Logistic models to minimize the material handling cost within a cross-dock

1.   Introduction

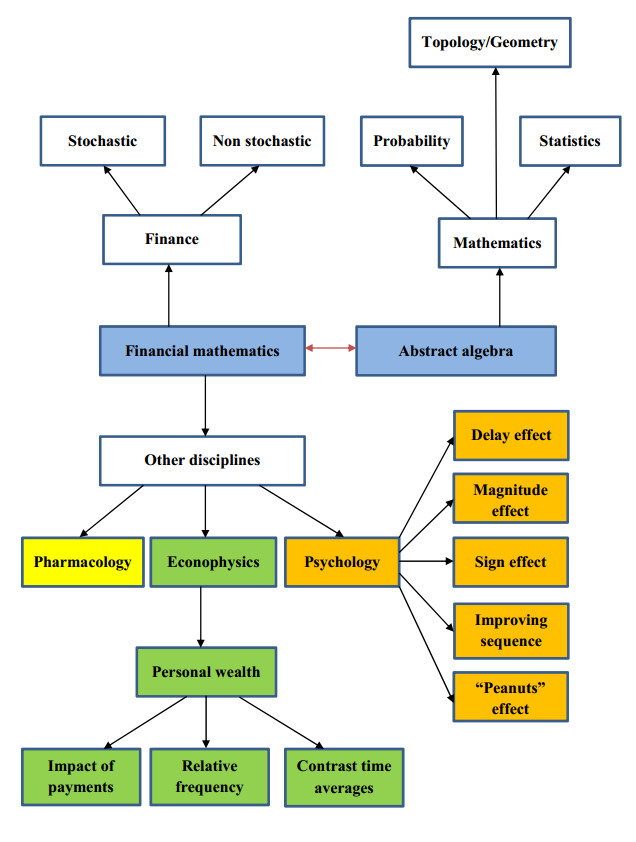
The field of finance is characterized by a high dynamism and its strong relationship with other disciplines such as psychology, physics, sociology, marketing, etc. Additionally, mathematics (in particular, probability, statistics, topology and, even, geometry) has become an essential instrument to analyze and assess the main financial models. However, abstract algebra has been scarcely used when modeling the foundations of finance, that is to say, the principles of financial mathematics.

In our opinion, this topic is very important because abstract algebra and financial mathematics deal with the grounds of mathematics and finance, respectively. Therefore, it is logical that a bridge between both disciplines should be built (see red arrow in Figure 1). On the other hand, the aforementioned dynamism exhibited by most financial instruments makes it necessary a flexible adaptation of axioms and structures describing the rational behavior of a decision maker in the real world.

Finally, the presence of mathematics is noteworthy in all disciplines and, undoubtedly, this can help to connect finance to the rest of scientific fields (see, again, Figure 1). More specifically, actions of semigroups (or $A$-modules, $A$-operands ^[4], $A$-acts ^[21], $A$-sets ^[23], $A$-systems ^[22] for $A$ being a semigroup) represent a classical and fundamental notion in semigroup theory and category theory (see the above mentioned references). Moreover, this concept has applications to many areas of mathematics, computation (automata theory), criptography ^[26] and physics.

In order to reach the objectives pointed out in this section, this paper is organized as follows. Section 2 provides a revision of the main interrelations between the research in intertemporal choice and other disciplines. After providing the preliminary concepts in Section 3, Section 4 analyzes the main binary relations in the context of intertemporal choice, by paying a special attention to the equivalence relation between dated rewards and its relationship with the additivity of discount functions. In this paper, we will use actions of semigroups in order to characterize additive discount functions (see propositions 1 and 3). Moreover, homomorphisms between two different actions are studied in this context (see Theorem 1). On the other hand, Corollary 1 is a nice result which characterizes separable discount function where the order of times acting on a reward does not matter (without needing that the discount function is additive). We hope that the approach to discount functions with actions will become a central reference in this topic. Although this paper has been focused on discount functions, the analysis of capitalization functions is analogous. Another interesting algebraic structure, related with discount functions, is quiver algebra, analyzed in Section 5. In this way, a characterization of additive discount functions is obtained by using this notion (see Proposition 5). Sections 6 and 7 introduce, respectively, novel structures of vector and affine spaces, associated to the map of indifference lines generated by a discount function. Specifically, Sections 6 is devoted to the description of the vector space constructed with the factors associated to a discount function $F_d$, where the benchmark $d$ has been given. Finally, Section 7 describes the partial affine space ($E_d$) associated to the former vector space $V_d$ (see Proposition 6), and the way to construct a reference system of the partial affine space and a change of reference with the complete discount function. Finally, Section 8 summarizes and concludes.

2.   Literature review

In the context of intertemporal choice, discounting has shown to be an important topic with applications to many disciplines. In order to provide some real life examples of this model, the literature review is going to be summarized in different streams by following Figure 1.

2.1.   Applications to psychology

With respect to the relationship between psychology and financial mathematics (see Figure 1, in orange), we have to point out the analysis of the "anomalies" derived from the Discounted Utility Model: Delay effect ^[10,14], magnitude effect ^[15], sign effect, improving sequence effect ^[9,13,20], "peanuts effect" ^[16]. The study of these "paradoxes" is of great importance en Marketing, specifically in consumer's behavior.

On the other hand, the subjective perception of time in intertemporal choice can be modeled by distorting the parameter "time" in a discount function ^[36]. In this way, Cruz Rambaud and Ventre ^[18] and Cruz Rambaud et al. ^[8] introduced the general concept of time deformation which derives from the more general definition of deformation in the area of abstract algebra. Specifically, Stevens ^[33] and Takahashi ^[35] proposed the so-called "power" and Weber-Fechner laws, respectively, which are particular cases of time deformations. Other concepts, shared by financial mathematics, psychology and pharmacology, are impulsiveness (or impatience) and inconsistency (or variation of impatience) (see ^[11,12]). In particular, the consideration of the so-called moderately and strongly decreasing impatience ^[32] gave rise to the novel concept of derivative of a differentiable real function $F$, relative to another function of two variables $f$ (see ^[17]).

2.2.   Applications to econophysics

Deforming time is also a usual topic in econophysics (see Figure 1, in green). In this way, the $q$-exponential discount function was already familiar to Bernoulli and Euler ^[25] and was already formalized in the periodic compound interest. However, this function has recently become well-known among nonextensive statistical theorists. Among them, Cajueiro ^[3] introduced the so-called $q$-exponential discount function as the reciprocal (with respect to the product of real-valued functions) of the $q$-exponential function, used in nonextensive thermodynamics ^[39]. Later, Cruz Rambaud and Muñoz Torrecillas ^[10] and Takeuchi ^[36] deformed the parameter "time" in the $q$-exponential discount function by using the Stevens "power" law, giving rise to the Weibull discount function. In this way, Cruz Rambaud et al. ^[8] endowed the set of deformations with the structure of monoid with which deforming time can be considered as an action of such monoid over the set of discount functions.

In ^[31], the authors consider additive in contrast to multiplicative dynamics in analyzing games, from a dynamic perspective. In particular, the repetition of a gamble, additive or multiplicative, is investigated. Thus, we will follow the ideas on ergodicity economics^*, presented by ^[29], as time is essential in our model. In this way, we can state that our approach to discount functions is dynamic.

^*Ergodicity economics (see ^[30]) seeks to build realistic models of its temporal evolution. The main concepts are the growth optimality, the maximization of the time average growth, and the choice of suitable utility functions. In particular, when the utility function follows a Brownian motion with an invertible drift, optimizing expected changes in utility functions is equivalent to optimizing the time average growth. Moreover, starting from given dynamics, we can determine the existence of an associated utility function.

Adamou et al. ^[2] introduced the so-called Riskless Intertemporal Payment Problem (RIPP) where the decision maker compares the growth rates of the wealth arising from each payment and chooses the payment with the higher growth rate. This methodology is based on three items: the decision maker's existing wealth, the wealth dynamics, and the time frame, giving rise to four scenarios: no discounting, exponential, hyperbolic and hybrid discounting. More specifically, these scholars proposed a general riskless model with no behavioral biases:

where $x(t)$ denotes the wealth at time $t$, $f$ the growth function, and $g$ the growth rate. In particular, these models can adopt:

● A multiplicative dynamics (wealth grows exponentially in time, e.g., investing in income-generating assets):

● An additive dynamics (wealth grows linearly in time, e.g., net income from employment at a given salary with stable consumption costs):

Starting from the following expression for $g$:

instead of

one can derive the discount rate for two alternatives $a$ and $b$ with the restriction $g_a = g_b$ (denoted by $a \sim b$):

where $D$ is the delay and $H$ the horizon. In this setting, the future trajectories of each payment is essential to solve the temporal choice problem by distinguishing between the so-called fixed and adaptive time frames, giving rise to different cases of preference reversals.

Personal wealth is, apart from data on amounts and delays, one of the elements which define the discount function. From now on, the reasoning will be focused on the $q$-exponential function:

which generalizes the exponential, hyperbolic and quasi-hyperbolic discounting. According to Nascimento ^[19], three physical aspects have to be taken into account when dealing with personal wealth (see Figure 1):

● The impact of payments on personal wealth ^[2], analyzed by using the following ratios:

and

● The relative frequency between rewards.

● The contrast between time averages.

The second aforementioned item transforms the intertemporal choice in a stochastic growth problem. In effect, when unexpected every-days situations require an analysis without testable information, the uniform distribution maximizes the uncertainty. If payments can be delayed beyond the deadlines, then the cumulative probabilities ($P_m$ and $P_M$) increase their entropy, reaching the value 1 later, being the probabilities at this moment:

and

With respect to the third item, let $\tau(u)$ be the total time when $GF\Theta_M$ ("it will always be the case that I will at some time receive $M$") affirms that $\Theta_M$ is true, and $u$ the total time when $G\theta_M$ ("it will always be the case that I will receive an amount less than $M$") affirms that $\theta_M$ is true. In this case, one has:

In the case of a one-time payment, usually $(1+X_M)^{p_M} > (1+X_m)^{p_m}$, whereby the decision criterion will be:

Thus, payments with a low impact on wealth allow an additive dynamics because the time average does not change significantly between the first and the $n$-th periods:

for $0 < X_m < < 1$. Analogously, for an exponential discounter, one has:

for $0 < X_m < < 1$.

2.3.   Applications to abstract algebra

A first attempt to describe the grounds of finance with purely algebraic tools (see Figure 1, in blue) was provided by Torrecillas Jover and Cruz Rambaud ^[38] who used inverse limits to describe the evolution of a discount function through time. This approach makes it possible a general perspective of the main discounting models in the context of intertemporal choice. Later, Cruz Rambaud ^[5] defined a discount function as an algebraic automaton. This approach allows a very general concept of discount function able to describe any variant of the real practices performed by financial agents.

Finally, abstract algebra, and particularly algebraic automata, has been used to analyze the properties and characterizations of accounting systems (see ^[6,7,27,28]).

2.4.   Applications to Pharmacology and other fields

The progression of illnesses and addictions in connection with their treatment (see Figure 1, in yellow) can be described as discount functions ^[12] by considering that the "discounted disease" depends on three possible explanatory variables: the level of dose, the frequency of administration and the time to assess the (non)monetary rewards, all other things being the same. Thus, the level of disease is superadditive for an interval and subadditive otherwise. This is the case of the so-called exponentiated hyperbolic discount function:

where $i > 0$ and $k > 1$.

In Marketing, discount appears when analyzing the optimal timing and depth of retail discounts with the optimal timing and the quantity of the retailer's order over multiple brands and time periods ^[37]. Here, discount is the list price minus the actual price of the brand that day for each brand. Sun et al. ^[34] showed that there exists a negative and significant relation between investor sentiment and pension plan discount rate. This finding is very important for boards of directors and regulators during periods of high investor sentiment when pension plan sponsors are more likely to adjust down pension discount rate. Finally, Liu et al. ^[24] introduced a price discount, announced after a normal price, for the next period by promotions or coupons, in the context of the profit risk of the supply chain due to dual uncertain information.

As shown by this literature revision, the methodological foundations of intertemporal choice can be applied to many other disciplines such as psychology and pharmacology. Reciprocally, the mathematical tools used in other fields, such as physics, can be implemented in economics, giving rise to the so-called econophysics. This stream of methodological techniques between scientific disciplines makes it necessary the algebraic treatment of intertemporal choice in order to adequately analyze one of its central concepts, viz the additivity of the involved discount function or, equivalently, the transitivity of preferences.

Additivity is closely related to the other central concept in every discounting model: the instantaneous discount rate. In effect, in a stationary environment, the additivity of the discount function is equivalent to require that the instantaneous discount rate is constant. Moreover, these two conditions are equivalent to the absence of preference reversals. At this point, it is necessary to take into account that this last condition is the origin of almost all anomalies in the ambit of intertemporal choice and the description of subadditive (or superadditive) treatments in diseases and addictions.

Additivity of discount functions (or, equivalently, transitivity of preferences) takes part of the normative theory presented in the Discounted Utility (DU) model by Samuelson. Indeed, this is the core idea around which all observed behaviors revolve. Thus, taking into account the wide variety of perspectives from which intertemporal choice can be analyzed, additivity deserves a pure treatment, far from the particular features of the disciplines displayed in Figure 1.

3.   Preliminaries

Let ${\mathcal M}$ be the set $X \times D \times T$, where $X = [0, +\infty)$, $D = (-\infty, +\infty)$ and $T = [0, +\infty]$.

Definition 1. A dynamic discount function is a real-valued continuous function

such that

where $F(x, d, t)$ represents the value at $d$ (called delay, focal date or benchmark) of a ＄$x$ reward available at instant $d + t$. In order to make financial sense, this function must satisfy the following conditions:

1. For every $x \in X$ and every $d \in D$, $F(x, d, 0) = x$.

2. For every $d \in D$ and every $t \in T$, $F(0, d, t) = 0$.

3. $F(x, d, t)$ is strictly increasing with respect to $x$.

4. $F(x, d, t)$ is strictly decreasing with respect to $t$.

Observe the different nature of each variable involved in this definition: $d \in D$ is a calendar time, $t \in T$ is a period of time, and $x \in X$ and $F(x, d, t) \in X$ are amounts.

Remark 1. Sometimes, $F$ is not defined for every $(x, d, t) \in {\cal M}$. In such case, the maximal subset of ${\cal M}$ whose elements satisfy conditions 1, 2, 3 and 4 of Definition 1, will be called the domain of the discount function, denoted by ${dom}(F)$.

Example 1. The domain of the discount function $F(x, d, t) = x(1-kxdt)$, where $d \in \mathbb{R}^+$ and $k > 0$, is:

Usually, the discount function is linear with respect to $x$. In such case, the following definition can be introduced.

Definition 2. A dynamic discount function is said to be separable if

or, more generally,

with the same conditions as Definition 1, except for the first one.

Moreover, this discounting model can be simplified by using a function $F(t)$ independent of the delay $d$. More specifically,

Definition 3. A stationary discount function $F(t)$ is a real-valued continuous function

such that

where $F(t)$ represents the value at time $0$ of a ＄1 reward available at instant $t$ (usually, $t$ is called the interval), satisfying the following conditions:

1. $F(0) = 1$, and

2. $F(t)$ is strictly decreasing.

Table 1 summarizes the different types of discount functions.

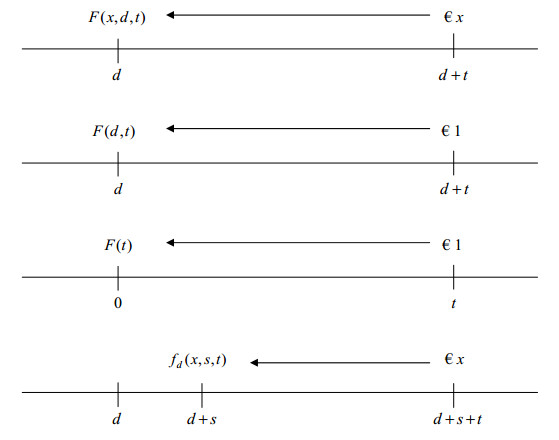
Definition 4. Let $F(x, d, t)$ be a dynamic discount function. For a given $d$, the discount operator associated to $d$ is the function

defined as:

$f_{d}(x, s, t)$ represents the value at $d + s$ of a $\$ x$ reward available at instant $d + s + t$. $f_{d}$ is well defined because $F(\cdot, d, s)$ is strictly increasing and then injective.

Remark 2. Obviously, $f_d$ is subject to the same restriction as $F$ regarding the valid triples $(x, s, t)$ to be used in Definition 4. More specifically, the domain of $f_d$, denoted by ${dom}(f_d)$, is the following subset of $X \times T^2$

where ${im}$ denotes the image of a function.

Figure 2 represents the four previous definitions.

Before presenting the next result, we need the following definition.

Definition 5. Given an additive semigroup $(S, +)$ and a set $X$, a semigroup action is a map

which satisfies the following condition:

Remark 3. If $\cdot$ is a partial map, the action is also labelled as partial.

Proposition 1. Assume ${dom}(F) = {\cal M}$. For every $d \in D$, denote theinterval $[d, +\infty[$ as $D_d$. The discount operator$f_{d}^{-1}$ defines an action $\triangleright_d$ of the semigroup $(T, +)$ on the set $(X, D_d)$ in the following way:

defined as:

^†$f_d^{-1}$ is called the counter-discount operator.

Proof. In effect,

Observe that:

Therefore,

This completes the proof.

Remark 4. We can stress the following two remarks:

1. If ${dom}(F) \neq {\cal M}$, then the action defined in Proposition 1 is partial.

2. A new action $\triangleleft_d$ could be defined instead of $\triangleright_d$:

with the restriction $s-t < 0$. Consequently, this action could be doubly partial.

4.   Equivalence relations associated to a discount function

Let $F(x, d, t)$ be a dynamic discount function. Given a specific value of $d$, the following binary relation, denoted by $\sim_d$, can be defined on $X \times T$^‡.

^‡Actually, it is defined on the set $\{ (x, t) \in X \times T: (x, d, t) \in {dom}(F) \}$. However, for the sake of simplicity, we will define the binary relation on $X \times T$.

Definition 6. For every $(x, s)$ and $(y, t)$, with $x < y$ and $s < t$, we will say that

if

Observe that, in this case,

or, equivalently,

Obviously, $\sim_d$ is an equivalence relation on $X \times T$^§. Thus, given an outcome $(x, s)$, its class of equivalence will be the set

^§This relation could be also defined on $X \times (d+T)$.

Observe that each class of equivalence is an indifference line when considering the amount and the interval time (with respect to $d$) as two economic goods. Additionally, we can define relations of preference between two couples $(x, s)$ and $(y, t)$.

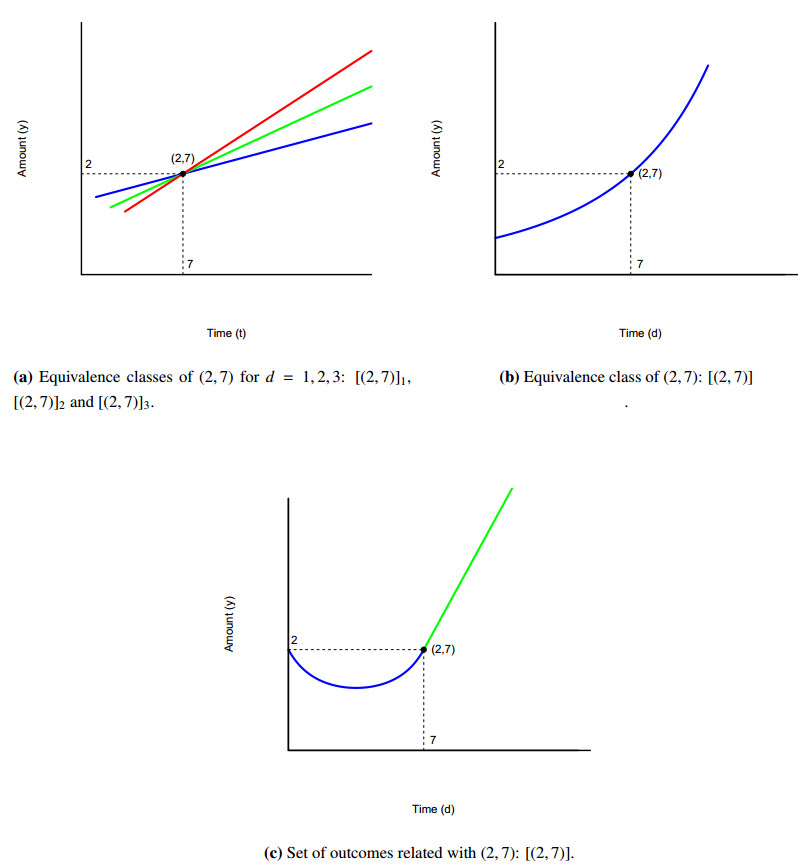
Example 2. If $F(d, t) = \frac{1}{1+kdt}$ ($d > 0$, $t \geq 0$ and $k = 0.05$), Figure 3(a) shows the equivalence classes of the outcome $(2, 7)$ for $d = 1$ (in blue), $d = 2$ (in green) and $d = 3$ (in red).

Example 3. If $F(x, t) = (x+1)^{\exp\{-kd\}}-1$, $t \geq 0$ and $k = 0.1$), Figure 3(b) shows the equivalence class of the outcome $(2, 7)$ (independent of $d$).

On the other hand, we are going to define the following binary relation on $X \times D$, denoted by $\sim$.

Definition 7. For every $(x, c)$ and $(y, d)$, $x < y$ and $c < d$, we will say that

if

In general, $\sim$ is not an equivalence relation because it is reflexive and symmetric but not necessarily transitive. Thus, given an outcome $(x, c)$, the set of its related outcomes is:

Example 4. If $F(d, t) = \frac{1}{1+kdt}$ ($d > 0$, $t \geq 0$ and $k = 0.05$), Figure 3(c) shows the set of outcomes related with $(2, 7)$.

Definition 8. A discount function $F$ is said to be additive if, for every $x \in X$, $d \in D$, and $s$ and $t \in T$, one has:

or, equivalently,

The next two propositions present two algebraic characterizations of additivity of discount functions by using equivalence relations (Proposition 2) and semigroup actions (Proposition 3). These two new characterizations allow us to use these two algebraic concepts in the study of additive discount functions.

As formerly indicated, in general the binary relation ($\sim$) associated to a given discount function (see Definition 7) is not an equivalence relation. However, the inclusion^¶ in $\sim$ of all the binary relations ($\sim_d$) associated to each benchmark of a given discount function (see Definition 6) is a necessary and sufficient condition to guarantee that $F$ is additive. Therefore, we can enunciate the following statement.

^¶Take into account that all considered relations are subsets of the Cartesian product $X \times D$.

Proposition 2. The discount function $F$ is additive if, and only if, for every$d \in D$, $\sim_d$ (defined on $X \times (d+T)$) is included in$\sim$.

Proof. Necessity. Let us consider that $F$ is additive. Assume that $(x, d+s) \sim_d (y, d+t)$, with $x < y$ (which implies $s < t$). By definition of $\sim_d$, $F(x, d, s) = F(y, d, t)$. As $F$ is additive, we can write the former equality as $F(\cdot, d, s)(x) = [F(\cdot, d, s) \circ F(\cdot, d+s, t-s)](y)$. By simplifying $F(\cdot, d, s)$ on the left, one has $x = F(y, d+s, t-s)$ and so $(x, d+s) \sim (y, d+t)$. Consequently, $\sim_d$ is included in $\sim$.

Sufficiency. Assume that for every $d \in D$, $\sim_d$ is included in $\sim$ and consider the outcome

Obviously,

and so

Consequently,

and so $F$ is additive.

Given a dynamic discount function, we can define the following map:

defined as:

Remark 5. Observe that this definition is a particular case of Proposition 1 since:

Intuitively, a discount function can be think as times (whose algebraic structure is semigroup) acting on dated rewards. So, it is reasonable to characterize additivity as an algebraic action of the semigroup of times on the set of dated rewards. Consequently, we can enunciate the following proposition.

Proposition 3. A discount function $F$ is additive if, and only if, $\triangleright$ is a semigroup action.

Proof. In effect, given $s_1, s_2 \in S$, on the one hand, one has:

On the other hand,

Observe that

if, and only if, $F$ is additive.

Remark 6. Let us recall that a partial action of a group $G$, with identity element $1$, on a set $X$ is a collection ${\alpha_g}$ ($g \in G$) of partial bijections of $X$, such that $\alpha_1$ is the identity bijection of $X$ and, for every $g, h \in G$, the composition of the partial maps $\alpha_g \circ \alpha_h$ is the restriction of $\alpha_{gh}$ to the domain of $\alpha_g \circ \alpha_h$.

Here the domain of $\alpha_g \circ \alpha_h$ is the largest subset of $X$ for which $\alpha_g \circ \alpha_h$ is applicable. On the other hand, a partial bijection of $X$ is a bijection between two (non necessarily proper) subsets of $X$. In particular, if $g = 1$, the domain of $\alpha_g$ is allowed to be the empty set. This notion allows us to study discount functions in a more general way. But this idea will be considered for a future paper.

Definition 9. A homomorphism between two $S$-actions is given by a map $h_0: X \times D \longrightarrow X \times D$ and a semigroup morphism $h_1: S \longrightarrow S$ satisfying:

Let $F$ be a discount function. For every $a \in D$ and $b \in D$, $a \geq b$, we define:

such as

Theorem 1. $h_{a, b}$ is a homomorphism between the actions$\vartriangleright_a$ and $\vartriangleright_b$, that is to say, the following diagram is commutative:

Proof. To do this, we have to show the following equality:

that is to say, that the following diagram is commutative:

In effect, let us calculate the left-hand side of the former equality:

On the other hand, the right-hand side can be displayed as follows:

Observe that the two results coincide. Then, the theorem holds.

Remark 7. The following remarks have to be taken into account:

1. If $a < b$, we define

2. Observe that, in the general definition of a homomorphism between actions, $h_1(s) = s$.

Theorem 2. If $a > b$ and $F$ is additive, then $h_{a, b}(x, d) = F(x, b+d, a-b)$.

Proof. In effect, if $F$ is additive, one has:

from where:

Remark 8. In general, the converse implication does not hold. In effect, if $h_{a, b}(x, d) = F(x, b+d, a-b)$, one has:

which could be written as:

Let us consider the real-valued function

where $f$ is a unitary, stationary discount function. Under these conditions, $F$ is a stationary discount function:

● $F(0, t) = 0$, for every $t \in {dom}(f)$.

● $F(x, 0) = x$, for every $x \in \mathbb{R}^+$.

● $\frac{\partial F(x, t)}{\partial x} = \frac{1}{(e^x-1) f(t) + 1} e^x f(d) > 0$.

● $\frac{\partial F(x, t)}{\partial t} = \frac{1}{(e^x-1) f(t) + 1} (e^x-1) f^{\prime}(d) < 0$.

In general, one has:

On the other hand,

Therefore, $F$ is additive if, and only if, $f$ is additive. However, observe that

Thus, making $t_1 = a-b$ and $t_2 = d$, the counterexample follows.

However, if moreover $F(x, t)$ is separable, that is to say, $F(x, t) = u(x)F(t)$, a characterization can be provided in the following way.

Corollary 1. Let $F(x, t) = u(x)F(t)$ be a separable discount function such that $\lim_{x \to +\infty} u(x) = + \infty$. In theseconditions, $u(x) = kx$ ($k > 0$) if, and only if,

Proof. In effect, if $u(x) = kx$ ($k > 0$) then the conclusion is obvious. Reciprocally, if $F[F(x, t_1), t_2] = F[F(x, t_2), t_1]$, one has:

In particular, if $t_1 = t$ and $t_2 = t+h$, then:

Taking natural logarithms in both sides of the former equality, dividing by $h$ and letting $h \to 0$, one has:

or, equivalently,

By simplifying $F^{\prime}(t)$ and rearranging terms,

Making the change of variable $u(x)F(t) = z$, one has:

which is a differential equation:

whose solution is:

where $k > 0$. This completes the proof.

5.   The vector space $(V_d, +, \cdot)$

Let $F$ be a dynamic discount function. For every date $d \in D$, we can consider the function

such that

defined by:

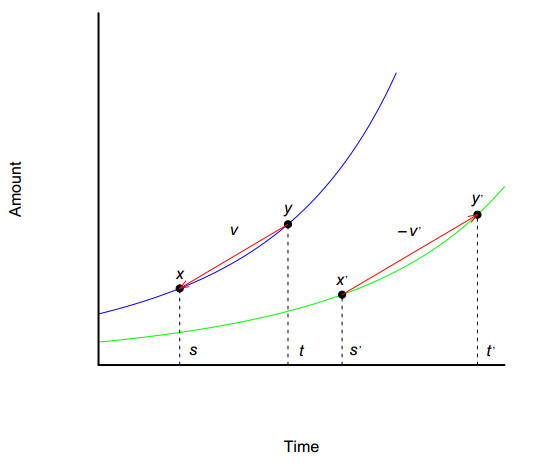
This "truncated" discount function will be called the discount function (referenced) at time $d$. Given two dated rewards $(x, s)$ and $(y, t)$, where $s < t$, we will say that the vector

does exist if $(x, s) \sim_d (y, t)$, that is to say, $x = f_d(\cdot, s, t-s)(y)$. In such a case, the vector

also exists because, by the symmetric property, $(y, t) \sim_d (x, s)$, that is to say, $y = f_d^{-1}(\cdot, s, t-s)(x)$ (see Figure 4).

Remark 9. In the particular case in which $F_d$ is separable, i.e., $F_d(x, t) = u(x)F_d(t)$, the vector $\vec{v} : = ((y, t), (x, s))$ does exist if

Moreover, as $u(y) = u(x) \frac{F_d(s)}{F_d(t)}$, then the vector $-\vec{v} : = ((x, s), (y, t))$ also exists.

The set of all so-defined vectors will be denoted by $V_d$.

5.1.   Path algebra associated to a set of dynamic discount functions

Let ${\cal F}$ be a set of dynamic discount functions. Consider the set $X \times D$, where $X = \mathbb{R}^+$ is the set of amounts and $D = \mathbb{R}$ is the set of calendar times.

Definition 10. A quiver on ${\cal F}$ is a quadruple $Q_{\cal F} = (Q_0, Q_1, s, t)$, where:

● $Q_0 : = X \times D$ is the set of vertices.

● $Q_1$ is the set of arrows. Specifically, there will be an arrow $a$ between two vertices $v_1 = (x, d)$ and $v_2 = (x^{\prime}, d^{\prime})$, represented by $v_1 \stackrel{a}\to v_2$, if there is a dynamic discount function, $F \in {\cal F}$, such that $F(x^{\prime}, d, d^{\prime}-d) = x$^‖.

^‖Obviously, between two given vertices there can be several arrows.

● $s, t: Q_1 \to Q_0$ are two functions, called the source and the target, respectively, such that $s(a) = v_1$ and $t(a) = v_2$.

Definition 11. A path of length $n$ between two vertices $v$ and $w$ is a sequence $(v, a_1, a_2, \ldots, a_n, w)$, where $a_1, a_2, \ldots, a_n$ are arrows, $s(a_1) = v$ and $t(a_i) = s(a_{i+1})$, for every $1 \leq i \leq n-1$, and $t(a_n) = w$. Schematically,

The set of all paths of length $n$ will be denoted by $Q_n$. To the just-defined quiver $Q_{\cal F}$ we can associate a path, denoted by $\mathbb{R} Q_{\cal F}$ and defined as follows. Consider the $\mathbb{R}$-vector space whose basis is the set of all paths of length $n$, for every $n \in \mathbb{N}$, and whose product is defined by the concatenation of paths, i.e., given two basis vectors $(v, a_1, \ldots, a_n, w)$ and $(v', a'_1, \ldots, a'_m, w')$ of $\mathbb{R} Q_{\cal F}$, its product is:

if $w = v'$, and the empty path, if $w \neq v'$.

One has the following $\mathbb{R}$-vector space direct sum decomposition:

where $\mathbb{R} Q_k$ is the subspace of $\mathbb{R} Q_{\cal F}$ generated by all paths of length $k$. Clearly, $\mathbb{R} Q_k \cdot \mathbb{R} Q_l \subseteq \mathbb{R} Q_{k+l}$, for every $k, l \in \mathbb{N}$. Thus, $\mathbb{R} Q_{\cal F}$ is a $\mathbb{N}$-graded algebra.

5.2.   Particular cases

$1.$ If ${\cal F} = \{F\}$, being $F$ a dynamic discount function, then $Q_{\cal F}$ is called the quiver associated to $F$.

$2.$ $\cal F$ composed by all dynamic discount functions.

We will say that two paths in the quiver algebra are equivalent if they have the same starting vertex and the same ending vertex.

Proposition 4. A dynamic discount function is additive if, and only if, everypath in the quiver algebra is equivalent to a path of length one.

When the set $D$ is discrete, we can obtain other characterizations of additive discount functions by using the representation of quivers. In effect, take as vertices the set $D$ of calendar times. Indeed, we can think that this set is discrete, then obtaining a quiver of the following form:

This quiver is denoted as $A^\infty$. Moreover, it is possible to consider the quiver $A_\infty^\infty$, i.e., the quiver of the form:

Each vertex corresponds to a calendar time, say $t_i$, for the vertex $i$. Recall that a $\mathbb R$-representation of a quiver consists in associating to each vertex $v \in Q$ an $\mathbb R$-vector space $V_v$ and, for each arrow $a: v \to w$, a $\mathbb R$-linear map $f_a: V_v \to V_w$. We denote this representation by $(\{V_v\}_{v \in Q_0}, \{f_a\}_{a \in Q_1})$.

Given a discount function $F$, we can construct a representation in the quiver $A^\infty$ (or $A_\infty^\infty)$. In effect, we can associate $\mathbb R$ (the set of amounts) to any vertex $v \in A^\infty$ and, to any arrow $a: n \to n+1$, the $\mathbb R$-linear map defined as:

For a nontrivial path $p = a_1 a_2 \cdots a_k$ from $v$ to $w$:

we can define a map from $V_v = \mathbb R$ to $V_w = \mathbb R$, called the evaluation, by:

This evaluation can be extended to linear combinations of paths with the same origin and target:

from which:

Proposition 5. A discount function is additive if, and only if, for every path in the quiver algebra $p$, the evaluation $f_p$ coincides with $F(\cdot, t_v, t_w -t_v)$.

Given two discount functions $F_1$ and $F_2$, we can define a homomorphism between the representations that they define. A homomorphism between these two representations is given by a set of $\mathbb R$-linear maps:

which are compatible with the maps associated to the arrows in the representations, i.e., for an arrow $a: v \to w$ then

6.   The vector space $(V_d^{\prime}, +, \cdot)$

6.1.   Equivalence relation in $V_d$

Given two vectors $\vec{v} = ((x, s), (y, t))$ and $\vec{v}^{\prime} = ((x^{\prime}, s^{\prime}), (y^{\prime}, t^{\prime}))$ (observe that nothing is said about the relationship between $s$ and $t$, and between $s^{\prime}$ and $t^{\prime}$), we will say that

if

that is to say,

Remark 10. In the particular case in which $F_d$ is separable, one has:

if

Obviously, $\bot_d$ is an equivalence relation. The quotient set $V_d/\bot_d$ will be denoted by $V_d^{\prime}$. In the next subsection, we are going to define a "sum" and a "scalar product" on $V_d^{\prime}$. But before, we need the following definition.

Definition 12. A discount function referenced at time $d$ is said to be regular if

In what follows, we are going to assume that $F_d$ is regular.

6.2.   Defining a sum in $V_d^{\prime}$

For the sake of clarity in the presentation, we are going to start with the separable case. Let $\boldsymbol{\vec{v}} = [(x, s), (y, t)]$, $s < t$, and $\boldsymbol{\vec{v}^{\prime}} = [(x^{\prime}, s^{\prime}), (y^{\prime}, t^{\prime})]$, $s^{\prime} < t^{\prime}$, two vectors in $V_d^{\prime}$. In this case, one has:

and

Let us see if it is possible to find a representative $\vec{w} : = ((y, t), (z, u))$, $t < u$, of $\boldsymbol{\vec{v}^{\prime}}$. In this case,

This equation is equivalent to require:

from where:

As $F_d$ is regular, the existence of $u$ is guaranteed. Therefore, we define:

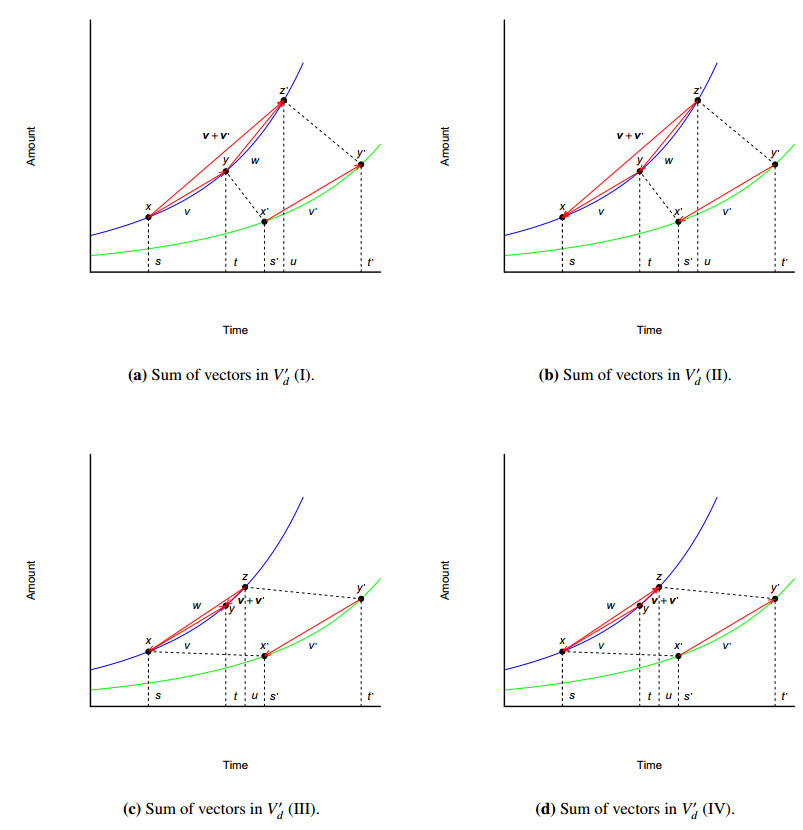
which, obviously, is well defined (see Figure 5(a)).

Let us see now the general case. Let $\boldsymbol{\vec{v}} = [(x, s), (y, t)]$, $s < t$, and $\boldsymbol{\vec{v}^{\prime}} = [(x^{\prime}, s^{\prime}), (y^{\prime}, t^{\prime})]$, $s^{\prime} < t^{\prime}$, two vectors in $V_d^{\prime}$. In this case, one has:

and

The values of $z$ and $u$ can be obtained from the following system of equations:

or

As before, we define:

Other cases are briefly described in the following items:

● $\boldsymbol{\vec{v}} = [(y, t), (x, s)]$, $s < t$, and $\boldsymbol{\vec{v}^{\prime}} = [(y^{\prime}, t^{\prime}), (x^{\prime}, s^{\prime})]$, $s^{\prime} < t^{\prime}$, in whose case $\vec{w} : = ((z, u), (y, t))$, $t < u$, and $\boldsymbol{\vec{v}} + \boldsymbol{\vec{v}^{\prime}} : = [(z, u), (x, s)]$ (see Figure 5(b)).

● $\boldsymbol{\vec{v}} = [(x, s), (y, t)]$, $s < t$, and $\boldsymbol{\vec{v}^{\prime}} = [(y^{\prime}, t^{\prime}), (x^{\prime}, s^{\prime})]$, $s^{\prime} < t^{\prime}$, in whose case $\vec{w} : = ((z, u), (x, s))$, $s < u$, and $\boldsymbol{\vec{v}} + \boldsymbol{\vec{v}^{\prime}} : = [(z, u), (y, t)]$ (see Figure 5(c)).

● $\boldsymbol{\vec{v}} = [(y, t), (x, s)]$, $s < t$, and $\boldsymbol{\vec{v}^{\prime}} = [(x^{\prime}, s^{\prime}), (y^{\prime}, t^{\prime})]$, $s^{\prime} < t^{\prime}$, in whose case $\vec{w} : = ((x, s), (z, u))$, $s < u$, and $\boldsymbol{\vec{v}} + \boldsymbol{\vec{v}^{\prime}} : = [(y, t), (z, u)]$ (see Figure 5(d)).

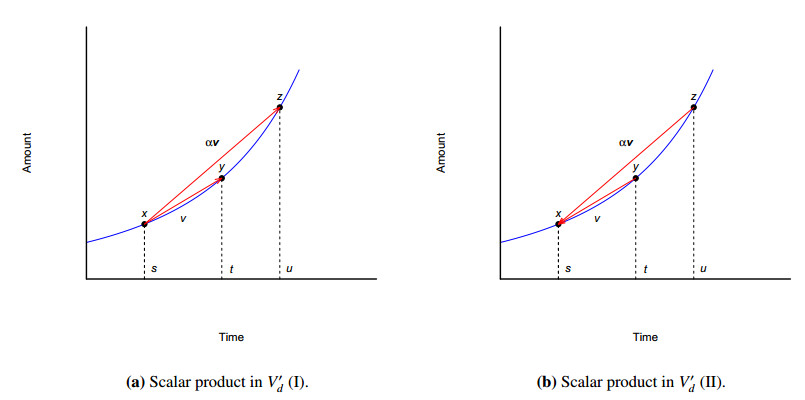
6.3.   Defining a scalar product in $V_d^{\prime}$

For the sake of clarity in the presentation, we are going to start with the separable case. Let $\boldsymbol{\vec{v}} = [(x, s), (y, t)]$, $s < t$, a vector in $V_d^{\prime}$ and $\alpha$ a real number. In this case, one has:

We will consider two cases:

$1.$ $\alpha \geq 0$. In this case,

such that

or, equivalently,

From the last equation, one has:

As $F_d$ is regular, the existence of $u$ is guaranteed.

$2.$ $\alpha < 0$. In this case,

such that

or, equivalently,

From the last equation, one has:

As $F_d$ is regular, the existence of $u$ is again guaranteed (see Figure 6).

Let us see now the general case. Let $\boldsymbol{\vec{v}} = [(x, s), (y, t)]$, $s < t$, a vector in $V_d^{\prime}$ and $\alpha$ a real number. In this case, one has:

We will consider two cases:

$1.$ $\alpha \geq 0$ (see Figure 6(a)). In this case,

such that

and

From the former system of equations, we can obtain the values of $z$ and $u$.

$2.$ $\alpha < 0$ (see Figure 6(b)). In this case,

such that

and

From the former system of equations, we can obtain the values of $z$ and $u$.

It is straightforward to show that $(V_d^{\prime}, +, \cdot)$ is a vector space of dimension 1.

Remark 11. Observe that the former construction could analogously be made on a given indifference line. Specifically, the indifference line crossing the point $(x, 0) \in X \times D$, denoted by $E_{d, x}$, gives rise to a vector subspace of $(V_d^{\prime}, +, \cdot)$. Moreover, is is straightforward to see that all these subspaces are isomorphic. Finally, each indifference line is an affine space whose reference system is $R_{d, x} = ((x, 0), \{ ((F^{-1}(\cdot, d, t)(x), 0), (x, t)) \})$.

6.4.   Defining a norm on $V_d^{\prime}$

Each vector in $V_d^{\prime}$ is characterized by its norm, defined as::

● If $\boldsymbol{\vec{v}} = [(y, t), (x, s)]$, $s < t$, then:

● If $\boldsymbol{\vec{v}} = [(x, s), (y, t)]$, $s < t$, then:

Obviously, $\|\cdot\|$ satisfies the properties of a norm in a vector space.

7.   Affine space generated by a discount function

Let $d$ be a given date in $D$ and let us denote the interval $[d, +\infty[$ as $D_d$. Consider the set $E_d : = X \times D_d$. We will say that there exists a vector $v$ from $(x, d+s)$ to $(y, d+s+t) \in E_d$:

where $x$, $y$, $s$ and $t \in \mathbb{R}^+$, if $f_d(x, s, t) = y$, that is to say,

The elements of this vector space, denoted by $V_d$, are the finite concatenations of $\mathbb{R}$-multiples of the just defined vectors.

Proposition 6. $E_d$ is a partial affine space associated to the vector space$V_d$.

Proof. In effect, the function $\varphi_{(x, s)}: E_d \longrightarrow V_d$, such that $\varphi_{(x, s)}(y, t) : = ((x, s), (y, t)$ is injective (partially bijective). Moreover, the concatenation of vectors $((x, s), (y, t))$ and $((y, t), (z, u))$ is the vector $((x, s), (z, u))$. In effect, the existence of vector $((x, s), (y, t))$ is guaranteed because:

Analogously, vector $((y, t), (z, u))$ exists because:

By replacing $y$ of the first equation into the second equation and simplifying, one has:

which defines the vector $((x, s), (z, u))$. Consequently, Chasles' equality holds and $E_d$ is a partial affine space.

Proposition 7. $R_d = (d, \{ ((F(x, d, t), 0), (x, t)) \})$ is a reference system ofthe partial affine space $E_d$.

Corollary 2. The change of the affine reference $R_d$ to the reference $R_{d'}$($d' < d$) is given by the function $F(\cdot, d', d)$.

Remark 12. A similar alternative approach is the following. Let $P$ be an ordered set. An increasing subset (or order filter) of $P$ is a subset $U \subseteq P$ such that $x \in U$ and $y \geq x$ imply $y \in U$. The increasing subsets of $P$ can be easily seen as the open sets of a topology on $P$. Thus, every point $x \in P$ is included in a unique smallest open set

called the principal filter of $x$.

A sheaf $\cal F$ of discount functions over $P$ associates to every element $x \in P$, ${\cal F}_x$, the set of all discount functions defined on $V_x$ and, if $x \leq y$, there is a function $f_{xy}: {\cal F}_x \to {\cal F}_y$. Moreover, if $x \leq y \leq z$, then $f_{xz} = f_{yz} \circ f_{xy}$.

This approach will be examined in detail in further research.

8.   Conclusions

This paper has provided a wide range of algebraic concepts and structures able to fit the logic and rationality behind the behavior of financial decision makers. This research is justified by the dynamism which characterizes the working of financial markets and institutions. The main contribution of this manuscript is the involvement of abstract algebra to lay the foundations of financial mathematics, role which traditionally has been leaded by other disciplines such as statistics, probability, calculus and topology.

On the other hand, this paper has analyzed, from different points of view, the concept of additivity of discount functions which guarantees the transitivity in the choice of dated rewards. Indeed, this is a central topic in financial mathematics as it points out the limits of rationality of decision makers in intertemporal choices. In this way, another contribution of this paper is the characterization of financial processes, in particular the so-defined discount operators, as affine spaces and quivers by analyzing the property of additivity in these algebraic contexts.

Crossed product is a very important construction in the theory of actions of semigroups on sets. Unfortunately, in the problem studied in this paper, it has not been possible to construct such object.

Acknowledgments

We are very grateful for the comments and suggestions offered by two anonymous referees. The first author has been partially supported by the Mediterranean Research Center of Economy and Sustainable Development (CIMEDES), University of Almería (Spain). The second author has been partially supported by grants FEDER-UAL18-FQM-B042-A and PY20_00770 from Junta de Andalucía.

Conflict of interest

All authors declare no conflicts of interest in this paper.