Numerical investigations of pattern formation in binary systems with inhibitory long-range interaction

1.   Introduction

In the Ohta-Kawasaki theory of diblock copolymers ^[1,2], the density field of A-monomers is given by a function $u$ on domain $M$, the density of B-monomers is given by $1-u$ and the free energy of a diblock copolymer is

We suppose that $\epsilon > 0, \beta > 0, \gamma > 0$ are fixed. These parameters are related to the Flory-Huggins interaction parameter, the index of polymerization and the molecular weight of the minority phase. See ^[3] where a rigorous derivation of Eq (1.1) can be found. For the purposes of this paper $M$ is a compact 2-dimensional manifold, $0 < \epsilon < < 1$, $\nabla$ is the surface gradient on $M$ and $u$ satisfies a mass conservation constraint

where ${\mathit{{\rlap{-} \smallint }}_M u dS = |M|^{-1} \int_M u dS}$, $|M|$ is the measure of $M$, and ${ u \in {{\mathcal A}} = W^{1, 2}(M) \cap \left\lbrace \mathit{{\rlap{-} \smallint }}_M u dS = \omega \right\rbrace }$.

We denote the first integral in Eq (1.1) by ${L}(u)$ where

is a Landau-type free energy that is common in phase separation problem. ${L}$ is said to be attractive in the sense that its minimizers favor domains of a single phase with boundaries that minimize perimeter. The minimizers of ${L}(u)$ are the stationary solutions of the Cahn-Hilliard model whose solutions are characterized by the phenomenon known as Ostwald ripening or coarsening where small sets of one phase combine to form larger sets that are more energetically favored than the smaller sets (see, e.g., ^[4]). The variety of patterns exhibited by the minimizers of Eq (1.3) are limited by this coarsening effect. On the other hand, the case $\gamma > 0$ exhibits a wide variety of patterns. An approach that has proven to be successful in the analysis of problems related to Eq (1.1) has been to study the stationary solutions of the $\Gamma$-limit, $\epsilon^{-1}{I} \rightarrow J$ as $\epsilon\rightarrow 0$, i.e.,

where $\Sigma$ is the collection of all measurable subsets of $M$ of finite measure and finite perimeter and $P_M(E)$ is the perimeter of $E$ (see ^[5,6,7]). The Liapunov-Schmidt method and asymptotic analysis applied to $J$ have demonstrated the existence of stable single droplet and stable droplet assemblies when the droplet diameter is sufficiently small. For example, in ^[8], the small parameter $\epsilon$ is used to carry out perturbation analysis and $\gamma$ (an order 1 parameter) is used for bifurcation analysis to find wriggled lamellar solutions bifurcating from the perfect lamellar solutions (i.e., solutions of the companion $\Gamma$-limit problem). The existence and stability of localized patterns (spots, stripes, annuli) and period patterns (lamellar, hexagonal) in two dimensions are established in ^[9]. In one space dimension, it can be shown that the minimizers of (1.1) or its companion sharp interface $\Gamma$-limit problem are periodic (see, e.g., ^[10,11]). Sternberg and Topaloglu have shown that for a similar problem on a flat torus, the lamellar solution is stable for $0 < \gamma < < 1$ and becomes unstable when $\gamma$ is sufficiently large (see ^[12,13]).

The previously mentioned analytical approaches require additional conditions (e.g., $\epsilon$ is small, $\gamma$ is not too large, the domain is a flat tori, etc.) that limit the type of pattern that the analysis can reveal. To apply the singular perturbation theory to droplets, the droplet size must be sufficiently small. In a disk assembly where the droplet radius is $\rho$ and $n_d$ is the number of droplets, the relation $\rho \approx \left(\omega |M| /(\pi n_d) \right)^{1/2}$ implies that either $\omega > 0$ is very small or that $n_d$ is very large. However, in our numerical model with a properly chosen mesh size, we are not constrained by these restrictions and are able to determine solutions with moderately sized droplets and non-standard droplets.

In the present work, we study the minimizers of Eq (1.1) and so we define

Our investigations are carried out by numerically solving Eq (1.5). We compute the analytic gradient and Hessian of the discretization of ${I}$. In the following, $h$ denotes the average edge length of a triangle in a discretization of the domain which is used to describe the fidelity of the mesh. The parameter $\beta$ in Eq (1.1) is an order 1 parameter that controls the fidelity of the interface between the two constituents. Large $\beta$ encourages solutions with a sharper interface, while a small $\beta$ encourages a more diffuse interface. In the $\Gamma$-limit problem, the value of $\beta$ is not significant. However, for the minimizers of Eq (1.1), $\beta$ plays a minor role in influencing what solutions are realizable at a particular mesh size $h$.

The analytical results in ^[5] offer some insight into the number and distribution of droplets in a droplet assemblies and conditions under which solutions are stable. [5,Theorem 2.2] asserts that for every $\epsilon' > 0$ there is a $\delta > 0$, depending on $\epsilon'$ and $\omega$ such that if $\gamma \rho^3 < 12 - \epsilon'$ and $\rho < \delta$, then the Euler-Lagrange equation of Eq (1.4) admits a stable solution in the shape of a single geodesic disk of radius $\rho$ where the location of the disk depends on $\gamma$ as described in the following three cases:

(C₁) If $\gamma$ is small, a single geodesic disk is located near a point of maximum Gauss curvature of $M$;

(C₂) If $\gamma$ is of order $O(\frac{1}{\rho})$, the center of the geodesic disk is near a global minimum of a function that is a linear difference of a remnant function (the regular part of the Green's function) and the Gauss curvature. Section 2 for a discussion of the Green and remnant function.

(C₃) If $\gamma$ is large, the droplet is located near the global minimum of the remnant function.

Although the results in ^[5] apply to a sphere, the conclusions based on order of magnitude estimates for $\gamma$ and $\rho$ are applicable to other geometries and in Section 2, we present numerical solutions that are representative of Cases C$_1$-C$_3$. for a triaxial ellipsoid. We conjecture that the maximum of the remnant function for a triaxial ellipsoid with semi-major axes $a < b < c$ is near $(a, 0, 0)$ when $\gamma > 0$ is not too large. The curvature of $M$ plays a role for small values of $\gamma$, but for large $\gamma$, the inhibitory term drives pattern formation.

The case of large $\gamma$ and disk assemblies is addressed by [5,Theorem 2.3]) which asserts that if $\epsilon' > 0$ is sufficiently small, there exists $\delta > 0$ depending on $\epsilon', n_d, \omega$ such that if $\rho < \delta$, $\gamma \rho^3 \log \frac{1}{\rho} > 1 + \epsilon'$, $\rho^3\gamma < 12 - \epsilon'$, then there exists a minimizer of Eq (1.4) consisting of $n_d$ droplets that is stable and the size of a droplet is approximately $(\omega |M|/ (n_d\pi))^{1/2}$.

In Cases C$_1$-C$_3$, the single droplet solution is stable. When the number of interior droplets is $n\ge 2$, [5,Theorem 2.3] asserts there is a stable disk assembly $E$ consisting of $n$-droplets. As the radii of these disks approach zero, their centers $\zeta^1, \zeta^2, \dots, \zeta^n$ tend to a local minimum of

where $G$ is the Green's function and $R$ is the remnant function (see Section 2). Since we will focus on domains that are conformal to a sphere we can explicitly compute $G$ and $R$ in terms of the fundamental solution of the Neumann Problem on a sphere. This enables us to show how the features of the solutions of the inhibitory system are influenced by a variation in the parameter $\gamma$ as well as parameters that determine $K$.

In Section 3, the sharp interface problem is discussed. In Section 4, the inhibitory term of the free energy is expressed in terms of an auxiliary function $v = (-\triangle)^{-1}(u-\omega)$, leading to an efficient algorithm for computing numerical minimizers of Eq (1.1). In Section 5, the numerical model for the diffuse interface problem is introduced and (1.5) is discretized. Numerical solutions are presented in Section 6. We present examples of disk assemblies with $n_d$ droplets. We include numerical solutions that describe droplet assemblies when $n_d$ is large or small. We extend the solution space to include patterns with stripes, wriggles and combinations of these features. We discover new stable solutions that include elongated droplets, dog-bone shaped droplets and annular rings for cases of small and large $\gamma > 0$. Concluding remarks are presented in Section 7.

2.   The Green's function

In this paper, $M$ is a triaxial ellipsoid

with $a < b < c$. The maximum Gauss curvature is $K(0, 0, \pm c) = c^2/(ab)^2$ and the minimum Gauss curvature is $K(\pm a, 0, 0) = a^2/(bc)^2$. $K$ has saddle points at $(0, \pm b, 0)$ where $K(0, \pm b, 0) = b^2/(ac)^2$.

A collection of sets on $M$ is best viewed using stereographic projection. We define $\Pi: M \rightarrow {\mathbb{R}}^2$ where $(u, v) = (cx/(c-z), cy/(z-c))$; $\Pi^{-1}: {\mathbb{R}}^2 \rightarrow M\subset {\mathbb{R}}^3$ is given by

where we see from Eq (2.1) that $M \cap \lbrace{z = 0\rbrace}$ maps to $(u/a)^2 + (v/b)^2 = 1$, $M \cap \lbrace{z > 0\rbrace}$ maps to $(u/a)^2 + (v/b)^2 > 1$ and $M \cap \lbrace{z < 0\rbrace}$ maps to $(u/a)^2 + (v/b)^2 < 1$.

Let $\triangle_\Sigma$ denote the spherical Laplacian, $d\sigma$ surface measure and $\delta$ the delta-function on $\Sigma$. The solution $\psi(\theta, \phi, \theta', \phi')$ satisfying

and the constraint

is given by (see, e.g., ^[14])

where

$\Lambda = d(p, p')$ is the arc-length measured along the shorter segment of the great circle passing through $p(1, \theta, \phi)$ and $p'(1, \theta', \phi')$.

In our applications, the Green's function $G$ satisfies

and Eq (2.2). It follows that

From [14,Eq A.5]), we have

which follows from the identities

Since $\zeta' \bar \zeta = \cot \frac{\theta'}{2}\cot \frac{\theta}{2} e^{i(\phi'-\phi)}$ and $\zeta \bar{ \zeta'} = \cot \frac{\theta}{2}\cot \frac{\theta'}{2} e^{i(\phi -\phi')}$, it follows that

Applying Eq (2.5), we have

Thus, for $\zeta, \zeta' \in \mathbb{C}$ and $\zeta \not = \zeta'$,

If we can find a mapping $D \mapsto \Sigma_{p_0}$ that is one-to-one, onto and conformal, we can use the Green's function on $\Sigma_{p_0}$ to express the Green's function for $D$. For example, let $D = {{ \mathbb{E} }}(a, b, c) \setminus \lbrace (0, 0, c)\rbrace$. Let $\zeta = \zeta(p)$ be a one-to-one conformal mapping from $D$ to ${{{\mathbb{C}}}} \setminus \lbrace \infty\rbrace$. The Green's function for $D$ is

Using the value $\zeta$ as the independent parameter, we write

The second term in Eq (2.8) is the regular part of the Green's function and is denoted by

For future reference, we define the remnant function as

Thus, for the ellipsoid where $\zeta = \cot({{ {\frac{1}{2}}}}\hat\theta) \thinspace e^{i\hat \phi}$, we have

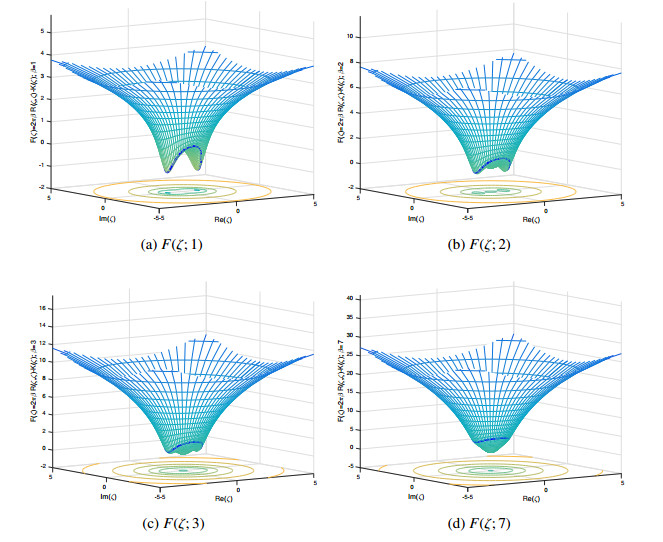
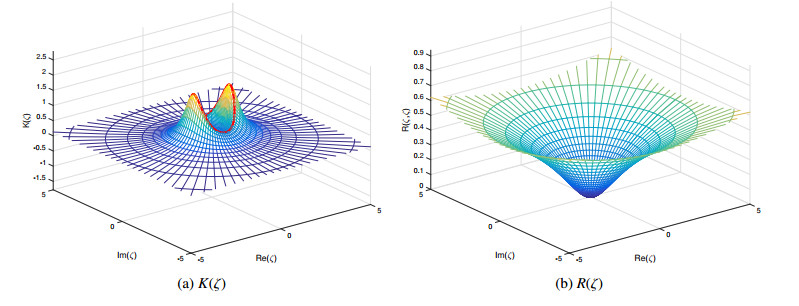
In Figure 1, we consider an ellipsoid ${{{ \mathbb{E} }}}(2, 1.5, 1)$. We present a graph of $K(\xi)$ for

The equatorial curve $(\zeta, K(\zeta))$ is displayed in red and clearly indicates the points of maximum Gauss curvature that correspond to the stereographic projections of $(\pm 2, 0, 0)$. The function $R(\zeta)$ is presented in Figure 1(b). $R$ is bounded below and is minimized at $\zeta = 0 + 0i$. When

3.   The sharp interface model

We refer to Eqs (1.1)–(1.2) as the diffuse interface model. The stationary solutions of Eq (1.1) subject to Eq (1.2) satisfy the corresponding Euler-Lagrange equations, a nonlinear integro-partial differential equation. The system presented here is nearly identical in form to the one presented in ^[15], except that in the present work, $M$ is a compact 2-manifold without boundary.

Consider the $\Gamma$-limit, $\epsilon^{-1}{I} \rightarrow {\cal J}$ as $\epsilon\rightarrow 0$, i.e.,

where $\Sigma$ is the collection of all measurable subsets of $M$ of finite measure and finite perimeter, $\tau > 0$ and $P_M(E)$ is the perimeter of $E$. The sharp interface problem is the problem of finding the stationary points of Eq (3.1) subject to the condition $|E| = \omega|M|$. We divide Eq (1.1) by $\tau$ and set $\gamma' = \gamma/\tau$ and rescale ${\cal J}$ and $\gamma$. For convenience, we assume $\tau = 1$ and drop the "prime" in $\gamma'$.

As discussed in Section 3, stationary solutions of the sharp interface problem reveal droplet locations at equilibrium for small $\rho$. We summarize a number of asymptotic estimates that are relevant to the sharp interface analysis and refer to ^[5,16] for detailed derivations of these estimates. For a single droplet of radius $\rho$, there are three energy estimates corresponding to how $\gamma$ compares with $\rho^{-2}$ corresponding to C$_1$–C$_3$ discussed in Section 1.

3.1.   Single droplet

(C₁) When $0\le \gamma < < 1$, the total energy of a single disk of diameter $\rho$ centered at $\xi$ is dominated by the local part of ${\cal J}(D)$ and

(see ^[16]). This expression is minimized when $\xi$ maximizes the Gauss curvature $K$.

(C₂) When $\gamma = O(\frac{1}{\rho})$ or $\gamma\rho \rightarrow \beta$, then a droplet centers near the minimum of

(C₃) When $\gamma$ is large ($\gamma > > 1$),

and a droplet centers near a minimum of $R(\xi)$

While the original problem is formulated on the ellipsoid ${{ \mathbb{E} }}(a, b, c)$, it is easier to interpret the results when quantities are expressed as a function of $\xi\in{{\mathbb{C}}}$. We will assume an orientation, where the $z$-axis of the ellipsoid is aligned with the north pole of the unit sphere. Since $a > b > c = 1$, $K$ is minimized when $K(0, 0, \pm 1) = 1/(ab)^2$. $K$ is maximized when $K(\pm a, 0, 0) = (a/b)^2$. $(0, \pm b, 0)$ are saddle points of $K$ where $K(0, \pm b, 0) = (b/a)^2$. $\gamma = O(\frac{1}{\rho})$, ${\cal J}$ is minimized when $F(\zeta; \beta) = 2\pi \beta R(\zeta) - K(\zeta)$ is minimized. A graph of $F(\zeta; \beta)$ is presented in Figures 2(a)–(d) for $\beta = 1, 2, 3, 7$. The curve $(\zeta, F(\zeta))$ for $\zeta$ corresponding to the equator of the ellipsoid $z = 0$ is highlighted in dark blue. For small $\beta$, the droplet locates near $(\pm a, 0, 0)$. However, when $\beta$ is sufficiently large the droplet moves away from $(\pm a, 0, 0)$ and towards $(0, 0, \pm c)$. Analysis suggests there is a range of $\beta$ where $F(\zeta; \beta)$ has three local minima (see Figure 2(b) where $\beta = 2$). When $\beta$ (or $\gamma$) is sufficiently large, there is single global minima located near $\zeta = 0+0i$. See Figure 2(d).

3.2.   Droplet assemblies

For disk assemblies, we following the notation in ^[5], we let $r_j > 0$ be the radius of a geodesic disk centered at $p_j$ for $j = 1, 2, \dots, n$, i.e.,

A droplet assembly is denoted ${ E = \cup^{n}_{j = 1} E^j. }$ When $\gamma$ is sufficiently large, the first integral in Eq (1.1) is approximately the total perimeter of all the disks and the total energy of a disk assembly $E$ is given by (see [5, Lemma 2.7])

If the droplets have the same radius $r_i = \rho$, using symmetry ($G(\xi_i, \xi_j) = G(\xi_j, \xi_i)$), we have

Remark The parameter $\rho$ denotes the radius of a flat disk and not the (geodesic) radius of a geodesic disk, but a comparison between the geodesic distance and the Euclidean distance shows $d(p, p') = |p-p'| + O(\rho^2)$ and the estimates for ${\cal J}(E)$ are valid for $\rho$ small.

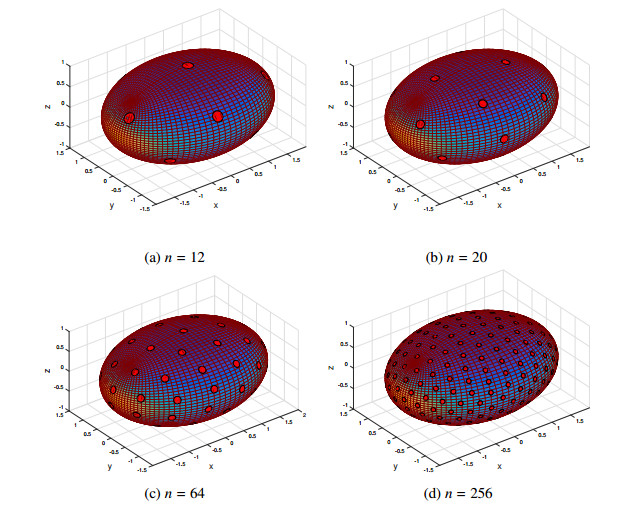
In Figure 3(a)–(d), we present assemblies with $12, 20, 64$ and 256 droplets on an ellipsoid ${{ \mathbb{E} }}(2, 1.5, 1)$ whose locations are determined by minimizing Eq (3.2). Regions of large Gauss curvature on ${{ \mathbb{E} }}$ are colored yellow; regions of low Gauss curvature are dark blue. In general, the droplets are nearly uniformly distributed when viewed on $\Sigma$; but on the ellipsoid, the droplets pack closer together near the equator $z = 0$, where the curvature of ${{ \mathbb{E} }}$ is greatest.

4.   Otha-Kawasaki model on a compact two-dimensional manifold

Let $C^1_{pw}(M; {\mathbb{R}})$ denote the set of piecewise continuously differentiable functions $u: M \rightarrow {\mathbb{R}}$. ${{\mathcal H }}(M)$ denotes the Hilbert space $W^{1, 2}(M)$ which is the completion of $C^1_{pw}(M; {\mathbb{R}})$ with respect to the Sobolev norm ${{{ }} ||u||_{1, 2} = \sqrt{ (u, u)_H} }$ where

We define the subspace

It will be convenient to rewrite Eq (1.1) in a form that lends itself to numerics. With this in mind, we define $v$ to be a solution of the Neumann Problem:

The second condition in Eq (4.2) holds because ${{{ }} \mathit{{\rlap{-} \smallint }}_M u\; dS = \omega}$ where $0 < \omega < 1$. It follows that $v = (-\triangle)^{-1}(u-\omega)$. Formally, $(-\triangle)^{-1}$ is an integral operator expressed in terms of a Green's function (see ^[17]). Using Green's identity, we can rewrite the second integral in Eq (1.1) as follows

With $W(u) = u^2(1-u)^2$, the free energy can be expressed as

which, as we shall see, lends itself well to the computation of numerical minimizers.

For future reference, we record the weak formulation of Eq (4.2): Given a fixed $u\in {{\mathcal H }}(M)$ and $0 < \omega < 1$, find $v \in {{\mathcal V}}(M)$ such that

where

and $(u, \phi) = \int_M u \phi dS$ is the usual inner product on $L^2(M)$.

5.   Numerical model for the diffuse interface problem

We will follow the usual finite element approach to discretizing Eq (1.5) (see, e.g., ^[18]). Because the problem is formulated on a compact two-dimensional manifold (see ^[17]), we present some additional details for the convenience of the reader.

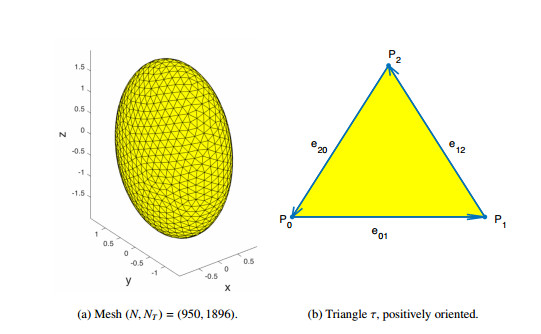
Let $M_h$ be a triangulation of $M$ with positive orientation, i.e., ${{{ }} M_h = \cup^{{{N_T}}} _{j = 1} \tau_j}$ where $\tau_j$ denotes a typical triangle and $N_T$ is the number of triangles in $M_h$. Let $P = \lbrace P_1, P_2, \dots, P_N \rbrace$ denote the vertices in the triangulation $M_h$. The average edge length of the triangles in $M_h$ is denoted by $h$. In Figure 4(a), we present a mesh with $(N, N_T) = (950, 1896)$. In Table 1, we present a summary of the meshes used in our calculations.

To insure an accurate finite element solution, the meshes for triangular discretization used in our numerical calculations are generated by Persson's mesh generator ^[19] which produces high quality meshes consisting of triangles that are almost equilateral. This is a desirable property when solving PDEs with the finite element method. Upper bounds on the errors depend only on the smallest angle in the mesh, and if all angles are close to $60^{ \circ }$, good numerical results are achievable. A mesh of a triaxial ellipsoid with $(a, b, c) = (1.0, 1.5, 2.0)$ and $h = 0.19$ is shown in Figure 4(a). A typical triangle $\tau$ is shown in Figure 4(b). We will use the terms coarse, medium and fine mesh when referring to meshes with parameters $(h, \epsilon) = (0.10, 0.05)$, $(0.05, 0.025)$, $(0.025, 0.0125)$, respectively. Typically, $\epsilon \approx {{ {\frac{1}{2}}}} h$ produced reasonable results. With an unstructured grid, we found that the computation time was prohibitively long with a fine mesh, but the coarse and medium grids were sufficient to capture the important features characterizing the patterns in the solutions at the respective scales.

From a practical standpoint, if the features in a pattern are too fine, a coarse mesh will not be able to capture those features. In this case, the solution process terminates with the solver evolving a constant solution. However, if $h$ is chosen to be at the proper scale when compared with the features of the pattern of interest then a coarse or medium grid will suffice.

Let $P_0, P_1, P_2$ denote vertices in a typical triangle $\tau$. The vertices are positively oriented so that ${\bf{e_{01}}} = P_1 - P_0$, ${\bf{e_{12}}} = P_2 - P_1$, ${\bf{e_{20}}} = P_0 - P_2$ and ${\bf{e_{01}}} \times {\bf{e_{12}}}$ is the outer normal to $M_h$. In our discretization, the geometry is fixed and the degrees of freedom are the values of the phase function $u$ at vertices $P_i$ for $i = 1, ..., N.$ There should be no confusion between elements of the set $\{ P_0, P_1, P_2 \}$ denoting vertices of a generic triangle $\tau$ and elements of the set $\{ P_1, P_2, P_3, ...., P_N\}$ denoting vertices of the triangulation $M_h$.

A finite element solution is sought in the finite dimensional space

where by linear we mean a function of the form $w(x, y, z) = a + bx + cy + dz$ for $(x, y, z) \in \tau_j$. When $a\not = 0$, such a function is said to be affine. Let $P_j = (x_j, y_j, z_j)$ and define $\Phi_i(x, y, z)$ so that

where $\lbrace \Phi_i : i = 1, \dots, N \rbrace$ is a set of basis functions. Hence, any $v_h \in S_h$ can be written as

where $v_j = v(P_j)$. The finite dimensional version of (4.2) is to find $v_h \in S_h$ such that

where $a(v, \psi)$ is defined in Eq (4.4) and the last equation in Eq (5.1) is the discrete version of the mass constraint. Expressing $v_h$ in terms of the basis functions $\left \lbrace \Phi_j, j = 1, \dots, N \right\rbrace$ and then inserting into Eq (5.1), we are led to the linear system

The first $N$ Eq (5.2) can be written in the form $A V = F$ where $A = (a_{ij}) = a(\Phi_j, \Phi_i)$ is the $N \times N$ stiffness matrix and $F\in {\mathbb{R}}^{N}$ is the forcing term. If we augment the matrix $A$ by appending a row derived from Eq (5.3) and appending a zero to $F$, we are led to a matrix equation $\tilde A V = \tilde F$ where $\tilde A$ is $(N+1) \times N$ and $\tilde F \in {\mathbb{R}}^{N+1}$. The rank of $\tilde A$ is $N$, so we form

Note, for fixed $0 < \omega < 1$, the solution of Eq (5.4) is unique. To emphasize the dependence of $V$ on $\omega$ and $U = (u_1, \dots, u_N)^T$, we write

A function $u \in {{\mathcal H }}(M)$ is approximated by a $u_h \in S_h$, i.e.,

where $u_j = u(P_j)$. The linear mass constraint ${\mathit{{\rlap{-} \smallint }}_{M_h} u_h dS = \omega}$ is included in the definition of feasible solutions. In particular, we let

In this case, $\partial M_h = \emptyset$ and there are no boundary conditions placed on the density function $u$. The mass constraint can be written in the form of

It follows that

and

where $V$ is given by Eq (5.5). For the second term in ${I}(u)$, we have

where the integration over $M_h$ is carried out exactly for the piecewise linear function $u_h$, leading to the nonlinear functional $N(U) : {\mathbb{R}}^N \rightarrow {\mathbb{R}}$.

We are lead to the discrete variational problem

where

and $V = V(U, \omega)$ denotes the unique solution of Eqs (5.2) and (5.3).

We say a solution $U^*$ (or $u_h^*$) of Problem ${{\mathcal P}}_h$ is stable in $S_h$ if the Hessian matrix

is positive definite, i.e., all eigenvalues of $H^*$ are positive. We say that a solution $U^*$ of Problem ${{\mathcal P}}_h$ is unstable in $S_h$ if at least one eigenvalue is negative. Otherwise, we say that the stability in $S_h$ is indeterminate. An equivalent way of saying this is a solution $U^*$ is stable in $S_h$ if

for $U = U^* + \delta U$ and $|\delta U|$ sufficiently small. Stability in $S_h$ does not take into account the conservation of mass constraint. For this reason, we define stability with respect to $\tilde S_h$ and consider small perturbations $U \rightarrow U^*+ \delta U$ which satisfy the mass constraint. To this end, we say that a solution $U^*$ is stable in $\tilde S_h$ if

for $U = U^* + \delta U$ and $|\delta U|$ sufficiently small. Stability with respect to $S_h$ implies stability with respect to $\tilde S_h$, but stability with respect to $\tilde S_h$ does not imply the converse. Moreover, if a stable solution in $\tilde S_h$ undergoes a change in topology, then one cannot assume there is a minimizer $u_h^*$ that is $S_h$-stable in a neighborhood of that solution. In our numerical exploration of the solution space, we find it informative to include discussion of stable and unstable solutions in $S_h$ and $\tilde S_h$ as the key parameters $\gamma$ and $\omega$ are varied.

6.   Numerical solutions

Numerical solutions are computed using an interior-point large-scale algorithm implemented in the MATLAB-Optimization Toolbox solver fmincon. Analytic expressions for the gradient ${{ }} D {I^h} = \left[ \frac{\partial {I}}{\partial u_j} \right]$, ${{ }} 1\le j\le N$, and the $N\times N$ Hessian matrix ${{{ }} D^2{I^h} = \left[ \frac{\partial^2 {I^h}}{\partial u_i \partial u_j} \right], 1\le i, j\le N}$ are computed.

In the following, we denote the $k$-th iterate from an fmincon evolution by $u_h^k$ and the final solution by $u_h^*$. The initial guess is denoted by $u_h^0$. Note, even though ${ \rm {supp} }(u_h)$ may be concentrated, the ${ \rm {supp} }(v_h)$ may be the entire manifold $M$, meaning that the Hessian matrix of ${I^h}$ need not be sparse.

Due to the complexity of the solution space and the nonlinear nature of the problem, we will see that the solution found by fmincon will depend on the initial guess $u_h^0$ and the scale $h$. The interior-point method produces a local minimum, not necessarily a global one.

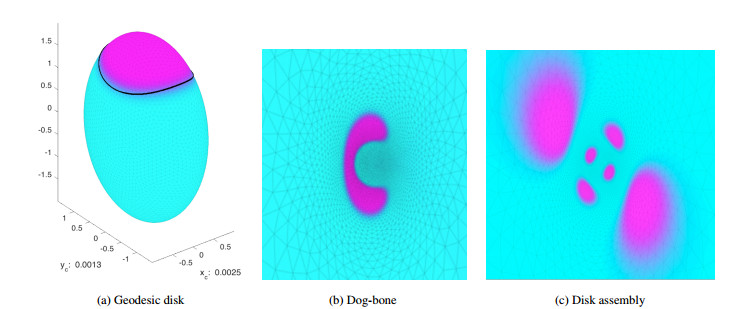
We found the solution process to be robust in the following sense. If we were seeking a disk assembly with $n_d$ disks and total mass $\omega|M|$, we could determine a good $u_h^0$ by distributing $n_d$ sets each with roughly the area of a disk of radius ${{{ }} \rho = \left({\omega |M| }/{(n_d \pi)} \right)^{1/2}.}$ If $\gamma > 0$ is small and $n_d$ is not too large, an initial assembly of $n_d$ sets would converge to $n_d$ geodesic disks of radius roughly size $\rho$. When a typical droplet size is not small, individual droplet shapes need not be a geodesic disk. Other interesting stable shapes, such as the dog-bone droplet and the elongated droplet are observed. To probe the solution space of Problem ${{\mathcal P}}_h$, we consider a number of parametric studies.

When discussing a solution that is a single droplet (or droplet assembly), it is instructive to determine the centroid of the droplet to easily assess its position on the ellipsoid. The center of mass of the minority constituent represented by a solution $u^*_h$ is denoted by $(\bar x, \bar y, \bar z)$ where

In the following, we investigate how parameter variations in $\gamma, \beta, h, \omega$ influence pattern formation on a triaxial ellipsoid when $(a, b, c) = (1, 1.5, 2)$.

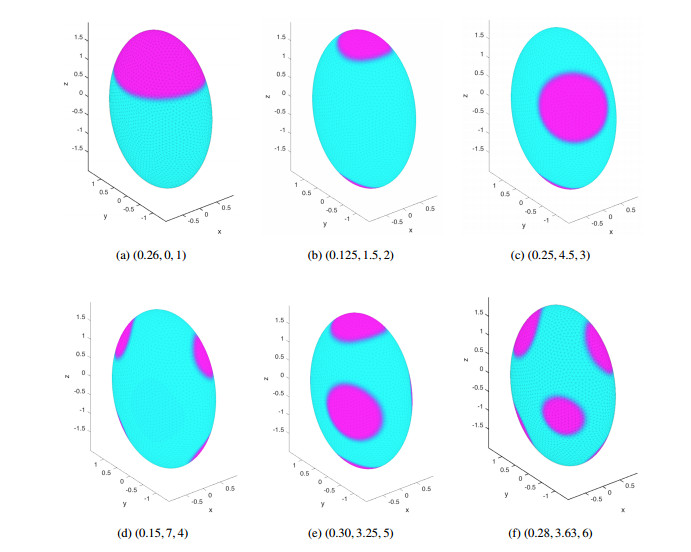
6.1.   Solutions with $0\le \gamma < 7.5$

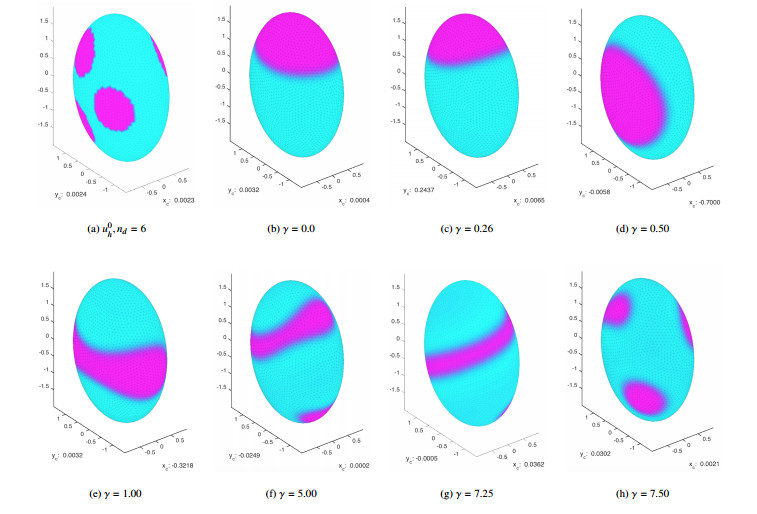
For these studies, we began the solution process with an initial configuration consisting of six disjoint droplets (see Figure 5(a)). The colormap in Figure 5 identifies the minority constituent ($u\approx 1$) with the dark (magenta) color, while the second constituent ($u\approx 0$) is represented by the light (cyan) color. This convention is followed throughout the paper.

Setting $\gamma = 0$ in Eq (5.7), we evolved $u^0_h$ to a minimizer. In the process, we observed the coarsening effect as the six droplets combined to form a single droplet that converged to a set that was roughly a geodesic disk centered at $(\bar x, \bar y) = (0.0004, 0.0032)$ (see Figure 5(b)). Figure 5(b) corresponds to Case 1 in Section 1. This problem was discussed in ^[20] which used an SQP-algorithm and a numerical Hessian. We found the solutions produced by the two different methods were in agreement, but the interior-point method with analytic Hessian implemented in this paper, was significantly faster.

Using $u_h^*$ from Figure 5(b) as the initial guess for a solution with $\gamma = 0.26$, a single disk-like solution was found, but its center of mass was displaced to $(\bar x, \bar y) = (0.0065, 0.2437)$ (see Figure 5(c) corresponding to Case 2 in Section 1). As $\gamma$ increased, we found that the solution jumped to a geodesic disk centered at $(\bar y, \bar z) = (0, 0)$. In particular, for $\gamma = 0.5$, we found $(\bar y, \bar z) = (-0.0058, -0.0007)$ (see Figure 5(d)). Figure 5(d) corresponds to Case 3 in Section 1 and suggests that the remnant function is minimized near $(\pm 1, 0, 0)$. We note that for Cases 1–3, the condition $\gamma \rho^3 < 12$ is satisfied: $\rho\approx1.655$ when $\gamma\approx 0$ (droplet centered at $(0, 0, 2)$, Figure 5(b)–(c))) and $\rho\approx 1.5021$ when $\gamma = 0.5$ (droplet centered at $(1, 0, 0)$, Figure 5(d)). As $\gamma$ was increased beyond $0.5$, we found that the droplet became elongated, transforming into a dog-bone-like shape at $\gamma = 1$ (see Figure 5(e)). A further increase in $\gamma$ led to an elongation of the dog-bone that wrapped itself around the ellipsoid (see Figure 5(f)-(g)). The transition from Figure 5(d) to Figure 5(g) was smooth. At $\gamma = 7.25$, the solution is unstable in $\tilde S_h$. The single elongated droplet breaks into one elongated droplet and two disk-like droplets when $\gamma = 7.5$ (see Figure 5(h)). The solution for $\gamma = 7.5$ was found to be unstable in $\tilde S_h$. For $0 < \gamma < 5$, solutions in $\tilde S_h$ were found to be stable

In Table 2, we present a summary of the findings related to the solutions presented in Figure 5. We have carried out similar numerical simulations for a sphere ($a = b = c = 1$) and a prolate ellipsoid $(a = b = 1, c = 2)$ and found similar qualitative behavior, but with a different range of $\gamma$. For the prolate ellipsoid, a single droplet centers at $(0, 0, 2)$ when $\gamma = 0$. As $\gamma$ is increased slightly, the droplet "jumps" to a position centered on the equator. With increasing $\gamma$ the droplet elongates into a dog-bone droplet which then elongates and wraps around the prolate ellipsoid until the single elongated droplet breaks into smaller droplets.

In Table 2, $n_d$ is the number of droplets and $n_s$ is the number of stripes in the solution. Note, the dog-bone and geodesic disk are topologically the same. A stripe or wriggled stripe is an annulus.

6.2.   Stable disk assemblies in $S_h$

The interior-point method used to minimize ${I^h}$ terminated when it was no longer possible to reduce ${I^h}$ with $u_h \in \tilde S_h$. In many cases, the solution process terminated at a solution that was stable in $\tilde S_h$. Most solutions found in this manner were unstable in $S_h$ with one unstable mode (i.e., the Hessian matrix at $u_h^*$ had one negative eigenvalue with geometric multiplicity one). For a $u^*_h$ stable in $\tilde S_h$, but unstable in $S_h$, we attempted to find a "nearby" solution that was stable in $S_h$. By adjusting $\omega, \beta$ and $\gamma$, we found it was possible to do so for disks and disk assemblies. For example, increasing $\beta$ from $0.25$ to $1.00$ with $(\omega, \gamma) = (0.25, 0)$ had the effect of sharpening the interface, but we found $(\bar x, \bar y) = (-0.001, 0.031)$ for the center of mass in Figure 6(a) (see also the first entry in Table 3). Parameter values related to Figure 6 are presented in Table 3.

In Table 2(b), we see a solution that was stable in $\tilde S_h$, but unstable in $S_h$ for $(\omega, \gamma, \beta) = (0.25, 0, 0.25)$. By increasing $\omega$ to $0.26$ and $\beta$ to $1$, we were able to find a solution that was stable in $S_h$ (see Figure 6(a)). The remaining solutions presented in Figure 6(b)–(f) were computed in a similar manner and were found to be stable in $S_h$. The methodology that was followed was crude. Essentially, we monitored how the lowest eigenvalue of the Hessian matrix behaved as $\omega$ and $\gamma$ were varied.

6.3.   Solutions with stripes and wriggles

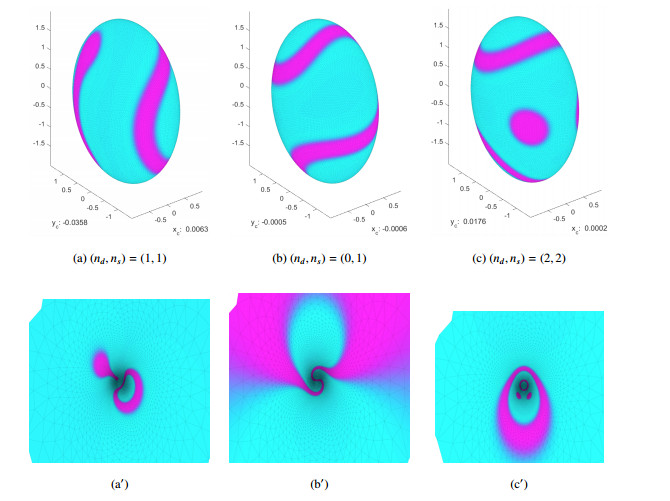
In this section, we fix $\beta = 1$ and vary $\gamma$. We present solutions (see Figure 7(a)–(h)) where the dominant feature is the stripe (or wriggle). Table 4 contains related parameters for these solutions. For $\gamma = 2.5$, we set $u^0_h$ equal to an assembly with geodesic disks at $(0, 0, \pm 2)$ and a stripe around the equator. With $\omega = 0.15$, the two disks disappeared and only the stripe around the equator remained after a solution was evolved (Figure 7(a)). We continued by using the solution from a previous set of parameters as the initial guess for a solution with a new set of parameters. We varied $\omega, \gamma$ as shown in Table 4. This is not a complete inventory of solutions, but is meant to convey how the solutions depend on the parameters. At certain values of $\gamma$, there is a change in the nature of a solution (e.g., the number of stripes change, the orientation of the stripes change, etc.). Eventually, when $\gamma$ is sufficiently large, a stripe is elongated then breaks into a disk assembly. For larger values of $\gamma$ only the constant solution is observed.

In Figure 7(a)–(d) and (f), we present solutions with either one, two or three stripes where the stripes are parallel to the $xy$-plane. In Figure 7(c)–(d), the stripes are parallel to the $yz$-plane with $\omega = 0.1$ and $\omega = 0.4$, respectively. In Figure 7(e), we found an assembly with two droplets and one strip. In Figure 7(g)–(h), we found solutions with one stripe and two elongated disks. It is only when $\gamma$ is very large (say $\gamma = 800$), that the stripe-disk assembly breaks into a pure disk assembly. It should noted that the solutions presented in Figure 7(g)–(h) are unstable in $\tilde S_h$, but those in Figure 7(a)–(e) are stable in $\tilde S_h$.

6.4.   Comparisons with $\Gamma$-limit solutions

In the following, $E$ will denote a subset of $M$ whose area is $\omega |M|$. If $E$ has a $C^1$ boundary and is enclosed by one or more curves, then $J(E)$ denotes the total length of the curves. Let $\tau = \int^1_0 \sqrt{\frac{1}{2} t^2(1-t)^2}dt = {\sqrt{2}}/{12}$. As $\epsilon \rightarrow 0$, ${(\epsilon\tau)^{-1}}{L}$ has a $\Gamma$-limit denoted by $J(E)$ where $L$ is defined in Eq (1.3). (see ^[16]). $L^h$ will denote the discretization of $L$. We will use this result to evaluate how well our numerical formulation approximates the perimeter of $E$ when $\epsilon$ is small. In the first problem, we numerically computed the family of geodesic disks $E_\omega$ centered at $(0, 0, 2)$ and the corresponding radius of $E_\omega$ (denoted by $\rho_{\omega}$) for $\omega \in \lbrace 0.10, 0.15, 0.20, 0.25 \rbrace$. The values $J(E_\omega)$ are presented in the fourth column of Table 5. The absolute value of the relative difference between ${(\epsilon\tau)^{-1}}{{L^h}}(u^*_h)$ and $J(E_\omega)$ was about 1% or less in all cases. Note, the analytical results in ^[16] shows there exists a sharp interface solution in a neighborhood of $\epsilon = 0$ and a numerical solution is a good representation of such a solution. We should note that in a numerical solution, the interface between the two constituents is not sharp and the change from $u^*_h\approx 0$ to $u^*_h\approx 1$ takes place in an annular regions of width $\approx3h$ that borders $E$. See Figure 8(a).

When $\gamma = 1$, a dog-bone-shaped simply connected set $E$ is a solution of Problem ${{{\mathcal P}}_h}$ (see Figure 5(e)). To estimate the perimeter of $E$, we considered the stereographic projection of the dog-bone solution (see Figure 8(b)). We estimated the boundary of the set $\Lambda = \partial(\Pi(E))$, calculated $\Pi^{-1}(\Lambda)$ and found its length was $12.730$ and ${(\epsilon\tau)^{-1}}{{L^h}}(u^*_h) = 12.907$. The absolute relative difference was 1.39%.

For a third comparison, we computed a solution consisting of an assembly (again denoted by $E$) of six disks with $\gamma = 4.0$. We estimated the boundary of the set $\Lambda = \partial(\Pi(E))$, calculated $\Pi^{-1}(\Lambda)$ and found the total length of the curves was $21.75$ while ${(\epsilon\tau)^{-1}}{{L^h}}(u^*_h) = 22.35128$.

6.5.   Mesh dependence

In order to investigate how the solution depends on the mesh size, we considered two mesh sizes $h = 0.09$ and $h = 0.045$. This essentially increases the number of triangles by a factor of 4. See Table 1.

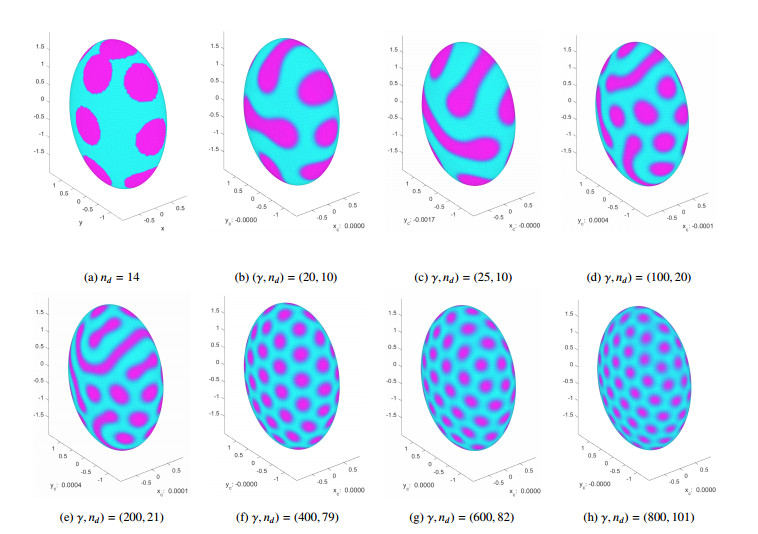
In Section 6.3, we found that on a coarse grid $(h = 0.09)$ with $\gamma$ sufficiently large, solutions with stripes were no longer achievable. To investigate, how this conclusion may be affected by the fidelity of the grid, we computed a family of solutions for $h = 0.045$. Setting $\omega = 0.40$ and starting with an initial distribution of 14 droplets as shown in Figure 9(a), we then proceeded to compute solutions for $\gamma = 20, 25,100,200,400,600,800$. None of the computed solutions had stripes or wriggled stripes, although some of the droplets were elongated and/or dog-bone shaped. It is interesting to note that using the solutions in Figure 7(a)–(c) as the initial guess, and re-evolving solutions with $\beta = 0.25$ led to a constant solution, demonstrating the stabilizing role of the parameter $\beta$.

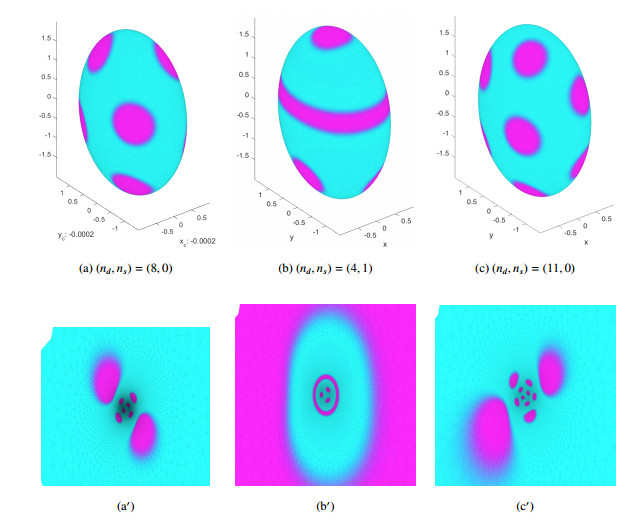
While we were able to observe solutions with stripes on the coarse mesh, typically these solutions would degenerate into disk assemblies as $\gamma$ increased. However, on a finer mesh $h = 0.045$, it was possible to find a variety of solutions for a fixed value of $\gamma$, even when $\gamma$ is not large. For example, in Figure 10, we present solutions: (a) with one dog-bone and one wriggled stripe, (b) one wriggled stripe, (c) two disks and two wriggled stripes. In Figure 11, we present solutions with (a) eight disks, (b) four disks and one stripe, and (c) eleven disks. Figure 10(a')–(c') and Figure 11(a')–(c') present the stereographic projections of the respective solutions.

We also computed disk assemblies with $n_d = 5, 6, 7, 9, 10, 11$. In this case, the total energy was found to be decreasing as a function of $n_d$ for $n_d < 8$ and increasing for $n_d > 8$. We conclude that the disk assembly with $n_d = 8$ had the minimum energy among those solutions presented.

7.   Concluding remarks

In this paper, we investigate pattern formation in a two-phase system on a two-dimensional manifold by numerically computing the minimizers of the Otha-Kawasaki model for micro-phase separation of diblock copolymers. Where analytical results are available, we find our numerical solutions are in agreement. In the case of a single droplet, our numerical model demonstrates a single droplet forms in the shape of a geodesic disk centering near a point of maximum Gauss curvature when $\gamma$ is zero or very close to zero. When $\gamma > 0$ but small and comparable in magnitude to $\rho^{-1}$, then the location of the droplet is located near point where a function that is the linear difference between the remnant function and the Gauss curvature is a minimum. When $\gamma$ is sufficiently large, our numerical results suggest that the remnant function is minimized at $(\pm a, 0, 0)$ and this is the location where the single droplet forms.

If $\omega$ is small, then under suitable conditions, analytical results predict the existence of assemblies of geodesic disks of nearly identical radius $\rho$. For our numerical model, this means that $\rho$ is small and we must use a very fine mesh to capture a droplet assembly with hundreds of droplets. On the other hand, when $\omega$ is sufficiently large our numerical model is able to compute stable assemblies consisting of geodesic disks, elongated droplets, dog-bone droplets, stripes, wriggled stripes, annular rings, and combinations thereof.

Our numerical work for small $\gamma$ is in agreement with previous analytical work that predicts the existence of stable equilibria. Our numerical work demonstrates the existence of disk assemblies and stripes in this regime. When $\gamma$ is moderate to large, the size of a typical facet played an important role. For if $h$ is too large when compared to the size of of $E$, the solution process would converge to a constant solution. The same effect is observed when $\gamma$ is large and the number of disks in a disk assembly solution is large. While we found a disk assembly with 101 droplets for $\gamma = 800$ in one of our test cases, it is certainly possible that an assembly with the same number of droplets could exist for a smaller value of $\gamma$ and the same $\omega$. Our method was not limited by computing resources. The coarse grid solutions easily run on a desktop PC; the medium grids were run on the ColonialOne, a high performance computing facility at The George Washington University.

Although we focused on the triaxial ellipsoid in this paper for demonstration purposes, our methods are general and can be applied to higher genus surfaces and surfaces with boundaries and we look to consider these cases in future work.

Acknowledgements

The authors acknowledge the ColonialOne high performance computing resource at The George Washington University.

Conflict of interest

The authors declare there is no conflicts of interest.

Appendix

Ellipsoid geometry:

In the following, we suppose $\mathbb{E}(a, b, c)$ is a triaxial ellipsoid

with $a > b > c > 0$. The maximum Gauss curvature is $K(\pm a, 0, 0) = a^2/(bc)^2$ and the minimum Gauss curvature is $K(\pm a, 0, 0) = a^2/(bc)^2$; $K(0, 0, \pm c) = c^2/(ab)^2$. $K$ has saddle points at $(0, \pm b, 0)$ and $K(0, \pm b, 0) = b^2/(ac)^2$. In our benchmark case, $(a, b, c) = (2, 1.5, 1)$, we find $K(\pm 2, 0, 0) = 16/9$, $K(0, \pm1.5, 0) = 9/16$ and $K(0, 0, \pm 1) = 1/9$.

In the following, $\Sigma = \lbrace (x, y, z) \ | \ x^2 + y^2 + z^2 = 1 \rbrace$ is the unit sphere. Let $(1, \theta, \phi)$ and $(1, \theta', \phi')$ denote spherical coordinates for the points, $p, p' \in \Sigma$, respectively.

for $0 \le \theta \le \pi, 0 \le \phi\le 2 \pi$. Let $\zeta, \zeta'$ denote the respective stereographic projections of $p, p'$ into the complex plane, i.e., $\zeta = \cot({{ {\frac{1}{2}}}}\theta) e^{i\phi}$ and $\zeta' = \cot({{ {\frac{1}{2}}}}\theta') e^{i\phi'}$. $\Sigma_{p_0} = \Sigma \setminus \left\lbrace p_0 \right\rbrace$ denotes the unit sphere with $p_0$ removed. With $p_0 = (0, 0, 1)$, stereographic projection $\Sigma_{p_0} \rightarrow {{\mathbb{C}}}$ is conformal.

We will show there is a mapping $A:{{ \mathbb{E} }}(a, b, c) \setminus \lbrace (0, 0, c) \rbrace \rightarrow \Sigma \setminus (0, 0, 1)$ that is affine and conformal, we can use it to define a Green's function for $D = {{ \mathbb{E} }}(a, b, c)$. Let $A$ be the matrix with columns ${\bf{f}}_1 = a {\bf{e}}_1$, ${\bf{f}}_2 = b {\bf{e}}_2$ and ${\bf{f}}_3 = c {\bf{e}}_3$ where $\lbrace {\bf{e}}_1, {\bf{e}}_2, {\bf{e}}_3 \rbrace$ is the standard basis for ${{ \mathbb{R} }}^3$. ${{ \mathbb{E} }}(a, b, c)$ is parametrized by

where $0 \le \theta \le \pi, 0 \le \phi\le 2 \pi$. It is easy to check that

${ {{\boldsymbol{ n }}}(\theta, \phi) = {\bf{f}}_2 \times {\bf{f}}_3 \cos\phi\sin\theta + {\bf{f}}_3 \times {\bf{f}}_1 \sin\phi\sin\theta + {\bf{f}}_1 \times {\bf{f}}_2 \cos\theta }$ is normal to $D$ at $p = {{\boldsymbol{ x }}}(\theta, \phi)$. Moreover, since

a unit normal at $p\in D$ is ${ \hat {{\boldsymbol{ n }}}(\theta, \phi) = \frac{ {{\boldsymbol{ n }}}(\theta, \phi) }{ |{{\boldsymbol{ n }}}(\theta, \phi)| }. }$

Define the mapping $p\in D \rightarrow q \in \Sigma$ in the following way. Let

and define

Finally, stereographic projection of $q \in \Sigma_{p_0} \rightarrow \zeta \in {{\mathbb{C}}}$ is given by