Mathematical modeling and optimal control strategies of Buruli ulcer in possum mammals

1.   Introduction

Mycobacterium ulcerans (MU) infection is considered to be the most common condition in human society that causes both disability and deformity. This mycobacterium ulcerans (MU) is one of several mycobacteria classified as potentially pathogenic to animals and humans ^[2,20]. It is most often observed in tropical wetlands, and especially in the West and Central African region, see for more information ^[3,27]. Due to the environmental variations, presently Buruli ulcer (UB) worldwide is considered to be the reason of morbidity. Infected cases are present in many countries around the world and frequently in tropical areas mention ^[4,18]. Furthermore, in non-tropical areas, such as China and Australia, infected cases have been identified ^[20].

Several studies have investigated the potential for Mycobacterium ulcerans (MU) infection in wildlife. The authors in ^[19] studied inoculation of MU in brushtail opossums and found that an unoinoculated opossum in the same room in a separate cage had been infected. Among Australian koalas, there was a natural infection with ringed-tailed opossums and an alpaca ^[27]. The lesions identified clinically were found the same as in humans. It is shown in ^[27] that in January 1998, an adult ringed tail opossum (Pseudocheirusperegrinus) in east Cowes is a clinically identified lesion that is consistent with Mycobacterium ulcerans infection. However, no other studies have been shown for this infected animal about its PCR or culture to be diagnosed. Similarly, in May 1998, an additional case of ring-tailed possum was reported at East Cowes with ulcers on the nose and posterior. In both cases, PCR IS2404 confirmed that Mycobacterium ulcerans infection occurred east of Cowes in January 2000 ^[27]. Some recent discoveries suggest that aquatic insects, some of which are responsible for transmission of infection to the populations of anaemia as well as humans, see more for further details ^[26]. Koalas or possum which are considered to be small mammals eat the M. ulcerans through environment using aerosols and then transferring the M. ulcerans, see for details ^[1,27]. The possum individuals can be infected through the insect vectors which are infected or the mosquitoes that siting on mammals and transmit the infection further. A vector that attacks small infected mammals can get infected. Infected mammals increase infection and ultimately spread Mycobacterium ulcerans into the environment. This cycle is under way for the spread of the disease among mammals and vector and vice versa.

The mathematics regarding the modeling of infectious diseases is thought to be the fruitful for disease understanding mechanism and to provide useful control mechanism for the eliminations of many infectious diseases. Through the effective controls modeling one can be able to understand efficiently the disease preventive mechanism. The models with controls have gotten attentions from scientists and researchers around the world, see ^[4]. For example a mathematical model suggested in ^[4] is used to study BU model with optimal controls with the main aims to minimizing the infections in the infective compartments vectors and humans. The Ebola virus which produced a lot of infections and death cases has been formulated mathematically in ^[2] where the authors put appropriate controls for the minimizations of disease infections. In another study suggested in ^[15], where an effort have been made to use control modeling by addressing effectively the dynamics of an Ebola disease model. The authors considered the controls combinations and provided useful strategies for the minimization of infection.

Optimal control is considered to be the best tools in order to study the dynamics of infectious diseases and its possible control. In epidemiological models, this theory have been used widely and restrainable results have been obtained about the current disease progress and its controls. A few recent papers using optimal control theory for outbreak models, can be seen ^{[9,10,11,12,13]}. For example, the authors in ^[9] investigated the dynamics of the novel coronavirus using actual Pakistani data using optimal control theory. Modeling the Zika dynamics through optimal control theory using actual data was examined in ^[10]. The development of a new mathematical model for the dynamics of pine wilt disease using optimal control theory has been discussed in ^[11]. The application of optimal control analysis for vaccinated TB individuals is provided in ^[12]. A hepatitis B model including isolation, immunization, treatment and optimal control analysis is examined in ^[13]. Moreover, in ^[8], the authors constructed a mathematical model with optimal time-dependent controls to study malaria dynamics. They suggest immunization and treatment strategies for potential malaria elimination in society. The authors of ^[6] used the theory of optimal time-dependent control and suggested the control straggles for the spread of malaria among infective immigrants. A dynamical model to assess the Zika infection has been formulated and discussed through optimal control analysis in ^[7]. Furthermore, the authors of ^[5] examined a mathematical model to study malaria disease with detailed control strategies.

According to the authors knowledge, no study has yet been mathematically designed to understand BU's mathematical modeling of possum and explore its dynamics. This work is categorized by section is as follows: The work is organized as follows: In section 2 we provide a detailed formulation of mathematical modeling for the given problem. A brief analysis of the equilibrium points of the model and its stability both locally and globally are shown in Section 3. The theory of optimal control and its application to the proposed model using Pontraygin's Maximum Principle for characterizing optimal control is presented in Section 4. Section 5 looks at the numerical simulation of an optimum control problem. Sections 6 and 7 summarize the ecological impacts and key findings of the study, respectively.

2.   Mathematical model formulation

We provide here the brief descriptions of model formulation by denoting the population of possum by $N_m (t)$, and further splitting into two compartments, namely, the healthy or the susceptible individuals which are possibly to attract the infections, by $S_m (t)$, and those who are infectious with Mycobacterium ulcerans is given by $I_m (t)$. Thus,

We denote the vector (mosquitoes) population by $N_v (t)$ at time $t$ is partitioned into susceptible and infected mosquitoes shown respectively by $S_v (t)$ and $I_v (t).$ So that,

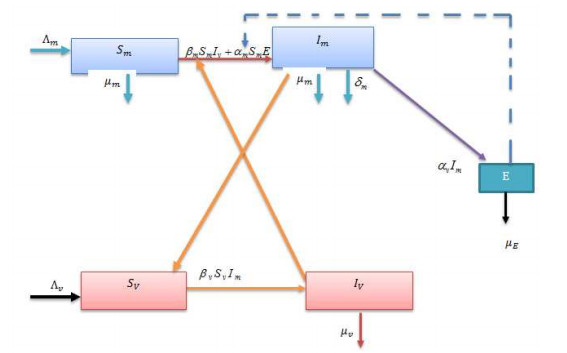
The density of the Mycobacterium ulcerans in the environment is shown by $E$. The parameter $\Lambda _m$ defines the birth rate of the healthy possum that attract the Buruli ulcer infections by contacting the infectious mosquitoes by the rate $\beta _m$, while $\beta _m$ defines to be the transmission probability of contact through the infected mosquitoes. The death of the possum individuals that die naturally is given by $\mu_m$. Through the contact rate given by $\beta _m S_m I_v$, the infection goes to the infected class of the possum. Also, it is reasonable to highlight and also we mentioned it in our modeling that possum infected individuals through the rate $\alpha_m$ getting infection. The parameter $\alpha _m$ defines to be the transmission probability of contact through Mycobacterium ulcerans from the environment and is given by the route $\alpha _m S_m E$. The death due to infection of the possum infected individuals is given by $\delta _m$. The birth of the susceptible mosquitoes population is shown by $\Lambda_v$ while the individuals in the vector class die naturally and is shown by $\mu_v$. The transmission route given by $\beta _v S_v I_m$ that generate the infection through the contact among susceptible vector and infected humans, where $\beta _v$ is defines to be the probability of the mosquitoes to be infected possum by contacting an infectious possum. The removal of infected possum from the environment is given by $\alpha_E$ while $\mu_E$ denotes the decay of Mycobacterium ulcerans from the environment. It is assumed that all news born are to be susceptible. The above discussion is presented in the diagram of Figure 1 while its transmission process through mathematical model is given in the following equations:

subject to non-negative initial conditions

3.   Mathematical analysis of the model

This section investigate some related properties of the model (2.1) which will be discussed in this section. This include the positivity of the system, equilibrium points and its stability.

3.1.   Solution positivity

The following result regarding the nonnegativity of the model (2.1) is presented.

Theorem 1. Let for the model (2.1) the initial conditions to be $S_m(0) > 0$, $I_m(0) > 0$, $S_v(0) > 0$, $I_v(0) > 0$ and $E(0) > 0$. Then there exists $(S_m(t), I_m(t), S_v(t), I_v(t), E(t)):(0, \infty)\longrightarrow(0, \infty)$ that solve the system (2.1).

Proof. Consider

So, $t^* > 0$, we have the result below for the system (2.1) by considering its first equation,

So, we have

So,

giving

The following is obtained suing second equation of model (2.1),

which implies

The similar process can be used to show that $S_v(t) > 0, \; I_v(t) > 0$ and $E(t) > 0$.

3.2.   Invariant region

Adding the first two equations of system (2.1), we get

i.e.,

Using the theory in ^[21], we have

Taking, $t\rightarrow \infty$, we obtain $0 < N_m\leq\frac{\Lambda_m}{N_m}$.

The dynamics of the total mosquito population is

The solution of (3.2) when $t$ approaches $\infty$ is

So, the region that is feasible biologically for the system (2.1) is presented by

where the fundamental results are hold in this region. To present the results for the positive invariance of $\Phi$, we have

and $E\leq E^*$, where $E^* = \frac{\alpha_E}{\mu_E}$. So, it is worthy to determine the results of system in $\Phi$, where epidemiologically and mathematically the model is well posed.

3.3.   Equilibria and basic reproduction number

Before establishing results for the computations of basic reproduction number, first, we need to obtain the infection free equilibrium by denoting it $E_0$ for system (2.1) and can be get through the following way:

We follow the method and notation considered in ^[22] to have the expressions for $\mathcal{R}_0$. The sentential matrices that needs during computations can be arranged as follows:

Inverse of V

The spectral radius of the above is to be the required basic reproduction number for our proposed model (2.1) after some computations given by:

3.4.   Local stability

The local stability for the given system (2.1) has been established in the following theorem.

Theorem 2. The model (2.1) is locally asymptotically stable, if ${\cal{R}}_0 < 1$ at the disease free case $E_0$.

Proof. At $E_0$, we have the following Jacobian system:

The respective characteristics equation of $J(E_0)$ is given by

where

We have for Eq (3.3) the roots which are $-\mu_m < 0$, $-\mu_v < 0$, while the remaining are easy to obtained by satisfying the Routh-Hurtwiz criteria ($a_j > 0$ for $j = 1, ..., 3$ and further $a_1a_2 > a_3$). Thus, the model (2.1) when ${\cal{R}}_0 < 1$ at the infection free equilibrium is locally asymptotically stable.

3.5.   Endemic equilibria

To have the expressions for the model (2.1) at the endemic case, we denote its endemic equilibrium by

and is given by

We use the above result into first equation of the model (2.1), and obtain

where,

The coefficient $a$ in (3.4) is positive while the positivity of the coefficient $c$ depends when ${\cal{R}}_0 < 1$ otherwise negative. So, the sign of $b$ and $c$ can determine the positive solution of (3.4). For the case when ${\cal{R}}_0 > 1$, two solutions can be obtained for (3.4), that are positive and negative. For the case when considering $c = 0$ if and only if ${\cal{R}}_0 = 1$, then a solution of the form exists $I^{**}_m = -b/a$, when $b < 0$. It can be concluded that the equilibria depends on the changing value of ${\cal{R}}_0$, that shows the existing of an interval for ${\cal{R}}_0$ with two equilibria,

We have no solution for the Eq (3.4) in such a case when $c > 0$ and either $b\geq0$ or $b^2 < 4ac$.

3.6.   Stability of the endemic equilibrium

Theorem 3. The possum model (2.1) at $E_1$ is locally asymptotically stable if ${\cal{R}}_0 > 1$.

Proof. At $E_1$, the following Jacobian matrix is presented,

where $Q_1 = I^{**}_v \beta _m+ \alpha _mE^{**} +\mu _m, \; Q_2 = I^{**}_v \beta _m+E^{**} \alpha _m, \; \; Q_3 = (\delta _m+\mu _m), \; \; Q_4 = \beta _v I^{**}+\mu _v, \\\; \; Q_5 = \beta _m S^{**}_m, \; \; Q_6 = \alpha _m S^{**}_m, \; \; Q_7 = \beta _v S^{**}_v.$

The characteristics equation of $J(E_1)$ is

where

$k_i > 0$ for $i = 1, 2, ...5$ where

In order to have $k_i > 0$ for $i = 1, 2, ...5$, an algebraic computation software can be used to satisfies these conditions. If all these conditions are fulfilled, then it in ensured that the system (2.1) is locally asymptotically stable at the endemic state.

3.7.   Global stability of DFE

In this subsection, we investigates the global asymptotical stability of the system (2.1) at DFE $E_0$. Stating the result given below:

Theorem 4. The possum model (2.1) is globally asymptotically stable at $E_0$ when ${\cal{R}}_0 < 1$.

Proof. Let define the Lyapunov function given by

The time derivative of $\mathfrak{L(t)}$ and further use of model (2.1) gives,

where $b_i$, for $i = 1, 2, ...5$ are constants.

Using $S^0_m = \frac{\Lambda_m}{\mu_m}$ and $S^0_v = \frac{\Lambda_v}{\mu_v}$, we get

Choosing the constants $b_1 = b_2 = \mu_v$, $b_3 = b_4 = \beta_m\frac{\Lambda_m}{\mu_m}$ and $b_5 = \frac{\Lambda_m\mu_v\alpha_m}{\mu_E\mu_m}$ and further simplification, the following is achieved,

Thus, $\mathfrak{L'(t)}$ is negative when ${\cal{R}}_0\leq1$ and it can be equal to zero if $S_m = S^0_m$, $S_v = S^0_v$, $I_m = I_v = E = 0$. Thus, for the $\Phi$, the largest sect is $E_0$. Finally, it can be stated that the model (2.1) is globally asymptotically stable at the disease free case whenever ${\cal{R}}_0 < 1$.

3.8.   Global stability endemic case

We study the global stability of the endemic case for the model (2.1) by using the following result:

Theorem 5. The possum system (2.1) at the endemic case $E_1$ is stable globally asymptotically when ${\cal{R}}_0 > 1$.

Proof. We define the Lapunove function given by:

Differentiation and further using of model (2.1) leads to the following,

After some calculations, we get

and

It follows from (3.8-3.12)

Thus, the largest invariant subset, $L'(t) = 0$ is $E_1$. The result in ^[14], confirms the equilibrium $E_1$ is globally asymptotically stable for ${\cal{R}}_0 > 1$.

4.   Optimal control analysis

Modeling of infectious diseases and its control analysis is considered useful tool in disease epidemiology, where some recent publications use this control analysis for their proposed work ^[23,24,25]. Considering the optimal control theory and its applications to model (2.1) by incorporating the controls variables and using the Pontryagin's Maximum Principle to obtain the required optimal controls results. We endeavor to ensure minimizing the individuals infected through mycobacterium ulcerans and the related measure of cost and the uses of the prevention mechanisms, insecticide controls and the related possible treatment of the infected possum individuals. The term given by $(1-u_1)$, is used in order to keep the infection possibly minimum by reducing the interactions among the susceptible possum, MU in the environment or the infected vector, where $u_1$ is defined to the control preventive mechanism effort, a useful and intensive necessary education/informatios for officers of the wildlife. The control variable $u_2$ denotes the possible effort that can be brought by making spraying on the population of vectors and its reservoirs to decrease better the minimizations or reduction of the infectious vector population. While $u_3$ is the treatment control effort in order to minimize the infected possum by reducing the discard rate and death of the infection of the possum infected individuals. Keeping the above discussions in mind the following optimal control system is given:

with the non-negative initial conditions.

In model (4.1), we taking into account the three controls variables that are time dependent, and given by $u(t) = (u_i)\in {\cal{U}}$ with $i = 1, ..., 3$ which have been discussed and defined above. These controls variables shown by $u(t) = (u_1, u_2, u_3)\in {\cal{U}}$ are associated with the state variables $S_m, I_m, S_v, I_v$ and $E$. It is bounded and measure with the set given by

Now, let define the objective functional for the optimal control problem above, given by

associated to the model (4.1). The constants in (4.3), $W_1$, $W_2$, $W_3$, $a_1$, $a_2$ and $a_3$ respectively denote the balancing and weight constants. The first weight constant given by $a_1$ is related possum infected individuals, $a_2$ related with the infected vectors while $a_3$ is used for the MU in the environment. Further, the given constants $W_1, W_2, W_3$ and $a_1, a_2, a_3$ describe the cost related to the interventions in the given interval $[0, T]$. To have an optimal control problem, $u^*_1, u^*_2, u^*_3$ such that

where the set $\cal{U}$ is defined in (4.2). The Hamiltonian equation for the control system is defined through the equation given below:

where $\lambda _{S_m }, \lambda _{I_m }, \lambda _{S_v }, \lambda _{I_v }$ and $\lambda _E$ are the adjoint variables.

4.1.   Existence of the control problem

This section determine the existence of the control problem (4.1) by using the approach given in ^[16]. The system (4.1) is clearly bounded above, which make enable us to follow the results given in ^[16] for our considered system (4.1) with the suggested assumptions to be fulfilled.

$G_1:$ Both the state and controls variables are non empty.

$G_2:$ The given set ${\cal{U}}$ is closed and convex.

$G_3:$ The equations in (4.1) where its right side is continuous and bounded and can be shown in form in $u$ given by with coefficients hinging on time and state.

$G_4:$ The existence of constants $i_1, i_2 > 0$ and $n > 1$ in such a manner that the term inside the objective functional $J$ is convex and holds the following,

For the fulfillment of the conditions above the results in ^[28] will be used to show the existence of the model (4.1). The first condition is satisfied with the fulfillment of the state and controls variables which is nonempty and bounded. The second conditions about the boundedness and the convex property are fulfilled as the system does. The conditions is valid due to the characterization of the system in bilinear in control variables. For the condition four the following is shown,

where $W_1, W_2, W_3, a_1, a_2, a_3, i_1, i_2 > 0$ and $n > 1$. Therefore, we have the result below:

Theorem 6. For the objective functional (4.3) with the control set (4.2) and the optimality system (4.1) there exists an optimal control $u^* = (u^*_1, u^*_2, u^*_3)$ such that $J(u^*_1, u^*_2, u^*_3) = \min_{\cal{U}}J(u_1, u_2, u_3)$.

To get the solution of the optimal control system (4.1), it is require to determine the Lagrangian and Hamiltonian for (4.1). The Lagrangian $I$ can be defined in the following way for the control model (4.1):

For obtaining the marginal value of the Lagrangian $I$, writing the Hamiltonian $H$, by choosing $\underline{Y} = (S_m, I_m, S_v, I_v, E)$, ${\cal{U}} = (u_1, u_2, u_3)$ and $\lambda = (\lambda _{S_m }, \lambda _{I_m }, \lambda _{S_v }, \lambda _{I_v }, \lambda_E)$, to get:

where $H$ = $(\underline{Y}, \cal{U}, \lambda)$

4.2.   Optimal control solution

Using the Pontryagins Maximum principles we present the optimal control solutions ^[17]. Using this principal to reformulate (4.1-4.3) into a problem of minimizing pointwise a Hamiltonian $H$ with regard to $u_1, u_2$ and $u_3.$

Theorem 7. Given optimal controls $u_1^ *, u_2^ *, u_3^ *$ and solutions $S_m, I_m, S_v, I_v, E$ of the optimality (4.3 -4.1) that minimize $J\left({u_1, u_2, u_3 } \right)$ over $U.$ Then adjoint variables $\lambda _{S_m }, \lambda _{I_m }, \lambda _{S_v }, \lambda _{I_v }, \lambda _E$ are exists and satisfying,

where $i$ is $S_m, I_m, S_v, I_v, E$ and with transversality conditions

Proof. Corollary 4.1 of ^[16] leads to guarantee the existence of an optimal control. The convexity and other properties related to the control system and the solution of the control are fulfilled. Therefore, the differential equations associated to the adjoint variables are achieved through differentiating the Hamiltonian equation together with the optimal control. The adjoint equations obtained and then rearranged is as follows:

The solution of $u^*_i$ for $i = 1, 2, 3$ subjected to the given conditions, the required results are obtained in (24)-(26).

5.   Numerical simulation

For us to depict the results of the numerical solution of the proposed model with and without control, the following parameter values given in Table 1 are used which are defined briefly. We consider the time unit for the entire numerical results in per day. For illustrations perspective, some parameter values are assumed for this exercise.

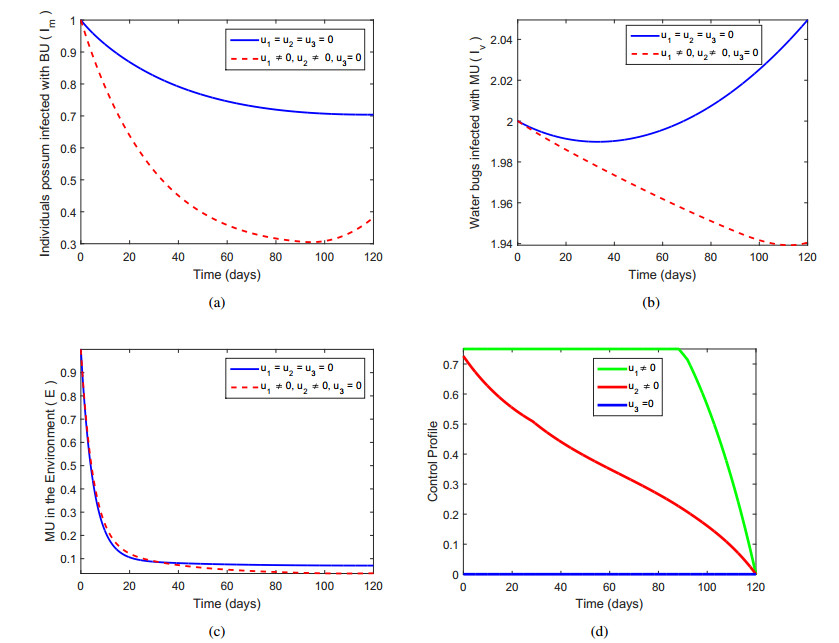
5.1.   Prevention ($u_1$) and ($u_2$) of Buruli ulcer

The two prevention controls $u_1$ and $u_2$ (proper educations to wildlife officers and spraying of insecticide on mosquitos) is employed for the optimization of the objective functional J in the absence of control $u_3 = 0$ and the desired results are obtained graphically in Figure 2. With this strategy, the result shown in Figure 2(a-d) for the infected compartments together with controls variables are useful for the infection minimization. Figure 2(a) determine the BU infected possums $I_m$ compared to the non-controlled system is decreasing significantly. The combination of controls $u_1$ and $u_2$ is very effective strategy that can minimize the BU infection effectively. It is obvious in Figure 2(b) that there is a vast and a clear difference between the case with control and without control. The proper educations to the wildlife officers regarding the infections mechanism and its preventions, and using the quality insecticide spray can best reduce the population of infected vector $I_v$. In Figure 2(c) there is a little variations among the two system of control and without control. The proper and effective education to the officers of the wildlife and proper straying of insecticides mechanism enhance the reduction of the concentrations of MU in the environment $E$. The control profile in Figure 2(d) indicates one requires 25% efforts control $u_1$ for almost 110 days before getting to 120 days while one needs control $u_2$ effort of 90 days at 100 % maximum before reducing to 26% and kept constant for the rest of the 120 days.

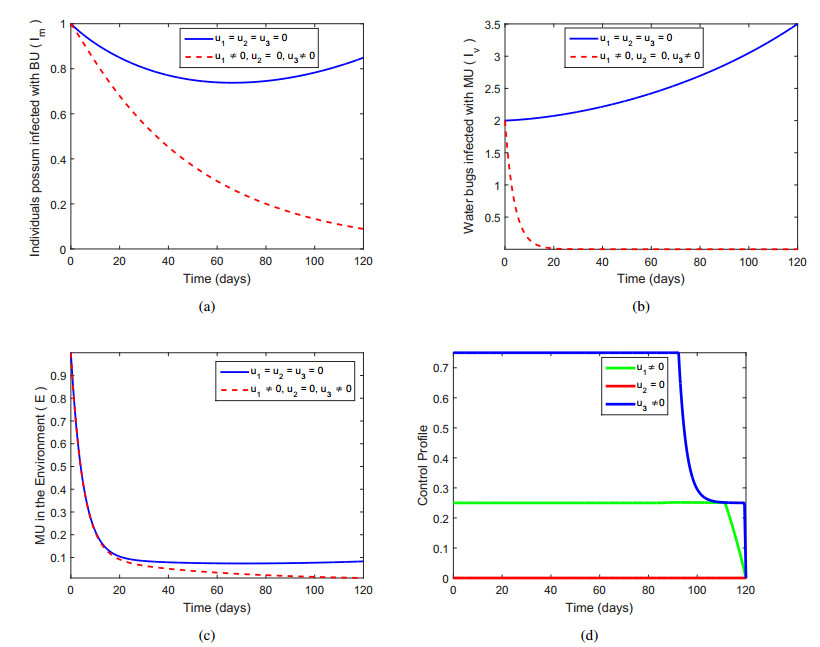
5.2.   Prevention ($u_1$) and treatment ($u_3$) of Buruli ulcer

This set of controls that is the prevention ($u_1$) and treatment ($u_3$) of Buruli ulcer are used and obtained the desired results graphically while $u_2$ is set to be zero. The controls in the form of prevention and treatment $u_1, \; u_3$ (insecticide spraying and the treatment of possum infected individuals) are considered and the numerical experiment is performed and desired results are depicted in Figure 3. Figure 3(a) shows that the number of infected possums $I_m$ is considerably less as compared to the system with no control. This combination of controls is effective because in developed countries like Australia where there is a better veterinary practitioners compare to the less developed countries. In Figure 3(b) there is a clearly evidence that the infected number of water bugs is quit substantially different from the case with controlled and without controlled. It can be inferred from Figure 3(b) that the present set of controls show good behavior for the minimization of infection in the infected compartment such as the water bugs $I_v$. Figure 3(c) describes the MU in the environment, and a decrease is observed in the minimization of MU in the environment $E$ after day 80 fully. It shows that the two combined mechanism is good to reduce the concentration of MU in the environment. In Figure 3(d) the control profile $u_1$ indicates that one requires about 26% effort and maintained constantly for 110 days before getting to 120 days. The control profile $u_3$ in Figure 3(d) is at 100% effort for 90 days period before it reduce to 25% effort which is maintained the for the entire 120 days while the control $u_2$ is set to zero.

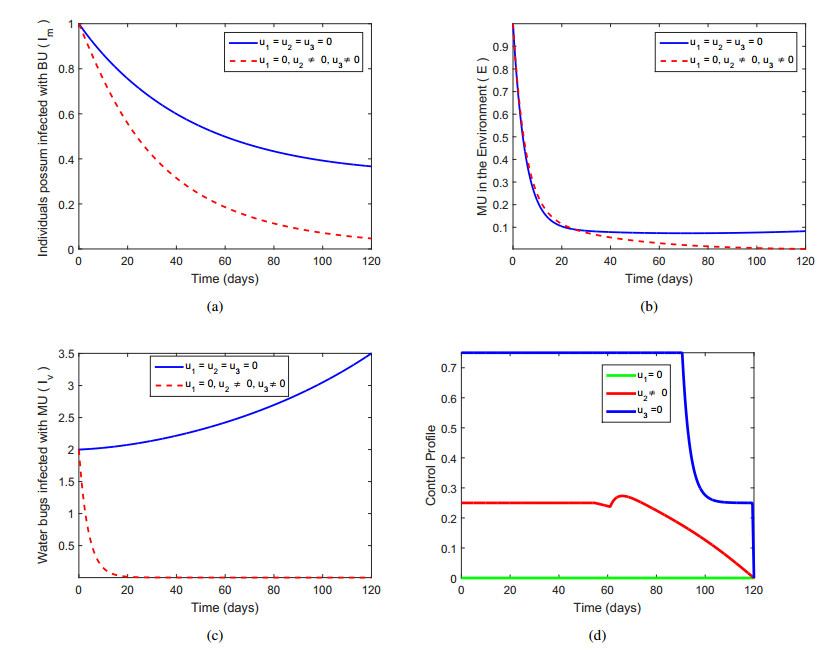
5.3.   Prevention ($u_2$) and treatment ($u_3$) of Buruli ulcer

In the present set of combinations of controls, the prevention and treatment control $u_2, u_3$ (intensive education for wildlife officers and treating infected possums) are used and the simulated results of the model with and without controls systems are obtained in Figure 4 in the absense of $u_1$ control. In Figure 4(a), it is obvious that the infected possums with BU $I_m$ is significantly different from activation of control and without control which can be seen as effective control strategy. Figure 4(b) describes that a highly substantial difference among the two systems. It can be seen in 4(b) that the combination of such controls capable of reducing the infected water bugs that eventually bit the possum to bring about the BU. Figure 4(c) indicates that there is a different between the activation of control and without control in the concentration of MU in the environment $E.$ Thus, this strategy minimizes the concentration level of MU in the environment $E$. Figure 4(d) shows the control profile $u_3$ which is maintained at 100% effort for 90 days then reduce to 24% which is maintained for the rest of the 120 days while control $u_2$ is also kept at 26% effort for 70 days before gradually reducing till the 120 days and control $u_1$ is set to zero.

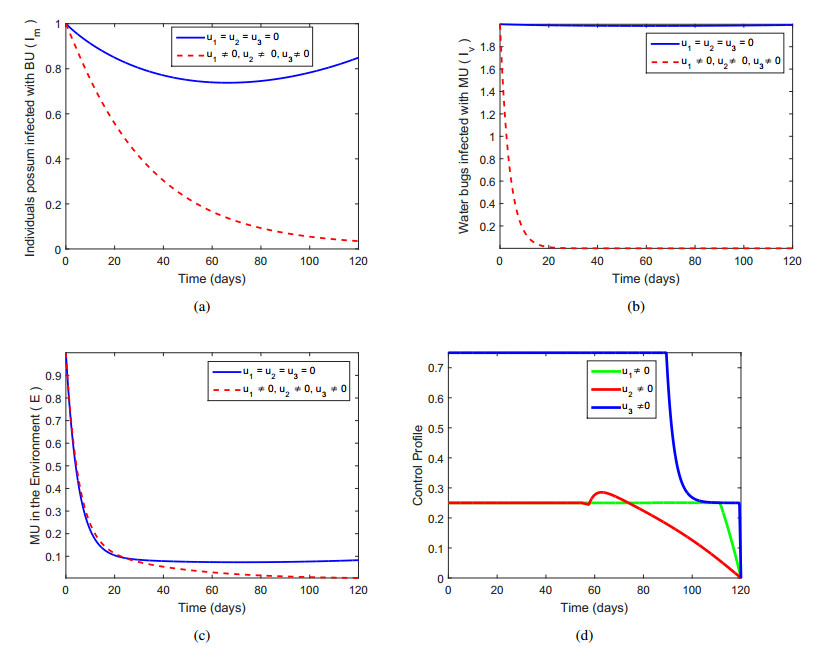
5.4.   Prevention ($u_1$), ($u_2$) and treatment ($u_3$) of Buruli ulcer

The entire controls which are $u_1, u_2, u_3$ (intensive education for wildlife officers, spraying of insecticides and treating infected possums) are used and the simulated results of the system are obtained graphically in Figure 5. Figure 5(a) shows that there is significantly different between the application of the three controls and the case of without control. This appears to infer that the combination of all the three controls at the same time minimize the number of infected possum with BU. A similar situation is depicted in Figure 5(b) and therefore, keeping and practicing of this mechanism is a potential tool of reducing the number of infected water bugs $I_v$. The result shown in 5(c) describes that the infection may decrease little but meaningful after day 80 to 120. This shows that putting all the controls active and employing each strategy appropriately can best reduce the level of concentration of MU in the environment $E$. The control profile in 5(d) shows that one needs to maintain the control $u_1$ at 25% for the period of 113 days before reducing in effort the rest of 120 days. The control $u_2$ requires same effort as in control $u_1$ but sharply reduces after 72 days for the rest of the days. In 5(d), the control $u_3$ is maintained at 100% for the maximum of 84 days and then reducing to 25% and has be maintained till 120 days.

6.   Ecological implications environmental studies

Australia confirmed the ingestion of the M. ulcerans due to insect vector or through the environment. It is considered to be the reason for shedding the virus into the environment. With the implementation of the controls strategies properly, the rate of possums M. ulcerans infection can be brought to a minimum level which is to be the useful ecological implications. The literature ^[30,31,32] suggest that the Buruli ulcer is identified and has been associated with the aquatic environment. In some other studies ^[29], it has been mentioned that the infection can be identified in terrestrial mammals. The use of prevention that can reduce better the infection of M. ulcerans in possums, can be more effective, and possibly it will help by reducing the M. ulcerans recycle in the soil which possibly to back in the populations of mammals. The use of insecticide spraying can also an effective control for the reduction of infection. It will reduce the infections in the reservoirs as well as the vectors populations. That vectors reservoirs that are sprayed can reduced M.ulcerans, and hence the bite to the possums will not lead to an infection. The proper controls strategies can also give a proper preventive mechanism and at the same time, the right medications in order to treat the infected possums which are identified can better reduce the disease spread in the species. Since the preventive mechanism as shown by the control $u_1$ includes the proper training of the wildlife department and its workers that can improve the quality of handling the infected possum with M.ulcerans. Although, the implementation of all the control strategies at the same time can reduce possibly better the infection minimization. If these discussions are kept in mind well and applied properly then the ecosystem that enhances the survival of these bacteria will be broken and eventually will be reduced.

7.   Conclusions

We studied a possum mammal deterministic mathematical model and carried out the detailed mathematical results. We obtained the fundamental results of the model and examined its results using the threshold quantity ${\cal{R}}_0$ which usually driven the spread of the disease is determined. The fixed points are obtained and its stability results are explored. We found that the model possess two equilibrium points. Each of the fixed is used to present its stability for the case when the threshold less or greater than unity. The analysis of the equilibrium points for the infection free and endemic case are discussed and obtained the results that the model is globally asymptotically stable. We considered time dependent controls and formulated an optimal control system. The necessary results for the optimality system are carried out in details. We proved that control model exists. We presented in deep the simulation of the model and presented the numerical results considering different set of controls combination. Each set of control is used and the desired results are obtained and discussed graphically. Finally, we utilized all the effective controls at the same time and the results are obtained by which we found that the infection can be eliminated best by considering all the controls active such as the intensive wildlife officer's education, praying of insecticide and treatment of infected possum. The numerical solution showed that optimizing all the three controls is the best strategy to curtail the spread of BU among possum. In addition, given any one of the two preventive control and treatment is also an effective way particularly for the minimizing the spread of BU in possum mammal and infection of MU in water bugs.

Acknowledgment

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia for funding this work through research groups program under grant number R.G.P-2/97/42.

Conflict of interest

No conflict of interests exists regarding the publication of this paper.