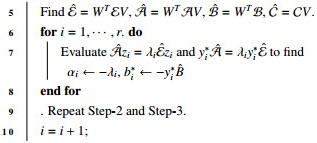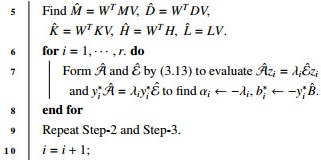SVD-Krylov based techniques for structure-preserving reduced order modelling of second-order systems

1.   Introduction

Mathematical modeling of physical systems plays a significant role in assessing, simulate, control, or optimize the implementation of real-world problems in technological development. It is an alternative approach to avoid extensive laboratory works engaged with a great deal of equipment. On the other hand, mathematical modeling can save not only time or labor but also help to enhance the performance of the physical system. The models are originated in different ways, such as finite element method (FEM) or finite difference method (FDM) discretization, and often represented by linear time-invariant (LTI) continuous-time system. The second-order LTI continuous-time system can be represented in state-state form as

where $M, D, K \in \mathbb{R}^{n\times n}$ are time-invariant matrices, $H\in \mathbb{R}^{n\times p}$ is the input matrix describing the external access to the system, $L\in \mathbb{R}^{m\times n}$ represents the output of the measurement and $D_a \in \mathbb{R}^{m\times p}$ is the direct feed-through of the system. The number of states or dimensions of the system is n while $\xi(t)\in \mathbb{R}^n$ is the vector of states, $u(t)\in \mathbb{R}^p$ is the vector of control input and $y(t)\in \mathbb{R}^m$ is the measured output of the system. The input and output of the system are defined in continuous-time over the interval $[0, \infty)$ and thus the system is known as a continuous-time system of second-order. If $M = I$, then the system is called a standard state-space system, or if $M$ is an invertible matrix then the system can also be converted into a standard state-space system. If $p = m = 1$, the system is called single-input single-output (SISO) system, otherwise, it is called the multi-input multi-output (MIMO) system. In the MIMO system, we consider $p, m < < n$, i.e., the number of input and output of the system is much less than the number of states. Applying Laplace transformation, the transfer function of second-order LTI continuous system can be found as

Many physical phenomena of science and engineering can be modeled as second-order systems (see e.g., ^[1,2,3]). For example, in mechanics, mechatronics ^[4], and multi-body dynamics ^[5], where the velocity is taken into account in the modeling, and thus the acceleration becomes part of the system. In mechanics, usually, the matrices M, D, and K describe the mass, damping, and stiffness distributions, respectively, and the vector $\xi(t)$ is known as mechanical displacement ^[6]. Such systems also appear in electrical engineering when RLC circuits are designed for nodal analysis ^[7]. There the matrices M, D, and K are called the conductance, capacitance, and susceptance matrices, respectively, and the vector $\xi(t)$ is denoted as electric charge.

To generate an exact model of a physical system, through discretization, a sufficient number of grid points needs to create because the system may obstruct by several bodies with factious devices. As a result, the size of the developing model usually becomes too large and sparse, and additionally well-structured also. A large-scale system demands extraordinary computational effort to deal with and consume additional computer memory to store it. It also prohibits rapid simulation processes that are obligatory in many installations. To avoid these types of complications, reducing the size of the system becomes unavoidable in many cases. The technique to reduce the size or dimension of a model is known as model order reduction (MOR) ^[8,9,10]. The r-dimensional reduced-order model (ROM) of (1.1) can be written as

where $\hat{M}, \hat{D}, \hat{K} \in \mathbb{R}^{r \times r}$, $\hat{H}\in \mathbb{R}^{r \times p}$, $\hat{L}\in \mathbb{R}^{m \times r}$, $\hat{D}_a = D_a$ and $r \ll n$. The target is to minimize the value of $r$ by the trial and error basis such that system (1.3) approximates to the system (1.1) by conserving the system properties invariant. The transfer function corresponding to the ROM (1.3) is denoted by $\hat{G}(s)$ and is defined as

The aspect of model order reduction is to reduce the unwanted enormous computational interruptions in analyzing or improving the performance in the implementation of modern technology. Among several model reduction techniques, SVD based balanced truncation (BT) ^[11,12] and Krylov-based techniques iterative rational Krylov algorithm (IRKA) ^[13,14] are well-known and efficient in this arena. Both techniques have some advantages or disadvantages such as IRKA is computationally cheap, whereas BT is comparatively expensive, BT has a priori error bound, in contrast, IRKA has no error bound. Also, BT preserves the stability of the system, contrariwise IRKA does not depend on it. By going beyond these issues, combining the features of both these techniques S. Gugercin in ^[15] developed an efficient way for model-order reduction of large-scale linear dynamical systems that assures the system stability asymptotically with minimized $\mathcal{H}_2$ approximation. We propose a two-sided projection-based model-order reduction method iterative SVD-Krylov algorithm (ISKA) for the second-order linear dynamical system. The method is susceptible to provide the best approximation to the full model by preserving the second-order structure and stability of the system with minimized $\mathcal{H}_2$ norm.

2.   Preliminaries

Consider the k-dimensional linear dynamical system represents in state-space form of first-order ordinary differential equation as

where $\mathcal{E} \in \mathbb{R}^{k\times k}$ is non-singular, $\mathcal{A}\in\mathbb R ^{k\times k}$, $\mathcal{B}\in\mathbb R^{k\times p}$, $\mathcal{C}\in\mathbb R ^{m\times k}$ and ${\mathcal D}_a\in\mathbb R^{m\times p}$.

However, the second-order system (1.1) can be converted into an equivalent first-order form (2.1) in several ways ^[16]. Due to the structural requirement of the system, a feasible first-order representation of the second-order system is needed to be constructed. To design a suitable arrangement of the second-order system (1.1), we are choosing the following first-order form

The systematize observability Lyapunov equation of (2.1) is

Since the direct computation of the observability Gramian by solving equation (2.3) is almost impossible for large-scale settings, one needs to find the corresponding Gramian factor by any suitable techniques, for instance, Low-rank Cholesky-factor based Alternating Direction Implicit (LRCF-ADI) method as in ^[17,18,19]. If $Z_q$ the observability Gramian factor, then the Gramian, $\mathcal{Q} = Z_qZ_q^T$ can be treated as the approximate solution of the Lyapunov equation (2.3). The techniques for finding $Z_q$ of first-order system is provided in Algorithm 1.

Now consider the computationally feasible $r$-dimensional reduced order model of (2.1) is given by

where $\hat{\mathcal{E}} \in \mathbb{R}^{r\times r}$, $\hat{\mathcal{A}}\in\mathbb R ^{r\times k}$, $\hat{\mathcal{B}}\in\mathbb R^{r\times p}$, $\hat{\mathcal{C}}\in\mathbb R ^{m\times r}$ and $\hat{\mathcal{D}}_a\in\mathbb R^{m\times p}$.

The reduced coefficient matrices of (2.4) is formed by the following way

Here the projector $V$ is constructed by following the prominent Krylov-based interpolatory MOR techniques IRKA in ^[14,20] as

in which $\{\alpha_i\}_{i = 1}^r$ and $\{b_i\}_{i = 1}^r$ are the assuming interpolation points and tangential directions respectively, where $r$ is the size the desired ROM. The other projector $W$ is formed with observability Gramian $\mathcal{Q}$ according to the SVD-based MOR techniques in ^[15,21,22] as

The detailed procedure of computing the ROMs (2.4) of first-order system is illustrated in Algorithm 2. In [15,Theorem 3.2] S. Gugercin showed that the ROMs (2.4) achieved by Algorithm 2 maintaining the stability of the system asymptotically as the original system.

3.   Structure-preserving model-order reduction of second-order system by ISKA

The main intention of this work is to reduce the dimension of the second-order system (1.1) by keeping the system structure invariant through the ISKA approach. To do this, it is essential to modify some steps of first-order ISKA and LRCF-ADI algorithms in terms of second-order matrices of (1.1).

3.1.   Structure-preserving LRCF-ADI for second-order system

The LRCF-ADI method of first-order was discussed in ^[19,23,24]. The modification of the LRCF-ADI algorithm for the structure-preserving second-order form can be derived as follows.

Let us consider $\mathcal{V}_i = \begin{bmatrix} \mathcal{V}^{(1)}_i \\ \mathcal{V}^{(2)}_i \end{bmatrix}$ and $\mathcal{W}_i = \begin{bmatrix} \mathcal{W}^{(1)}_i \\ \mathcal{W}^{(2)}_i \end{bmatrix}$, then for the first iteration of the Step-3 of Algorithm 1 can be written as

From (3.1) we get

As a consequence, for $i \geq 2$, the next $i-$th iterations take the forms

If the shift parameter has no imaginary part, then the Step-6 of Algorithm 1 can be written as

which implies

and if it contains an imaginary part, then for $\delta_i = \frac{Re(\mu_i)}{Im(\mu_i)}$, the Step-10 of Algorithm 1 can be expressed as

This results in

The re-organized second-order structure-preserving form of LRCF-ADI is exhibited in Algorithm 3.

3.2.   Structure-preserving ISKA for second-order system with $\mathcal{H}_2$ optimality

Algorithm 2 needs to reform in the structure-preserving shape with the system matrices of (1.1). In the Step-2 of this algorithm, projector $V$ needs to be re-structured utilizing the second-order matrices. Let us consider the $i-$th iteration of $V$ be expressed as $V_i$ and due to the structure of the system, it can be partitioned as $V_i = \begin{bmatrix} V^{(1)}_i \\ V^{(2)}_i \end{bmatrix}$, then for the MIMO dynamical systems, it can be configured as

Equation (3.8) implies to

Likewise for the SISO case, without considering the tangential direction $b_i$, (3.9) can be written as

Now, the error system associated with the reduced-order model (1.3) of the considering second-order system (1.1) by maintaining the first-order representation (2.2) has the form

where $G(s)$ and $\hat{G}(s)$ are defined in (1.2) and (1.4), respectively. In (3.11), we have constituted

Here, $\mathcal{E}, \mathcal{A}, \mathcal{B}$ and $\mathcal{C}$ are the matrices provided in the first-order representation (2.2) of the second-order system (1.1) and also $\mathcal{\hat{E}}, \mathcal{\hat{A}}, \mathcal{\hat{B}}$ and $\mathcal{\hat{C}}$ have the following compositions

The observability Lyapunov equation corresponding to the Graminan $\mathcal{Q}_{err}$ of the error system (3.11) is

Authors in ^[25] evolved an efficient approach to estimate the $\mathcal{H}_2$ norm of the error system (3.11) as

Here, $\|G(s)\|_{\mathcal{H}_2}$ is the $\mathcal{H}_2$ norm of the full model which we need to evaluate at one time in computation but this is infeasible to investigate for a large-scale system by any direct solver. Suppose $Z_q$ is the low-rank Gramian factor of the Gramian $\mathcal{Q}_{err}$ of the Lyapunov equation (3.14) then

and that can be successfully determined by Algorithm 3.

Again, the $\mathcal{H}_2$ norm of the reduced-order model, $\|\hat{G}(s)\|_{\mathcal{H}_2}$ can be enumerated by the Gramian $\mathcal{\hat{Q}}$ of the low-rank Lyapunov equation

that consists of reduced-order matrices. Due to the small size of these matrices, the Lyapunov equation (3.17) is solvable by the MATLAB library command $\texttt{lyap}$.

Finally, $\text{trace}(\mathcal{B}^T \mathcal{Q}_s \mathcal{\hat{B}})$ can be measured by the low-rank Gramian $\mathcal{Q}_s$ of the sparse-dense Sylvester equation

that can be efficiently solved by the techniques provided in Algorithm 4 of ^[26].

The second-order structure-preserving modified form of Algorithm 2 with the computation technique of $\mathcal{H}_2$ norm is summarised in Algorithm 4.

The author in ^[3] showed that the second-order systems are equivalent to the corresponding first-order systems, hence system (1.3) is equivalent to (2.4). Thus, according to ^[15] the reduced-order system (1.3) achieved by Algorithm 4 is asymptotically stable.

4.   Numerical results

The proposed method ISKA is validated by applying to some data generated from real-world problems. International Space Station Model (ISSM), Clamped Beam Model (CBM), Scalable Oscillator Model (SOM), and Butterfly Gyro Model (BGM) are under our attention. The numerical computations are carried out with MATLAB^Ⓡ R2015a (8.5.0.197613) on a board with 4$\times$Intel^Ⓡ$\text{Core}^{\text{TM}}$i5-6200U CPU incorporating a 2.30 GHz clock speed and 16 GB RAM.

Table 1 displays the dimensions of the discussing models, their types with analogous input-output structures, and the size of the corresponding ROMs gain by the developed technique ISKA as illustrated in Algorithm 4. Detailed of those models are available on the web-page for the Oberwolfach Benchmark Collection^*.

^*https://sparse.tamu.edu/Oberwolfach

4.1.   Frequency domain analysis

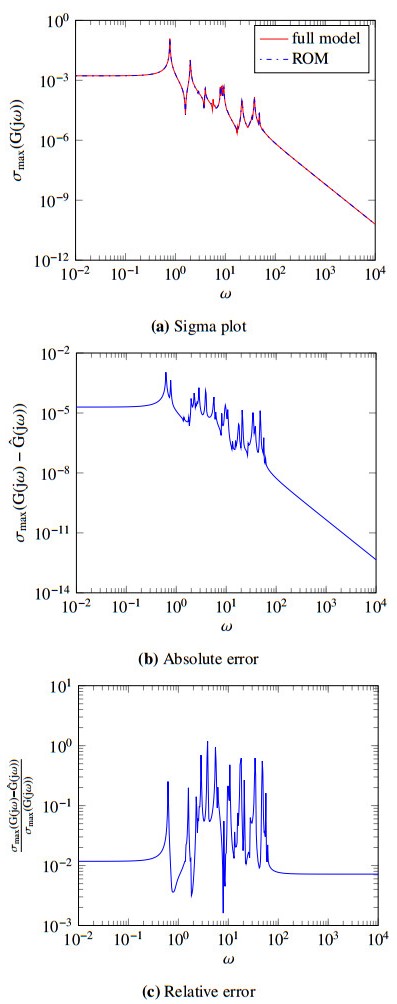
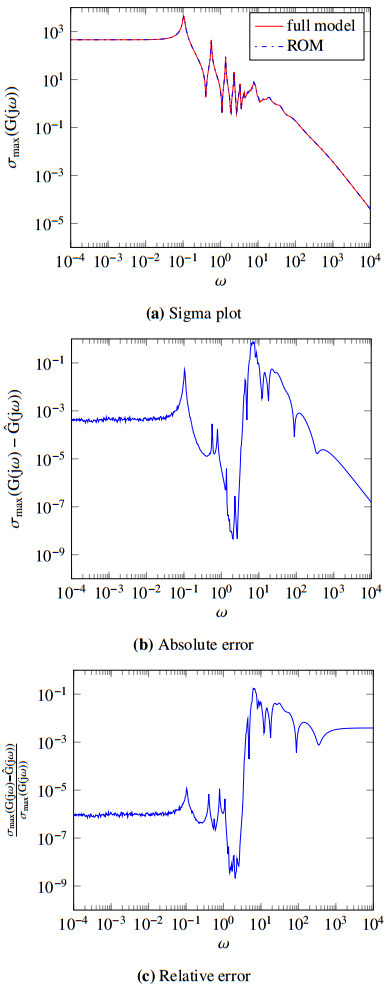
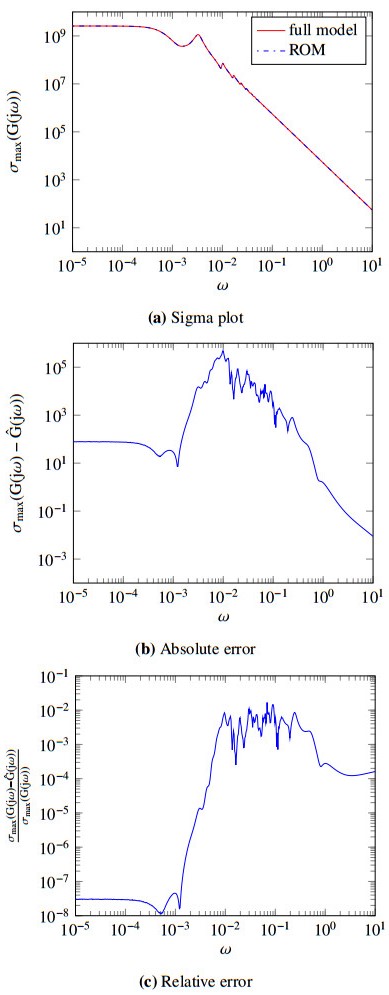
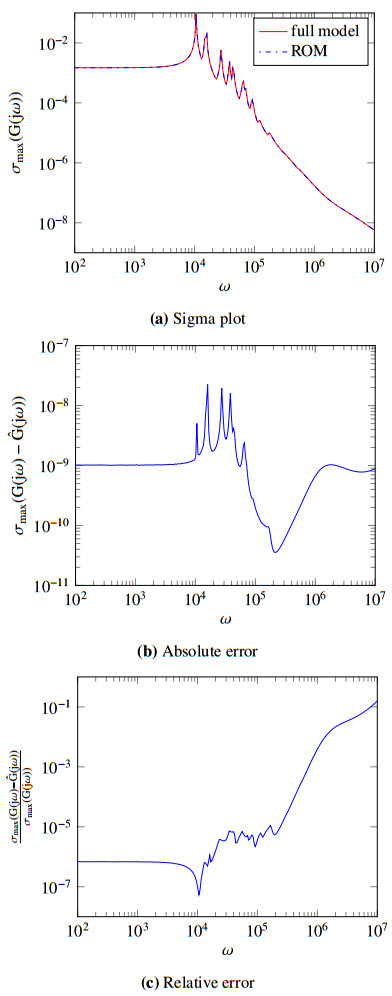
Figure 1a, Figure 2a, Figure 3a and Figure 4a display the well-matching of the transfer functions of the full models with analogous ROMs in the desired dimensions. Figure 1b, Figure 2b, Figure 3b and Figure 4b depict the absolute errors in computing ROMs of the relating second-order models, whereas Figure 1c, Figure 2c, Figure 3c and Figure 4c illustrate the corresponding relative errors in attaining the ROMs.

From the displaying figures achieved by ISKA, it is conspicuous that the proposed method is sufficiently efficient and robust for the target models in finding ROMs of the second-order systems by conserving the second-order structure.

In comparison with the previous work ^[25], it is noticed that Algorithm 4 can generate a better approximation to the full model. Since the graphical presentations are almost the same, to compendious the article, we are avoiding the graphical comparison here but we will present the $\mathcal{H}_2$-norm comparisons next.

4.2.   Stability analysis

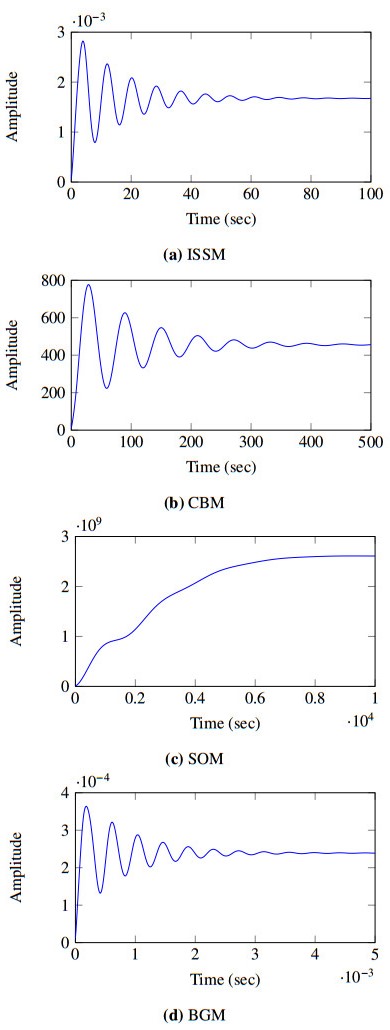
Sub-figures of Figure 5 exhibit the step-responses of the ROMs of the target models originate from Algorithm 4. The horizontal axis depicts the time required for the step-response to be converged to the equilibrium, whereas the vertical axis is for the amplitude. The ROM of BGM converged within a fraction of a second, and the ROMs of ISSM, CBM, and SOM need $100$, $500$, and $10000$ seconds, respectively, to be converged.

It is perceivable from Figure 5 that all the ROMs computed by Algorithm 4 of the considering models are stable after a certain period of time, i.e, the ROMs are asymptotically stable.

4.3.   $\mathcal{H}_2$-norm comparisons

Table 2 represents the comparisons of the $\mathcal{H}_2$ error norm of the ROMs achieved by IRKA and our newly developed technique as represents in Algorithm 4. Here, we compared the $\mathcal{H}_2$ error norm estimated by ISKA in the present work with that of the previous work for concerning models in ^[25] by IRKA.

It has been observed that the developed approach ISKA is well-efficient to minimize the $\mathcal{H}_2$ error norms of all the considering models in comparison to IRKA and that ascertain the proposed technique can provide a better approximation to the original model by conserving system properties.

Moreover, from Table 2, it is evident that the MIMO systems are more feasible in terms of $\mathcal{H}_2$ norm optimality in comparison to the SISO systems.

5.   Conclusion

We have introduced a two-sided projection-based structure-preserving model-order reduction approach for the second-order linear dynamical systems. Here we have following the features of the SVD and Krylov-based model reduction methods. We have successfully modified the LRCF-ADI and ISKA algorithms of first-order to preserve the second-order structure in the reduced-order model. Structure-preservation of the system is significant for getting a better approximation to the full model. It conserves some fundamental physical properties of the system that is essential for more exploration of the system. The SVD-based method has a priori error bound but it has computational complexities, and the Krylov-based technique is computationally efficient but it has neither an error bound nor the stability guarantee. The numerical investigations of the proposed method on some real-world models manifest that it is productive to provide the reduced-order model by preserving the second-order structure and system stability with minimized $\mathcal{H}_2$ norm of the reduced system.

Acknowledgment

This research is funded by University Grant Commission (UGC), Bangladesh. The reference of the funding is ugc/fellowship/1.157/ph.d/2015/part-2 and has been started from December 02, 2018.

Conflict of interest

The authors declare that they have no conflicts of interest to this work.