1.
Introduction and preliminaries
Suppose that G is connected, simple and undirected graph having edge set E(G) and vertex set V(G), respectively. The order of graph G is |V(G)| and size of graph G is |E(G)|. Moreover, Δ(G) and δ(G) represent the maximum and minimum degree of graph G respectively. Let W={v1,v2,…,vk} be an ordered set of V(G) and let u be a vertex of G. The representation r(u∣W) of u with respect to W is the k-tuple (d(u,v1),d(u,v2),…,d(u,vk)). If distinct vertices of G have distinct representation with respect to W, then W is called metric generator for G. A metric generator of minimum cardinality is metric basis for G, and its cardinality is called metric dimension of G, denoted by dim(G) (see [1]). A metric generator ˊW for G is called fault-tolerant metric generator if ˊW∖{v} is also a metric generator, for each v∈ˊW. The fault-tolerant metric dimension of G is the minimum cardinality of this set ˊW and is denoted by fdim(G) (see [2]).
Let d(x,e) denotes distance between edge e and vertex x, defined as d(x,e)=min{d(x,a), d(x,b)}, where e=ab (see [3]). A vertex x distinguishes two edges e1 and e2, if d(e1,x)≠d(e2,x). Let WE={w1,w2,…,wk} be an ordered set of vertices of G and let e be an edge of G. The representation r(e∣WE) of e with respect to WE is the k-tuple (d(e,w1),d(e,w2),…,d(e,wk)). If distinct edges of G have distinct representation with respect to WE, then WE is called edge metric generator for G (see [3]). An edge metric generator of minimum cardinality is an edge metric basis for G, and its cardinality is called edge metric dimension of G, denoted by edim(G) [4,5,6,7].
Slater proposed the idea of metric dimension to find the location of intruder in a network (see [1,8]). The proposed idea was further extended by Melter and Harary in [9]. Metric dimension is important in robot navigation, chemistry, problems of image processing and pattern recognition etc. (see [10,11,12,13,14,15]). The use of metric dimension of graphs was also observed in games like mastermind and coin weighing (see [16]).
Kelenc in [3] extended the idea of metric dimension to edge metric dimension and make a comparison between them. He also discussed some useful results for paths Pn, cycles Cn, complete graphs Kn and wheel graphs. In [8], Zubrilina classified the graphs on n vertices for which edge metric dimension is n−1. In [17], Kratica computed the edge metric dimension of generalized petersen graphs GP(n,k) for k=1 and 2 while for the other values of k the lower bound is given. In [18], Ahsan computed the edge metric dimension of convex polytopes related graphs [19,20,21].
In 2008, Hernando, Slater, Mora and Wood introduced the new idea of fault-tolerant metric dimension in [2]. Further in 2017, Voronov calculated the fault-tolerant metric dimension of the king's graph (see in [22]). In 2018, Raza et al. computed the fault-tolerant metric dimension of generalized convex polytopes [23]. Recently in 2019, Liu, Munir, Ali, Hussain and Ahmed have computed the fault-tolerant metric dimension of wheel related graphs like gear graphs [24]. Basak has computed the fault-tolerant metric dimension of circulant graphs [25].
A framework where failure of any single unit, another chain of units not containing the defective unit can substitute the initially utilized chain is called fault-tolerant self-stable framework. These graphs can tolerate the failure of one part (vertex) keeping consistent execution (see [24,26]). For this purpose we propose the concept of fault-tolerant edge metric dimension. Let ˊWE be edge metric generator of graph G, then ˊWE is called fault-tolerant edge metric generator of G if ˊWE∖{v} is also an edge metric generator of graph G for each v∈ˊWE. A fault-tolerant edge metric generator of minimum cardinality is a fault-tolerant edge metric basis for graph G, and its cardinality is called fault-tolerant edge metric dimension of G, we are denoting it by fedim(G) [27,28]. In this concept, we will extend the work of edge metric dimension to fault-tolerant edge metric dimension.
The lemmas given below are very helpful for calculating the fault-tolerant edge metric dimension of graphs:
Lemma 1.1. [3] For any n≥2, edim(Pn)=dim(Pn)=1, edim(Cn)=dim(Cn)=2, edim(Kn)=dim(Kn)=n−1. Moreover, edim(G)=1 if and only if G is path.
Lemma 1.2. [3] For a connected graph G, edim(G)≥log2(△(G)).
Lemma 1.3. [3] For a connected graph G of order n, edim(G)≥1+⌈log2δ(G)⌉.
From the definition of fault-tolerant edge metric dimension, it can be seen that
Lemma 1.4. For a connected graph G,
1. fedim(G)≥1+edim(G).
2. 2≤fedim(G)≤n.
The rest of paper is structured as follows: In the second section, we will study the fault-tolerant edge metric dimension of family of path, cycle and complete graphs. In third section, we will investigate the fault-tolerant edge metric dimension of family of cycle with chord graphs Cmn. In fourth section, fault-tolerant edge metric dimension of family of tadpole graphs Gln will be determined. In last section, we will compute the fault-tolerant edge metric dimension of family of kayak paddle graphs Gln,m.
2.
Fault-tolerant edge metric dimension of family of path, cycle and complete graphs
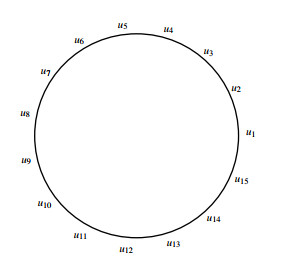
In this section, we will investigate the fault-tolerant edge metric dimension of family of paths, cycles and complete graphs. The family Pn have V(Pn)={u1,u2,…,un} and E(Pn)={uiui+1:1≤i≤n−1}. The family Pn for n=10 is shown in Figure 1. The following theorem tells us the edge metric dimension of Pn.
Theorem 2.1. [3] For any integer n≥2, edim(Pn)=1.
Now, we will compute the fault-tolerant edge metric dimension of Pn.
Theorem 2.2. For any integer n≥2, fedim(Pn)=2.
Proof. In order to compute fault-tolerant edge metric dimension of Pn, we have ˊWE={u1,un} ⊂V(Pn), we have to show that ˊWE is a fault-tolerant edge metric generator of Pn. For this, we give representations of each edge of Pn.
r(uiui+1|ˊWE)=(i−1,n−i−1), where 1≤i≤n−1.
We see that there are no two tuples having the same representations. This shows that fault-tolerant edge metric dimension of Pn is less than or equal to 2. Since by Lemma 1.4, Pn has fault-tolerant edge metric dimension greater than or equal to 2. Hence fault-tolerant edge metric dimension is equal to 2.
The family Cn have V(Cn)={u1,u2,…,un} and E(Cn)={uiui+1:1≤i≤n−1}∪{unu1}. The family Cn for n=15 is shown in Figure 2. The following theorem tells us the edge metric dimension of Cn.
Theorem 2.3. [3] For any integer n≥3, edim(Cn)=2.
Now, we will compute the fault-tolerant edge metric dimension of Cn.
Theorem 2.4. For any integer n≥3, fedim(Cn)=3.
Proof. In order to compute fault-tolerant edge metric dimension of Cn, we have the following cases.
Case (i). n is odd. Take ˊWE={u1,u2,u3} ⊂V(Cn), we have to show that ˊWE is a fault-tolerant edge metric generator of Cn. For this, we give representations of each edge of Cn.
r(unu1|ˊWE)= (0,1,2).
Case (ii). n is even. Take ˊWE={u1,u2,u3} ⊂V(Cn), we have to show that ˊWE is a fault-tolerant edge metric generator of Cn. For this, we give representations of each edge of Cn.
r(unu1|ˊWE)= (0,1,2).
We see that there are no two tuples having the same representations. This shows that fault-tolerant edge metric dimension of Cn is less than or equal to 3. Since by Lemma 1.4, Cn has fault-tolerant edge metric dimension greater than or equal to 3. Hence fault-tolerant edge metric dimension of Cn is equal to 3.
Theorem 2.5. For any integer n≥2, fedim(Kn)=n.
Proof. The proof is straight forward from Lemma 1.1 and Lemma 1.4.
3.
Fault-tolerant edge metric dimension of family of cycle with chord graphs Cmn
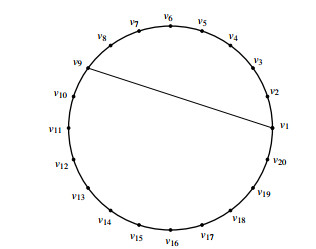
In this section, we will investigate the fault-tolerant edge metric dimension of family of cycle with chord graphs Cmn. The family Cmn have V(Cmn)={v1,v2,…,vn} and E(Cmn)={vivi+1:1≤i≤n−1}∪{vnv1,v1vm}. It suffices to consider 2<m≤⌊n2⌋. The family Cmn for n=20 and m=9 is shown in Figure 3. The following theorem tells us the edge metric dimension of Cmn.
Theorem 3.1. [29] For all n≥4, edim(Cmn)=2.
Now, we will compute the fault-tolerant edge metric dimension of Cmn.
Theorem 3.2. For all n≥4, fedim(Cmn)=3.
Proof. In order to compute fault-tolerant edge metric dimension of Cmn, we have the following cases.
Case (i). Both n and m are even. Let ˊWE={v2,vm2+1,vm+1} ⊂V(Cmn), we have to show that ˊWE is a fault-tolerant edge metric generator of Cmn. For this, we give representations of each edge of Cmn.
r(vnv1|ˊWE)= (1,m2,2) and r(v1vm|ˊWE)= (1,m2−1,1).
Case (ii). n is odd and m is even. Let ˊWE={v2,vm2+1,vm+1} ⊂V(Cmn), we have to show that ˊWE is a fault-tolerant edge metric generator of Cmn. For this, we give representations of each edge of Cmn.
r(vnv1|ˊWE)= (1,m2,2) and r(v1vm|ˊWE)= (1,m2−1,1).
Case (iii). n is even and m is odd. Let ˊWE={v2,vm+12+1,vn2+m+12} ⊂V(Cmn), we have to show that ˊWE is a fault-tolerant edge metric generator of Cmn. For this, we give representations of each edge of Cmn.
r(vnv1|ˊWE)= (1,m−12,m−2) and r(v1vm|ˊWE)= (1,m−12−1,m−1).
Case (iv). Both n and m are odd. Let ˊWE={vm+12,vm+1,vn} ⊂V(Cmn), we have to show that ˊWE is a fault-tolerant edge metric generator of Cmn. For this, we give representations of each edge of Cmn.
r(vnv1|ˊWE)= (m−12,2,0) and r(v1vm|ˊWE)= (m−12,1,1).
We see that there are no two tuples having the same representations in all the four cases. This shows that fault-tolerant edge metric dimension of Cmn is less than or equal to 3. Since by Lemma 1.4, Cmn is not a path so fault-tolerant edge metric dimension of Cmn is greater than or equal to 3. Hence fault-tolerant edge metric dimension of Cmn is 3.
4.
Fault-tolerant edge metric dimension of family of tadpole graphs Gln
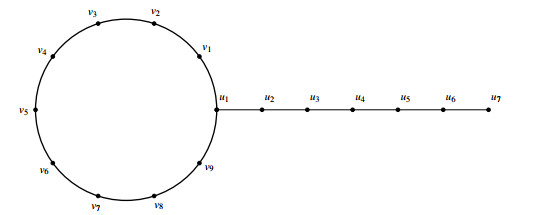
In this section, we will compute the fault-tolerant edge metric dimension of family of tadpole graphs Gln. The family Gln have V(Gln)={v1,v2,…,vn,u1,u2,…,ul} and E(Gln)={vivi+1:1≤i≤n−1}∪{usus+1,:1≤s≤l−1}∪{vnu1,u1v1}. The graph Gln for n=9 and l=7 is shown in Figure 4. The following theorem tells us the edge metric dimension of Gln.
Theorem 4.1. [29] For all n≥2, l≥3, edim(Gln)=2.
Now, we will compute the fault-tolerant edge metric dimension of Gln.
Theorem 4.2. For all n≥2, l≥3, fedim(Gln)=3.
Proof. In order to compute fault-tolerant edge metric dimension of Gln, we have the following cases.
Case (i). n is odd. Let ˊWE={v1,vn,um} ⊂V(Gln), we have to show that ˊWE is a fault-tolerant edge metric generator of Gln. For this, we give representations of each edge of Gln.
r(uiui+1|ˊWE)=(i,i,m−i−1) where 1≤i≤m−1,
r(vnu1|ˊWE)= (1,0,m−1) and r(u1v1|ˊWE)= (0,1,m−1).
Case (ii). n is even. Let ˊWE={v1,vn,um} ⊂V(Gln), we have to show that ˊWE is a fault-tolerant edge metric generator of Gln. For this, we give representations of each edge of Gln.
r(uiui+1|ˊWE)=(i,i,m−i−1) where 1≤i≤m−1,
r(vnu1|ˊWE)= (1,0,m−1) and r(u1v1|ˊWE)= (0,1,m−1).
We see that there are no two tuples having the same representations. This shows that fault-tolerant edge metric dimension of Gln is less than or equal to 3 and now we try to show that fault-tolerant edge metric dimension of Gln is greater than or equal to 3. Since by Lemma 1.4, Gln is not a path so fault-tolerant edge metric dimension of Gln is greater than or equal to 3. Hence fault-tolerant edge metric dimension of Gln is equal to 3.
5.
Fault-tolerant edge metric dimension of family of kayak paddle graphs Gln,m
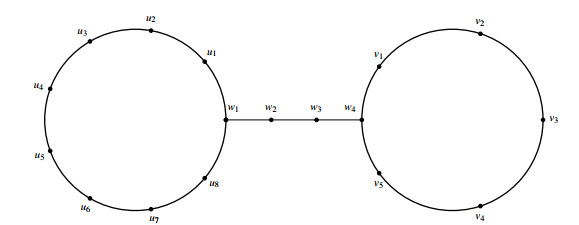
In this section, we will compute the edge metric dimension of family of kayak paddle graphs Gln,m. The family Gln,m have V(Gln,m)={u1,u2,…,um,v1,v2,…,vn,w1,w2,…,wl} and E(Gln,m)={vivi+1:1≤i≤n−1}∪{wjwj+1:1≤j≤l−1}∪{usus+1:1≤s≤m−1}∪{vnw1,w1v1,wlu1,umwl}. The family Gln,m for n=8, m=5 and l=4 is shown in Figure 5. The following theorem tells us the edge metric dimension of Gln,m.
Theorem 5.1. [29] For every n≥2, m≥2 and l≥4, edim(Gln,m)=2.
Now, we will compute the fault-tolerant edge metric dimension of Gln,m.
Theorem 5.2. For n≥2, m≥2 and l≥4, fedim(Gln,m)=4.
Proof. In order to compute fault-tolerant edge metric dimension of Gln,m, we have the following cases.
Case (i). n is odd and m is even. Let ˊWE={v1,v2,u1,u2} ⊂V(Gln,m), we have to show that ˊWE is a fault-tolerant edge metric generator of G_{n, m}^l . For this, we give representations of each edge of G_{n, m}^l .
r(w_i w_{i+1}|\acute{W}_E) = (i, i+1, l-i, l-i+1) where 1 \leq i \leq l-1,
r(v_{n}w_{1}|\acute{W}_E) = \ (1, 2, l, l+1) , r(w_{1}v_{1}|\acute{W}_E) = \ (0, 1, l, l+1) , r(w_{l}u_{1}|\acute{W}_E) = \ (l, l+1, 0, 1) and r(u_{m}w_{l}|\acute{W}_E) = \ (l, l+1, 1, 2) .
Case (ii). Both n and m are even. Let \acute{W}_E = \{v_1, v_2, u_1, u_2 \} \ \subset V(G_{n, m}^l) , we have to show that \acute{W}_E is a fault-tolerant edge metric generator of G_{n, m}^l . For this, we give representations of each edge of G_{n, m}^l .
r(w_i w_{i+1}|\acute{W}_E) = (i, i+1, l-i, l-i+1) where 1 \leq i \leq l-1,
r(v_{n}w_{1}|\acute{W}_E) = \ (1, 2, l, l+1) , r(w_{1}v_{1}|\acute{W}_E) = \ (0, 1, l, l+1) , r(w_{l}u_{1}|\acute{W}_E) = \ (l, l+1, 0, 1) and r(u_{m}w_{l}|\acute{W}_E) = \ (l, l+1, 1, 2) .
Case (iii). Both n and m are odd. Let \acute{W}_E = \{v_1, v_2, u_1, u_2 \} \ \subset V(G_{n, m}^l) , we have to show that \acute{W}_E is a fault-tolerant edge metric generator of G_{n, m}^l . For this, we give representations of each edge of G_{n, m}^l .
r(w_i w_{i+1}|\acute{W}_E) = (i, i+1, l-i, l-i+1) where 1 \leq i \leq l-1,
r(v_{n}w_{1}|\acute{W}_E) = \ (1, 2, l, l+1) , r(w_{1}v_{1}|\acute{W}_E) = \ (0, 1, l, l+1) , r(w_{l}u_{1}|\acute{W}_E) = \ (l, l+1, 0, 1) and r(u_{m}w_{l}|\acute{W}_E) = \ (l, l+1, 1, 2) .
We see that there are no two tuples having the same representations. This shows that fault-tolerant edge metric dimension of G_{n, m}^l is less than or equal to 4 and now we try to show that fault-tolerant edge metric dimension of G_{n, m}^l is grater than or equal to 4 .
For this purpose, we have to show that there is no fault-tolerant edge metric generator having cardinality 3 , we suppose on contrary that fault-tolerant edge metric dimension of G_{n, m}^l is 3 and let \acute{W}_E = \{v_i, v_j, v_k \} . Then the Table 1 shows all order pairs of edges (e, f) for which r(e|\acute{W}_E) = r(f|\acute{W}_E) .
In all possibilities, we conclude that there is no fault-tolerant edge metric generator of 3 vertices. Hence fault-tolerant edge metric dimension of G_{n, m}^l is 4 .
6.
Conclusions
In this paper, we have computed the fault-tolerant edge metric dimension of some planar graphs path, cycle, complete, cycle with chord, tadpole and kayak paddle. It is observed that the fault-tolerant edge metric dimension of these graphs is constant and does not depend on the number of vertices. It is concluded that the fault-tolerant edge metric dimension of families of path graphs is two, the fault-tolerant edge metric dimension of families of cycle graphs, cycle with chord graphs, tadpole graphs is three and the fault-tolerant edge metric dimension of kayak paddle graphs is found to be four. Here we end with an open problem.
Open Problem
Characterize all families of graphs for which difference of fault-tolerant metric dimension and edge metric dimension is one.
Acknowledgment
Authors are thankful to the reviewers for their valuable comments.
Conflict of interest
The authors declare that no competing interests exist.










 DownLoad:
DownLoad: