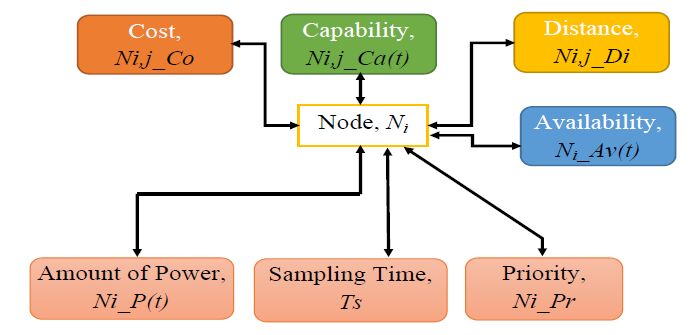
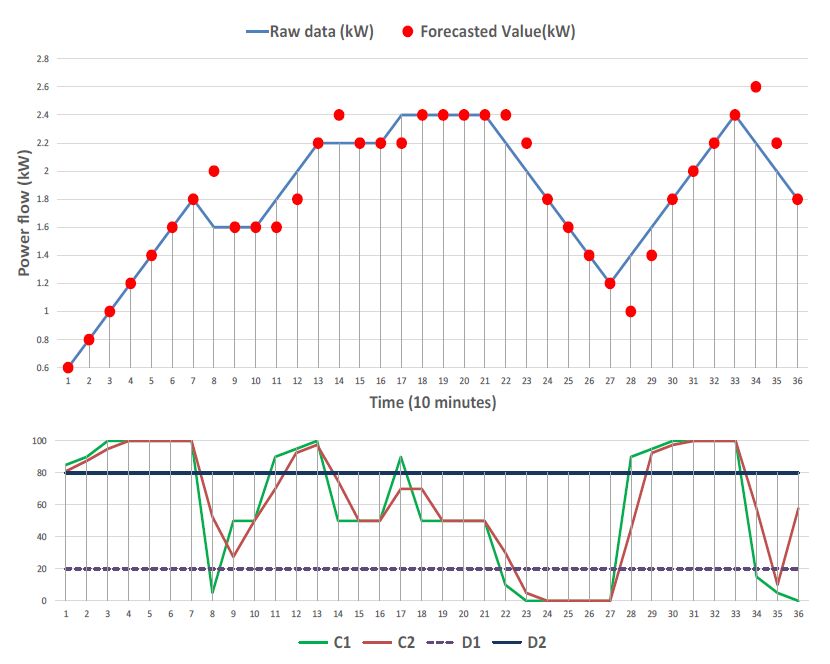
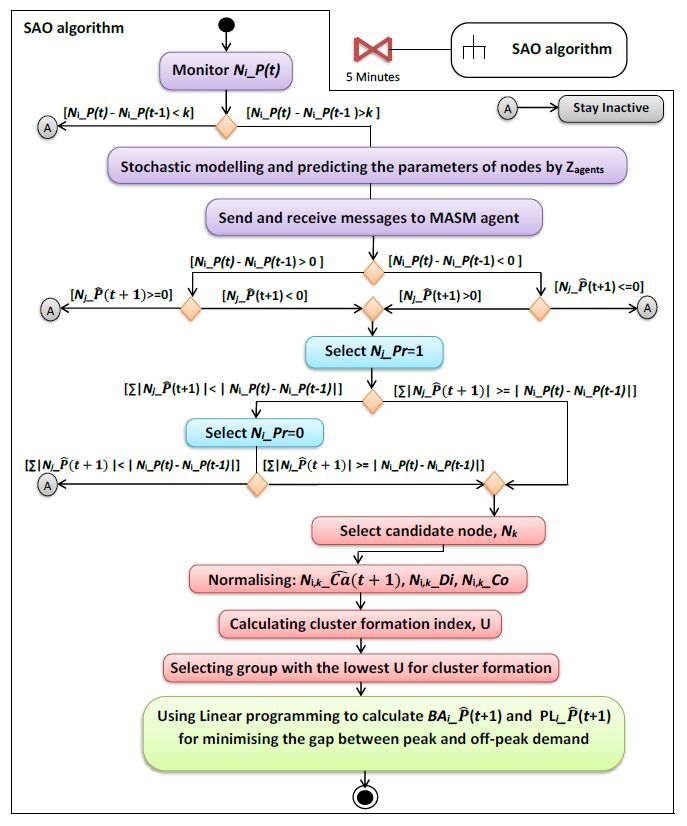
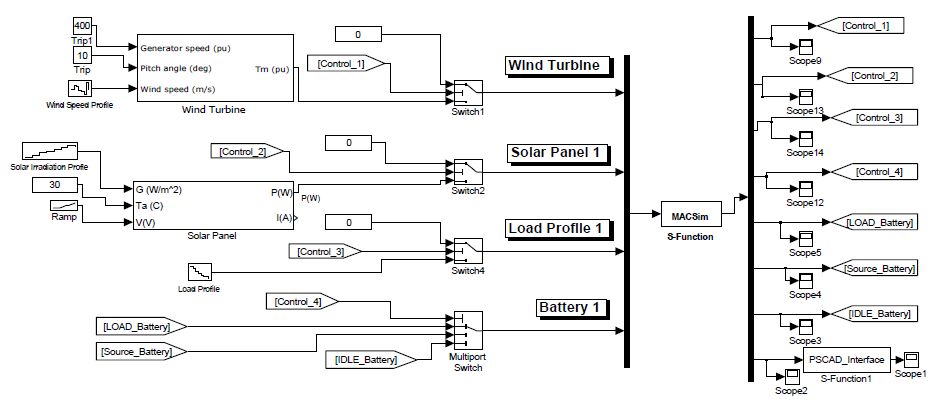
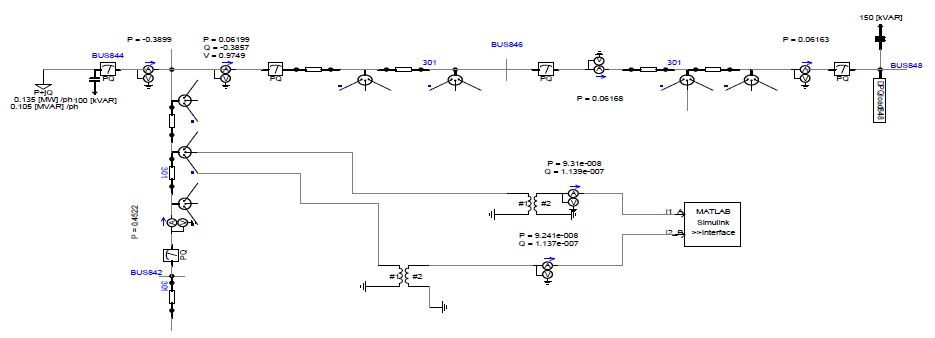
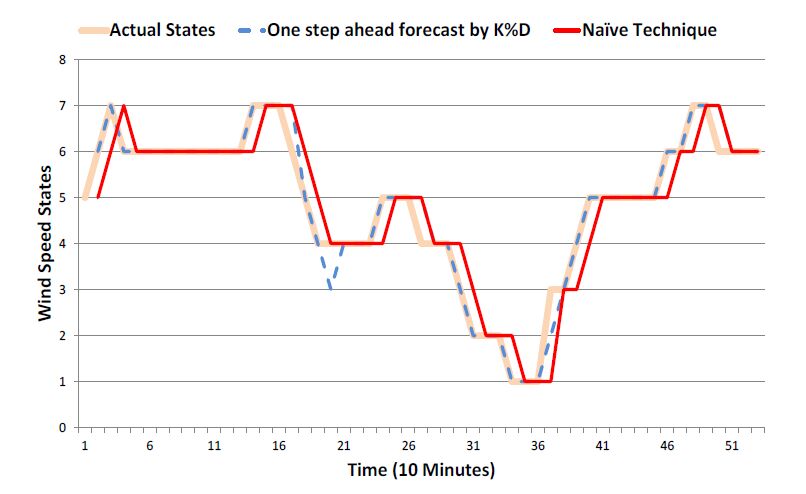
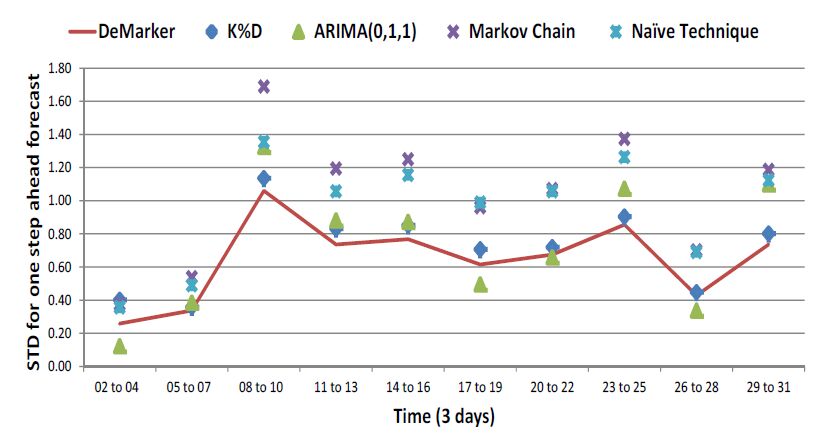
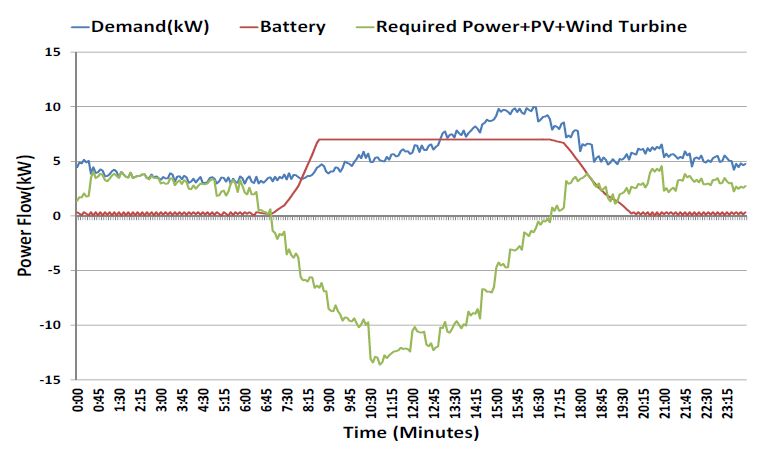
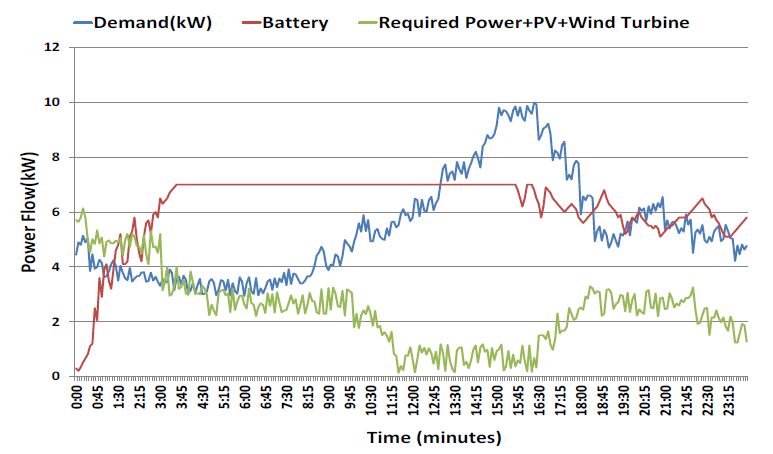
In the current research, a smart grid is considered as a network of distributed interacting nodes represented by renewable energy sources, storage and loads. The source nodes become active or inactive in a stochastic manner due to the intermittent nature of natural resources such as wind and solar irradiance. Prediction and stochastic modelling of electrical energy flow is a critical task in such a network in order to achieve load levelling and/or peak shaving in order to minimise the fluctuation between off-peak and peak energy demand. An effective approach is proposed to model and administer the behaviour of source nodes in this grid through a scheduling strategy control algorithm using the historical data collected from the system. The stochastic model predicts future power consumption/injection to determine the power required for storage components. The stochastic models developed based on the Box-Jenkins method predict the most efficient state of the electrical energy flow between a distribution network and nodes and minimises the peak demand and off-peak consumption of acquiring electrical energy from the main grid. The performance of the models is validated against the autoregressive moving average (ARIMA) and the Markov chain models used in previous work. The results demonstrate that the proposed method outperforms both the ARIMA and the Markov chain model in terms of forecast accuracy. Results are presented, the strengths and limitations of the approach are discussed, and possible future work is described.
1.
Introduction
The chemostat refers to a laboratory device used for the growth of micro-organisms in a culture environment [1,2], that has been regarded as an idealization of the nature to study microbial ecosystems in stationary stage [3]. It turned out to be an important investigation field due to a large number of applications, especially in waste water treatment [4,5] but also in ecological and environmental sciences (see [6,7,8,9,10]).
It is worth mentioning that the chemostat has been subject to a large number of scientific publications and books, not only in biology and ecology but also in mathematics. Indeed there exists a specific research area about the so-called "theory of the chemostat" [11,12] where many researchers have been involved in the last years. This interest has been strengthened by the fact that the chemostat device can be mathematically modeled in a simple way which reproduces quite faithfully real bio-processes.
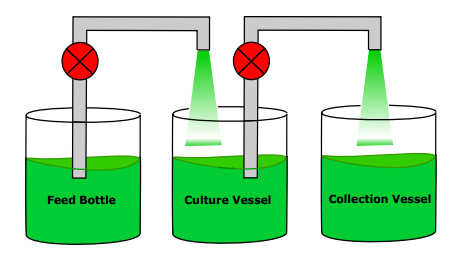
Let us recall quickly in what consists the original chemostat device. It is composed of three tanks, the feed bottle, the culture vessel and the collection vessel, which are interconnected by pumps (see Figure 1). The substrate is stored in the feed bottle and provided with a given flow rate to the culture vessel, where interactions between nutrient and microbial biomass take place. The media from the culture vessel is also withdrawn towards the collection vessel with the same flow rate, to keep the volume in the culture vessel constant.
The mathematical model of the chemostat is given by the following dynamical system
where $ s = s(t) $ and $ x = x(t) $ denote the concentration of substrate and species, respectively, $ s_{in} $ is the input concentration of nutrient, $ D $ is the removal rate (also called input flow rate), and $ \mu(\cdot) $ is the specific growth function describing the kinetics of the nutrient consumption by the bacterial species. Here, we assume that the yield coefficient of the conversion of the substrate into biomass is equal to $ 1 $ (that is always possible to impose by a change of the unit of the biomass concentration). More specifically, we consider in the present work the Haldane growth function
where $ k_s $ is the affinity constant and $ k_i $ a parameter modeling the growth inhibition under large concentrations of substrate. Since it will be useful later, let us define the number
Many works have been dedicated to this classical deterministic model of the chemostat (see for instance [11,12]) but most of time the removal rate $ D $ is kept constant, although it is well-known that in practice it is frequently subject to disturbances (see for instance [13] where some chronicles of time varying removal rates are depicted).
Motivated by this fact, it has been proposed to model the perturbations on the input flow rate in the chemostat model (1.1)–(1.2) by $ D+\Phi(z^*(\theta_t\omega)) $, where $ z^*(\theta_t\omega) $ denotes the Ornstein-Uhlenbeck process (introduced in more detail in Section 2) and $ \Phi $ is a bounded function defined as
where $ d > 0 $ (see, for instance, [14,15] for other possible functions). Indeed, any odd function $ \Phi $ which is increasing and such that $ lim_{z\to +\infty}\Phi(z) = d $ can be considered.
In this way, once practitioners provide an interval $ [D^l, D^r]\subset{\mathbb{R}} $, $ 0 < D^l < D < D^r < \infty $, (typically obtained from observations) we can define $ d = D^r-D = D-D^l $ and then the perturbed input flow is bounded for every time and any realization of the noise, i.e.,
Then, the random chemostat model becomes
One may wonder the reason why we consider this way of modeling bounded random fluctuations to perturb the input flow $ D $ in the model (1.1)–(1.2), instead of considering other stochastic process, such as for instance the well-known standard Wiener process. Indeed, this way has been typically used to model real perturbations and provides several advantages from both mathematical and biological points of view, see for instance [15].
On the one hand, this way of modeling noise fits in a loyal way the bounded variations of the input flow rate observed in real life. On the contrary, the Wiener process is unbounded with probability one which leads to arbitrary large (possibly negative) values of the corresponding perturbed input flow rate, which is not realistic at all from the biological point of view. We refer readers to [15,16] where the authors explain the relevant drawbacks found when perturbing the input flow in the classical deterministic chemostat (1.1)–(1.2) with a Wiener process (where $ \mu $ is a Monod growth function).
Moreover, the approach proposed in this paper allows to prove the persistence of the bacterial species (under some conditions on the growth function), as it is observed by practitioners on very long time periods despite variations of the input flow rate. This is not the case when considering the Wiener process where persistence cannot be ensured (see [16] and [17] where the Wiener process is used to model disturbances on the input flow and environmental perturbations in the classical deterministic chemostat).
In industrial setup, large concentrations of the input substrate $ s_{in} $ can be observed and it is also well-known that bacterial species may suffer from growth inhibition under very large concentrations $ s $. The non-monotonic growth function (1.3) precisely models this fact (see [18]). Differently to the classical case, where the growth function $ \mu $ is assumed to be increasing (as this is the case for the Monod function), the dynamics of the deterministic chemostat model with such non-monotonic growth function may exhibit a bi-stability for certain values of the dilution rate $ D $ (see for instance [11]). Depending on the initial condition, the state of the system converges asymptotically to the wash-out of the biomass (which is not a desirable state) or to a positive equilibrium. This kind of instability is observed in practice and present an issue in industrial applications because it requires a good monitoring of the system to detect if the state belongs the attraction basin of the wash-out equilibrium [19,20,21,22]. Most of the time, practitioners prefer to size the process to avoid such a behavior, i.e. such that the system admits an unique globally stable equilibrium (see also [23,24]). This mathematically amounts to have the following condition
(this result is recalled later). The purpose of the present work is to study the behavior of the random dynamics when the constant removal rate is replaced by $ D+\Phi(z^*(\theta_t\omega)) $ where $ D $ satisfies condition (1.9).
The realizations of this variable may satisfy or not condition (1.9) at some times $ t $. If not, one may wonder if this could lead the biomass to extinction. This question is of primer importance for the practitioners for the good health of the bio-process. In other words, for a nominal removal rate that satisfies condition (1.9), is the persistence of the biomass always guaranteed, even when the realizations of the noise provide effective values of the removal rate that do not satisfy this condition? Precise definitions of persistence in the framework of the chemostat will be given later.
Let us underline that stochastic modeling of the chemostat has received a great attention in the literature, considering different kinds of demographic noise [25,26,27,28,29,30], but few works have dealt with noise on the input, and much less in the case of considering Haldane consumption function, whereas this is quite natural for an open system as the chemostat, which is often the main source of fluctuations.
The paper is organized in the following way: in Section 2 we provide preliminaries and classical results about the deterministic chemostat model (1.1)–(1.2). In Section 3 we study the properties of the solutions of the random chemostat model with Haldane consumption kinetics (1.7)–(1.8). Then, in Section 4 we give conditions to ensure both uniform weak and strong persistence of the species. In Section 5, several simulations are presented to support the theoretical study. Finally, we present some conclusions in Section 6.
2.
Preliminaries
In this section we recall briefly some results that are useful in this paper. For the sake of clarity, we split this preliminary section in three different parts: the first one concerns classical results of the deterministic chemostat model (1.1)–(1.2), the second one is about the Ornstein-Uhlenbeck process and the third one recalls the definitions of persistence.
2.1. The deterministic chemostat model
The next proposition recalls the classical results about the chemostat model (1.1)–(1.2) when $ \mu $ is a non-monotonic function. We refer readers to [11,12] for proofs and more details.
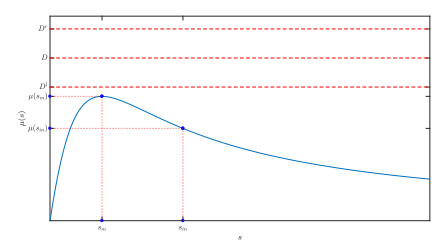
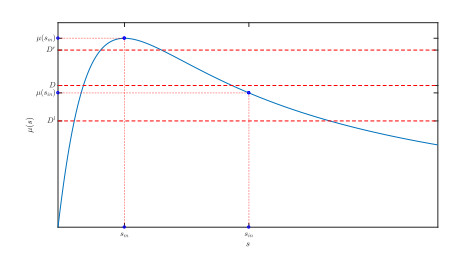
Proposition 2.1. Assume that there exists $ \hat s \in (0, s_{in}) $ such that the function $ \mu $ is increasing on $ (0, \hat s) $ and decreasing on $ (\hat s, s_{in}) $. Define the break-even concentrations $ \lambda^-(D) $, $ \lambda^+(D) $ as follows
1. If $ D > \mu(\hat s) $, the system (1.1)–(1.2) possesses a unique equilibrium $ E^0: = (0, s_{in}) $, which is globally asymptotically stable on $ {\mathbb{R}}_+^2 $.
2. If $ D < \mu(s_{in}) $, the system (1.1)–(1.2) admits a unique positive equilibrium $ E^-: = (s_{in}-\lambda^-(D), \lambda^-(D)) $ which is globally asymptotically stable on $ {\mathbb{R}}_+^\star\times{\mathbb{R}}_+ $.
3. If $ D \in [\mu(s_{in}), \mu(\hat s)] $, the system (1.1)–(1.2) presents a bi-stability between $ E^- $ and $ E^0 $. From any initial condition in $ {\mathbb{R}}_+^\star\times{\mathbb{R}}_+ $ excepted on a set of null measure, the solution converges asymptotically to $ E^- $ or $ E^0 $.
Remark 1. In practice, only the second case is desirable because it guarantees that in any situation the wash-out of the biomass is avoided.
Remark 2. For the Haldane expression (1.3), one has explicit expressions of the functions $ \lambda^{\pm} $
Let us recall that the concept of break-even concentrations has been revisited in the context of stochastic models of the chemostat [31,32] but we will not need it here. We keep the classical deterministic definition.
In the rest of the paper, we shall consider that we are in conditions of Proposition 2.1, that is $ \mu $ non-monotonic on the interval $ [0, s_{in}] $ (otherwise the analysis is similar to monotonic growth function and cannot present bi-stability). Throughout the paper we shall consider the following hypothesis
Assumption 1. There exists $ s_m\in(0, s_{in}) $ such that the function $ \mu $ is increasing on $ (0, s_m) $ and decreasing on $ (s_m, s_{in}) $.
2.2. The Ornstein-Uhlenbeck process
We present here briefly the Ornstein-Uhlenbeck (OU) process. For more details we refer readers to [13,33,34].
The Ornstein-Uhlenbeck (OU) process is a stationary mean-reverting Gaussian stochastic process defined as
where $ \omega $ denotes a standard Wiener process in a probability space $ (\Omega, \mathcal{F}, \mathbb{P}) $, $ \beta $ is the mean reversion constant representing the strength with which the process is attracted by the mean, $ \nu > 0 $ is the volatility constant describing the variation or the size of the noise and $ \theta_t $ denotes the usual Wiener shift flow given by
We note that the OU process (2.1) can be obtained as the stationary solution of the Langevin equation
Typically, the OU process (2.1) can model the position of a particle by taking into account its friction in a fluid (which is the main difference with the typical standard Wiener process). Indeed, it can be considered as a generalization of the standard Wiener process and provides a link between the standard Wiener process ($ \beta = 0 $, $ \nu = 1 $) and no noise at all ($ \beta = 1 $, $ \nu = 0 $).
From now on we consider $ \beta $ and $ \nu $ fixed and $ z^*(\theta_t\omega) $ the OU process defined above.
We recall in the next proposition some of its properties.
Proposition 2.2 (See [35,36]). There exists a $ \theta _t $-invariant set $ \widetilde{\Omega }\in \mathcal{F} $ of $ \Omega $ of full measure such that for $ \omega \in \widetilde{\Omega} $ and $ \beta, \nu > 0 $, we have
(i) the random variable $ |z^*(\omega)| $ is tempered with respect to $ \{\theta_t\}_{t\in{\mathbb{R}}} $, i.e., for a.e. $ \omega\in\widetilde{\Omega} $,
(ii) this mapping is a stationary solution of (2.2) with continuous trajectories
(iii) for any $ \omega \in \tilde \Omega $ one has:
2.3. Persistence in the chemostat
We recall here the definitions of (uniform) persistence (see for instance [37]) that we consider in the present work.
Definition 2.1. The dynamics of (1.7)–(1.8) is strongly persistent if there exists $ \varepsilon > 0 $ such that for any initial condition $ (s(0), x(0)) $ in $ {\mathbb{R}}_+\times{\mathbb{R}}_+^\star $ and any realization of the $ D+\Phi(z^*(\theta_{(\cdot)} \omega)) $, the solution verifies
Definition 2.2. The dynamics of (1.7)–(1.8) is weakly persistent if there exists $ \varepsilon > 0 $ such that for any initial condition $ (s(0), x(0)) $ in $ {\mathbb{R}}_+\times{\mathbb{R}}_+^\star $ and any realization of $ D+\Phi(z^*(\theta_{(\cdot)} \omega)) $, the solution verifies
3.
Properties of the solutions of the random dynamics
In this section we study the random chemostat model (1.7)–(1.8) presented in the introduction. We prove the existence and uniqueness of a global positive solution and provide results about the existence of absorbing and attracting sets which, in addition, are deterministic (i.e. that do not depend on the realization of the noise). In addition, we derive first conditions under which extinction of species cannot be avoided.
In the sequel, we denote $ \mathcal{X}: = \{(s, x)\in{\mathbb{R}}^2\, :\, s, x\geq 0\} $ for the positive cone.
Theorem 3.1. For any initial condition $ u(0)\in\mathcal{X} $, system (1.7)–(1.8) possesses a unique global solution $ u(t; 0, \omega, u(0)) = (s(t; 0, \omega, u(0)), x(t; 0, \omega, u(0)))\in \mathcal{C}^1([0, +\infty); \mathcal{X}) $. In addition, it remains in $ \mathcal{X} $ for every $ t > 0 $.
Proof. Let us first write system (1.7)–(1.8) as
where
and
$ F(\cdot, \theta_t\omega)\in\mathcal{C}^1(\mathcal{X}\times[0, +\infty); \mathcal{X}) $ whence $ F $ is locally Lipschitz respect to $ u \in\mathcal{X} $. Therefore, for each realization of the noise, $ du/dt = L(\theta_t\omega)u+F(u, \theta_t\omega) $ is an non-autonomous differential equation with a right member Lipschitz with respect to $ u $ and continuous with respect to $ t $ (recall that $ z^*(\theta_t\omega) $ is continuous respect to $ t $ and $ \Phi $ is also continuous). Therefore, the solution of the Cauchy problem admits an unique local solution of system (1.7)–(1.8) from the theory of ordinary differential equations.
Let us first show that both $ x $ and $ s $ remain in $ \mathcal{X} $ for any $ u_0\in\mathcal{X} $. To this end, we notice first that $ x(t) = 0 $ solves (1.7). By uniqueness of the Cauchy problem, we deduce that any other solution is such that $ x(t) \ne 0 $ for any $ t $. Notice also that one has, thanks to (1.6),
which proves that the axis $ s = 0 $ is repulsive in $ \mathcal{X} $. This demonstrates the positiveness of the solution of system (1.7)–(1.8).
Now we prove that both the substrate and the microorganisms concentrations remain bounded for every time. To this end, define $ v(t): = s(t)+x(t) $. Then the variable $ v $ is solution of the following differential equation
and, thanks to (1.6),
By comparison of solutions of scalar ODEs (see [38]) we obtain
Then, $ v $ is forward bounded and since $ v = s+x\geq 0 $, we deduce that both the solution $ s $ and $ x $ are also bounded for positive time. The unique solution of system (1.7)–(1.8) is thus defined for any $ t\geq 0 $.
Now, we prove the existence of deterministic attracting and absorbing sets for the solutions of the random chemostat model (1.7)–(1.8).
Theorem 3.2. The system (1.7)–(1.8) possesses a deterministic (forward) attracting set
Proof. Define the variable $ q(t): = s(t)-s_{in}+x(t) $. Then $ q $ satisfies the following differential equation
whose solution is given by
From (1.6), we have
and taking limit when $ t $ goes to infinity we have
which means that, for any $ \varepsilon > 0 $, there exists $ T(\omega, \varepsilon) > 0 $ such that
This proves that
is a (forward) deterministic absorbing set for system (1.7)–(1.8). As $ \varepsilon > 0 $ is arbitrary, the proof is done.
Remark 3. Let us underline that the attracting set (3.1) obtained in Theorem 3.2 does not depend on the event $ \omega\in\Omega $. This is another particularity that we obtain when considering this way of modeling random bounded realizations.
Our aim now is to provide first conditions on the parameters of system (1.7)–(1.8) under which extinction of the species occurs.
Theorem 3.3. Assume that the inequality
is fulfilled, where $ s_m $ is defined in (1.4). Then, the singleton
is a (forward) attracting set.
Proof.
From the equation describing the dynamics of the species (1.8) and (1.6) one has
and by comparison of solutions of scalar ordinary differential equations [38], we have
Taking limit when $ t $ goes to infinity in (3.4), we obtain from (3.3) and Proposition 2.2 (ⅲ),
4.
Conditions for persistence
In this section our aim is to provide conditions to ensure persistence of the species in the sense defined in Section 2.3.
We shall distinguish in the following weak and strong persistence, as defined for instance in [37]. Before stating a result concerning the weak persistence of species, let us first provide a property linked to the choice of the function $ \Phi $.
Proposition 4.1. Let be $ \Phi(z) = \frac{2d}{\pi}\arctan(z) $ defined as in (1.5). Then
Proof. Since $ \Phi(z) = \frac{2d}{\pi}\arctan(z) $, then we have
whence $ \Phi(z^*(\cdot))\in L^1(\Omega, \mathcal{F}, \mathbb{P}) $. Then, since $ \mathbb{P} $ is invariant by $ \theta $ (see [34,35]), from the Birkhoff ergodic theorem it yields that
Hence, it is enough to show that $ \mathbb{E}[\Phi(z^*(\omega))] = 0 $. In fact, we have
where $ f_{\text{OU}} $ denotes the density function of the random variable $ z^*(\cdot) $, which is an even function since it is gaussian, and $ \Phi $ is an odd function.
Remark 4. From Proposition 4.1 we notice that we could model random perturbations as in this paper, i.e., by means of $ \Phi(z^*(\theta_t\omega)) $, and the ergodic property (4.1) remains true as long as $ \Phi $ is an odd measurable function.
Theorem 4.1. Assume that the inequality
is fulfilled. Then, the random chemostat model (1.7)–(1.8) is weakly persistent, that is there exits $ \varepsilon > 0 $ such that for any initial condition $ x(0)\in\mathcal{X} $, any realization satisfies
Proof. Let $ \varepsilon > 0 $ be such that $ \mu(s) > D $ for all $ s\in[s_{in}-\varepsilon, s_{in}+\varepsilon] $ and define
From Theorem 3.2, we know that $ s(t; 0, \omega, s(0)) $ converges asymptotically to the set $ [0, s_{in}] $. Therefore, there exists $ T(\omega, \varepsilon) > 0 $ such that $ s(t; 0, \omega, s(0)) < s_{in}+\varepsilon $ for any $ t > T(\omega, \varepsilon) $.
Consider now, for $ t > T(\omega, \varepsilon) $, the sets
and the functions in $ [0, 1] $
Then, from (1.8), one can write the following inequality
and by integration between $ T(\omega, \varepsilon) $ and $ t > T(\omega, \varepsilon) $ one obtain
Assume that one has
From Proposition 4.1, one has
and then (4.3) gives
which is a contradiction since $ x $ is bounded. We deduce thus that the sets $ U(\cdot) $ are necessarily such that
that is
which shows that one has
or equivalently
since $ s(t)+x(t) $ converges to $ s_{in} $ for any realization (see the proof of Theorem 3.2).
Remark 5. Theorem 4.1 proves the weak (uniform) persistence of species as long as $ D < \mu(s_{in}) $ is fulfilled, the same condition that guarantees the persistence in the deterministic case (see Proposition 2.1). However, let us underline that we do not impose the upper bound $ D^r $ of the variations of the removal rate to fulfill this inequality. This means that one could have realizations of the disturbances such that the effective value of the removal rate is above $ \mu(s_{in}) $ on large periods of time making the species to be arbitrary closed to the extinction but it will always persist.
In the next result we consider a stronger condition on the upper bound $ D^r $ of the removal rate which ensures the strong persistence of the species.
Theorem 4.2. Assume that the inequality
is fulfilled. Then, the random chemostat model (1.7)–(1.8) is strongly persistent and the set
is (forward) attracting, where the function $ \lambda^- $ is defined in Proposition 2.1.
Proof. Take $ \varepsilon > 0 $ such that $ \mu(s) > D^r $ for any $ s\in[s_{in}-\varepsilon, s_{in}+\varepsilon] $ and posit
From now on, we will $ s(t) $, $ x(t) $ and $ q(t) $ instead of $ s(t; 0, \omega, s(0)) $, $ x(t; 0, \omega, x(0)) $ and $ q(t; 0, \omega, q(0)) $ to make the readability easier even though we recall that every state variable depends on the noise.
From Theorem 3.2, we know that the variable $ q(t) = s(t)-s_{in}+x(t) $ converges asymptotically to zero for any realization, and thus any solution $ s(t) $ of the random model (1.7)–(1.8) converges to the set $ [0, s_{in}] $. Consequently, there exists $ T(\omega, \varepsilon) > 0 $ such that
where
If $ s(t)\in[s_{in}-\varepsilon, s_{in}+\varepsilon] $ for any $ t > T(\omega, \varepsilon) $, then one has, from (1.8), $ \dot x(t) > \eta x(t) $ for any $ t > T(\omega, \varepsilon) $, which implies that $ x $ is unbounded, thus a contradiction. We deduce that there exists a finite time $ \bar{T}(\omega)\geq T(\omega, \varepsilon) $ such that $ s(\bar{T}(\omega))\leq s_{in}-\varepsilon/2 $. On another hand, from (1.7), $ s(t) $ can be written as the solution of the non-autonomous dynamics
Note that one has
and then
(from the definition of $ \kappa $). We deduce that the set $ [0, s_{in}-\varepsilon/2] $ is forward invariant for the semi-flow $ \{\dot\sigma = F(t, \sigma), \; t > T(\omega, \varepsilon)\} $. Therefore, one has
Then, once identified $ \sigma $ with $ s $, from (4.5)
and from the comparison of solutions of scalar ordinary differential equations [38], one has the inequality $ s(t) \leq s^+(t) $ for any $ t > \bar{T}(\omega) $, where $ s^+(t) $ is solution of the Cauchy problem
Note that the solution $ s^+(t) $ belongs to the interval $ [0, s_{in}] $ for any $ t\geq \bar{T}(\omega) $ (and is thus bounded) and that its dynamics is asymptotic autonomous with limiting dynamics
Under assumption $ D^r < \mu(s_{in}) $, one has necessarily $ \lambda^-(D^r) < s_{in} $ and the property
is fulfilled. One finally obtains that any solution of (4.6) in $ [0, s_{in}] $ is such that $ s^{†}(t)\to \lambda^-(D^r) $ when $ t \to +\infty $. From the theory of asymptotically autonomous dynamical systems [39], one concludes that $ s^+(t) $ converges also to $ \lambda^-(D^r) $ when $ t \to +\infty $, which proves that one has
or equivalently
since $ s(t)+x(t) $ converges to $ s_{in} $ for any realization. This demonstrates the strong persistence of the random dynamics (1.7)–(1.8) with the explicit lower bound $ s_{in} - \lambda^-(D^r) $.
Now we consider the last situation when $ \mu(s_{in}) < D < \mu(s_m) $ which corresponds to the bi-stability in the deterministic case. In the random framework, one cannot guarantee persistence nor wash-out of the biomass. As we shall see later on simulations, the asymptotic behavior of the solutions depends on the initial condition and the realization of the noise. However we show that an upper bound on the biomass can be provided.
Theorem 4.3. Assume $ x(0) > 0 $. Then, the upper bound
for any solution of the random dynamics (1.7)–(1.8) as long as $ D^l < \mu(s_m) $.
Proof. Let us remark that in this proof we will write $ x(t) $, $ s(t) $ and $ q(t) $, or simply $ x $, $ s $ and $ q $, instead of $ x(t; 0, \omega, x(0)) $, $ s(t; 0, \omega, s(0)) $ and $ q(t; 0, \omega, q(0)) $ for the sake of simplicity.
Consider $ x(0) > 0 $. Then, from (1.8) one has
where $ q = s_{in}-x-s $.
We know that $ \lim_{t\rightarrow+\infty}q(t) = 0 $ then, for every $ \varepsilon > 0 $ there exists $ T(\omega, \varepsilon) > 0 $ such that $ |q(t)| < \varepsilon $ for every $ t > T(\omega, \varepsilon) $. Thus $ x(t) < s_{in}+\varepsilon $ for every $ t > T(\omega, \varepsilon) $.
Moreover, for all $ x\in(s_{in}-\lambda^-(D^l)+\varepsilon, s_{in}+\varepsilon) $, one has $ s_{in}-x-q\in(-q-\varepsilon, \lambda^-(D^l)-q-\varepsilon) $. In fact, since $ s_{in}-x-q = s\geq 0 $ (see Theorem 3.1), then we have $ s_{in}-x-q\in(0, \lambda^-(D^l)-q-\varepsilon)\subset(0, \lambda^-(D^l)) $ whence $ F(t, x) < 0 $ since $ \mu(0, \lambda^-(D^l)) < D^l $ and $ D+\Phi(z^*(\theta_t\omega))\geq D^l $.
Thus,
for every $ \varepsilon > 0 $.
5.
Numerical simulations
In this section we present several numerical simulations to support our theoretical results in three different cases: extinction, strong persistence and weak persistence of species.
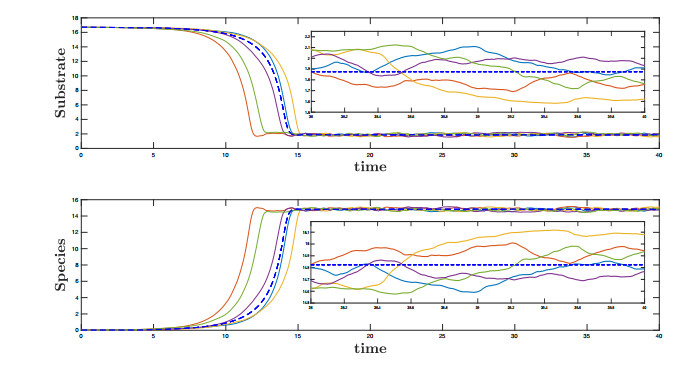
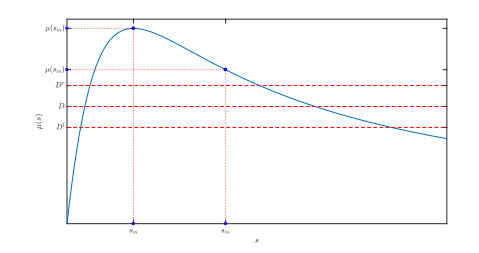
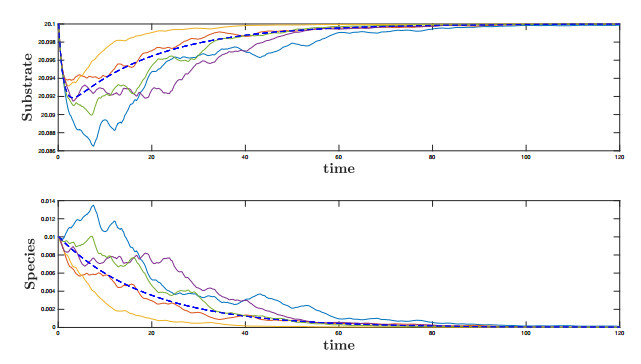
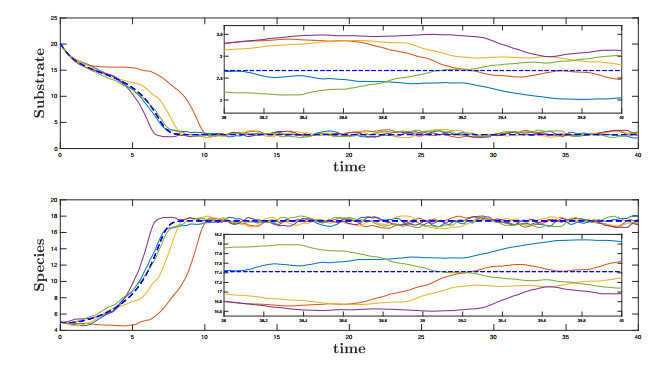
Two different figures are presented in each case. The first figure (with two panels) concerns the dynamics of the substrate (top) and the species (bottom) in the random chemostat model (1.7)–(1.8) for different realizations of the noise (in colored continuous lines) along with the case without noise i.e. the deterministic chemostat model (in blue dashed lines). In addition, in each panel we display a little box with a zoom to illustrate better the dynamics around the attracting set. The second figure offers information about the consumption function of the consumer species and those parameters involved in conditions to have extinction, weak persistence and strong persistence of species.
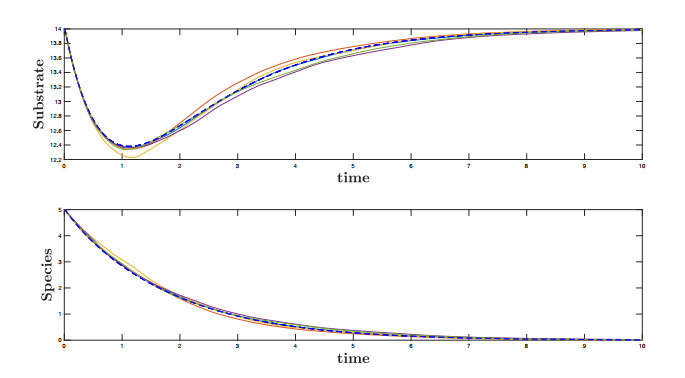
We first present the case of extinction in Figure 2. We consider $ s(0) = 14 $, $ x(0) = 5 $ as initial conditions and set $ s_{in} = 14 $, $ \mu_0 = 4 $, $ k_s = 7.5 $, $ k_i = 4 $, $ D = 1.4 $ and the interval given by practitioners from observations is $ [D^l, D^r] = [1.15, 1.65] $, then $ d = 0.25 $. In addition, $ \nu = 1 $ and $ \beta = 1 $. We can observe in Figure 3 that $ D^l > \mu(s_m) $ holds true and then, as proved in Theorem 3.3, the species extinguishes (the attracting set in this case is $ \{(0, s_{in})\} $).
This is indeed quite intuitive as condition (3.3) basically means that the nominal value $ D $ of the removal rate is too large large compared to the growth kinetics (recall that $ D^l > \mu(s_m) $ implies $ D > \mu(s_m) $), even though we start far away from the washout $ (s_{in}, 0) $.
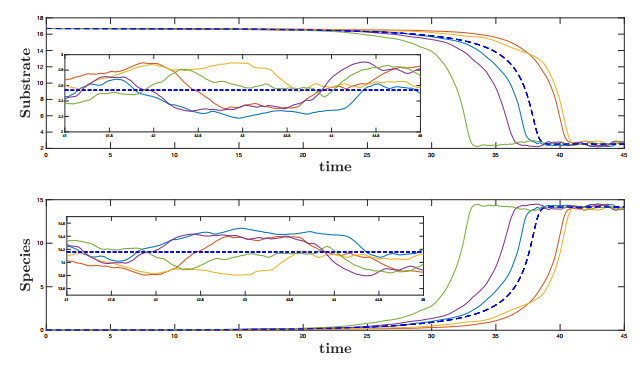
Now we present situations where weak and strong persistence is ensured. To compare, we start with the case of weak persistence by considering $ s(0) = 16.7 $, $ x(0) = 0.01 $ as initial conditions and set $ s_{in} = 16.7 $, $ \mu_0 = 7 $, $ k_s = 7 $, $ k_i = 7 $. In addition, $ \beta = 1 $ and $ \nu = 1 $. Once fixed these parameters, the removal rate $ D $ will be the set to allow conditions (4.4) and (4.2) be true or false.
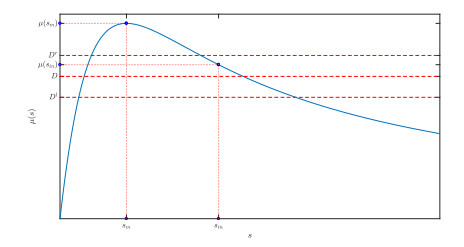
In Figure 4 we set $ D = 1.7 $ and the interval $ [D^l, D^r] = [1.45, 1.95] $ then $ d = 0.25 $. In this case $ D < \mu(s_{in}) $ is fulfilled (observe Figure 5) then we have weak persistence of species, see Theorem 4.1. Although we start very closed to the washout $ (s_{in}, 0) $, we observe persistence of species.
In Figure 6 we set $ D = 1.4 $ and the interval $ [D^l, D^r] = [1.15, 1.65] $ then $ d = 0.25 $. In this case $ D^r < \mu(s_{in}) $ holds true (see Figure 10) and then strong persistence of species is obtained from Theorem 4.1.
Moreover, we would like to notice that OU process proves again to be a powerful tool when modeling real (bounded) noises. In addition, it allows us to observe clearly the difference between weak and strong persistence.
Finally we present some numerical simulations to observe that both extinction and persistence can be obtained when $ D^l < \mu(s_{in}) < D $ is fulfilled, as in the deterministic case. However, the issue here depends also on the realization of the noise.
6.
Conclusion
We have considered the chemostat model (1.1)–(1.2) with Haldane consumption kinetics, under bounded perturbations on the input flow rate, motivated by real cases in industrial setup and biotechnology. To this end, we use a bounded saturated function of the Ornstein-Uhlenbeck process that allows us to ensure the noise to be bounded in realistic intervals.
We prove in Theorem 3.1 existence and uniqueness of global positive solution of the corresponding random chemostat (1.7)–(1.8) by means of standard results from the theory of ODEs and thanks to properties of the Ornstein-Uhlenbeck process. Then, in Theorem 3.2 we establish the existence of an absorbing and attracting set which has the nice property to be deterministic, i.e. that does not depend on the realization of the noise.
We then focused on the long-time behavior of the random dynamics inside this attracting set. To this end, we first proved in Theorem 3.3 that extinction of species cannot be avoided as long as $ D^l > \mu(s_m) $ whatever is the input concentration $ s_{in} $. On the opposite, we proved in Theorem 4.1 the weakly uniform persistence of species when $ D < \mu(s_{in}) $, which means that species can be temporarily arbitrary closed to the extinction but still persist even when having random disturbances in the input flow. The condition $ D < \mu(s_{in}) $ ensures persistence in the deterministic case but the effective removal rate does not necessarily fulfill this condition depending on the realizations. Finally, we prove the strong persistence of the species in Theorem 4.2 under the stronger condition $ D^r < \mu(s_{in}) $. In this case, we provide an explicit lower bound for the asymptotic concentration of the species, a useful information for practitioners.
In addition, we support the theoretical results with several numerical simulations which depict the possible behaviors of the random dynamics. Moreover, this allows us to illustrate the difference between weak and strong persistence: once fixed every parameter we change the removal rate $ D $ to let conditions $ \mu(s_{in}) > D $ and $ \mu(s_{in}) > D^r $ be true or not. Condition to have weak persistence ($ \mu(s_{in}) > D $) does not involve the noise and then the random realizations of the species can fluctuate closed to zero and we still ensure persistence whereas condition to have strong persistence ($ \mu(s_{in}) > D^r $) only fulfills for realizations of the perturbed removal rate inside a small enough interval.
To conclude, we would like to stress that the Ornstein-Uhlenbeck process has proved once again to be relevant tool to model random disturbances in a biological framework. This stochastic process fits in a quite loyal way the bounded fluctuations that are observed in practice, and justify the (weak or strong) persistence of the biomass despite the possible realizations of noise, as also observed in practice.
Acknowledgments
This work has been partially supported by Proyecto de Excelencia P12-FQM-1492 from Junta de Andalucía, Project PGC2018-096540-B-I00 from Ministerio de Ciencia, Innovación y Universidades (Spanish government) and Project US-1254251 from Consejería de Economía y Conocimiento (Junta de Andalucía).
Conflict of interest
The authors declare there is no conflict of interests.









 DownLoad:
DownLoad: