Dynamical behaviour of fractional-order atmosphere-soil-land plant carbon cycle system

1.   Introduction

From the researches and reports in recent years, it has been known that the earth is confronting with environmental pollution and energy crisis and people from all walks of life are trying hard to find solutions. The most important point is to understand the process of terrestrial carbon cycle, which plays the prominent position in the global carbon cycle. In different fields, theoretical issues concerning the carbon cycle have been studied differently, such as in atmosphere science ^[1], ocean science ^[2,3], forest ecological system ^[4], geological sciences ^[5] and so on ^[6,7]. Research achievements mainly concentrate on the carbon source and sink, carbon footprint and carbon exchange. This study established a dynamical system to investigate the evolution of the carbon cycle.

Carbon cycle change, increases in the NOx emission to the atmosphere and in the atmospheric aerosol (Black carbon, PM2.5 etc) amount, will perturb the Earth's radiative budget and exert large impact on the Earth’s climate. In ^[8], Leonid et al. proposed a terrestrial ecosystem carbon life cycle model to investigate the intensity of carbon source and sink. Enting^[9] used Laplace transform to analyze the carbon cycle. Michela et al. ^[10] built a carbon cycle dynamic system for Italy, Siena province and examined the carbon footprint of six carbon emission scenarios. Pan et al. ^[11] estimated the global forest carbon balance and Piao et al. ^[12] described China's carbon budget and its change mechanism by remote sensing data and a biogeochemical model. According on China's regional terrestrial ecosystem carbon cycle, Fu et al. ^[13] studied regional atmosphere-soil-land plant carbon cycle system based on the analysis of the carbon flux. The dynamic behaviour of the system is studied from the point of view of stability.

On the other hand, fractional-order calculus has gained much popularity from theoretical as well as application viewpoints. It used to be considered as the generalization of classical integer-order calculus to real or complex order. Compared with integer calculus, the major merit of fractional calculus lies in the fact that it has memory. Many people are interested in developing the theoretical analysis and numerical methods for fractional-order differential equations. Actually, fractional-order differential equations have recently proved to be an effective and valuable measures in various fields such as in engineering ^{[14,15,16,17]}, physics ^[18,38], mathematical biology ^[19,20,21], psychological and life sciences ^{[22,23,24,25,26]} and other scientific fields. Furthermore, more and more researchers have performed investigation to study the mathematical properties and numerical solutions of the fractional-order ecological system recently. In ^[19], Ahmed et al. investigated the fractional-order predator-prey system and the fractional-order rabies system to obtain the existence and uniqueness of solutions, the stability of equilibrium points and numerical solutions for these systems. In ^[26], authors showed us fractional-order energy demand-supply system which confirmed the energy resource attractor with a necessary condition about the existence of chaotic behaviors and two different control strategies. In song et al. ^[27], a fractional-order delayed predator-prey system was proposed and analyzed. The main work is investigating the stability of the system. Furthermore, the authors find that fractional-order can affect the stability of the system without harvesting terms.

We here want to make a more precise depiction to the atmosphere-soil-land plant carbon cycle by using the time fractional differential operator which lies in the system itself that the memory data of it. It can characterize the real cycle which also affected by the history. Therefore, by investigating this system, we may have a better perception and the performer could refer to our result to make some change when facing some environmental problem. Based on the above analysis, we consider a class of fractional-order differential system to describe the dynamics of atmosphere-soil-land plant carbon cycle. The system consists of $x_{1}(t)$, $x_{2}(t)$ and $x_{3}(t)$, where $x_{1}(t)$ is the time-dependent variable of carbon flux in atmosphere, $x_{2}(t)$ is the carbon flux of soil and $x_{3}(t)$ is the carbon flux of animals and plants. According to the law of carbon flow, we give the following assumptions:

Assumption $1$: in order to maintain a balance, the inflow and outflow is equal to the total carbon flow.

Assumption $2$: the internal carbon flux is determined by the carbon flow of three cycles (atmosphere cycle, soil cycle and land plant cycle).

Assumption $3$: the internal flow of each cycle obeys the rules of supply pattern, receive pattern, Lotka-Volterra pattern and diffusion pattern.

Assumption $4$: the rest of carbon flow is ignored except the large carbon flow changed in the atmosphere-soil-land cycle.

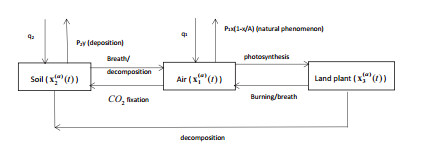
On the basis of Assumptions 1–4, we could build the atmosphere-soil-land plant terrestrial ecosystem carbon cycle dynamic system as shown in Figure 1.

In this paper, we assume the carbon inflow $q_{1}$ of the atmosphere cycle and the carbon inflow $q_{2}$ of the soil cycle are both constant.

From Figure 1, it shows that a part of carbon flow escapes out with the change of natural phenomenon in the atmosphere cycle and this carbon flow represents the release of carbon dioxide from the atmosphere under the combined action of the atmosphere cycle and the land plant cycle ultimately. And some of it flows into soil cycle by carbon dioxide fixation. What's more, in the soil cycle, a part of carbon flow sinks into the atmosphere cycle by breath and decomposition and another part of it goes out with deposition. In the land plant cycle, a part of carbon flow flows into the atmosphere cycle by breath and burning and another part of it goes into the soil cycle by decomposition.

Under the premise of the above hypothesis and Figure 1, the three-dimensional fractional-order atmosphere-soil-land plant carbon cycle system is obtained as follows:

where $\alpha$ is the fractional order satisfying $0 < \alpha\leq1$ and $\frac{d^{\alpha}}{dt^{\alpha}}$ is in the sense of the Caputo fractional derivative, and the coefficients of the system have specific meanings: $m_{i}$ $(i = 1, 2)$ are the carbon outflow coefficients; $A_{i}$ $(i = 1, 2)$ are the positive constants; $\beta_{12}$ is the receive coefficient of carbon flow from the atmosphere cycle to the soil cycle; $\alpha_{21}$ is the supply coefficient of carbon flow from the soil cycle to the atmosphere; $\beta_{1}$ is the diffusion coefficient of the atmosphere cycle that depends on the carbon reserve of the land plant cycle; $\alpha_{32}$ is the supply coefficient of carbon flow from the land plant cycle to the soil cycle; $\alpha_{22}$ is the diffusion coefficient of the soil cycle; $\beta_{2}$ is the diffusion coefficient of the soil cycle that depends on the carbon reserve of the atmosphere cycle; $\alpha_{32}$ is the supply coefficient of carbon flow from the land plant cycle to the soil cycle; $\alpha_{31}$ is the supply coefficient of carbon flow from the land plant cycle to the atmosphere cycle; $\gamma_{31}$ is the Lotka-Volterra coefficient of carbon flow from the land plant cycle to the atmosphere cycle.

A simplified formula is

where $\alpha_{1} = \alpha_{21}-\beta_{12}$, $K_{1} = A_{1}$, $\alpha_{2} = \beta_{12}-m_{2}-\alpha_{21}$, $\alpha_{3} = \alpha_{32}$, $K_{2} = \frac{\alpha_{22}}{\alpha_{32}}A_{2}$, $\alpha_{4} = \alpha_{32}+\alpha_{31}$, $\gamma_{1} = \gamma_{31}$. System (1.2) reflects the interactive relationships among the atmosphere cycle, soil cycle and land plant cycle. In the above system, there are complicated dynamics existing between the variables and parameters. In addition, it is beneficial to us for more intuitive analysis of the system.

In this article, we first put forward a fractional-order system of atmosphere-soil-land plant carbon cycle. Moreover, to show more realistic conditions, we give system parameter estimation method. Then we discuss the sufficient condition for existence and uniqueness of the solution. And the conditions of local stability of the fractional-order system are analyze by calculating equilibrium points. We also find the existence of the asymptotically stable attractor of the system and the carbon cycle in the planet is balanced by numerical simulations. Furthermore, we construct a discretization process of fractional-order system and study the necessary and sufficient conditions of the stability of the discretization system. It shows that the fractional-order parameter has an impact on the stability of the discretization system.

This paper is arranged as follows. Section $2$ analyzes the sufficient condition for existence and uniqueness of the solution of the fractional-order atmosphere-soil-land plant carbon cycle system and investigates conditions of the local stability of the system. Section $3$ discretizes the fractional-order atmosphere-soil-land plant carbon cycle system and analyzes the necessary and sufficient conditions of stability of discretization system. We use numerical simulations which not only illustrate our results with the theoretical analysis, but also exhibit the complex dynamical behaviors in Section $2$ and Section $3$, respectively.

2.   The fractional-order atmosphere-soil-land plant carbon cycle system

In this section, we use a class of fractional-order differential system called atmosphere-soil-land plant carbon cycle system to analyze the carbon flux relationship among the atmosphere cycle, the soil cycle and the land plant cycle.

2.1.   Basics of fractional-order calculus

The Caputo definition of fractional derivative ^[28] is given as

where the operator $D^\alpha$ is referred as the ``$\alpha$-order Caputo differential operator", $f^{(l)}$ represents the $l$-order derivative of $f(t)$, $l$ is the smallest integer which is not less than $\alpha$ and $J^{\theta}$ is the $\theta$-order Riemann-Liouville integral operator which can be described as

where $\Gamma(\theta)$ is the Euler's Gamma function.

In ^{[29,30,31,32,33]}, stability conditions and their applications to systems of fraction-order differential equations were reported. We consider the following nonlinear autonomous fractional-order system

where $X(t) = (x_{1}, x_{2}, x_{3})^{T}\in R^{3}$, $F:R^{3}\rightarrow R^{3}$ is a nonlinear vector function in terms of $X$. The Jacobian matrix evaluated at the equilibrium point $X^{*} = (x^{*}_{1}, x^{*}_{2}, x^{*}_{3})$ is

The local stability of the equilibrium points of a linearized fractional-order system can be obtained from the following lemma ^[29] :

Lemma 2.1. If all the eigenvalues $\lambda_{1}, \lambda_{2}, \lambda_{3}$ of the equilibrium point $X^{*}$ of system (2.1), satisfy the Matignon's conditions ^[30] which can be described as

where $|\arg\lambda_{i}|(i = 1, 2, 3)$ denotes the argument value of the eigenvalue $\lambda_{i}$. Then $X^{*}$ is locally asymptotically stable.

2.2.   Existence and uniqueness of the solution

The fractional-order atmosphere-soil-land plant carbon cycle system can be written in the following form

where

Define the supermum norm as

then, the norm of the matrix $M = [m_{ij}[t]]$ is defined by ^[35]

We investigate the existence and uniqueness of the solution in the region $\Omega\times(0, T]$ where

thus, we get the solution of the system as follows

so

Finally, according to the above conditions, we get the following inequality

where

If $L < 1$, then the mapping $X = H(X)$ is a contraction mapping and we get the sufficient condition for existence and uniqueness of the solution of system as follows.

Theorem 2.1. The sufficient condition for existence and uniqueness of the solution of system in the region $\Omega\times(0, T]$ with initial conditions $X(0) = X_{0}$ and $t\in(0, T)$ is

2.3.   Parameter estimation of the atmosphere-soil-land plant carbon cycle system

In the practical application, it is very important to estimate parameters of the system. Next, we give a simple estimation method for the various parameters involved in the system.

$\rm(i)$ Estimate of the coefficients of diffusion $\beta_{1}$, $\beta_{2}$.

We use the following formulas to estimate the diffusion coefficients.

where $\nu_{1}$ represents the quantity of diffusion in the atmosphere cycle, $\omega_{1}$ represents the total carbon dioxide, $\eta_{1}$ represents the total quality of diffusion in the soil cycle, $\xi_{1}$ represents the total carbon dioxide.

$\rm(ii)$ Estimate of the coefficient of supply $\alpha_{1, 2, 3, 4}$ and the Lotka-Volterra coefficient $\gamma_{1}$.

In the case of $\alpha_{1}$. Let $x_{1}(0) = 0$, when $t$ is small, we ignore the role of carbon in atmosphere cycle and land plant cycle, and the approximate assumption $x_{2} = x_{21}$, then the first formula in system (1.2) becomes

So, when $t = t_{1}$, $x_{1} = x_{21}$, then from the above formula, we get

thus, the above formula implies that: in the case of a certain speed of carbon in atmosphere cycle, $\alpha^{-1}_{1}$ equals the time which carbon supply becomes $0$ required. So, estimation of the supply coefficient, we can convert to estimate from the time perspective.

$\rm(iii)$ Estimation of the parameter $q_{1}$, $m_{1}$, $K_{1}$, $q_{2}$, $K_{2}$.

According to statistical data fitting, we can get the estimated value of $q_{1}$, $m_{1}$, $K_{1}$, $q_{2}$, $K_{2}$.

2.3.1.   Stability analysis of fraction-order atmosphere-soil-land plant carbon cycle system

To analyze system and discuss the stability of the system, we first find out the equilibrium points of system (1.2). Let

After calculating, the system has three equilibrium points

For system (1.2), the Jacobian matrix of equilibrium point $(x^*, y^*, z^*)$ is as below

Theorem 2.2. The atmosphere cycle and soil cycle equilibrium point $E_{0} = (\frac{\alpha_{1}\alpha_{3}K_{2}-\alpha_{1}q_{2}+\alpha_{2}q_{1}}{-\alpha_{1}\beta_{2}+\alpha_{2}m_{1}}, -\frac{q_{1}}{\alpha_{1}}+\frac{m_{1}}{\alpha_{1}}(\frac{\alpha_{1}\alpha_{3}K_{2}-\beta_{2}q_{2}+\alpha_{2}q_{1}}{-\alpha_{1}\beta_{2}+\alpha_{2}m_{1}}), 0)$ is locally asymptotically stable if $\alpha_{4} > \gamma_{1}\frac{\alpha_{1}\alpha_{3}K_{2}-\alpha_{1}q_{2}+\alpha_{2}q_{1}}{-\alpha_{1}\beta_{2}+\alpha_{2}m_{1}},$ $\alpha_{2} < m_{1}$ and $m_{1}\alpha_{2}-\alpha_{1}\beta_{2} < 0$.

Proof. The Jacobian matrix of equilibrium point $E_{0}$ is

The corresponding characteristic polynomial is

So the eigenvalues of the Jacobian matrix $J(E_{0})$ are

If $\alpha_{2} < m_{1}$ and $m_{1}\alpha_{2}-\alpha_{1}\beta_{2} < 0,$ then both eigenvalues $\lambda_{1, 2}$ are negative. If $\alpha_{4} > \gamma_{1}\frac{\alpha_{1}\alpha_{3}K_{2}-\alpha_{1}q_{2}+\alpha_{2}q_{1}}{-\alpha_{1}\beta_{2}+\alpha_{2}m_{1}},$ then $\lambda_{3}$ is negative. Therefore, all the eigenvalues of the atmosphere cycle and soil cycle equilibrium point $E_{0}$ satisfy Matignon's conditions (2.2).

Next, the eigenvalues of the two-species equilibrium points $E_{1}$ and $E_{2}$ are given by

where

Remark 2.1. Since $E_{0}$ is a land plant free equilibrium and the discriminant of eigenvalues is greater than zero, which verifies the first statement in Theorem 2.3, we notice that the conditions of Theorem 2.2 is free with the order $\alpha$.

Now, we use the following theorem to determine the local stability of interior equilibrium points $E_{1}$ and $E_{2}$.

Theorem 2.3. ^[29] If the discriminant of the eigenvalues of equation (2.3.1) is given as

then equilibrium points $E_{1}$ and $E_{2}$ are locally asymptotically stable if they satisfy the following fractional Routh-Hurwitz conditions:

$\rm (i)$ If $D(P) > 0$, then the necessary and sufficient condition for equilibrium point $E_{1}(E_{2})$, to be locally asymptotically stable, is $A_{1} > 0$, $A_{3} > 0$, $A_{1}A_{2}-A_{3} > 0$.

$\rm (ii)$ If $D(P) < 0$, $A_{1}\geq{0}$, $A_{2}\geq{0}$, $A_{3} > 0$, then $E_{1}(E_{2})$ is locally asymptotically stable for $\alpha < \frac{2}{3}$. However, if $D(P) < 0$, $A_{1} < 0$, $A_{2} < 0$, $\alpha > \frac{2}{3}$, then all roots of equation (2.3.1) satisfy the condition $|arg(\lambda)| < \alpha\pi/2$.

$\rm (iii)$ If $D(P) < 0$, $A_{1} > 0$, $A_{2} > 0$, $A_{1}A_{2}-A_{3} = 0$, then $E_{1}(E_{2})$ is locally asymptotically stable for all $\alpha\in(0, 1)$.

$\rm (iv)$ The necessary condition for equilibrium point $E_{1}(E_{2})$, to be locally asymptotically stable, is $A_{3} > 0$.

2.4.   Numerical simulations

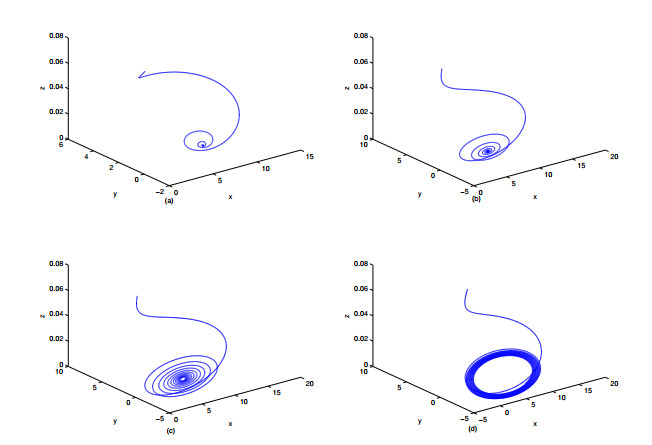
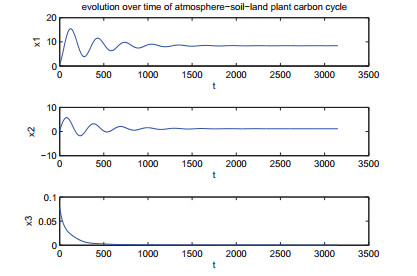
In this subsection, to briefly illustrate the system dynamics, we use a modified Adams-Bashforth-Moulton algorithm method proposed by ^[34] to solve the system. The numerical simulation results show that there is a rather complex nonlinear relationship among the atmosphere cycle, soil cycle and land plant cycle. As in ^[13], we select the following parameter values: $q_{1} = 0.1$, $m_{1} = 0.03,$ $\alpha_{1} = 0.06,$ $\beta_{1} = 0.02,$ $K_{1} = 0.13,$ $q_{2} = 0.15,$ $\beta_{2} = 0.02,$ $\alpha_{2} = 0.02,$ $\alpha_{3} = 0.02,$ $K_{2} = 0.25,$ $\alpha_{4} = 0.02,$ $\gamma_{1} = 0.0005.$ Then numerical simulations are performed for $\alpha = 0.88$, $0.94$, $0.97$, and $0.99$. As can be seen from Figure 2, the dynamic behavior of the system has obvious differences under different values. When $\alpha = 0.88$ and $0.94$, an asymptotically stable attractor exists in Figure 2(a) and (b). When fractional-order parameter $\alpha$ is bigger, the speed of asymptotically stable of the system is faster. When $\alpha = 0.97$ and $0.99$, Figure 2 (c) and (d) show that the system has a stable limit cycle. Therefore, different fractional-order parameters $\alpha$ have different effects on the atmosphere-soil-land plant system. In addition, by observing the relationship among variables with time, we get Figure 3. From Figure 3, we find that the carbon reserve of the atmosphere has a maximum value with time and then keeps steady; the carbon reserve of the soil also has a maximum value with time, then it has a steady level; and the carbon reserve of the land plant cycle decreases to a minimal level and keeps steady finally. It shows that the carbon flow keeps a balance in the atmosphere cycle, soil cycle and land plant cycle.

3.   The discretized fractional-order atmosphere-soil-land plant carbon cycle system

In the following, we adopt the discretization ^[26,35] of fractional-order atmosphere-soil-land plant carbon cycle dynamic system and investigate the necessary and sufficient conditions for the stabilization of discretized system.

3.1.   Discretization process of the fractional-order system

Now, we assume that $x_{1}(0) = x_{10}, x_{2}(0) = x_{20}, x_{3}(0) = x_{30}$ are the initial values of system (1.2). So the discretization process of fractional-order atmosphere-soil-land plant carbon cycle dynamic system (1.2) with piecewise constant arguments is given as ^[35]

Firstly, let $t\in[0, s)$, so $\frac{t}{s}\in[0, 1)$, we obtain

and the solution of (3.2) is reduced to

where $I^{\alpha} = \frac{t^{\alpha}}{\alpha\Gamma(\alpha)}$.

Secondly, let $t\in[s, 2s)$, so $\frac{t}{s}\in[1, 2)$, we get

which has the following solution

So, after repeating the discretization process $n$ times, we gain

where $t\in[ns, (n+1)s)$. For $t\rightarrow(n+1)s$, system (3.4) is simplified to

3.2.   Stability of the fixed points of the discretized system

In what follows, we discuss the asymptotic stability of system (1.2) at the fixed equilibrium points. By considering the Jacobian matrix of these fixed points and calculating their eigenvalues, the local stability of these points based on the roots of the system's characteristic equation ^[36] is studied. The Jacobian matrix of system (3.5) is given by

Theorem 3.1. The fixed points $E_{0}$ of system (3.5) is locally asymptotically stable if and only if

and one of the following conditions holds:

$\rm (i)$ $\phi^{2}_{2} = \psi$ and $-4 < \frac{s^{\alpha}}{\alpha\Gamma(\alpha)}\phi_{1} < 0$;

$\rm (ii)$ $\phi^{2}_{2} > \psi$ and $-4 < \frac{s^{\alpha}}{\alpha\Gamma(\alpha)}(\phi_{1}\pm\sqrt{\phi^{2}_{2}-\psi}) < 0$;

$\rm (iii)$ $\phi^{2}_{2} < \psi$ and $\phi_{1}+\frac{s^{\alpha}}{4\alpha\Gamma(\alpha)}(\phi^{2}_{1}+\psi-\phi^{2}_{2}) < 0$,

where

$\phi_{1} = \alpha_{2}-m_{1}, \quad\beta_{2} = m_{1}+\alpha_{2}, \quad\psi = 4\alpha_{1}\beta_{2}.$

Proof. The Jacobian matrix evaluated at $E_{0}$ is given by

where $\vartheta = \frac{\alpha_{1}\alpha_{3}K_{2}-\alpha_{1}q_{2}+\alpha_{2}q_{1}}{-\alpha_{1}\beta_{2}+\alpha_{2}m_{1}}$.

The eigenvalues of $J(E_{1})$ are

So if the fixed point $E_{0}$ is locally asymptotically stable, it satisfies the stability conditions $|\lambda_{1}| < 1$ and $|\lambda_{2, 3}| < 1$ by the postulates in this theorem.

Next, let us discuss the stability of fixed points $E_{1, 2}$. To simplify calculations, we get the Jacobian matrix of these fixed points

where

and variables $\overline{x}_{1i}$, $\overline{x}_{2i}$, $\overline{x}_{3i}$, $i = 0, 1, 2$ are defined by equation (2.3). The characteristic equation of $J(E_{1, 2})$ is expressed as follows:

with the coefficients

where

$U_{1} = \frac{s^{\alpha}}{\alpha\Gamma(\alpha)}\frac{2\beta_{1}\overline{x}_{3i}}{K_{1}}$, $U_{2} = \frac{s^{\alpha}}{\alpha\Gamma(\alpha)}\gamma_{1}\overline{x}_{3i}$, $U_{3} = \frac{s^{\alpha}}{\alpha\Gamma(\alpha)}\gamma_{1}\overline{x}_{1i}$,

$V_{1} = \frac{s^{\alpha}}{\alpha\Gamma(\alpha)}(-m_{1})$, $V_{2} = \frac{s^{\alpha}}{\alpha\Gamma(\alpha)}\alpha_{1}$,

$V_{3} = \frac{s^{\alpha}}{\alpha\Gamma(\alpha)}(-\beta_{1})-U_{1}$, $V_{4} = \frac{s^{\alpha}}{\alpha\Gamma(\alpha)}(-\beta_{2})$,

$V_{5} = \frac{s^{\alpha}}{\alpha\Gamma(\alpha)}\alpha_{2}$, $V_{6} = \frac{s^{\alpha}}{\alpha\Gamma(\alpha)}\alpha_{3}$,

$V_{7} = \frac{s^{\alpha}}{\alpha\Gamma(\alpha)}(-\alpha_{4})+U_{3}$.

According to the Jury's criterion ^[37], if fixed points $E_{1, 2}$ are locally asymptotically stable, they should satisfy the following conditions:

$1+K_{1}+K_{2}+K_{3} > 0$, $1-K_{1}+K_{2}-K_{3} > 0$,

$1-K_{2}+K_{1}K_{3}-K_{3}^{2} > 0$, $1+K_{2}-K_{1}K_{3}-K_{3}^{2} > 0$.

Therefore, the above conditions indicate that fixed points $E_{1, 2}$ are locally asymptotically stable if the system's parameters belong to the following set

${\{H:[C-B-A-1]\in\Omega_{i}, \forall {i} = 1, 2, 3\}}$

where

$H = (\alpha_{1}, \alpha_{2}, \alpha_{3}, \alpha_{4}, \alpha_{5}, \beta_{1}, \beta_{2}, \alpha, s),$

$\Omega_{1} = \left(\frac{-A-3+\sqrt{(A^2-4B)-2A+1}}{2}, \frac{-A-3-\sqrt{(A^2-4B)-2A+1}}{2}\right),$

$\Omega_{2} = \left(-B-A-1, B+3A+7\right),$

$\Omega_{3} = \left(\frac{A+3+\sqrt{A^2+4B+14A+23}}{2}, \frac{A+3-\sqrt{A^2+4B+14A+23}}{2}\right),$

$A = V_{1}(V_{5}+V_{7})$,

$B = V_{1}(V_{5}+V_{7})-U_{2}V_{3}-V_{2}V_{4}$,

$C = U_{2}(-V_{2}V_{6}+V_{3}V_{5})V_{7}(V_{2}V_{4}-V_{1}V_{5}-V_{5})$.

3.3.   Numerical simulations

Discretization is a new method to analyze the fractional-order system. For discretized system, we mainly consider the stability of the fixed points of the system. However, even if we can obtain analytical conditions about stability, it would be a little difficult to deal with them thoroughly by theory.

So, in order to analyze the stability of the fixed points, we adopt numerical simulations to study the global dynamical behaviours of system (3.5). In the simulation process, some dynamical behaviours of system (3.5) can be shown, for example asymptotic behaviours near the equilibrium points and the stable limit cycle. In the following, we will find that when fractional-order parameters $\alpha$ and $s$ with different values, it will have strong effect on the stability of system (3.5).

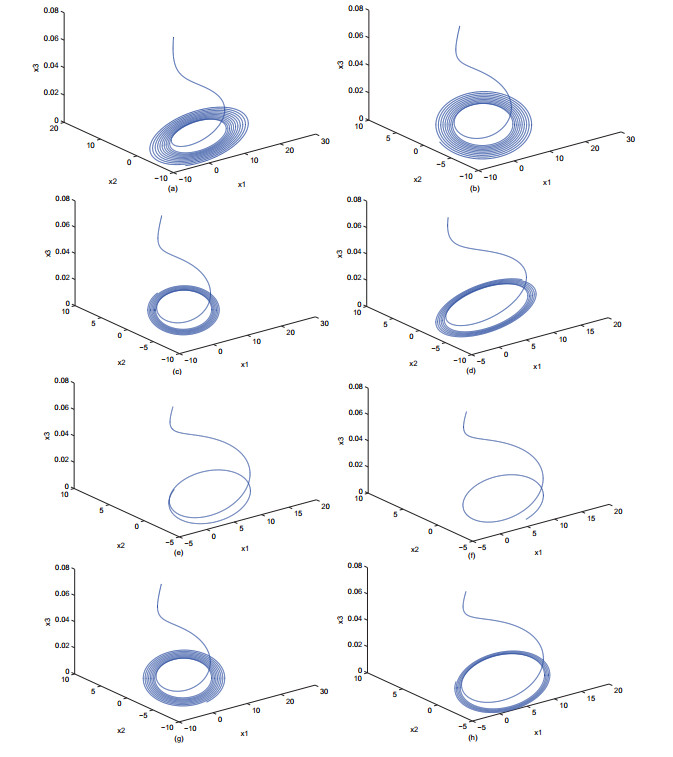
First, as in ^[13], we fix parameters $q_{1}$, $m_{1},$ $\alpha_{1},$ $\beta_{1},$ $K_{1},$ $q_{2},$ $\beta_{2},$ $\alpha_{2},$ $\alpha_{3},$ $K_{2},$ $\alpha_{4},$ $\gamma_{1}.$ Then we vary parameters $\alpha$ and $s$. On the basis of the above-mentioned parameters values and setting $\alpha = 0.9$, $\alpha = 0.98$ and $s = 0.6$, we get Figure 4(a) and (b) which depicts the phase portraits of the system (3.5). When $\alpha = 0.9$, $\alpha = 0.98$ and $s = 0.4$, we gain Figure 4(c) and (d). In the case of Figure 4(a)-(d), discretized system (3.5) is similar with fractional-order system (1.2) under increasing fractional-order parameter $\alpha$ and fixing parameter $s$. When $\alpha = 0.9, 0.98$ and $s = 0.09$, the phase portraits of system (3.5) are depicted in Figure 4(e)-(f), respectively. From Figure 4(c)-(f), we notice that increasing parameter $s$ and decreasing fractional-order parameter $\alpha$ make the behavior of system (3.5) stable. And when $\alpha = 0.3, 0.5$ and $s = 0.09$, Figure 4(g)-(h) shows that the stable limit cycle of system (3.5) which confirms the above result; because it is shown that the above result is reversible when $s$ is small and decreasing fractional-order parameter $\alpha$ destabilize the stable behaviour of system (3.5).

4.   Conclusions

In this paper, we introduced the fractional-order atmosphere-soil-land plant carbon cycle system and adopted discretization method to discretize this system. We analyzed some dynamic behaviours of the fractional-order atmosphere-soil-land plant carbon cycle system. We obtained the sufficient condition for existence and uniqueness of the solution and the conditions of local stability of the equilibrium points of the fractional-order system. Furthermore, for discretization system, the necessary and sufficient conditions of stability of the discretization system were also obtained. In discretization system, we knew that when applying the discretization process on fractional-order atmosphere-soil-land plant carbon cycle system as $\alpha\rightarrow{1}$, the discretization would be Euler's process. In addition, we found that, the stability of the discretization system were impacted by the fractional parameter. Numerical Simulations verified the correctness of our results.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant No. 11771216), the Major Program of the National Social Science Fund of China (Grant No. 17ZDA092), the Key Research and Development Program of Jiangsu Province (Social Development) [grant number BE2019725], the Six Talent Peaks Project in Jiangsu Province (Grant No. 2015-XCL-020), the Qing Lan Project of Jiangsu Province and the Laboratory Open Project of NUIST.

Conflict of interest

The authors state that there is no conflict of interest.