Exact wave solutions to the simplified modified Camassa-Holm equation in mathematical physics

1.   Introduction

Nonlinear evolution equations have much achieved importance and recognition recently. The differential equations have proved to be valuable tools to the modeling of many physical phenomena. The study of the traveling wave solutions for nonlinear differential equations (NLDEs) play an important role in various types of fields, such as, quantum mechanics, electricity, plasma physics, chemical kinematics, optical fibers, biological model, electromagnetic field, viscoelasticity, electrochemistry, physics, signal processing, optical fibers, control theory, fluid mechanics and population model ^[1,2,3,4], etc.

Now-a-days NLDEs have been creating important opportunity for the researchers. As a result, in the past few years different efficient and significant methods have been established and enhanced to obtain exact solutions to evolution equations, such as, the $\left( {G'/G} \right)$-expansion method ^[5,6,7,8], the variational iteration method ^[9,10,11], the modified decomposition method ^[12,13], the Jacobi elliptic function method ^[14], the modified Kudryashov method ^[15], the fractional sub-equation method ^[16], the homotopy perturbation method ^[17,18], the MSE method ^{[19,20,21,22]}, the tanh-function method ^[23], the finite difference method ^[24], the exp-function method ^[25,26,27], the F-expansion method ^[28,29], the operational method ^[30], the sine-cosine method ^[31], the first integral method ^[32], etc.

In 2006, Wazwaz ^[33] studies a family of important physical equations which is known as modified $\alpha$ - equation and he provides the following form of that modified $\alpha$ - equation:

where, $\alpha$ is a positive integer. By taking $\alpha = 2$, Wazwaz ^[33] reduces Eq. (1.1) to the following modified Camassa-Holm (MCH) equation:

Simplifying the MCH Eq. (1.2), we attain the following equation which is known as simplified modified Camassa-Holm (SMCH) equation with involving parameters $k\, \, {\rm{and}}\, \, \beta$ :

The study of the SMCH equation has explained many significant and sensible ambiences. In present literature, the SMCH equation has investigated through the $exp (-\phi (\eta))$-expansion method ^[34], the exp-function method ^[35], the improved $\left(G^{\prime} / G\right)$-expansion method ^[36], etc.

The aim of this article is to examine the fresh, useful and more general traveling wave solutions to the SMCH equation by aid of the MSE method. The MSE method is a recently developed effective, straightforward, powerful and rising method to investigate traveling wave solutions to the NLDEs. We also have shown the graphical representation of the attained solutions of its definite values of the involved parameters through depicting 3D and 2D figures.

The rest of the article is patterned as follows: In Section 2, we have described the MSE method. Section 3 is used to determine the fresh exact traveling wave solutions to the equation. In Section 4, we have shown the graphical representations and physical significance and in Section 5, we have represented the comparison and discussed the results. Finally, in Section 6, we have concluded this article.

2.   Outline of the MSE method

Now, we expressed the MSE method which is used by many researchers to observe the solitary wave solutions to nonlinear evolution equations (NLEEs). Let us consider the nonlinear evolution equations (NLEE) in two independent variables $x$ and $t$, in the following form:

where $u = u\left({x, t} \right)$ is an unknown function, $R$ is a polynomial of $u\left({x, t} \right)$ and its derivatives in which the highest order derivatives and nonlinear terms are involved and its partial derivatives is $u{}_t = \frac{{\partial u}}{{\partial t}}\, , \, \, {u_x} = \frac{{\partial u}}{{\partial x}}, \, \, {u_{tt}} = \frac{{{\partial ^2}u}}{{\partial {t^2}}}, \, \, {u_{xx}} = \frac{{{\partial ^2}u}}{{\partial {x^2}}}$.

To solve the NLEE (2.1) by aid of the MSE method, we represent the main steps in the following form:

Step 1: We consider the real variables $x$ and $t$ by the traveling wave variable $\xi$, in the following form:

where $w$ denotes the velocity of the traveling wave.

By using the traveling wave transformation Eq. (2.2) in Eq. (2.1) then reduces an ordinary differential equation (ODE) written in the form:

where $G$ is a polynomial of $F(\xi)$ and its derivatives while the highest order derivatives and nonlinear terms are connected and the superscripts indicate the ordinary derivatives with respect to $\xi$, in which $F^{\prime}(\xi) = \frac{d F}{d \xi}$.

Step 2: We assume that the Eq. (2.3) has the traveling wave solution in the following form:

where $N$ be the positive integer, $a_{j}(j = 0, 1, 2, \cdots \cdots, N)$ are unknown constants to be determined, in which $a_{N} \neq 0$, and the unknown function $s(\xi)$ to be evaluated, in which $s^{\prime}(\xi) = \frac{d s}{d \xi} \neq 0$.

Step 3: The positive integer $N$ showing in Eq. (2.4) can be determined by considering the homogeneous balance between the highest order derivatives and the nonlinear terms appearing in Eq. (2.3).

Moreover, if the degree of $F(\xi)$ is $deg \left[F(\xi) \right]=N$, therefore, the degree of any other expressions will be as follows:

Step 4: Substitute Eq. (2.4) into Eq. (2.3), we calculate all the necessary derivatives $F^{\prime}, F^{\prime \prime}, F^{\prime \prime \prime}$ and then estimate the function $s(\xi)$. Accordingly of this substitution, we get a polynomial of $\left(\frac{1}{s(\xi)}\right)^{j}, j =$ $0.1.2 \ldots$. In the resultant polynomial, we equate all the coefficients of $\left(\frac{1}{s(\xi)}\right)^{j}, j = 0.1.2 \ldots$. to zero, which yields a set of algebraic and differential equations for ${{a}_{j}}(j = 0, 1, 2, \cdots \cdots, N)$, $s(\xi)$ and other needful parameters.

Step 5: The solutions of the set of algebraic and differential equations obtained in Step 4, provide the values of $s(\xi)$ and other needful parameters.

3.   Formulation of the solutions

In this section, we examine the several new travelling wave solutions to the SMCH equation by the implementation of the MSE method. Let us consider the equation in of the form:

where $\beta>0$ and $k$ is arbitrary constant. It arises as a description of gravity water waves in the long-wave regime, water wave mechanics, turbulent motion, etc. Using the traveling wave transformation Eq. (2.2), the Eq. (3.1) converts into a nonlinear ODE

Integrating Eq. (3.2) once and choose the integrating constant to zero, yields

Balancing the linear term of the highest order derivative ${{u}^{\prime \prime }}$ and the nonlinear term of the highest order ${{u}^{3}}$ occurring in Eq. (3.3), gives $N = 1$. Therefore, the shape of the solution of Eq. (3.3) becomes:

where ${{a}_{0}}$ and ${{a}_{1}}$ are constants to be determined, such that ${{a}_{1}}\ne 0$ and $s(\xi)$ is an unknown function to be determined. Substituting the values of $u, {{u}^{3}}$ and ${{u}^{\prime \prime }}$ using Eq. (3.4) into Eq. (3.3) and then equating the coefficients of $s^{0}, s^{-1}, s^{-2}, s^{-3}$ to zero, these become

From Eq. (3.5) and Eq. (3.8), we determine

Using (3.6) and (3.7), we also obtain

Case 1:

When ${{a}_{0}} = 0$ then the solution is discarded.

Case 2:

When $a_{0} = \frac{\sqrt{3(w-2 k)}}{\sqrt{\beta}}, a_{1} = \pm \frac{i \sqrt{6 w}}{\sqrt{\beta}}$ and $s(\xi) = \mathrm{c}_{3}+\frac{\mathrm{c}_{1} \beta^{2} a_{0}^{2} a_{1}^{2} e^{\frac{3\left(-2 k+w-\theta a_{0}^{2}\right) \xi}{\beta a_{0} a_{1}}}}{9\left(\mathrm{w}-2 k-\beta a_{0}^{2}\right)^{2}}$, the solution (3.4) becomes below:

The solution in Eq. (3.10) is useful and further general travelling wave solution which does not exist in the previous literature. If we set different special values of ${c_1}$ and ${c_3}$ consistently further numerous solutions can be determined through this method, but for simplicity the remaining solutions have not been written down here.

When $w>2 k$, using the obtained results ${{a}_{0}}, {{a}_{1}}$ and $s(\xi)$ and if we choose, ${{c}_{\text{1}}}\text{ = }b\text{ }k\left(k\text{+}m \right)$ and $c_{3} = b^{2} k^{2} m^{2}$ and also by means of the computer algebra like Mathematica, converting the solution (3.10) from exponential to trigonometric function, we achieve the solution is simplified as the following soliton form:

Also, when $w>2 k$ if we choose, ${{c}_{\text{1}}}\text{ = }b\text{ }k\left(k\text{+}m \right)$ and $c_{3} = -b^{2} k^{2} m^{2}$, the above solution (3.2) reduces to the following soliton:

Solutions in Eq. (3.11) and Eq. (3.12) are the well-known periodic wave solutions.

Furthermore, when $w < 2 k$, using the obtained results ${{a}_{0}}, {{a}_{1}}$ and $s(\xi)$ and if we choose, ${{c}_{\text{1}}}\text{ = }b\text{ }k\left(k\text{+}m \right)$ and $c_{3} = -b^{2} k^{2} m^{2}$ and also by means of the computer algebra like Mathematica, converting the solution in Eq. (3.10) from exponential to trigonometric function, we achieve the solution is simplified as the following soliton form:

Also, for $w < 2 k$ if we choose, ${{c}_{\text{1}}}\text{ = }b\text{ }k\left(k\text{+}m \right)$ and ${{c}_{3}} =-{{b}^{2}}{{k}^{2}}{{m}^{2}}$, the above solution in Eq. (3.10) reduces to the following soliton:

Solutions in Eq. (3.13) and Eq. (3.14) are the well-known singular periodic wave solutions.

Case 3:

When $a_{0} = -\frac{\sqrt{3(w-2 k)}}{\sqrt{\beta}}, \quad a_{1} = \pm \frac{i \sqrt{6 w}}{\sqrt{\beta}}$ and $s(\xi ) = {{\rm{c}}_3} + \frac{{{{\rm{c}}_1}{\beta ^2}a_0^2a_1^2{e^{\frac{{3\left( { - 2k + w - \theta a_0^2} \right)\xi }}{{\beta {a_0}{a_1}}}}}}}{{9{{\left( {{\rm{w}} - 2k - \beta a_0^2} \right)}^2}}}$, the solution (3.4) reduces:

The solution in Eq. (3.15) is useful and further general travelling wave solution which does not exist in the previous literature. If we set different special values of ${{c}_{\text{1}}}$ and ${{c}_{3}}$ consistently further numerous solutions can be determined through this method, but for simplicity the remaining solutions have not been written down here.

When $w>2 k$ using the obtained results ${{a}_{0}}, {{a}_{1}}$ and $s(\xi)$ and if we choose, ${{c}_{\text{1}}}\text{ = }b\text{ }k\left(k\text{+}m \right)$ and ${{c}_{3}} =-{{b}^{2}}{{k}^{2}}{{m}^{2}}$ and also by means of the computer algebra like Mathematica, converting the solution in Eq. (3.15) from exponential to trigonometric function, we achieve the solution is simplified as the following soliton form:

And, when $w>\text{2 }k$ if we choose, ${{c}_{\text{1}}}\text{ = }b\text{ }k\left(k\text{+}m \right)$ and ${{c}_{3}} =-{{b}^{2}}{{k}^{2}}{{m}^{2}}$, the above solution in Eq. (3.15) reduces to the following soliton:

Solutions in Eq. (3.16) and in Eq. (3.17) are the well-known periodic wave solutions.

On the other hand, when $w < \text{2 }k$ using the obtained results ${{a}_{0}}, {{a}_{1}}$ and $s(\xi)$ and if we choose, ${{c}_{\text{1}}}\text{ = }b\text{ }k\left(k\text{+}m \right)$ and ${{c}_{3}} =-{{b}^{2}}{{k}^{2}}{{m}^{2}}$ and also by means of the computer algebra like Mathematica, converting the solution in Eq. (3.15) from exponential to trigonometric function, we achieve the solution is simplified as the following soliton form:

Also, when $w < \text{2 }k$ and if we choose, ${{c}_{\text{1}}}\text{ = }b\text{ }k\left(k\text{+}m \right)$ and ${{c}_{3}} =-{{b}^{2}}{{k}^{2}}{{m}^{2}}$, the above solution in Eq. (3.15) reduces to the following soliton:

Solutions in Eq. (3.18) and in Eq. (3.19) are the well-known singular periodic wave solutions.

Therefore, summarizing the solutions between Eqs. (3.11), (3.12), (3.16), (3.17) and also summarizing between Eqs. (3.14), (3.13), (3.18), (3.19) we attain the following subsequent solutions:

Now making use of the wave variable of Eq. (2.2), the solutions in Eqs. (3.20), (3.21), (3.22) and (3.23) become as follows:

The solutions in Eqs. (3.24), (3.25), (3.26) and (3.27) are fresh, important and further general to the SMCH equation can be extracted.

Therefore, it is remarkable to observe that the obtained traveling wave solutions arise to be suitable to seek for gravity water wave in the long-wave regime, the water wave mechanics, the turbulent motion, the driving a flow of fluid and singular periodic waves, etc.

4.   Graphical representations and physical significance

In this section, we show the graphical representations of the obtained solutions and discuss the physical significance to the MSCH equation is arranged below:

4.1.   Graphical representations of the obtained solutions

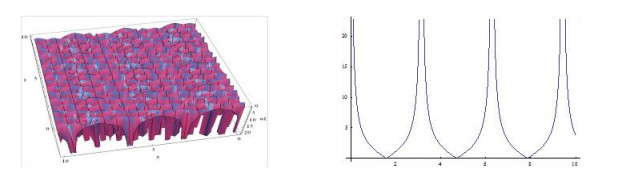
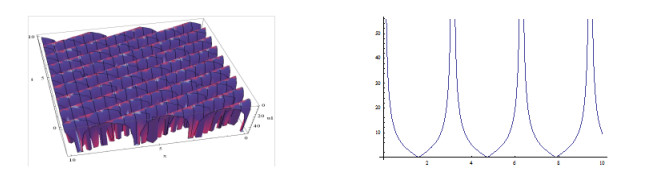
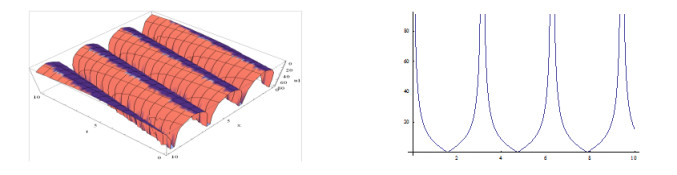
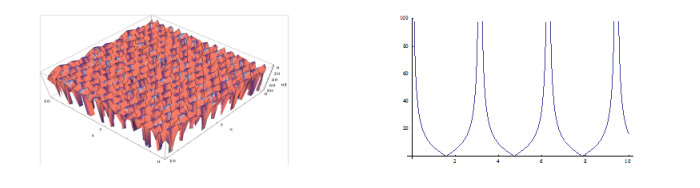
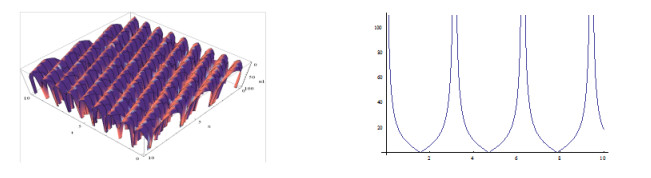
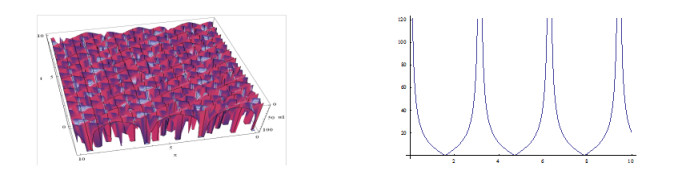
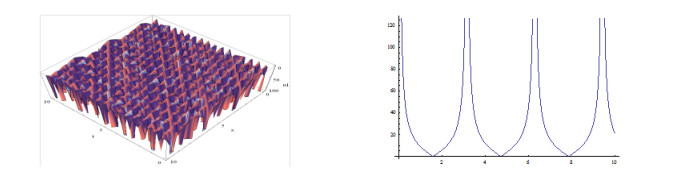
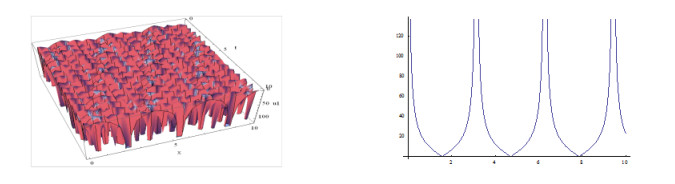
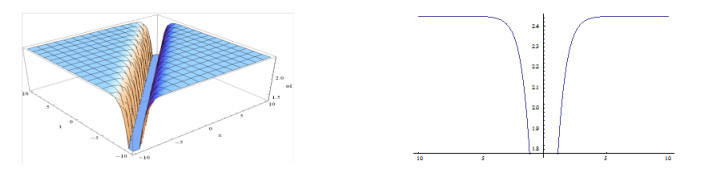
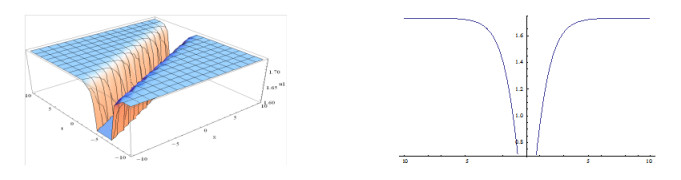
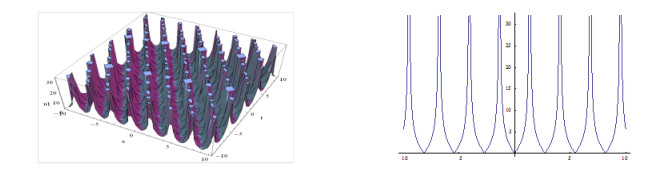
The shapes of the figures of the obtained solutions in Eq. (3.24) (positive and negative values) for the definite values of the parameters are given below:

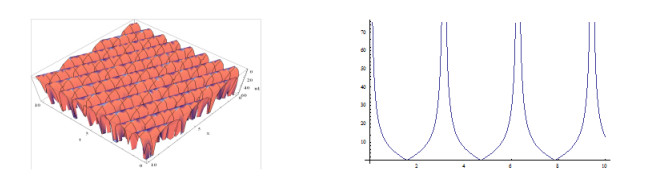
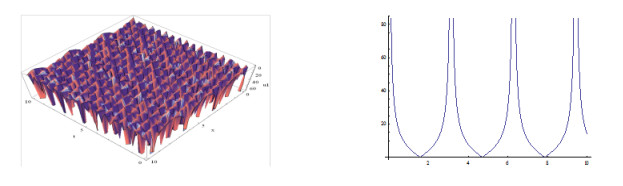
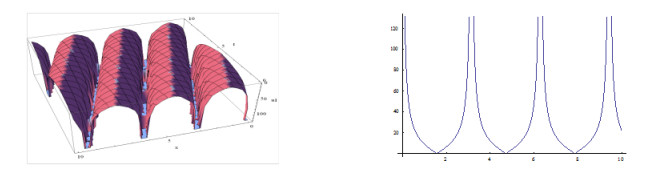
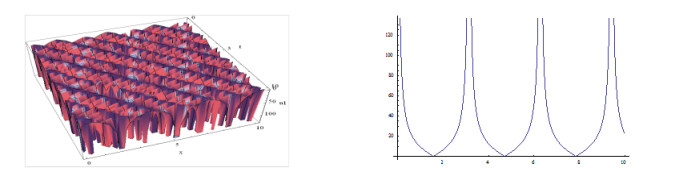
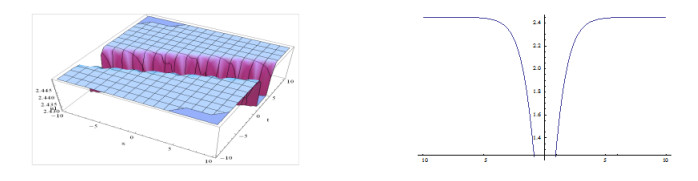
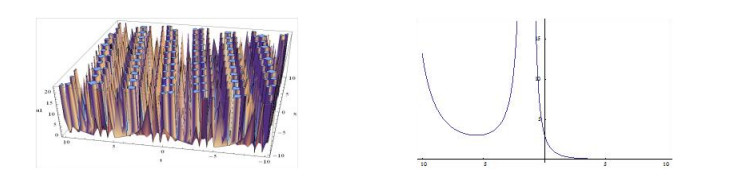
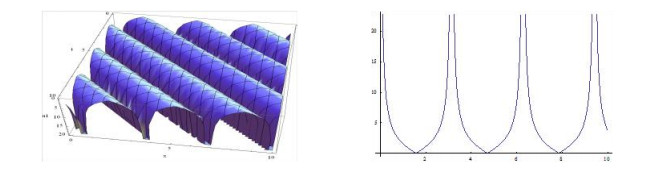
The shape of the figures of the obtained solution in Eq. (3.27) (positive and negative values) for the definite values of the parameters is shown below:

4.2.   Physical significance of the obtained solutions

In this sub-section, we have described the physical significance of the accomplished solutions through figures. We have obtained eight solutions where both the solutions in Eq. (3.24) and in Eq. (3.25) contain two solutions (positive and negative sign) which are in the trigonometry form and both the solutions in Eq. (3.27) and in Eq. (3.27) also contains two solutions (positive and negative sign) which are in the trigonometric hyperbolic form.

From the above graphical representations, we may assert that the solutions might be useful to inspect the physical significance in order to know the internal mechanisms of the related physical phenomena. We find different shapes of figures for the solutions in Eq. (3.24) and in Eq. (3.25), within intervals $0 \leq x, t \leq 10$ and for the solutions in Eq. (3.26) and in Eq. (3.27) within interval $-10 \leq x, t \leq 10$ for the different definite values of involved parameters.

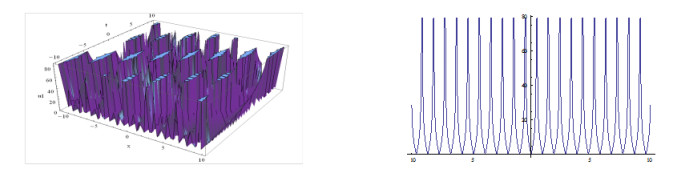
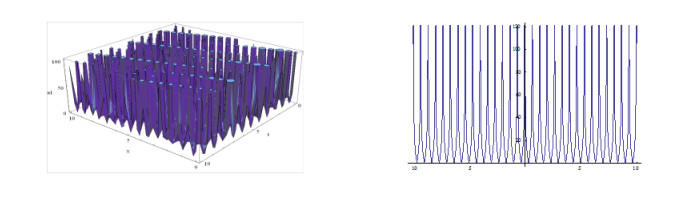
Plotting the figures of the solutions in Eq. (3.24) and in Eq. (3.25, ) we have observed that, for the different values of the velocity $w$ of the traveling wave, the figures of the obtained solutions become different shapes. Plotting the figures of the solutions in Eq. (3.24), we watch that when $w = 1$, the shape of the wave length is large and when $w = 5$, the shape of the wave length is small. Consequently when $w = 15$, the shape of the wave length larger than $w = 5$ and again when $w = 20$, the shape of the wave length is decreased. It is important to notice that when $w = 35$, the shape of the wave length becomes maximum i.e., larger than other values of the velocity of the travelling wave $w$. We also notice that for larger values of $w = 35$, the shape of the wave lengths decreasing and again increasing and when velocity arises to $w = 70$ then the shape of the figure becomes like $w = 35$. Furthermore, when larger values than $w = 70$, the shapes of the wave lengths decreasing and again increasing and when velocity arises to $w = 105$ then the shape of the figures become same to $w = 70$.

From the above discussion we have claimed that, the solutions in Eq. (3.24) to the MSCH equation are periodic wave solution and its period is $w = 35$.

Similarly, plotting the figures of the solutions in Eq. (3.25), we have found the same figures (periodic wave) like the shape of the figures in Eq. (3.24) and the same situation arises and also observed that its period is $w = 35$. Therefore, for minimalism, the shapes of the figures of the solutions in Eq. (3.25) have not shown here.

Furthermore, plotting the figures in the case of the solutions in Eq. (3.26) and in Eq. (3.27) we have observed that, when $w < 3, k = 1.5, {\rm{\beta }} = 1$ and $w = 3, k\ne 1.5, {\rm{\beta }} = 1$ and within interval $-10\le x, t\le 10$ the shapes of the figures are not singular periodic wave. But for other definite values of the including parameters within interval $-10\le x, t\le 10$, the shapes of the figures are singular periodic wave and for simplicity, only we have depicted the shapes of the figures of the solutions in Eq. (3.27) and the shapes of the figures of the solutions have omitted here.

5.   Results, discussion and comparison

In this section, we notice that, the solutions investigated by the $exp (-\phi (\eta))$ -expansion method, Ali et al. ^[34], obtained only five (05) wave solutions which were ordinary solutions (see Appendix-1) for the SMCH equation. But by using the MSE method, we have obtained eight (08) wave solutions which have not been found by the $exp (-\phi (\eta))$ -expansion method which are useful, efficient and more general and give well known shapes like periodic wave solutions and singular periodic wave solutions. The different choices of the integral constants from solutions in Eq. (3.10) and in Eq. (3.15), it might be obtained huge amount of exact wave solutions. Moreover, the attained solutions might be useful to analyze the physical significance. For the definite values of the parameters, different types of periodic and singular periodic solutions are derived in our article.

Therefore, comparing between the obtained solutions and the solutions obtained by the $exp (-\phi (\eta))$ -expansion method ^[34], we might claim that our obtained solutions are more general and useful.

6.   Conclusion

In this article, we have examined the new, significant and further general travelling wave solutions which are in the form of trigonometric and hyperbolic function to the SMCH equation by means of the efficient technique known as MSE method. The attained solutions are in general form and the definite values of the included parameters yield diverse known soliton solutions and the solutions might be useful to analyze many potential applications in mathematical physics and engineering. Furthermore, the MSE method has established better solutions than $exp (-\phi (\eta))$ -expansion method. We also have shown the graphical representation of the obtained solutions through depicting figures in order to interpret the physical phenomena of the tangible incidents. The established results have shown that the MSE method is straightforward, further general, efficient and more powerful and can be used to obtain exact traveling wave solutions for many other nonlinear differential equations.

Acknowledgments

We would like to thanks the honorable reviewers for their valuable comments and suggestions, which are really helpful to enrich the quality of our paper. Furthermore, we are grateful to the journal authority for their proper judgements and kind considerations.

Conflict of interest

The authors declare that they have no any competing interests.

Appendix-1

In this section, we have shown the list of the solutions to the simplified modified Camassa-Holm (SMCH) equation investigated by the $exp (-\phi (\eta))$ method (Ali et al., ^[34]) solutions, are arranged below:

where $\eta = x-v t.$