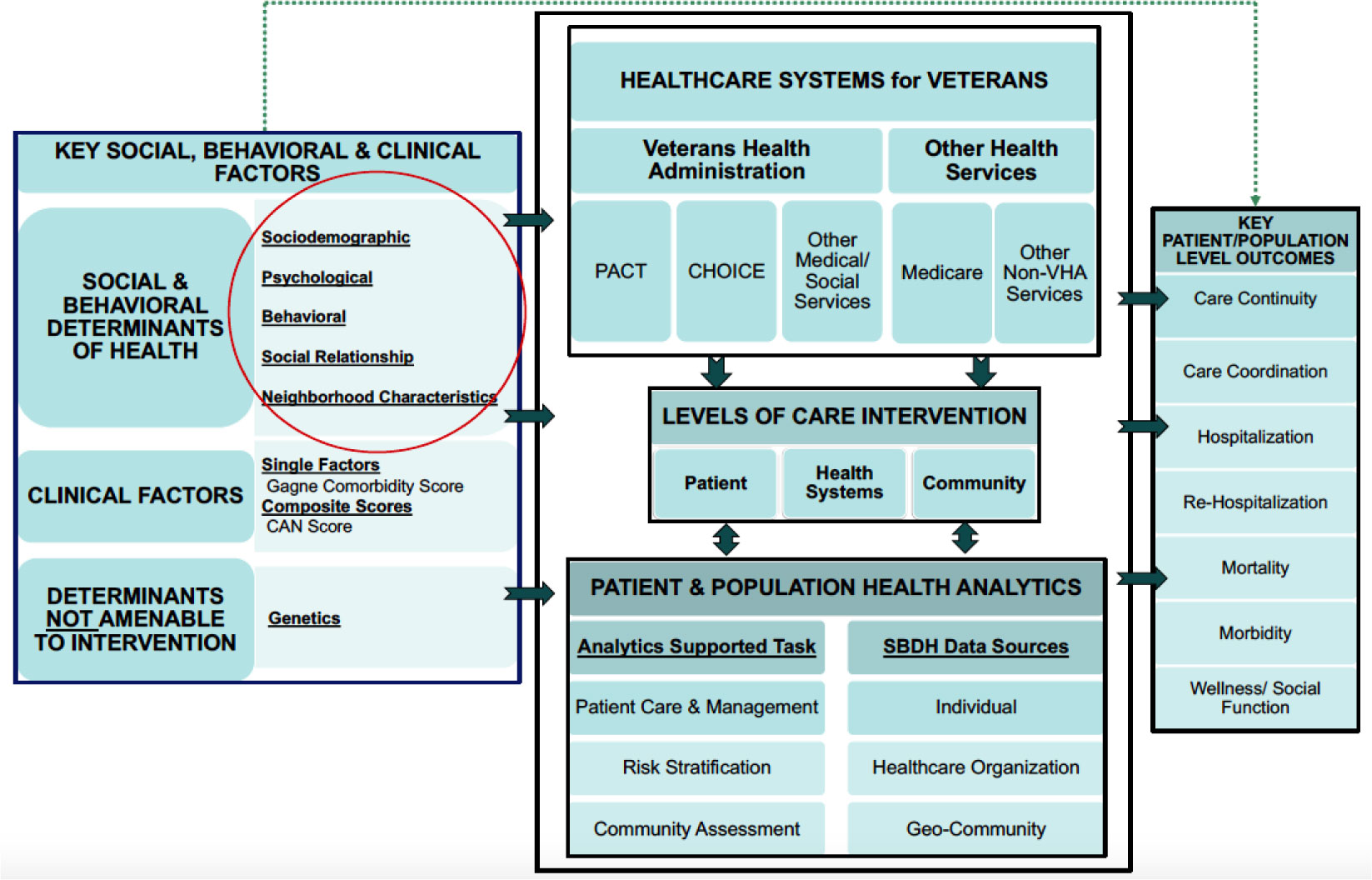
The premise of this project was that social and behavioral determinants of health (SBDH) affect the use of healthcare services and outcomes for patients in an integrated healthcare system such as the Veterans Health Administration (VHA), and thus individual patient level socio-behavioral factors in addition to the neighborhood characteristics and geographically linked factors could add information beyond medical factors mostly considered in clinical decision making, patient care, and population health. To help VHA better address SBDH risk factors for the veterans it cares for within its primary care clinics, we proposed a conceptual and analytic framework, a set of evidence-based measures, and their data source. The framework and recommended SBDH metrics can provide a road map for other primary care-centric healthcare organizations wishing to use health analytic tools to better understand how SBDH affect health outcomes.
1.
Introduction
Metal-hydrogen systems offer grand opportunities for studies on fundamental aspects of alloy thermodynamics [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. The interaction of solutes with structural defects of the metal can easily be assessed [2,6,15,16,17,18], as well as precipitation and growth of phases [5,9,10,19,20,21]. This is enabled by two unique properties of metal-hydrogen systems: First, the chemical potential of hydrogen in the metal can simply be controlled by the surrounding hydrogen gas pressure or by the electromotoric force in electrochemical loading experiments. This allows to directly link the chemical potential with other measured alloy properties. Second, hydrogen often is highly mobile in metals even at room temperature, facilitating experiments on reasonable time scales. Reducing the alloy size to the nano scale, the volume fraction of interfaces increases. This changes the systems properties due to interface effects, which relate to microstructural defects as well as to mechanical stress [6,8,10,11,18,19,22,23,24]. Interface effects modify the hydrogen atoms’ site occupancy in the solid solution regime as well as the stability of hydride phases. In turn, hydrogen can be utilized as a probe for the systems’ microstructure.
Hydrogen absorption usually accompanies with a hydrogen-induced volume expansion of the metal. Depending on the specific metal-hydrogen system, the volume expansion reaches 10-20%, when one hydrogen atom is dissolved per metal atom [1,3]. In metal thin films adhered to rigid substrates, the in-plane expansion is hindered by the substrate, yielding large compressive in-plane stresses of the order of several GPa [25,26]. This changes the thermodynamics of the system. Recently [10,19], we proposed a quasi-thermodynamic model to reveal the interplay of substrate-induced stress, chemical potential and hydride formation in metal-hydrogen thin films. This enables the determination of the attractive H-H interaction energy and of the critical temperature of hydride formation. For the model case of palladium-hydrogen (Pd-H) thin films with different microstructures, in the present manuscript we complete this model by focusing on interface contributions via the hydrogens’ site occupancy in the presence of microstructural defects. Evaluating the chemical potential in the low concentrated solid solution regime allows for the reconstruction of the related distribution of site energies. This enables us to evaluate the volume fractions of interface regions in the films and to reveal the character of the occupied defect sites.
Hence, in this paper we aim to investigate the distribution of site energies in palladium-hydrogen thin films of different thickness and microstructure in the solid solution regime. We propose a model taking the substrate-induced stress contribution to the chemical potential of the films into account. Fitting measured chemical potentials of the films with respect to this model enables us to determine the related densities of sites, including interstitial sites and different kinds of defect sites. From this, we estimate volume fractions and the character of the defect sites in the films.
2.
Methods and materials
2.1. σDOS-model
In the undistorted Pd metal lattice hydrogen occupies octahedral interstitial sites. At low H-concentrations a solid solution $ \alpha $-phase forms, until the precipitation of a high concentration hydride $ \alpha \text{'} $-phase sets in at the solid solution limit$ {x}_{\alpha }^{max} $. In bulk Pd, hydrogen absorption results in an isotropic lattice expansion (Eq 1)
with the expansion factor $ {\eta }_{H} = 0.063\left(3\right) $ [1] and the lattice constant $ a = 0.389\mathrm{n}\mathrm{m} $ of pure palladium. This relation also holds for the two-phase region [16], taking the mean hydrogen concentration $ {x}_{H} $ of the sample into account. Thereby, $ {x}_{H} $ is defined as dissolved hydrogen atoms per palladium atom [H/Pd]. Hence, each dissolved H-atom is surrounded by an elastic strain field of the Pd lattice. The H atoms attractively interact via these strain fields, yielding an elastic contribution to the chemical potential [27] and initiating hydride formation at the solid solution limit$ {x}_{\alpha }^{max} $. As first described by Lacher [28], within a linear approximation of the elastic interaction the chemical potential $ {\mu }_{H} $of H in bulk Pd is commonly given by (Eq 2) [3,29]
with gas constant $ R $ and absolute temperature $ T $. The first term in Eq 2 describes the configurational entropy of H dissolved on the octahedral sites and the maximum fraction $ r $ of sites that can be occupied by hydrogen. $ r $ is determined both by the electronic structure [30] and the microstructure [31] of the metal host and accounts mainly for the composition of the hydride phase. Within this model the hydrogen atoms enter sites with a sharp site energy $ {E}_{0} $, while the H-H interaction energy is characterized by an interaction strength parameter $ {E}_{HH} $. Standard values for bulk Pd have been determined by Wicke or Kirchheim, Mütschele and others to be $ {E}_{0} = 3.9-7.7\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l} $ [22,27,32] and $ {E}_{HH} = 30\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l} $ [22].
Mechanical stress resulting from elastic constraints changes the chemical potential. Cahn and Larché [33,34,35] have shown for the general case of systems exposed to stress that the chemical potential is modified in leading order by (Eq 3)
where $ {v}_{0} $ is the partial molar volume of sites occupied by an interstitial species and $ {\sigma }_{ii} $ is the sum of axial stresses. Considering octahedral sites in Pd, the volume density is $ {v}_{0} = 8.56\times {10}^{-6}{\mathrm{m}}^{3}/\mathrm{m}\mathrm{o}\mathrm{l} $ [27].
In thin films the stress contribution to the chemical potential mainly depends on the substrate-induced in-plane stress, while vertical interface stress contributions resulting at phase interfaces within the film cancel out [10,19]. In total, with a superposition of the H-H interaction and of the substrate-induced stress-contribution, the chemical potential of thin films can be written Eq 4 [10,19]
with $ i = \left(\mathrm{1, 2}\right) $.
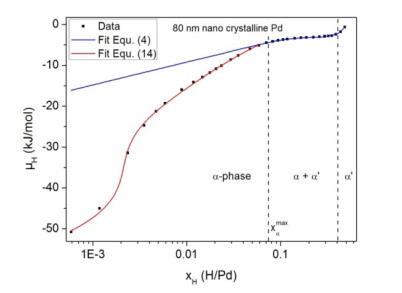
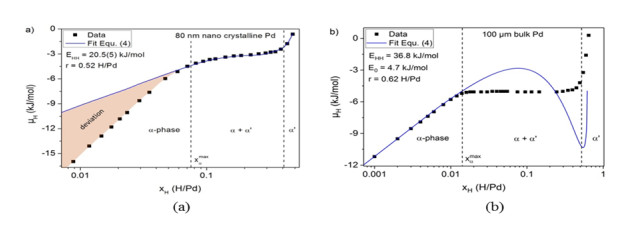
The substrate-induced stress $ {\sigma }_{ii} $ can be measured by a substrate deflection method [36,10]. With this measured stress dependency, Eq 4 enables a description of the thermodynamic conditions of hydride formation in the Pd-H thin films adhered to substrates, converging to the measured sloped chemical potential plateau in the two-phase field in terms of a Maxwell-construction—reflecting the measured two-phase co-existence [10,19]. However, as exemplarily shown in Figure 1a for the example of an 80 nm nano crystalline Pd-H film on a silicon substrate, the fit function of Eq 4 (blue line) remarkably deviates from the measured chemical potential in the $ \alpha $-phase region below the solid solution limit. This differs from the measured chemical potential of the Pd-H bulk system (with $ {\sigma }_{ii} = 0) $ shown in Figure 1b, where the fit function of Eq 4 nicely describes the low concentration regime. We note that deviations of the bulk isotherm from the measured data in the two-phase region of the bulk system in Figure 1b are self-evident: In the concentration range of the two-phase equilibrium, the isotherm oscillates around the measured chemical potential. The constant potential data can be obtained by the Maxwell-construction; this has been targeted in reference [10].
Isotherms of Pd thin films of other microstructures and thicknesses are presented in the supplemental information. They show a similar behavior to the film in Figure 1a. Hence, in the manuscript we picture results of the 80 nm nano crystalline Pd film as case examples.
Within the framework of this model, the observed deviation is caused by the restriction to a sole site energy $ {E}_{0} $ in Eq 4: In thin films a number of microstructural defects such as surfaces, interfaces and dislocations with additional site energies for hydrogen are present. Open-volume defects like grain boundaries, vacancies and the dilatation fields of edge dislocations with a locally expanded lattice can interact attractively with hydrogen induced strain fields and hence offer more negative site energies than the conventional interstitial sites. This results in a preferable H-occupation of open-volume defects [6,18,31]. Re-writing Eq 4 as Eq 5
illustrates that in case of defective metals the left hand side of the equation has to be replaced by a distribution of sites and site energies [22,31]. Subsequently, we will show that this approach enables a reasonable fit of the measured chemical potential curves of Pd-H thin films in the solid solution regime. Following the approach of an additive contribution of substrate-induced stresses to the chemical potential, the measured stress contribution $ {v}_{0}{\eta }_{H}{\sigma }_{ii}\left({x}_{H}\right) $ has to be substracted from the measured chemical potential $ {\mu }_{H} $ to determine pure site energies. Any change in the H-H-interaction contribution $ {E}_{HH}{x}_{H} $ is neglected, here. It has a minor impact on the isotherm in the low concentration regime, and it would yield a self-referred contribution to the hydrogen concentration $ {x}_{H} $ of the film. Its effect on the fitting parameters in the low concentration regime is discussed in the supplemental information.
Following an approach of Kirchheim et al. [2,22,24,37,38], within the framework of statistical thermodynamics the distribution of hydrogen atoms among a number of different sites can be described by using Fermi-Dirac statistics and the related density of sites (DOS), given by $ Z\left(E\right) $. Since the chemical potential of hydrogen atoms in different sites is equal at a given overall hydrogen concentration of the film, in turn the total concentration $ {x}_{H} $ of hydrogen atoms in the metal at a given chemical potential $ {\mu }_{H} $ is determined by integrating over the energies $ E $ of $ Z\left(E\right) $ multiplied with the Fermi-Dirac function (Eq 6) [2,37],
In turn, this enables the reconstruction of the density of sites $ Z\left(E\right) $, when $ {\mu }_{H}\left({x}_{H}\right) $ is measured.
Considering conventional interstitial lattice sites with a sharp site energy $ {E}_{0} $, the DOS transforms to a delta-distribution (Eq 7) [2],
In defective metals a fraction $ f $ of the interstitial lattice sites is replaced by sites with a different energy distribution. Considering sites like grain boundaries with a distribution of atom arrangements, following an idea of White et al. the DOS can be described by a Gaussian distribution (Eq 8) with half width $ {\sigma }_{1} $ around peak energy $ {E}_{1} $ [39,2],
For dislocations the situation is more complicated [2,37]. Here, hydrogen atoms tend to form elongated hydrides in the dilatation fields of edge dislocations at low overall hydrogen concentrations in the metal. Considering the related DOS with an energy $ {E}_{V} $ of hydride formation close to the dislocation and assuming an octahedral symmetry of the dislocation sites [2], it is Eq 9 [37]
with the dislocation areal density $ \rho $ and the partial volume of hydrogen atoms in metals, $ {V}_{H} = 1.69\times {10}^{-6}{\mathrm{m}}^{3}/\mathrm{m}\mathrm{o}\mathrm{l} $ [3]. Furthermore, the parameter $ A $ is given by $ A = \frac{Gb\left(1+v\right)}{3\pi \left(1-v\right)} $ with shear modulus $ G = 44.7\mathrm{G}\mathrm{P}\mathrm{a} $, Burgers vector $ b = 0.275\mathrm{n}\mathrm{m} $ and Poisson ratio $ v = 0.523 $ in the (111) plane of a Pd thin film with [111] texture [10].
To fit the measured chemical potential curves of Pd-H thin films, depending on the film structure we will take into account one or two kinds of sites with sharp site energy $ {E}_{0} $ and $ {E}_{0}^{il} $ (representing interstitial sites) and two different kinds of sites with Gauss distributed site energies $ {E}_{1} $ and $ {E}_{2} $. The two Gaussians may represent grain/domain boundary sites and deep traps. As discussed below, we will not consider dislocations. For simplicity, we will furthermore assume $ r = 1\mathrm{H}/\mathrm{P}\mathrm{d} $, neglecting the blocking of octahedral interstitial sites. This is justified at low overall hydrogen concentrations, regarded here. Within our approach we use as few fitting parameters as possible, that can be clearly distinguished from a physical point of view.
In the regular fcc Pd lattice the number of octahedral interstitial sites equals that of the Pd atoms, yielding the relation $ {f}_{0} = 1-{f}_{1}-{f}_{2} $ for the number density $ {f}_{0} $ of available interstitial sites in Pd. For some Pd films (see below), an additional adhesive vanadium interlayer was placed in-between the Pd film and the substrate. This layer offers additional interstitial sites $ {f}_{0}^{il} $ of site energy $ {E}_{0}^{il} $, that add on top of the sites in the Pd film. Then, in total the DOS of the Pd films is given by (Eq 10)
Evaluating the total hydrogen concentration in a film referring to Eq 6, all partial DOS of Eq 10 can be treated separately, and the partial hydrogen concentrations can be summed up, subsequently. Integrating the first two parts of Eq 6 with 10 (Eq 11)
yields the common result (Eq 12)
which is equivalent to $ {\mu }_{H} = RTln\left(\frac{{x}_{H}}{1-{x}_{H}}\right)+{E}_{0} $ for $ {f}_{1} = {f}_{2} = {f}_{0}^{il} = 0 $.
For the Gaussian parts of Eqs 6 and 10 no primitives exist. However, the partial hydrogen concentration $ {x}_{H, \mathrm{1, 2}} $ in sites with Gaussian site energy distribution can be calculated numerically, when the integral is transformed into a sum over $ n $ discrete energies $ ∆{E}_{j} = \left({E}_{j}-{E}_{j-1}\right) $ on a properly chosen energy interval $ \left[a, b\right] $. Then (Eq 13),
This sum can be calculated stepwise for discrete values of $ {\mu }_{H} $. Together with Eq 12 it yields the total hydrogen concentration as a function of the chemical potential (Eq 14)
in the film for each given $ {\mu }_{H} $, with $ {{E}_{0}, {E}_{0}^{il}, E}_{1}, {E}_{2}, {\sigma }_{1}, {\sigma }_{2}, {f}_{1} $ and $ {f}_{2} $ left as fitting parameters of the DOS to represent the measured chemical potential. $ {f}_{0}^{il} $, on the other hand, can be calculated from the thickness of the V interlayer. Relative to the Pd layer thickness it is (Eq 15)
with the thicknesses $ {d}_{V} $ and $ {d}_{Pd} $ of the V interlayer and the Pd film, and the molar volumes $ {v}_{V} = 8.32\times {10}^{-6}{\mathrm{m}}^{3}/\mathrm{m}\mathrm{o}\mathrm{l} $ of vanadium and $ {v}_{Pd} = 8.56\times {10}^{-6}{\mathrm{m}}^{3}/\mathrm{m}\mathrm{o}\mathrm{l} $ of palladium [27]. Since we correct the measured chemical potential data for the measured substrate-induced stress contribution, we call our model the “σDOS model”.
The Gaussian functions in Eq 13 decrease rapidly to the left and to the right hand sides of the peak energies. Setting $ a = -80\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l} < {E}_{j}\le b = +40\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l} $ and $ ∆{E}_{j} = 0.2\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l} $ is a reasonable choice in case of the investigated Pd-H thin films: with the fitting parameters in Table 1, the incremental concentration steps are $ ∆{x}_{H, \mathrm{1, 2}}^{j} < 1\times {10}^{-14} $ H/Pd at the borders of [a, b].
2.2. Experimental details
24-200 nm Pd films were Ar-ion beam sputtered at $ 2\times {10}^{-4}\mathrm{m}\mathrm{b}\mathrm{a}\mathrm{r} $ in an UHV chamber with a background pressure of the order of $ {10}^{-10}\mathrm{m}\mathrm{b}\mathrm{a}\mathrm{r} $. The sputter rate was $ 1\mathrm{n}\mathrm{m}/\mathrm{m}\mathrm{i}\mathrm{n} $. Microstructure and adhesion conditions of the films were adjusted by choosing two different substrates (Silicon (Si) $ \left[001\right] $ with its native surface oxide layer and sapphire (Al2O3) $ \left[0001\right] $), by choosing the substrate temperature between 300 and 1073 K, and by adding a $ 1\mathrm{n}\mathrm{m} $ adhesive V-interlayer (V//Al2O3) for the epitaxial films. All films contained a small amount of iron $ {x}_{Fe} = 1-2\mathrm{a}\mathrm{t}\mathrm{\%} $, resulting from the film’s cathode beam sputtering in the UHV vessel. The substrates dimensions were 30 mm × 7 mm × (0.1-0.5) mm. The Pd films’ microstructures were described elsewhere [40]. At 300 K, Pd grows with $ \left[111\right] $ fibre texture and in-plane grain sizes of 30-50 nm on silicon substrates. These films are called “nano crystalline films”. Pd on sapphire sputtered at 673 K has a multi-oriented, polycrystalline microstructure with twinned domains. These films are named “multi-oriented films”. Pd on sapphire with an adhesive V-interlayer grows seeded epitaxially at 673 K. The films are called “epitaxial films”.
After film preparation, XRD stress analysis yields compressive intrinsic in-plane stresses of the order of $ {\sigma }_{0} = -1.3\mathrm{G}\mathrm{P}\mathrm{a} $ for nano crystalline Pd films on Si. Multi-oriented films on Al2O3 and epitaxial films on V//Al2O3 are strained in tension with stresses of $ {\sigma }_{0} = +0.2\mathrm{t}\mathrm{o}+0.8\mathrm{G}\mathrm{P}\mathrm{a} $, see reference [41].
The Pd films were loaded stepwise with hydrogen by electrolytical charging in 2/3 glycerin (80%) and 1/3 phosphoric acid (80%) [19]. The chemical potential $ {\mu }_{H} $of hydrogen in the films (Eq 16a) was determined in reference to a saturated Ag/AgCl-electrode, as from Nernst equation [12,13,31]
with Faradays constant $ F $, electromotive force (EMF) $ U $ and standard potential $ {U}_{0} = 0.181\mathrm{V} $. The standard potential was determined for a 100 µm thick Pd bulk sheet. The offset term in Eq 16a refers to the standard chemical potential of gaseous hydrogen. It is (Eq 16b)
at $ T = 297\mathrm{K} $, see the supplemental information for details. As conventionally done in the corresponding literature on metal hydrogen systems [2,22,31,37,38,42], we here shift the energy scale by adding $ -{\mu }_{H2}^{0}/2 $ to the chemical potential, essentially neglecting the offset term.
H-induced changes $ ∆{\sigma }_{11}\equiv ∆\sigma $ of the Pd films’ in-plane stress were determined in-situ by substrate curvature measurement in the long substrate direction. According to Stoney’s equation (Eq 17) [36].
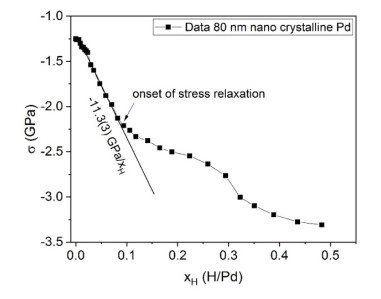
with the substrates’ elastic moduli $ {E}_{S} $ and $ {v}_{S} $, substrate thickness $ {d}_{S} $, film thickness $ {d}_{f} $, radius $ R $of substrate curvature and initial radius $ {R}_{0} $. The change of the radius of curvature was measured utilizing an induction sensor with a resonant circuit. A metal plate was glued to the backside of the substrates’ front end and placed close to the sensor. When the distance between plate and sensor changes due to substrate-bending, the measured capacity of the sensor changes due to eddy currents induced in the plate. This enables calibration of the substrate curvature [43]. A typical stress-concentration curve is shown in Figure 2 for the exemplary case of the 80 nm nano crystalline Pd-H film. Further stress data of the films was published in references [10] and [41].
3.
Results
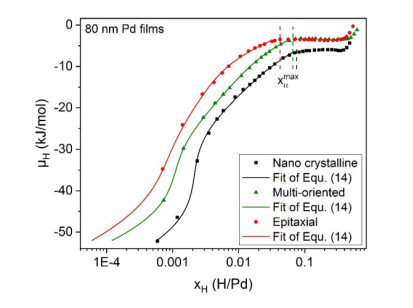
Figure 3 shows the measured, stress-corrected chemical potentials (data points) of 80 nm Pd-H thin films with nano crystalline, multi-oriented and epitaxial microstructures and best fits (lines) according to Eq 14. For the nano crystalline and the multi-oriented film $ {f}_{0}^{il} $ is $ {f}_{0}^{il} = 0 $, while it is $ {f}_{0}^{il} = 0.0127 $ for the epitaxial film. Apparently, the measured chemical potentials of the films with different microstructures differ systematically, with the smallest chemical potential at a given H-concentration for the nano crystalline film. This is in accordance with the expectation that nano crystalline films contain the largest number of open-volume defects.
As can be seen, the data points are well represented by the fitted curves. This is also expressed in Figure 4. There, the original, uncorrected $ {\mu }_{H} $ data of the 80 nm nano crystalline Pd-H thin film is plotted together with the fit according to the quasi-thermodynamic approach of Eq 4 and with the fitted line according to Eq 14. In accordance with the data treatment described before, thereby the measured substrate-induced stress contribution was added back to the curve of Eq 14 after the fitting procedure. While the fit of Eq 4 strongly deviates from the measured chemical potential in the $ \alpha $-phase region, Eq 14 fits well, there. Hence, the fitted DOS with one delta and two Gaussian distributions well represents the measured chemical potential. In the supplemental information, we furthermore show that it is mandatory to use two Gaussian site energy distributions next to the interstitial sites to fit the chemical potential.
The fitted σDOS model parameters of Eq 14 are summarized in Table 1 for all investigated Pd-H films. Related isotherms are presented in the supplemental information. Reference data for bulk Pd according to references [10,22,32] is given in Table 1, as well. The fits are very sensitive to small changes in the fit parameters, yielding considerably small confidence intervals. This is discussed in more detail in the supplemental information.
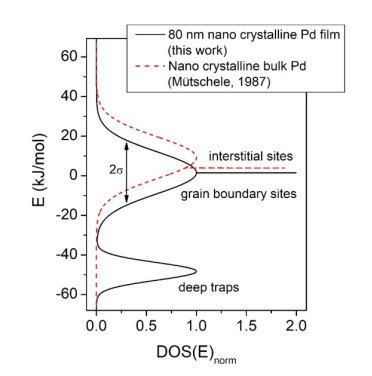
In Figure 5, the fitted density of sites of the 80 nm nano crystalline Pd-H film is compared to the DOS determined by Mütschele and Kirchheim for nano crystalline bulk in reference [22].
4.
Discussion
Figure 4 exemplarily shows the measured data for one chosen Pd-H film, and two related fit curves of the quasi-thermodynamic approach and the σDOS model. For both fit curves, the measured stress contribution to the chemical potential is separated from the fitting procedure. The quasi-thermodynamic approach (blue line) considers octahedral interstitial sites only, which hydrogen occupies in bulk material. The red line according to the fitted DOS in Figure 5 touches the curve of the quasi-thermodynamic approach close to the solid solution limit$ {x}_{\alpha }^{max} $ of the film. This observation hints on saturation of sites different from octahedral interstitial sites within the films’ $ \alpha $-phase region. Furthermore, it shows that the onset of hydride formation in the films is determined by hydrogen located in interstitial sites.
On a closer look the slope of the σDOS model curve is larger than that of the quasi-thermodynamic approach close to $ {x}_{\alpha }^{max} $. This effect is caused by the H-H interaction not implemented in Eq 14, that bends down $ {\mu }_{H}\left({x}_{H}\right) $ when the film enters the plateau region of the two-phase field [10,22]. This aspect is discussed in the supplemental information.
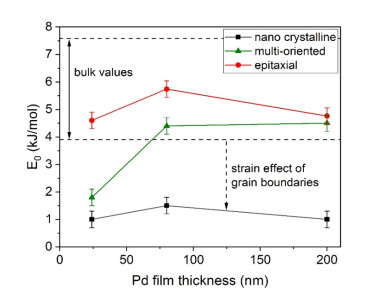
The absolute values of $ {E}_{0} $ of the interstitial sites in Pd are plotted in Figure 6 together with the marked range (between the dashed lines) of bulk values [10,22,32] for the energy range determined for octahedral interstitial sites in Pd.
Apparently, the site energy values $ {E}_{0} $ of the thicker multi-oriented (green triangles) and of the epitaxial (red spheres) Pd-H films fall into the range of the bulk values, while that of the nano crystalline films (black squares) and of the thinnest 24 nm multi-oriented film are reduced by $ 2-3\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l} $. This hints on an interfacial stress contribution of the grain boundaries on the grains, as proposed by Weissmüller and Lemier [23,44]: In their model, the hydrogen filled grain boundaries affect the grain interior of nano crystalline Pd-H samples. In the low concentration $ \alpha $-phase regime the H-occupation of grain boundary sites leads to a tensile straining of the grain interior, which increases the H binding energy to the interstitial sites, expressed by a reduction of the site energy $ {E}_{0} $.
In thin films adhered to rigid substrates, all straining effects are anisotropic, yielding a surplus vertical expansion and hence a tetragonal distortion of the films [41]. Hence, the grain-boundary straining effect will be anisotropic, as well, and it should increase with an increasing volume fraction of grain boundaries. This is confirmed by the fitting parameters in Table 1.
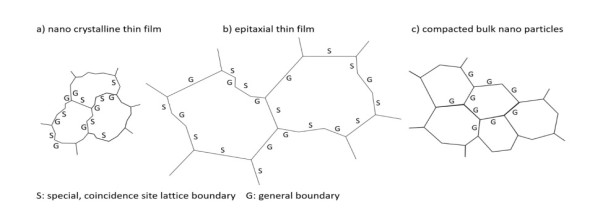
According to Table 1, for all investigated Pd-H thin films the obtained grain boundary energies $ {E}_{1} $ and the half widths $ {\sigma }_{1} $ of the energy distributions are similar within $ {E}_{1} = 0.5-0.7\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l} $ and $ {\sigma }_{1} = 15-19\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l} $, respectively. This remarkable result is not expected at first hand, since the grain boundary structure of nano crystalline films and of films of other microstructures can be assumed to differ. However, it has been shown both for fibre textured as well as for epitaxial metal thin films that the crystalline texture assists the formation of special low-Σ grain boundary fractions [45,46,47], forming a two dimensional network with general grain boundary fractions [45,48]. This supports the experimental result that grain/domain boundaries in Pd-H thin films of different microstructures can be described by similar model parameters. Interestingly, the half widths $ {\sigma }_{1} $ of the site energy distributions are also similar to the bulk value of $ 15\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l} $ determined for nano crystalline Pd in reference [22]. But, the absolute grain boundary energy $ {E}_{1} $ is shifted to less positive values for the thin films compared to the value of $ 9.1\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l} $ for Mütscheles and Kirchheims nano crystalline bulk Pd [22]. Hence, hydrogen is bound more strongly to grain/domain boundary sites in thin films compared to their nano crystalline bulk Pd samples. This observation suggests that the grain boundary structure of sputtered thin films differs from that of these nano crystalline bulk samples. This may result from the different preparation process of compacting gas phase condensated nano particles, the consolidating inert gas condensation (IGC) method [22,49]. As shown in Refs. [49,50], IGC nano crystalline bulk Pd samples similar to those investigated in reference [22] contain light element impurities (O, N, H) by preparation. The impurity content linearly increases with an increasing surface-to-volume ratio of the particles. This indicates that the impurities segregate to the grain boundaries of the samples, where they can block absorption sites for further hydrogen occupation. This might increase the mean grain boundary energy $ {E}_{1} $ of nano crystalline bulk Pd. At a particle size of $ 5-10\mathrm{n}\mathrm{m} $ like in reference [22], a total impurity content of $ 4.5-9\mathrm{a}\mathrm{t}\mathrm{\%} $ is expected [50], with atom ratios O:H:N of 6:4:3 [49]. Complementary, possible segregation of substrate material, i.e. Si or V, in the grain/domain boundaries of the sputtered Pd films would change the film’s site energies compared to bulk material. Gemma et al. have investigated the interdiffusion of V and Pd by means of atom probe tomography, resulting in a steady V content of the order of $ 5\mathrm{a}\mathrm{t}\mathrm{\%} $ in Pd close to the interface [51].
Another cause of reduced grain/domain boundary energies in thin films might be related to structural changes due the tetragonal distortion of adhered thin films, like it is observed for the interstitial site energies, as well.
Furthermore, for nano crystalline bulk Pd consisting of randomly oriented nano particles, grain boundaries with a partially amorphous intergranular phase have been reported [17,49,52]. Consideration of the similar widths $ {\sigma }_{1} $ of the energy distributions suggests that the general grain boundary fraction of the thin films contains amorphous parts, as well.
The grain/domain boundary structures proposed for nano crystalline and epitaxial Pd thin films as well as for nano crystalline bulk Pd are schematically compared in Figure 7.
Next to grain/domain boundary sites, deep traps are found for the Pd-H thin films. Their energy values $ {E}_{2} $ range between $ {E}_{2} = -42\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l} $ and $ {E}_{2} = -48\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l} $. However, they group for the different microstructures with more positive values for the epitaxial films and more negative values for the nano crystalline films. Regarding the nature of these deep traps, three constituents of the films’ microstructure are at hand: the films’ surface, a natural surface oxide layer, and vacancies. Additionally, for the case of epitaxial Pd thin films the thin vanadium interlayer acts as a hydrogen trap, see Table 1. This was expected, since the binding energy of H to vanadium is larger than that to palladium [27,51]. In the present study, the chemical potential of the Pd thin films’ surface oxide layer was determined by anodic polarization of the films in the electrolyte, see the supplemental information for details. It ranges between $ -45 $and $ -80\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l} $, depending on the degree of oxidation. Hence, the measured deep trap energies fall into the range of Pd oxide potentials. Furthermore, literature data for the adsorption energy of hydrogen atoms on clean Pd(111) surfaces are of a similar order of magnitude. Ferrin et al. and Dong et al. calculated H trapping energies of $ -46\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l} $ [53] (the values therein were corrected by $ -{\mu }_{H2}^{0}/2 $) to $ -49\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l} $ [54] on Pd(111) surfaces. Conrad and Ertl et al. measured $ -44\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l} $ [55]. All of these energy values indicate the presence of deep traps at the Pd-H films surfaces. Additionally, hydrogen can be trapped in vacancies in the bulk of the films [18]. The trapping energy of Pd vacancies decorated with H-atoms changes with the number of trapped H. According to reference [56] the trapping energy is $ -22\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l} $ for one H atom, $ -45\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l} $ for two H atoms, and it decreases down to $ -112\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l} $ for six trapped H atoms. With this, it is improbable that vacancies widely contribute to hydrogen trapping in the investigated Pd-H thin films, since their filling should not saturate at two hydrogen atoms.
To evaluate the nature of the deep traps in more detail, the site fractions $ {f}_{2} $ given in Table 1 are compared to the number density of surface sites of Pd thin films. Owing to the Burgers vector $ b = 0.275\mathrm{n}\mathrm{m} $, the $ \left(111\right) $ surface plane of the Pd thin films consists of $ {N}_{S} = 2.54\times {10}^{-9}\mathrm{m}\mathrm{o}\mathrm{l}/{\mathrm{c}\mathrm{m}}^{2} $ Pd atoms. With the molar volume $ {v}_{Pd} = 8.56\times {10}^{-6}{\mathrm{m}}^{3}/\mathrm{m}\mathrm{o}\mathrm{l} $ [27] of Pd, a $ 1{\mathrm{c}\mathrm{m}}^{2} $ film of $ 80 nm $ thickness consists of $ {N}_{V} = 9.35\times {10}^{-7}mol $ Pd atoms in total. Hence, for this film $ {N}_{S}/{N}_{V} = 0.0027 $. Surface atom fractions $ {N}_{S}/{N}_{V} $ of films with other thicknesses are listed in the last column of Table 1. Assuming that at maximum 1 H atom is adsorbed per Pd surface atom [55], $ {N}_{S}/{N}_{V} $ represents the maximum surface site fraction of H atoms on the films.
For all investigated films apart from $ 200\mathrm{n}\mathrm{m} $nano crystalline Pd-H, Table 1 reveals $ {f}_{2} < {N}_{S}/{N}_{V} $. Thus, hydrogen adsorption to surface sites can explain the experimental findings. However, for most films a certain amount of surface sites seems to be blocked for hydrogen adsorption. For other surface sites, the natural surface oxide will be reduced by the formation of water molecules, which are dissolved in the electrolyte and open surface trap sites for H atoms. Thereby, the loss of hydrogen atoms by water formation in the electrochemical loading experiments results in an apparent lowering of the chemical potential in the plots of $ {\mu }_{H}\left({x}_{H}\right) $ in Figures 3 and 4. The related effect will be three times that of direct H trapping on the Pd surface: Two hydrogen atoms bind to one surface oxygen atom, and a further hydrogen atom binds to the nascent surface site after dissolution of the generated water molecule. According to the values of $ {f}_{2} $, hydrogen trapping in vacancies, again, is of minor importance in the measured Pd-H thin film isotherms.
One can estimate the volume fraction $ {v}_{1} $ of grain/domain boundary sites in the Pd films, when the site fractions $ {f}_{1} $ are identified with the defects’ volume fraction in the metal [22,37]. This implies that each defect site has the partial volume $ {v}_{0} $ of an octahedral interstitial site, compare Eq 10. This is analogous to an attempt of Löffler et al. [49], who successfully described the contribution of disordered grain boundaries to X-ray scattering intensities of nano crystalline bulk Pd, assuming that the atom density of disordered grain boundaries matches that of the crystal lattice.
Nano crystalline thin films often consist of columnar grains, ranging from the top close to the bottom of the film [57]. The multi-oriented and the epitaxial Pd films investigated in this study consist of large domains [41,58], that can be described as columns, as well. Assuming columnar grains/domains with diameter $ D $ and grain/domain boundaries of width $ ∆ $, the grain boundary volume fraction is given as (Eq 18)
With the established value of $ ∆ = 0.9 nm $ for grain boundaries in nano crystalline bulk Pd [2,59] according mean grain/domain sizes were calculated and are listed in the left column of Table 2 for the different Pd-H films.
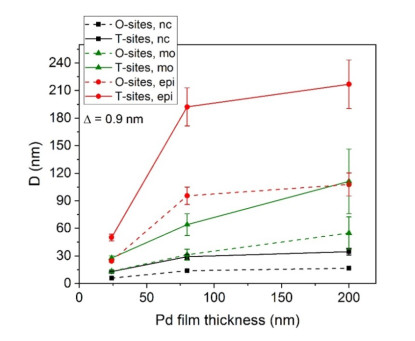
The resulting grain/domains sizes are of a reasonable order of magnitude, but they are systematically too small compared to measured lateral grain/domain sizes of the films as determined by SEM. For the example of the $ 200\mathrm{n}\mathrm{m} $ nano crystalline Pd film a lateral grain size of $ 30-50\mathrm{n}\mathrm{m} $ was measured [41,57,58]. But, the domains were measured to span more than $ 100 nm $ in the multi-oriented films and several hundred $ nm $ in the epitaxial films [41,57,58].
Considering this observation, different explanations are at hand. (ⅰ) first, the defect volume fractions might be over-estimated by Eq 14, if a significant kind of defect was neglected in Eq 10, for example dislocations. Another possible explanation might be linked to the assumption underlying Eq 18, e.g. that (ⅱ) the partial volume of grain boundary sites equals that of octahedral interstitial sites. Finally, (ⅲ) the adapted bulk grain boundary width $ ∆ $ might be too small for the thin films. These aspects are discussed subsequently.
To determine (ⅰ) the dislocation effect on the chemical potential of metal-hydrogen systems, the respective DOS of Eq 9 needs to be introduced into Eq 6. With a step-function approximation of the site occupancy, Kirchheim has shown that Eq 6 then yields the chemical potential contribution (Eq 19) [37].
with the hydrogen concentration $ {x}_{V} $ of dislocations.
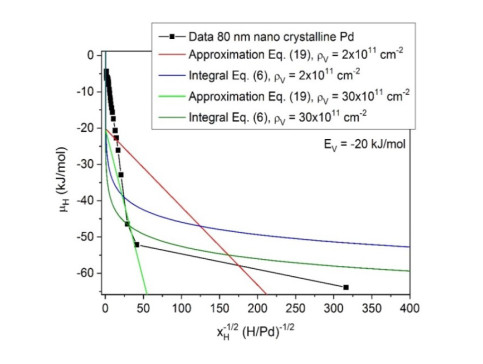
If $ {x}_{V} $ is not small, Eqs 6 with 9 needs to be integrated numerically. Both results are shown in Figure 8 for differently assumed dislocation densities $ \rho $ and compared to the data of the 80 nm nano crystalline Pd-H film. The hydride formation energy of the dislocations was set to $ {E}_{V} = -20\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l} $ [37]. The dislocation densities were set to $ \rho = 2\times {10}^{11}{\mathrm{c}\mathrm{m}}^{-2} $, which is typical for strongly deformed metals, and (for the plot) to $ \rho = 30\times {10}^{11}{\mathrm{c}\mathrm{m}}^{-2} $.
Figure 8 shows that the film data are not represented by the curves for reasonable dislocation densities. An un-physically high dislocation density would be needed to approach the data. The reason is that the measured chemical potential of hydrogen in the Pd films increases much slower with the film’s hydrogen concentration than predicted by a primary dislocation effect, see the supplemental information. Hence, in the chemical potential of the solid solution regime of Pd-H thin films dislocations do not play a major role, and they can be neglected in the DOS evaluation.
Assuming the site fractions $ {f}_{1} $ to be correct, (ⅱ) a possibility to explain too small calculated grain/domain sizes $ D $ can be found in the geometry of the grain/domain boundary sites. Boundary sites with different character than octahedral (O)-sites might be occupied—such as tetrahedral (T)-sites. In the fcc lattice two T-sites exist per metal atom, while there is only one O-site per atom [3]. The DOS in Eq 10, however, represents the numbers $ {f}_{i}^{O} $ of sites replacing O-sites. Hence, assuming T-boundary sites, Eq 10 needs to be re-written (Eq 20):
with $ {f}_{1}^{T} = 2\cdot {f}_{1}^{O}\dot{ = }{f}_{1} $ in Table 1. We note that in principle only $ 50\% $ of these T-sites (according to a maximum concentration of $ 1 H/Pd $) can be occupied by H atoms, since the nearest neighbour distance of the T-sites is 1.95 Å or 2.75 Å in the unit cell of palladium, respectively. The value of 1.95 Å is slightly smaller than Switendicks criterion for the minimum distance of 2.1 Å for neighbouring H atoms in the metal lattice due to a short ranged, repulsive electronic H-H interaction [59]. However, with a certain degree of disorder in the general grain/domain boundary fractions of the Pd thin films, one can assume that the positions of the T-sites are slightly distorted, making more T-sites available for hydrogen. Furthermore, in general it is not expected that the grain boundary sites are entirely occupied by H atoms, since the grain boundaries do not undergo hydride formation [22].
Since $ {f}_{1} $ is small, the consideration of T-sites does not significantly change the fitting parameters in Table 1. In case of the 80 nm nano crystalline Pd film $ {E}_{0} $ is reduced by $ 0.2\mathrm{k}\mathrm{J}/\mathrm{m}\mathrm{o}\mathrm{l} $, while the other fitting parameters remain constant. For most other films $ {f}_{1} $ is even smaller, yielding smaller corrections.
But, the change of the type of grain/domain boundary sites changes the volume density of domain boundaries in Eq 18, since (Eq 21)
yields (Eq 22)
for T-sites, when no restrictions apply for the T-site occupancy. Since $ ∆\ll D $, this scales up the lateral domain diameters $ D $ approximately by a factor of 2. The resulting domain sizes are listed in the right column of Table 2, as well. All domain sizes are plotted as a function of film thickness in Figure 9.
ⅲ) The third explanation could be a different grain boundary width $ ∆ $. According to Eq 22, the calculated grain/domain size $ D $ scales linearly with the geometrical boundary width $ ∆ $ (Eq 23),
Hence, the grain/domain sizes would scale up, if the grain/domain boundary width $ ∆ $ were larger than expected. This might be interpreted by a certain underestimation of the grain boundary width $ ∆ $ for the nano crystalline bulk Pd in reference [22], taking the possible fraction of surplus atoms into account, that may block sites for hydrogen occupation at the grain boundaries. If this assumption were correct, the enhanced open-volume of the grain/domain boundaries of the thin films would deliver further arguments for a lowered site energy of grain/domain sites of Pd-H thin films compared to the nano crystalline bulk Pd-H grain boundaries.
In total, the fitted DOS and the resulting domain sizes suggest that H atoms are occupying T-sites in the domain boundaries of Pd thin films rather than O-sites. This suggestion matches the observed site occupancy in amorphous metals [14,38,42]. It fits to the proposition of partly amorphous intergranular phase fractions in the nano crystalline bulk as well as the Pd-H thin films. Additionally, the grain boundary width seems to be slightly larger than 0.9 nm.
5.
Conclusions
The site energy distribution in Pd-H thin films can be successfully described by the proposed σDOS model which considers the substrate-induced stress impact as well as interstitial sites, grain boundary sites and deep trap sites for hydrogen. Within this σDOS model we can reveal information about the films’ microstructure.
This model is not restricted to Pd-H thin films, but it will be applicable to a variety of systems, where substrate-induced stresses and microstructural constituents significantly contribute to the site occupancy of solute atoms, that segregate to open-volume defects. This pure thermodynamic approach can supplement the microstructural analysis of alloy systems by other quantitative techniques, such as positron annihilation spectroscopy, neutron diffraction or transmission electron microscopy. This will be of high interest in the investigation of thin film metal-hydrogen systems containing special microstructural constituents of high content. Other examples are light elements such as carbon, nitrogen, oxygen or lithium in metals, but segregating metallic alloys such as bismuth in copper, as well.
Acknowledgements
Financial support of the Deutsche Forschungsgemeinschaft (DFG) via Projects PU131/7-2, PU131/9-1 and PU131/12-1 is gratefully acknowledged.
Conflict of interests
The authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: