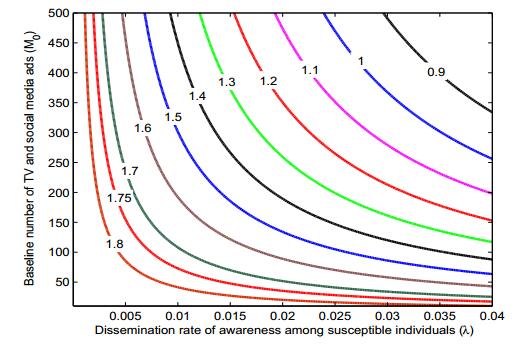
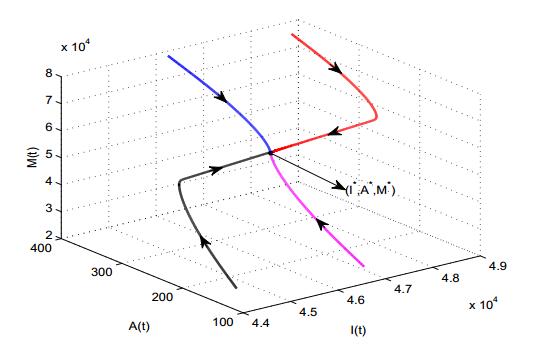
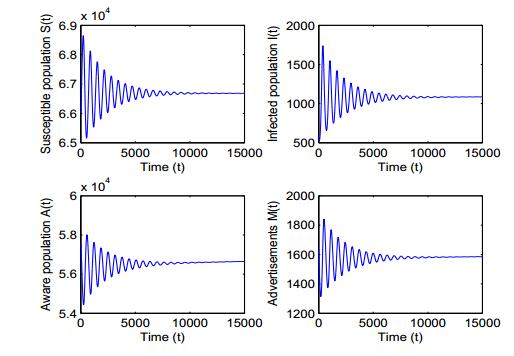
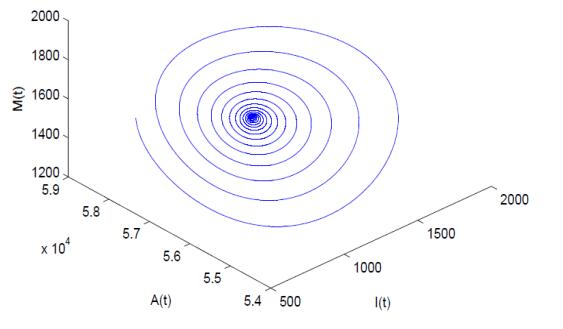
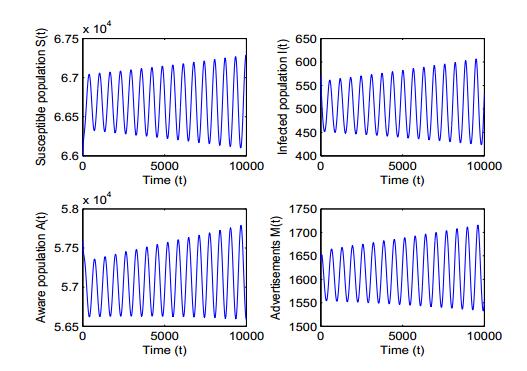
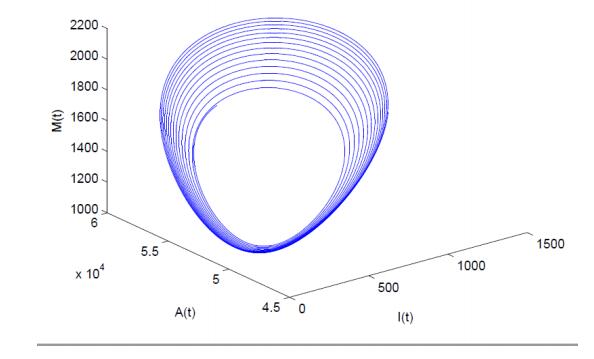
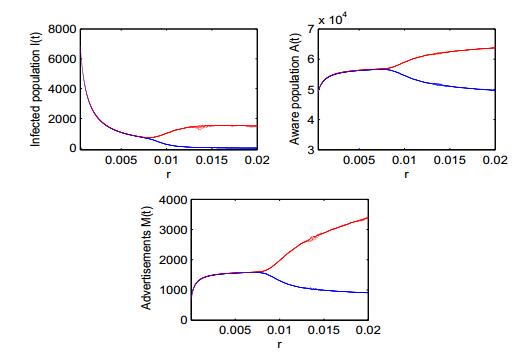
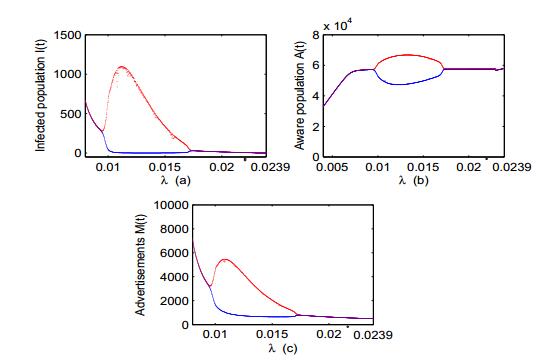
Public health information through media plays an important role to curb the spread of various infectious diseases as most of the populations rely on what media projects to them. Social media and TV advertisements are important mediums to communicate people regarding the spread of any infectious disease and methods to prevent its spread. Therefore, in this paper, we propose a mathematical model to see how TV and social media advertisements impact the dynamics of an infectious disease. The susceptible population is assumed vulnerable to infection as well as information (through TV and social media ads). It is also assumed that the growth rate of TV and social media ads is proportional to the number of infected individuals with decreasing function of aware individuals. The feasibility of possible equilibria and their stability properties are discussed. It is shown that the increment in growth rate of TV and social media ads destabilizes the system and periodic oscillations arise through Hopf-bifurcation. It is also found that the increase in dissemination rate of awareness among susceptible population also gives rise interesting dynamics about the stability of endemic equilibrium and causes stability switch. It is observed that TV and social media advertisements regarding the spread of infectious diseases have the potential to bring behavioral changes among the people and control the spread of diseases. Numerical simulations also support analytical findings.
1.
Introduction
Maize is a major crop of the North China Plain (NCP), which accounts for approximately more than 31% of the national grain production. To increase yield per unit area, farmers in this region typically apply 5–7 times of irrigation to crop via the conventional border irrigation method, with each time pumping of more than 60 mm water. As a result, annual groundwater withdrawal ranges from 600 to 800 mm yr–1 [1]. According to a report, over 7.6 million tubewells are used to pump groundwater across the region [2]. Consequently, excessive water pumping, continuously causing groundwater to drop at a rate of more than 1 m yr–1 [3]. The first aquifer is completely depleted, and the second aquifer is about to be depleted, as farmers pump water from the ground faster than it can refill. Furthermore, because of little precipitation, annual natural water replenishment is uncertain [4]. In the near future, the situation may become more difficult. For example, the water table in the counties surrounding Beijing is declining year after year, and rapid urbanisation has increased demand for water while reducing its availability [5–7]. Presently, the water shortage drastically limiting crop yield [8].
On the other hand, excessive use of N fertilizer in crop production posed a hazard to both terrestrial and aquatic ecosystems. A typical plant can only utilize half of the applied N fertilizer and remaining enters in water bodies via drainage [9]. In an estimate, 249 kg N ha–1 year–1 exceeds the crop N uptake capacity [10]. The N fertilizer is highly water–soluble, it transports with water on the wide range of soil types [11]. Many researchers showed that about 20% of N fertilizer loss takes place due to leaching [12]. Therefore, fertilizer N use efficiency in the region is often less than 20 to 25%, because farmers apply N fertilizer through broadcasting, which is an inefficient method as compared to modern techniques, such as application of water and nutrients through drip irrigation system [13,14].
The drip irrigation system consists of small diameter plastic pipes with outlets that drip a low rate of water into the soil. Unlike traditional border irrigation system, which saturate the entire soil, water is supplied near to the root-zone of plants, wetting only the region of the soil in which the roots grow. Water is applied more frequent with the drip irrigation system, ensuring full utilization of water stored in the soil profile and a very favourable high moisture content in the soil for plants to flourish. Despite the fact that drip irrigation system is only practiced on a small scale, it has a great potential for increasing production [15] improving photosynthesis rate [16], reducing evaporation, deep drainage, and save irrigation when compared to border irrigation method [14,17]. Drip irrigation significantly reduces evaporation without affecting transpiration rate of wheat crop [18]. Drip irrigation also enhances WUE of different crops and reduces water loss via drainage and runoff [19,20]. There are also many other advantages of drip irrigation system. Drip irrigation, in particular, maintains soil aeration, which promotes plant root growth, increases leaf area index, and improves grain quality. Despite these advantages, the drip is not well adopted in the agricultural system of the region. Due to water shortages in most areas, maize is frequently cultivated under rainfed conditions after border irrigation.
Many researchers have focused on spring maize and examined its yield potentiality under the impact of different agronomic methods to offset the effect of water shortage on crop production in the study area [1]. Still, modelling based information on water and nitrogen balance of spring maize under different irrigation methods is limited. In present study, we used WHCNS model as a tool to determine the N fate and water consumption, and to answer how much the WUE and FNUE changes under border irrigation method, drip irrigation and rainfed conditions. The model has been successfully applied in the NCP [21]. Wang et al. [22] reported that simulated soil water content, soil N content, crop biomass and N uptake matched well with the measured data.
The objectives were to; (i) compare grain yield, water consumption, N fates, WUE and FNUE of spring maize under different irrigation methods, (ii) evaluate simulation performance of WHCNS model, (iii) study effect of long-term dry and rainy seasons on spring maize.
2.
Materials and methods
2.1. Study area
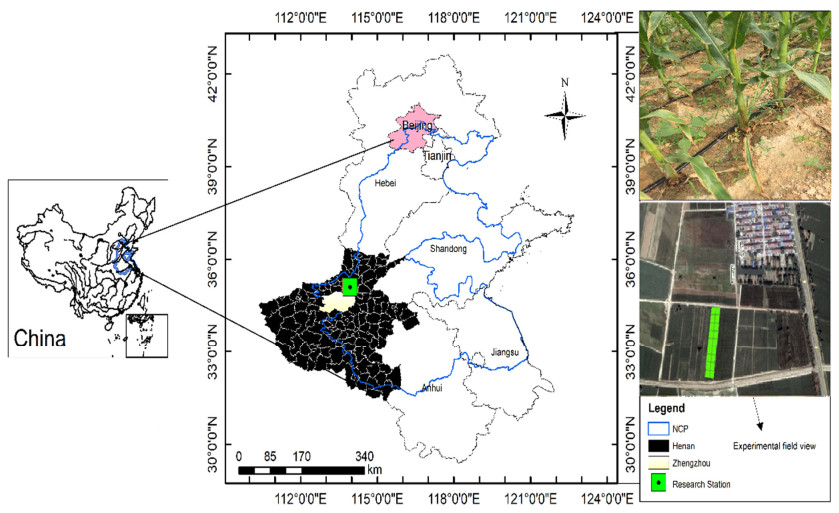
The research station is located in Yuanyang county (34.47° N, 113.38° E) of Zhengzhou, Henan province, China. The study area experiences warm temperate, sub–humid, and continental monsoon weather conditions (Figure 1). The mean annual temperature is 14.4 ℃ and rainfall is about 641 mm. Maximum rainfall (60–70%) occurs during spring maize growing season. Soil of experimental site has sandy loam texture (USDA classification), pH 8.2, organic matter 11.2 g kg–1, nitrate (N) 76.5 g kg–1, phosphorus (P) 8.2 g kg–1 and exchangeable (K) 67.3 g kg–1 [23,24]. The layer-wise basic soil properties are given in Table 1.
2.2. Experimental design
A two-year field experiment was conducted from 2018–2019. The experimental design was a randomized complete block design (RCBD), with four replications. There were three treatments, including conventional border irrigation method, drip irrigation and rainfed conditions. The plot size was 108 m2 (12 m long × 9 m wide). Each drip irrigation plot consisted of lateral pipes that delivered water directly to the root zones of the crops, while the sub–main pipeline system supplied water to the laterals. With a flow rate of 1.2 L h-1, the inner diameter of lateral drip pipes was 1.60 cm. For border irrigation and drip irrigation methods, there were separate water outlets and water meters to record the amount of irrigation. The irrigation system was controlled by a computer and a smartphone application [25].
2.3. Crop management
Spring maize variety Luobai–3 was sown on 13 April in 2018 and 14 April in 2019 at a row spacing of 60 cm with a seed rate of 30 kg ha–1. Total amount of irrigation under drip irrigation method was 90 mm (20–30 mm each time). Irrigation was applied when the field moisture level fell below 50% of the field capacity and irrigated to 80% of the field capacity. In the border irrigation method, the total irrigation amount was 150 mm (50 mm each time). For the strong seedling establishment, the full dose of phosphorus (25 kg P ha−1) and potassium (21 kg K ha−1) fertilizers was applied as a basal fertilizer. Superphosphate was used as a source of P fertilizer, and potassium chloride was used as a source of K fertilizer. For each treatment, the total amount of nitrogen (N) was 200 kg ha–1, from which 65% of the N fertilizer was incorporated in the soil before sowing. The plant density was 6–8 plants m2 at harvest time. Weed control, insect pest control, and disease control measures were all according to the local farmer practices. Manual hand hoeing was performed during the 2–3 leaf stage and mechanical plough operation was performed at 4–6 leaf stage. The crop was harvested on 24–25 September.
2.4. Observations and measurement procedures
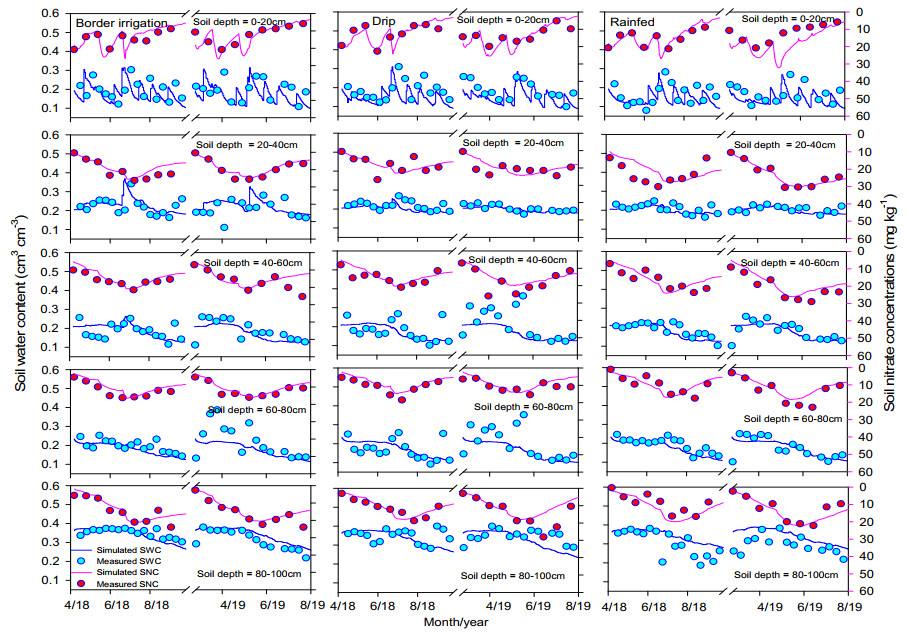
The soil bulk density and soil particle fraction were determined by the cutting ring method [26] and using hydrometer [27], respectively. Soil saturated and residual water contents were determined with the water retention curve [28]. Soil saturated hydraulic conductivity was measured using KSAT instrument. While soil water content was measured from different soil depths (0–100 cm at 20 cm intervals) in each experimental plot using on–field installed WiTu technology tubular moisture sensors. This sensor is new, modern, and most accurate to determine soil water content [29]. While, for determination of soil nitrate concentrations, soil samples were sieved with 4 mm sieves, extracted with 1 mol L–1 KCL (1:10, soil/water), and filtered. Ready samples were analyzed by a continuous flow analyzer (AA3, Bran and Luebbe, Germany). The grain yields and crop biomass were measured at harvest and different growth stages [30].
2.5. Detail of WHCNS model
Integrated WHCNS (Soil-Water-Heat-Carbon-Nitrogen-Simulator) model simulates crop growth and yield as a function of the soil–plant–atmosphere dynamics. The model consists of five primary modules, including (i) soil water, (ii) soil temperature (iii), carbon, (iv) nitrogen, and (v) crop growth. In the functional system of model, the simulation methods for soil water and temperature are imported from HYDRUS1D [31] and RZWQM models [32]. The FAO Penman–Monteith equation is used to compute the reference ET0 [33]. While water infiltration and redistribution are modelled via modified Green–Ampt [34] and Richard's [35] equations, respectively. Runoff is estimated using the SCS curve method [36]. Soil carbon and nitrogen cycles are adopted from the Daisy model [37] and crop growth and yields were projected using an improved PS123 model [38].
2.5.1. Input data of model
The model runs on a daily time step and requires latitude and longitude of site, soil saturated water content (θs), water content at field capacity (θfc), permanent wilting point (θwp), saturated hydraulic conductivity (Ks), soil C/N ratio (kg h–1), root, shoot and leaf weight (g), plant type (C3 or C4), sowing date, seed rate, and fertilizer dose, harvesting date, as well as daily rainfall, relative humidity, maximum, minimum and mean air temperature. The soil data, which were calibrated, is presented in Table 1, and basic crop parameters are given in Table 2. The meteorological data used in the model were acquired from an on–field established weather station.
2.5.2. Evaluation of model performance
To evaluate the WHNCS model simulations goodness of fit, the Relative Root Mean Square Error (RRMSE), Index of Agreement (IA) and Pearson Correlation Coefficient (r) were used.
where Oi is observed (or measured) value, Piis predicted value, and ˉO is the mean of the observed (or measured) values, n is the number of data values.
Statistically, RRMSE is a good indicator of model accuracy, lower the RRMSE (%), better the model performance [39], and IA valueranges from 0–1, close to 1, IA value represents a perfect match of simulated data with measured, and 0 specify no agreement [40]. Whereas Pearson correlation coefficient r value equal to either 1 or –1 illustrates perfect correlation between simulated and measured data [41].
In addition, the analysis of variance (ANOVA) was applied using Statistix 8.1 software (Analytical Software, Tallahassee, FL, USA) to calculate the overall effect of border, drip and rainfed conditions on spring maize. The significant differences among irrigation methods were determined using Fisher's LSD at P < 0.05 through the All–pairwise comparison method [42]. Furthermore, water balance and water use efficiency (WUE), nitrogen balance and nitrogen fertilizer use efficiency (FNUE), savings, and yield variations (%) were calculated using the following equations.
where, Wbal is water balance, I is Irrigation (mm); P is precipitation (mm); ET is evapotranspiration (mm) and D is drainage (mm), R is runoff (mm); WUE is water use efficiency; GY is grain yield (kg ha–1); WS is water-saving; WU is water use (mm); BI is border irrigation; DI is drip irrigation; RF is rainfed [43]; FNUE is fertilizer nitrogen use efficiency; YV is yield variation.
2.6. Scenario analysis on dry and rainy years from 2000 to 2017
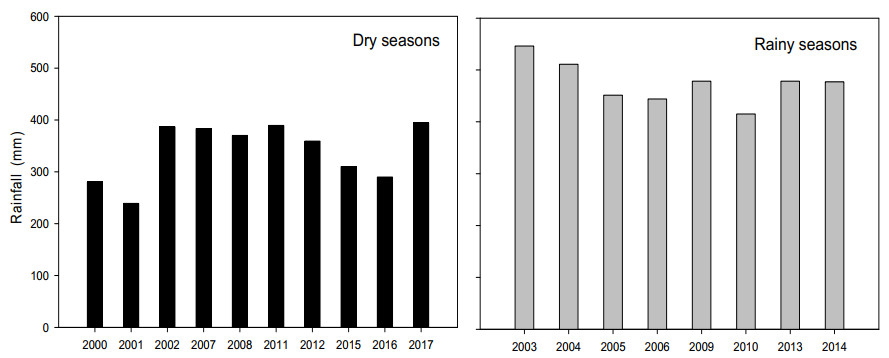
To extensively explore the effect of long-term dry and rainy seasons on spring maize yield, water movement, and N fate, we performed 18 years scenario analysis from 2000–2017. The border irrigation method was used as a basic treatment. The dry and rainy years were differentiated according to the method used by Murray-Tortarolo et al. [44] and Gao et al. [45]. Years with annual seasonal rainfall greater than the mean annual seasonal rainfall over 2000–2017 were identified as rainy years, while those that were less than the mean annual seasonal rainfall were separated as dry years. There was total 10 dry years and 8 rainy years (Figure 2). There is no broadly recognized criteria to justify rainy and dry years; therefore, separation is relative [45]. To avoid complexity, we used the long term mean annual season rainfall as a threshold level in the study. Figure 2 shows the differentiated dry and rainy seasons.
3.
Results
3.1. Calibration and evaluation of the model
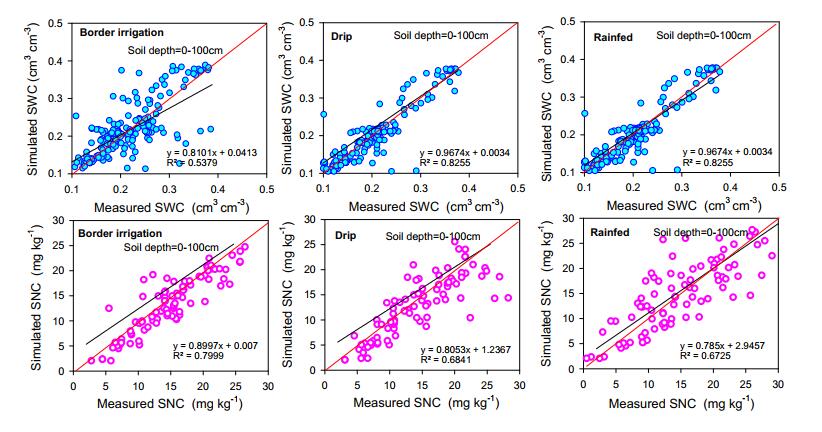
The model was calibrated using measured data (season 2018) of soil water content (cm3 cm–3), N concentrations (mg kg–1), crop biomass (kg ha–1), and grain yield under border irrigation method, drip irrigation and rainfed conditions, and then validated using data from the next year (season 2019). Highly sensitive crop and soil indicators were adjusted using a trial–and–error method during calibration to reduce the chance of error between simulated and measured data [46]. When compared to prior investigations, statistical evaluation of simulated data using absolute values revealed good model performance [47,48]. The model precisely predicted soil water content, N concentrations, crop biomass, and grain yield. The measured data points fluctuated up–down, close to the projected curve with the acceptable ranges of RRMSE values. The RRMSE varied under effect of different irrigation method and variables. Thus, top to deep soil layer (0–100 cm) RRMSE ranged from 5.0–36.0% for soil water content, 14.0–38.0% for soil nitrate concentrations, 19.0–24.0% for crop biomass and 1.0–2.0% for grain yield. In general, there is no threshold limit of RRMSE value. The model's performance considered good as the RRMSE or RMSE value decreases [49]. The maximum range of RRMSE for soil variables was relatively larger than crop growth and yield variables due to relatively high uncertainty and complex soil processes. Whereas IA values were between 0.53–0.91 for soil water content, 0.75–0.96 for soil nitrate concentrations, 0.97–0.98 for crop biomass, and 0.55–0.64 for grain yield. In the case of correlation coefficients, the r equal to 1 or close 1 existed between simulated and measured crop biomass and grain yields. Similarly, simulated soil water content and N concentrations had moderate to strong correlation with a minimum and maximum range of r corresponding to 0.43–0.98 (Table 3 and Figures 3 and 4). A strong correlation (r > 0.85) between measured and simulated for grain yield and biomass also reported by Shi et al. [46] with simulation error less than 10%.
3.2. Effect of different irrigation methods on spring maize yield
The farmer-based border irrigation method consumed a high amount of irrigation (300 mm) as compared to drip irrigation and showed a total grain yield of 20184 kg ha–1 (10021 kg ha–1 in 2018 and 10,163 kg ha–1 in 2019). Significantly (P < 0.05) high total grain yield 22949 kg ha–1 (11567 kg ha–1 in 2018 and 11382 kg ha–1 in 2019) obtained from drip irrigated maize at 40% decreased water (180 mm) for the two years. Thus, drip irrigation increased grain yield by 14 and 73% than border irrigation and rainfed maize, respectively. The rainfed maize exhibited total grain yield of 13249 kg ha–1 (6666 kg ha–1 in 2018 and 6584 kg ha–1 in 2019), which was 42% lower than drip irrigated maize because the rainfed plot was highly under water–stress. Throughout the experimental period, the distribution of precipitation was uneven. While vigorous plant growth and development, which promoted root growth, increased biomass accumulation, grain number, and cob length, was the key reason for better production from the drip irrigated maize. Figures 5 and 6 indicate the changes in yield from season to season as well as the physiological response of spring maize under different irrigation methods.
3.3. Effects of different irrigation methods on evaporation, transpiration, drainage, runoff, water balance, and water use efficiency
The simulated soil evaporation, crop transpiration, field drainage, and runoff as well as water balance and water use efficiencies under different irrigation methods, are present in Table 4. Both drainage and runoff were negligible under the drip irrigation method, and rainfed conditions and border irrigation had higher average drainage by 22.2 mm, and evaporation rates were decreased in the rainfed and drip fields. The rainfed and drip plots had an average evaporation rate of 139.5 and 153.5 mm, respectively. While border irrigation method exhibited 173.4 mm evaporation, which was 13% increased evaporation as compared to drip plot. In the case of crop transpiration, the drip and rainfed plots had 6–24% decreased water loss through transpiration than border irrigation method. The border irrigated plot had 209.4 mm transpiration. Minimum evapotranspiration from the drip plot indicates increased crop water use [50]. Furthermore, the drip field increased water balance by 46% as compared to border irrigation method. The border irrigation method showed an average 58.25 mm water balance. The lower water balance was under rainfed condition with 48.38 mm. Due to minimum water loss, the WUE of drip irrigated maize was 3.23 kg m–3, significantly higher than border irrigation method and rainfed maize. In the first season, the WUE under drip irrigation method was 3.41 kg m–3, and the subsequent year was 3.15 kg m–3. Thus, the order of WUE was drip irrigation > border irrigation > rainfed condition.
3.4. Effects of different irrigation methods on N fates, N balance, and N use efficiency
The summary of nitrogen fate under different irrigation methods is given in Table 5. Results showed that the N leaching was negligible under drip irrigation method and rainfed condition and higher in border method. The border irrigation treatment had an average N leaching of 21.8 kg ha–1. Whereas the ammonia volatilization was higher in both drip and rainfed plots and lowered in border irrigation method. The average ammonia volatilization was 19.5 kg ha–1 in drip irrigation method and 30 kg ha–1 in rainfed condition, significantly higher than border irrigation method. The N denitrification rates were minor in all treatments. The maximum N leaching under border irrigation method could be attributed to excessive application of water, and the reason of increased ammonia volatilization from rainfed and drip fields could be due to low moisture at the soil surface layer. In the case of N mineralization and crop N uptake. The border irrigated maize had an average 54.1 kg N ha–1 mineralization, and drip plot had 41 kg N mineralization ha–1. Despite this difference in N mineralization, the drip irrigated maize had almost equal N utilization. The average crop N uptake of the drip irrigated crop was 191 kg ha–1, which was only 1.2% lower than border irrigated maize and 4% higher than rainfed maize. Moreover, the drip irrigated maize field had significantly good N balance as compared to border irrigated and rainfed maize. The drip field had 27.2 kg ha–1 N balance, 51.3–63.7% higher than border and rainfed fields. Result showed that the drip irrigated maize also had higher FNUE. The FNUE of drip irrigated maize increased by 24.1%. Thus, the order of FNUE was drip irrigation > border irrigation > rainfed condition.
3.5. The long–term effect of dry and rainy years on spring maize yield, water and N dynamics
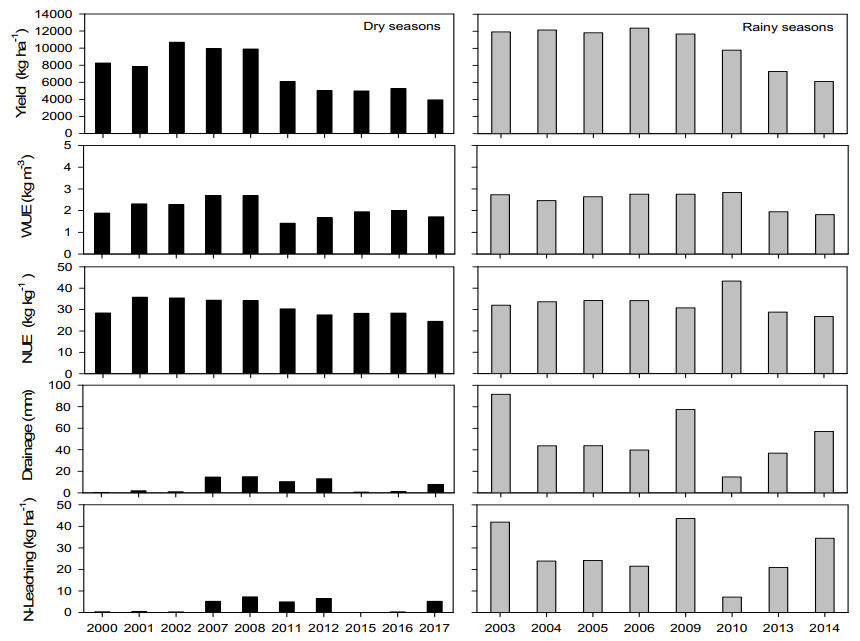
To evaluate the impact of climate change on spring maize yield, water, and nitrogen fate, we ran the model for the long-term period from 2000–2017. We selected conventional border irrigation method as a treatment. The model well-captured effect of dry and rainy seasons. The results showed that the rainfall anomaly significantly influences spring maize yield, water, and N balances. The yield bars were fluctuated high-low according to the rainfall variability. The lower the rate of rainfall, the lower the spring maize yield [46]. The dry season produced 30.8% low yield as compared to rainy season. The average yield for rainy years simulated as 10,386 kg ha–1 and for dry years as 7188 kg ha–1. Among the rainy years, maximum yields were 12,147 and 12,360 kg ha–1 in 2004 and 2006, respectively, whereas simulated yields in 2013 and 2014 rainy years were lowest. The reason of low yield during these seasons was rainfall uncertainty. Over 70% of rainfall occurred after 60 days of sowing. Consequently, both WUE and FNUE also affected. In dry and rainy seasons, the average WUEs were 2.06 and 2.49 kg m–3, and FNUEs were 30.71 and 32.97 kg kg–1, respectively. Furthermore, we found that N leaching was highly correlated with drainage amounts. Increased and decreased amount of drainage resulted in increased and decreased N leaching. The maximum average drainage was 50.6 mm, which resulted in 27.2 kg ha–1 N leaching. The year–wise simulated results are shown in Figure 6.
4.
Discussion
4.1. Water productivity of spring maize under different irrigation methods
Crop water productivity is strongly related to irrigation methods [52]. Farmers' based border irrigation methods tend to induce excessive soil water content in the topsoil layer, which possibly caused water-stress and subsequently affected grain yield [53]. The soil of the study area is predominantly sandy clay loam. It has hard surface layer due to low organic content [54]. Therefore, in current study, the border irrigation method showed 13% higher evaporation rate as compared to drip irrigation method. The drip irrigated maize not only reduced evaporation, but also maintained plant transpiration, thus increased yield by 14% with 40% water conservation. Compared to rainfed maize, the drip irrigated maize highly increased yield. The increase of yield under drip irrigation method, could be attributed to improved WUE. The results of yield increase, water saving and enhanced WUE of drip irrigated maize, agree with the findings of Zhou et al. [55] study, which showed that keeping soil moisture at an optimal level via reducing irrigation amounts and increasing number of irrigations, maximizes crop yield as compared to increasing soil water content by apply full irrigation [56]. In our study, drip irrigation primarily promoted growth of roots, biomass accumulation and then grain–filling. Figure 5 shows the effects of border irrigation method, drip and rainfed conditions on spring maize. Previously, also demonstrated by Sandhu et al. [57] and Yang et al. [18], they found that drip irrigation method improved maize yield by > 13% while reducing ET by 20 mm with significantly reduction in runoff rates and deep–drainage water losses. Similarly, Leghari et al. [21] compared yield and water-saving of spring maize under different irrigation methods and stated that drip irrigation increased yield by 9.8% at 62.5% reduced water consumption, improved WUE by 24.5% than border irrigation method. The increase of WUE was mainly due to a significant decrease in water loss. Overall, results suggesting that the drip irrigation method would ensure food security by increasing yield and maintain ecosystem.
4.2. Nitrogen use efficiency of spring maize under different irrigation methods
The loss of N due to volatilization, denitrification, and leaching is not only yield affecting factor, but it is also the main cause of maximal N deposition in terrestrial and aquatic systems. Because N in the form of NO3− is highly water–soluble, it moves freely with excessive water [58]. Plants can uptake half of the applied N and remaining resulting in environmental contamination. Wang et al. [22] reported that border irrigation method resulted in 97 to 186 kg N ha−1 leaching, while drip irrigation method reduced N leaching by 68%. The N emission losses including ammonia volatilization and denitrification were also higher under border irrigation method. Similarly, our study showed that border irrigation method is inefficient as compared to drip irrigation method, which is efficient due to high N productivity. The drip irrigated maize produced maximum yield while reducing N leaching loss by 97%, improving N utilization, and enhancing FNUE by 24%. These findings are in line with those of Li et al. [59] who found less than 40 kg and more than 50 kg ha–1 N leaching when irrigation application was less and greater than 300 mm ha–1. Reduced N losses in drip-irrigated maize could be due to direct N supplementation to the plant root zone in the required amount. Drip irrigation enhanced soil moisture first, then N uptake and thus improved nutrient management [60].
4.3. Spring maize response to long–term dry and rainy seasons
Maize is a drought-tolerance crop (ABA accumulates in leaf tissue, which induces stomatal closure). However, prolonged drought stress could adversely affect vegetative growth, biomass accumulation, formation of reproductive organs and yield attributes [48–61]. Deficit water-stress mainly reduces plant height due to decrease in photosynthesis and osmotic potential [62]. Scenario analysis on the long-term impact of climate change exhibited that rainfall distribution during the growing season is critical. For example, simulated yields in 2012 and 2017 seasons were 3943 and 5018 kg ha–1, respectively, lower than the rest of growing seasons due to rainfall irregularity from sowing to harvesting. On average, the dry years reduced yield by 30.8% as compared to rainy season. Similar yield response of spring maize according to the season to season variation in local weather conditions, also observed by Shi et al. [46] who found that the crop yields were decreased as rainfall decreased in 2011 and 2012. During the dry season, the supplemental application of water is recommended at the critical growth stage or when the crop is profoundly suffering from water stress and finally wilting up [63].
4.4. Limitations and future works
In this study, we simulated effect of border irrigation method, drip irrigation and rainfed conditions under farmer-based fertilizer application rate. The model was evaluated for crop growth and soil hydraulic parameters, except for N leaching and drainage, as well as evaporation and transpiration due to the unavailability of measured data. In future works, the model should be assessed for these factors under different irrigation methods. Furthermore, the exhibited results of model to the dry and rainy years, should be examined under long term field experiments for better understanding of the impact of dry and rainy seasons on crop yield, water, and N balances.
5.
Conclusions
The statistical indicators exhibited that the WHCNS model could be potentially used in the region to analyze the water movement and N cycling quantitatively. Based on the measured and modelled results, we found that the drip irrigation method would significantly improve crop yield as compared to conventional border irrigation method and rainfed. The drip irrigation not only increased grain yield but also conserved water by decreasing evaporation, drainage, and runoff. Moreover, the drip irrigation had a negligible amount of N leaching. Both WUE and FNUEs were higher in drip irrigated maize. Whereas border irrigation method resulted in increased evaporation as compared to drip irrigation, and this was a major pathway of water loss under the conventional border irrigation method. Despite drip irrigation system is costly, the water saving, and yield increase under drip irrigation suggesting suitability of this system in the NCP. Furthermore, considering rainfall variability based on long–term dry and rainy seasons, the scenario analysis showed that although maize is a drought tolerance crop, the rainfall uncertainty during the crop growth period could result in low yield.
Acknowledgments
The study was funded by China Agriculture Research System of MOF and MARA (CARS-02), National Key Research and Development Program of China (2017YFD0301102–5) and Leading Talent Project of Science and Technology Innovation of Central Plains (194200510008).
Conflicts of interest
The authors have declared that no competing interests exist.









 DownLoad:
DownLoad: