On circuital topologies and reconfiguration strategies for PV systems inpartial shading conditions: A review

Antonino Laudani; Gabriele Maria Lozito; Valentina Lucaferri; Martina Radicioni; Francesco Riganti Fulginei; Antonino Laudani; Gabriele Maria Lozito; Valentina Lucaferri; Martina Radicioni; Francesco Riganti Fulginei

doi:10.3934/energy.2018.5.735

AIMS Energy

2018, Volume 6, Issue 5: 735-763. doi: 10.3934/energy.2018.5.735

Previous Article Next Article

Review Topical Sections

On circuital topologies and reconfiguration strategies for PV systems inpartial shading conditions: A review

Department of Engineering, Roma Tre University, Via Vito Volterra 62, Rome, Italy

Received: 26 June 2018 Accepted: 06 September 2018 Published: 19 September 2018

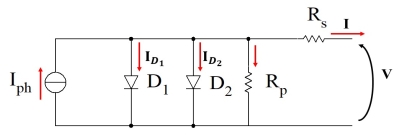
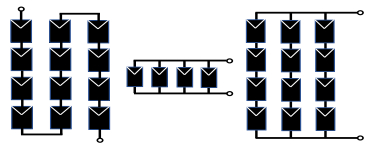
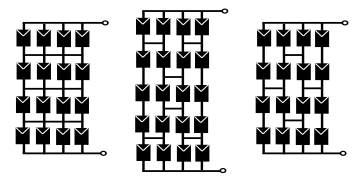
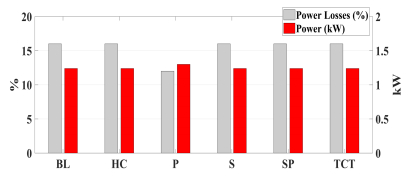
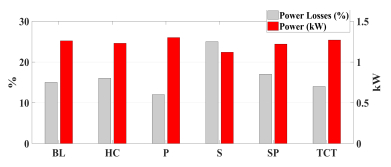
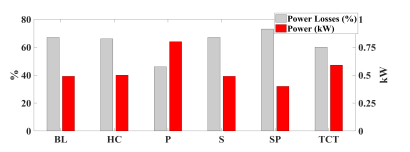
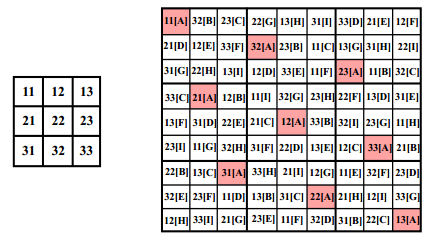
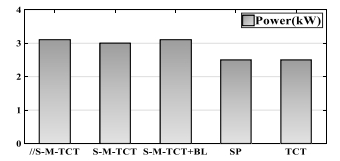
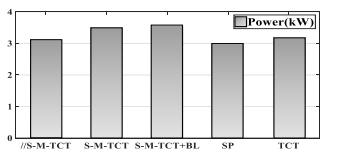
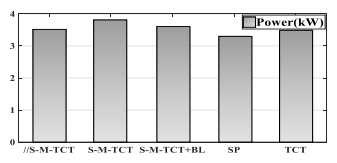
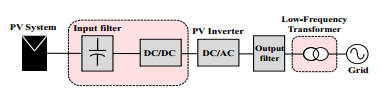
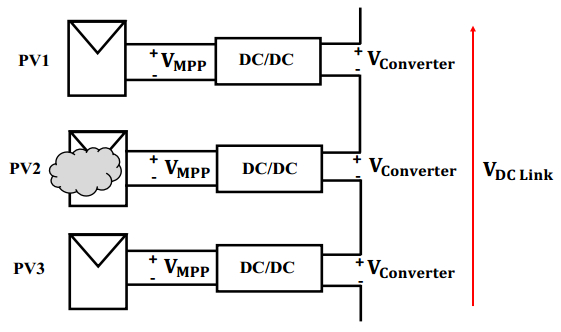
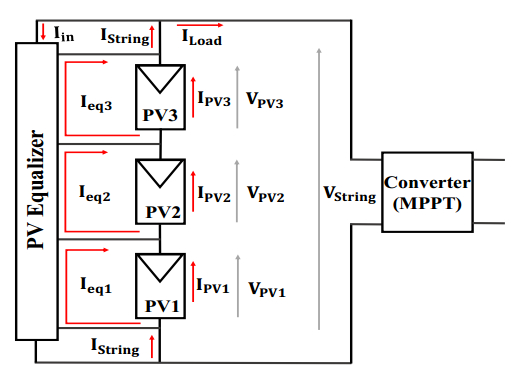
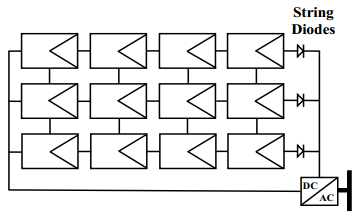
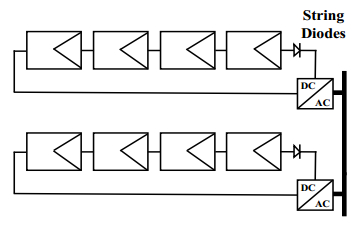
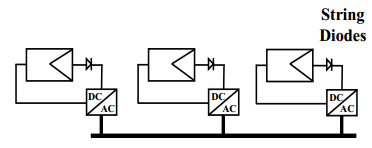
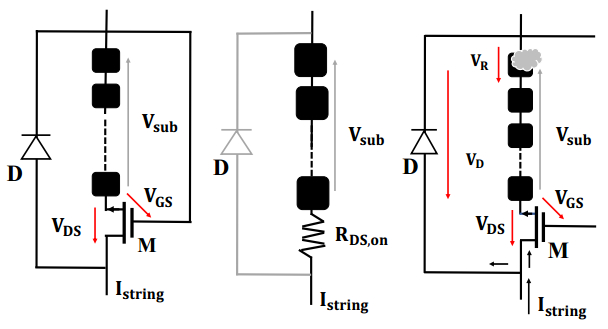
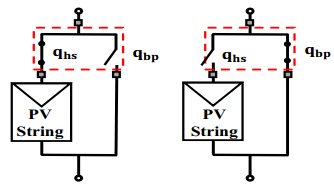
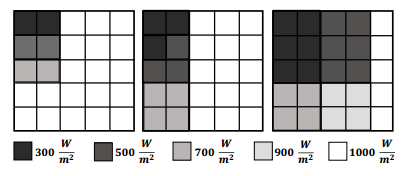
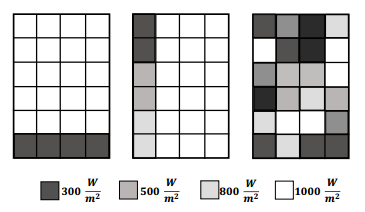
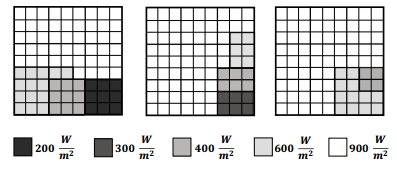
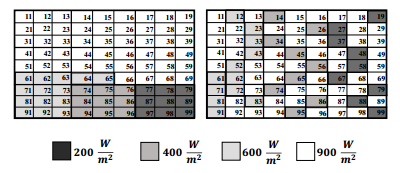
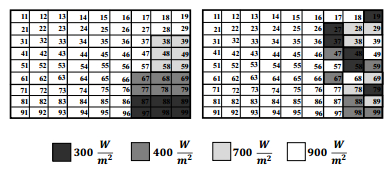
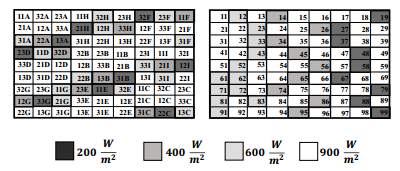
Photovoltaic (PV) power generation is heavily influenced by mismatching conditions, mainly caused by partial or full shading of an array portion. Such a non-uniform irradiation can lead to severe reductions in the power produced; some techniques, such as array reconfiguration or microconverters and microinverters technology are aimed at retrieving this power together with the use of Maximum Power Point (MPP) tracker algorithms, while others tend to mitigate the effects that power losses have on the PV system, i.e. overheating and aging. Solutions based on the use of bypass diodes and their re-adapted forms belong to this latter case. The complexity of the problem has shown the need of analyzing the role played by each one of the mentioned aspects; the focus of this paper is to give the reader a detailed review of the main solutions to PV arrays shading present in literature.

Keywords:

Citation: Antonino Laudani, Gabriele Maria Lozito, Valentina Lucaferri, Martina Radicioni, Francesco Riganti Fulginei. On circuital topologies and reconfiguration strategies for PV systems inpartial shading conditions: A review[J]. AIMS Energy, 2018, 6(5): 735-763. doi: 10.3934/energy.2018.5.735

Related Papers:

[1]	Guy M. Toche Tchio, Joseph Kenfack, Joseph Voufo, Yves Abessolo Mindzie, Blaise Fouedjou Njoya, Sanoussi S. Ouro-Djobo . Diagnosing faults in a photovoltaic system using the Extra Trees ensemble algorithm. AIMS Energy, 2024, 12(4): 727-750. doi: 10.3934/energy.2024034
[2]	Lasanthika Dissawa, Nirmana Perera, Kapila Bandara, Prabath Binduhewa, Janaka Ekanayake . Thirteen-level inverter for photovoltaic applications. AIMS Energy, 2016, 4(2): 397-413. doi: 10.3934/energy.2016.2.397
[3]	David Ludwig, Christian Breyer, A.A. Solomon, Robert Seguin . Evaluation of an onsite integrated hybrid PV-Wind power plant. AIMS Energy, 2020, 8(5): 988-1006. doi: 10.3934/energy.2020.5.988
[4]	M Saad Bin Arif, Uvais Mustafa, Shahrin bin Md. Ayob . Extensively used conventional and selected advanced maximum power point tracking techniques for solar photovoltaic applications: An overview. AIMS Energy, 2020, 8(5): 935-958. doi: 10.3934/energy.2020.5.935
[5]	J. Appelbaum . Shading and masking affect the performance of photovoltaic systems—a review. AIMS Energy, 2019, 7(1): 77-87. doi: 10.3934/energy.2019.1.77
[6]	Mesude Bayrakci Boz, Kirby Calvert, Jeffrey R. S. Brownson . An automated model for rooftop PV systems assessment in ArcGIS using LIDAR. AIMS Energy, 2015, 3(3): 401-420. doi: 10.3934/energy.2015.3.401
[7]	Zijian Hu, Hong Zhu, Chen Deng . Distribution network reconfiguration optimization method based on undirected-graph isolation group detection and the whale optimization algorithm. AIMS Energy, 2024, 12(2): 484-504. doi: 10.3934/energy.2024023
[8]	Kaovinath Appalasamy, R Mamat, Sudhakar Kumarasamy . Smart thermal management of photovoltaic systems: Innovative strategies. AIMS Energy, 2025, 13(2): 309-353. doi: 10.3934/energy.2025013
[9]	Sabir Rustemli, Zeki İlcihan, Gökhan Sahin, Wilfried G. J. H. M. van Sark . A novel design and simulation of a mechanical coordinate based photovoltaic solar tracking system. AIMS Energy, 2023, 11(5): 753-773. doi: 10.3934/energy.2023037
[10]	Abdollah Kavousi-Fard, Amin Khodaei . Multi-objective optimal operation of smart reconfigurable distribution grids. AIMS Energy, 2016, 4(2): 206-221. doi: 10.3934/energy.2016.2.206

Abstract

1. Introduction

In 1960, Opial ^[12] established the following inequality:

Theorem A Suppose $f\in C^{1}[0, h]$ satisfies $f(0) = f(h) = 0$ and $f(x) > 0$ for all $x\in (0, h).$ Then the inequality holds

$\begin{align} \int_{0}^h\left|f(x)f'(x)\right|dx\leq\frac{h}{4}\int_{0}^{h}(f'(x))^{2}dx, \end{align}$

(1.1)

where this constant $h/4$ is best possible.

Many generalizations and extensions of Opial's inequality were established ^{[2,4,5,6,7,8,9,10,11,15,16,17,18,19]}. For an extensive survey on these inequalities, see ^[13]. Opial's inequality and its generalizations and extensions play a fundamental role in the ordinary and partial differential equations as well as difference equation ^{[2,3,4,6,7,9,10,11,17]}. In particular, Agarwal and Pang ^[3] proved the following Opial-Wirtinger's type inequalities.

Theorem B Let $\lambda\geq 1$ be a given real number, and let $p(t)$ be a nonnegative and continuous function on $[0, a]$ . Further, let $x(t)$ be an absolutely continuous function on $[0, a]$ , with $x(0) = x(a) = 0$ . Then

$\begin{align} \int_{0}^{a}p(t)|x(t)|^{\lambda}dt\leq\frac{1}{2}\int_{0}^{a}[t(a-t)]^{(\lambda-1)/2}p(t)dt\int_{0}^{a}\left|x'(t) \right|^{\lambda}dt. \end{align}$

(1.2)

The first aim of the present paper is to establish Opial-Wirtinger's type inequalities involving Katugampola conformable partial derivatives and $\alpha$ -conformable integrals (see Section 2). Our result is given in the following theorem, which is a generalization of (1.2).

Theorem 1.1 Let $\lambda\geq 1$ be a real number and $\alpha\in (0, 1]$ , and let $p(s, t)$ be a nonnegative and continuous functions on $[0, a]\times [0, b]$ . Further, let $x(s, t)$ be an absolutely continuous function and Katugampola partial derivable on $[0, a]\times [0, b]$ , with $x(s, 0) = x(0, t) = x(0, 0) = 0$ and $x(a, b) = x(a, t) = x(s, b) = 0$ . If $p > 1,$ $\frac{1}{p}+\frac{1}{q} = 1$ Then

$\int_{0}^{a}\int_{0}^{b}p(s, t)|x(s, t)|^{\lambda}d_{\alpha}sd_{\alpha}t\leq\frac{p+q}{pq} \left(\frac{1}{\alpha^{2}}\right)^{\lambda-1}\left(\int_{0}^{a}\int_{0}^{b}\Gamma_{abpq\lambda\alpha}(s, t)\cdot p(s, t)d_{\alpha}sd_{\alpha}t\right)$

$\begin{align} \times\int_{0}^{a}\int_{0}^{b}\left|\frac{\partial^{2}}{\partial s\partial t}(x)_{\alpha^{2}}(s, t)\right|^{\lambda}d_{\alpha}sd_{\alpha}t, \end{align}$

(1.3)

where

$\Gamma_{abpq\lambda\alpha}(s, t) = \left\{(st)^{1/p}[(a-s)(b-t)]^{1/q}\right\}^{\alpha(\lambda-1)}.$

Remark 1.1 Let $x(s, t)$ reduce to $s(t)$ and with suitable modifications, and $p = q = 2$ and $\alpha = 1$ , (1.3) become (1.2).

Theorem C Let $\lambda\geq 1$ be a given real number, and let $p(t)$ be a nonnegative and continuous function on $[0, a]$ . Further, let $x(t)$ be an absolutely continuous function on $[0, a]$ , with $x(0) = x(a) = 0$ . Then

$\begin{align} \int_{0}^{a}p(t)|x(t)|^{\lambda}dt\leq\frac{1}{2}\left(\frac{a}{2} \right)^{\lambda-1}\left(\int_{0}^{a}p(t)dt\right)\int_{0}^{a}\left|x'(t)\right|^{\lambda}dt. \end{align}$

(1.4)

Another aim of this paper is to establish the following inequality involving Katugampola conformable partial derivatives and $\alpha$ -conformable integrals. Our result is given in the following theorem.

Theorem 1.2 Let $j = 1, 2$ and $\lambda\geq 1$ be a real number, and let $p_{j}(s, t)$ be a nonnegative and continuous functions on $[0, a]\times [0, b]$ . Further, let $x_{j}(s, t)$ be an absolutely continuous function and Katugampola partial derivable on $[0, a]\times [0, b]$ , with $x_{j}(s, 0) = x_{j}(0, t) = x_{j}(0, 0) = 0$ and $x_{j}(a, b) = x_{j}(a, t) = x_{j}(s, b) = 0$ . Then for $\alpha\in(0, 1]$

$\int_{0}^{a}\int_{0}^{b}\left(p_{1}(s, t)|x_{1}(s, t)|^{\lambda}+p_{2}(s, t)|x_{2}(s, t)|^{\lambda}\right)d_{\alpha}sd_{\alpha}t\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \;$

$\leq\frac{1}{2^{\lambda}}\left(\frac{1}{\alpha^{2}}\right)^{\lambda-1}\Bigg[\left(\int_{0}^{a}\int_{0}^{b}(st)^{\alpha(\lambda-1)}p_{1}(s, t) d_{\alpha}sd_{\alpha}t\right)\int_{0}^{a}\int_{0}^{b}\left|\frac{\partial^{2}}{\partial s\partial t}(x_{1})_{\alpha^{2}}(s, t)\right|^{\lambda} d_{\alpha}sd_{\alpha}t$

$\begin{align} +\left(\int_{0}^{a}\int_{0}^{b}(st)^{\alpha(\lambda-1)}p_{2}(s, t)d_{\alpha}sd_{\alpha}t\right)\int_{0}^{a}\int_{0}^{b}\left|\frac{\partial^{2}}{\partial s\partial t}(x_{2})_{\alpha^{2}}(s, t)\right|^{\lambda}d_{\alpha}sd_{\alpha}t\Bigg]. \end{align}$

(1.5)

2. Katugampola conformable partial derivatives

Here, let's recall the well-known Katugampola derivative formulation of conformable derivative of order for $\alpha\in(0, 1]$ and $t\in[0, \infty)$ , given by

$\begin{align} {\cal D}_{\alpha}(f)(t) = \lim\limits_{\varepsilon\rightarrow 0}\frac{f(te^{\varepsilon t^{-\alpha}})-f(t)}{\varepsilon}, \end{align}$

(2.1)

and

$\begin{align} {\cal D}_{\alpha}(f)(0) = \lim\limits_{t\rightarrow 0}D_{\alpha}(f)(t), \end{align}$

(2.2)

provided the limits exist. If $f$ is fully differentiable at $t$ , then

${\cal D}_{\alpha}(f)(t) = t^{1-\alpha}\frac{df}{dt}(t).$

A function $f$ is $\alpha$ -differentiable at a point $t\geq 0$ , if the limits in (2.1) and (2.2) exist and are finite. Inspired by this, we propose a new concept of $\alpha$ -conformable partial derivative. In the way of (1.4), $\alpha$ -conformable partial derivative is defined in as follows:

Definition 2.1 ^[20] ( $\alpha$ -conformable partial derivative) Let $\alpha\in (0, 1]$ and $s, t\in[0, \infty)$ . Suppose $f(s, t)$ is a continuous function and partial derivable, the $\alpha$ -conformable partial derivative at a point $s\geq 0$ , denoted by $\frac{\partial}{\partial s}(f)_{\alpha}(s, t)$ , defined by

$\begin{align} \frac{\partial}{\partial s}(f)_{\alpha}(s, t) = \lim\limits_{\varepsilon\rightarrow 0}\frac{f(se^{\varepsilon s^{-\alpha}}, t)-f(s, t)} {\varepsilon}, \end{align}$

(2.3)

provided the limits exist, and call $\alpha$ -conformable partial derivable.

Recently, Katugampola conformable partial derivative is defined in as follows:

Definition 2.2 ^[20] (Katugampola conformable partial derivatives) Let $\alpha\in (0, 1]$ and $s, t\in[0, \infty)$ . Suppose $f(s, t)$ and $\frac{\partial}{\partial s}(f)_{\alpha}(s, t)$ are continuous functions and partial derivable, the Katugampola conformable partial derivative, denoted by $\frac{\partial^{2}}{\partial s\partial t}(f)_{\alpha^{2}}(s, t)$ , defined by

$\begin{align} \frac{\partial^{2}}{\partial s\partial t}(f)_{\alpha^{2}}(s, t) = \lim\limits_{\varepsilon\rightarrow 0}\frac{\frac{\partial}{\partial s}(f)_{\alpha}(s, te^{\varepsilon t^{-\alpha}})-\frac{\partial}{\partial s}(f)_{\alpha}(s, t)}{\varepsilon}, \end{align}$

(2.4)

provided the limits exist, and call Katugampola conformable partial derivable.

Definition 2.3 ^[20] ( $\alpha$ -conformable integral) Let $\alpha\in (0, 1]$ , $0\leq a < b$ and $0\leq c < d$ . A function $f(x, y):[a, b]\times[c, d]\rightarrow {\Bbb R}$ is $\alpha$ -conformable integrable, if the integral

$\begin{align} \int_{a}^{b}\int_{c}^{d}f(x, y)d_{\alpha}xd_{\alpha}y: = \int_{a}^{b}\int_{c}^{d} (xy)^{\alpha-1}f(x, y)dxdy \end{align}$

(2.5)

exists and is finite.

3. Main results

Theorem 3.1 Let $\lambda\geq 1$ be a real number and $\alpha\in (0, 1]$ , and let $p(s, t)$ be a nonnegative and continuous functions on $[0, a]\times [0, b]$ . Further, let $x(s, t)$ be an absolutely continuous function and Katugampola partial derivable on $[0, a]\times [0, b]$ , with $x(s, 0) = x(0, t) = x(0, 0) = 0$ and $x(a, b) = x(a, t) = x(s, b) = 0$ . If $p > 1,$ $\frac{1}{p}+\frac{1}{q} = 1$ Then

$\begin{align} \times\int_{0}^{a}\int_{0}^{b}\left|\frac{\partial^{2}}{\partial s\partial t}(x)_{\alpha^{2}}(s, t)\right|^{\lambda}d_{\alpha}sd_{\alpha}t, \end{align}$

(3.1)

where

$\Gamma_{abpq\lambda\alpha}(s, t) = \left\{(st)^{1/p}[(a-s)(b-t)]^{1/q}\right\}^{\alpha(\lambda-1)}.$

Proof From (2.4) and (2.5), we have

$x(s, t) = \int_{0}^{s}\int_{0}^{t}\frac{\partial^{2}}{\partial s\partial t}(x)_{\alpha^{2}}(s, t)d_{\alpha}sd_{\alpha}t.$

By using Hölder's inequality with indices $\lambda$ and $\lambda/(\lambda-1)$ , we have

$|x(s, t)|^{\lambda/p}\leq \left[\left(\int_{0}^{s}\int_{0}^{t}\left|\frac{\partial^{2}}{\partial s\partial t} (x)_{\alpha^{2}}(s, t)\right|d_{\alpha}sd_{\alpha}t\right)^{\lambda}\right]^{1/p}\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \;$

$\begin{align} \leq\left(\frac{1}{\alpha^{2}}(st)^{\alpha}\right)^{(\lambda-1)/p}\left(\int_{0}^{s}\int_{0}^{t}\left|\frac{\partial^{2}}{\partial s\partial t}(x)_{\alpha^{2}}(s, t)\right|^{\lambda}d_{\alpha}sd_{\alpha}t\right)^{1/p}. \end{align}$

(3.2)

Similarly, from

$x(s, t) = \int_{s}^{a}\int_{t}^{b}\frac{\partial^{2}}{\partial s\partial t}(x)_{\alpha^{2}}(s, t)d_{\alpha}sd_{\alpha}t,$

we obtain

$\begin{align} |x(s, t)|^{\lambda/q}\leq \left(\frac{1}{\alpha^{2}}[(a-s)(b-t)]^{\alpha}\right)^{(\lambda-1)/q} \left(\int_{s}^{a}\int_{t}^{b}\left|\frac{\partial^{q}}{\partial s\partial t}(x)_{\alpha^{2}}(s, t)\right|^{\lambda}d_{\alpha}sd_{\alpha}t\right)^{1/q}. \end{align}$

(3.3)

Now a multiplication of (3.2) and (3.3), and by using the well-known Young inequality gives

$\begin{eqnarray*} |x(s, t)|^{\lambda}&\leq &\left(\frac{1}{\alpha^{2}}\right)^{\lambda-1}\cdot\Gamma_{abpq\lambda\alpha}(s, t)\cdot\left(\int_{0}^{s}\int_{0}^{t} \left|\frac{\partial^{2}}{\partial s\partial t}(x)_{\alpha^{2}}(s, t)\right|^{\lambda}d_{\alpha}sd_{\alpha}t\right)^{1/p}\\ &\times&\left(\int_{s}^{a}\int_{t}^{b}\left|\frac{\partial^{2}}{\partial s\partial t}(x)_{\alpha^{2}}(s, t)\right|^{\lambda}d_{\alpha}sd_{\alpha}t\right)^{1/q}\\ &\leq &\left(\frac{1}{\alpha^{2}}\right)^{\lambda-1}\cdot\Gamma_{abpq\lambda\alpha}(s, t)\cdot\Bigg(\frac{1}{p}\int_{0}^{s}\int_{0}^{t}\left|\frac{\partial^{2}}{\partial s\partial t}(x)_{\alpha^{2}}(s, t)\right|^{\lambda}d_{\alpha}sd_{\alpha}t\\ &+&\frac{1}{q}\int_{s}^{a}\int_{t}^{b}\left|\frac{\partial^{2}}{\partial s\partial t}(x)_{\alpha^{2}}(s, t)\right|^{\lambda}d_{\alpha}sd_{\alpha}t\Bigg) \end{eqnarray*}$

$\begin{align} \; \; \; \; \; \; \; \; \; \; = \frac{p+q}{pq}\left(\frac{1}{\alpha^{2}}\right)^{\lambda-1}\cdot\Gamma_{abpq\lambda\alpha}(s, t)\int_{0}^{a}\int_{0}^{b}\left|\frac{\partial^{2}}{\partial s\partial t}(x)_{\alpha^{2}}(s, t)\right|^{\lambda}d_{\alpha}sd_{\alpha}t, \end{align}$

(3.4)

where

$\Gamma_{abpq\lambda\alpha}(s, t) = \Big\{(st)^{1/p}[(a-s)(b-t)]^{1/q}\Big\} ^{\alpha(\lambda-1)}.$

Multiplying the both sides of (3.4) by $p(s, t)$ and $\alpha$ –conformable integrating both sides over $t$ from $0$ to $b$ first and then integrating the resulting inequality over $s$ from $0$ to $a$ , we obtain

$\int_{0}^{a}\int_{0}^{b}p(s, t)|x(s, t)|^{\lambda}d_{\alpha}sd_{\alpha}t\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \;$

$\leq\frac{p+q}{pq}\left(\frac{1}{\alpha^{2}}\right)^{\lambda-1}\cdot\int_{0}^{a}\int_{0}^{b}\Gamma_{abpq\lambda\alpha}(s, t)\cdot p(s, t)\left(\int_{0}^{a}\int_{0}^{b}\left|\frac{\partial^{2}}{\partial s\partial t}(x)_{\alpha^{2}}(s, t)\right|^{\lambda}d_{\alpha}sd_{\alpha}t\right)d_{\alpha}sd_{\alpha}t$

$= \frac{p+q}{pq}\left(\frac{1}{\alpha^{2}}\right)^{\lambda-1}\cdot\left(\int_{0}^{a}\int_{0}^{b}\Gamma_{abpq\lambda\alpha}(s, t)\cdot p(s, t)d_{\alpha}sd_{\alpha}t\right)\int_{0}^{a}\int_{0}^{b}\left|\frac{\partial^{2}}{\partial s\partial t}(x)_{\alpha^{2}}(s, t)\right|^{\lambda}d_{\alpha}sd_{\alpha}t.$

This completes the proof.

Remark 3.1 Let $x(s, t)$ reduce to $s(t)$ and with suitable modifications, (3.1) becomes the following result.

$\begin{align} \int_{0}^{a}p(t)|x(t)|^{\lambda}d_{\alpha}t\leq\frac{p+q}{pq}\left(\frac{1}{\alpha^{2}}\right)^{\lambda-1}\cdot\int_{0}^{a} \Gamma_{apq\lambda\alpha}(t)p(t)d_{\alpha}t\int_{0}^{a}\left|{\cal D}_{\alpha}(x)(t) \right|^{\lambda}d_{\alpha}t, \end{align}$

(3.5)

where ${\cal D}_{\alpha}(x)(t)$ is Katugampola derivative (2.1) stated in the introduction, and

$\Gamma_{apq\lambda\alpha}(t) = \Big\{t^{1/p}(a-t)^{1/q}\Big\} ^{\alpha(\lambda-1)}.$

Putting $p = q = 2$ and $\alpha = 1$ in (3.5), (3.5) becomes inequality (1.2) established by Agarwal and Pang ^[3] stated in the introduction.

Taking for $\alpha = 1$ , $p = q = 2$ and $p(s, t) = {\rm constant}$ in (3.1), we have the following interesting result.

$\int_{0}^{a}\int_{0}^{b}|x(s, t)|^{\lambda}dsdt\leq \frac{1}{2}(ab)^{\lambda}\left[B\left(\frac{\lambda+1}{2}, \frac{\lambda+1}{2}\right)\right] ^{2}\int_{0}^{a}\int_{0}^{b}\left|\frac{\partial^{2}}{\partial s\partial t}x(s, t)\right|^{\lambda}dsdt,$

where $B$ is the Beta function.

Theorem 3.2 Let $j = 1, 2$ and $\lambda\geq 1$ be a real number, and let $p_{j}(s, t)$ be a nonnegative and continuous functions on $[0, a]\times [0, b]$ . Further, let $x_{j}(s, t)$ be an absolutely continuous function and Katugampola partial derivable on $[0, a]\times [0, b]$ , with $x_{j}(s, 0) = x_{j}(0, t) = x_{j}(0, 0) = 0$ and $x_{j}(a, b) = x_{j}(a, t) = x_{j}(s, b) = 0$ . Then for $\alpha\in(0, 1]$

(3.6)

Proof Because

$x_{1}(s, t) = \int_{0}^{s}\int_{0}^{t}\frac{\partial^{2}}{\partial s\partial t}(x_{1})_{\alpha^{2}}(s, t)d_{\alpha}sd_{\alpha}t = \int_{s}^{a}\int_{t}^{b}\frac{\partial^{2}}{\partial s\partial t}(x_{1})_{\alpha^{2}}(s, t)d_{\alpha}sd_{\alpha}t.$

Hence

$|x_{1}(s, t)|\leq\frac{1}{2}\int_{0}^{a}\int_{0}^{b}\left|\frac{\partial^{2}}{\partial s\partial t}(x_{1})_{\alpha^{2}}(s, t)\right|d_{\alpha}sd_{\alpha}t.$

By Hölder's inequality with indices $\lambda$ and $\lambda/(\lambda-1)$ , it follows that

$p_{1}(s, t)|x_{1}(s, t)|^{\lambda}\leq\frac{1}{2^{\lambda}}p_{1}(s, t)\left(\int_{0}^{a}\int_{0}^{b}\left|\frac{\partial^{2}}{\partial s\partial t} (x_{1})_{\alpha^{2}}(s, t)\right|d_{\alpha}sd_{\alpha}t \right)^{\lambda}\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \;$

$\begin{align} \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \leq\frac{1}{2^{\lambda}}\left(\frac{1}{\alpha^{2}}\right)^{\lambda-1}(st)^{\alpha(\lambda-1)}p_{1}(s, t)\int_{0}^{a}\int_{0}^{b}\left|\frac{\partial^{2}}{\partial s\partial t}(x_{1})_{\alpha^{2}}(s, t)\right|^{\lambda}d_{\alpha}sd_{\alpha}t, \end{align}$

(3.7)

Similarly

$\begin{align} p_{2}(s, t)|x_{2}(s, t)|^{\lambda}\leq\frac{1}{2^{\lambda}}\left(\frac{1}{\alpha^{2}}\right)^{\lambda-1}(st)^{\alpha(\lambda-1)}p_{2}(s, t)\int_{0}^{a}\int_{0}^{b} \left|\frac{\partial^{2}}{\partial s\partial t}(x_{2})_{\alpha^{2}}(s, t)\right|^{\lambda}d_{\alpha}sd_{\alpha}t, \end{align}$

(3.8)

Taking the sum of (3.7) and (3.8) and $\alpha$ -integrating the resulting inequalities over $t$ from $0$ to $b$ first and then over $s$ from $0$ to $a$ , we obtain

$\int_{0}^{a}\int_{0}^{b}\left(p_{1}(s, t)|x_{1}(s, t)|^{\lambda}+p_{2}(s, t)|x_{2}(s, t)|^{\lambda}\right)d_{\alpha}s d_{\alpha}t\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \;$

$\begin{eqnarray*} &\leq&\frac{1}{2^{\lambda}}\left(\frac{1}{\alpha^{2}}\right)^{\lambda-1}\Bigg\{\int_{0}^{a}\int_{0}^{b}\left((st)^{\alpha(\lambda-1)}p_{1}(s, t) \int_{0}^{a}\int_{0}^{b}\left|\frac{\partial^{2}}{\partial s\partial t}(x_{1})_{\alpha^{2}}(s, t)\right|^{\lambda}d_{\alpha}sd_{\alpha}t\right)d_{\alpha}sd_{\alpha}t\\ &+&\int_{0}^{a}\int_{0}^{b}\left((st)^{\alpha(\lambda-1)}p_{2}(s, t)\int_{0}^{a}\int_{0}^{b}\left|\frac{\partial^{2}}{\partial s\partial t}(x_{2})_{\alpha^{2}}(s, t)\right|^{\lambda}d_{\alpha}sd_{\alpha}t\right)d_{\alpha}sd_{\alpha}t\Bigg\}\\ & = &\frac{1}{2^{\lambda}}\left(\frac{1}{\alpha^{2}}\right)^{\lambda-1}\Bigg[\left(\int_{0}^{a}\int_{0}^{b}(st)^{\alpha(\lambda-1)}p_{1}(s, t) d_{\alpha}sd_{\alpha}t\right)\int_{0}^{a}\int_{0}^{b}\left|\frac{\partial^{2}}{\partial s\partial t}(x_{1})_{\alpha^{2}}(s, t)\right|^{\lambda} d_{\alpha}sd_{\alpha}t\\ &+&\left(\int_{0}^{a}\int_{0}^{b}(st)^{\alpha(\lambda-1)}p_{2}(s, t)d_{\alpha}sd_{\alpha}t\right)\int_{0}^{a}\int_{0}^{b}\left|\frac{\partial^{2}}{\partial s\partial t}(x_{2})_{\alpha^{2}}(s, t)\right|^{\lambda}d_{\alpha}sd_{\alpha}t\Bigg]. \end{eqnarray*}$

Remark 3.2 Taking for $x_{1}(s, t) = x_{2}(s, t) = x(s, t)$ and $p_{1}(s, t) = p_{2}(s, t) = p(s, t)$ in (3.6), (3.6) changes to the following inequality.

$\int_{0}^{a}\int_{0}^{b}p(s, t)|x(s, t)|^{\lambda}d_{\alpha}sd_{\alpha}t\leq\frac{1}{2^{\lambda}}\left(\frac{1} {\alpha^{2}}\right)^{\lambda-1}\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \;$

$\begin{align} \times\left(\int_{0}^{a}\int_{0}^{b}(st)^{\alpha(\lambda-1)}p(s, t) d_{\alpha}sd_{\alpha}t\right) \int_{0}^{a}\int_{0}^{b}\left|\frac{\partial^{2}}{\partial s\partial t} (x)_{\alpha^{2}}(s, t)\right|^{\lambda}d_{\alpha}sd_{\alpha}t. \end{align}$

(3.9)

Putting $\alpha = 1$ in (3.9), we have

$\begin{align} \int_{0}^{a}\int_{0}^{b}p(s, t)|x(s, t)|^{\lambda}dsdt\leq\frac{1}{2^{\lambda}}\left(\int_{0}^{a}\int_{0}^{b}(st)^{\lambda-1}p(s, t) dsdt\right)\int_{0}^{a}\int_{0}^{b}\left|\frac{\partial^{2}}{\partial s\partial t} x(s, t)\right|^{\lambda}dsdt. \end{align}$

(3.10)

Let $x(s, t)$ reduce to $s(t)$ and with suitable modifications, and $\lambda = 1$ , (2.10) becomes the following result.

$\begin{align} \int_{0}^{a}p(t)|x(t)|dt\leq\frac{1}{2}\left(\int_{0}^{a}p(t)dt\right)\int_{0}^{a}\left|x'(t)\right|dt. \end{align}$

(3.11)

This is just a new inequality established by Agarwal and Pang ^[4]. For $\lambda = 2$ the inequality (3.11) has appear in the work of Traple ^[14], Pachpatte ^[13] proved it for $\lambda = 2m$ ( $m\geq 1$ an integer).

Remark 3.3 Let $x_{j}(s, t)$ reduce to $x_{j}(t)$ ( $j = 1, 2$ ) and $p_{j}(s, t)$ reduce to $p_{j}(t)$ ( $j = 1, 2$ ) with suitable modifications, (3.6) becomes the following interesting result.

$\int_{0}^{a}\left(p_{1}(t)|x_{1}(t)|^{\lambda}+p_{2}(t)|x_{2}(t)|^{\lambda}\right)d_{\alpha}t\leq\frac{1}{2^{\lambda}}\left(\frac{1} {\alpha^{2}}\right)^{\lambda-1}\Bigg[\left(\int_{0}^{a}t^{\alpha(\lambda-1)}p_{1}(t)d_{\alpha}t\right)\int_{0}^{a}\left|{\cal D }_{\alpha}(x'_{1})(t)\right|^{\lambda} d_{\alpha}t$

$\begin{align} \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; +\left(\int_{0}^{a}t^{\alpha(\lambda-1)}p_{2}(t)d_{\alpha}t\right)\int_{0}^{a}\left|{\cal D}_{\alpha}(x'_{2})(t)\right|^{\lambda}d_{\alpha}t\Bigg]. \end{align}$

(3.12)

Putting $\lambda = 1$ and $\alpha = 1$ in (3.12), we have the following interesting result.

$\int_{0}^{a}\left(p_{1}(t)|x_{1}(t)|+p_{2}(t)|x_{2}(t)|\right)dt\leq\frac{1}{2}\Bigg(\int_{0}^{a}p_{1}(t)dt\int_{0}^{a}\left|x'_{1}(t)\right| dt+\int_{0}^{a}p_{2}(t)dt\int_{0}^{a}\left|x'_{2}(t)\right|dt\Bigg).$

Finally, we give an example to verify the effectiveness of the new inequalities. Estimate the following double integrals:

$\int_{0}^{1}\int_{0}^{1}\Big[st(s-1)(t-1)\Big]^{\lambda}dsdt,$

where $\lambda\geq 1$ .

Let $x_{1}(s,t)=x_{2}(s,t)= x(s, t) = st(s-1)(t-1)$ , $p_{1}(s,t)=p_{2}(s,t)= p(s, t) = (st)^{1-\alpha}$ , $a = b = 1$ and $0 < \alpha\leq 1$ , and by using Theorem 3.2, we obtain

$\int_{0}^{1}\int_{0}^{1}\Big[st(s-1)(t-1)\Big]^{\lambda}dsdt\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \;$

$\begin{eqnarray*} & = &\int_{0}^{1}\int_{0}^{1}p(s, t) \left|x(s, t)\right|^{\lambda}d_{\alpha}sd_{\alpha}t\\ &\leq&\frac{1}{2^{\lambda}}\left(\frac{1} {\alpha^{2}}\right)^{\lambda-1}\left(\int_{0}^{1}\int_{0}^{1}(st)^{\alpha(\lambda-1)}p(s, t) d_{\alpha}sd_{\alpha}t\right) \int_{0}^{1}\int_{0}^{1}\left|\frac{\partial^{2}}{\partial s\partial t} (x)_{\alpha^{2}}(s, t)\right|^{\lambda}d_{\alpha}sd_{\alpha}t\\ & = &\frac{1}{2^{\lambda}}\left(\frac{1} {\alpha^{2}}\right)^{\lambda-1}\left(\frac{1}{\alpha(\lambda-1)+1}\right)^{2} \int_{0}^{1}\int_{0}^{1}\Big[(2s-1)(2t-1)\Big]^{\lambda}(st)^{\alpha-1}dsdt\\ & = &\frac{1}{2^{\lambda}}\left(\frac{1} {\alpha^{2}}\right)^{\lambda-1}\left(\frac{1}{\alpha(\lambda-1)+1}\right)^{2} \left(\frac{1}{2^{\alpha-1}}\int_{-1}^{1}t^{\lambda}\frac{1}{(t+1)^{1-\alpha}}dt\right)^{2}\\ &\leq&\frac{1}{2^{\lambda}}\left(\frac{1} {\alpha^{2}}\right)^{\lambda-1}\left(\frac{1}{\alpha(\lambda-1)+1}\right)^{2} \left(\frac{1}{2^{\alpha-1}}\frac{2^{\alpha}}{\alpha}\right)^{2}\\ & = &\frac{2^{2-\lambda}}{\alpha^{2\lambda}\left(\alpha(\lambda-1)+1\right)^{2}}. \end{eqnarray*}$

4. Conclusions

We have introduced a general version of Opial-Wirtinger's type integral inequality for the Katugampola partial derivatives. The established results are generalization of some existing Opial type integral inequalities in the previous published studies. For further investigations we propose to consider the Opial-Wirtinger's type inequalities for other partial derivatives.

Acknowledgments

I would like to thank that research is supported by National Natural Science Foundation of China(11471334, 10971205).

Conflict of interest

The author declares no conflicts of interest.

References

[1]	Hariharan R, Chakkarapani M, Ilango GS, et al. (2016) A method to detect photovoltaic array faults and partial shading in PV systems. IEEE J Photovoltaics 6: 1278–1285.
[2]	Silvestre S, Kichou S, Chouder A, et al. (2015) Analysis of current and voltage indicators in grid connected pv (photovoltaic) systems working in faulty and partial shading conditions. Energy 86: 42–50. doi: 10.1016/j.energy.2015.03.123
[3]	Pendem SR, Mikkili S (2018) Modelling and performance assessment of pv array topologies under partial shading conditions to mitigate the mismatching power losses. Sol Energy 160: 303–321. doi: 10.1016/j.solener.2017.12.010
[4]	Ghanbari T (2017) Permanent partial shading detection for protection of photovoltaic panels against hot spotting. IET Renew Power Gen 11: 123–131.
[5]	Rossi D, Omana M, Giaffreda D, et al. (2015) Modeling and detection of hotspot in shaded photovoltaic cells. IEEE T VLSI Syst 23: 1031–1039.
[6]	Oliveri A, Cassottana L, Laudani A, et al. (2017) Two FPGA-oriented high-speed irradiance virtual sensors for photovoltaic plants. IEEE T Ind Inform 13: 157–165.
[7]	Carrasco M, Laudani A, Lozito GM, et al. (2017) Low-cost solar irradiance sensing for pv systems. Energies 10: 998.
[8]	Pendem SR, Mikkili S (2018) Modeling, simulation and performance analysis of solar pv array configurations (series, seriesparallel and honey-comb) to extract maximum power under partial shading conditions. Sol Energy 4: 274–287.
[9]	Hemalatha R, Ramaprabha R, Radha S (2015) A comprehensive analysis on sizing of solar energy harvester elements for wireless sensor motes. Renew Sust Energ Rev 8: 291–315.
[10]	El-Dein MZS, Kazerani M, Salama MMA (2012) Optimal total cross tied interconnection for photovoltaic arrays to reduce partial shading losses. In Power and Energy Society General Meeting, IEEE, 1–6.
[11]	Deshkar SN, Dhale SB, Mukherjee JS, et al. (2015) Solar pv array reconfiguration under partial shading conditions for maximum power extraction using genetic algorithm. Renew Sust Energ Rev 43: 102–110.
[12]	Mohanty S, Subudhi B, Ray PK (2016) A new mppt design using grey wolf optimization technique for photovoltaic system under partial shading conditions. IEEE T Sustain Energ 7: 181–188. doi: 10.1109/TSTE.2015.2482120
[13]	Mahmoud Y, El-Saadany EF (2016) Fast power-peaks estimator for partially shaded PV systems. IEEE T Energy Conver 31: 206–217.
[14]	Celik B, Karatepe E, Silvestre S, et al. (2015) Analysis of spatial fixed pv arrays configurations to maximize energy harvesting in bipv applications. Renew Energ 75: 534–540. doi: 10.1016/j.renene.2014.10.041
[15]	Cristaldi L, Faifer M, Rossi M, et al. (2014) Simplified method for evaluating the effects of dust and aging on photovoltaic panels. Measurement 54: 207–214. doi: 10.1016/j.measurement.2014.03.001
[16]	Faba A, Gaiotto S, Lozito GM (2017) A novel technique for online monitoring of photovoltaic devices degradation. Sol Energy 158: 520–527.
[17]	Bai J, Cao Y, Hao Y, et al. (2015) Characteristic output of pv systems under partial shading or mismatch conditions. Sol Energy 112: 41–54. doi: 10.1016/j.solener.2014.09.048
[18]	Ahmed J, Salam Z (2015) A critical evaluation on maximum power point tracking methods for partial shading in pv systems. Renew Sust Energ Rev 47: 933–953. doi: 10.1016/j.rser.2015.03.080
[19]	Kofinas P, Dounis AI, Papadakis G, et al. (2015) An intelligent mppt controller based on direct neural control for partially shaded pv system. Energ Buildings 90: 51–64. doi: 10.1016/j.enbuild.2014.12.055
[20]	Kotti R, ShireenW(2015) E_cient mppt control for pv systems adaptive to fast changing irradiation and partial shading conditions. Sol Energy 114: 397–407.
[21]	Sundareswaran K, Vignesh kumar V, Palani S (2015) Application of a combined particle swarm optimization and perturb and observe method for mppt in pv systems under partial shading conditions. Renew Energ 75: 308–317.
[22]	Benyoucef AS, Chouder A, Kara K, et al. (2015) Artificial bee colony based algorithm for maximum power point tracking (mppt) for pv systems operating under partial shaded conditions. Appl Soft Comput 32: 38–48.
[23]	Laudani A, Fulginei FR, Salvini A, et al. (2014) Implementation of a neural mppt algorithm on a low-cost 8-bit microcontroller. In Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), 2014 International Symposium on, IEEE, 977–981.
[24]	Lozito GM, Bozzoli L, Salvini A (2014) Microcontroller based maximum power point tracking through fcc and mlp neural networks. In Education and Research Conference (EDERC), 2014 6th European Embedded Design in, 207–211.
[25]	Belhachat F, Larbes C (2015) Modeling, analysis and comparison of solar photovoltaic array configurations under partial shading conditions. Sol Energy 120: 399–418.
[26]	Belhaouas N, Cheikh MSA, Agathoklis P, et al. (2017) Pv array power output maximization under partial shading using new shifted pv array arrangements. Appl Energ 187: 326–337. doi: 10.1016/j.apenergy.2016.11.038
[27]	Bastidas-Rodrgueza JD, Trejos-Grisalesb LA, Gonzlez-Montoyac D, et al. (2018) General modeling procedure for photovoltaic arrays. Electr Pow Syst Res 155: 67–79.
[28]	Gonzlez-Montoyac D, Bastidas-Rodrgueza JD, Trejos-Grisalesb LA, et al. (2018) A procedure for modeling photovoltaic arrays under any configuration and shading conditions. Energies 11: 767.
[29]	Babu TS, Ram JP, Dragievi T, et al. (2018) Particle swarm optimization based solar PV array reconfiguration of the maximum power extraction under partial shading conditions. IEEE T Sustain Energ 9: 74–85. doi: 10.1109/TSTE.2017.2714905
[30]	Ram JP, Rajasekar N (2017) A novel flower pollination based global maximum power point method for solar maximum power point tracking. IEEE T Power Electr 32: 8486–8499.
[31]	Iraji F, Farjah E, Ghanbari T (2018) Optimisation method to find the best switch set topology for reconfiguration of photovoltaic panels. IET Renew Power Gen 12: 374–379. doi: 10.1049/iet-rpg.2017.0505
[32]	Dhimish M, Holmes V, Mehrdadi B, et al. (2017) Seven indicators variations for multiple pv array configurations under partial shading and faulty pv conditions. Renew Energ 113: 438–460.
[33]	Potnuru SR, Pattabiraman D, Ganesan SI, et al. (2015) Positioning of pv panels for reduction in line losses and mismatch losses in pv array. Renew Energ 78: 264–275. doi: 10.1016/j.renene.2014.12.055
[34]	Vijayalekshmy S, Bindu GR, Iyer SR (2016) A novel zig-zag scheme for power enhancement of partially shaded solar arrays. Sol Energy 135: 92–102.
[35]	Dhanalakshmi B, Rajasekar N (2018) Dominance square based array reconfiguration scheme for power loss reduction in solar photovoltaic (pv) systems. Energ Convers Manage 156: 84–102.
[36]	Rezaii R, Ameri MH, Varjani AY, et al. (2018) Overcoming partial shading issue of pv modules by using a resonant switched capacitor converter. In Power Electronics, Drives Systems and Technologies Conference (PEDSTC), 2018 9th Annual, 38–43.
[37]	Uno M, Kukita A (2015) Single-switch voltage equalizer using multistacked buck–boost converters for partially shaded photovoltaic modules. IEEE T Power Electr 30: 3091–3105.
[38]	Chub A, Vinnikov D, Kosenko R, et al. (2017) Wide input voltage range photovoltaic microconverter with reconfigurable buck–boost switching stage. IEEE T Ind Electron 64: 5974–5983. doi: 10.1109/TIE.2016.2645891
[39]	Vinnikov D, Chub A, Roasto I, et al. (2016) Multi-mode quasi-z-source series resonant DC/dc converter for wide input voltage range applications. In Applied Power Electronics Conference and Exposition (APEC),IEEE, 2533–2539.
[40]	Ikkurti HP, Saha S (2015) A comprehensive techno-economic review of microinverters for building integrated photovoltaics (bipv). Renew Sust Energ Rev 47: 997–1006. doi: 10.1016/j.rser.2015.03.081
[41]	Hasan R, Mekhilef S (2017) Highly e_cient flyback microinverter for grid-connected rooftop pv system. Sol Energy 146: 511–522.
[42]	Uno M, Kukita A (2013) Two-switch voltage equalizer using series-resonant inverter and voltage multiplier for partially-shaded series-connected photovoltaic modules. In Energy Conversion Congress and Exposition, IEEE.
[43]	Famoso F, Lanzafame R, Maenza S, et al. (2015) Performance comparison between micro-inverter and string-inverter photovoltaic systems. Energy Procedia 81: 526–539.
[44]	Bauwens P, Doutreloigne J (2014) Reducing partial shading power loss with an integrated smart bypass. Sol Energy 103: 134–142.
[45]	Daliento S, Di Napoli F, Guerriero P, et al. (2016) A modified bypass circuit for improved hot spot reliability of solar panels subject to partial shading. Sol Energy 134: 211–218. doi: 10.1016/j.solener.2016.05.001
[46]	Kim KA, Krein PT (2015) Reexamination of photovoltaic hot spotting to show inadequacy of the bypass diode. IEEE J Photovolt 5: 1435–1441. doi: 10.1109/JPHOTOV.2015.2444091
[47]	Dhimish M, Holmes V, Mehrdadi B, et al. (2018) Output-power enhancement for hot spotted polycrystalline photovoltaic solar cells. IEEE T Device Mat Re 18: 37–45.
[48]	Winston DP, Kumar BP, Christabel SC, et al. (2018) Maximum power extraction in solar renewable power system - a bypass diode scanning approach. Comput Electr Eng.
[49]	Daliento S, Chouder A, Guerriero P, et al. (2017) Monitoring, diagnosis, and power forecasting for photovoltaic fields: A review. Int J Photoenergy 2017: 1–13.
[50]	Mellit A, Tina GM, and Kalogirou SA (2018) Fault detection and diagnosis methods for photovoltaic systems: A review. Renew Sust Energ Rev 91: 1–17. doi: 10.1016/j.rser.2018.03.062
[51]	Ali MH, Rabhi A, Hajjaji AE, et al. (2017) Real time fault detection in photovoltaic systems. Energy Procedia 111: 914–923.
[52]	Laudani A, Fulginei FR, Salvini A (2014) High performing extraction procedure for the one-diode model of a photovoltaic panel from experimental iv curves by using reduced forms. Sol Energy 103: 316–326.
[53]	Laudani A, Fulginei FR, and Salvini A (2014) Identification of the one-diode model for photovoltaic modules from datasheet values. Sol Energy 108: 432–446. doi: 10.1016/j.solener.2014.07.024
[54]	Laudani A, Fulginei FR, Salvini A, et al. (2014) Very fast and accurate procedure for the characterization of photovoltaic panels from datasheet information. Int J Photoenergy.
[55]	Silvestre S, da Silva MA, Chouder A, et al. (2014) New procedure for fault detection in grid connected pv systems based on the evaluation of current and voltage indicators. Energ Convers Manage 86: 241–249. doi: 10.1016/j.enconman.2014.05.008
[56]	Mahendran M, Anandharaj V, Vijayavel K, et al. (2015) Permanent mismatch fault identification of photovoltaic cells using arduino. ICTACT J MICROELECTRON 01: 79–82. doi: 10.21917/ijme.2015.0014
[57]	Stauffer Y, Ferrario D, Onillon E, et al. (2015) Power monitoring based photovoltaic installation fault detection. In 2015 International Conference on Renewable Energy Research and Applications (ICRERA).
[58]	Mekki H, Mellit A, Salhi A (2016) Artificial neural network-based modelling and fault detection of partial shaded photovoltaic modules. Simul Model Pract Th 67: 1–13. doi: 10.1016/j.simpat.2016.05.005
[59]	Garoudja E, Chouder A, Kara K, et al. (2017) An enhanced machine learning based approach for failures detection and diagnosis of pv systems. Energ Convers Manage 151: 496–513. doi: 10.1016/j.enconman.2017.09.019
[60]	Belaout A, Krim F, Mellit A (2016) Neuro-fuzzy classifier for fault detection and classification in photovoltaic module. In Proc. Identification and Control (ICMIC) 2016 8th Int. Conf. Modelling, 144–149.
[61]	Dhimish M, Holmes V, Mehrdadi B, et al. (2017) Photovoltaic fault detection algorithm based on theoretical curves modelling and fuzzy classification system. Energy 140: 276–290. doi: 10.1016/j.energy.2017.08.102
[62]	Tsanakas JA, Ha LD, Al Shakarchi F (2017) Advanced inspection of photovoltaic installations by aerial triangulation and terrestrial georeferencing of thermal/visual imagery. Renew Energ 102: 224–233. doi: 10.1016/j.renene.2016.10.046
[63]	Tsanakas JA, Ha L, Buerhop C (2016) Faults and infrared thermographic diagnosis in operating c-si photovoltaic modules: A review of research and future challenges. Renew Sust Energ Rev 62: 695–709.
[64]	Zorn C, Kaminski N (2015) Acceleration of temperature humidity bias (thb) testing on igbt modules by high bias levels.a In 2015 IEEE 27th International Symposium on Power Semiconductor Devices & IC's (ISPSD).
[65]	Laudani A, Lozito GM, Lucaferri V, et al. (2017) An analytical approach for maximum power point calculation for photovoltaic system. In Circuit Theory and Design (ECCTD), 2017 European Conference on, 1–4.

This article has been cited by:

1.	Samah LAAMAMI, Aicha ABID, Mouna BENHAMED, Lassaad SBITA, 2020, Investigation on Protection Diodes in PV Generator, 978-1-7281-1080-6, 1069, 10.1109/SSD49366.2020.9364119
2.	A. Laudani, G. M. Lozito, 2019, Smart Distributed Sensing for Photovoltaic Applications, 978-1-7281-3403-1, 2908, 10.1109/PIERS-Spring46901.2019.9017556
3.	Laudani Antonino, Lozito Gabriele Maria, Radicioni Martina, 2019, Areal-time MCU-based wireless system for PV applications, 978-8-8872-3745-0, 1, 10.23919/AEIT.2019.8893319
4.	G. Sai Krishna, Tukaram Moger, Reconfiguration strategies for reducing partial shading effects in photovoltaic arrays: State of the art, 2019, 182, 0038092X, 429, 10.1016/j.solener.2019.02.057
5.	G. Sai Krishna, Tukaram Moger, Improved SuDoKu reconfiguration technique for total-cross-tied PV array to enhance maximum power under partial shading conditions, 2019, 109, 13640321, 333, 10.1016/j.rser.2019.04.037
6.	Mohammed Alkahtani, Zuyu Wu, Colin Sokol Kuka, Muflah S. Alahammad, Kai Ni, A Novel PV Array Reconfiguration Algorithm Approach to Optimising Power Generation across Non-Uniformly Aged PV Arrays by Merely Repositioning, 2020, 3, 2571-8800, 32, 10.3390/j3010005
7.	Antonino Laudani, Gabriele Maria Lozito, Martina Radicioni, Francesco Riganti Fulginei, Alessandro Salvini, 2020, Chapter 40, 978-3-030-37160-9, 525, 10.1007/978-3-030-37161-6_40
8.	Bo Yang, Haoyin Ye, Jingbo Wang, Jiale Li, Shaocong Wu, Yulin Li, Hongchun Shu, Yaxing Ren, Hua Ye, PV arrays reconfiguration for partial shading mitigation: Recent advances, challenges and perspectives, 2021, 247, 01968904, 114738, 10.1016/j.enconman.2021.114738
9.	Jun Zhou, Chong Liu, Kun Li, PV array reconfiguration with electrical energy storage system for power system frequency regulation, 2022, 10, 2296-598X, 10.3389/fenrg.2022.971628
10.	Shahroz Anjum, Vivekananda Mukherjee, Static and Dynamic Reconfiguration Strategies for Reducing Partial Shading Effects in Photovoltaic Array: A Comprehensive Review, 2022, 10, 2194-4288, 2200098, 10.1002/ente.202200098
11.	Shahroz Anjum, V. Mukherjee, Gitanjali Mehta, Hyper SuDoKu-Based Solar Photovoltaic Array Reconfiguration for Maximum Power Enhancement Under Partial Shading Conditions, 2022, 144, 0195-0738, 10.1115/1.4051427
12.	Gabriele Maria Lozito, Emanuele Grasso, Francesco Riganti Fulginei, 2022, A Neural-Enhanced Incremental Conductance MPPT Algorithm with Online Adjustment Capabilities, 978-1-6654-8537-1, 1, 10.1109/EEEIC/ICPSEurope54979.2022.9854781
13.	Long Wang, Xucheng Chang, Xiang Li, Wenli Huang, Yingying Jiao, Power Grid Frequency Regulation Strategy for Photovoltaic Plant Based on Multi-Objective Harris Hawks Optimization, 2021, 9, 2296-598X, 10.3389/fenrg.2021.806263
14.	Rupendra Kumar Pachauri, Ahmad Faiz Minai, Piyush Kuchhal, Vandana Jha, , 2022, PV Array Reconfiguration Methods based on Game Theory to Eliminate Shading Effect during Non-uniform Irradiations: Experimental Feasibility, 978-1-6654-6047-7, 1, 10.1109/STCR55312.2022.10009493
15.	Shahroz Anjum, V. Mukherjee, Gitanjali Mehta, Advanced SuDoKu-Based Reconfiguration Strategies for Maximum Power Extraction From Partially Shaded Solar Photovoltaic Array, 2021, 143, 0199-6231, 10.1115/1.4051090
16.	Shahroz Anjum, V. Mukherjee, Irregular SuDoKu Modeling of Solar Photovoltaic Arrays for Partial Shading Optimization, 2023, 2193-567X, 10.1007/s13369-023-07864-z
17.	Divya Ahluwalia, Shahroz Anjum, V. Mukherjee, Boost in energy generation using robust reconfiguration: A novel scheme for photovoltaic array under realistic fractional partial shadings, 2023, 290, 01968904, 117211, 10.1016/j.enconman.2023.117211
18.	Mohd Faisal Jalil, Dushyant Sharma, R.C. Bansal, Cross kit reconfiguration algorithm for enhanced output power of PV array during shading mismatch conditions, 2023, 288, 00304026, 171218, 10.1016/j.ijleo.2023.171218
19.	Md Khursheed Alam, Salman Rafi, Mohd Faisal Jalil, Sheeraz Kirmani, 2023, Exploring the PV Topologies in Comparison with Loshu Reconfiguration: Estimate Output Power, 979-8-3503-1997-2, 1, 10.1109/SeFeT57834.2023.10245818
20.	Rupendra Kumar Pachauri, Jai Govind Singh, Chess Game Rook‐Icon Movement‐Based Photovoltaic Array Reconfiguration for Higher Shade Dispersion and Improved Global Power Peaks Under Partial Shading Conditions: An Experimental Study, 2024, 2194-4288, 10.1002/ente.202301145
21.	Lingzhi Yi, Jingxuan Tan, Yahui Wang, Bote Luo, Lü Fan, Siyue Cheng, Static reconfiguration method of photovoltaic array based on improved competence square, 2024, 99, 0031-8949, 115002, 10.1088/1402-4896/ad7d4e
22.	Antonino Laudani, Fabio Corti, Matteo Intravaia, Gabriele Maria Lozito, Michele Quercio, Francesco Riganti Fulginei, 2024, Monitoring of BIPV by Means of a Low Cost Wireless Sensor Network, 979-8-3503-5518-5, 01, 10.1109/EEEIC/ICPSEurope61470.2024.10751001
23.	Marium Jalal, Ihsan Ullah Khalil, Azhar Ul Haq, Aymen Flah, Saad A. Mohamed Abdel Wahab, Advancements in PV Array Reconfiguration Techniques: Review Article, 2024, 12, 2169-3536, 183751, 10.1109/ACCESS.2024.3509955

Reader Comments

Your name:*

Email:*
© 2018 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)