Optimal information dissemination strategy to promote preventivebehaviors in multilayer epidemic networks

1.   Introduction

In the literature, special functions have a great importance in a variety of fields of mathematics, such as mathematical physics, mathematical biology, fluid mechanics, geometry, combinatory and statistics. Due of the essential position of special functions in mathematics, they continue to play an essential role in the subject as well as in the geometric function theory. For geometric behavior of some other special functions, one can refer to ^{[1,2,3,4,5,6,7,8,9,10,11,12]}. An interesting way to discuss the geometric properties of special functions is by the means of some criteria due to Ozaki, Fejér and MacGregor. One of the important special functions is the Mathieu series that appeared in the nineteenth century in the monograph ^[13] defined on $ \mathbb{R} $ by

Surprisingly, the Mathieu series is considered in a variety of fields of mathematical physics, namely, in the elasticity of solid bodies ^[13]. For more applications regarding the Mathieu series, we refer the interested reader to [14, p. 258, Eq (54)]. The functions bear the name of the mathematician Émile Leonard Mathieu (1835–1890). Recently, a more general family of the Mathieu series was studied by Diananda ^[15] in the following form:

In 2020, Gerhold et al. ^[16], considered a new Mathieu type power series, defined by

where $ \alpha, \mu\geq0, \beta, r > 0 $ and $ |z|\leq1, $ such that $ \alpha < \beta(\mu+1). $

In ^[17], Bansal and Sokól have determined sufficient conditions imposed on the parameters such that the normalized form of the function $ S(r, z) $ belong to a certain class of univalent functions, such as starlike and close-to-convex. In ^[18], the authors presented some generalizations of the results of Bansal and Sokól by using the same technique. In addition, Gerhold et al. [18, Theorems 5 and 6] has established some sufficient conditions imposed on the parameter of the normalized form of the function $ S_{1, 2, \mu}(r; z) $ defined by

to be starlike and close-to-convex in the open unit disk. The main focus of the present paper is to extend and improve some results from ^[18] by using a completely different method. More precisely, in this paper we present some sufficient conditions, such as the normalized form of the function $ S_{1, \beta, \mu}(r; z) $ defined by

satisfying several geometric properties such as starlikeness, convexity and close-to-convexity.

We denoted by $ \mathcal{H} $ the class of all analytic functions inside the unit disk

Assume that $ \mathcal{A} $ denoted the collection of all functions $ f\in \mathcal{H}, $ satisfying the normalization $ f(0) = f^\prime(0)-1 = 0 $ such that

A function $ f\in\mathcal{A} $ is said to be a starlike function (with respect to the origin zero) in $ \mathcal{D} $, if $ f $ is univalent in $ \mathcal{D} $ and $ f(\mathcal{D}) $ is a starlike domain with respect to zero in $ \mathbb{C} $. This class of starlike functions is denoted by $ \mathcal{S}^*. $ The analytic characterization of $ \mathcal{S}^* $ is given ^[19] below:

If $ f(z) $ is a univalent function in $ \mathcal{D} $ and $ f(\mathcal{D}) $ is a convex domain in $ \mathbb{C} $, then $ f\in\mathcal{A} $ is said to be a convex function in $ \mathcal{D} $. We denote this class of convex functions by $ \mathcal{K}, $ which can also be described as follows:

An analytic function $ f $ in $ \mathcal{A} $ is called close-to-convex in the open unit disk $ \mathcal{D} $ if there exists a function $ g(z), $ which is starlike in $ \mathcal{D} $ such that

It can be noted that every close-to-convex function in $ \mathcal{D} $ is also univalent in $ \mathcal{D} $ (see, for details, ^[19,20]).

In order to show the main results, the following preliminary lemmas will be helpful. The first result is due to Ozaki (see also [21, Lemma 2.1]).

Lemma 1.1. ^[22] Let

be analytic in $ \mathcal{D}. $ If

or if

then $ f $ is close-to-convex with respect to the function $ -\log(1-z) $.

Remark 1.2. We note that, as Ponnusamy and Vuorinen pointed out in ^[21], proceeding exactly as in the proof of Lemma 1.1, one can verify directly that if a function $ f: \mathcal{D}\rightarrow \mathbb{C} $ satisfies the hypothesis of the above lemma, then it is close-to-convex with respect to the convex function

The next two lemmas are due to Fejér ^[23].

Lemma 1.3. Suppose that a function $ f(z) = 1+\sum_{k = 2}^\infty a_k z^{k-1} $, with $ a_k\geq0\; (\forall k\geq2) $ as analytic in $ \mathcal{D}. $ If $ (a_k)_{k\geq1} $ is a convex decreasing sequence, i.e., $ a_k-2a_{k+1}+a_{k+2}\geq0 $ and $ a_k-a_{k+1}\geq0 $ for all $ k\geq1, $ then

Lemma 1.4. Suppose that a $ f(z) = z+\sum_{k = 2}^\infty a_k z^{k} $, with $ a_k\geq0\; (\forall k\geq2) $ as analytic in $ \mathcal{D}. $ If $ (ka_k)_{k\geq1} $ and $ (ka_k-(k+1) a_{k+1})_{k\geq1} $ both are decreasing, then $ f $ is starlike in $ \mathcal{D}. $

Lemma 1.5 (^[24]). Assume that $ f\in\mathcal{A}. $ If the following inequality

holds for all $ z\in\mathcal{D}, $ then $ f $ is starlike in

Lemma 1.6 (^[25]). Assume that $ f\in\mathcal{A} $ and satisfies

for each $ z\in \mathcal{D}, $ then $ f $ is convex in $ \mathcal{D}_{\frac{1}{2}} $.

2.   Main results

Theorem 2.1. Let $ \mu, \beta > 0 $ and $ 0 < r\leq1 $ such that $ \beta\geq1+\frac{2}{\mu+1}. $ In addition, if the following condition holds:

then the function $ \mathcal{Q}_{\mu, \beta}(r; z) $ is close-to-convex in $ \mathcal{D} $ with respect to the function $ -\log(1-z). $

Proof. For the function $ \mathcal{Q}_{\mu, \beta}(r; z) $, we have

To prove the result, we need to show that the sequence $ \left\{ka_k\right\}_{k\geq1} $ is decreasing under the given conditions. For $ k\geq2 $ we have

where

However, we have

In addition, for all $ k\geq2 $, we have

which is positive by our assumption. Having (2.1)–(2.3), we conclude that the sequence $ (ka_k)_{k\geq2} $ is decreasing. Finally, we see that the condition $ (H) $ implies that $ a_1\geq 2 a_2, $ then the function $ \mathcal{Q}_{\mu, \beta}(r; z) $ is close-to-convex in $ \mathcal{D} $ with respect to the function $ -\log(1-z) $ by Lemma 1.1. □

If we set $ \beta = \frac{3}{2} $ in Theorem 2.1, we derive the following result as follows:

Corollary 2.2. Let $ 0 < r\leq1. $ If $ \mu\geq3, $ then the function $ \mathcal{Q}_{\mu, \frac{3}{2}}(r; z) $ is close-to-convex in $ \mathcal{D} $ with respect to the function $ -\log(1-z) $.

Upon setting $ \mu = 2 $ in Theorem 2.1, we get the following result:

Corollary 2.3. Let $ 0 < r\leq1. $ If $ \beta\geq\frac{5}{3}, $ then the function $ \mathcal{Q}_{2, \beta}(r; z) $ is close-to-convex in $ \mathcal{D} $ with respect to the function $ -\log(1-z). $

Remark 2.4. In ^[18], it is established that the function $ \mathcal{Q}_{\mu,2}(r; z) = :\mathbb{Q}_\mu(r;z) $ is close-to-convex in $ \mathcal{D} $ with respect to the function $ \frac{z}{1-z} $ for all $ 0 <r\leq\sqrt{\mu}. $ Moreover, in view of Remark 1.2, we conclude that the function $ \mathcal{Q}_{\mu,2}(r; z) $ is close-to-convex in $ \mathcal{D} $ with respect to the function $ -\log(1-z) $ for all $ 0<r\leq\sqrt{\mu} $. However, in view of Corollaries 2.2 and 2.3, we deduce that Theorem 2.1 improves the corresponding result available in [18, Theorem 5] for $ 0<r\leq1. $

Theorem 2.5. Assume that $ \mu, \beta>0, 0<r\leq 1 $ such that $ \beta\geq 1+\frac{1}{\mu+1}. $ In addition, if the condition $ (H) $ holds, then

for all $ z\in \mathcal{D}. $

Proof. For $ k\geq1 $, we get

Further, for all $ k\geq1, $ we have

Hence, in view of (2.4) and (2.5), we deduce that the sequence $ (a_k)_{k\geq1} $ is decreasing. Next, we prove that $ (a_k)_{k\geq1} $ is a convex decreasing sequence, then, for $ k\geq2 $ we obtain

Moreover, we get

Keeping (2.6) and (2.7) in mind, we have $ a_k-2a_{k+1} > 0 $ for all $ k\geq2. $ In addition, the condition $ (H) $ implies $ a_1-2a_2\geq0. $ This in turn implies that the sequence $ (a_k)_{k\geq1} $ is convex. Finally, by Lemma 1.3, we obtain the desired result. □

Taking $ \beta = \frac{3}{2} $ in Theorem 2.5, we derive the following result:

Corollary 2.6. Assume that $ r\in(0, 1]. $ If $ \mu\geq\frac{\log(4)}{\log(2^{\frac{3}{2}}+1)-\log(2)}-1\sim 1.14, $ then

Setting $ \mu = 1 $ in Theorem 2.5, we established the following result which reads as follows:

Corollary 2.7. Let $ 0 < r\leq1. $ If $ \beta\geq\frac{\log(3)}{\log(2)}, $ then

Remark 2.8. The result obtained in the above theorem has been derived from [18, Theorem 6] for $ \beta = 2, \mu>0 $ and $ 0<r<\sqrt{\mu}. $ Hence, in view of Corollaries 2.2 and 2.6, we deduce that Theorem 2.5 improves the corresponding result given in [18, Theorem 6] for $ 0<r\leq1. $

Theorem 2.9. Assume that $ \min(\mu, \beta)>0, 0<r\leq1 $ such that $ \beta\geq1+\frac{3}{\mu+1}, $ then the function $ \mathcal{Q}_{\mu,\beta}(r;z) $ is starlike in $ \mathcal{D}. $

Proof. We see in the proof of Theorem 2.1 that the sequence $ (k a_k)_{k\geq1} $ is decreasing. Hence, with the aid of Lemma 1.4 to show that the function $ \mathcal{Q}_{\mu,\beta}(r; z) $ is starlike in $ \mathcal{D}, $ it suffices to prove that the sequence $ (ka_k-(k+1)a_{k+1})_{k\geq1} $ is decreasing. We have

where

For $ k\geq2, $ we have

which in turn implies that

for all $ k\geq2, $ and consequently, the sequence $ (ka_k-(k+1)a_{k+1})_{k\geq2} $ is decreasing. Further, a simple computation gives

Therefore, $ (ka_k-(k+1)a_{k+1})_{k\geq1} $ is decreasing, which leads us to the asserted result. □

In the next Theorem we present another set of sufficient conditions to be imposed on the parameters so that the function $ \mathcal{Q}_{\mu, \beta}(r; z) $ is starlike in $ \mathcal{D}. $

Theorem 2.10. Let the parameters be the same as in Theorem 2.1. In addition, if the following conditions

hold true, then the function $ \mathcal{Q}_{\mu, \beta}(r; z) $ is starlike in $ \mathcal{D}. $

Proof. First of all, we need to prove that the sequences $ (u_k)_{k\geq2} $ and $ (v_k)_{k\geq2} $ defined by

are decreasing. Indeed, we have

In addition, for any $ k\geq2, $ we have

According to (2.10) and (2.11) we conclude that the sequence $ (u_k)_{k\geq2} $ is decreasing. Also, for $ k\geq2, $ we have

Moreover, for all $ k\geq2 $, we find

Since the sequence $ (k/(k-1))_{n\geq2} $ is decreasing, we deduce that $ \frac{k}{k-1}\leq 2 $ for all $ k\geq2 $ and consequently,

Hence, in view of the above inequality combined with (2.13) and (2.12), we conclude that the sequence $ (v_k)_{k\geq2} $ is decreasing. Now, we set

We see that the function $ \tilde{\mathbb{Q}}_{\mu, \beta}(r; z) $ is analytic in $ \mathcal{D} $ and satisfies $ \tilde{\mathbb{Q}}_{\mu, \beta}(r; 0) = 1. $ Hence, to derive the desired result, it suffices to prove that, for any $ z\in\mathcal{D}, $ we have

For this goal in view, it suffices to show that

For all $ z\in\mathcal{D}, $ we get

In addition, in view of the inequality:

we obtain

By using (2.14) and (2.15), for $ z\in\mathcal{D} $, we get

Furthermore, by using the fact that the function $ r\mapsto \chi_{\mu, \beta}(r) = \left(\frac{r^2+1}{r^2+2^\beta}\right)^{\mu+1} $ is strictly increasing on $ (0, 1] $, and with the aid of condition $ (H^*) $, we obtain

Finally, by combining (2.16) and (2.17), we derived the desired results. □

By setting $ \beta = 2 $ in Theorem 2.10, we obtain the following corollary:

Corollary 2.11. If $ 0 < r\leq1 $ and $ \mu\geq1 $, then the function $ \mathbb{Q}_\mu(r; z) $ defined in (1.4) is starlike in $ \mathcal{D} $.

Taking $ \beta = \frac{3}{2} $ in Theorem 2.10, we obtain:

Corollary 2.12. Under the assumptions of Corollary 2.2, the function $ \mathcal{Q}_{\mu, \frac{3}{2}}(r; z) $ is starlike in $ \mathcal{D}. $

Setting in Theorem 2.10 the values $ \mu = 2 $, we compute the following corollary:

Corollary 2.13. Suppose that all hypotheses of Corollary 2.3 hold, then the function $ \mathcal{Q}_{2, \beta}(r; z) $ is starlike in $ \mathcal{D} $.

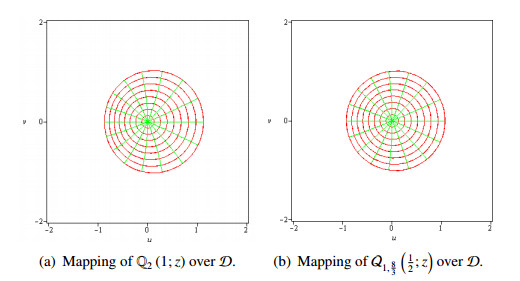
Example 2.14. The functions $ \mathcal{Q}_{3, \frac{3}{2}}(1/2; z) $ and $ \mathcal{Q}_{2, \frac{5}{3}}(1/2; z) $ are starlike in $ \mathcal{D} $.

Figure 1 illustrates the mappings of the above examples in $ \mathcal{D} $.

Theorem 2.15. Let $ \mu, \beta > 0 $ and $ 0 < r\leq1 $ such that $ \beta\geq1+\frac{3}{\mu+1}. $ If the following condition

holds true, then the function $ \mathcal{Q}_{\mu, \beta}(r; z) $ is convex in $ \mathcal{D}. $

Proof. We define the sequences $ (x_k)_{k\geq2} $ and $ (y_k)_{k\geq2} $ by

Let $ k\geq2, $ then

However, we have

Hence, in view of (2.18) and (2.19), we get that $ (x_k)_{k\geq2} $ is decreasing. Also, we have

Moreover, for $ k\geq2 $, we find that

Having (2.20) and (2.21) in mind, we deduce that the sequence $ (y_k)_{k\geq2} $ is decreasing. To show that the function $ \mathcal{Q}_{\mu, \beta}(r; z) $ is convex in $ \mathcal{D}, $ it suffices to establish that the function

is starlike in $ \mathcal{D} $. For this objective in view, it suffices to find that

For all $ z\in\mathcal{D} $ and since $ (y_k)_{k\geq2} $ is decreasing, we get

Further, for any $ z\in\mathcal{D}, $ we obtain

Keeping (2.22) and (2.23) in mind, for $ z\in\mathcal{D} $, we get

Again, by using the fact that the function $ r\mapsto \chi_{\mu, \beta}(r) $ is increasing on $ (0, 1] $ and with the aid of hypothesis $ (H^{**}) $ we obtain that

Finally, by combining the above inequality and (2.24), we obtain the desired result asserted by Theorem 2.15. □

Taking $ \beta = 2 $ in Theorem 2.15, in view of (1.4), the following result holds true:

Corollary 2.16. Let $ 0 < r\leq1. $ If $ \mu\geq2, $ then the function $ \mathbb{Q}_\mu(r; z) $ is convex in $ \mathcal{D}. $

If we set $ \mu = 1 $ in Theorem 2.15, in view of (1.5), we derive the following result:

Corollary 2.17. Let $ 0 < r\leq1. $ If $ \beta\geq\frac{\log(8\sqrt{e-2}-1)}{\log(2)}, $ then the function $ \mathcal{Q}_{1, \beta}(r; z) $ is convex in $ \mathcal{D}. $

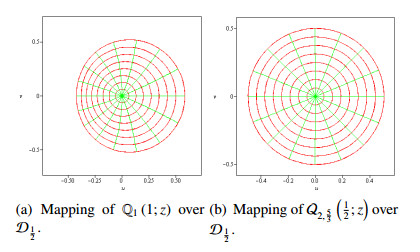
Example 2.18. The functions $ \mathbb{Q}_2(r; z) $ and $ \mathcal{Q}_{1, \frac{8}{3}}(r; z) $ are convex in $ \mathcal{D}. $

Figure 2 gives the mappings of the above presented examples in $ \mathcal{D} $.

Theorem 2.19. Let the parameters be the same as in Theorem 2.1, then the function $ \mathcal{Q}_{\mu, \beta}(r; z) $ is starlike in $ \mathcal{D}_{\frac{1}{2}}. $

Proof. For any $ z\in\mathcal{D} $ we get

where

Straightforward calculation gives

Furthermore, for $ k\geq2 $, we get

Thus, the sequence $ (c_k)_{k\geq2} $ is decreasing. However, in view of (2.26), for $ z\in\mathcal{D} $ we obtain

According to the monotony property of the function $ r\mapsto\chi_{\beta, \mu}(r) $ on $ (0, 1) $ we get

Hence, in view (2.29) and (2.30) we find for all $ z\in\mathcal{D} $ that

With the help of Lemma 1.5, we deduce that the function $ \mathcal{Q}_{\mu, \beta}(r; z) $ is starlike in $ \mathcal{D}_{\frac{1}{2}}. $ □

Corollary 2.20. Assume that all conditions of Corollary 2.2 are satisfied, then the function $ \mathcal{Q}_{\mu, \frac{3}{2}}(r; z) $ is starlike in $ \mathcal{D}_{\frac{1}{2}}. $

Corollary 2.21. Suppose that all hypotheses of Corollary 2.3 hold, then the function $ \mathcal{Q}_{2, \beta}(r; z) $ is starlike in $ \mathcal{D}_{\frac{1}{2}} $.

If we set $ \beta = 2 $ in the above Theorem, in view of (1.4), the following result is true:

Corollary 2.22. Let $ 0 < r\leq1 $ If $ \mu\geq1, $ then the function $ \mathbb{Q}_\mu(r; z) $ is starlike in $ \mathcal{D}_{\frac{1}{2}}. $

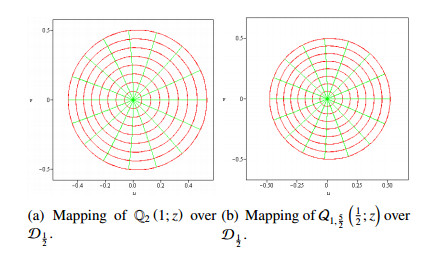
Example 2.23. The functions $ \mathcal{Q}_{3, \frac{3}{2}}(1/2; z), \mathbb{Q}_1(1;z) $ and $ \mathcal{Q}_{2, \frac{5}{3}}(1/2; z) $ are starlike in $ \mathcal{D}_{\frac{1}{2}} $.

In Figure 3, we give the mappings of the above presented examples in $ \mathbb{D} $.

Theorem 2.24. Let $ \beta, \mu > 0 $ and $ 0 < r < 1. $ If $ \beta\geq1+\frac{3}{\mu+1}, $ then the function $ \mathcal{Q}_{\mu, \beta}(r; z) $ is convex in $ \mathcal{D}_{\frac{1}{2}}. $

Proof. For all $ z\in\mathcal{D}, $ it follows that

where

For all $ k \geq2 $, we get

However, for all $ k\geq2 $ and under the conditions imposed on the parameters, we have

Hence, in view of (2.32) and (2.33) we conclude that the sequence $ (d_k)_{k\geq2} $ is decreasing. Therefore, by (2.31), we conclude

Moreover, since $ \beta\geq1+\frac{3}{\mu+1} $ and $ r\in (0, 1] $, we get

and consequently, for all $ z\in\mathcal{D}, $ we obtain

Finally, with the means of Lemma 1.6, we conclude that the function $ \mathcal{Q}_{\mu, \beta}(r; z) $ is convex in $ \mathcal{D}_{\frac{1}{2}}. $ □

If we take $ \beta = 2 $ in Theorem 2.15, in view of (1.4), the following result holds true:

Corollary 2.25. Let $ 0 < r\leq1. $ If $ \mu\geq2, $ then the function $ \mathbb{Q}_\mu(r; z) $ is convex in $ \mathcal{D}_{\frac{1}{2}}. $

If we let $ \mu = 1 $ in Theorem 2.15, in view of (1.5), we derive the following result:

Corollary 2.26. Let $ 0 < r\leq1. $ If $ \beta\geq\frac{5}{2}, $ then the function $ \mathcal{Q}_{1, \beta}(r; z) $ is convex in $ \mathcal{D}_{\frac{1}{2}}. $

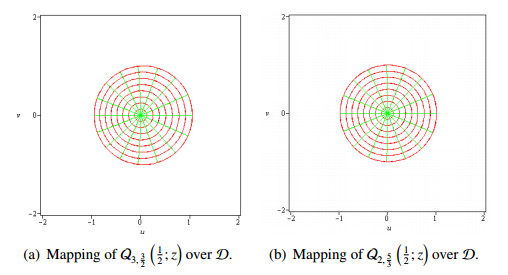
Example 2.27. The functions $ \mathbb{Q}_2(r; z) $ and $ \mathcal{Q}_{1, \frac{5}{2}}(r; z) $ are convex in $ \mathcal{D}_{\frac{1}{2}}. $

In Figure 4, we present the mappings of these examples in $ \mathbb{D } $.

Remark 2.28. The geometric properties of the function $ \mathbb{Q}_\mu(r; z) $ derived in Corollaries 2.16, 2.22 and 2.25 are new.

3.   Conclusions

In our present paper, we have derived sufficient conditions such that a class of functions associated to the generalized Mathieu type power series are to be starlike, close-to-convex and convex in the unit disk $ \mathcal{D}. $ The various results, which we have established in this paper, are believed to be new, and their importance is illustrated by several interesting corollaries and examples. Furthermore, we are confident that our paper will inspire further investigation in this field and pave the way for some developments in the study of geometric functions theory involving certain classes of functions related to the Mathieu type powers series.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA for funding this research work through the project number "NBU-FFR-2023-0093".

Conflict of interest

The authors declare that they have no conflicts of interest.