Figure 1.
Results of iterative phase retrieval for 30 iteration times placed at inverse s-shaped arrangement. Each kernel is of size 21 × 21.
Citation: Dario Siniscalco, Anna Lisa Brigida, Nicola Antonucci. Autism and neuro-immune-gut link[J]. AIMS Molecular Science, 2018, 5(2): 166-172. doi: 10.3934/molsci.2018.2.166
| [1] | Xiaolei Gu, Wei Xue, Yanhong Sun, Xuan Qi, Xiao Luo, Yongsheng He . Magnetic resonance image restoration via least absolute deviations measure with isotropic total variation constraint. Mathematical Biosciences and Engineering, 2023, 20(6): 10590-10609. doi: 10.3934/mbe.2023468 |
| [2] | Peixian Zhuang, Xinghao Ding, Jinming Duan . Subspace-based non-blind deconvolution. Mathematical Biosciences and Engineering, 2019, 16(4): 2202-2218. doi: 10.3934/mbe.2019108 |
| [3] | Yan Huo, Diyuan Guan . Size measurement and prediction for L-glutamic acid crystal growth during stirred crystallization based on imaging analysis. Mathematical Biosciences and Engineering, 2021, 18(2): 1864-1878. doi: 10.3934/mbe.2021097 |
| [4] | Sanjaykumar Kinge, B. Sheela Rani, Mukul Sutaone . Restored texture segmentation using Markov random fields. Mathematical Biosciences and Engineering, 2023, 20(6): 10063-10089. doi: 10.3934/mbe.2023442 |
| [5] | Chaofeng Ren, Xiaodong Zhi, Yuchi Pu, Fuqiang Zhang . A multi-scale UAV image matching method applied to large-scale landslide reconstruction. Mathematical Biosciences and Engineering, 2021, 18(3): 2274-2287. doi: 10.3934/mbe.2021115 |
| [6] | Qing Luo, Xiang Gao, Bo Jiang, Xueting Yan, Wanyuan Liu, Junchao Ge . A review of fine-grained sketch image retrieval based on deep learning. Mathematical Biosciences and Engineering, 2023, 20(12): 21186-21210. doi: 10.3934/mbe.2023937 |
| [7] | Pavithra Latha Kumaresan, Subbulakshmi Pasupathi, Sindhia Lingaswamy, Sreesharmila Thangaswamy, Vimal Shunmuganathan, Danilo Pelusi . Fruit-Fly optimization based feature integration in image retrieval. Mathematical Biosciences and Engineering, 2021, 18(5): 6178-6197. doi: 10.3934/mbe.2021309 |
| [8] | Hong-an Li, Min Zhang, Zhenhua Yu, Zhanli Li, Na Li . An improved pix2pix model based on Gabor filter for robust color image rendering. Mathematical Biosciences and Engineering, 2022, 19(1): 86-101. doi: 10.3934/mbe.2022004 |
| [9] | Xuwen Wang, Yu Zhang, Zhen Guo, Jiao Li . Identifying concepts from medical images via transfer learning and image retrieval. Mathematical Biosciences and Engineering, 2019, 16(4): 1978-1991. doi: 10.3934/mbe.2019097 |
| [10] | Xianyi Chen, Anqi Qiu, Xingming Sun, Shuai Wang, Guo Wei . A high-capacity coverless image steganography method based on double-level index and block matching. Mathematical Biosciences and Engineering, 2019, 16(5): 4708-4722. doi: 10.3934/mbe.2019236 |
In an information era, owing to hardware and software advances, the development of technologies in engineering is tented to high computational ability. Intelligent computing and machine learning provide a good strategy to solve the complicated problems and a fast computational ability to reduce the complexity of the procedure. In the computer vision field, it usually operates in the frequency domain to extract the essential information in order to model the events. However, the procedure operated in the frequency domain is a kind of complex computation. Involving the intelligence into the modeling technique to solve the confronted problems of computer vision is the current trend. Intelligent computing is the integration of many technologies and decisions of knowledge for the computing environment. Computational photography scheme, image processing, requests the intelligent computing to deal with the object model and feature extraction. Motion blur is usually presented in many practical scenarios, such as hand-held cameras especially mobile material. The motion-blurred picture is caused by the relative motion between the camera and an imaged scene during exposure. Generally, the relative motion can be divided into two kinds: camera shake and object motion. Sensor movement during exposure leads to unwanted blur in the acquired image. Assuming a scene and ignoring the effects of defocus and lens abnormality, each point in the blurred image can be modeled as the convolution of the unblurred image by a global point spread function (PSF). Image deblurring aims to achieve a deconvolution process to recover the clear image from the acquired blurry image. Based on intelligent computing strategy, image deblurring could be reduced the computing complexity and improved the computational time.
Artificial neural networks (NNs) have been used extensively in image processing [1,2]. Schuler et al. [3] proposed a learning-based neural network (NN) to estimate the features and then estimate blur kernel for deblurring by using the deconvolution. Additionally, a common assumption in motion deblurring methods is that the motion PSF is spatially invariant. This implies that all pixels are convolved with the same motion blur kernel. The problem of blur kernel estimation and more generally blind deconvolution is a long-existing problem in computer vision. Restoration of blurry images is highly dependent on estimation of motion blur kernel after implementing the appropriate image restoration method. Many well-known PSF algorithms to estimate blur kernel have been proposed [4,5,6,7,8]. When the PSF is known, or can be estimated, a deconvolution algorithm, such as Richardson-Lucy [9,10,11,12], can be used to deblur the image. Motion blur is a type of the relative motion of the camera and shooting scene during exposure. Mathematically, the corresponding motion blur information is usually modeled as a linear image degradation process.
|
$ B=I⊗K+N, $
|
(1.1) |
where $ \otimes $ denotes the convolution operator, $ B $, $ I $, $ K $, and $ N $ denote the blurred image, true sharp image, unknown blur kernel, and noise term, respectively. Blind image deconvolution is an inherently ill-posed problem since the blurred image $ B $ does not provide enough information for determining both $ I $ and $ K $. Therefore, how to estimate blur kernel $ K $ from blurred image $ B $ is an important issue in motion-blurred image restoration. Many of studies have been proposed. Some studies are briefly described in the following.
Blurred kernel information is usually hidden in the regions with edges, if the edge of an image suffered serious damage, it will result in inaccurate blur kernel estimation. Tai et al. [10] proposed a modified Richardson-Lucy (RL) method to incorporate space-invariant blur model under a projective motion path for image scenes. Yang et al. [11] proposed blur kernel estimation and non-blind image deconvolution to deblur image by using bilateral filter and Gradient attenuation Richardson-Lucy deconvolution algorithm. Dobeš et al. [13] and Goldstein and Fattal [5] proposed the kernel estimation in frequency domain. The blur kernel is then recovered using a phase retrieval algorithm with improved convergence and disambiguation capabilities. Deblurring approaches, based on spectral properties and edge information of an image have presented by [5,14,15] to retrieval the blur kernel information. In addition, one of many deblurring techniques is to incorporate image priors to impose on the deblurred results. Deshpande and Patnaik [16] proposed an image motion deblurring algorithm based on dual Fourier spectrum combined with bit plane slicing algorithm and Radon transform (RT) for accurate estimation of PSF parameters (blur length and blur angle). Shao et al. [17] used non-stationary Gaussian prior to estimate the salient edges of image as the cues to blur kernel estimation. He et al. [18] proposed motion blurring which used different priors for the local region and the motion blur kernel to formulate a minimization energy function that alternates between blur kernel estimation and deblurring image restoration. Jia [19] relied on color mixtures to estimate the motion blur kernel of moving objects given their boundary alpha values. Levin et al. [20] used a maximum a posteriori estimation (MAP) to estimate blur kernel and achieve the deblurring results. Except MAP methods [21,22], many methods are being developed [13,23,24,25,26].
In this paper, we propose a motion deblurring method based on fast PSF (FPSF) to achieve image restoration. The advantages of this system can speed up the running time and find an optimal blur kernel, as well as obtain a good image quality for deblurring. In addition, in order to verify the reliability of our proposed system, the experimental data include the real motion-blurred images and artificial blurred images.
The rest of this paper is organized as follows. Section 2 describes the related techniques. Section 3 describes the proposed method which includes blur kernel clustering, blur kernel integration, and the optimal blue kernel searching. Section 4 presents the experimental results. Finally, a conclusion is given in Section 5.
In this section, we briefly describe the techniques related to our proposed approach.
A particular property of natural image scenes can be illustrated by the following power-law relationship [27,28].
|
$ ∣ˆI(ω)∣2∝∥ω∥−β, $
|
(2.1) |
where $ \omega $ is the coordinates in frequency domain, $ \hat{I} $ denotes Fourier transform of a natural image ($ I $), according to the literature, $ \beta\approx 2 $.
As the researches indicated, the blur information is hidden in the power-law of the neighborhoods of edges, therefore, filtering an image forming Eq. (2.1) can be acquired this information and is expressed as
|
$ |^I∗d(ω)|2=|ˆI(ω)|2⋅|ˆd(ω)|2≈π2∥ω∥−2∥ω∥2=c, $
|
(2.2) |
for constant $ c $, $ d $ is a first-order Laplacian filter. Thus, a blurry image $ B = I\ast k $, this filtering process can be used to estimate the following blur-kernel power spectrum $ |\hat{k}(\omega)|^2 $.
|
$ |^(B∗d)(ω)|2=|ˆI(ω)|2⋅|ˆd(ω)|2⋅|ˆk(ω)|2≈c|ˆk(ω)|2. $
|
(2.3) |
The power spectrum of any signal $ F $ can relay to its autocorrelation according to the Wiener-Khinchin theorem [29].
|
$ ˆRF(ω)=|ˆF(ω)|2, $
|
(2.4) |
where the autocorrelation is defined by $ R_F(x) = (\bar{F}\ast F)(x) $. The blur approximation in Eq. (2.3) can be identified by real-space parts for the spectrum and can be expressed as
|
$ RB∗d(x)≈cRk(x). $
|
(2.5) |
Evidently, the power spectrum of a natural image varies by multiplicative factors along the different directions, that is,
|
$ |ˆI(ω)|2≈cθ(ω)⋅∥ω∥−2, $
|
(2.6) |
where $ \theta(\omega) = \arctan(\omega_x, \omega_y) $ is the angle of the vector $ \omega $.
Blur kernel information, like $ c_{\theta(\omega)} $ and the kernel phase, can be recovered by means of the Fourier slice theorem and Wiener-Khinchin theorem, given autocorrelation functions computed from the input blurry image $ B(x) $. From Eq. (2.6) known, only single parameter $ c_\theta $ is unknown. Based on Fourier theorem and Wiener-Khinchin theorem, Eq.(2.3) can be rewritten in real-space and expressed as Eq.(2.7) [5].
|
$ fθ(x)≈cθ⋅RPθ(k)(x),θ∈[−π,π], $
|
(2.7) |
where $ P_\theta $ is a projection of a 2D signal into 1D by integrating it along the direction orthogonal to $ \theta $. By repeating this procedure for all the $ \theta $, an approximation for the 2D blur-kernel power spectrum function $ |\hat{k}(\omega)|^2 $ can be obtained. In [5], this procedure repeated three times. In addition, based an iterative phase-retrieval algorithm, this approximation can recover the blur kernel $ k $.
The phase recovery also called phase retrieval. As described above, recovering the kernel $ k $, given its power spectrum $ |\hat{k}|^2 $ requires estimating the phase component of $ \hat{k}(\omega) $. However, this procedure only obtains the spectrum information, the phase information is still unknown because it iteratively switches between Fourier and real-space domains. In addition, the input $ |\hat{k}|^2 $ and the spatial constraints may not guarantee a unique solution. Moreover, as [30] discussed, it may converge to local minima formation, therefore, the phase retrieval procedure is repeated multiple times under starting randomly phase component to further estimate the blur kernel.
According to GS algorithm [31], this algorithm is a common method for phase retrieval. It is based on iterative Fourier transform and inverse Fourier transform between the object domain and the Fourier domain. A hybrid input-output method is used to estimate the blur kernel in iterative phase retrieval procedure under the appropriate frequency/spatial domain constraints [5,31]. Therefore, based on iterative phase retrieval algorithm, the blur kernel can be recovered. Thus, the blurry image can be deblurred through a deconvolution. The procedures of phase retrieval algorithm are briefly described as follows. Its pseudo code is shown in Algorithm 1 (see [5] for details).
Step 1) Given the initial phase $ \phi(\omega) $ within $ [-\pi, \pi] $ randomly generated.
Step 2) Transfrom the real-space domain $ g $ using inverse Fourier transform.
Step 3) Transform $ g $ into $ \hat{g} $ using Fourier domain constraints.
Step 4) Transform to real-space $ g_2 $ using the phase information of $ \hat{g} $.
Step 5) Compute the constraint $ R(x) $ using the space domain constraints.
Step 6) Obtain a hybrid input-output constraint $ \Omega $ which is the union of $ R(x) $ and $ s $.
Step 7) Repeat Steps 3 - 6 for $ m $ times, and output the $ k_n $ based on the constraint $ \Omega $ which is the union of $ g_2(x) $ and $ s $.
| Algorithm 1 Iterative phase retrieval |
| 1: Input: kernel magnitude spectrum, $p(\omega)=\mid\hat{k}(\omega)\mid$ and kernel size $=s$ 2: for $n=0$ to $N_{guesses}$ do 3: //initiate the phase $\phi(\omega)$ randomly; 4: Sample $\phi(\omega)$ uniformly from $[-\pi, \pi]$ 5: //transform to real space using inverse Fourier transform 6: $g=F^{-1}(p\cdot \textrm{e}^{i\phi})$ 7: for $m=1$ to $N_{inner}$ do 8: //appply fourier domain constraints; 9: $g_2=F^{-1}((\alpha p+(1-\alpha)\mid\hat{g}\mid)\cdot \exp^{i\cdot\phi(\hat{g})})$ 10: //apply space domain constraints 11: $R(x)=2g_{2}(x)-g(x)$ 12: $\beta =\beta_{0}+(1-\beta_{0})(1-\exp(-m/7)^3)$ 13: $\Omega=\{x:R(x) < 0\}\cup\{x:x\notin [0, s]\times [0, s]\}$ 14: $g(x)=\left \{ βg(x)+(1−2β)g2(x),ifx∈Ω,g2(x),ifx∉Ω; \right.$ 15: end for 16: $\Omega=\{x:g_2(x) < 0\}\cup\{x:x\notin [0, s]\times [0, s]\}$ 17: $k_n(x)= \left \{ 0,ifx∈Ω,g2(x),ifx∉Ω \right. $ 18: end for 19: Output: $k_n$ |
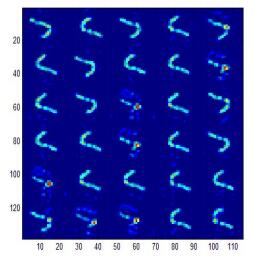
However, using the phase retrieval method, it cannot guarantee to obtain the same kernel in each of iterations and cannot decide which one is the best blur kernel, as shown in Fig. 1. Figure 1 shows thirty blur kernels which include the symmetric or failure blur kernels after performing thirty iterations in phase retrieval. Assuming that repeating phase retrieval for $ n $ times, it can find $ n $ blur kernels. Afterwards, an optimal kernel can be obtained from these $ n $ kernels. [5] takes the final kernel to deconvolve the blurry image. In our experiments, we utilize a normalized sparsity measure (NSM) [24] to decide the optimal blur kernel from $ n $ blur kernels and to estimate the quality of blur kernel.
As known above, it can obtain $ n $ blur kernels after iterating $ n $ times. Each of NSM values for deconvolution by using the corresponding kernel can be calculated. Figure 1 shows an example of blur kernel for thirty iteration times. From Fig. 1, it is obvious that the symmetric relationship exists among blur kernels and the estimated blur kernel for each iteration is also different. Hence, the measure of blur kernel quality will test the symmetry of blur kernel and will make a score. In order to estimate the symmetric characteristic of blur kernel, it has to calculate the NSM score twice. For example, if there are thirty kernels, it will calculate the NSM for sixty times. After computing NSM value, the smaller the NSM score, the better the reconstructed image, as shown in Fig. 2. According to our experimental results, a kernel with the minimum NSM value is a good kernel more confidently.
In our system, we modify the number of computing NSM times and thus speed up an optimal blur kernel acquirement from $ n $ blur kernels.
Natural image signals are highly structural information, such as pixels exhibiting strong dependencies and containing important information about the structure of the objects in the visual scene. In order to estimate the structural performance of the reconstructed image after deconvolution, we adopt the structural-similarity-based image quality measure (SSIM) [32] instead of the mean squared error (MSE). The SSIM mainly compute the structural similarity between the reference and the distorted signals. However, one usually requires the overall image quality measure, a mean SSIM (MSSIM) derived from SSIM is used to achieve this measure, which can exhibit much better consistency with the qualitative visual appearance. In our experiments, we adopt the MSSIM to estimate the quality of the reconstructed image. The MSSIM index is briefly defined as
|
$ MSSIM(X,Y)=1MM∑j=1SSIM(xj,yj), $
|
(2.8) |
where $ X $ and $ Y $ are the reference and the distorted images, respectively; $ x_j $ and $ y_j $ are the image contents at the $ j $th local window; and $ M $ is the number of local windows of the image. The higher the MSSIM, the closer both images.
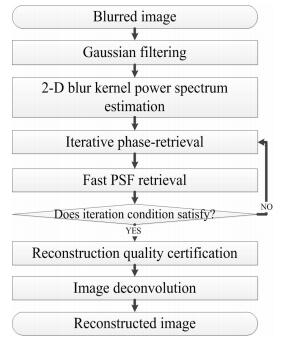
In this paper, we propose an image deblurring using fast point spread function (FPSF) method to efficiently and quickly search the optimal blur kernel. Because the method by [5] is time-consuming, in our approach, we will further improve the computational time and speed up decide the optimal blur kernel to deblur the blurred image. Figure 3 illustrates the flowchart of the proposed system. The details of the procedures are described in the following.
In order to improve the blur kernel estimation which is seriously affected by high-frequency components [5], we use Gaussian filter [33] to reduce this influence and improve the blur kernel estimation for a blurred image. Here, we use Gaussian filter with size $ 5\times5 $, $ \sigma = 0.6 $, and a mean of zero, it is proportional to the size of the neighborhood on which the filter operates. Pixels more distant from the center of the operator have smaller influence. After filtering the blurry image, it can improve the power spectrum of 2D blur kernels, afterwards, the optimal blur kernel can be acquired by our proposed method.
After doing blur kernel estimation and iterative phase retrieval described by the previous section, it can obtain the corresponding kernels in each of iterative times in phase retrieval. However, from Figure 1, it is clearly obvious that each of these kernels is different. In other words, it does not guarantee that these kernels can yield a good deblurring result. Based on this reason, we propose a FPSF method to estimate an optimal blur kernel. Using this estimated optimal blur kernel, it can deblur the blurry image by deconvolution. Figure 4 illustrates the flowchart of the FPSF.
This method consists of blur kernel clustering and blur kernel integration. The blur kernel clustering based on MSSIM is to classify these blur kernels obtained by phase retrieval. After performing the clustering, we use the integration to find the optimal kernel from the clusters. For clustering, we use the MSSIM to estimate the similarity of all candidate kernels, kernel which has a high MSSIM will be clustered into the same cluster. The procedures of the clustering method are described as follows.
First of all, assuming that there are $ k_n $ blur kernels.
Step 1) Select the first kernel in these kernels as an initial base.
Step 2) Calculate the MSSIM values for this base and the rest of candidate kernels.
Step 3) If MSSIM value is more than or equal to a threshold, then this candidate kernel is classified into the corresponding cluster.
Step 4) If MSSIM value is less than a threshold, then a new base is yielded and it will serve as a new cluster.
Step 5) Repeat Steps 2 - 4, until all candidate kernels are clustered.
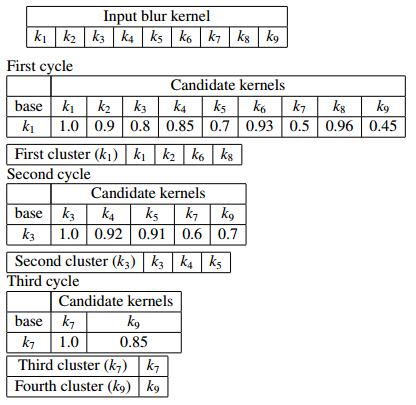
Based on MSSIM characteristic, the higher the MSSIM value, more similar both kernels. According to our experiments, this threshold is set 0.9. An example of kernel clustering algorithm is illustrated as follows. Assuming there are nine blur kernels, they will be clustered.
|
First, kernel $ k_1 $ is chosen as a base, next, the MSSIM value is computed. The first cycle can obtain the first cluster called $ k_1 $ which includes $ k_2 $, $ k_6 $, and $ k_8 $ kernels. Then, kernel $ k_3 $ is a new cluster. After computing the clustering procedures, all candidate kernels can be classified into the corresponding clusters.
Based on above clustering process, assume there are $ n $ blur kernels, they will be classified into $ C_m $ kernel clusters where $ m\leq n $. As described above, a good kernel can be obtained after computing the NSM for sixty times, but, it is very time-consuming. Therefore, in order to reduce the number of computing NSM times, we propose a blur kernel integration technique to gain this performance. This kernel integration technique consists of mean blur kernel calculation and refining described as follows.
◆ Mean blur kernel: We calculate an average blur kernel corresponding to each of kernel clusters with the relative coordinates. The average blur kernel for each of kernel clusters is defined as
|
$ Km,avg(x,y)=1gg∑i=1Cm(i)(x,y), $
|
(3.1) |
where $ g $ denotes the number of kernels corresponding to kernel cluster, $ m $ denotes the number of kernel clusters, $ C_m(\cdot)(x, y) $ denotes a kernel value corresponding to the $ x $ and $ y $ coordinates at the $ m $th kernel cluster.
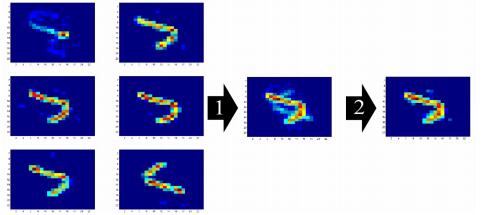
◆ Refining: Owing to the difference between kernels in cluster, the average kernel may involve noise (as shown in Figure 5 number 1's result). As described above, the noise will affect the deblurring process, hence, in order to reduce the influence of the noise and keep the important information of the kernel, we further refine the mean blur kernel to gain performance. We make a weight matrix to achieve the refining. First, we define a weight matrix of a kernel cluster which represents the number of nonzero kernel values corresponding to the coordinates in the same kernel cluster, the weight matrix is defined as
|
$ wm(x,y)={wm(x,y)+1,ifCm(i)(x,y)>0,wm(x,y),otherwise, $
|
(3.2) |
where the initial $ w_m(x, y) $ sets to zero for $ m $ clusters. An average weight value is computed by
|
$ aveWm=∑x∑ywm(x,y)Sm, $
|
(3.3) |
where $ S_m $ is the number of nonzero kernel values corresponding to the relative cluster. The refining mean blur kernel is expressed as
|
$ RKm,avg(x,y)={Km,avg(x,y),ifwm(x,y)≥aveWm,Km,avg(x,y)=0,otherwise. $
|
(3.4) |
Figure 5 illustrates an example of kernel integration processing in a kernel cluster.
Based on the blur kernel integration, we can obtain a refining mean blur kernel corresponding to each of kernel clusters. Afterwards, using the measure of blur kernel quality again described by subsection 2.3 for $ m $ refining mean blur kernels, we obtain the best mean blur kernel and its corresponding cluster. Because we have recorded the symmetry of the cluster in searching cluster process, thus, we can greatly reduce the computational time and quickly find an optimal blur kernel. The procedures of searching an optimal blur kernel (OBK) are described as follows.
Step 1) Give a set of blur kernels which belong to the best kernel cluster, and the corresponding symmetric property of the phase.
Step 2) Deconvolve all the blurred images using these kernels.
Step 3) Compute the relative NSM values for all deconvolution results.
Step 4) Find the minimum NSM value from these NSM values and its corresponding kernel, this kernel serves as an optimal kernel.
To verify the performance of our proposed method, the experimental results are compared with Goldstein and Fattal [5] and Krishnan et al. [24] to perform the visual quality of the reconstruction image and computational time. Based on the above procedures, we can obtain the optimal kernel for the corresponding blurry image, then each of three components (red, green, blue) for the color image is individually used this optimal kernel to work the non-blind deconvolution method based on [34]; finally, all blurry color images can be reconstructed.
All experiments are implemented in Microsoft Visual Studio 2010 C$ \sharp $, an Intel © i5 dual Core 3.2 GHz, and 4 GB RAM computer with window 7 64 bits platform.
First, we need to make the experimental data by using predefined blur kernels. How to decide the number of predefined blur kernels is a trade-off between objectivity and variety of the experimental data. In order to perform these attributes, in our experiments, we make ten blur kernels with size $ 21\times 21 $ shown in Figure 6 to simulate ten kinds of blurred images. A database including ten images with size $ 768\times 1024 $, $ 682\times 1024 $, $ 1024\times 682 $, and $ 720\times 960 $ pixels separated 4, 3, 2, and 1 is given. Then we blurred each of these images using ten blur kernels, it can obtain 100 motion-blurred images for test. In order to avoid noise disturbance to affect kernel estimation, all of experimental data are firstly filtered by Gaussian filter. After filtering, we can obtain more convergent blur kernel by means of our proposed method. Here, we use Gaussian filter with the standard deviation $ \sigma = 0.6 $ and run thirty iterations for phase retrieval to demonstrate our experiments.
For performance measure, we use the peak signal-to-noise ratio (PSNR) and MSSIM to estimate the performance of the system. The PSNR and mean square error (MSE) are defined as
|
$
PSNR=10logS2MaxMSE,MSE=1h×wh∑iw∑j|I1(i,j)−I2(i,j)|2,
$
|
(4.1) |
where $I_1(i,j)$ and $I_2(i,j)$ denote the reconstructed image and the original one corresponding to the coordinates $(i,j)$. $h$ and $w$ denote the height and width of the image, respectively. For a gray-level image, $S_{Max}$ is 255 gray value.
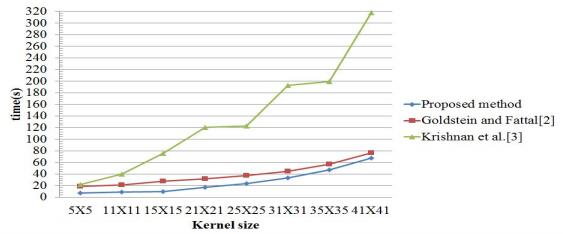
Because our proposed method improved Goldstein and Fattal method, the power spectrum of blur kernel for each iteration in phase retrieval may be not equal. Hence, in order to obtain the stable performance in our experiments, each blurry image is doing blur kernel estimation and its convolution for ten times. In addition, the size of blur kernel will seriously affect the execution time and reconstructed image quality, therefore, we test the different kernel sizes to demonstrate the execution speed. First of all, we take an average execution time in which the blurry image is doing blur kernel estimation with the different kernel sizes for ten iterations. Figure 7 shows the average execution time for the different blur kernel sizes in our experimental data. From Figure 7, it is clear that the execution time increases with increasing kernel size, and our proposed method is more upgraded than those of methods. Hence, considering the computational time and the visual quality of the reconstructed images, we adopt the blur kernel of size 21 $ \times $ 21.
Table 1 illustrates the PSNR value and MSSIM value. Image deblurring results of a part of tests are shown in Figures 8-9. Besides man-made test data, we also use the real motion-blurred images to demonstrate our proposed method, as shown in Figures 10-11.
| Kernel | Method | ||
| Proposed | [5] | [24] | |
| $k_1$ | 22.13/0.94 | 22.15/0.81 | 20.47/0.70 |
| $k_2$ | 23/0.96 | 23.24/0.85 | 20.36/0.73 |
| $k_3$ | 23.95/0.96 | 24.36/0.53 | 25.94/0.85 |
| $k_4$ | 22.6/0.95 | 22.47/0.83 | 22.04/0.79 |
| $k_5$ | 21.69/0.93 | 21.48/0.79 | 20.16/0.65 |
| $k_6$ | 22.42/0.94 | 22.49/0.82 | 22.8/0.83 |
| $k_7$ | 19.43/0.88 | 19.33/0.68 | 18.77/0.57 |
| $k_8$ | 24.27/0.95 | 24.28/0.95 | 21.16/0.88 |
| $k_9$ | 22.13/0.94 | 22.14/0.80 | 21.63/0.78 |
| $k_{10}$ | 23.4/0.95 | 23.54/0.82 | 20.23/0.66 |
| Ave. | 22.5/0.94 | 22.55/0.82 | 21.36/0.75 |
DownLoad:
CSV
The experimental results have been presented above. For computational time, our proposed method is superior to Goldstein and Fattal's method and Krishnan et al.'s method, as shown in Figure 7. For MSSIM and PSNR values, our proposed method is superior to Krishnan et al.'s method and is close to Goldstein and Fattal's method, illustrated in Table 1. For real blurry images, because many factors caused the motion-blurred images are unknown beforehand, the recovered image still existed the failure, as shown in Figure 11. In summary, the global performance for MSSIM and computational time is superior to that for the methods of Goldstein and Fattal and Krishnan et al.
In this paper, we have proposed an image deblurring based on FPSF and clustering to recover the sharp image. Based on FPSF method applied the intelligence computing on the estimated image, the advantage of the computing strategy could reduce much more the computational complexity, at the same time, the optimal blur kernel could be estimated efficiently. As the experimental results, our proposed algorithm could efficiently reduce computational time. Also, for the blurry images, the proposed algorithm could restore the images with a good visual quality. It could enhance the image quality shown in many kinds of the view devices.
There is no conflict of interest in this paper.
| [1] |
Blikslager AT, Moeser AJ, Gookin JL, et al. (2007) Restoration of barrier function in injured intestinal mucosa. Physiol Rev 87: 545. doi: 10.1152/physrev.00012.2006
|
| [2] | Podolsky DK (1999) V. Innate mechanisms of mucosal defense and repair: The best offense is a good defense. Am J Physiol 277: G495–G499. |
| [3] |
Kunzelmann K, Mall M (2002) Electrolyte transport in the mammalian colon: Mechanisms and Implications for disease. Physiol Rev 82: 245–289. doi: 10.1152/physrev.00026.2001
|
| [4] |
Ferraris RP, Diamond J (1997) Regulation of intestinal sugar transport. Physiol Rev 77: 257–302. doi: 10.1152/physrev.1997.77.1.257
|
| [5] |
Groschwitz KR, Hogan SP (2009) Intestinal barrier function: Molecular regulation and disease pathogenesis. J Allergy Clin Immunol 124: 3–22. doi: 10.1016/j.jaci.2009.05.038
|
| [6] |
Bischoff S, Barbara G, Buurman W, et al. (2014) Intestinal permeability-A new target for disease prevention and therapy. BMC Gastroenterol 14: 189–214. doi: 10.1186/s12876-014-0189-7
|
| [7] |
Van Itallie CM, Holmes J, Bridges A, et al. (2008) The density of small tight junction pores varies among cell types and is increased by expression of claudin-2. J Cell Sci 121: 298–305. doi: 10.1242/jcs.021485
|
| [8] |
Ulluwishewa D, Anderson RC, Mcnabb WC, et al. (2011) Regulation of tight junction permeability by intestinal bacteria and dietary components. J Nutr 141: 769–776. doi: 10.3945/jn.110.135657
|
| [9] | De Magistris L, Picardi A, Sapone A, et al. (2014) Intestinal barrier in autism, In: Patel VB (ed.), Comprehensive guide to autism, New York: Springer, 123. |
| [10] |
Catassi C, Fasano A (2008) Celiac disease. Curr Opin Gastroenterol 24: 687–691. doi: 10.1097/MOG.0b013e32830edc1e
|
| [11] |
Bjarnason I, Macpherson A, Hollander D (1995) Intestinal permeability: An overview. Gastroenterology 108: 1566–1581. doi: 10.1016/0016-5085(95)90708-4
|
| [12] |
Fasano A (2011) Zonulin and its regulation of intestinal barrier function: The biological door to inflammation, autoimmunity and cancer. Physiol Rev 91: 151–175. doi: 10.1152/physrev.00003.2008
|
| [13] |
Lerner A, Matthias T (2015) Changes in intestinal tight junction permeability associated with industrial food additives explain the rising incidence of autoimmune disease. Autoimmun Rev 14: 479–489. doi: 10.1016/j.autrev.2015.01.009
|
| [14] |
Siniscalco D, Cirillo A, Bradstreet JJ, et al. (2013) Epigenetic findings in autism: New perspectives for therapy. Int J Environ Res Public Health 10: 4261–4273. doi: 10.3390/ijerph10094261
|
| [15] |
Siniscalco D, Antonucci N (2013) Possible use of Trichuris suis ova in autism spectrum disorders therapy. Med Hypotheses 81: 1–4. doi: 10.1016/j.mehy.2013.03.024
|
| [16] |
Wakefield AJ (2002) The gut-brain axis in childhood developmental disorders. J Pediatr Gastroenterol Nutr 34: S14–S17. doi: 10.1097/00005176-200205001-00004
|
| [17] | Siniscalco D (2014) Gut bacteria-brain axis in autism. Autism 4: e124. |
| [18] | Siniscalco D, Antonucci N (2013) Involvement of dietary bioactive proteins and peptides in autism spectrum disorders. Curr Protein Pept Sci 14: 674–679. |
| [19] |
Trivedi MS, Shah JS, Al-Mughairy S, et al. (2014) Food-derived opioid peptides inhibit cysteine uptake with redox and epigenetic consequences. J Nutr Biochem 25: 1011–1018. doi: 10.1016/j.jnutbio.2014.05.004
|
| [20] |
Frustaci A, Neri M, Cesario A, et al. (2012) Oxidative stress-related biomarkers in autism: Systematic review and meta-analyses. Free Radic Biol Med 52: 2128–2141. doi: 10.1016/j.freeradbiomed.2012.03.011
|
| [21] |
Melnyk S, Fuchs GJ, Schulz E, et al. (2012) Metabolic imbalance associated with methylation dys-regulation and oxidative damage in children with autism. J Autism Dev Disord 42: 367–377. doi: 10.1007/s10803-011-1260-7
|
| [22] |
Shattock P, Whiteley P (2002) Biochemical aspects in autism spectrum disorders: Updating the opioid-excess theory and presenting new opportunities for biomedical intervention. Expert Opin Ther Targets 6: 175–183. doi: 10.1517/14728222.6.2.175
|
| [23] |
Siniscalco D, Sapone A, Giordano C, et al. (2013) Cannabinoid receptor type 2, but not type 1, is up-regulated in peripheral blood mononuclear cells of children affected by autistic disorders. J Autism Dev Disord 43: 2686–2695. doi: 10.1007/s10803-013-1824-9
|
| [24] |
Siniscalco D, Bradstreet JJ, Cirillo A, et al. (2014) The in vitro GcMAF effects on endocannabinoid system transcriptionomics, receptor formation, and cell activity of autism-derived macrophages. J Neuroinflammation 11: 78. doi: 10.1186/1742-2094-11-78
|
| [25] |
Fiorentino M, Sapone A, Senger S, et al. (2016) Blood-brain barrier and intestinal epithelial barrier alterations in autism spectrum disorders. Mol Autism 7: 49. doi: 10.1186/s13229-016-0110-z
|
| [26] |
Rose DR, Yang H, Serena G, et al. (2018) Differential immune responses and microbiota profiles in children with autism spectrum disorders and co-morbid gastrointestinal symptoms. Brain Behav Immun 70: 354–368. doi: 10.1016/j.bbi.2018.03.025
|
| [27] |
Lionetti E, Leonardi S, Franzonello C, et al. (2015) Gluten psychosis: Confirmation of a new clinical entity. Nutrients 7: 5532–5539. doi: 10.3390/nu7075235
|
| [28] |
O'Mahony SM, Clarke G, Borre YE, et al. (2015) Serotonin, tryptophan metabolism and the brain-gut-microbiome axis. Behav Brain Res 277: 32–48. doi: 10.1016/j.bbr.2014.07.027
|
| [29] |
Theije CGMD, Koelink PJ, Korte-Bouws GA, et al. (2014) Intestinal inflammation in a murine model of autism spectrum disorders. Brain Behav Immun 37: 240–247. doi: 10.1016/j.bbi.2013.12.004
|
| [30] |
Baganz NL, Blakely RD (2013) A dialogue between the immune system and brain, spoken in the language of serotonin. ACS Chem Neurosci 4: 48–63. doi: 10.1021/cn300186b
|
| [31] |
Van Elst K, Bruining H, Birtoli B, et al. (2014) Food for thought: Dietary changes in essential fatty acid ratios and the increase in autism spectrum disorders. Neurosci Biobehav Rev 45: 369–738. doi: 10.1016/j.neubiorev.2014.07.004
|
| [32] |
Halliwell B (2006) Oxidative stress and neurodegeneration: Where are we now? J Neurochem 97: 1634–1658. doi: 10.1111/j.1471-4159.2006.03907.x
|
| [33] |
Cartocci V, Catallo M, Tempestilli M, et al. (2018) Altered brain cholesterol/isoprenoid metabolism in a rat model of autism spectrum disorders. Neuroscience 372: 27–37. doi: 10.1016/j.neuroscience.2017.12.053
|
| [34] |
Brigida AL, Schultz S, Cascone M, et al. (2017) Endocannabinod signal dysregulation in autism spectrum disorders: A correlation link between inflammatory state and neuro-immune alterations. Int J Mol Sci 18: 1425. doi: 10.3390/ijms18071425
|
| [35] |
Acharya N, Penukonda S, Shcheglova T, et al. (2017) Endocannabinoid system acts as a regulator of immune homeostasis in the gut. Proc Natl Acad Sci USA 114: 5005–5010. doi: 10.1073/pnas.1612177114
|
| [36] |
Gyires K, Zádori ZS (2016) Role of cannabinoids in gastrointestinal mucosal defense and inflammation. Curr Neuropharmacol 14: 935–951. doi: 10.2174/1570159X14666160303110150
|
| [37] |
Maríbauset S, Llopisgonzález A, Zazpe I, et al. (2016) Nutritional Impact of a Gluten-Free Casein-Free Diet in Children with Autism Spectrum Disorder. J Autism Dev Disord 46: 673–684. doi: 10.1007/s10803-015-2582-7
|
| [38] |
Iovene MR, Bombace F, Maresca R, et al. (2017) Intestinal Dysbiosis and Yeast Isolation in Stool of Subjects with Autism Spectrum Disorders. Mycopathologia 182: 349–363. doi: 10.1007/s11046-016-0068-6
|
| [39] | Siniscalco D, Mijatovic T, Bosmans E, et al. (2016) Decreased Numbers of CD57 + CD3- Cells Identify Potential Innate Immune Differences in Patients with Autism Spectrum Disorder. Vivo 30: 83–89. |
| [40] |
de Theije CG, Wopereis H, Ramadan M, et al. (2014) Altered gut microbiota and activity in a murine model of autism spectrum disorders. Brain Behav Immun 37: 197–206. doi: 10.1016/j.bbi.2013.12.005
|
| [41] |
Needham BD, Tang W, Wu WL (2018) Searching for the gut microbial contributing factors to social behavior in rodent models of autism spectrum disorder. Dev Neurobiol 78: 474–499. doi: 10.1002/dneu.22581
|
| [42] |
Fung TC, Olson CA, Hsiao EY (2017) Interactions between the microbiota, immune and nervous systems in health and disease. Nat Neurosci 20: 145–155. doi: 10.1038/nn.4476
|
| [43] |
Santocchi E, Guiducci L, Fulceri F, et al. (2016) Gut to brain interaction in Autism Spectrum Disorders: A randomized controlled trial on the role of probiotics on clinical, biochemical and neurophysiological parameters. BMC Psychiatry 16: 183. doi: 10.1186/s12888-016-0887-5
|
Dario Siniscalco, Anna Lisa Brigida, Nicola Antonucci. Autism and neuro-immune-gut link[J]. AIMS Molecular Science, 2018, 5(2): 166-172. doi: 10.3934/molsci.2018.2.166
| Kernel | Method | ||
| Proposed | [5] | [24] | |
| $k_1$ | 22.13/0.94 | 22.15/0.81 | 20.47/0.70 |
| $k_2$ | 23/0.96 | 23.24/0.85 | 20.36/0.73 |
| $k_3$ | 23.95/0.96 | 24.36/0.53 | 25.94/0.85 |
| $k_4$ | 22.6/0.95 | 22.47/0.83 | 22.04/0.79 |
| $k_5$ | 21.69/0.93 | 21.48/0.79 | 20.16/0.65 |
| $k_6$ | 22.42/0.94 | 22.49/0.82 | 22.8/0.83 |
| $k_7$ | 19.43/0.88 | 19.33/0.68 | 18.77/0.57 |
| $k_8$ | 24.27/0.95 | 24.28/0.95 | 21.16/0.88 |
| $k_9$ | 22.13/0.94 | 22.14/0.80 | 21.63/0.78 |
| $k_{10}$ | 23.4/0.95 | 23.54/0.82 | 20.23/0.66 |
| Ave. | 22.5/0.94 | 22.55/0.82 | 21.36/0.75 |
DownLoad:
CSV
| Kernel | Method | ||
| Proposed | [5] | [24] | |
| $k_1$ | 22.13/0.94 | 22.15/0.81 | 20.47/0.70 |
| $k_2$ | 23/0.96 | 23.24/0.85 | 20.36/0.73 |
| $k_3$ | 23.95/0.96 | 24.36/0.53 | 25.94/0.85 |
| $k_4$ | 22.6/0.95 | 22.47/0.83 | 22.04/0.79 |
| $k_5$ | 21.69/0.93 | 21.48/0.79 | 20.16/0.65 |
| $k_6$ | 22.42/0.94 | 22.49/0.82 | 22.8/0.83 |
| $k_7$ | 19.43/0.88 | 19.33/0.68 | 18.77/0.57 |
| $k_8$ | 24.27/0.95 | 24.28/0.95 | 21.16/0.88 |
| $k_9$ | 22.13/0.94 | 22.14/0.80 | 21.63/0.78 |
| $k_{10}$ | 23.4/0.95 | 23.54/0.82 | 20.23/0.66 |
| Ave. | 22.5/0.94 | 22.55/0.82 | 21.36/0.75 |
