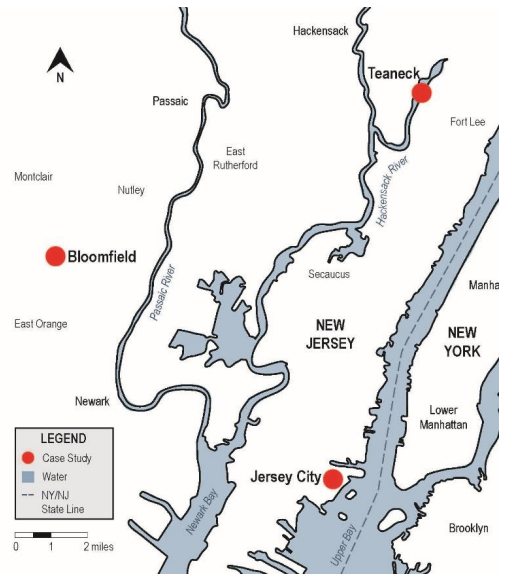
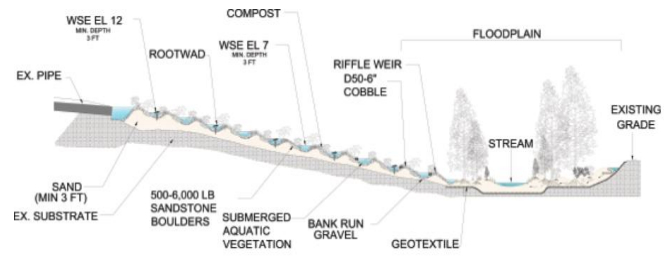
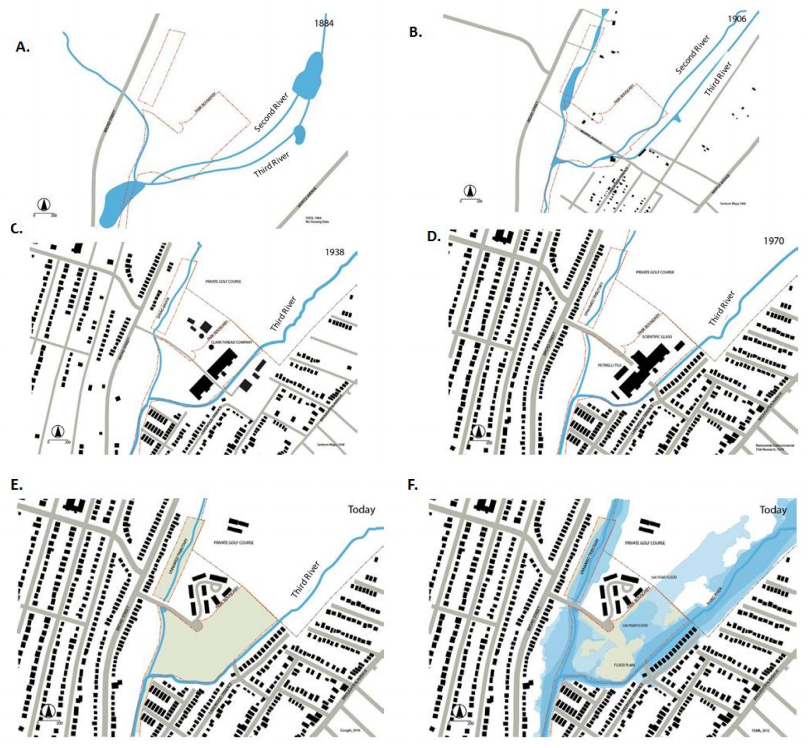
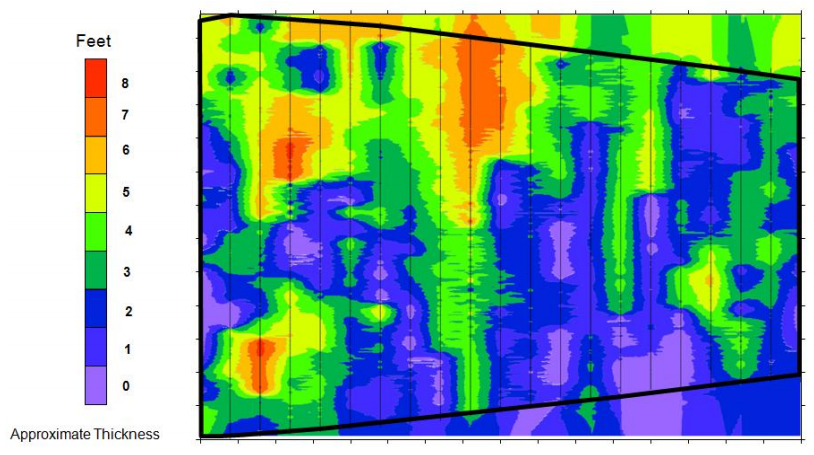
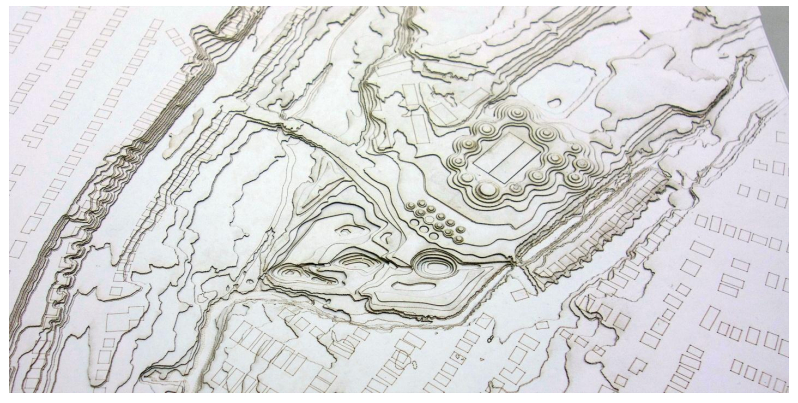
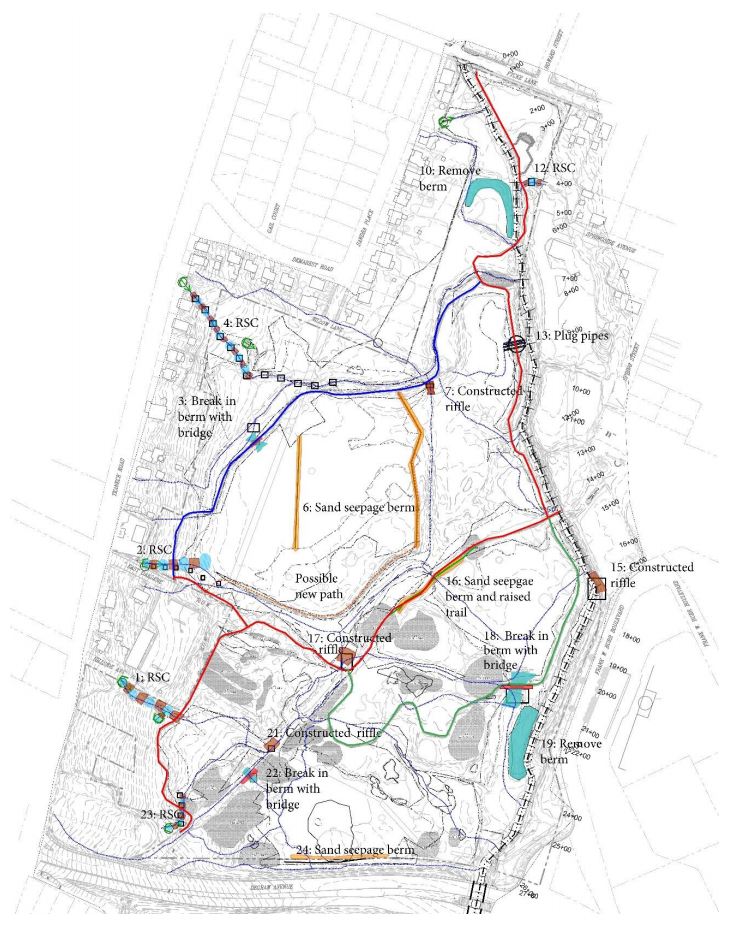
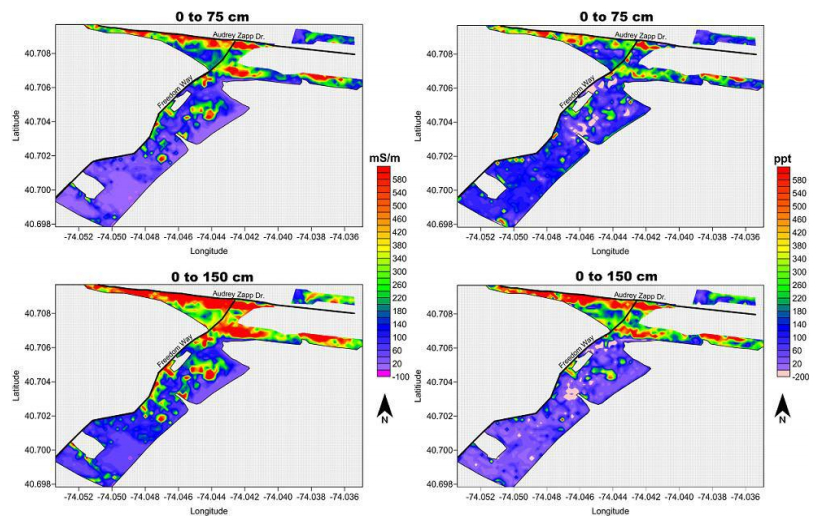
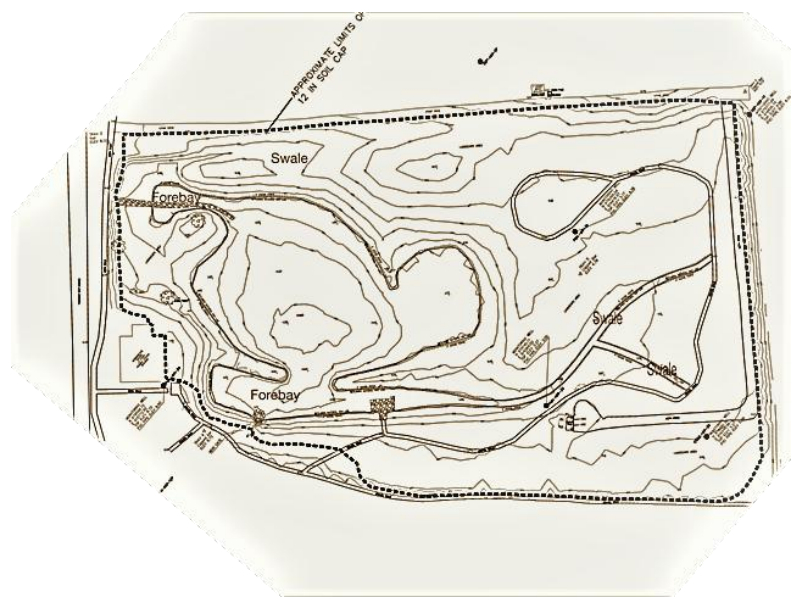
The continuing loss of urban wetlands due to an expanding human population and urban development pressures makes restoration or creation of urban wetlands a high priority. However, urban wetland restorations are particularly challenging due to altered hydrologic patterns, a high proportion of impervious surface and stormwater runoff, degraded urban soils, historic contamination, and competitive pressure from non-native species. Urban wetland projects must also consider human-desired socio-economic benefits. We argue that using current wetland restoration approaches and existing regulatory “success” criteria, such as meeting restoration targets for vegetation structure based on reference sites in non-urban locations, will result in “failed” urban restorations. Using three wetland Case Studies in highly urbanized locations, we describe geophysical tools, stormwater management methods, and design approaches useful in addressing urban challenges and in supporting “successful” urban rehabilitation outcomes. We suggest that in human-dominated landscapes, the current paradigm of “restoration” to a previous state must shift to a paradigm of “rehabilitation”, which prioritizes wetland functions and values rather than vegetation structure in order to provide increased ecological benefits and much needed urban open space amenities.
1.
Introduction
Molecular biology research on the molecular basis of biological activity requires data. Biologists acquire these data by using approaches and technologies such as microarray and RNA-sequencing (RNA-seq) techniques. Microarray technology is used to detect the sequences of nucleic acids and simultaneously thousands of gene transcripts from samples [1]. RNA-seq is a sequencing technique that can show the existence and amount of RNA in a biological sample by using next generation sequencing. Both techniques produce a high-dimensioanal gene expression data matrix with rows that indicate genes, columns that indicate experimental conditions, and cells that indicate the expression of that gene under those conditions. Gene expression data are very important for acquiring knowledge about cells, but there are frequently missing values. These missing values are often caused by experimental errors such as hybridization failures in microarray datasets and missing read counts in RNA-seq datasets. However, further analysis of these datasets requires a complete data matrix. Therefore, missing-value imputation approaches that use coherence the data are needed.
Two well-known missing-value imputation methods are LLS and BPCA. BPCA estimates missing values in the target gene (gene that contains missing values) by using a linear combination of principal components with parameters estimated using a Bayesian method. LLS uses a linear combination of the target gene and its similar genes to estimate the missing values in the target gene, and it uses clustering to measure gene similarities. In reality, genes are similar only under certain experimental conditions, so this similarity should only be measured by considering the related experimental conditions instead of all of the conditions. This is why clustering should be performed in rows and columns simultaneously, which is called biclustering [2]. Biclustering aims to identify local patterns in genes and conditions at the same time. The output of the biclutering technique is biclusters [3]. The use of this technique in LLS gives a better estimation of the missing values. Biclustering collates genes and conditions based on a weighted distance and correlation, respectively. Then, a regression model is used for least square-based missing-value estimation. An iterative framework is applied to improve the selection of coherent genes and correlated conditions. This method is called iterative bicluster-based least squares or bi-iLS [4].
Bi-iLS uses the row average to fill in all of the missing values in the target gene to obtain a temporary complete matrix. However, the row average is viewed as being flawed. The row average cannot reflect the real structure of the dataset because it only uses the information from an individual row. Thus, BPCA is considered better than the row average due to it reflecting the global covariance structure in all genes [5]. In this study, BPCA was used to obtain the temporary complete matrix in bi-iLS instead of the row average. This modification resulted in a new imputation method called bi-BPCA-iLS.
In this paper, the framework and implementation of our proposed bi-BPCA-iLS algorithm for missing-value imputation has been presented. The proposed missing-value imputation method will be implemented on a microarray dataset of Saccharomyces cerevisiae and an RNA-seq dataset of Schizosaccharomyces pombe.
2.
Missing values
In theory, every data point has a probability of being missing. The process of setting this probability is called the missing-data mechanism or response mechanism, while the models of these processes are called missing-data or response models [6,7,8,9]. Missing values can be categorized into three groups [10]. If the probability of a data point becoming missing is the same for all, then the missing values are called missing completely at random (MCAR). If the probability of a data point becoming missing is the same only for certain groups based on observational data, then the missing values are called missing at random (MAR). If missing values are neither MCAR nor MAR, then they are called missing not at random (MNAR) or not missing at random (NMAR). In other words, missing values in NMAR are independent of unobserved data [11].
3.
Clustering and biclustering
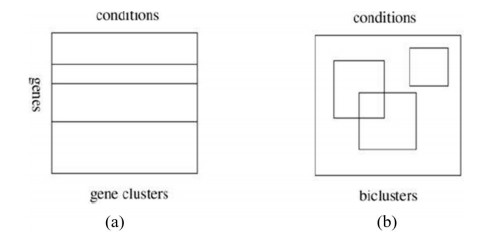
Clustering is a technique that groups data points into several groups or clusters. In gene expression data, the purpose of clustering is to group genes into clusters where each cluster consists of genes that are similar to each other and dissimilar to genes from other clusters [12]. Biclustering in gene expression data is the simultaneous clustering of rows and columns [13]. The aim of biclustering is to find groups of similar genes based only on correlated experimental conditions. The output of biclustering is a bicluster. Genes are similar under certain experimental conditions, so biclustering is preferable to clustering. A comparison of biclustering and clustering in two-dimensional gene expression data matrices can be seen in Figure 1 [14]. Figure 1(a) indicates a clustering technique of genes based on all conditions, while Figure 1(b) shows a biclustering technique of genes based only on correlative experimental conditions.
4.
Imputation method
4.1. LLS
LLS is a missing-value imputation method that identifies tne coherent information in gene expression data. There are two steps to the LLS method. The first step is to select k similar genes using Euclidean distance. The second step is to estimate the missing values [16,17]. This neighbor-based imputation method suits datasets that have a structure with dominant local similarities and high complexity [18].
Let a matrix E be the expression matrix consisting of m genes and n conditions. Assuming that the gene g1 has k similar genes (gs1, gs2, …, gsk) given the Euclidean distance and p missing values in the first p conditions, then the target gene y can be defined.
where α is a vector of 1×p consisting of p missing values, w is a vector of 1×(n−p) consisting of the non-missing values in the target gene and the matrices B and A are the k similar genes' corresponding columns with α and w, respectively. Vector X can be defined as the solution to the least squares problem with AT and w.
The solution of this least squares problem is
where A+ is the pseudoinverse of the matrix A. Hence, the missing values in the target gene g1 can be estimated using
To choose the proper value of k, LLS uses a heuristic algorithm by applying artificial missing values to genes. These artificial missing values will be estimated using different values of k, then the value of k that produces the lowest estimation error will be chosen as the proper value of k [16].
4.2. bi-iLS
Bi-iLS is updated from the imputation method called LLS [16] in two aspects, i.e., the use of biclustering and an iterative framework. Bi-iLS can recognize gene similarities only under certain correlative conditions (biclustering), while LLS takes account all of the conditions in a data matrix. This makes bi-iLS preferable to LLS for gene expression data [4]. This imputation method suits data that have a dominant local similarity structure [18]. There are two parameters that need to be defined in the early stage of this process, namely k (for k similar genes) and T0.
Let the matrix E be the expression matrix consisting of m genes and n conditions. A gene that has p missing values is called the target gene. Assuming that all p missing values are in the first p conditions without a loss of generality, the target gene is defined as
where α is a vector of 1×p comprising p missing values and w is a vector of 1×(n−p) consisting of the non-missing values in the target gene. Similar to LLS, the first step of bi-iLS is to select k similar genes of target genes by using the Euclidean distance. The measurement of Euclidean distance requires a complete matrix, so bi-iLS uses the row average to fill n all of the missing values and obtain the temporary complete matrix. After selecting k similar genes, they are defined as
where g(s1)T denotes k similar genes, while the matrices B and A denote, respectively, the expression values for the first p conditions and remaining (n−p) conditions of the selected similar genes. Every condition has a different correlation with the other conditions. So, to account for the correlation or weight of each condition in the identification of the missing values, matrix R is defined as
Matrix R, with the size of p×(n−p), represents the weighted correlations between other conditions and the condition where the missing values in the target gene are found. The (j,v)th element of R is denoted by rj(v). The larger the value of rj(v), the larger are the weights and stronger are the correlations between the conditions with the missing values. Then, using R, k similar genes are reselected. Reselection of the k similar genes uses the weighted Euclidean distance of the target gene gt and other genes gs based on the location of the jth missing values. The equation is
where g(v) denotes the vth element of gt or gs. Then, upon estimating the jth missing values for the target gene, conditions that are uncorrelated are removed from the least squares framework. Let
then the conditions are said to be related if
where T0 is a pre-defined parameter using the same heuristic algorithm to find the proper value of k. The removal of uncorrelated conditions redefines matrices A and B and w. Hence, we have
where αj denotes the jth missing values and wj denotes the non-missing values of correlated conditions. Also, we have
where Bj represents the jth columns of the data and Aj denotes a matrix consisting of the correlated columns of the k similar genes. Similar to LLS, a regression model αj=BTjxj is needed to estimate the jth missing value where xj contains the regression coefficient for k similar genes. xj can be obtained by minimizing the least squares error, as follows:
Thus, the jth missing value in the target gene can be estimated by using
where (AT)+j is the pseudoinverse of ATj.
An iterative framework is applied to improve the selection of similar genes. A complete matrix output from the ith iteration will be the temporary complete matrix in the (i+1)th iteration. This iteration process will be repeated until it reaches the maximum iteration or a specific criterion. The complete framework of bi-iLS can be seen in Figure 2.
4.3. BPCA
There are three main steps of the BPCA based imputation method: principal component (PC) regression, Bayesian estimation and application of an expectation-maximization (EM) repetitive algorithm [19]. In PC regression, Principal Component Analysis (PCA) represents the D-dimensional vector y as a linear combination of K principal axis vectors wl (1≤l≤K and K<D), as follows:
where D is the quantity of columns in data, xl is a factor score and ∈ is the residual error. Assuming that there are no missing values, PCA can find wl=√λlul where λl and ul respectively denote the eigenvalues and eigenvectors of the corresponding covariance matrix of y. If missing values are present, then the principal axis vectors are split into two parts, i.e., W=(Wobs,Wmiss) where Wobs and Wmiss denote a matrix that has column vectors wobs1,…,wobsK and wmiss1,…,wmissK, respectively. Factor scores x=(x1,…,xK) are obtained by minimizing the residual error of the observed part as follows:
This is a simple least squares problem that can be solved easily. Hence, the missing part of y can be estimated as
However, these parameters are still unknown. BPCA uses a probabilistic PCA model under the assumption that the residual error ∈ and xl (1≤l≤K) obey normal distributions. The parameters W, μ and τ form a parameter set θ≡{W,μ,τ}. BPCA uses Bayesian estimation to estimate these parameters. It is used here because it can locate the best dimensions for latent space. This estimation is done by applying the EM algorithm until convergence is reached. This imputation method is appropriate for data with lower complexity structures [20].
5.
Proposed imputation method
The proposed bi-BPCA-iLS algorithm updates the bi-iLS algorithm during the process of obtaining the temporary complete matrix. Other than the process of obtaining the temporary complete matrix, bi-BPCA-iLS and bi-iLS are the same. In bi-ILS, the row average is used to fill in all of the missing values for the target genes to obtain a temporary complete matrix. However, the use of the row average to fill in the missing values is considered unsatisfactory. Row averages cannot reflect the structure of the data because they only use the information of a single row or gene [21]. Also, use of the row average is not an effective approach when there is an outlier in the target gene. Hence, the use of BPCA to get a temporary complete matrix is thought to be better than the use of the row average. BPCA can reflect the global covariance structure of all genes [5]. The main idea behind the proposed bi-BPCA-iLS method is to use BPCA instead of the row average to get a temporary complete matrix in the bi-iLS framework. This alteration means that bi-BPCA-iLS becomes an updated and improved missing-value imputation method. As mentioned before, bi-iLS matched to data that have a dominant local similarity structure and high complexity, while BPCA suits data with a structure of lower complexity. The idea of combining BPCA with bi-iLS makes bi-BPCA-iLS become more robust for data with a lower complexity structure. The complete framework of bi-BPCA-iLS can be seen in Figure 3. The differences table for the LLS, bi-iLS and bi-BPCA-iLS methods is given as Table 1.
Table 1 shows the differences between the three least squares-based imputation algorithms. LLS uses clustering to measure gene similarity, while bi-iLS and bi-BPCA-iLS use biclustering, which, as mentioned before, is considered to have higher efficacy. The row average is used in LLS and bi-iLS to obtain the temporary complete matrix, while bi-BPCA-iLS uses BPCA. Only bi-iLS and bi-BPCA-iLS iterates the imputation process. Our proposed imputation algorithm is the newest among these.
6.
Experiments
The proposed method has been implemented and evaluated on two-dimensional gene expressions: a microarray dataset and an RNA-seq dataset [22]. Bi-iLS was proven to perform well on the microarray datasets of Spellman 1998 for Saccharomyces cerevisiae [4], so bi-BPCA-iLS was also implemented on this dataset to make a performance comparison. Also, both bi-BPCA-iLS and bi-iLS were implemented on RNA-seq to analyze their performances on different gene expression datasets.
6.1. Microarray Data
The microarray dataset is a cell cycle expression dataset for the yeast Saccharomyces cerevisiae; it has been synchronized using a CDC15 temperature-sensitive mutant [23]. According to Spellman et al., the samples of mRNA were taken every 10 minutes for 300 minutes. However, there were several missing time points in the published data. In fact, samples were taken every 20 minutes from 10 min to 70 min, and then every 10 minutes from 70 min to 250 min and every 20 minutes from 250 min to 290 min. Therefore, the CDC15 dataset contains the expression level of 6178 genes at 24 different time points which gives a matrix size of 6178 × 24. An example of the CDC15 dataset is shown in Table 2.
The CDC15 dataset had missing values, so genes that contained missing values were removed to get the ground truth. The ground truth was used to calculate the estimation error or NRMSE of each imputation methods. After removing genes that contained missing values, the size of the matrix became 4381 × 24. In the experiments for this dataset, r% of the observation values was set to be missing randomly where r = 1, 5, 10, 15, 20, 25 and 30. The estimation was repeated five times for each missing rate to generate the average result.
6.2. RNA-seq data
The RNA-seq dataset was gene expression data from the Schizosaccharomyces pombe or GSE150544 [24]. The technique of RNA sequencing was used to identify the differences between the gene expression levels of four different INO80 mutant strains, each with two replicates; this resulted in eight samples for each gene. The four strains were wt (control), Nht1, Iec1 and Iec5. The length for each gene, which indicates how many nucleotides are in that gene, was also included. In this experiment, only coding genes were observed. This dataset contained the expression of 5137 genes under nine different conditions, i.e., the length, wt_rep1, wt_rep2, nht1_rep1, nht1_rep2, Iec1_rep1, Iec2_rep2, Iec5_rep1 and Iec5_rep2, resulting in a matrix size of 5137 × 9. The data were not normalized to ensure the real expression of each gene and positive gene expression. An example of the GSE150544 dataset is shown in Table 3.
A value of zero indicates that a gene was not detected because the gene was not expressed, or was minimally expressed; therefore the value of zero is not a missing value. Then, r% of the observation values was set to be missing randomly where r = 1, 5, 10, 15, 20, 25 and 30. The estimation was repeated five times for each missing rate to generate the average result.
6.3. Imputation results
Our proposed imputation method was implemented in MATLAB. The parameters k and T0 were estimated automatically using the integrated function in our algorithm. The estimation process was iterated five times for each test. We carried out five tests for each missing rate to obtain the most accurate and convergent results. The imputation results applying our proposed method to the microarray dataset can be seen in Table 4 and Figure 4 below, where mr denotes the missing rate in Tables 4 and 5.
The imputation results of applying our proposed method to the RNA-seq dataset can be seen in Table 5 and Figure 5 below.
Based on Table 5 and Figure 5, the average value of the NRMSE for a missing rate of 1% was 0.29626, for a missing rate of 5% was 0.23798 and for a missing rate of 10% was 0.24662. The lowest estimation error was achieved when the missing rate was 5%; it was highest when the missing rate was 1%. The NRMSE values were predominantly below 0.3 at every missing rate, indicating that our proposed imputation method, bi-BPCA-iLS, performed well on the GSE150544 dataset.
7.
Evaluation and analysis
Two existing methods, LLS and bi-iLS, were compared to our proposed imputation method. This comparison entailed the use of the the average value of NRMSE and computational time generated from five trials for every missing rate. The difference between the NRMSE values of Method A and Method B divided by the NRMSE value of Method A shows the improvement of Method B relative to Method A. If the improvement value is positive, then Method B results in a higher imputation accuracy compared to Method A. If the improvement value is negative, then method B has a decrease in imputation accuracy compared to Method A.
7.1. CDC15 dataset
The averages of the improvement values across all missing rates for the CDC15 dataset are shown in Table 6 below. Based on these figures, the bi-iLS algorithm showed a significant overall improvement in NRMSE value (10.07%) relative to the LLS algorithm. Our proposed method, bi-BPCA-iLS, also showed a significant overall improvement in NRMSE value: 10.612% relative to LLS and 0.582% relative to bi-iLS.
As shown in Table 6 and Figure 6, the imputation method that produced the lowest overall NRMSE across all missing rates for the CDC15 dataset was our proposed method, bi-BPCA-iLS.
After comparing the values of NRMSE, the computational times of the imputation methods were also compared in MATLAB. Based on Table 7, bi-iLS is shown to add an overall average of 320.134 seconds of computational time compared to LLS. bi-BPCA-iLS is shown to add an overall average of 343.850 seconds of computational time relative to LLS and only 23.716 seconds relative to bi-iLS.
As shown in Figure 7, LLS displayed a consistent computational time for every missing rate, while bi-iLS and bi-BPCA-iLS had additional computational time following the increase in missing rates. In conclusion, the fastest imputation method was LLS; this is related to the high NRMSE it generated compared to the other methods. Regarding bi-iLS and bi-BPCA-iLS, there was no significant computational time difference between these two methods. If the goal is achieving a lower NRMSE, then one can use bi-BPCA-iLS instead of bi-iLS.
7.2. RNA-Seq
The average improvement values across all missing rates for the RNA-seq dataset (GSE150544) are shown in Table 8. We can see that the bi-iLS algorithm showed an overall improvement in NRMSE value of 5.12% relative to the LLS algorithm. Our proposed method, bi-BPCA-iLS, had an overall improvement in NRMSE value of 8.20% relative to LLS and 3.09% relative to bi-iLS.
The performances of LLS, bi-iLS, and bi-BPCA-iLS on the GSE1505544 data can be seen in Table 8. Bi-BPCA-iLS and bi-iLS had negative performances when the missing rate was 1% and 5%, so LLS performed well when the missing rate was below 5% in this dataset. But when the missing rate moved above 5%, the performance of bi-BPCA-iLS was superior to the other methods. As shown in Figure 8, the average NRMSE from bi-BPCA-iLS tended to be lower than those of the other methods.
After comparing the values of NRMSE, the computational times of the imputation methods were compared in MATLAB. Based on Table 9 and Figure 9, bi-iLS is shown to add an overall 117.200 seconds of computational time relative to LLS. While bi-BPCA-iLS is shown to add an overall 126.549 seconds of computational time relative to LLS and only 9.349 seconds relative to bi-iLS. There is no significant computational time difference between bi-BPCA-iLS and bi-iLS, only 9.349 seconds.
8.
Conclusions
Early approaches toward missing-value imputation tended to consider all experimental conditions in measuring gene similarity. However, genes are only similar under certain experimental conditions. This meant that an bi-iLS algorithm for imputing missing values has to be developed. This algorithm uses the row average to obtain a temporary complete matrix, which has become to be considered as a flawed approach. The row average cannot reflect the real structure of the dataset because it only leverages the information of an individual row. Thus, in this study, we used BPCA to obtain a temporary complete matrix instead of using row average. The proposed algorithm is called bi-BPCA-iLS. After finding the temporary complete matrix using BPCA, the required parameters can be found. Our proposed algorithm performs clustering on genes and conditions alternately to find biclusters that consist of a subset of genes that are similar under a subset of conditions. After the biclusters related to the target genes are found, least squares estimation of the missing values can be performed while considering only related genes and conditions. This estimation process can be iterated to improve the selection of similar genes and conditions in every iteration, which improves the accuracy of the missing-value imputation.
Experiments were conducted on two gene expression datasets: a microarray dataset for Saccharomyces cerevisiae (CDC15) and an RNA-seq dataset for Schizosaccharomyces pombe (GSE150544). The results show that our proposed method is best suited to impute missing values in microarray datasets and RNA-seq datasets based on the NRMSE, compared to preceding imputation methods such as LLS and bi-iLS. Significant NRMSE improvements of 10.612% for CDC15 and 8.20% for GSE150544 were observed when using bi-BPCA-iLS instead of LLS, indicating the importance of using biclustering and iterative frameworks. Also, bi-BPCA-iLS showed NRMSE improvements of 0.582% for CDC15 and 3.09% for GSE150544 relative to bi-iLS, indicating that the temporary complete matrix is better obtained with BPCA rather than via the row average. The additional computational time of bi-BPCA-iLS compared to bi-iLS was only 23.716 seconds for CDC15 and 9.349 seconds for GSE150544, which can be concluded as not significant. These experimental results show that our proposed method outperforms the other two existing methods. Thus, our proposed method is applicable to other datasets that fit our assumption.
The missing-value imputation method bi-BPCA-iLS outperformed other methods such as LLS and bi-iLS in selected microarray and RNA-seq datasets in terms of the NRMSE. The improvement relative to LLS indicates the importance of using biclustering and iterative framework in the imputation, while the improvement relative to bi-iLS indicates that the temporary complete matrix is better obtained with BPCA rather than via the row average.
Acknowledgments
Universitas Indonesia funded this research with grant number NKB-030/UN2.F3/HKP.05.00/2021.
Conflict of interest
The authors declare that there is no conflict of interest.









 DownLoad:
DownLoad: