1.
Introduction
Malnutrition in its various forms continues to be a public health concern worldwide. From undernutrition, over-nutrition, micronutrient deficiencies, and diet-related non-communicable diseases, countries face one or more of these burdens at a time [1,2]. Most people have diets that fall short of a healthy one and are unable to eliminate hunger, be safe, reduce and protect against all forms of malnutrition, promote health, or be produced sustainably [1,3]. Even in the presence of adequate food where energy requirements are met, micronutrient deficiencies can prevail if micronutrient-rich foods such as fruits, vegetables, and animal source foods are regularly lacking from the diet [4]. The undernourishment, low food quantity, poor dietary quality and diversity scenario is common among rural communities in Africa and Asia, many of whom are smallholder farmers [5,6]. In these cases, dietary diversity has been found to be a good indicator of the dietary quality and households' access to food [7,8]. Consumption of high-quality diets varies depending on culture and food availability and is limited by poverty and affordability of food [3,9]. Rural households spend more of their income on food compared to their urban counterparts, and though they primarily consume what is produced, it has been noted that they are now selling more food for income beyond the traditional cash crops [10,11].
Agriculture is central to the livelihoods and food security of households in Uganda, with 80% of the smallholder farmers contributing 70% of the national food production [12]. However, production by smallholder farmers, who are mainly in the rural areas, is hindered by low technology adoption; limited access to inputs, information, and financial services; poor pests and diseases management practices and food handling and storage practices; and poor infrastructure [12,13,14,15]. Agricultural production is promoted and supported by national policies, plans and interventions that emphasize an increase of production and food security through use of suitable skills, technologies, inputs, and markets, to shift farmers from subsistence farming to commercial farming [16]. Within this context, where strategies and efforts are in place to improve food security and livelihoods through agriculture with focus on selected crops [17], it is important to ascertain the dietary quality of rural smallholder farmers to ensure that their nutrition security is being also addressed. Agricultural interventions have improved production and consumption of specific foods and have shown mixed results on their impact on diets, income, and nutritional status, where impact has varied depending on context [18,19]. This study therefore explored the dietary diversity of children under five and the food security of smallholder farming households in Central Uganda to understand the current dynamics around dietary diversity and food security in order to inform development of context specific strategies to improve the dietary diversity of the children in rural smallholder households.
2.
Materials and methods
2.1. Study site and sample
A cross sectional study was conducted among rural smallholder farming households from Kiboga district in August 2016 to assess household characteristics, dietary diversity, and food security status. Kiboga district located in Central region about 120 kilometers from Kampala, the capital city of Uganda has two main rain seasons a year with both perennial and annual production systems. Dominant systems include agroforestry (with fruit trees and/or indigenous trees), banana-coffee, and maize systems. Livestock keeping especially cattle, pigs, goats, and poultry is also present [20]. Smallholder farming households in the study site (district and parishes) are representative of those in banana growing regions of Eastern Africa, given similarities in farming systems [21]. The cooking banana is a starchy staple food cooked when unripe in the central and western parts of the country. As a banana-growing region, the production of this staple food was severely affected by the banana bacterial wilt from 2004. This disease, which led to total yield losses within a year of infection for some farmers, greatly affected the food security status and income of the affected households. Various efforts to contain the disease have been employed and productivity recovery is ongoing [22,23]. It is on this basis that the food security and dietary diversity was assessed as households recover their former main source of livelihood. In addition to cooking bananas, other banana types such as the dessert bananas are also grown and consumed when raw and unripe [24].
A multi-stage sampling procedure was used. Two parishes were purposively selected on their accessibility and location, ensuring that they were not neighbors, and having predominantly farming households. Within selected parishes, 10 villages were randomly selected, from which 182 households were sampled using systematic random sampling.
With the assistance of village leaders, a list of households in each village that met the criteria of farming households and having at least one child aged between 6 and 59 months physically present was compiled. The households were numbered, and a list of random numbers was generated using Microsoft excel. The sample size of 182 households was based on guidelines by [25]. Calculations accounted for the number of households with children below 59 months in the selected villages and the prevalence of malnutrition among children in the Northern Central region where Kiboga district is located, 28% stunted and 7% underweight [25,26]. The overall number of households as per the 2014 national census was 595 in Kisweeka Parish and 414 households in Ssinde Parish. Discounting these to the proportion of households that had children aged 6–59 months and for the household population of interest, the study sample size was estimated to be adequate to obtain estimates at a confidence interval of 95%. Where more than one eligible child was present, the data was obtained on the youngest child (referred to as the index child). Eight enumerators (four men and four women) were recruited based on previous data collection experience and relevant language skills. Enumerators were trained and a pre-test of the questionnaire was conducted prior to actual data collection.
2.2. Data collection and analysis
A validated structured questionnaire was administered by trained enumerators to the mother or caregiver of the selected child within sampled households. Data on household demographics, crop and livestock production; household food consumption frequency over seven days prior to the survey; food consumption of the child over the 24 hours preceding the survey; and anthropometric measurements of weight and length/height of the children to determine their nutritional status was collected.
2.2.1. Household food security
Food Insecurity Access Scale (HFIAS) was used to determine whether households experienced any of the nine-food insecurity-related conditions during the four weeks prior to the survey; and the frequency of occurrence was recorded for each condition [27]. The frequency of occurrence for each of the nine conditions were scored: never = 0, rarely = 1, sometimes = 2, and often = 3. Scores were summed to obtain the HFIAS, which could range from 0 to 27. The higher the HFIAS, the more food insecure the household. Households were further defined as food secure, mild, moderately, or severely food insecure, using the categorization procedure described by Coates et al (2007), based on which of the nine-food insecurity-related conditions a household faced during the four-week reference period and the frequency of occurrence. For example, a household that was unable to eat preferred foods, and/or had a monotonous diet, and/or had foods considered undesirable rarely was categorized as mildly food insecure, while a household that faced any of these three conditions often was categorized as moderately food insecure. Also, a household running out of food, going to bed hungry, or going a whole day and night without eating, even if rarely, was categorized as severely food insecure [27,28]. The three sub-domains of the HFIAS relate to anxiety and uncertainty, insufficient food quality, and insufficient food intake. If a household reported the presence of the first food insecurity-related condition, it qualified the occurrence of the first domain—anxiety and uncertainty. Presence of any of the next three food insecurity-related conditions (second to fourth conditions) qualified the occurrence of the second domain- insufficient food quality and presence of any of the next five food insecurity-related conditions (fifth to ninth) qualified the occurrence of the third domain - insufficient food intake [27,28].
To identify the number of months during which the household had adequate access to food regardless of source, respondents reported whether they had very little, little, just enough, enough food to feed and store, or more than enough to feed and store in each of the past 12 months. Months with very little or little food were considered food shortage months. This information was also used to calculate the Months of Adequate Household Food Provision (MAHFP) score by summing up for each household the number of months without food shortage [29].
2.2.2. Household food consumption
Foods consumed by the household over the past seven days were recorded using a food frequency questionnaire; consumption, frequency of consumption, and source of these food groups was assessed, as well as the food items within 11 food groups: (ⅰ) cereals and grains (ⅱ) white roots, tubers, cooking bananas (ⅲ) legumes (ⅳ) meat (ⅴ) fish (ⅵ) milk and milk products and eggs, (ⅶ) orange and dark yellow foods (ⅷ) dark green leafy vegetables (ⅸ) other fruits (ⅹ) other vegetables (xi) condiments including sugar and oil [7].
The Household Food Consumption Score (HFCS) considers both quality and quantity of food group access and was therefore calculated in addition to household dietary diversity. The HFCS was generated by summing the household food group consumption frequency over seven days, applying set weightings to each food group based on nutrient density versus caloric density. The weights applied to the food groups were starchy staples 2, legumes 3, vegetables and fruits 1, meat and milk 4, sugars and oils 0.5, and condiments 0 [30]. The HFCS was categorized as poor (0–21), borderline (21.5–35), and acceptable (>35) where scores could range from 0 to 100 [30].
2.2.3. Child health and nutrition
An infant and young child feeding questionnaire, based on WHO guidelines [31], was used to obtain information on breastfeeding practices, food frequency and dietary diversity. An unquantified 24-hour dietary recall was used to determine dietary diversity as proxy indicator of the micronutrient adequacy of the index child's diet [7]. The respondent was asked to recall all foods and beverages consumed by the index child over the last 24 hours; as well as the sources of these foods. The dietary diversity for children ≥24 months old was based on nine food groups: (ⅰ) cereals, white roots, tubers, cooking bananas (ⅱ) legumes (ⅲ) milk and milk products, (ⅳ) eggs, (ⅴ) organ meats, (ⅵ) meat and fish, (vii) dark green leafy vegetables, (viii) other vitamin A-rich plant foods, and (ix) other fruits and vegetables. A score of one was given for each food group if consumed at least once and zero otherwise. The scores were summed to obtain the dietary diversity score (DDS) [7].
For children aged 6–23 months, minimum dietary diversity as recommended by WHO was assessed following the same procedures above except that is was based on seven food groups: (ⅰ) cereals, white roots, tubers, cooking bananas (ⅱ) legumes (iii) milk and milk products, (ⅳ) eggs, (ⅴ) meat and fish, (ⅵ) vitamin A-rich fruits and vegetables, (vii) other fruits and vegetables [31]. Both household and child food consumption questionnaires distinguished consumption of orange-fleshed sweet potatoes but not biofortified iron-rich beans. Vitamin A supplementation status was obtained from the child's immunization card or mother or caregiver's recall.
Anthropometric measurements, weight, and length/height of the index child were taken to determine their nutritional status following recommend procedures [32,33]. Weight was measured using Seca 874 U digital weighing scales that can measure the child's weight while being held by an adult. The scales were calibrated using a known weight. Wooden child measuring boards were used to measure both recumbent length for children < 24 months and height for children ≥24 months. Children were undressed for assessment of weight and for length/height, hair clips were removed as appropriate. The age and date of birth of the child was obtained by recall and where possible, verified using the health and/or immunization cards. The ENA for SMART 2011 software using the WHO 2005 growth standards was used to generate Z-scores for weight-for-age (WAZ), weight-for-height (WHZ) and height-for-age (HAZ) and the corresponding malnutrition classifications; with Z-scores more than two SDs below the reference median indicating underweight, wasting, or stunting respectively [32,33].
2.2.4. Statistical analysis
All data were analyzed using SPSS version 17. Data was summarized using descriptive statistics. Cross tabulations, chi square tests, and bivariate correlations were used to establish any relationships between categorical and ordinal variables such as household characteristics; food security status; nutritional status and diet diversity. Coefficients (r) such as Pearson's and Spearman were applied depending on whether variables were ordinal or interval data. T-tests were also used to establish any differences between the two parishes.
Principal component analysis (PCA) and cluster analysis were carried out using STATA 14 software to develop household food access typologies. Typologies were created to understand the variability of food security and inform development of best-fit strategies to improve dietary diversity [34]. Key variables included in the PCA were household size, total land size, MAHFP, HFIAS, HFCS, child dietary diversity score, and nutritional status indicators for the children (WAZ, WHZ, and HAZ) to further understand the variance between households. These indicators were all included in the PCA to control for multi-collinearity to determine the appropriateness of all the indicators included. All variables used were first normalized to Z-scores. Only indicators that loaded well were retained for the final PCA analysis. The resulting three principal components were then used in cluster analysis using wards linkages to develop four group/ typologies at an L2 dissimilarity measure of 40.
The study protocol was approved by the Health Research Ethics Committee 2 of Stellenbosch University, Reference Number S16/06/099. Communication and permission were sought from the district health office. Informed consent was obtained from the household head, spouse, or caregiver prior to each interview and before measurement of the child's weight and height.
3.
Results
3.1. Household demographics and food production
Of the 182 households surveyed, eight were excluded from analysis due to incomplete or inconsistent data especially regarding dietary intake and index child information. Exclusion did not significantly affect results for the household demographics (data not shown). Therefore, 174 households were analyzed, with 67% from Kisweeka and 33% from Ssinde parishes. Twenty-five percent of children were aged 6–11 months; 36% aged 12–23 months; 30% aged 24–36 months; and 9% aged 36–51 months. Fifty-three percent were girls and 47% boys.
Majority of the respondents (89%) were women (Table 1). Eighty-three percent of households were headed by men while 17% were headed by women. Average household size was 5.8 ± 0.2, with households in Kisweeka (6.1 ± 0.2) significantly larger than in Ssinde (5.1 ± 0.3) (p < 0.01). In terms of household composition, 57% of all household members were ≤14 years and 26% were aged 15–34 years. The main source of income for majority of households (63%) was farming, followed by income from a business (25%). The most attended markets by households were bi-weekly markets (98%–100%), located 6.5 ± 0.3 km from the homesteads. Concerning livestock ownership, 42% of the households owned at least one animal type. Of those that had livestock, 59% had poultry (6.3 ± 6.7 birds), 41% had pigs (2.0 ± 1.3), and 19% had goats (3.1 ± 3.0).
Households had access to 1.5 ± 0.06 plots of land for agriculture, that was owned, rented, borrowed or any other form of access. The mean area of each plot was 0.04 ± 0.01 hectares. The mean total area of land that the households had access to was 0.96 ± 0.88 hectares.
Twenty-three different crops were grown at the time of the survey. This included three cereals and grains (maize, sorghum and rice); six roots, tubers or cooking bananas (banana, cassava, sweet potatoes, potatoes, arrow root, and coco yam); three legumes (beans, groundnuts and soybean); ten fruits and vegetables (amaranth, pumpkin, mangoes, jack fruit, tomatoes, watermelon, passion and citrus fruits, avocado and onions); and one cash crop (coffee). Banana was the most frequently grown crop (71% of households), followed by other staples like cassava (56%), maize (64%) and sweet potatoes (38%). Beans were the main legume grown by 63%, while groundnuts were grown by 10% of households. Mangoes were the only fruit grown by > 10% of households. The three vegetables reported were each grown by < 10% of households. Overall, of the 23 crops recorded, 15 were grown by < 10% of the households.
3.2. Household food consumption
On average, households consumed 2.6 ± 0.7 meals a day. Majority (82%) consumed > 6 food groups over seven days. Food groups consumed at least once per week by > 80% of households were legumes (100%), roots, tubers, and cooking bananas (97%), cereals and grains (88%) and other fruits (83%; jack fruit, bananas, avocado and passion fruits) (Table 2). Intake of animal source foods (meats, fish, and diary and eggs, respectively) in this period ranged from 53% to 60% of households.
Cereals and grains and the other vegetables food group (cabbage, tomatoes, onions, eggplant, African eggplant, and mushrooms) were consumed on 4.5 ± 2.3 and 4.3 ± 1.3 days respectively over the seven-day period. Roots, tubers, cooking bananas; and other fruits were consumed on 2.7 ± 1.0, and 2.3 ± 1.2 days, respectively. Legumes consumption (1.7 ± 0.5 days) was similar to that for meat (1.7 ± 0.9 days). No consumption of orange-fleshed sweet potato was reported.
Diversity within food groups showed an average consumption of two foods within a food group. Food groups with the highest mean number of food items consumed in seven days were other vegetables (3.4 ± 2.1); roots, tubers, cooking bananas (2.6 ± 1.1); other fruits (1.9 ± 1.4), cereals and grains (1.8 ± 1.1) and legumes (1.7 ± 0.5). The major foods consumed within each food group are shown in Table 2.
For 74%–89% of households, their farmland was the source of roots, tubers, cooking bananas; vitamin A-rich fruits and vegetables; legumes and other fruits food groups, respectively. Meanwhile, meat; fish; other vegetables and other food items respectively were sourced from markets by 79%–95% of households. Cereals and grains, and dairy were the only two food groups for which sourcing from farms (40%–44%) matched that from the market (55%–59%). The mean HFCS was 68.0 ± 23.6; with 96% of households having an acceptable HFCS (>35) and 4% a borderline HFCS (21.5–35).
3.3. Household food security
Households had 7.6 ± 0.2 months a year of adequate food access (MAHFP). The MAHFP corresponded with the annual food availability which showed two peak seasons from November to February and June to July (six months) in which > 60% of households reported having just enough food, enough food to feed and store, or more than enough food to feed and store. In addition, two lean seasons were observed from March to May and August to September (five months) where > 50% of the households reported having little or very little food available. Over the 12-month period prior to the study, 39% of households reported little or very little food availability, 34% had enough food and more than enough food to feed and store, while 27% had just enough food.
According to the HFIAS, 71% of households faced anxiety and uncertainty over food in the preceding month while 59% had insufficient quality of food, having consumed less preferred foods and/or limited variety of foods and/or foods they did not want (Table 3). Sleeping hungry and going for a day and night hungry were the least faced conditions by only 8% and 6% of the households respectively. The mean HFIAS score was 10.7 ± 5.9, out of a maximum of 27 which occurs when a household has faced each of the conditions often. Standard categorization of HFIAS scores showed that only 34% were food secure; 6% had mild food insecurity; 31% had moderate food insecurity; and 29% faced severe food insecurity. In response to food insecurity, households coped in the following ways: reduced number of meals (37%), reduced quantity of foods (21%), worked for food/money (19%), and borrowed from friends/relatives (19%).
3.4. Child nutrition
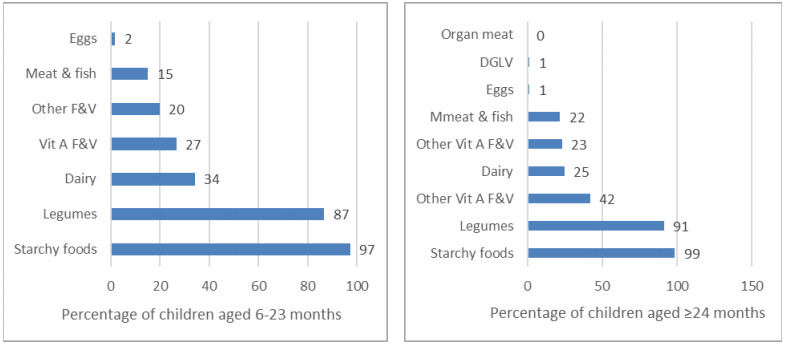
Among children aged 6–23 months, 66% were still breastfeeding. For those no longer breastfeeding, the average duration of breastfeeding was 14.3 ± 0.6 months. There was no significant difference between breastfeeding patterns of boys and girls. Ninety-one percent of the children aged 6–23 months had received Vitamin A supplementation in the last 12 months. Only 22% of children aged 6–23 months met the minimum dietary diversity of ≥4 food groups, while 23% met the minimum acceptable diets, that is consumed four food groups and two meals (6–8 months old) or 3 meals (9–23 months old). Food groups consumed were mostly starchy staples (97%) and legumes (87%), followed by dairy (34%) (Figure 1).
For children ≥24 months, 71% consumed ≤3 food groups, while 29% consumed 4–5 food groups. Less than half of the children aged ≥24 months consumed an animal source food (dairy, meat, fish or eggs), a vitamin A-rich fruit or vegetable (23%) or any kind of fruit or vegetable (42%) (Figure 1). No consumption of organ meats was reported.
The average number of food groups consumed by children aged 6–23 months was 2.8 ± 1.2, while for the 24–36 months old, 3.0 ± 0.8 food groups, and for children > 36 months 3.2 ± 0.9 food groups. The average number of meals was 3.3 ± 0.1 (girls 3.4 ± 0.1 and boys 3.3 ± 0.1). No significant relationship was observed between the sex of the child, and the number of meals and total number of food groups consumed. There was however a significant positive relationship between the number of meals and number of food groups consumed (Pearson's correlation analysis; r = 0.4; p < 0.01). Significant positive correlations were noted between consumption of starchy staples and legumes (r = 0.3 at p < 0.01), and dark green leafy vegetables and other vitamin A-rich vegetables (r = 0.2 at p < 0.01). The total number of food groups was also significantly related with all food groups except eggs and organ meats. The food groups with the strongest relationship with the total number of food groups (r ≥ 0.4 at p < 0.01) included dairy, meat and fish, other vitamin A-rich fruits and vegetables, and other fruits and vegetables. Meanwhile, significant negative correlations were found between consumption of legumes and dairy (r = -0.2 at p < 0.05); and legumes and meat (r = -0.2 at p < 0.01).
In terms of nutritional status, 4.6% of the children were wasted, 9.2% were underweight and 33.3% were stunted. There was a significant monotonic relationship between age and prevalence of stunting, with a higher prevalence of stunting among children > 36 months (75%), and those aged 12–23 months (42%) (r = -0.3, p < 0.01). Of the children aged 6–11 months, 14% were stunted while 26% of 24–36 months old were stunted. No relationship between gender and nutritional status was found.
3.5. Household typologies
The three principal components retained together explained 74.8% of the variation in household food security and child nutritional status (Table 4). While HFCS, MAHFP, WAZ and child DDS had significant factor loadings for the three final principal components, HFIAS was not significant, and the following variables had low loadings and were not retained for the final PCA analysis, household size, total land size, HAZ and WAZ. MAHFP and HFIAS had a strong correlation with component 1, HFCS and child dietary diversity score had a strong correlation with component 2. It is important to note that while MAHFP showed food insecurity for over 50% over five out of 12 months, and HFIAS showed food insecurity for 60% of households in the previous month, HFCS was in contrast with 96% having an acceptable score. Only WAZ had a strong correlation with component 3. An inference was made that component 1 explained the household food group consumption; component 2 the household food availability and access while component 3 explained the nutritional status of the children.
As a result, four household typologies with a fair distribution of households 19%–29% were generated (Table 5). The 1st and 2nd typologies had the more food secure households based on the HFCS, MAHFP and HFIAS. The 3rd typology had households facing mild food insecurity with HFIAS of 2.8 and MAHFP of 7 months while the 4th typology had the most food insecure households with HFIAS of 3.9 and a MAHFP of 5 months. The average child dietary diversity score was lowest in the 3rd typology. The household typologies also reflected that households with higher food consumption scores, had more months of adequate food provisioning and were more food secure.
The 2nd household typology had the highest FCS (Table 5). This is further reflected by the consumption of the various food groups across the different typologies (Table 6), which showed that for the 2nd household typology, food groups were each consumed by ≥70%, except for dark-green leafy vegetables (Table 6). The 3rd typology had the lowest consumption of dark-green leafy vegetables, other fruits and vegetables, and milk, while the 4th typology had the lowest consumption of orange and dark-yellow foods, meat, and fish. The 4th typology had the highest percentage of households consuming food from their own production and did not purchase any vitamin A-rich vegetables and other fruits. They also had the lowest percentage of households purchasing legumes, other vegetables, milk, and fish (Table 6). The 3rd and 4th typologies therefore had vulnerable households facing more food insecurity and low dietary diversity.
4.
Discussion
Limited diversity of crops grown, low consumption of micronutrient rich foods, child stunting, and household food insecurity were observed. Starchy staples (cereals, grains, roots, tubers, cooking bananas) and legumes were the most consumed food groups by both children and households. Roots, tubers, cooking bananas; legumes, vitamin A-rich fruits and vegetables; and other fruits were mainly sourced from on-farm production. Animal source foods, and other vegetables were sourced mainly from the market.
The prevalence of childhood undernutrition, low dietary diversity, low consumption of vitamin A-rich and iron-rich foods observed in the study were similar to the national and regional values reported in the 2016 national Demographic Health Survey [26], that also reflected dietary gaps among rural households. Aside from cereals and grains, other vegetables (those not rich in vitamin A) were the second most frequently consumed food group and were consumed on average on four out of seven days. This frequent consumption of other vegetables is probably skewed as tomatoes, onions and egg plants are usually added to dishes as condiments, and the amounts used are insufficient to provide nutritional benefits. This reflects the need for nutrition education to promote consumption of dark green leafy and orange/ dark yellow vegetables in sufficient quantities [37,38]. Although legumes were consumed by all households during the past seven days, it was consumed on average on only two out of the seven days.
The low dietary diversity for children under five in the study corresponds with previous reports [39,40,41,42]. While a study indicated that children aged 9–17 months are twice as likely to meet the minimum dietary diversity of four food groups compared to 6–8 and 18–23 month old children [43], another report indicates that as children age, dietary diversity decreases but meal frequency increases [44]. These changes have been attributed to introduction of complementary foods, and the shift from complementary foods to family diets [43]. The increased mobility and communication skills of the children as they grow could also be an additional factor. Changes in diet quality across these age groups can be further explored through qualitative studies. None of the children consumed organ meat during the recall period. This can possibly be attributed to the limited access to the market and storage/preservation facilities, and high cost which limits regular consumption [45]. A higher consumption of liver has been reported in urban areas [46].
The consumption patterns were in tandem with the crops grown, showing more dependence on starchy staples and legumes. Indeed, beans and starchy staples such as bananas, maize, and sweet potatoes are the key crops produced in the study site [13,47]. Vegetable production is limited by availability of water, access to quality seed, with larger and consistent production mainly among farmers growing for the urban market [37]. A reduction in the available African indigenous vegetable species has been reported from at least 160 species in 1989 to 23 species in 2017 [48]. This has implications on available agrobiodiversity and the need for conservation, improvement of the seed system and promotion particularly among smallholder farmers that produce 70% of the national agricultural produce [12].
Even though 42% of households had at least one type of livestock and < 30% of children consumed animal source foods, no significant relationship was found between livestock ownership and animal source food consumption. Some studies have however reported significant positive relationships between livestock production and consumption [49,50], while others did not [51]. Given that livestock in developing countries are often reared as a source of income and not for consumption, nutrition education on how income can be used to achieve dietary diversity is important [52].
In addition to own production, markets also had a role in household access to diverse diets. Occasional markets were the most accessible markets. These markets are common in rural areas of East Africa, where traders set up at the same location for one day and community members travel to the market to sell or make purchases not limited to foodstuffs. From the study, households travelled on average 7km to these markets, a distance that can influence the sell and purchase of perishable items such as animal source foods. Access to markets influences dietary diversity even for farming households and improving this access can positively affect dietary diversity [53,54].
Household food security was a challenge for more than half of the surveyed households. Food availability and access are reported as the main limiting factors affecting household food security in the region, mainly due to drought, crop and livestock diseases that reduce crop harvests and food stocks, high food prices and low household incomes [55]. According to the MAHFP, over 50% of households faced food shortages for five out of 12 months; while the HFIAS showed that 60% of households were food insecure in the previous month. In contrast, according to the HFCS 96% of household had an acceptable food consumption score and thus likely to be food secure. This difference between HFCS and HFIAS has been previously reported where food security measures such as HFCS, HFIAS, Coping Strategies Index and reduced Coping Strategies Index though well corelated, they presented different elements of food security. HFCS was more strongly correlated with household dietary diversity capturing more of the food quality and diversity than HFIAS which captures food quantity and stability [56]. Though the food at hand over the preceding seven days may have been acceptable (HFCS), the households were experiencing food insecurity with anxiety over food and months of inadequate food (HFIAS and MAHFP). As such, dietary diversity and food security in this population need to be addressed.
Food availability is also influenced by the agricultural seasons where the contribution of different food groups and food species to the diet and nutrition of the households is reported to change with seasons [57,58]. This was reflected by the peak food availability and lean seasons, and months of adequate food observed in the study. In addition to seasonality, other factors that influence adequate food availability and access include limited diversity produced, poor postharvest handling and limited infrastructure which are typical in rural areas in sub-Saharan Africa thus reducing food stocks [59]. In the lean seasons when production diversity contributed less to dietary diversity, incomes and markets can be harnessed [60]. However, based on panel data, improving production diversity remains an important avenue to improving food and nutrition security [61]. The seasonal variation of different foods and species offered by agrobiodiversity can also be harnessed to ensure availability and access to diverse nutrient dense foods across seasons [49,62].
Household agricultural production, income and market access have been reported to be associated with dietary diversity [53,54,59]. Based on findings in this study, these three factors need to be addressed in the smallholder farmer context. For farmers with some on-farm diversity, income and market access, particularly the 1st and 2nd typologies, access to diverse foods through the market and capacity to efficiently utilize their incomes to contribute to dietary diversity may be of benefit [53,63]. For farmers with low on-farm diversity, income, and market access, particularly the 3rd and 4th typologies, increasing on-farm diversity, income and income use will be important [63,64]. Based on the identified household typologies, this study was followed-up with focus group discussions to further explore the dietary diversity and food security dynamics (results to be published elsewhere).
The study was limited by the cross-sectional design that did not enable collection of data across seasons. Seasonal data on food production and dietary diversity would have enhanced the study. Secondly, purposive selection of Parishes based on accessibility could have introduced bias as reduced accessibility has the likelihood of reducing food access and nutrition outcome.
5.
Conclusions
Although a wide range of crops could be grown, low diversity in production was noted and crops grown were mostly starchy staples and beans. Low consumption of micronutrient-rich foods, stunting, and household food insecurity were also observed. In the midst of the food access, availability, production, and consumption limitations, emphasis on dietary diversity remains paramount. Households mainly sourced their food from own production and markets. Therefore, in addition to improving production of fruits, vegetables and small livestock, the effective use and enhancement of available incomes and markets by households to improve access to and consumption of these food groups is needed. Policy and program recommendations from the study hinge on improving agricultural production, income and market access among smallholder farmers and their capacity to engage and utilize these three factors. Recommendations for programmes improving dietary diversity based on the household typologies are that for households with characteristics as those in the 1st and 2nd typologies, emphasis can be placed on enhancing income utilization and smallholder household market access to diverse foods. While for households with characteristics as those in the 3rd and 4th typologies, emphasis can be placed on increasing on-farm diversity and productivity, as well as household income. With nutrition education cutting across typologies. As such, further research into access to diverse foods within consumer markets commonly accessed by rural farming households will provide useful information for policy makers and intervention developers.
Acknowledgments
The authors acknowledge the Alliance of Bioversity International and CIAT for facilitating and supporting this study. Gratitude is extended to the study participants and enumerators who collected the data. This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
Conflict of interest
The Authors declare that there is no conflict of interest.









 DownLoad:
DownLoad: