Public Health Emergency of International Concern (PHEIC) has Declared Twice in 2014; Polio and Ebola at the Top

1.   Introduction

The most agammaessive and invasive tumor cells usually rely on extensive glycolysis to meet their large demand for energy and biosynthetic precursors ^[7,12,29,33]. The increase in glycolytic activity is often triggered by hypoxia, which derives from high cell density and insufficient vascularization ^[8,10,28]. However, up-regulation of glycolysis can also be observed in cancer cells under aerobic conditions, a phenomenon termed 'Warburg effect' ^[41,42]. The increase in glycolysis leads to vast production of lactate and protons, which have to be removed from the cell to prevent acidosis, which, among other effects, would result in inhibition of glycolysis and lead to cytostasis. Cancer cells are able to extrude the excess acidic byproducts via various pH sensitive membrane transporters.

Efflux of lactate from cancer cells is primarily mediated by the monocarboxylate transporters MCT1 and MCT4 ^{[28,30,31,40]}. The SLC16 gene family of MCTs comprises 14 isoforms, the first four of which (MCT1-4) carry lactate, but also other high-energy metabolites like pyruvate and ketone bodies, in cotransport with protons in a 1:1 stoichiometry across the cell membrane ^[11]. Lactate transport via the MCTs has been described by different kinetic models. By measuring influx of $^{14}$C-labeled lactate into red blood cells, de Bruijne and colleagues proposed a kinetic model that describes lactate transport as a symport system with ordered binding of lactate and $H^+$, where the proton binds first to the carrier, creating the binding site for the negatively charged lactate, followed by binding of lactate ^[9]. After translocation of lactate and $H^+$ across the membrane, lactate is released first from the transporter followed by $H^+$. As the rates of monocarboxylate exchange are substantially faster than those of net transport, the return of the free carrier across the membrane was considered as the rate-limiting step for net lactate flux ^[20]. However, based on single substrate inhibition experiments, it was also proposed that association and dissociation of the proton could be the step that limits the turnover-rate of MCT ^[1]. Transport activity of MCT1 and MCT4 is enhanced by non-catalytic function of the enzyme carbonic anhydrase Ⅱ (CAII) ^[3,4,5]. CAII, which directly binds to the C-terminal tail of the transporter ^[26,36], has been suggested to increase the effective rate constants of association and dissociation of protons from the transporter pore, possibly by working as a proton antenna which dissipates local proton microdomains to drive MCT-mediated lactate/proton co-transport ^[1,6,26]. Hypoxic cancer cells overexpress the hypoxia-regulated, membrane-tethered, extracellular carbonic anhydrase CAIX, which catalyzes the reversible hydration of $CO_2$ to $HCO_3^-$ and $H^+$. CAIX, the expression of which is usually linked to poor prognosis, has been shown to drive $HCO_3^-$ import via $Na^+/HCO_3^-$ cotransporters (NBCs) and $Cl^-/HCO_3^-$ exchangers (AEs) and facilitates $CO_2$ diffusion, leading to exacerbated intracellular alkalization and extracellular acidification ^{[25,34,37,38,39]}. Furthermore CAIX might function as a pro-migratory factor which facilitates cell movement and invasion ^{[23,34,35,37]}. We could recently demonstrate that CAIX facilitates transport activity of MCT1 in hypoxic MCF-7 breast cancer cells by a similar mechanism as observed for the interaction between MCT1/4 and CAII ^[2,19]. The CAIX-mediated increase in MCT1 activity was independent from the enzymes' catalytic activity, but required the intramolecular proton shuttle of CAIX, as well as the enzyme's proteoglycane-like domain, which was suggested to function as an intramolecular proton buffer ^[2,17,19]. Therefore it was concluded that CAIX, the expression of which was highly upregulated under hypoxia, could function as an extracellular proton antenna for MCT1 which facilitates the fast release of lactate and protons under hypoxic conditions ^[2,19]. In the present study we further evaluated the functional interaction between MCT1 and extracellular CAIX in cancer cells. We introduce a mathematical model aiming at a more theoretical characterization of the mentioned processes. The mathematical setting involves a system of stochastic differential equations for the dynamics of the intracellular and extracellular proton and lactate concentrations. The model predictions are validated against time series for intracellular proton concentration obtained experimentally in ^[19] and supplemented with data as described in Section 2 below. Our results suggest the existence of proton pools in the immediate proximity of the cell membrane, which seem to considerably influence the proton-coupled lactate transport across the plasma membrane of cancer cells.

2.   Material and Methods

2.1.   pH imaging in cancer cells

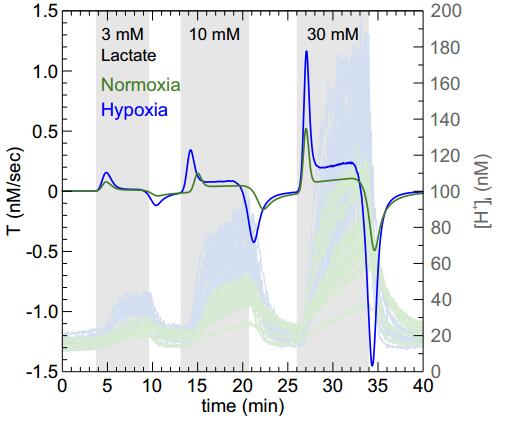
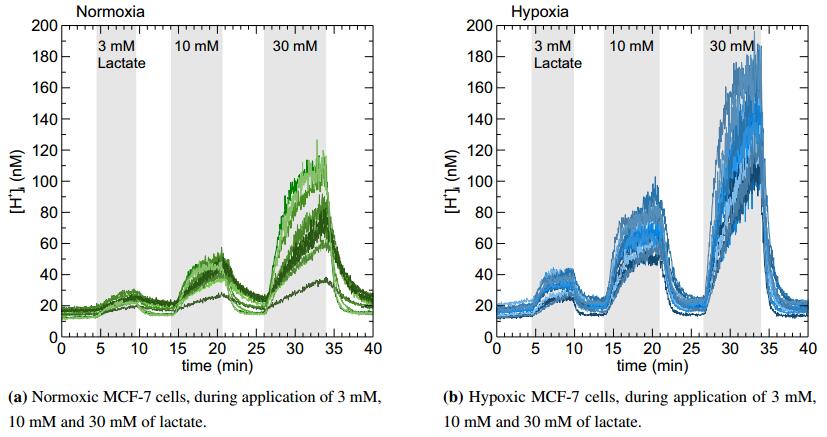
Imaging experiments on human MCF-7 breast cancer cells have been described in detail previously ^[19]. In brief MCF-7 cells, purchased from the German Collection of Microorganisms and Cell Cultures DSMZ (DSMZ-No. ACC-115), were cultured in RPMI-1640 medium (Sigma Aldrich, R1383), supplemented with $1.7\ {\rm mM}$ human insulin (Sigma Aldrich, 12643), $5\ {\rm mM}$ D-glucose (Sigma Aldrich, 16325), $16\ {\rm mM}$ sodium bicarbonate (Sigma Aldrich, 31437), $1\%$ penicillin/streptomycin (Sigma Aldrich, P4333), $2\%$ MEM amino acids (Sigma Aldrich, M5550), $10\%$ fetal calf serum (Sigma Aldrich, P4135), pH $7.2$, at 37 ℃ in $5\%$ $CO_2$, $21\%$ $O_2$, $74\%$ $N_2$ (normoxia) or $5\%$ $CO_2$, $1\%$ $O_2$, $94\%$ $N_2$ (hypoxia) in humidified cell culture incubators. Changes in intracellular proton concentration $[H^+]_i$ were measured with a Zeiss LSM 700 confocal laser scanning microscope, with a scanning frequency of 0.4 Hz. Cells were loaded with $10\ \mu M$ of the acetoxymethyl ester of Seminaphthorhodafluor 5- and 6-carboxylic acid 5F (Invitrogen$^{\text{TM}}$ SNARF 5F-AM, Life Technologies). SNARF was excited at $555\ {\rm nm}$ and the emitted light separated with a variable dichroic mirror at $590\ {\rm nm}$ in a $<590\ {\rm nm}$ and a $>590\ {\rm nm}$ fraction. For ratiometric imaging the signals of the $<590\ {\rm nm}$ fraction were divided by the signals of the $>590\ {\rm nm}$ fraction. The system was calibrated by the use of the ${K^+\over H^+}$ exchanging ionophore nigericin and the fluorescence signals converted to $[H^+]_i$. Image analysis was carried out with the program ImageJ. To measure changes in $[H^+]_i$ in single cells, a region of interest was drawn around individual cells and $[H^+]_i$ plotted against the time (Figure 1). %1a and Figure 1b). Transport activity of the monocarboxylate transporter was activated by application of $3$, $10$, and $30\ {\rm mM}$ of lactate (gray bars in Figure 1) in a physiological salt solution ($143\ {\rm mM}$ NaCl, $5\ {\rm mM}$ KCl, $2\ {\rm mM}$ CaCl$_2$, $1\ {\rm mM}$ MgSO$_4$, $1\ {\rm mM}$ Na$_2$HPO$_4$, $10\ {\rm mM}$ 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES), pH $7.2$). Application of lactate induced an intracellular acidification, indicating inward-directed co-transport of lactate and protons via MCT1, while removal of lactate resulted in an intracellular alkalization, which indicates outward-directed lactate and proton co-transport. Since lactate and protons are transported in a 1:1 stoichiometry by MCTs, the rate of change in $[H^+]_i$ is a direct measure for MCT transport activity. With these data we could previously show that MCT1 transport activity is almost doubled in MCF-7 cells under hypoxia ^[19]. As input for the models, developed in the present study, representative recordings of 12 normoxic (Figure 1a) and 15 hypoxic cells (Figure 1b) were used. To describe the intra- and extracellular proton and lactate dynamics we propose a mathematical model coupling ordinary (ODEs) and stochastic differential equations (SDEs) and using as input the original recordings presented in Figure 1. This setting includes pools of available/unavailable protons for the transport across the cell membrane and is obtained upon starting from a more rudimentary model not accounting for such supplementary compartments. The precise mathematical settings along with their respective performance are introduced and analyzed in the following section.

Figure 1.  Original recordings of intracellular proton concentration $[H^+]_i$.

DownLoad: Full-Size Img PowerPoint

3.   Data-based mathematical modeling and results

In this section we describe the mathematical model characterizing the dynamics of MCT1 as observed in the experiment. Figure 1 depicts the experimentally observed values of intracellular proton concentrations ($H_i$) after the application (removal) of $3 \ {\rm mM}$, $10 \ {\rm mM}$ and $30 \: {\rm mM}$ of lactate on (from) the extracellular side, after the cells were acclimatized for normoxic (Figure 1a) and hypoxic (Figure 1b) conditions.

Since the dynamics of $pH_i$ and also the MCT1 are time dependent (and we actually have time-series data for $H_i$), we develop a mathematical model relying on continuous time descriptions of the quantities of interest via ordinary and stochastic differential equations. Stochasticity plays an important role in pH dynamics; e.g., the distribution of $pH_i$ at any value of extracellular pH was found to be broader than predictions by theoretical models based on machine noise and stochastic variation in the activity of membrane-based mechanisms regulating $pH_i$ ^[22]. Our experimental data (see Figure 1) suggest themselves the presence of an important stochastic component in the dynamics of MCT transport. Recent multiscale mathematical models by the authors take into account stochastic fluctuations in the intracellular proton dynamics and connect them to acid-mediated tumor invasion ^{[13,14,15,16,21]}. Here we focus solely on the MCT-mediated transport of protons across the cell membrane. The variables of the model are: intracellular proton concentration ($H_i$), extracellular proton concentration ($H_e$), intracellular lactate concentration ($L_i$), and extracellular lactate concentration ($L_e$). The aim is to identify the key processes that affect the above quantities of interest. We investigate the following: (ⅰ) MCT1 transport kinetics, (ⅱ) intra/extracellular static buffers, (ⅲ) transporter domain, and (ⅳ) noncatalytic activity of CAII and CAIX. Subsequently we address the modeling of these processes in more detail.

3.1.   Modeling the MCT1 transporter

To model the transport activity of MCT1 we rely on the reaction kinetics model presented in ^[1], where the dynamics of the MCT1 is described as the transition between six states corresponding to:

1. state S1- binding of protons on the intracellular (IC) side,

2. state S2- binding of lactate on the IC side,

3. state S3- translocation of the loaded carrier from IC side to the extracellular (EC) side,

4. state S4- release of lactate on the EC side,

5. state S5- release of protons on the EC side,

6. state S6- translocation of the empty carrier from EC side to the IC side.

Transitions between these states (S1-S6) are modeled via simple first order reaction kinetics. Due to the difference in the relative speeds of each state transition, fast transitions are assumed to be in steady state. Using such quasi-steady state constraints, in ^[1] an algebraic expression for the net efflux (${\rm{Mol \over sec}}$) of intracellular protons ($H_i$) and intracellular lactate ($L_i$) has been obtained. This is represented by the function $T$, which is explicitly given as

where $k_{mj}$ with $m \ne j$ and $m, j \in \{1, 2, 3, 4, 5, 6\}$ represent the transition rates of the transporter from state $S_m$ into state $S_j$ and $K_o$, $K_e$, $K_l$, and $K_i$ denote constants obtained as fractions of such transition rates. Concretely we make the following choice:

3.2.   Modeling the stationary buffer

The buffer capacity $\beta$ of a solution is defined as the number of moles of $H^+$ that needs to be applied to 1L of the buffer solution in order to decrease the pH by 1 unit. Mathematically, $\beta$ can be expressed as (see ^[18,32])

The minus sign is due to the fact that increase of proton concentration results in decrease of pH, while conventionally the buffering power is a positive quantity. From this we deduce

The right hand side (RHS) in the last equation above represents the applied change in protons with respect to time, while the left hand side (LHS) represents the observed change in pH. In our case the applied change in protons is due to the MCT1 transporter, thus we get that

3.3.   A first approach to modeling the transporter domain (one-point model)

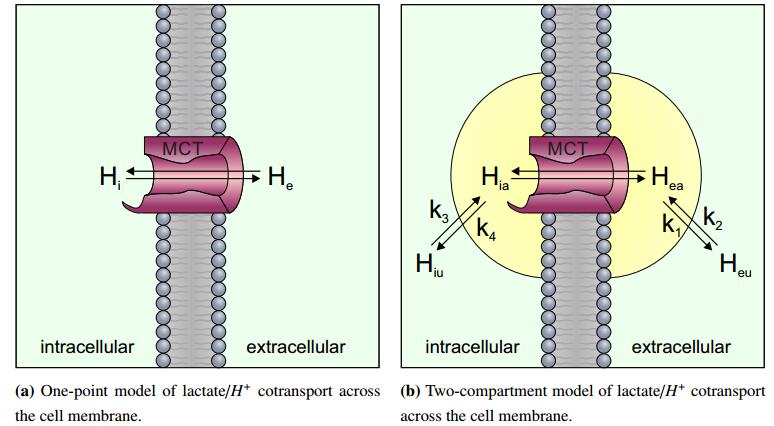
The experimental data in Figure 1 only feature time dependence without any spatial component. Therefore, a naive modeling approach would be to formulate a system of ordinary stochastic differential equations, thus not involving any partial derivatives, but accounting (by way of the noise terms) for randomness. Considering the key biological processes described above, we formulate the following SDE system (1) which we shall refer to as the one-point model. Figure 2a illustrates the corresponding proton exchange.

Figure 2.  Illustrations of the two models considered in this work.

DownLoad: Full-Size Img PowerPoint

with initial conditions

Thereby, $\xi_t^i$ ($i = 1, 2, 3$) represent Gaussian white noise. The corresponding processes are mutually independent and $c(t)$ denotes the control function, i.e. the function modeling the input of lactate into the system which is applied on the extracellular side during the course of the experiment. It will coincide with the function $C_2(t)$ introduced in Subsection 3.4 below. The diffusion coefficients in the noise terms are of multiplicative type in order to ensure nonnegativity of the solution to the SDE system.

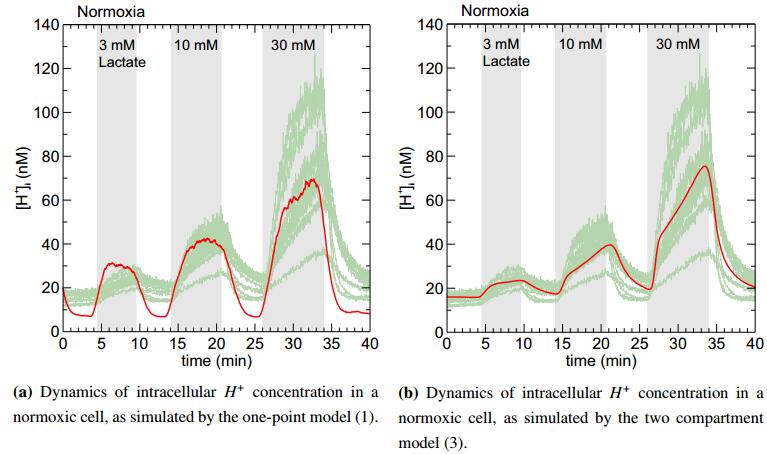
The simulation results for the one-point model (1) are shown in Figure 3 for the normoxic regime. The red curve depicts the mean value of the intracellular proton concentration averaged over 100 simulated cells (sample paths). It suggests that the time dynamics of $H_i$ exhibits undersaturation. The reason for this is that the initial concentrations of $H_e$, $H_i$, $L_i$ and $L_e$ are such that they facilitate the efflux of intracellular protons. The latter is so high that it leads to saturation of $H_i$ at a lower value in comparison to the actually observed level of $H_i$ saturation. This could be remedied by incorporating the spatial proton dynamics in the cell and its immediate extracellular region. This would in particular ensure that at any fixed time point MCT1 does not have access to the full $H_i$ and $H_e$ concentrations. However, in order not to complicate the setting by considering partial space-time derivatives and thus having to handle stochastic PDEs, we model instead some supplementary compartments. This can be seen as another way of introducing a hypothetical region called the transporter domain situated in the close intra- and extracellular neighbourhood of the cell membrane and representing the region of the cell containing molecules that are effectively involved in the activity of the transporter. We shall describe this in more detail below; here we only refer beforehand to Figure 3b to show the effect of modeling such a transporter domain on getting rid of the mentioned undersaturation of $H_i$ dynamics.

Figure 3.  Simulation results of the models (1) and (2)-(3) for the intracellular proton concentration of a cell in the normoxic regime (shown as red trace). The green traces show the experimental data.

DownLoad: Full-Size Img PowerPoint

3.4.   Modeling the transporter domain: A more careful approach

Since a cell is a 3D structure with non-zero volume, its constituents are subjected to spatial effects, like e.g., diffusion, spatial distribution of the MCT1 on the cell membrane, etc. It is of particular importance to note that no membrane transporter can have access to the full concentration of the required constituents at any time point. Instead, only a fraction of the total concentration in the vicinity of the transporters is actively involved. Following this line of argument, we consider the concentration of intracellular protons to be divided into $H_{ia}$ and $H_{iu}$. Thereby, the former represents the concentration of protons available for MCT-mediated extrusion, while the latter represents the intracellular proton concentration beyond the shuttling range of MCT. Similarly, the concentration of extracellular protons is divided into $H_{ea}$ and $H_{eu}$, with the former denoting the concentration of those available for MCT transport, while the latter represents the extracellular proton concentration not within the range of MCT.

Spatial movement (presumably diffusion) enables the conversion from unavailable to available protons and vice versa. This interconversion is modeled in this ODE-SDE setting via simple first order reaction kinetics between the respective compartments (or components):

The model constructed this way will be refered to as two-compartment model and its dynamics are illustrated in Figure 2b. The concrete mathematical setting will be described below in the equations (2)-(3) supplemented with the corresponding prescriptions of the coefficient functions on the right hand sides and the initial conditions. The model involves the major unknowns $H_{iu}$, $H_{ea}$, $H_{ia}$, $L_i$, and $L_{ea}$. Thereby, $L_i$ denotes the concentration of intracellular lactate and $L_{ea}$ that of extracellular lactate in the region available to the transporter. The dynamics of $H_{ea}$, $H_{ia}$, $L_i$, and $L_{ea}$ is directly related to the MCT1 shuttling activity, which makes up the main parts of the right hand sides in (3). The quantities $H_{eu}$ and $L_{eu}$ in the unavailable extracellular compartments can be obtained from $H_{eu}$ being constant (thus coinciding with its given initial value) and by directly integrating the decoupled equation (2b) below. Moreover, we will also take into account the influence of carbonic anhydrases CAII and CAIX on pH regulation, as explained in the following paragraph.

Modeling of CAII and CAIX

In the MCF-7 cell line used in this study, intracellular CAII is constantly expressed, both under normoxic and hypoxic conditions, while the expression of extracellular CAIX is strongly upregulated under hypoxia ^[19]. Both CAII and CAIX have been shown to facilitate transport activity of MCT1 via a non-catalytic mechanism, presumably by functioning as a proton collector and distributor for the transporter ^{[1,2,6,19,26]}. For extracellular CAIX the implications of this 'proton antenna' on the proton dynamics are as follows:

1. During $H_i$ efflux (i.e., when $T$ is positive), the protons released on the EC side are distributed away from the MCT1 site towards further away EC regions. This in turn facilitates faster cycles of MCT1 state transitions and thus enhances the efflux of protons.

2. During $H_i$ influx (i.e., when $T$ is negative), the protons on the EC side near the membrane are shuttled towards the MCT1 site, thus enhancing the influx of protons from the EC to the IC side.

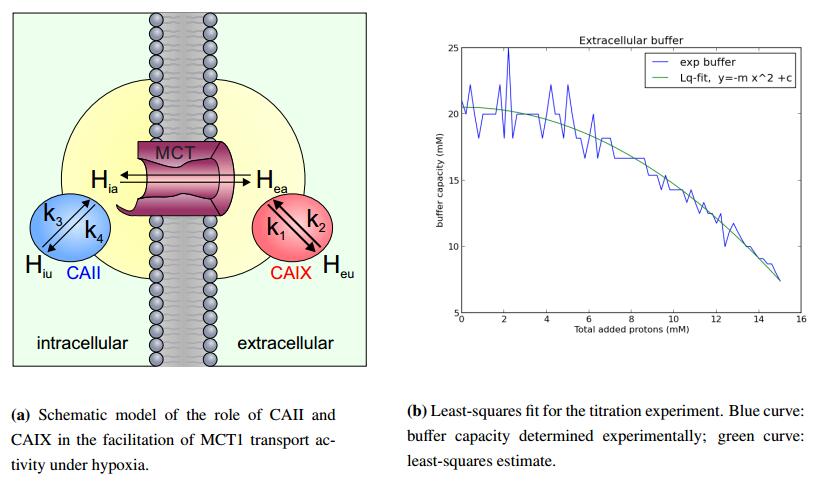
Since CAIX is only expressed under hypoxic conditions, these enhancing effects are only applied for hypoxic, but not for normoxic cells. CAII plays an analogous role at the IC side of the MCT1, both in normoxic and hypoxic cells. Figure 4 illustrates these influences in the hypoxic case.

Figure 4.  Illustration of the role of CAII and CAIX and least-squares fit for the titration experiment used to determine the functional form of the extracellular buffer modulator $k_6$.

DownLoad: Full-Size Img PowerPoint

The roles of CAIX and CAII are modeled in the following way:

1. The values of the parameters $k_1$ and $k_2$ in the hypoxic case are taken to be larger than their values in the normoxic case. This is in line with the observation that CAIX is activated during the hypoxic regime.

2. Comparatively, the values of the parameters $k_3$ and $k_4$ in the hypoxic case are taken to be only slightly larger than their values in the normoxic case.

Apart from this we make $k_1$ and $k_2$ time dependent. This time dependence characterizes the dynamic adaptation of the exchange of extracellular protons between the free and the available pools. This dynamic adaptation of protons represents the non-catalytic effect of CAIX. As hypothesised in ^[2,19], CAIX acts as a proton shuttler which effectively speeds up the spatial movement of extracellular protons and this in turn means that the exchange of extracellular protons between the free and available pools is also appropriately affected.

To properly capture the dynamic behavior of CAIX we need to adequately incorporate the time dependent behavior of the exchange coefficients $k_1$ and $k_2$. Since the accelerating effect of CAIX increases with increasing extracellular lactate concentration, the time dependence of CAIX must qualitatively mimick the dynamics of lactate application. Based on these considerations, the time evolution of $k_1$ is described as in (2c). Similarly, the time evolution of $k_2$ is given by (2d). Since there is no preference in the direction of proton movement, we have that $k_1(t) = k_2(t)$ for all $t >0$.

We also introduce two buffer modulators $k_5$ and $k_6$, the latter being time dependent. The former modulates the intracellular buffer $\beta _i$ as a dividing factor, while $k_6(t)$ modulates the extracellular buffer $\beta_e$ in a multiplicative way. For $0<k_5<1$ the internal buffer is amplified and hence the effect of the transporter is dampened, i.e., the protons released by MCT1 on the IC side are quickly absorbed. On the other hand, for $k_5>1$ the internal buffer capacity is reduced and therefore the effect of the transporter is enhanced. In contrast for a subunitary value of $k_6$ the external buffer is weakened, thus enhancing the effect of the transporter. On the other hand, for $k_6$ values larger than 1 the external buffer is enhanced, thus the effect of the transporter is reduced. Both $k_5$ and $k_6(t)$ influence indirectly the transport function $T$ by dynamically altering the buffer system. The extracellular buffer capacity $k_6(t)$ is modeled in (2e) as a quadratic function of $H_{ea}$. The precise form of that function was obtained after performing a least-squares fit of the titration experiment, as shown in Figure 4b. For the experimental determination of extracellular buffer capacity ($\beta _e$), the physiological salt solution used for the imaging experiments was titrated from pH $7.4$ to pH $6.4$ by stepwise addition of $0.2\ {\rm mM}$ HCl. The buffer capacity was then calculated for every single titration step, using the formula

with $\Delta $pH denoting the change in pH after addition of $0.2\ {\rm mM}$ HCl, and $\Delta $[HCl] being the amount of added HCl ($0.2\ {\rm mM}$). The calculated buffer capacity was then plotted against the total amount of added $H^+$.

The mathematical description: Equations for proton and lactate dynamics

where $H_{eu}$ is constant and $k_1$ and $k_2$ coincide,

with

Thereby $C_2(t)$ corresponds to the lactate control function in (1), and $H_i = H_{ia} + H_{iu}$ and $H_e = H_{ea} + H_{eu}$ in (3c) and (3d), respectively. They denote total available intra- and extracellular proton concentrations.

Initial conditions:

Observe that $C_1$ represents the lactate applied in the extracellular solution. There is no observable delay between its application and its actual availability in the solution. The high value of the exponent $p$ (i.e. $p = 40$) in the above expression of $C_1(t)$ is needed to mimic this instantaneous availability of extracellular lactate. Mathematically such high value of $p$ ensures very fast saturation of the extracellular lactate concentration. However, although the full amount of applied lactate is available on the extracellular side, the actual amount used by the transporter is less; the much smaller value $p = 4$ in the expressions of $C_2(t)$ and $C_3(t)$ represents the slow saturation of applied extracellular lactate as 'seen' by MCT1.

Numerical simulations

In order to validate the model (2) - (3) we perform numerical simulations and show that the model prediction fits the experimentally observed data in an appropriate manner. The choice of model parameters such as buffer capacity, pool exchange rates, MCT1 transporter rates etc. is crucial for reducing the error between the simulated result and the experimental data. Statistical methods should be used in order to estimate the involved parameters, however, of the 20 model parameters only at most 10 can be assigned fixed values directly based on experimental information. The rest are free variables that need to be statistically estimated. This is, however, a nontrivial problem, mainly due to the following challenges:

1. the model (3) is a coupled system of nonlinear stochastic differential equations involving several major unknowns: $H_{ia}$, $H_{ea}$, $L_i$, $L_{ea}$. The data necessary for the model validation is only available for one variable, namely $H_i$, which involves both $H_{ia}$ and $H_{iu}$. %The model (3) is thus an overdetermined system with respect to the available data, therefore the estimation problem is ill-posed.

2. since the parameters are present on the RHS of the equations and since there is no quantitative data for the derivatives, even if (3) consisted of only one equation (say for $H_{ia}$), the estimation task would still be challenging, as the unknown parameters appear as factors of the integrands and one has to minimize the error for every time integral.

3. finally, the nonlinear terms may render the error minimization task non-convex.

Taking these facts into consideration we tried the following error minimization approaches:

1. We first tried a maximum log-likelihood method. As $H_i$ is our only observable, we decided to maximize its log-likelihood. In order to compute the latter, we first needed to determine the probability density of $H_i$, for which we used the Gaussian kernel density estimator. Once the log-likelihood function was computed we applied the optimization algorithm to determine the best parameter. The optimization terminated only for very sparse time points, for relatively denser time points none of the optimization algorithm terminated. As mentioned above this could be due to the non-convexity and ill-posedness of the problem.

2. This led us to use Monte-Carlo based local search techniques. Since we already had a resonably good hand-picked guess of the parameters, we decided to randomly search, with $.5 \times 10^6$ iterations, for a parameter set in the neighborhood of this initial guess such that the L2-norm based error is minimized. Based on this we acquired the following parameter values:

Apart from the above, the parameter values for the environment type (i.e. normoxic and hypoxic) are given below.

1. Parameters for the simulation in the case of normoxic cells: %with $CO_2$ free buffer.

2. Parameters for the simulation in the case of hypoxic cells. %in $CO_2$ free buffer.

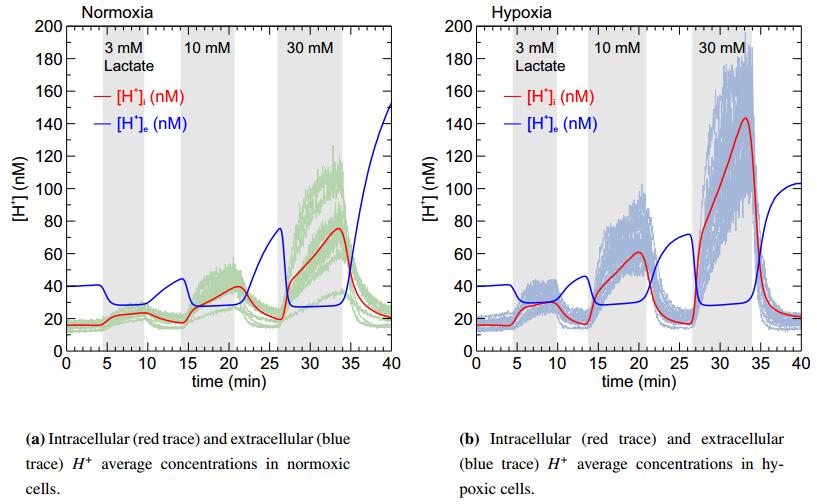
Using the above parameters we numerically simulated the model (2) - (3) by a finite difference scheme combined with an Euler-Maruyama time discretization. The 500 Monte-Carlo iterations were done in order to estimate the averages. Based on this we obtained the results in Figure 5 for intra- and extracellular proton concentrations in both the normoxic and the hypoxic regimes. Figure 6 shows the computed transport dynamics of MCT1. The numerical simulations indicate that the model is able to correctly predict the MCT1-induced dynamics of intracellular protons. In particular, the undersaturation of $H_i$ dynamics obtained with the simple one-point model is now eluded in both normoxic and hypoxic regimes.

Figure 5.  Simulation results of the two-compartment model (2)--(3). Shown are the average concentrations of intra- (red) and extracellular (blue) $H^+$. The light green and light blue traces depict the original data.

DownLoad: Full-Size Img PowerPoint

Figure 6.  Transport dynamics of MCT1, as expressed by the right-hand-side of (3c), during application and removal of lactate in a normoxic (green trace), respectively hypoxic (blue trace) cancer cell.

DownLoad: Full-Size Img PowerPoint

4.   Discussion

Our model suggests that extracellular and intracellular carbonic anhydrases can facilitate MCT1-mediated proton/lactate cotransport by accelerating the exchange of protons between the immediate surrounding of the transporter and the bulk solution. It has been shown that $H^+$ cotransporters such as MCTs, whose substrate is available only at very low concentrations, extract $H^+$ from the cytosol at rates well above the capacity for simple diffusion to replenish their immediate vicinity. Therefore the transporter must exchange $H^+$ with protonatable sites at the plasma membrane, which could function as a "proton-harvesting antenna" for the transporter ^[24]. Both intracellular CAII and extracellular CAIX are equipped with an intramolecular $H^+$ shuttle, which has been proposed to also mediate rapid shuttling of $H^+$ between MCTs and surrounding protonatable residues ^[2,6,19,26]. Thereby the CAs would stabilize the $H^+$ concentration in the immediate vicinity of the transporter pore, which in turn would facilitate proton-driven lactate flux via the transporter. In analogy to that, our model shows that increasing the rate constants for the exchange of protons between the free pool and the available pool enhances proton-coupled lactate transport across the membrane. Interestingly, the model could only fit the experimental data when the exchange of protons was enhanced on both sites of the membrane. Intracellular CAII is constantly expressed in MCF-7 cells, both under normoxic and hypoxic conditions, while extracellular CAIX is strongly upregulated under hypoxia ^[19]. According to the model, the rate of proton/lactate cotransport would therefore be limited by the slow exchange of $H^+$ between the free pool and the available pool on the extracellular site under normoxic conditions. However, cancer cells also produce only low amounts of lactate under normoxia, making the necessity for rapid proton/lactate transport obsolete. Under hypoxic conditions, when proton and lactate production is increased, CAIX would now enhance the exchange of $H^+$ between the free pool and the available pool on the extracellular site, while CAII would still facilitate intracellular $H^+$ movement. Thereby both carbonic anhydrases could stabilize the available proton pool for the MCT1 to drive proton-coupled lactate transport in hypoxic cancer cells. In line with this, we could recently show, that knockdown of CAII and CAIX, respectively, results in a significant reduction of MCT1 transport activity in MCF-7 breast cancer cells ^[2,19,27]. Performing mathematical modeling of this problem not only led to the above findings, but also allowed to assess the dynamics of the transport activity, which is hardly possible to do directly from data. The model is able to capture random effects which are inherent to such biological processes and the model development outlined the importance of compartmentalization of the protons closer and further away from the cell membrane and its transporters. Considering such "intermediate spatial stages" kept the mathematical setting in the ODE-SDE framework, as the handling of stochastic PDEs would be much more challenging, not only from the viewpoint of parameter estimation, but also merely concerning the numerical simulations.

Acknowledgments

This project has been supported by the BioComp Research Unit at the University of Kaiserslautern (TUK).

Conflict of interest

The authors declare there is no conflict of interest.