Most relevant genetic factors in ovarian cancer development

1.   Introduction

In a real Hilbert space $H$, with $D$ being a nonempty closed convex subset, where the inner product $\langle{\cdot, \cdot}\rangle$ and norm $\|\cdot\|$ are defined, the classical variational inequality problem (VIP) is to determine a point $x^*\in D$ such that $\langle{\mathscr{A}x^*, y-x^*}\rangle \ge 0$ holds for all $y\in D$, where $\mathscr{A}:H\rightarrow H$ is an operator. Then, we define $\lozenge$ as its solution set. Stampacchia ^[1] proposed variational inequality theory in 1964, which appeared in various models to solve a wide range of engineering, regional, physical, mathematical, and other problems. The mathematical theory of variational inequality problems was first applied to solve equilibrium problems. Within this model, the function is derived from the first-order variation of the respective potential energy. As a generalization and development of classical variational problems, the form of variational inequality has become more diverse, and many projection algorithms have been studied by scholars ^{[2,3,4,5,6,7,8,9,10]}. In ^[11], Hu and Wang utilized the projected neural network (PNN) to solve the VIP under the pseudo-monotonicity or pseudoconvexity assumptions. Furthermore, He et al. ^[12] proposed an inertial PNN method for solving the VIP, while Eshaghnezhad et al. ^[13] presented a novel PNN method for solving the VIP. In addition, in ^[14], a modified neurodynamic network (MNN) was proposed for solving the VIP, and under the assumptions of strong pseudo monotonicity and L-continuity, the fixed-time stability convergence of MNN was established.

The most famous method for solving the VIP is called the projection gradient method (GM), which is expressed as

Observably, the iterative sequence $\{x_n\}$ produced by this method converges towards a solution of the VIP, and $P_D:H\rightarrow D$ is a metric projection, with $\gamma$ denoting the stepsize parameter, and $\mathscr{A}$ being both strongly monotone and Lipschitz continuous. The projection gradient method fails when $\mathscr{A}$ is weakened to a monotonic operator. On this basis, Korpelevich ^[15] proposed a two-step iteration called the extragradient method (EGM)

where $\gamma$ is the stepsize parameter, and $\mathscr{A}$ is Lipschitz continuous and monotone. However, the calculation of projection is a major challenge in each iteration process. Hence, to address this issue, Censor et al. ^[16] proposed the idea of the half-space and modified the algorithm to

Recently, adaptive step size ^[17,18,19] and inertia ^{[20,21,22,23]} have been frequently used to accelerate algorithm convergence. For example, Thong and Hieu ^[24] presented the following algorithm:

where $\mathscr{H}_n = \{x\in H:\langle h_n-\tau_n\mathscr{A}h_n-s_n, x-s_n \rangle \le 0\},$ and

They also combined the VIP with fixed point problems ^[25] (we define $\Delta$ as a common solution set). For example, Nadezhkina and Takahashi ^[26] proposed the following algorithm:

where $\mathscr{A}$ is Lipschitz continuous and monotone, and $\mathscr{T}:D\rightarrow D$ is nonexpansive. The sequence produced by this algorithm exhibits weak convergence toward an element in $\Delta$. Another instance is the algorithm proposed by Thong et al. ^[27], which is as follows:

where $\tau_n$ is selected as the maximum $\tau$ within the set $\{\gamma, \gamma l, \gamma l^2, ...\}$ that satisfies the condition

Based on the preceding research, we present a self-adaptive step-size and alternated inertial subgradient extragradient algorithm designed for addressing the VIP and fixed-point problems involving non-Lipschitz and pseudo-monotone operators in this paper. The article's structure is outlined as follows: Section 2 contains definitions and preliminary results essential for our approach. Section 3 establishes the convergence of the iterative sequence generated. Finally, Section 4 includes a series of numerical experiments demonstrating the practicality and effectiveness of our algorithm.

2.   Preliminaries

For a sequence $\{x_{n}\}$ and $x$ in $H$, strong convergence is represented as $x_{n}\rightarrow x$, weak convergence is represented as $x_{n}\rightharpoonup x$.

Definition 2.1. ^[28] We define a nonlinear operator $\mathscr{T}:H\rightarrow H$ to have an empty fixed point set (${\rm Fix}(\mathscr{T}) \neq \emptyset$), if the following expression holds for $\{q_{n}\} \in H$:

where $I$ denotes the identity operator. In such cases, we characterize $I-\mathscr{T}$ as being demiclosed at zero.

Definition 2.2. For an operator $\mathscr{T}:H\rightarrow H$, the following definitions apply:

${\rm (1)}$ $\mathscr{T}$ is termed nonexpansive if

${\rm (2)}$ $\mathscr{T}$ is termed quasi-nonexpansive with a non-empty fixed point set $Fix(\mathscr{T})\neq\emptyset$ if

Definition 2.3. A sequence $\{q_n\}$ is said to be Fejér monotone concerning a set $D$ if

Lemma 2.1. For each $\zeta_1, \zeta_2 \in H$ and $\epsilon\in \mathbb{R}$, we have

Lemma 2.2. ^[26] Given $\psi\in H$ and $\varphi\in D$, then

${\rm (1)}$ $\|P_{D}\psi-P_{D}\varphi\|^2\leq\langle \psi-\varphi, P_{D}\psi-P_{D}\varphi\rangle$;

${\rm (2)}$ $\|\varphi-P_{D}\psi\|^{2}\leq \|\psi-\varphi\|^{2}-\|\psi-P_{D}\psi\|^{2}$;

${\rm (3)}$ $\langle \psi-P_D\psi, P_D\psi-\varphi \rangle\ge 0$.

Lemma 2.3. ^[29] Suppose $\mathscr{A}:D\rightarrow H$ is pseudomonotone and uniformly continuous. Then, $\varsigma$ is a solution of $\lozenge$ $\Longleftrightarrow$ $\langle \mathscr{A}x, x-\varsigma\rangle\ge 0, \quad\forall x\in D$.

Lemma 2.4. ^[30] Let $D$ be a nonempty subset of $H$. A sequence $\{x_n\}$ in $H$ is said to weakly converge to a point in D if the following conditions are met:

${\rm (1)}$ For every $x\in D$, $\mathop {\lim }\limits_{n \to \infty }\|{x_n-x}\|$ exists;

${\rm (2)}$ Every sequential weak cluster point of $\{x_n\}$ is in $D$.

3.   Main results

This section presents an alternated inertial projection algorithm designed to address the VIP and fixed point problems associated with a quasi-nonexpansive mapping $\mathscr{T}$ in $H$. We have the following assumptions:

Assumption 3.1.

${\rm (a)}$ The operator $\mathscr{A}:H\rightarrow H$ is pseudo-monotone, uniformly continuous over $H$, and exhibits sequential weak continuity on $D$;

${\rm (b)}$ $\varpi\in(\frac{1-\mu}{4}, \frac{1-\mu}{2})$, $0 < \kappa_n < \min\{\frac{1-\mu-2\varpi}{2\varpi}, \frac{1-\varpi}{1+\varpi}\}$.

The algorithm (Algorithm 1) is as follows:

To prove the algorithm, we first provide several lemmas.

Lemma 3.1. The sequence produced by Algorithm 1, denoted as $\{x_{2n}\}$, is bounded and $\mathop {\lim }\limits_{n \to \infty } \|x_{2n}-\varrho\|$ exists for all $\varrho\in \Delta$.

Proof. Indeed, let $\varrho\in \Delta$. Then, we have

According to $\varrho\in \Delta$, it follows that $\langle{\mathscr{A}\varrho, s-\varrho}\rangle\ge$ for all $s\in D$, and, at the same time, because of the pseudomonotonicity of $\mathscr{A}$, we establish $\langle{\mathscr{A}s, s-\varrho}\rangle\ge 0$ for all $s\in D$. If we set $s = s_n$, then $\langle{\mathscr{A}s_n, s_n-\varrho}\rangle\ge 0$. Thus, by (3.1), we can get

Subsequently, by (2.2), we obtain

Meanwhile, combined with (3.3), it is evident that

In particular,

By (2.2), we obtain

As another special case of (3.3), we have

and then, bringing (3.7) into (3.6), we can get

Plugging (3.8) into (3.5) gives

where

Thus, putting (3.10) into (3.9), we have

According to $\varpi\in(\frac{1-\mu}{4}, \frac{1-\mu}{2})$, $0 < \kappa_n < \min\{\frac{1-\mu-2\varpi}{2\varpi}, \frac{1-\varpi}{1+\varpi}\}$, we get the sequence $\{\|x_{2n}-\varrho\|\}$ is decreasing, and thus $\mathop {\lim }\limits_{n \to \infty } \|x_{2n}-\varrho\|$ exists. This implies $\{\|x_{2n}-\varrho\|\}$ is bounded, hence, $\{x_{2n}\}$ is bounded. For (3.7), we can get that $\{\|x_{2n+1}-\varrho\|\}$ is also bounded. Therefore, $\{\|x_n-\varrho\|\}$ is bounded. Thus, $\{x_n\}$ is bounded. □

Lemma 3.2. Consider the sequence $\{x_{2n}\}$ produced by Algorithm 1. If the subsequence $\{x_{2n_k}\}$ of $\{x_{2n}\}$ weakly converges to $x^*\in H$ and $\mathop {\lim }\limits_{k \to \infty }\|{x_{2n_k}-s_{2n_k}}\| = 0$, then $x^*\in \lozenge$.

Proof. Because of $h_{2n} = x_{2n}$, using the definition of $\{s_{2n_k}\}$ and Lemma 2.2, we get

and so

Hence,

Because of $\mathop {\lim }\limits_{k \to \infty }\|{x_{2n_k}-s_{2n_k}}\| = 0$ and taking the limit as $k\rightarrow \infty$ in (3.12), we acquire

Select a decreasing sequence $\{\epsilon_k\}\subset(0, \infty)$ to make $\mathop {\lim }\limits_{k \to \infty }\epsilon_k = 0$ hold. Then, for each $\epsilon_k$, based on (3.13) we use $M_k$ to represent the smallest positive integer satisfying

Since $\{\epsilon_k\}$ is decreasing, then $\{M_k\}$ is increasing. Also, for each $k$, $\mathscr{A}x_{2M_k}\neq0$, let

Here, $\langle \mathscr{A}x_{2M_k}, v_{2M_k} \rangle = 1$ for each $k$. Then, by (3.14), for each $k$ we have

Because $\mathscr{A}$ is pseudo-monotonic, we get

Since $x_{2n_k}\rightharpoonup x^*$ as $k\rightarrow \infty$, and $\mathscr{A}$ exhibits sequential weak continuity on $H$, it follows that the sequence $\{\mathscr{A}x_{2n_k}\}$ weakly converges to $\mathscr{A}x^*$. Then, based on the weakly sequential continuity of the norm, we obtain

Since $\{x_{M_k}\}\subset\{x_{n_k}\}$ and $\mathop {\lim}\limits_{k \to \infty }\epsilon_k = 0$, we have

which means $\mathop {\lim }\limits_{k \to \infty }\|\epsilon_kv_{2M_k}\| = 0$. Finally, we let $k\rightarrow \infty$ in (3.15) and get

This implies $x^*\in \lozenge$. □

Lemma 3.3. Considering $\{x_{2n}\}$ as the sequence produced by Algorithm 1, since $\{x_{2n}\}$ is a bounded sequence, there exists a subsequence $\{x_{2n_k}\}$ of $\{x_{2n}\}$ and $x^*\in H$ such that $x_{2n_k}\rightharpoonup x^*$. Hence, $x^*\in \Delta$.

Proof. From (3.11) and the convergence of $\{\|x_{2n}-\varrho\|\}$, we can deduce that

By the definition of $\{x_{2n+1}\}$, we have

then

and by (3.18) and $x_{2n_k}\rightharpoonup x^*$, we can get

Since $\mathscr{T}$ is demiclosed at zero, Definition 2.1, (3.17), and (3.19) imply

From (3.2), we deduce

This implies that

Based on the convergence of $\{\|x_{2n}-\varrho\|^2\}$, we can assume that

At the same time, according to (3.16), it can be obtained that

It follows from (3.4) that

Then,

It implies from (3.22)–(3.24) that

By (3.2), we get

Combining (3.25) and (3.26), we get

Combining with (3.21), (3.22), and (3.27), we have

Therefore, it implies from Lemma 3.2 that

Combining (3.20) and (3.28), we can derive

□

Theorem 3.2. $\{x_n\}$, a sequence produced by Algorithm 1, weakly converges to a point within $\Delta$.

Proof. Let $x^*\in H$ such that $x_{2n_k}\rightharpoonup x^*$. Then, by Lemma 3.3, it implies

Combining $\mathop {\lim }\limits_{n \to \infty } \|x_{2n}-\varrho\|^2$ exists for all $\varrho\in \Delta$, and by Lemma 2.4, we get that $\{x_{2n}\}$ converges weakly to an element within $\Delta$. Now, suppose $\{x_{2n}\}$ converges weakly to $\xi\in \Delta$. For all $g\in H$, it follows that

Furthermore, by (3.16), for all $g\in H$,

Therefore, $\{x_{2n+1}\}$ weakly converges to $\xi\in \Delta$. Hence, $\{x_n\}$ weakly converges to $\xi\in \Delta$ □

4.   Numerical experiments

This section will showcase three numerical experiments aiming to compare Algorithm 1 against scheme (1.6) and Algorithm 6.1 in ^[31], and Algorithm 3.1 in ^[32]. All codes were written in MATLAB R2018b and performed on a desktop PC with Intel(R) Core(TM) i5-8250U CPU @ 1.60GHz 1.80 GHz, RAM 8.00 GB.

Example 4.1. Assume that $H = \mathbb R^3$ and $D: = \{x\in\mathbb{R}^3:\Phi x\le \phi\}$, where $\Phi$ represents a $3\times3$ matrix and $\phi$ is a nonnegative vector. For $\mathscr{A}(x): = Qx+q$, with $Q = BB^T+E+F$, where $B$ is a $3\times3$ matrix, $E$ is a $3\times3$ skew-symmetric matrix, $F$ is a $3\times3$ diagonal matrix with nonnegative diagonal entries, and $q$ is a vector in $\mathbb{R}^3$. Notably, $\mathscr{A}$ is both monotone and Lipschitz continuous with constant $L = \|Q\|$. Define $\mathscr{T}(x) = x, \forall x\in\mathbb{R}^3$.

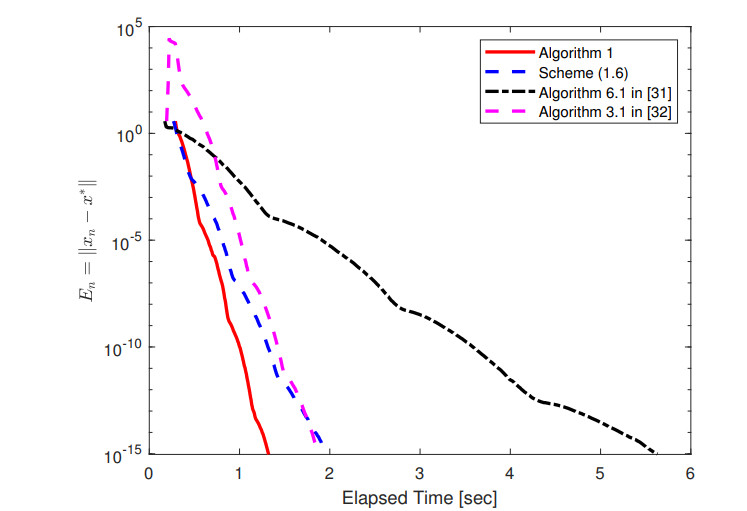
Under the assumption $q = 0$, the solution set $\Delta = \{0\}$, which means that $x^* = 0$. Now, the error at the n-th step iteration is measured using $\|x_n-x^*\|$. In both Algorithm 1 and scheme (1.6), we let $\mu = 0.5$, $\gamma = 0.5$, $l = 0.5$; in Algorithm 1, we let $\varpi = 0.2$, $\kappa_n = 0.2$; in scheme (1.6), we let $\alpha_n = 0.25$, $\beta_n = 0.5$; in Algorithm 6.1 in ^[31], we let $\tau = 0.01$, $\alpha_n = 0.25$; in Algorithm 3.1 in ^[32], we let $\alpha_n = \frac{1}{n+1}$, $\beta_n = \frac{n}{2n+1}$, $f(x) = 0.5x$, $\tau_1 = 1$, $\mu = 0.2$, $\theta = 0.3$, $\epsilon_n = \frac{100}{(n+1)^2}$. The outcomes of this numerical experiment are presented in Table 1 and Figure 1.

From Table 1, we can see that the algorithm in this article has the least number of iterations and the shortest required time. Therefore, this indicates that Algorithm 1 is feasible. According to the situation shown in Figure 1, we can see that Algorithm 1 is more efficient than the other two algorithms.

Example 4.2. Consider $H = \mathbb R$ and the feasible set $D = [-2, 5]$. Let $\mathscr{A}:H\rightarrow H$ be defined as

and $\mathscr{T}:H\rightarrow H$ be defined as

It is evident that $\mathscr{A}$ is Lipschitz continuous and monotone, while $\mathscr{T}$ is a quasi-nonexpansive mapping. Consequently, it is straightforward to observe that $\Delta = \{0\}$.

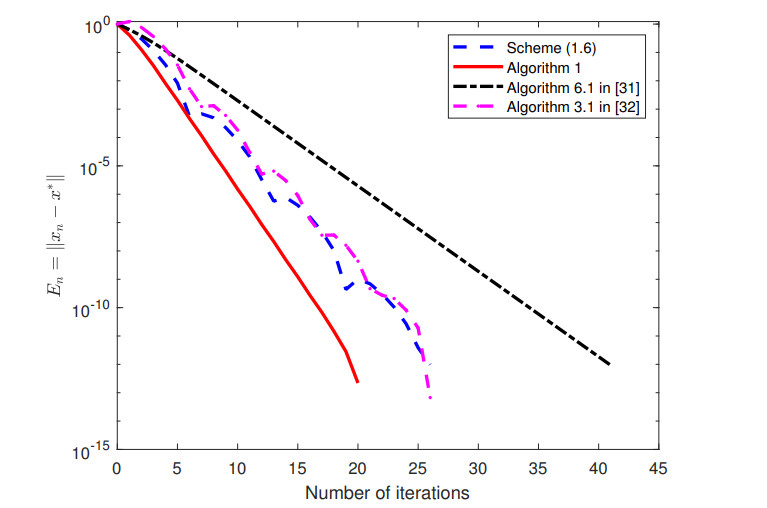
In Algorithm 1 and scheme (1.6), we let $\gamma = 0.5$, $l = 0.5$, $\mu = 0.9$; in Algorithm 1, we let $\kappa_n = \frac{2}{3}$, $\varpi = 0.03$; in scheme (1.6), we let $\alpha_n = 0.25$, $\beta_n = 0.5$; in Algorithm 6.1 in ^[31], we let $\tau = 0.4$, $\alpha_n = 0.5$, in Algorithm 3.1 in ^[32], we let $\alpha_n = \frac{1}{n+1}$, $\beta_n = \frac{n}{2n+1}$, $f(x) = 0.5x$, $\tau_1 = 1$, $\mu = 0.2$, $\theta = 0.3$, $\epsilon_n = \frac{100}{(n+1)^2}$. The results of the numerical experiment are shown in Table 2 and Figure 2.

Table 2 and Figure 2 illustrate that Algorithm 1 has a faster convergence speed.

Example 4.3. Consider $H = L^2([0, 1])$ with the inner product

and the induced norm

The operator $\mathscr{A}:H\rightarrow H$ is defined as

The set $D: = \{m\in H: \|m\|\le 1\}$ represents the unit ball. Specifically, the projection operator $P_D(m)$ is defined as

Let $\mathscr{T}:L^2([0, 1])\rightarrow L^2([0, 1])$ be defined by

Therefore, we can get that $\Delta = \{0\}$.

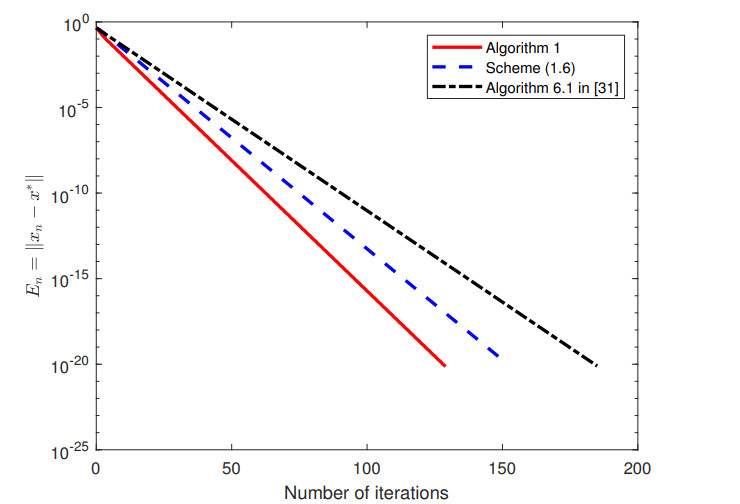
In Algorithm 1 and scheme (1.6), we let $\gamma = 0.5$, $l = 0.5$, $\mu = 0.5$; in Algorithm 1, we let $\kappa_n = 0.2$, $\varpi = 0.2$; in scheme (1.6), we let $\alpha_n = 0.25$, $\beta_n = 0.3$; in Algorithm 6.1 in ^[31], we let $\tau = 0.9$, $\alpha_n = 0.6$. The results of the numerical experiment are shown in Figure 3.

Figure 3 shows the behaviors of $E_n = \|x_n-x^*\|$ generated by all the algorithms, commencing from the initial point $x_0(p) = p^2$. The presented results also indicate that our algorithm is superior to other algorithms.

5.   Conclusions

This paper introduces a novel approach for tackling variational inequality problems and fixed point problems. Algorithm 1 extends the operator $\mathscr{A}$ to pseudo-monotone, uniformly continuous, and incorporates a new self-adaptive step size, and adds an alternated inertial method based on scheme (1.6). The efficiency of our algorithm is validated through the results obtained from three distinct numerical experiments.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant No. 12171435).

Conflict of interest

The authors declare that they have no competing interests.