Stationary solutions to a hybrid viscous hydrodynamic model with classical boundaries

1.   Introduction

Many modern semiconductor devices base their operation on quantum phenomena. These effects, often difficult to describe from a mathematical point of view, are localized only in a specific region of the device, therefore, it seems reasonable to use a hybrid approach, which involves the use of both quantum ^{[1,2,8,20,31]} and classical models ^{[10,21,23,24,28,29,30]}. Several interesting results are available in the literature, starting from the pioneering work by N. Ben Abdallah ^[4], where a set of physically reasonable conditions is prescribed at the interface between classical and quantum domains to link the Boltzmann equation and the stationary Schrödinger equations. A similar approach has been employed in ^{[3,5,7,11,12,17,25,32]}. The interface conditions used in these works are somewhat arbitrary since there are no direct measurements of the physical variables on the surface between classical and quantum domains. Furthermore, the transition between the classical and the quantum system does not take place abruptly in a precise section of the device but rather, there is a transition zone where the system behaves in a semi-classical way. Following this idea, in ^[9,13] an alternative approach was proposed for the first time. A smooth quantum function $Q(x)$ which multiplies the Bohm potential is introduced and it drives the classical system to become quantum and vice versa. Namely $Q(x) = 0$ in the classical part and $Q(x) = 1$ in the quantum one, but physically reasonable transition regions, where $0 < Q(x) < 1,$ are also included. In this way, no artificial interface condition are required, and the model naturally evolves from the classical to the quantum regimes ^{[14,15,16,18]}.

Unfortunately, the term $Q(x)$ adds some difficulties, especially in the treatment of the boundaries of the device. In our previous works in this line, to allow the existence of the weak hybrid solution, we necessarily had to consider boundary conditions in the quantum domain. Indeed, considering only quantum boundaries is the main limitation of the original model since the boundaries usually act as Ohmic contacts and they are well described by classical equations. To overcome this problem, here we introduce a suitable viscous term that regularizes the equations allowing us to consider classical boundaries. A similar viscosity has been employed by ^[19] to prove the existence of a solution to the quantum hydrodynamic model (QHD) for any positive values of the current density $J$.

In more detail, the aim of this paper is to study the existence of steady-state weak solutions to the following visco-hybrid quantum hydrodynamical equation (VH-QHD):

for $x\in \Omega = [0, 1]\,$ and $t\geq 0.$

In the system above $n$ is a strictly positive function modelling the electron density, $Q\!:\! \Omega \!\rightarrow \! [0, 1]$ is a regular function as introduced in ^[9,13]. In more detail the function $Q(x)$ is such that $Q = 0$ in the (classical) outer part of the device and $Q > 0$ in the central part, where the quantum effect normally occurs.

The system (1.1) must be coupled with another equation, named the Poisson equation, which describes the behavior of the self-consistent electrical potential $V$:

In (1.1) and (1.2) several positive scaled constants appear: $\tau$, $\lambda,$ $\nu$, and $T$; they represent the relaxation time, the Debye length, the viscosity coefficient, and the temperature, respectively. Finally $0 < \varepsilon < < 1$ is the scaled Plank's constant. The function $C(x)$ assigns the distribution of the fixed charge background of ions, that is the doping profile. Here we assume that $C$ is non-negative and in $C^0(\Omega)$.

The following boundary conditions for the stationary problem (1.1)-(1.2) are quite standard and have been already employed in many papers such as ^[13,16,22]; we have

and

where

Integrating (1.1)$_1$, from (1.5) and (1.6), it follows that

and, in view of the above boundary conditions (1.3)–(1.5), we have

We just point out that in the BVP above the condition $J = J_0$ replaces one of the two boundary conditions on the electric potential $V$, which are necessary to solve the Poisson equation. The equivalence between the two conditions is proved in ^[22].

The subject of this paper is therefore the following boundary problem associated with the steady-state VH-QHD model (1.1)-(1.2):

Here is the outline of the paper: In Section 2, in order to simplify the reading of the article, we state the main theorems that will be proved in the following sections. In Section 3 we study the approximating problem obtained from (1.9) assuming $Q(x)\geq q > 0$, for a given positive constant $q$. Then, in Section 4, the limit $q\rightarrow 0$ is considered. Finally, in Section 5, some simple numerical experiments are performed to analyze the effect of the viscosity on the classical boundaries.

2.   Main results

The main results of the paper will be presented in this section. We are looking for a solution to the visco-hybrid QHD (1.9) assuming with $Q = 0$ close to the boundaries and $Q > 0$ in the central part of the domain.

We remark that both the quantum function and the doping profile are assumed to be continuous functions.

We focus on the following fourth-order boundary value problem (BVP)

obtained differentiating (1.9)$_1$ in view of the Poisson equation (1.2).

In order to prove the existence of the solution to the system above we need to assume that the flow is subsonic, since this condition guarantees the uniform ellipticity of the problem, that is

and then

Remark 2.1. Similarly, on the boundary of the domain and for the doping profile $C(x)$, we must have

The 3rd order elliptic equation (2.1) is degenerate close to the boundaries where the quantum effects disappear. To overcome this technical difficulty we prove the existence of solutions for a regularized problem obtained assuming $Q = Q_q$ in (2.1), where $0 < q \leq Q_q\leq 1.$ As a consequence, we obtain a sequence of smooth functions $\{Q_q\}, \, q\in \mathbb{R}_+,$ and require that this sequence satisfies the following set of conditions:

where $\underline{n}: = \min\{1, C_0\} > n_\star$ and $n_\star$ as in (2.3). Now we consider the following modified visco-hybrid QHD equations (VH-Q$_q$HD) where we set $w_q = \sqrt{n_q}$ and replace $Q(x)$ by $Q_q(x)$. We will look for $(w_{q}, V_{q})(x)$, as solutions to the following VH-Q$_q$HD system:

As in ^[13], we start by proving the following theorem to asses the existence of solutions to (2.7).

Theorem 2.2 (Existence of VH-Q$_q$HD solution). Assume (2.4) and (2.5) are fulfilled, that $Q_q(x)$ is a non-negative, bounded smooth function on $\Omega = [0, 1]$ such that

and

where $\underline{n}: = \min\{1, C_0\}$. Then there exists at least one solution to (2.7) such that $(w_{q}, V_{q})\in H^4(\Omega) \times H^2(\Omega).$

Remark 2.3. Condition (2.6)$_3$ essentially means that ${|Q_q'|^2}/{Q_q}$ remains bounded when ${Q_q}\rightarrow 0$. We observe that this condition is verified when $Q_q$ behaves as $|x-x_0|^m$, for $m\geq 2$, when $x\rightarrow x_0$. Finally, we notice that the assumption (2.6)$_3$ is stronger than (2.9), required in the first part of the paper for $q > 0$.

To better assess the existence of the solution to a more realistic visco-hybrid QHD model, namely where $Q = 0$ on the classical part of the domain, we need to define what solution means in this contest. In this case, we do not expect a classical solution to exist and we look just for a weak solution defined as follows:

Definition 2.4. The couple $(w, V)(x)$ is a weak solution of (2.1) (where $w = \sqrt{n}$), if, for any $\phi\in C_0^\infty(\Omega)$ the following relations are verified

and

Since the limit problem behaves classically close to the boundaries, when we perform the hybrid limit we pass from the quantum to the classical regime then the quantum term disappears. Therefore we need to assume that

in a neighborhood of the boundaries $x = 0$ and $x = 1$.

The main result of this paper is the following theorem:

Theorem 2.5. (Hybrid limits and existence of VH-QHD solution). Assume (2.4), (2.5) and $Q\in C^1[0, 1]$ with $0\le Q\le 1$ and $C\in C^0[0, 1]$. Let $\{Q_q\}$ be a sequence satisfying (2.6), (2.12) and $(w_q, V_q)(x)$ be a solution to (2.7) corresponding to the approximating function $Q_q$. Then there exists a convergent subsequence of $(w_q, V_q)(x)$, which is not relabelled, with limit $(w, V)$, namely

Such a pair $(w, V)(x)$ is the weak solution to the VH-QHD system (2.1), where $w = \sqrt{n}$.

3.   Existence of a solution to the VH-Q$_q$HD problem

In this section, we prove that, under a suitable set of conditions, the BVP (2.7) admits a weak solution $(w_q, V_q)$. For this purpose, we rewrite (2.7) in the following equivalent form

In the next result we prove a set of useful a priori estimates, which allow to properly construct the fixed point theorem which guarantees the existence result for (3.1)-(3.2).

Lemma 3.1. (A priori estimates). Assume the subsonic conditions (2.4), (2.5) and $Q_q$ such that (2.8) and (2.9) are both satisfied. Let $w_q\in H^2(\Omega)$ be a solution of the BVP (3.1)-(3.2). Then $w_q$ verifies the following properties:

● Adjoint subsonic condition

● $L^\infty$ bound

● $H^2$ bound

where $w_M\ge \sqrt{\underline{n}}$, $\underline{c}_1 > 0$, $\underline{c}_2 > 0$, and $K > 0$ are constants with $\underline{c}_2$ independent of $q.$

Proof. Let

obtained multiplying (3.1) by $(w_q-1)\in H^1_0(\Omega),$ and integrating by parts. The integrals $I_1$ and $I_2$ can be estimated as follows:

Moreover, both $I_3$ and $I_4$ are equal to zero, indeed

In view of the estimate above, we get

Observing (3.8), we can see that the first three terms on the left side can be read as a quadratic form, namely

where $c_1$ and $c_2$ are positive constants. We notice that (3.9) is positive definite if and only if $\mathcal{B}^2_1-4 \mathcal{A}_1\mathcal{C}_1 < 0$. From (2.9), we get

that is always true, at least for a small (positive) values of $\varepsilon$.

Then, in view of (3.9) and (3.8), we get

which implies

observing that ${\frac{(w_q)_x^2}{w_q} = 4[(\sqrt{w_q})_x]^2}$ and taking ${K_1 = \sqrt{\frac{K_0}{c_2}}}$. The $L^\infty$ bound (3.4) follows by setting $w_M = (1+K_1)^2,$ while the $H^2$-bound (3.5) can be easily derived from (3.10), in view of (3.4).

Last step is to show that ${ w_q\geq \sqrt{\underline{n}}}$ for all $x\in\Omega$ and $\underline{n} = \min\{1, C_0\}.$

Let $(w_q-\sqrt{\underline{n}})^{-}: = \min(0, w_q-\sqrt{\underline{n}})$ used as a test function in the weak formulation of the problem (3.1) as follows

We recall that $w_q|_{\partial\Omega} = 1 > \sqrt{\underline{n}}$, so $(w_q-\sqrt{\underline{n}})^{-}|_{\partial\Omega} = 0$, and $(w_q-\sqrt{\underline{n}})^{-}\in H^1_0(\Omega)$. Concerning the first two terms on the right-hand side of the previous equation, one has

In order to estimate the $L_3$ term, we observe that the interval $\Omega$ can be seen as a disjoint union of the sub-intervals $\Omega^+ = \cup_i {\Omega_i}^+$, $\Omega^- = \cup_i {\Omega_i}^-$ plus isolated points, where

Therefore, $L_3$ can be rewritten as

and then

The integral $L_3$ must be computed on each interval ${\Omega_j}\!^-$. We just consider a single interval ${\Omega_j}\!^- = (a_j, b_j)$ contained in the open set $(0, 1)$ (the result can easily be generalized to a greater number of intervals), obtaining

Here we have used (3.5) to show that $w_q$ is a continuous function in $[a_j, b_j]$ and $w_q(a_j) = w_q(b_j) = \sqrt{\underline{n}}$.

Finally, we prove that also $L_4 = 0,$ indeed

In view of (2.9), (3.11), and (3.12), arguing as for (3.9), one can find two non negative constants named $\underline{c_1}$, $\underline{c_2}$ and $\underline{c_3}$ such that

therefore $(w_q-\sqrt{\underline{n}})^- = 0$ and then (3.3). □

Lemma 3.2. Set $u_q = \ln n_q$ and assume that the hypotheses of Lemma 3.1 hold, then

Proof. We consider the following equation

obtained from (2.7) setting $w_q = e^{u_q/2}$ and deriving with respect to $x$.

Clearly

Let's multiply (3.14) by $u_q$ and integrate by parts. In view of the boundary conditions (3.15), we get

According to the results in ^[22], we get

Moreover $N_2 = 0$, in view of the boundary conditions, and

Concerning $N_5,$ we have

Finally, in view of the estimation above, we obtain the following inequality

which implies (3.13). □

Theorem 3.3. Assume that the hypotheses of Lemma 3.1 and (2.2) hold. Then, the boundary value problem (3.14)-(3.15) admits at least one weak solution $u_q\in H^2(\Omega).$

Proof. As already noted in ^[13], Eq (3.14) is equivalent to the standard QHD model because $Q_q\ge q > 0$. Therefore, we can employ the same techniques applied in ^[22,26,27].

For $\sigma \in [0, 1]$ and $\rho\in X = C^{0, 1}(\Omega)$, we introduce the equation

and coupled it to (3.15). It is not difficult to see that for each $u_q, \phi \in H^2(\Omega)$ the following bi-linear form

is continuous and coercive in $H^2(\Omega)$.

Moreover a linear and continuous functional can be defined as follows:

Then the Lax-Milgram Lemma guarantees the existence of a unique solution $u_q\in H^2(\Omega)$ to the boundary value problem (3.15)–(3.18). Then a continuous and compact map $S$ on the functional space $X$ can be defined as

such that

● $S(\rho, 0) = 0$ for all $\rho\in X$,

● there is a constant $c > 0$ such that

Applying the Leray-Schauder fixed point theorem we can prove that $u_q$ is a fixed point for the map $S$ and also a weak solution to the BVP (3.14)-(3.15). □

Now we are ready to prove Theorem 2.2.

Proof of Theorem 2.2. We consider Eq (3.14)

from which we have

Observing that $u_q \in H^2(\Omega)$, by Theorem 3.3, and arguing as in Corollary 2.6 in ^[22], it is not difficult to prove that $({u_q}_{x}^2)_{xx} \in H^{-1}(\Omega)$. Concerning the viscous term $(e^{\frac{u_q}{2}})_{xxx}$ we have

It is easy to see that ${u_q}_x{u_q}_{xx}$ and ${u_q}_x^3$ both belongs to $L^{2}(\Omega)$ and ${u_q}_{xxx}\in H^{-1}(\Omega)$. Proceeding as in ^[22] and taking into account the regularity of $Q_q > q > 0$, we can deduce that $(u_q)_{xxxx}$ and then $(w_q)_{xxxx}$ are in $L^2(\Omega)$. Since problem (2.7) is equivalent to (3.14)-(3.15), the existence of a solution $w_q \in H^4$ follows easily. Finally, from the Poisson equation, we deduce $V_q\in H^2$ and that concludes the proof. □

4.   Hybrid limit

In this section we perform the hybrid limit for Eq (2.7), assuming $q\rightarrow0$. Unlike the previous works of the authors in this line ^{[13,15,16,17]}, in this paper we consider the quantum effects localized in the central part of the device, where $Q > 0$, which is more correct from the physical point of view. On the boundaries of the device we set $Q = 0$, assuming classical behaviour.

Now we present the proof of the main result of the paper.

Proof of Theorem 2.5. Let $\, 0 < \delta^{ * } < \delta^{ ** } < 1.$ Define the function $Q$ as follows:

and $\Omega_{c}: = [0, \delta^*]\, \cup\, \, [\delta^{ ** }, 1].$

Once the function $Q$ has been chosen as in (4.1), we construct the sequence of the approximating functions $\{Q_q\}$ to $Q,$ satisfying (2.6). Let $(w_q, V_q)(x)$ be the solutions to (2.7) corresponding to $Q_q$. In the sequel, we will denote constants independent from $q$ as $\bar{K}$ or $\bar{c_i}$.

We recall that from (3.3) and (3.5) the following $q$-independent estimate holds:

and we briefly prove also the following:

Proceeding as in Lemma 3.1, we rearrange the first three terms of the left-hand side in (3.8) as

The first term on the right-hand side is positive by (2.6), since $\mathcal{B}_2^2-4 \mathcal{A}_2\mathcal{C}_2 < 0$, where

As in the proof of Lemma 3.1, we obtain

By (2.9), we have $\frac{T}{{w_q}}-\frac{J^2}{{w_q}^5} > 0$ and recalling that $w_q\geq \sqrt{n_*},$ we can rewrite (4.4) as

and then we get (4.3).

Therefore, $\, \sqrt{Q_q}{w_q}_{xx}\,$ is uniformly bounded in $L^2(\Omega)$ and there exists a $w(x)$ as the hybrid limit of the sequence ${w_q}$ with

while, from (4.2), we have

Considering the weak form of (2.7)

we perform the hybrid limit $q\rightarrow 0.$

We just note that since $0\leq\sqrt{\underline{n}}\leq w_q \leq w_M$ for every $q$ and $w_q\rightarrow w\, \mbox{in} \, C^0(\Omega), \, \mbox{for}\, q\rightarrow 0,$ we can write $\frac{1}{w_q} \rightarrow \frac{1}{w}$ and $w_q^2 \rightarrow w^2\, \mbox{for}\, \, q\rightarrow 0,$ similarly for the other nonlinear terms.

So we obtain as limit

for any $\phi\in C_0^\infty(\Omega).$

Then $n = w^2$ satisfies (1.9)$_1$ in the weak sense.

In particular, the weak limit Eq (4.9) in $\Omega_c$ becomes

thanks to the hypothesis 2.12, in agreement with the previous estimates and (2.6)$_1$.

It follows that the limit solution $w$ satisfies

in $\Omega_c.$

Concerning the electric potential $V_q$, by integrating (1.1) with respect to $x$ and using (1.3), we obtain

The assumption (2.6) and the uniform estimates (4.3) imply that $\|V_q\|_{L^2}\leq \bar{K}$. Therefore, there exists $V$ such that

when $q\rightarrow 0.$

As before, we prove that the limit $V$ is the weak solution of the hybrid problem. To this end, we multiply (4.11) by $\phi\in C_0^\infty(\Omega)$ and integrate it in $\Omega$:

The uniform estimate in (4.2)-(4.3) and the properties of $\{Q_q\}$ allow that, for $q\rightarrow 0$, we have

Thus, the limit potential $V$ verifies the Poisson equation in the weak sense.

In order to conclude the proof, we need to verify the boundary conditions $(w)_{x}(0) = (w)_{x}(1) = 0$ for the limit solution. To this end, we have to prove that $(w_{q})_{xx}$ is weakly convergent in $L^2$ on a small region near each of the two extrema $0$ and $1$ of $\Omega.$ We write Eq (2.7) as follows:

By the previous uniform estimates, we can see that the right-hand side of the above equation is in $H^{-1}(\Omega)$. Then there exists a function $f \in L^2(\Omega)$ such that

which implies that

is in $\, L^2(\Omega).$

Then $2\varepsilon^2 \left(Q_q\frac{(w_{q})_{xx}}{w_{q}}+Q_q'\frac{(w_{q})_{x}}{w_{q}}\right)_{x} -\nu\, (w_q)_{xx}$ belongs to $L^2(\Omega)$ and, in view of the assumption (2.12), we conclude that, at least in a small region close to the boundaries, the convergence of the sequence $w_q\,$ to $\, w\,$ is weak in $H^2$.

By the inclusion $H^2(\Omega_c)\hookrightarrow C^1(\Omega_c),$ we can conclude that

and

The proof of Theorem 2.5 is complete. □

5.   Numerical simulations

In the previous sections, we have introduced a new hybrid viscous model (VH-QHD) and we have discussed how the viscous term $\nu (\sqrt{n})_{xx}$ allows the treatment of the classical boundaries making the problem well-posed.

In this section, we show the regularizing effects of viscosity by means of some numerical simulations on a simple $n^+|n|n^+$ transistor. For this device one usually assumes the following doping profile as in ^[13]

with $0 < C_m < 1$ and $0 < x_1 < x_2 < 1$. Within this paper the quantum regions is localized in the central part of the domain whereas the external ones, close to the Ohmic contacts, behave classically.

In this case we have

where $0 < y_1 < y_2 < 1$. To solve numerically the following boundary value problems we use COLNEW, a SCILAB tool (see ^[6]). To perform our computations, we consider the hybrid model in the following form:

coupled with the boundary conditions

where, as usual, $u = \ln n$. Both the doping profile $C(x)$ and the quantum function $Q(x)$ have been approximated by regular functions as follows:

where $x\in[0, 1]$, $C_m = 0.2$ and $q = 0.01$.

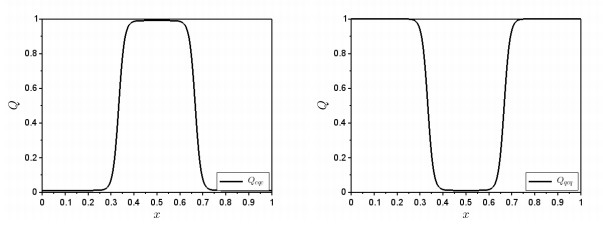
For sake of completeness we also consider the quantum boundary case, not included in the theoretical part, but extensively discussed in previous works ^[14,15,16]. In this case, the quantum function can be approximated by

The two quantum functions are displayed in Figure 1.

The other parameters, namely the scaled Debye length $\lambda$, the scaled temperature $T$, the scaled Plank constant $\varepsilon$, the current density $J$, and the relaxation time $\tau$ are assigned as follows:

To evaluate the effect of the viscosity, we compare the behavior of the charge density assuming $\nu = 0$ and $\nu = 0.001$, for both quantum functions $Q_{cqc}$ (Figures 2 and 3) and $Q_{qcq}$ (Figures 4 and 5). Observing Figure 2 we can see small oscillations of the charge density close to the boundaries, while this effect disappears by adding a small viscosity.

In Figure 3 the charge density behavior close to $x = 0$ is displayed in detail for three different viscosity values, namely $\nu = 0, \; 0.0001, \; 0.001$.

The behavior in the non-viscous case is the same as that obtained for very low viscosity. As the viscosity increases, the function's trend near the edges appears more regular. These fluctuations could be caused by the fact that the problem is not well-posed at the boundaries. However, it is also possible that these effects are related to the numeric scheme used by COLNEW. To better understand the cause of these fluctuations it is necessary to design an ad-hoc numerical scheme, which is beyond the aim of this article. Conversely, using (5.4) as a quantum function, the problem is well-posed on the boundaries and the behaviour of the charge density appears regular over the entire domain, both in the viscous and in the non-viscous cases, as in Figure 4.

6.   Conclusions

In this paper we discuss the existence of solutions for a hybrid classical-quantum hydrodynamic problem, assuming quantum effects localized in the central part of the domain. The existence of a weak solution is obtained as a limit-solution of a fully quantum regularised problem. Numerical simulations show that the viscous term contributes to limiting spurious oscillations on the boundary. However, a stationary one-dimensional model like the one discussed here cannot fully describe the complexity of the phenomenon under analysis. Further studies involving two-dimensional and time-dependent models are still in progress.

Acknowledgments

Bruno Rubino has been partially funded by the European Union - NextGenerationEU under the Italian Ministry of University and Research (MUR) National Centre for HPC, Big Data and Quantum Computing CN 00000013 - CUP: E13C22001000006.

Conflict of interest

The authors declare no conflicts of interest.