1.
Introduction
The term "flocking" refers to a phenomenon in which agents governed by an interacting many-body system converge at the same velocity while forming an appropriate group based on limited environmental information and simple laws. Flocking behaviors are ubiquitous in complex ecosystems. Examples include the flocks of birds, fish, sheep, spectators at sport events and the platooning of automated vehicles. Many mathematical models have been proposed in the mathematics community to describe flocking. Among them, the Cucker–Smale (CS) model introduced in [14] is a successful mathematical model representing flocking. The CS model is a Newtonian second-order system in terms of position-velocity, which is given by the following Cauchy problem concerning {(xi,vi)}Ni=1:
where N and ‖⋅‖ denote the number of agents and the standard Euclidean l2-norm, respectively, and we set R+:=[0,∞) throughout the paper. In addition, ϕ:R+→R+ is a communication weight satisfying the following conditions:
Due to the suitable dissipative structure regarding velocity in (1.1)2, the CS model and its variants have been actively studied from various perspectives. Examples include the mean-field limit [22,23], kinetic descriptions [7,25], hydrodynamic descriptions [17,27], time delay [13], stochastic analysis [8], relativistic correction [3,21], bi-cluster flocking [9], unit-speed constraint [1,10], temperature fields [16,24], collision avoidance [12] and extension to manifolds [2,4]. For the survey paper, refer to [11].
However, the literature on the CS model has only been investigated through a Markovian approach. Indeed, the behaviors of many agents (humans, animals, plants, etc.) in an ecosystem tend to be influenced by their memories and experiences, at least their short-term memory. Therefore, instead of the CS system (1.1) ignoring memory effects, we are primarily interested in studying the flocking system in a non-Markovian sense to investigate more realistic flocking mathematically. We consider the following fractional CS system by changing the usual time-derivative to the Caputo fractional derivative of order α∈(0,1):
where Dcα denotes the Caputo fractional derivative of order α∈(0,1) (see Definition 2.1).
The Caputo fractional derivative is used in memory-preserving dynamic systems because it incorporates historical information into the derivative operator, reflecting the system's dependence on past states. This feature allows for more accurate modeling of systems with memory effects, such as viscoelastic materials, biological tissues, and economic systems. The flexibility of fractional derivatives enables the capture of complex temporal behaviors and nonlinear characteristics that integer-order derivatives cannot adequately describe. Consequently, the Caputo derivative is essential for representing the intricate dynamics of various natural and engineered systems.
Because dealing with a fractional derivative is more complicated than dealing with the usual derivative, (1.2) has been less lively studied than that in (1.1) (e.g., the discrete model [18,19], the Riemann–Liouville fractional derivative under a constant communication weight [29], optimal control problems [32,33], and mono-clustser flocking dynamics under a general communication weight [20] and under general network topologies [26]).
From the mentioned literature on (1.2), the multi-cluster flocking of the system (1.2) has not yet been addressed. Multi-cluster flocking behavior is often observed in nature and human society, for example, in social opinion disagreement, animal herding invaded by predators, K-means algorithms, flight multi-formation, and groups with members with similar characteristics.
Throughout this paper, we are primarily concerned with the following problem: Under what conditions in terms of initial data and system parameters does multi-cluster flocking occur in the proposed fractional system (1.2)?
Next, we provide concept definitions for the mono-, bi- and multi-cluster flocking of the system (1.2) as follows:
Definition 1.1. (n-cluster flocking) Let Z={(xi,vi)}Ni=1 be the solution of (1.2).
(1) The configuration Z exhibits n-cluster flocking behavior if there exist n-cluster groups Zβ={(xβi,vβi)}Nβi=1 such that the following assertions hold:
(2) The configuration Z exhibits mono-cluster flocking when n=1, bi-cluster flocking when n=2, and multi-cluster flocking when n≥3.
The rest of the paper is organized as follows: In Section 2, we briefly introduce basic materials to be used in Section 3 and Section 4 based on fractional calculus and present several basic estimates for (1.2). In Section 3, we study a sufficient framework guaranteeing the bi-cluster flocking of (1.2). In Section 4, we demonstrate a sufficient framework for the multi-cluster flocking of (1.2). In Section 5, we provide several numerical simulations and compare them with the analytical results. Finally, Section 6 is devoted to a brief summary of the main results and some discussion on the remaining issues to be investigated in future work.
Notation. We employ the following notations for concision:
2.
Preliminaries
In this section, we revisit basic materials for fractional calculus to be crucially employed in Sections 3 and 4. Subsequently, we present two preliminary lemmas to study the bi- and multi-cluster flocking of the proposed fractional system (1.2).
2.1. Fractional calculus
In this subsection, we briefly introduce basic concepts and the backgrounds based on fractional calculus, beginning with defining the Caputo fractional derivative.
Definition 2.1 (Caputo derivative). [31] For α∈(0,∞), if the right sides are well defined, the Caputo fractional derivative Dcαf of order α is defined as
Next, we recall the gamma function and beta function as follows:
Definition 2.2 (Gamma and beta functions). Let C and Z≤0 be the set of complex numbers and the set of nonpositive integers, respectively and let Re(w) be the real part of w∈C. The gamma function Γ=Γ(z) for z∈C and beta function B=B(z,w) for Re(z)>0 and Re(w)>0 are given by
(1) (Gamma function) Γ(z):=∫∞0e−ttz−1dt,z∈C.
(2) (Beta function) B(z,w):=∫10tz−1(1−t)w−1dt, for Re(z),Re(w)>0.
Thus, the following basic properties hold for Γ and B:
Remark 2.1. (Basic properties for Γ and B)
(1) Γ(1)=1,Γ(n)=(n−1)!for all positive integer n,Γ(z+1)=zΓ(z).
(2) B is symmetric, i.e., B(z,w)=B(w,z), B(z,w)=Γ(z)Γ(w)Γ(z+w).
The following text provides the basic concepts and essential relations for the Mittag-Leffler function. This function is often employed when addressing the convergence analysis of fractional ordinary differential equations, especially when deriving bi- and multi-flocking estimates.
Definition 2.3 (Mittag-Leffler function). For given α,β∈C, the Mittag-Leffler function, denoted by Eα,β, is defined as
Proposition 2.1 (Basic facts (Ⅰ)). [20,31] For α,β,γ∈C, one has the following assertions:
(1) Eα,β(z)=zEα,α+β(z)+1Γ(β).
(2) For β,γ>0 and α,λ∈C,
(3) For α,y,z∈C, and β,γ>0,
The proposition below guarantees that the flocking estimates for Eα,β(⋅) that we obtain later are related to an algebraic decay rate.
Proposition 2.2 (Basic facts (Ⅱ)). [20,31] Suppose that α,β and γ satisfy
Let N be the set of all natural numbers. Then, we have the following relations for n∈N:
(1) For |arg(z)|≤γ,
(2) For γ≤|arg(z)|≤π,
(3) As a direct consequence of (2),
Subsequently, we define "completely monotone" to treat the fractional Caputo derivative of order α∈(0,1) in more detail.
Definition 2.4 (Completely monotone). [30] A C∞-function f is completely monotone if
In addition, every completely monotone function is always nonnegative, monotonically decreasing, and convex.
Next, we present a previous result regarding the necessary and sufficient conditions for Eα,β(−t) to be completely monotone.
Proposition 2.3 (Complete monotonicity of Eα,β(−t)).[34] The term Eα,β(−t) is completely monotone on t∈R+−{0} if and only if α∈(0,1] and β≥α.
Next, for α∈(0,1) and T>0, we consider
Then, (2.1) can be transformed into the following integral equation when f is continuous:
For a constant matrix A∈Rd×d and f(t,x(t))=Ax(t)+y(t), (2.1) is written as
In this case, under the appropriate conditions for y(t), a unique solution x(t) exists on [0,T]. Moreover, the solution can be expressed in a more specific form than (2.2).
Proposition 2.4 (Solution of (2.3)). [5,20] Let x(t) be the solution of (2.3) of order α∈(0,1) and let y(t) be an element of a space C1−α([0,T]), where C1−α([0,T]) is given by
Then, the solution of (2.3) uniquely exists and is expressed by
where Eα,β(A) is defined as
In the sequel, we briefly describe the Cauchy–Lipschitz theory for the fractional ODE of order α∈(0,1] as follows:
Proposition 2.5 (Cauchy–Lipschitz theory for a fractional ODE). [6] We consider the following fractional ODE system of order α∈(0,1]:
If f is locally Lipschitz continuous in x and continuous in t, then for some strictly positive number ϵ, there exists a unique solution x(t) of (2.4) on the interval [t0−ϵ,t0+ϵ].
Finally, we state the comparison principle for the fractional ODE system (2.1).
Proposition 2.6 (Comparison principle for a fractional ODE). [28] Suppose that f(t,x) and F(t,x) are two continuous functions defined on G:=[0,T]×R satisfying
Next, assume that x=ψ(t) and x=ϕ(t) are the solutions of the following initial value problem for α∈(0,1):
(1) Dαcx(t)=f(t,x(t)),x(0)=x0,
(2) Dαcx(t)=F(t,x(t)),x(0)=x0, respectively.
Then, we have
For readers interested in several relations between the monotone function and the sign change of its Caputo derivative, we recommend [15].
2.2. Preparatory lemmas
In this subsection, we estimate the uniform boundedness of ‖V‖ in terms of the initial data motivated by the arguments employed in [20] and offer the previous lemma proven in [16]. First, we define the following functional:
where δij denotes the Kronecker delta, and for simplicity, we set the following throughout the paper:
Then, it is straightforward to check that, for i,j∈[N], the functional Ψij satisfies
In the following text, we convert (1.2) into a matrix formulation in terms of X, V and the system parameters using the above functional Ψij, as follows:
where Φ(X(t))∈RN×N is given by
Then, combining (2.5) and Proposition 2.4 results in
Next, we consider the following recurrence relation {V(i)}∞i=0 based on (2.6):
We observe that, for t∈R+,
where ‖⋅‖op denotes the operator norm of a matrix. Because Ψij≥0 and ∑Nj=1Ψij=1, we derive
Hence, we prove that ‖V‖ is uniformly bounded by ‖V(0)‖ from the above frameworks.
Lemma 2.1 (Uniform boundedness of ‖V‖). In the recurrence relation (2.7), the following assertion holds for i∈N∪{0}:
Furthermore, if V is the solution of (2.5), we also demonstrate that, for t∈R+,
Proof. We employ an inductive argument to verify the assertion.
● (The case ofi=0): Definition 2.3 and (2.7) yield that
Therefore, we reach the desired assertion when i=0.
● (The case ofi>0): We assume that the assertion holds for k≤i, where k∈N∪{0}. Then, the inductive assumption, (2.7), (2.8), and Definition 2.3 imply that
From the beta function (see Definition 2.2) and the second assertion of Remark 2.1, we immediately have that for z, w\in\mathbb{C} satisfying {\rm{Re}}(z) > 0 and {\rm{Re}}(w) > 0 ,
and we obtain
Thus, we combine (2.9) and (2.10) to attain the desired assertion. Subsequently, we estimate from (2.10), Definition 2.3, Proposition 2.3, and (2.8) that
The outcome induces that \{V^{(i)}\}_{i = 0}^\infty is a Cauchy sequence, and if we set V^\infty: = \lim_{i\to\infty}V^{(i)} , then V^\infty is the unique solution of (2.6) (i.e., V = V^\infty ). Therefore, the desired lemma holds due to
□
Moreover, we introduce the following crucial lemma to investigate the velocity alignment estimate in terms of D_V in (1.2):
Lemma 2.2 (Key estimate). [16] Assume that A\in\mathbb{R}^{N\times N} is a nonnegative stochastic matrix (\mathit{\text{i.e.}}, \; A_{ij}\geq 0 and \sum_{j = 1}^N A_{ij} = 1 for i, j\in [N]) and Z, W\in\mathbb{R}^{N\times d} are matrices satisfying
Then, it follows that
where \mu(A) denotes the ergodicity coefficient of A\in \mathbb{R}^{N\times N} defined by
and we set
3.
Bi-cluster flocking dynamics
In this section, we demonstrate the bi-cluster flocking of the fractional system (1.2) under admissible data in terms of the initial data and system parameters. For this, we reorganize (1.2) to discriminate two cluster groups Z_1 = \{(x_{1i}, v_{1i})\}_{i = 1}^{N_1} and Z_2 = \{(x_{2j}, v_{2j})\}_{j = 1}^{N_2} from each other, where N_1+N_2 = N and N_1, N_2\geq 1 , as follows:
3.1. Sufficient frameworks
In this subsection, we present several sufficient frameworks for the bi-cluster flocking of (3.1) and employ notation for simplicity. First, we set the following deviations and averages for position-velocity: For i\in [N_1] and j\in [N_2] ,
● (Position averages and deviations)
● (Velocity averages and deviations)
Then, we define the configuration vectors for each cluster group by
● (Configuration vectors for each cluster group)
Moreover, we set
● (Reordering of configuration vectors)
Similarly, we let
● (Configuration vectors for the deviation of each cluster group)
and
● (Configuration vectors for deviation)
Next, we define \Delta_v as
where a^k denotes the k -th component of a\in \mathbb{R}^d . The functional \Delta_v measures the difference between velocity averages in the two cluster groups Z_1 and Z_2 .
Subsequently, we obtain basic estimates concerning the mentioned notation as follows:
Lemma 3.1 (Basic estimate). Suppose that (X, V) is the solution of the fractional system (3.1). Then, the following relations hold for t\in \mathbb{R}_+ :
Proof. To prove the first assertion, from \sum_{i = 1}^{N_1}(v_{1i}-v_{1cen}) = 0 , we get
Likewise, one has
□
In what follows, we reinterpret the bi-cluster fractional system (3.1) in terms of position–velocity averages to later estimate \Delta_v^k and the rate at which the bi-cluster formation occurs.
Lemma 3.2 (Fractional systems for averages and deviations). Let (X, V) be the solution of the system (3.1). Then, (x_{1cen}, v_{1cen}) , (x_{2cen}, v_{2cen}) , (\hat{x}_{1i}, \hat{v}_{1i}) , and (\hat{x}_{2j}, \hat{v}_{2j}) satisfy
and
Proof. We take \sum_{i = 1}^{N_1} and \sum_{j = 1}^{N_2} in (3.1)_2 and (3.1)_3 , respectively, and then use the standard technique of interchanging i(j) and k and dividing by 2 to these, respectively, to reach the desired first equation. To get the second equation, we use (3.1) and the definitions of \hat{x}_{1i} , \hat{v}_{1i} , \hat{x}_{2j} , and \hat{v}_{2j} . □
In the following, we define position-velocity diameters for each cluster group as follows:
● (The position-velocity diameter of each cluster group)
In addition, we set
● (Total position-velocity diameter)
Before we end this subsection, we provide several sufficient frameworks concerning the initial data and system parameters to derive the bi-cluster flocking estimate of the fractional system (3.1). Now, we display the admissible set (\mathcal {F}) as follows:
\diamond (\mathcal{F}_1)\; (\text{Separated initial data}) : For some k\in [d] , there is a nonnegative number r_0 satisfying that initial position configurations are selected to be split suitably as below:
\diamond (\mathcal{F}_2)\; (\text{Assumption for group formation}) : There exists a nonnegative number D_X^\infty\geq 0 such that
\diamond (\mathcal{F}_3)\; (\text{Closeness to the bi-cluster}) : The initial data are in a formation state close to the bi-cluster as follows: For \beta\in [2] ,
Herein, we briefly comment on the described sufficient framework (\mathcal {F}) . In (\mathcal {F}_1) , the initial positions of the two clusters Z_1 and Z_2 are sufficiently far apart to attain the desired bi-cluster flocking. In addition, (\mathcal {F}_2) is the condition ensuring the group formation of each cluster group, and (\mathcal {F}_3) is the condition that the initial state of (3.1) is close to a bi-cluster. Finally, we notice that (\mathcal {F}) is not empty when we take a sufficiently large r_0 and appropriate initial data and system parameters, for instance, \phi with a compact support or an exponential decay rate, etc.
3.2. Bi-cluster flocking estimate
In this subsection, we verify the bi-cluster flocking of (3.1) under the sufficient framework (\mathcal {F}) . To do this, we begin with demonstrating that the distance between two cluster groups is greater than some function proportional to t^\alpha for t\in \mathbb{R}_+ . Throughout this subsection, we define the following:
Lemma 3.3 (Estimate for D_\alpha^c(\Delta_v^k(t)) ). Suppose that (X, V) is the solution of (3.1). Then, it follows that, for t\in \mathbb{R}_+ ,
Proof. By Lemma 3.2, we have
Then, we employ Cauchy–Schwarz's inequality and Lemma 2.1 to find
Thus, we conclude the desired lemma. □
Next, we set
S_1^*: = \sup S_1 and
S^*: = \sup S . From (\mathcal{F}_2) and the continuity of D_X , we observe that S_1\neq \emptyset and S_1^*\in (0, \infty] . In addition, since (\mathcal{F}_1) yields that
and \min_{i\in [N_1], j\in [N_2]}\|x_{1i}-x_{2j}\| is continuous, we can obtain that S\neq \emptyset and S^*\in (0, S_1^*] .
Subsequently, for \beta\in [2] , let
and we employ the following functional:
Then, it is straightforward to check that
Based on the recurrence Eq (2.7) and motivated by the second assertion of Lemma 3.2 with the definitions of \Psi_{\beta ij} , \hat{V}_1 and \hat{V}_2 , we consider the following recurrence relation with respect to \{\hat{V}_\beta^{(i)}\}_{i = 0}^\infty for \beta\in [2] :
where \hat{V}_\beta^{(i)}(s)\in \mathbb{R}^{N_\beta\times d} and \Phi_\beta(X(s))\in \mathbb{R}^{N_\beta\times N_\beta} are given by
Furthermore, \hat{\mathcal{R}}_\beta\big(X(s), V_\beta^{(i)}(s)\big)\in \mathbb{R}^{N_\beta\times d} is written by
and \mathcal{Q}_\beta(V^{(i)})\in \mathbb{R}^{1\times d} is defined as
Now, we study the uniform boundedness of D_{\hat{V}_1} and D_{\hat{V}_2} .
Lemma 3.4 (Estimates of D_{\hat{V}_1} and D_{\hat{V}_2} ). Assume that (X, V) is the solution of (3.1) such that (\mathcal{F}_1) – (\mathcal{F}_3) hold. Then, for \beta\in [2] and t\in [0, S^*] ,
Proof. We divide the proof into several steps.
● (Step A: Estimate of \mu(\Phi_\beta(X(s))) ) For t\in [0, S^*] , because the following assertions hold:
it follows from the definitions of the ergodicity coefficient (see Lemma 2.2) and (\Phi_\beta(X(t)))_{ij} and the monotonicity of \phi that, for t\in [0, S^*] ,
● (Step B: Recurrence relation) We take a diameter to (3.2) and apply (3.3) and Lemma 2.2 to this to get that, for t\in [0, S^*] ,
To estimate D_{\hat{\mathcal{R}}_\beta\big(X(s), V_\beta^{(i)}(s)\big)} , we note that, for j\in [N_\beta] and \gamma\neq \beta ,
where we used the proof of Lemma 2.1 to employ that
Then, D_{\hat{\mathcal{R}}_\beta\big(X(s), V_\beta^{(i)}(s)\big)} can be estimated as follows:
Thus, we combine the above relations and Proposition 2.3 to obtain that, for t\in [0, S^*] ,
From the above estimate, we construct the following recurrence relation for \{\hat{W}^{(i)}\}_{i = 0}^\infty :
In (3.5), we can immediately know that, for each i\in \mathbb{N}\cup\{0\} ,
● (Step C: Iterative method) We claim that
Proof of (3.6). We use induction to prove the desired claim.
\diamond\; (\mbox{The case of}\; i = 0) : From Definition 2.3 and (3.5), we have that
\diamond\; (\mbox{The case of}\; i > 0) : Suppose that the desired assertion holds for 0\leq k\leq i , and we obtain from (3.5) that, for i\in \mathbb{N}\cup\{0\} ,
where we applied the following relation induced by the first and third assertions of Propositions 2.1 and 2.3:
Next, if we employ the same methods as (2.9) and (2.10), then we estimate that
Hence, we reach the desired claim. □
● (Step D: Desired result) Using Lemma 2.1 and (3.6) yields that
Because
it follows from Proposition 2.3 and (\mathcal{F}_3) that, for t\in [0, S^*] ,
Finally, we conclude the desired lemma. □
From Lemmas 3.3 and 3.4, we can show that \min_{i\in [N_1], j\in [N_2]}\|x_{1i}-x_{2j}\| is greater than a function that increases proportionally to t^\alpha under (\mathcal{F}_1) – (\mathcal{F}_3) .
Lemma 3.5. [Estimate of \min_{i\in [N_1], j\in [N_2]}\|x_{1i}-x_{2j}\| ] Assume that (X(0), V(0)) satisfies (\mathcal{F}_1) – (\mathcal{F}_3) , and let (X, V) be the solution of (3.1). Then, we can derive S^* = S_1^* , which leads to
Proof. For the proof by contradiction, suppose that S^* < S_1^* . Then, we notice that
Thus, by the definition of \phi_M(t) and the monotonicity of \phi , we attain that, for t\in[0, S^*] ,
This relation and Lemme 3.3 induce that, for t\in[0, S^*] ,
If we apply Proposition 2.6 and (2.2) to the above inequality, then we can estimate that, for t\in [0, S^*] ,
Using (\mathcal{F}_3) implies that, for t\in [0, S^*] ,
Therefore, from the above outcome, (\mathcal{F}_3) , and Lemma 3.4, we deduce that, for t\in [0, S^*] ,
where we applied the below relations:
Because of the above relation, the first assertion of Remark 2.1, (\mathcal{F}_1) , (1.2)_1 , and (2.2), we reach the following inequality:
which reveals that
This results in a contradiction. Accordingly, S^* = S_1^* , and we prove the desired lemma. □
In what follows, we study the velocity alignment estimate for each cluster group based on the iterative method dealt with in Section 2.2. For \beta\in [2] , we recall
and again employ the following functional:
Then, we remind that
From the recurrence Eq (2.7) and \Psi_{\beta ij} with V_1 and V_2 defined in Section 3.1, we consider the following subrecurrence relation \{V_\beta^{(i)}\}_{i = 0}^\infty for \beta\in [2] :
where V_\beta^{(i)}(s)\in \mathbb{R}^{N_\beta\times d} , \Phi_\beta(X(s))\in \mathbb{R}^{N_\beta\times N_\beta} is given by
and \mathcal{R}_\beta\big(X(s), V_\beta^{(i)}(s)\big)\in \mathbb{R}^{N_\beta\times d} is defined by
Next, for t\in [0, S_1^*] , we note that (3.3) holds in this case as follows:
Taking a diameter to (3.8), and then applying (3.9) and Lemma 2.2 to this derives that, for t\in [0, S_1^*] ,
To estimate D_{\mathcal{R}_\beta\big(X(s), V_\beta^{(i)}(s)\big)} , we observe from (3.4) that, for j\in [N_\beta] ,
Then, D_{\mathcal{R}_\beta\big(X(s), V_\beta^{(i)}(s)\big)} can be estimated as follows:
Hence, combining the above outcomes implies that, for t\in [0, S_1^*] ,
Therefore, we have from Proposition 2.3 and Lemma 3.5 that, for t\in [0, S_1^*] ,
which leads to
Since the first and third assertions of Proposition 2.1 yield that
for t\in [0, S_1^*] , one has
Now, we investigate D_{V_\beta^{(i)}} to demonstrate the velocity alignment of each cluster group. To do this, we address the following recurrence relation in terms of \{W^{(i)}\}_{i = 0}^\infty :
In (3.14), we can easily check that, for each i\in \mathbb{N}\cup\{0\} ,
Next, we estimate |W^{(i+1)}-W^{(i)}| for each i\in \mathbb{N}\cup \{0\} to deduce the decay rate of D_{V_\beta} .
Lemma 3.6 (Estimate of |W^{(i+1)}-W^{(i)}| ). In the recurrence relation (3.14), the following assertion holds for i\in \mathbb{N}\cup\{0\} and t\in [0, S_1^*] :
Proof. We employ an inductive method to show the desired lemma.
● (\mbox{The case of}\; i = 0) : From (3.14), we directly attain that
Then, we reach the desired lemma when i = 0 .
● (\mbox{The case of}\; i > 0) : Suppose that the desired assertion holds for 0\leq k\leq i , and we note from (3.14) that, for i\in \mathbb{N}\cup\{0\} ,
We employ the inductive assumption, Proposition 2.1, Definition 2.3, and (3.13) to estimate that
where we used the same methodology as in (2.10) to the last equation. Finally, we obtain the desired lemma. □
As a direct consequence of Lemma 3.6, we verify from Lemma 2.1 and Definition 2.3 that, for t\in [0, S_1^*] ,
Moreover, we see from (3.7) that, for t\in [0, S_1^*] ,
In conclusion, we deduce that, for t\in [0, S_1^*] ,
Now, we are ready to demonstrate the bi-cluster flocking of the fractional system (3.1) by proving that S_1^* = \infty .
Theorem 3.1 (Bi-cluster flocking). Assume that (X(0), V(0)) satisfies (\mathcal{F}_1) – (\mathcal{F}_3) , and suppose that (X, V) is the solution of the system (3.1). Then, we get the following bi-cluster flocking estimate for t\in \mathbb{R}_+ :
(1) (Group formation and bi-cluster formation)
(2) (Velocity alignment)
Proof. Due to Lemma 3.5 and (3.15), it suffices to derive that S_1^* = \infty . For the proof by contradiction, suppose that S_1^* < \infty . Then, we have
Subsequently, from (2.2) and
one has
Thus, taking a diameter to the above relations leads to
and we obtain D_{X(t)}\leq D_{X(0)}+\frac{1}{\Gamma(\alpha)}\int_{0}^t \frac{D_{V(s)}}{(t-s)^{1-\alpha}} ds.
Herein, (3.15), Propositions 2.1 and 2.3 yield that
which gives that
This is contradictory to D_{X(S_1^*)} = D_X^\infty ; thus, S_1^* = \infty , and we demonstrate the desired bi-cluster flocking estimate. □
4.
Multi-cluster flocking dynamics
In this section, we obtain the multi-cluster flocking of the fractional system (1.2) under admissible data in terms of the initial data and system parameters. As in the bi-cluster system (3.1), we reformulate (1.2) to distinguish several cluster groups Z_\beta = \{(x_{\beta i}, v_{\beta i})\}_{i = 1}^{N_\beta} for \beta\in [n] from Definition 1.1, where \sum_{\beta = 1}^n N_\beta = N and N_\beta\geq 1 , as follows:
The methodology in this section is an extended version of that in Section 3, where n = 2 extends to a general n ; thus, the detailed proof and arguments are omitted.
4.1. Sufficient frameworks
In this subsection, we provide suitable sufficient frameworks guaranteeing the multi-cluster flocking of (4.1) and handy notation for brevity. Similar to Section 3.1, for \beta\in [n] , we define
● (Position averages and deviations)
● (Velocity averages and deviations)
● (Configuration vectors for each cluster group)
● (Reordering of configuration vectors)
● (Configuration vectors for the deviation of each cluster group)
● (Configuration vectors for deviation)
● (Difference between velocity averages)
● (The position-velocity diameters of each cluster group)
● (Total position-velocity diameters)
Then, we describe the following two lemmas counterparts of Lemmas 3.1 and 3.2 without the proof:
Lemma 4.1 (Basic estimate). Suppose that (X, V) is the solution of the system (4.1). Then, we get the following assertions for \beta\in [n] and t\in \mathbb{R}_+ :
Lemma 4.2 (Fractional systems for averages and deviations). Let (X, V) be the solution of the system (4.1). Then, (x_{\beta cen}, v_{\beta cen}) and (\hat{x}_{\beta i}, \hat{v}_{\beta i}) satisfy
and
Finally, we present several sufficient frameworks (\mathcal {G}) in terms of the initial data and system parameters for the multi-cluster flocking of (4.1) as follows:
\diamond (\mathcal{G}_1)\; (\text{Separated initial data}) : For some k\in [d] , there exists a nonnegative number r_0\geq 0 such that the initial position configurations are chosen to be split as follows:
\diamond (\mathcal{G}_2)\; (\text{Condition for group formation}) : There is a nonnegative number D_X^\infty\geq 0 satisfying
\diamond (\mathcal{G}_3)\; (\text{Closeness to the multi-cluster}) : The initial data are in a formation state close to the multi-cluster as follows: For \beta, \gamma \in [n] ,
4.2. Multi-cluster flocking estimate
In this subsection, we demonstrate the multi-cluster flocking of (4.1), assuming (\mathcal {G}) . Throughout the subsection, we set the following:
Next, we prove that the distance between two distinct cluster groups is greater than some function proportional to t^\alpha . To achieve this, we provide the following lemma counterpart of Lemma 3.3:
Lemma 4.3 (Estimate of D_\alpha^c(\Delta_{v, \beta, \gamma}^k(t)) ). Let (X, V) be the solution of the system (4.1). Then, we obtain that, for \beta, \gamma \in [n] and t\in \mathbb{R}_+ ,
Proof. Employing Lemma 4.2 gives that
Thus, we attain the following estimates from Cauchy–Schwarz's inequality and Lemma 2.1:
In conclusion, we get the desired lemma. □
In what follows, as in Section 3, we consider
S_1^*: = \sup S_1 and
S^*: = \sup S . By the continuity of D_X and (\mathcal{G}_2) , one has S_1\neq \emptyset and S_1^*\in (0, \infty] . Moreover, because (\mathcal{G}_1) implies that
and \min_{i\in [N_\beta], j\in [N_\gamma]}\|x_{\beta i}-x_{\gamma j}\| is continuous, it follows that S\neq \emptyset and S^*\in (0, S_1^*] .
Then, we can obtain the same result as Lemma 3.4 on [0, S^*] .
Lemma 4.4 (Estimate of D_{\hat{V}_\beta} ). Assume that (X(0), V(0)) satisfies (\mathcal{G}_1) – (\mathcal{G}_3) , and suppose that (X, V) is the solution of (4.1). Then, for \beta\in [n] and t\in [0, S^*] ,
Proof. We omit this proof because it is similar to the proof of Lemma 3.4. □
In the same manner as the proof of Lemma 3.5, when the three frameworks (\mathcal{G}_1) – (\mathcal{G}_3) are assumed, we verify that for \beta\neq \gamma , \min_{i\in [N_\beta], j\in [N_\gamma]}\|x_{\beta i}-x_{\gamma j}\| is greater than a function that increases proportionally to t^\alpha , as follows:
Lemma 4.5. [Estimate of \min_{i\in [N_\beta], j\in [N_\gamma]}\|x_{\beta i}-x_{\gamma j}\| ] Suppose that (X(0), V(0)) satisfies (\mathcal{G}_1) – (\mathcal{G}_3) , and let (X, V) be the solution of (4.1). Then, S^* = S_1^* holds, which asserts that
To derive the velocity alignment estimate concerning each cluster group based on the iterative method, we extend (3.8) to the multi-cluster setting. For this, for \beta\in [n] , we let
and set the following functional:
Then, we immediately have that
Similar to the construction of (3.8), we consider a subrecurrence relation \{V_\beta^{(i)}\}_{i = 0}^\infty for \beta\in [n] , as follows:
where V_\beta^{(i)}(s)\in \mathbb{R}^{N_\beta\times d} , and \Phi_\beta(X(s))\in \mathbb{R}^{N_\beta\times N_\beta} is given by
and \mathcal{R}_\beta\big(X(s), V_\beta^{(i)}(s)\big)\in \mathbb{R}^{N_\beta\times d} is written by
Subsequently, as in (3.9), it is easy to check that, for \beta\in[n] and t\in [0, S_1^*] ,
Hence, if we take a diameter to (4.3) and apply (4.4) and Lemma 2.2 to this, we reach that, for t\in [0, S_1^*] ,
where D_{\mathcal{R}_\beta\big(X(s), V_\beta^{(i)}(s)\big)} can be estimated as follows, with the same argument as that for (3.10):
Accordingly, under the frameworks (\mathcal{G}_1) – (\mathcal{G}_3) , using (3.13), (4.2), and the same methodologies employed in (3.11) and (3.12), we induce that, for t\in [0, S_1^*] ,
In the sequel, we consider the following recurrence relation concerning \{W^{(i)}\}_{i = 0}^\infty to study the velocity alignment estimate of (4.1):
Herein, we crucially notice that for each i\in \mathbb{N}\cup\{0\} , D_{V_\beta^{(i)}}\leq W^{(i)} .
Then, as in the proof of Lemma 3.6, the inductive argument yields a relation regarding |W^{(i+1)}-W^{(i)}| for i\in [N] as below:
Lemma 4.6 (Estimate for |W^{(i+1)}-W^{(i)}| ). In the recurrence relation (4.5), the following assertions hold for i\in \mathbb{N}\cup\{0\} and t\in [0, S_1^*] :
Therefore, due to (3.7) and Lemma 3.6, it follows from Lemma 2.1 and Definition 2.3 that, for t\in [0, S_1^*] ,
which implies that, for t\in [0, S_1^*] ,
Finally, we prove the multi-cluster flocking of the system (4.1) under (\mathcal{G}_1) – (\mathcal{G}_3) .
Theorem 4.1 (Multi-cluster flocking). Suppose that (X(0), V(0)) satisfies (\mathcal{G}_1) – (\mathcal{G}_3) , and assume that (X, V) is the solution of (4.1). Then, the following multi-cluster flocking estimate holds for t\in \mathbb{R}_+ :
(1) (Group formation and multi-cluster formation)
(2) (Velocity alignment)
Proof. By Lemma 4.5 and (4.6), it suffices to demonstrate that S_1^* = \infty . For the proof by contradiction, suppose that S_1^* < \infty . Then,
Similar to the proof of Theorem 3.1, one has
Moreover, based on the arguments employed in (3.16), we can derive from (4.6), Propositions 2.1 and 2.3 that, for t\in [0, S_1^*] ,
This causes a contradiction to D_{X(S_1^*)} = D_X^\infty . Eventually, S_1^* = \infty , and we conclude the desired multi-cluster flocking of (4.1). □
5.
Numerical simulations
In this section, we present several numerical descriptions using the Grunwald–Letnikov approximation to compare with the analytical result of Theorem 4.1. For all simulations, we set
and choose the below communication weight:
Then, we select the following initial data satisfying
and consider the 3 -cluster groups as follows:
where we denote
Subsequently, we now briefly check that the above initial data and system parameters satisfy the sufficient framework (\mathcal{G}_1) – (\mathcal{G}_3) addressed in Section 4. To do this, we observe through direct calculation that
Hence, it remains to verify the framework (\mathcal{G}_2) - (\mathcal{G}_3) . When using the Python code, it follows that the following relations hold:
Therefore, it is straightforward to see that (\mathcal{G}_2) is satisfied because one has
Furthermore, we can show that (\mathcal{G}_3) is satisfied due to for \beta, \gamma \in [3] ,
and for \beta\in [3] ,
Next, we describe several numerical results concerning the multi-cluster flocking result studied in Theorem 4.1.
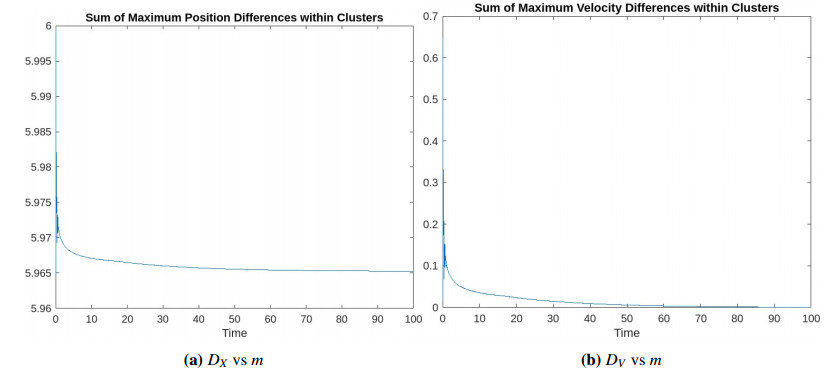
First, Figure 1 shows the emergence of multi-cluster flocking, substantiating the analytical results of Theorem 4.1. Second, Figure 2 illustrates the emergence of multi-cluster formation, validating the analytical results of Theorem 4.1. In particular, Figure 2(B) indicates that
tends to increase as a constant multiple of t^{0.5} .
6.
Conclusions
In this paper, we have studied the multi-cluster flocking of the fractional CS model with the Caputo fractional derivative. In the proposed fractional system, we offered appropriate admissible data consisting of well-separated initial data, well-prepared system parameters, and a communication weight satisfying suitable conditions to demonstrate the desired multi-cluster flocking. Afterward, we observed that multi-cluster flocking does not rapidly occur, unlike exponential decay. The rate of occurrence depends on the algebraic decay rate and communication weight. However, we are unsatisfied with the current results and still have some topics to explore in future research. Examples include the mean-field limit (i.e., N\to \infty ), extension to the Riemannian manifold, and collision avoidance of the fractional CS system. We leave these issues as future work.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The work of H. Ahn was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (2022R1C12007321).
Conflict of interest
The author declares no conflict of interest.









 DownLoad:
DownLoad:




