Conditional stability for an inverse source problem and an application to the estimation of air dose rate of radioactive substances by drone data

1.   Motivation

The Fukushima Daiichi Nuclear Disaster in March 2011 has released radioactive substances such as cesium-137 into environments. In particular, radioactive substances fall on the ground and some of them diffuses in the soil. These radioactive substances are a source and generate the air dose rate of radiation, which can be considerd as influences to inhabitants. Possible sources for such air dose rates and possible sources are in the air and on the ground, in the underground. The sources in the air could be created by floating radioactive substances, but we can assume that such sources in the air can be neglected after 9 years passed after the disaster in 2011 and the susbstances have sufficiently diffused in the air to a very low level. Thus we assume that the air dose rates can be generated by sources on the ground and the underground. As for related works on the several kinds of sources, we refer to Malins et al.^[8] and Saito ^[9] for example.

Moreover these substances on and in the ground can move for example by refloating on dry days and may run-off into rivers, so that the sources may not be stationary. However for a feasible model, we can assume that we can neglect also the time change of sources. In some areas of Fukushima prefecture, inhabitants have already returned to daily lives, and the estimation of the air dose rate of radioactive substances in towns and villages is crucial for the sake of the health of them. The air dose rate at the human height level (e.g., 1m) is considered as very influential factor to the health through exposures by breathing the air. The observation of air dose rates can be done by drones containing measurement equipments. However direct observations of air dose rates at the human height level is not realistic because of many obstacles against the flights of drones such as houses and other many artificial structures such as walls. Moreover we do not a priori know the source, that is, the density disribution of radioactive substances on the ground and in the shallow underground. Thus, not knowing sources themselves, we can observe only data at higher altitude (e.g., 30–50 m).

Therefore our task is an inverse problem where we are required to determine the dose rate at the human height level by means of high-altitude data. This motivates our theoretical research for the correponding inverse problem and our theoretical result shows not bad stability under adequate conditions and suggests how to control flight orbits for a reasonable accuracy in solving an inverse problem.

2.   Mathematical model and the main result.

We describe a mathematical model, by which we can discuss our inverse problem from a general point of view.

Let $D \subset \mathbb{R}^3$ be an open domain. Henceforth we set $x = (x_1, x_2, x_3)$, $y = (y_1, y_2, y_3)$ and

We set

Here $4\pi\mu(y)$, $y \in D$ describes the density of e.g., radioactive substances. We consider $f(x)$ as the air dose rate at $x\in \mathbb{R}^3$. For an arbirarily fixed constant $M > 0$, we set

Let $\gamma, \Gamma_1 \subset \mathbb{R}^3$ be sets and $\overline{\gamma} \cap \overline{\Gamma_1} = \emptyset$.

Our inverse problem is: determine $f\vert_{\Gamma_1}$ by $f\vert_{\gamma}$.

Here we note that we assume $\mu\in \mathcal{M}$ but we do not know $\mu$.

Example: Taking into consideration the observation by drones, we choose curves $\Gamma_1, \gamma$ on the same curve $\Gamma$ which is an orbit of a drone. For example, we choose two segments $\gamma$ and $\Gamma_1$. Let $x_3 = 0$ and $x_3 > 0$ correspond to the flat ground and the underground respectively. Let $\widetilde{D} \subset \mathbb{R}^3$ be an open domain such that $\widetilde{D} \cap \{ x_3 < 0\} \ne \emptyset$. Then we set $D = \widetilde{D} \cap \{ x_3 < 0\}$. In particular, the case of $\widetilde{D} \subset \{0 < x_3 < \delta\}$ with small $\delta > 0$ and $\mu \ne 0$ in $D$, means that the substances concentrate on the ground and the shallow underground. Let $(a, b) \in \mathbb{R}^2$ be a fixed planar location and $\delta < h_1 < h_2 < H_1 < H_2$ and

This setting describes that we are requested to determine the dose rate at the heights $h_1 \sim h_2$ by high-altitude data at $H_1\sim H_2$.

Let $L$ be an infinite straight line and let $\Gamma$ be a connected component of $L \cap E$. For an arbitrarily fixed $\delta > 0$, we set

Theorem. Let $\gamma, \Gamma_1 \subset \Gamma$ be finite segments on $\Gamma$ such that $\overline{\gamma} \cap \overline{\Gamma_1} = \emptyset$. We assume that

Then there exist constants $C > 0$ and $\theta \in (0, 1)$ such that

Here $C > 0$ depends on $\frac{M}{\delta^2}$, $\gamma, \Gamma_1$, and $\theta$ depends only on $\gamma, \Gamma_1$.

We can expect that $\theta$ is smaller when dist $(\gamma, \Gamma_1)$ is larger. The theorem implies the uniqueness, that is, if $f = 0$ on $\gamma$, then $f = 0$ on $\Gamma_1$.

As can be seen by the proof in Section 3, data $f$ on $\gamma$ cannot give any information of $f$ outside of the straight line $L$ where $\gamma$ and $\Gamma_1$ are included. In other words, we can determine $f$ only in the extended direction of $\gamma$ by data on $\gamma$, provided that the extended segment is in $E$. In particular, we assume that $0 < \delta < h_1 < h_2 < H_1 < H_2$ and recall (2.2). Then $\gamma, \Gamma_1 \subset \Gamma: = (\delta, \infty)$. The theorem asserts a stability estimate of Hölder type in determining $f(x)$, $x\in \Gamma_1$ by $f(x)$, $x \in \gamma$, and the Hölder exponent $\theta$ depends only on a geometric configuration of the two segments $\gamma$ and $\Gamma_1$. Our main theorem guarantees a rather good rate of the stability when we use drone data at high-altitude for determining the dose rate at lower-level.

Here we do not discuss the determination of the source $\mu(x)$ itself, and we do not know whether we can extract some information of $\mu$ from $f\vert_{\gamma}$. On the other hand, as data we choose $f$ in a domain $D_1 \subset \mathbb{R}^3$ such that $\overline{D \cap D_1} = \emptyset$, and Cheng et al. ^[2] proves some stability for an inverse problem of determining $\mu\vert_{D}$ by $f\vert_{D_1}$ which are not data on a segment. The stability is conditional under assumption that unknown $\mu$ satisfies (2.3) and is of logarithmic rate which is much weaker than (2.4). We emphasize that data $f$ on $\gamma$ cannot determine the source $\mu$ but can determine $f$ on $\Gamma$ with Hölder stability rate which is much better than the logarithmic rate.

3.   Proof of Theorem

The proof is based on a harmonic extension of $f$ and the line unique continuation for a harmonic function.

First Step: harmonic extension of $f$.

We recall $E = \{x\in \mathbb{R}^3;\, \mbox{dist}\, (x, D) > \delta\}$ with arbitrarily fixed $\delta > 0$. We set

We can directly verify

Clearly

which means that $G$ is a harmonic extension of $f$.

We note that the harmonic extension $G$ defined by (3.1) is applied for the determination of $\mu$ (e.g., Cheng et al. ^[2], Cheng and Yamamoto ^[4]).

Second Step: line unique contination.

The following line unique continuation is a key, which is proved as Theorem 2.1 in Cheng et al. ^[1]: Theorem 0. Let $\Omega \subset \mathbb{R}^n$, $n\ge 3$ be a domain and a straight line $L$ intersect $\partial\Omega$ at two points such that $\Gamma = L \cap \Omega$ is a segment. Moreover we assume that two segments $\gamma, \Gamma_1$ satisfy $\gamma \subset \Gamma_1 \subset \overline{\Gamma_1} \subset \Gamma$ and $\overline{\Gamma_1}\ne \Gamma$. Let $u \in C^2(\Omega)$ satisfy $\Delta u = 0$ in $\Omega$. If $\Vert u\Vert_{C(\overline{\Omega})} \le M$ with some constant $M > 0$, then there exist constants $C > 0$ and $\theta\in (0, 1)$ such that

Here the constant $C > 0$ depends on $M, \gamma, \Gamma_1$, while $\theta\in (0, 1)$ depends on $\gamma$ and $\Gamma_1$.

For the two dimensional case, see Cheng and Yamamoto ^[3].

We set

Then $\widetilde{\Gamma}, \widetilde{\gamma}, \widetilde{\Gamma_1} \subset E\times \{0\}$ are lines. Moreover for any $\mu \in \mathcal{M}$, we can estimate

In view of (3.3), we apply Theorem 0 where we replace $\Gamma_1, \gamma, \Gamma, M$ by $\widetilde{\Gamma_1}, \widetilde{\gamma}, \widetilde{\Gamma}, \frac{M}{\delta^2}$ respectively, so that we can choose constants $C = C\left(\frac{M}{\delta^2}, \gamma, \Gamma_1 \right) > 0$ and $\theta = \theta(\gamma, \Gamma_1)\in (0, 1)$ such that

that is,

by (3.2). Thus the proof is complete.

4.   Numerical examples

In the numerical computation, we here propose a method via the determination of $\mu(x)$. More precisely, we choose $\{p_1, p_2, ..., p_M\}\subset \gamma\subset\mathbb{R}^3$ and $\{q_1, q_2, ..., q_N\}\subset D\subset\mathbb{R}^3$ as collocation points, and construct the matrix $\mathbf{A} = [A_{ij}]$ as $A_{ij} = w_j/r^2_{p_iq_j}$ where $w_j$ are the volume integral coefficients, i.e.,

Then find the least-norm solution $\tilde{\mu}$ to the equation $\mathbf{A}\tilde{\mu} = \mathbf{b}$, where $\mathbf{b} = (f(p_1), ..., f(p_M))$. Taking into consideration observation data $f_{meas}$ with errors, the Tikhonov regularization is adopted and $\tilde{\mu}$ is then the minimizer to the cost functional

Here $\alpha > 0$ is a regularizing parameter which we should choose suitably according to the noise level. A discretized form is

where $l_i$ are the line integral coefficients. The regularization parameter $\alpha$ is chosen as $\alpha\sim \delta^2$, where $\delta$ is the noise level of observation data measured by the $L^2(\gamma)$-norm and we refer to Cheng and Yamamoto ^[5] as for a choice strategy of $\alpha$. The approximation solution can be constructed by $\tilde{\mu}$ as

In the following numerical examples, we assume that the source distribution has a compact support in $B: = \{x = (x_1, x_2, x_3)\in \mathbb{R}^3; \, \vert x\vert < 1, \, x_3 < 0\}$. The exact source distribution is given as $\mu(x) = (1+0.5\sin(2\pi \vert x\vert))\exp(-\vert x\vert^2) \chi_B(x)$ where $\chi_B(x)$ is the characteristic function of $B$.

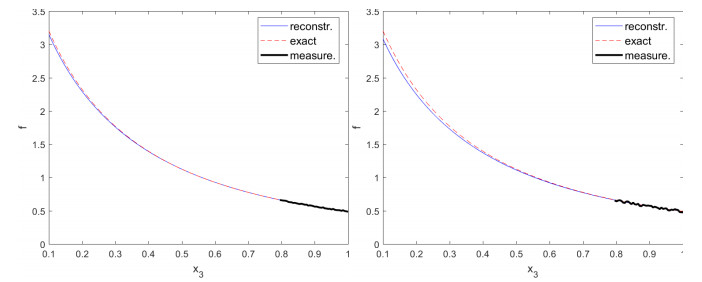
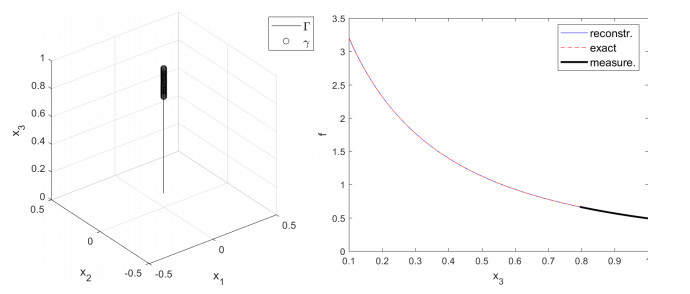
The present example is to reconstruct the dose rate along the line $\Gamma = \{0, 0, x_3\}$ with measurement on $\gamma = \{0, 0, x_3\}, x_3\in [0.8, 1]$. There are 20 uniformly distributed collocation points on the measured segment and $40\times40\times 20$ integral points in $[-1.0, 1.0]\times[-1.0, 1.0] \times[-1.0, 0]$. Figure 1 shows the comparison between the reconstructed solution and the exact solution along $\Gamma_1 = (0, 0, x_3), x_3\in [0.1, 1]$ in the case of no observation noises. The exact solution are obtained by numerical integration and the difference is less than $10^{-4}\|f\|_{C(\Gamma)}$ with finer grid resolution.

In order to further illustrate the performance of the method, a random noise is added on the exact observation. Figure 2 gives the results with observation error of level $1\%$ and $3\%$ respectively, which coincide well with the exact solution with the relative error less than $5\%$ at $x_3 = 0.1$.

5.   Conclusion

In this paper, we dicuss the estimation of air dose rates of radioactive substances at the human height level by high-altitude data by means by drone. We establish a Hölder stability estimate for this inverse problem on the basis of a mathematical model. For determination of air dose rates in more directions, the main theorem suggests that a drone orbit should include the corresponding many directions. More precisely, let $\gamma$ be a curve composed of $N$-segments $\gamma_1, ..., \gamma_N \subset E$. Let $\ell_k$, $1\le k \le N$ be the extended straight lines of $\gamma_k$ such that $\ell_k$ and $\gamma_k$ are in the same connected component of $E$. The line $\ell_k$ may be a finite segment, an infinite straight line or a half straight line. The theorem means that $f\vert_{\gamma}$ determines $f$ on $\cup_{k = 1}^N \ell_k$ uniquely. In other words, when a drone flies zigzag, drone data can determine $f$ on all the extended directions of the components of the zigzag. Moreover the stability is rather good in determining the dose rate along the orbit direction.

The key of the proof is the harmonic extension and the line unique continuation, which asserts stable continuation (3.4) of a harmonic function along the segment and is different from usual unique continuation of solutions to elliptic equations (e.g., Isakov ^[6], Lavrent'ev et al. ^[7]). The uniqueness corresponding to (3.4) can be easily proved. Indeed let $x(\tau)$ with $\tau \in J$: some open interval, be a parametrization of the straight line $\Gamma$. Since $\Delta G = 0$ in some domain $\widetilde{E} \subset \mathbb{R}^4$, the interior real analyticity of a harmonic function yields that $G$ is real analytic in $(x, \xi) \in \widetilde{E}$. This analyticity can be proved also by the representation (3.4) of $G$. Therefore $G(\tau): = G(x(\tau), 0)$ is analytic in $\tau \in J$. Consequently with some non-empty open interval $J_0 \subset J$, the unicity theorem of an analytic function implies that if $G(\tau) = 0$ for $\tau \in J_0$, then $G(\tau) = 0$ for $\tau \in J$. For more details on the line unique continuation, we refer to ^[1] and ^[3].

We give numerical examples by a method by first determining a source. Our numerical results indicated acceptably good accuracy also with noisy data. Our rather good stability can support our numerical results.

Acknowledgments

This work was partially supported by Grant-in-Aid for Scientific Research (S) 15H05740 of Japan Society for the Promotion of Science, Subsidy Program for R & D in Innovation Coast Framework, NSFC (No. 11771270, 91730303) and the "RUDN University Program 5-100". J. Cheng is supported by NSFC (No. 11941121). Most of the paper was completed during the stay of the fourth author at the Università degli Studi di Napoli Federico Ⅱ in January 2019. The authors thank the anonymous referee for the valuable comments.

Conflict of interest

The authors have no conflict of interest.