1.
Introduction
Pilonidal Sinus Disease (PSD) was previously referred to as Jeep driver disease when it was noticed amongst American soldiers driving the eponymous vehicles in World War II [1]. It is a common problem in the medical practice, affecting young-to-middle-aged males more commonly as compared to females due to the presence of excess body hair [2]. For unknown reasons, the incidence of PSD has increased steadily over the past 50 years [3],[4]. Previously, in Norwegian study it was represented at 26 per 100,000 population. A recent estimate specifies an incidence range from 0.11% for women at the university to 8.8% for Turkish soldiers. Risk factors include stiff hair, obesity, a bathroom habit of less than twice a week, and a sedentary occupation or lifestyle (i.e., sitters of more than six hours a day) [1].
Its pathophysiology is debatable as it has been commonly thought to be embryonic; however, currently it is accepted to be an acquired pathology with multiple contributing factors [5]–[7]. Due to upright body posture in sitting and standing position, the broken hair tends to accumulate in the midline in the natal cleft [2]. Hair penetrates into the skin of the gluteal cleft causes a cyst and sinus formation because of reaction to a foreign matter, leading to secondary infections and abscess formation [5]. It was notified that its incidence increased among people sitting for long hours working with computers [8]. It is unknown whether hairs (either loose or native to the region) are the primary cause of PSD or whether hair follicles become affected by the physical environment which leads to micro-abscesses and PSD [1].
Its management is surgical for more than 100 years, despite that the optimal approach remains controversial, because no method satisfies all requirements for the ideal treatment, so many reports have advocated various different approaches with different outcomes [9],[10].
We perceived that there are scarce studies that estimate the incidence of pilonidal sacrococcygeal sinus, so, the current study aimed to estimate the incidence of PSD among patients presented to surgical department, their presentation and the mode of management employed and its outcome in term of SSI, recurrence and patients' satisfaction.
2.
Material and methods
2.1. Study design
The patients in this cohort study were recruited from patients who were treated in the department of general surgery in Almikhwah General Hospital in Al-Baha southern of KSA (MGH) during the period from Jan 2014 to April 2020. Patients were divided into non complicated PS and complicated PA (abscess). Patients with recurrent disease were excluded from the study. Using a predesigned questionnaire, socio-demographic, clinical, and data concerned with diagnosis, treatment, therapeutic responses, recurrence, patient's satisfaction and overall survival were recorded. Each patient was enrolled once, even if he was seen more than once. Accordingly, a patient diagnosed as non-complicated PS and developed abscess during follow-up was included in group of patients with PA. The patients were followed up for at least two years. Recurrence is assumed as recurrence of symptoms and signs some of time after complete wound healing.
2.2. Ethics approval of research
This study was congruous with the Declaration of Helsinki for medical research. Moreover, the study design and protocol were approved by Almikhwah General Hospital Administration, as well as the Institution Human Research Ethical Committee (HREC-0030/MGH-12/2013), and patients' written informed consent was obtained before to conduct the study. Confidentiality was insured through the stages of the study by substituting patients' names with research codes and introducing data into a personal computer.
2.3. Data analysis
The collected data were dispersed in master sheet, entered computer and analysed using SPSS software, version 17 (SPSS Inc., Chicago). Descriptive data has been presented as percentage for qualitative variables, whereas the quantitative data were presented as mean and standard deviation (SD). By setting the level of significant at P value <0.05, Chi-square test was used to verify the associations between the categorical variables.
3.
Results
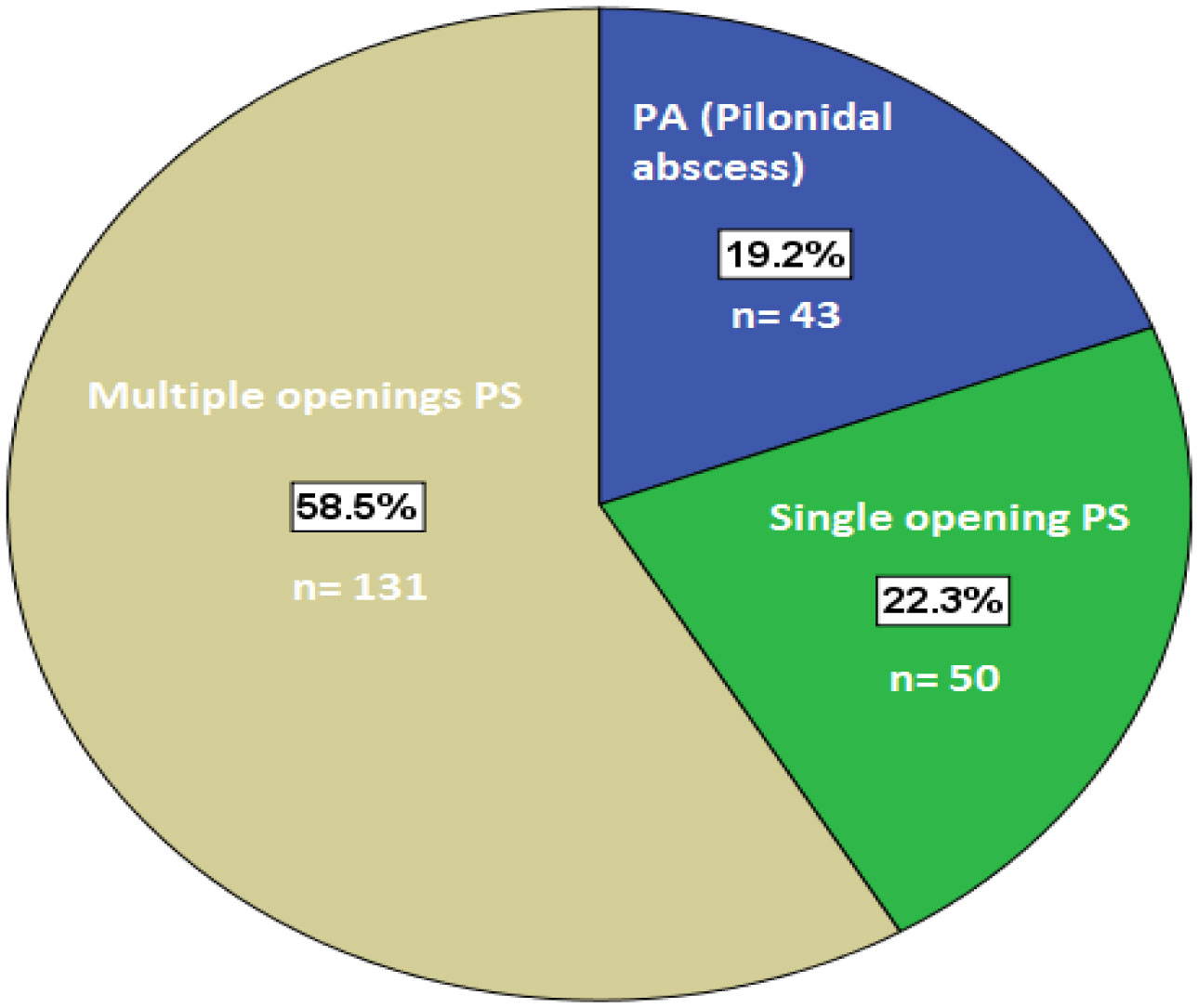
Of the 7729 of new cases registered in general surgery clinic at MGH during the study period a total of 224 patients were identified to have the diagnosis of PSD. This produced an incidence rate of 2.9% of the total surgical clinic population. Male to female ratio was 2.25:1 (male: 155, female: 69) diagnosed with PSD. Hundred eighty-one (80.8%) had PS and the remainder 43 (19.2%) had PA that treated surgically. Table 1 shows the characteristics of patients with PSD. In PS surgical modality was fashioned according to the extent of the disease and the number of sinus opening (Figure 1), whereas, all PA were managed by incision and drainage (Figure 2).
There was no any significant difference concerning duration of postoperative pain control, antibiotics usage, and patient's satisfaction, P = 0.8, P = 0.14, and P = 0.1 respectively. The main purpose of the use of analgesics was to control pain, so, it was discontinued as soon as the patient became pain free.
Patients with PS managed by primary repair (simple closure and Limberg flap) had significantly shorter recovery time when compared to patients managed by lay open method. Post-operative histopathology results returned in concordance with the primary diagnosis in all specimens.
Patients with PS were received prophylactic antibiotics perioperatively. Patients with PA were managed surgically by incision and drainage followed by a 5 days course of antibiotics and analgesics. Whereas, patients with HS were treated medically with extended 5 days of oral and topical antibiotics plus oral Diclofenac sodium if not contraindicated.
Mean hospital stay was 2.1 ± 0.83 days (range, 1 to 4), and it was shorter in the group of patients treated by lay open and primary simple closure techniques than that treated with Limberg flap, the difference was statistically significant (P = 0.002).
Surgical site infection was defined as infection at the operative site occurs within 30 days postoperatively. Whereas, recurrence was defined as the presence of persistent blood-stained or purulent discharge from the formerly operated or adjacent zone during the follow up period.
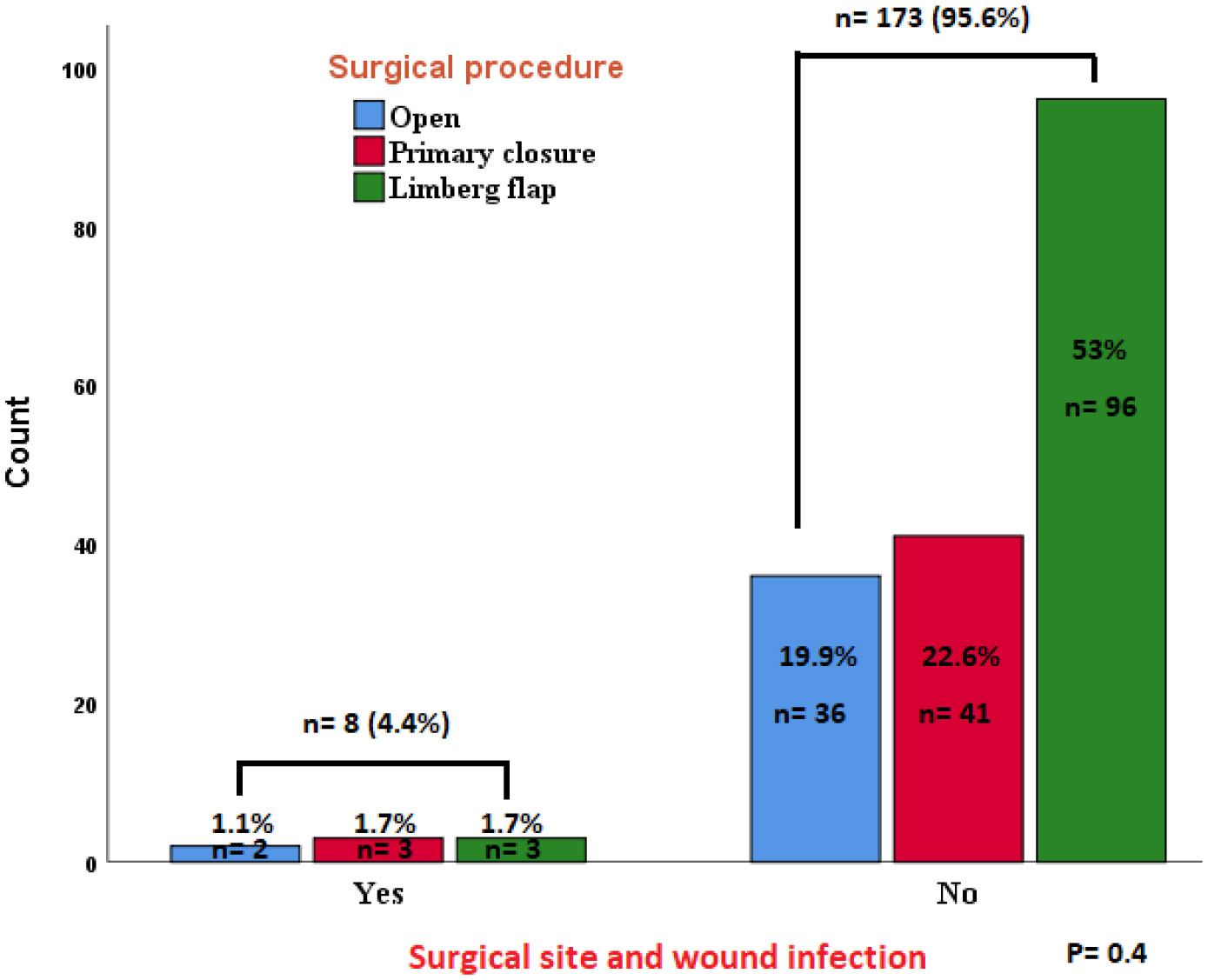
Surgical site infection was evolved in 8 (4.4%) patients (Figure 3), and its occurrence was not affected by the type of the surgical procedure (P = 0.4).
During follow up period, 16 patients had experienced recurrence of the disease with an agammaegate incidence rate of 7.1%, and there was significant difference between the groups of PS and PA (P = 0.000) as patient with PA has a tendency of recurrence. Whereas, among the group of patients with PS there was no significant difference in the recurrence rate between the type of surgery (P = 0.4) (Table 2).
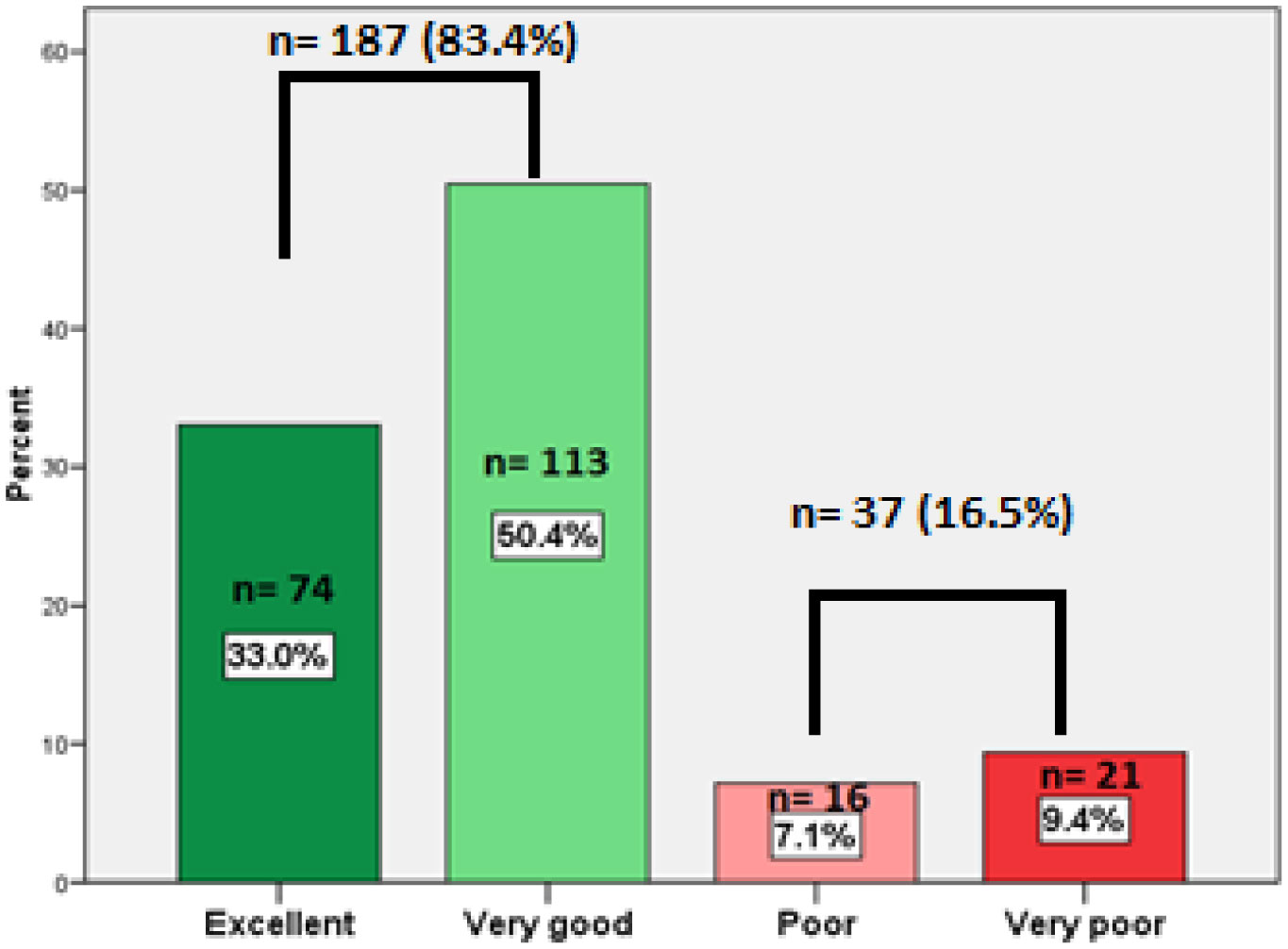
Over all patients' satisfaction was of note worth as it was very good/excellent in 187 (83.4%) as shown in Figure 4. There was co-incidence with hidradenitis suppurativa (HS) in 79 (35.3%).
Presence of HS did not affect the incidence of SSI nor recurrence as P = 0.8 and P = 0.6 respectively.
As PSD is affecting younger age groups, usually these patients had no comorbidities. Diabetes Miletus was found in only 4 patients, bronchial asthma in 3 patients whom into which receiving steroid inhaler. Presence of diabetes or Asthma did not affect the outcome as P = 0.7 and P = 0.4 respectively.
4.
Discussion
The global perception of PSD, is a simple disease concerning the pilus, but upon detailed inspection PSD is more complicated with several aspects of the disease remaining unclear [11].
There is a substantial socio-economic burden associated with this kind diseases, as it is affecting young males and having a considerable time off normal activities following surgery, together with its significant recurrence rate [12].
Its incidence is different between races, being low among Africans and Asians, and high among white people, particularly those from the Mediterranean [8]. In the current study, the incidence of PSD among presenters to surgical clinic was 2.9%. It was in conformity with the incidence estimated in the study in Turkey as it was ranging between 0.11% in women at college to 8.8% in soldiers [13].
Despite numerous publications in the past eight decades, there are still significant differences worldwide in the elective treatment of patients with pilonidal diseases [14]. Most surgeons lack experience and/or skills or interest in the treatment of pilonidal disorders. Easy extirpation by simple excision with or without a primary closure is cushy and rapid. Alternative techniques such as Limberg flaps are more complicated. In general, the operations for PSD may be delegated to juniors or the condition is not of sufficiently enough interest to many surgeons to keep up to date with the literature or learn new techniques [15].
In literature search, there is controversary on the use of prophylactic antibiotic in the surgical treatment of PSD. Several authors do not advise antibiotics in judgment of the fact that preoperative bacterial isolates usually anaerobes and do not affect the complication rate in chronic PSDs. Conversely, bacterial isolates from infected wounds after surgery are mostly aerobes [5],[16].
However, others advocate a single dose of metronidazole [5],[17]. Several studies concluded that prophylactic antibiotics seem to be unnecessary in patients undergoing the lay-open procedure, whilst antibiotic prophylaxis may be beneficial to prevent infectious complications during removal with primary closure [5],[18]. On regards, the practice of prophylactic antibiotic in current study was employed in all patients as a single preoperative dose of metronidazole and ceftriaxone. Whereas, antibiotics as a treatment was given only to patients whom treated by closure with secondary intention or those with accompanied with HS.
Herein, in the current study, the computed mean hospital stay was around 2.1 days (range, 1 to 4). This was longer than the results reported in Egypt by Awad and Saad, in which it was 1.5 days (range, 1 to 5) [19]. Conversely, it was noted shorter than the results reported by others [20]–[23].
Post-surgery, wound infection is well documented complication of pilonidal sinus, it was noted in 4.4% of patients and this was less than that reported by Al-Khayat et al. [24] and Kanlioz & Ekici [25] where the incidence of wound infection was 12.8% and 14.2% respectively.
The current study was in line with the conclusion of others as the time laps of recovery in patients underwent primary wound closure was shorter than those treated by lay open wound technique [19].
The recurrence rate has become an important parameter for evaluating the treatments' effects. In previous series, a recurrence rate between 0% and 100% had been declared for PSD, and a wide range of recurrence can also be seen even within the different surgical approach techniques [3],[23],[26],[27].
Previous studies had confirmed the links between the recurrence PDS and the length of the follow up period [3]. Dependent on the type of surgical procedure in patients with PS, recurrence rate in this study was 1.4%, but when including PA this will rise to 7.1%, it is comparable to the findings of other where the incidence of recurrence of 7–56% have been reported by Mustafi and Engels [28], as well as 13.3% that reported by Kayaalp and colleagues [29].
Recurrence of the disease is likely to affect long-term patient satisfaction after PSD surgery. In the current study patients' satisfaction was of note worth as it was very good/excellent in 83.4%. This was in concomitant with the short hospitalization, short term of analgesics usage, low incidence of postoperative surgical site infection, and low recurrence rate observed in the study.
5.
Conclusions
The pilonidal sinus is a disease that needs frequent and detailed examination since it affects the younger population and its treatment is usually associated with an economic burden. In this respect, we are of the opinion that estimating its incidence, making it preventable disease and minimizing recurrences are crucial major steps to improve patients' quality of life in our locality.
Pilonidal sinus disease is best dealt with under the umbrella of interested surgeons. Emergency treatment of pilonidal abscess should primarily consist of midline incision and drainage with subsequent arrangement for elective surgical excision. Many techniques for elective surgical management of pilonidal disease are classified basically into two groups: total excision of the sinus followed by either leaving the wound open for secondary healing or its primary closure with techniques ranging from simple suturing to complex method for coverage with Limberg flap.
Management by means of primary repair technique (Limberg flap or simple closure) had recovery time significantly shorter compared to patients managed by secondary healing. Thence, treatment of PS with primary repair is advisable. Patient satisfaction and success rate are substantially high, making the option and preference of a suitable surgical interference mode an appealing for the majority of the patients with pilonidal disease. Future large prospective studies are prudent to improve the current techniques. In particular, improvements are need to be verified, aiming to further lessen the recurrence rates.
To reduce pressure and congestion in the operating lists of the central hospitals, we can use a clear criterion based on the extent of the disease and the number of sinus openings that will facilitate the management of pilonidal sinus disease in peripheral hospital settings, and comparable results can be achieved in terms of recurrence rate as well as patient satisfaction.









 DownLoad:
DownLoad: