Self-mastery among Chinese Older Adults in the Greater Chicago Area

1.   Introduction

Some human pathogens, such as hepatitis B virus (HBV), hepatitis C virus (HCV) and human immunodeficiency virus (HIV), possess the ability to suppress the immune response and damage the immune system, ultimately leading to the development of certain chronic diseases and even tumors ^[1]. In recent years, researchers have extensively studied numerous models pertaining to these infections ^[2,3,4]. In recent years, there has been notable progress in treating these infections. For example, the latest direct-acting antiviral drugs (DAA) for HCV can cure the majority of cases quickly, with cure rates reaching up to 95%^[5,6]. For HBV, the optimal approach involves long-term medication to manage the condition, reduce viral transmission and stabilize host immune system^[7,8]. Similarly, antiretroviral therapy (ART) is commonly used to suppress HIV replication^[9]. Notably, a small group of elite controllers can naturally manage HIV without treatment^[10]. However, challenges persist, including drug resistance and the risk of viral replication or recurrence^[5,6,7,8,9]. In the past few years, immune checkpoint therapy, a method that shows significant efficacy in completely eliminating tumor cells for certain types of tumors, has been discovered, which activates the host's own immune system to inhibit tumor growth and spread ^[11,12,13]. Enhancing antiviral treatment by strengthening specific immune responses has become a hot topic among researchers.

In 2003, Komarova et al. ^[1] first established an immunosuppressive infection model to investigate the relationship between drug efficacy and treatment duration, the model is given as follows:

where $ y $, $ z $ denote the population size of viruses and immune cells at time $ t $, respectively. Viral reproduction follows logistic growth, $ r $ represents the viral replication rate at a viral load $ K $. It is hypothesized that the virus population undergoes decay at a rate $ a $, and immune cells eliminate the viruses at a rate $ pyz $. Furthermore, immune cells are suppressed by the viruses at a rate $ qyz $ and die at a rate $ b $. In the context of antigenic stimulation, the proliferation of immune cells relies on both the viruses and immune cells, and it can be quantified by the expansion function

where $ \eta $ represents the inhibitory effects of the viruses on the proliferation of immune cells.

In 2014, Shu et al. ^[14] introduced a time delay in the immune expansion function of the model described in ^[1] and studied the existence of Hopf bifurcation and periodic solutions. In 2017, Tian et al. ^[15] incorporated diffusion into the model presented in ^[14] and studied the direction and stability of Hopf bifurcations. However, viruses require a certain amount of time to effectively stimulate immune cells. We refer to this time period as the virus stimulation delay, denoted as $ \tau $. The immune cells at time $ t $ are essentially activated by the viruses at time $ t-\tau $. Therefore, in 2021, Li et al. ^[16] studied the function as follows:

However, it has been noted by Wodarz (see pp 31, Chapter 2 in ^[17]) that the growth rate of immune cells, denoted as $ zf(y) $, in all of these models was assumed to be directly proportional to $ z $, but nonlinearity can better capture the realistic dynamics. Thus, a more realistic model, proposed by De Boer and Perelson ^[18,19] in 1995–1997, has been suggested to provide a better representation of the actual dynamics. In this model, the immune expansion function is described by the well-known Beddington-DeAngelis functional response ^[20,21], the form of which is as follows:

It was initially used in predator-prey models ^[22,23,24]. The parameter $ s $ in the function represents the strength of competition between immune responses. This immune expansion function provides a more biologically realistic description of the interactions and competitive relationships between virus populations and immune cell populations within a host ^[25]. Thus the Beddington-DeAngelis functional response has also been widely discussed in immunosuppressive infection models ^[26,27,28].

In 2023, Chen et al. ^[29] introduced the Beddington-DeAngelis functional response into the immunosuppressive infection model established by Komarova et al. ^[1], the model is as follows:

In ^[29], Chen et al. discussed the local and global stability of equilibrium points in the absence of delay, as well as the stability and Hopf bifurcation of model (1.2) when delay is present. They designed antiviral drug treatment strategies from the perspectives of adaptivity and feasibility of immune competition strength and viral suppression intensity.

In practical problems, the spread of viruses within a host is possible. Thus we introduce the diffusion into the model proposed by Chen et al. in ^[29]. As far as we know, this task has not been attempted yet. Therefore, we study the reaction-diffusion system under the Neumann boundary condition as follows:

where $ \Omega = (0, l \pi) $ with $ l > 0 $, $ y = y(x, t) $ and $ z = z(x, t) $ denoting the population densities of viruses and immune cells at location $ x $ and time $ t $, respectively. The parameters $ s $ and $ \tau $ stand for the competition intensity between immune responses and the viral stimulation delay, respectively. The diffusion rates of viruses and immune cells are $ d_1 $ and $ d_2 $, respectively. The same parameters as in model (1.1) have the same biological meanings. Note that all parameters in (1.3) remain nonnegative.

The remaining sections of the paper are organized as follows: Section 2 discusses the local asymptotic stability of the positive constant steady state solution and the existence of Hopf bifurcation. In Section 3, we derive the normal form of the Hopf bifurcation by using the multiple time scales (MTS) method. Section 4 presents numerical simulations to illustrate the theoretical analysis, and the conclusion is given in Section 5.

2.   Stability of the positive constant steady state solution and existence of Hopf bifurcation

In this section, we concentrate on studying the local asymptotic stability of the positive constant steady state solution and the existence of Hopf bifurcation for system (1.3). From a biological perspective, we only focus on the positive constant steady state solution $ (y_*, z_*) $. It is evident that $ (y_*, z_*) $ satisfies the following equations:

Then we can write $ y_* $ in terms of $ z_* $ as

substituting Eq (2.2) into Eq (2.1), we obtain

where

Denote

Lemma 1. For the positive constant steady state solution of system (1.3), we have the following results.

(i) If $ \Delta_1 > 0 $, $ AC > 0, \; AB < 0, \mathit{\text{and}} a+pz_* < r $ holds, then system (1.3) has two positive constant steady state solutions, $ E_{*_{1}} = (y_{*_{1}}, z_{*_{1}}) $ and $ E_{*_{2}} = (y_{*_{2}}, z_{*_{2}}) $. Here $ z_{*_{1}} = \frac{-B + \sqrt{\Delta_1}}{2A} $, $ z_{*_{2}} = \frac{-B - \sqrt{\Delta_1}}{2A} $, with $ y_{*_{1}} = K\left(1 - \frac{a + pz_{*_{1}}}{r}\right) $ and $ y_{*_{2}} = K\left(1 - \frac{a + pz_{*_{2}}}{r}\right) $;

(ii) If $ \Delta_1 > 0 $, $ AC < 0, \mathit{\text{and}} a+pz_* < r $ holds, then system (1.3) has one positive constant steady state solution $ E_{*_{3}} = (y_{*_{3}}, z_{*_{3}}) $. Here $ z_{*_{3}} = \frac{-B + \sqrt{\Delta_1}}{2A} $, with $ y_{*_{3}} = K\left(1 - \frac{a + pz_{*_{3}}}{r}\right) $;

(iii) If $ \Delta_1 = 0 $, $ AB < 0, \mathit{\text{and}} a+pz_* < r $ holds, then system (1.3) has one positive constant steady state solution $ E_{*_{4}} = (y_{*_{4}}, z_{*_{4}}) $. Here $ z_{*_{4}} = \frac{-B}{2A} $, with $ y_{*_{4}} = K\left(1 - \frac{a + pz_{*_{4}}}{r}\right) $.

Without loss of generality, we denote $ E_{*_{1}} $, $ E_{*_{2}} $, $ E_{*_{3}} $, and $ E_{*_{4}} $ as $ E_* $. Therefore, when the parameters of system (1.3) satisfy any one of the conditions (ⅰ)–(ⅱ) of Lemma 1, the positive constant steady state solution $ E_* = (y_*, z_*) $ exists.

Now, we analyze the stability of $ E_* = (y_*, z_*) $. Set $ U(x, t) = (y(x, t), z(x, t))^{\mathrm{T}} $, then the linearization of system (1.3) at $ E_* $ can be written as

where

Therefore, the characteristic equation of the linearization of system (1.3) at $ E_* $ can be obtained as

with

Lemma 2. When $ \tau = 0 $, the positive constant steady state solution $ E_* $ of system (1.3) is locally asymptotically stable if $ b_0-q > 0 $.

Proof. When $ \tau = 0 $, characteristic Eq (2.6) becomes

It is clear that $ T_n > 0 $, $ N_n > 0 $, thus if $ b_0-q > 0 $ holds, the real parts of the roots of Eq (2.6) are negative. Thus, $ E_* $ is locally asymptotically stable.

This completes the proof. □

Suppose that $ \lambda = $i$ \omega\; (\omega > 0) $ is a root of Eq (2.6), then we have

Square and add above equations, then denote $ g\mathrel{\overset{\triangle}{ = }}\omega^2. $ We obtain

Next, we will discuss the existence of $ \omega $. For the sake of convenience in our discussion, we present the following assumed conditions:

where $ \Delta_2 = (2C_0 q - 2 N_n+T_n^2)^2-4\left[(C_0 q-N_n)^2-C_0^2 b_0^2\right] $, and $ N_n, T_n, b_0, C_0 $ are given in Eq (2.6).

Lemma 3. When $ \tau > 0 $, concerning the cases of positive roots of Eq (2.9), we have the following results:

(i) Equation (2.9) has a unique positive root if $ \mathrm{(H1)} $ or $ \mathrm{(H2)} $ is satisfied, then the positive constant steady state solution of system (1.3) will not exhibit stability switches,

(ii) Equation (2.9) has two positive roots if $ \mathrm{(H3)} $ is satisfied, then the positive constant steady state solution of system (1.3) will exhibit stability switches,

(iii) Equation (2.9) has no positive root if $ \mathrm{(H4)} $ or $ \mathrm{(H5)} $ is satisfied.

Proof. If the condition $ \mathit{\text{(H1)}} $ is satisfied, we have $ g_1 = g_2 $, $ g_1+g_2 = -(2C_0 q - 2 N_n+T_n^2) > 0 $. If the condition $ \mathit{\text{(H2)}} $ is satisfied, we have $ g_1\cdot g_2 = (C_0 q-N_n)^2-C_0^2 b_0^2 < 0 $. Both of them imply that there is a unique positive root $ g $ satisfying Eq (2.9). This proves (ⅰ).

Similarly, we conclude (ⅱ)–(ⅲ). □

Considering the scenario with only a pair of purely imaginary roots, the unique positive $ \omega $ that satisfies Eq (2.9) can be described as follows:

Denote

Now, define a set

From Eq (2.11), we obtain

From Eq (2.13), we find that $ \{\tau_{n, j}^+\}_{j = 0}^{\infty} $ is increasing about $ j $ for some fixed $ n \in I_1 $. Thus, for fixed $ n $, one has $ \tau_{n, 0}^+ = \min _{j \in \mathbb{N}_0}\left\{\tau_{n, j}^ + \right\} $. To investigate the stability of $ E_* $, we define the smallest critical value of time delay

Theorem 1. If $ b_0-q > 0 $ and one of the two conditions $ {{\text{(H1)}}} $ or $ {{\text{(H2)}}} $ is satisfied, then the positive constant steady state solution $ E_* $ of system (1.3) is locally asymptotically stable when $ \tau \in [0, \tau_c) $, and unstable when $ \tau \in \left(\tau_c, \infty\right) $. Moreover, system (1.3) undergoes the Hopf bifurcation at $ E_* $ when $ \tau = \tau_c $, where $ \tau_c $ is given in Eq (2.14).

Proof. Differentiating the both sides of the characteristic Eq (2.6) with respect to time delay $ \tau $ gives rise to

As a result, one has

This means that the transversality condition is satisfied.

This completes the proof. □

3.   Normal form of the Hopf bifurcation

We have obtained that under certain conditions, the characteristic Eq (2.6) of system (1.3) has a unique pair of purely imaginary roots $ \lambda = \pm $i$ \omega_n^+ $, then system (1.3) undergoes the Hopf bifurcation at $ E_* $ when $ \tau = \tau_c $, with $ \tau_c $ as given at $ (2.14) $. In this section, we will utilize the method of MTS to derive the normal form of the Hopf bifurcation.

Denote that

and

Perform a Taylor expansion of $ f(y(x, t-\tau), z(x, t)) $ at $ E_* $, then we obtain

Now, we set $ \hat{y}(x, t) = y(x, \tau t)-y_* $, $ \hat{z}(x, t) = z(x, \tau t)-z_* $, and still denote $ \hat{y}(x, t) $ and $ \hat{z}(x, t) $ by $ y(x, t) $ and $ z(x, t) $, respectively. Then system (1.3) takes the form

Let $ h = \left(h_{11}, h_{12}\right)^{\mathrm{T}} $ be the eigenvector of the characteristic matrix of the linearization of system Eq (3.4) at $ E_* $ corresponding to the eigenvalue $ \mathrm{i} \omega \tau $ and $ h^* = d\left(h_{21}, h_{22}\right)^{\mathrm{T}} $ be the eigenvector of the adjoint matrix corresponding to the eigenvalue $ -\mathrm{i} \omega \tau $. They satisfy the inner product

By calculating, we have

Consider the delay $ \tau $ as a bifurcation parameter, let $ \tau = \tau_c+\varepsilon \mu $, where $ \tau_c $ is the critical point of the Hopf bifurcation, given as Eq (2.14). $ \mu $ is a small perturbation parameter, and $ \varepsilon $ is the characteristic scale used for non-dimensionalization. The solution of Eq (3.4) is assumed to take the form:

where

The derivative with respect to $ t $ is now transformed into

with the differential operator $ D_i = \frac{\partial}{\partial T_i}, \; i \in \mathbb{N}_0. $ Let

where $ j\in \mathbb{N} = \{1, 2, 3, ...\} $. According to Eqs (3.7) and (3.8), we get

To deal with the delayed terms, we expand $ y(x, t-1) $ at $ y(x, T_0-1, T_1, T_2, \cdots) $, then we have

where $ y_{j1} = y_j\left(x, T_0-1, T_1, T_2, \cdots\right), \; j\in \mathbb{N} $.

Substituting Eqs (3.6)–(3.11) into Eq (3.4) will lead to some perturbation equations. By collecting the coefficients with respect to different powers of $ \varepsilon $, we can obtain a set of ordered linear differential equations. First, for the $ \varepsilon $-order terms, we have

where $ L, \alpha, \beta $ are given by Eq (3.2). Thus the solution of Eq (3.12) can be expressed in the form as follows:

where $ h_{11}, h_{12} $ are given by Eq (3.5), and $ c. c. $ represents the complex conjugate of the previous term. Next, for the $ \varepsilon^2 $-order terms, we obtain

where $ L, \alpha, \beta $ are given by Eq (3.2). We substitute solution Eq (3.13) into the right side of Eq (3.14), and denote the coefficient vector of $ \mathrm{e}^{\mathrm{i} \omega \tau_c T_0} $ as $ m_1 $, which satisfies the solvability condition

Then one has

where

with

Suppose that the solution of Eq (3.14) is

Let $ C_k = \langle\cos (n x) \cos (n x), \cos (k x)\rangle = \int_0^{l\pi} \cos (n x) \cos (n x) \cos (k x) \mathrm{d} x $. Besides, we have

We substitute solution Eqs (3.13) and (3.17) into Eq (3.14), then make the inner product with $ \cos (kx) $ on both sides of the obtained equation, where $ k\in \mathbb{N}_0 $. By adding the obtained results, we can compare the coefficients in front of terms $ G^2 $ and $ G \bar{G} $, then we get

where

Specifically, if $ n = 0 $, the condition for $ C_k \neq0 $ is $ k = 0 $. Thus we consider $ n = k = 0 $, then we have $ C_k = l \pi $, $ \int_0^{l\pi} \cos (n x) \cos (k x) \mathrm{d} x = l \pi $. Thus we can simply get the value of $ \eta_{1, 0} $, $ \eta_{0, 0} $, $ \zeta_{1, 0} $, $ \zeta_{0, 0} $. For the $ \varepsilon^3 $-order terms, we get

where $ L, \alpha, \beta $ are given by Eq (3.2). We substitute solution Eqs (3.13) and (3.17) into Eq (3.19), then denote the coefficient vector of $ \mathrm{e}^{\mathrm{i} \omega \tau_c T_0} $ as $ m_2 $, which satisfies the solvability condition

Since $ \mu $ is the disturbance parameter and $ \mu^2 $ has very little influence on the result, the items containing $ \mu^2 G $ can be ignored. Then we obtain

where

with

Therefore, the normal form of the Hopf bifurcation for system Eq (1.3) reduced on the center manifold is

where $ M $ and $ \chi $ are given by Eqs (3.16) and (3.20), respectively. Now introduce $ G = r \mathrm{e}^{\mathrm{i} \theta } $ and put it into the normal form Eq (3.21), then one has

For the stability of the periodic solutions of system (1.3), we have the following result.

Theorem 2. When $ \frac{\mathrm{Re}(M)\mu}{\mathrm{Re}(\chi)} < 0 $, system Eq (1.3) exists as periodic solutions near the positive constant steady state solution $ E_* $. Moreover,

(i) If $ \mathrm{Re}(M)\mu < 0 $, the bifurcating periodic solutions reduced on the center manifold are unstable, and when $ \mu > 0 $ ($ \mu < 0 $), the direction of bifurcation is forward (backward);

(ii) If $ \mathrm{Re}(M)\mu > 0 $, the bifurcating periodic solutions reduced on the center manifold are stable, and when $ \mu > 0 $ ($ \mu < 0 $), the direction of bifurcation is forward (backward).

4.   Numerical simulations

In this section, we will perform numerical simulations for different values of $ \tau $. Based on the work of Komarova et al. ^[1], we fix

For the remaining parameters, we consider the actual meaning of the parameters and choose

It is easy to check that the condition (ⅱ) of Lemma 1 is satisfied, which implies that the system (1.3) has only one positive constant steady state solution,

In addition, we can also find that this set of parameters satisfies the condition $ \text{(H2)} $ of Lemma 3. Furthermore, by Eqs (2.10), (2.12) and (2.14), we obtain

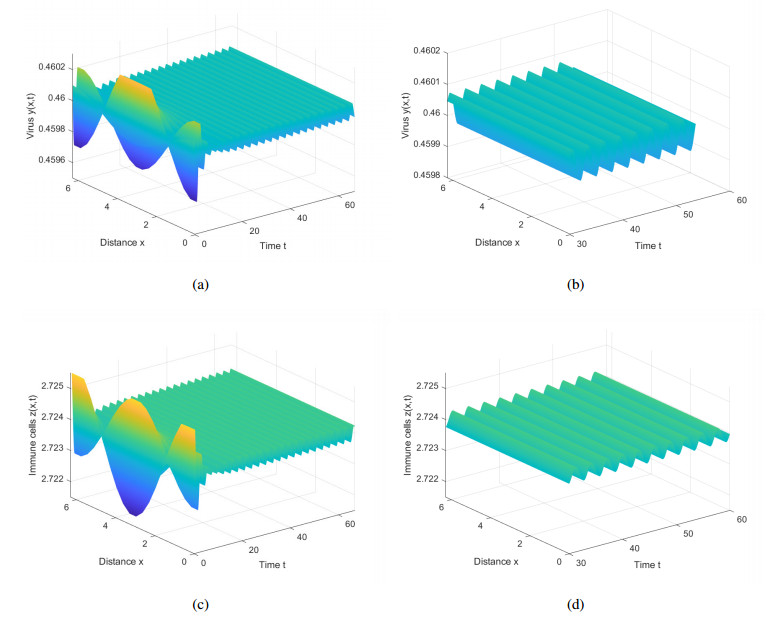
Therefore, by Theorem 2.1, $ E_* $ is locally asymptotically stable when $ \tau \in [0, \tau_c) = [0, 0.0667) $, and unstable when $ \tau \in \left(0.0667, +\infty\right) $. Take $ \tau = 0.055 \in [0, 0.0667) $ as an example, then $ E_* $ is locally asymptotically stable as is illustrated by the computer simulations (see Figure 1).

Figure 1.  Choose the initial function as ($ 0.4600+0.0001\cos x, 2.7239+0.002\cos x $), then the constant steady state solution $ E_* = (0.4600, 2.7239) $ of system (1.3) is locally asymptotically stable when $ \tau = 0.055 < \tau_c $.

DownLoad: Full-Size Img PowerPoint

Biologically, when the virus stimulation delay does not exceed the threshold, immune cells can control the virus in the long-term at low levels. Although the virus is not completely eliminated, it does not cause serious disease deterioration, this is the ideal scenario that we hope for.

According to Eqs (3.16) and (3.20), we can get

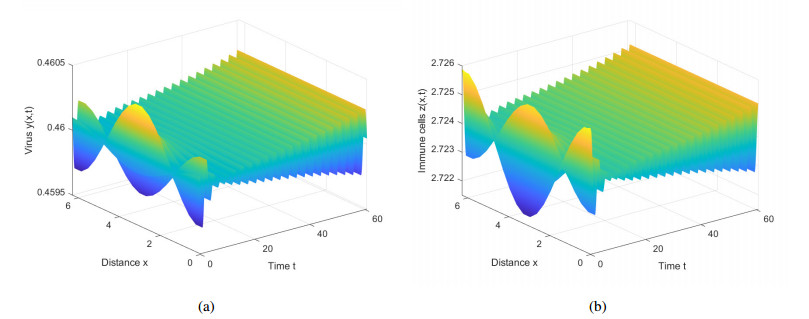
which implies that $ \mathrm{Re}(M) > 0 $, and $ \mathrm{Re}(\chi) < 0 $. From Theorem 2, when $ \mu > 0 $, system (1.3) has stable bifurcating periodic solutions. In addition, the direction of the Hopf bifurcation is forward. Take $ \tau = 0.067\in \left(0.0667, +\infty\right) $ as an example, then system (1.3) generates a spatially homogeneous stable periodic solution (see Figure 2, where Figure 2(a), (c) depict simulations of the virus and immune cell dynamics, respectively, while Figure 2(b), (d) represent their respective local zoom-in plots).

Figure 2.  Choose the initial function as ($ 0.4600+0.0001\cos x $, $ 2.7239+0.002\cos x $), then system (1.3) has a spatially homogeneous stable periodic solution when $ \tau = 0.067 > \tau_c $.

DownLoad: Full-Size Img PowerPoint

Biologically, when the virus stimulation delay slightly exceeds the threshold $ \tau_c $, the densities of immune cells and virus exhibits periodic oscillations. As the number of immune cells increases, they effectively control the virus and reduce the viral load. After a while, an immunoevasion mechanism for the virus may emerge and cause the number of immune cells to drop, allowing the virus to remultiply. This scenario is not ideal, but it is still manageable.

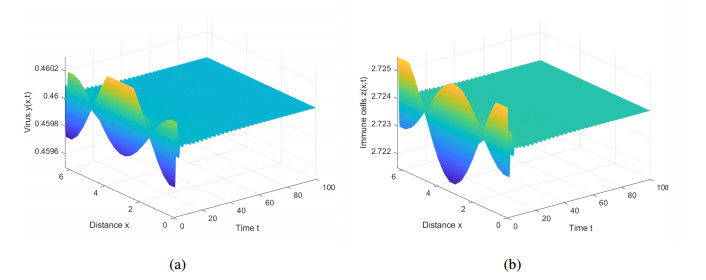
Once $ \tau $ significantly exceeds the threshold, take $ \tau = 0.076\in \left(0.0667, +\infty\right) $ as an example, the virus proliferates rapidly (see Figure 3). This is the worst-case scenario, as the virus could spread rapidly and pose significant risks to the host.

Figure 3.  Choose the initial function as ($ 0.4600+0.0001\cos x $, $ 2.7239+0.002\cos x $), then the constant steady state solution $ E_* $ of system (1.3) is unstable when $ \tau = 0.076 > \tau_c $.

DownLoad: Full-Size Img PowerPoint

5.   Conclusions

In this paper, we incorporated diffusion into an immunosuppressive infection model with virus stimulation delay and Beddington-DeAngelis functional response. We studied the stability of the constant steady state solution of the model and provided conditions for the occurrence of Hopf bifurcation. Moreover, we analyzed the stability and direction of the Hopf bifurcation, and further derived the normal form. By analyzing the model, we obtained a threshold $ \tau_c $ for the virus stimulation delay $ \tau $ and discovered that when $ \tau $ was less than this threshold, the constant steady state solution was locally asymptotically stable. However, once $ \tau $ exceeded the threshold, the constant steady state solution lost stability, and the model exhibited stable periodic solutions. This implied that when the virus could quickly stimulate immune cells, the host possessed strong immunity, which could inhibit virus growth and spread. Conversely, rapid virus proliferation posed significant risks to the host. The discovery of the threshold could help biologists predict, judge, and control the growth of virus cells and select effective treatment strategies.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This study was funded by Fundamental Research Funds for the Central Universities of China (Grant No.2572022DJ07).

Conflict of interest

The authors declare there is no conflicts of interest.