Papillary renal cell carcinoma (PRCC) is a malignant neoplasm of the kidney and is highly interesting due to its increasing incidence. Many studies have shown that the basement membrane (BM) plays an important role in the development of cancer, and structural and functional changes in the BM can be observed in most renal lesions. However, the role of BM in the malignant progression of PRCC and its impact on prognosis has not been fully studied. Therefore, this study aimed to explore the functional and prognostic value of basement membrane-associated genes (BMs) in PRCC patients. We identified differentially expressed BMs between PRCC tumor samples and normal tissue and systematically explored the relevance of BMs to immune infiltration. Moreover, we constructed a risk signature based on these differentially expressed genes (DEGs) using Lasso regression analysis and demonstrated their independence using Cox regression analysis. Finally, we predicted 9 small molecule drugs with the potential to treat PRCC and compared the differences in sensitivity to commonly used chemotherapeutic agents between high and low-risk groups to better target patients for more precise treatment planning. Taken together, our study suggested that BMs might play a crucial role in the development of PRCC, and these results might provide new insights into the treatment of PRCC.
Citation: Yujia Xi, Liying Song, Shuang Wang, Haonan Zhou, Jieying Ren, Ran Zhang, Feifan Fu, Qian Yang, Guosheng Duan, Jingqi Wang. Identification of basement membrane-related prognostic signature for predicting prognosis, immune response and potential drug prediction in papillary renal cell carcinoma[J]. Mathematical Biosciences and Engineering, 2023, 20(6): 10694-10724. doi: 10.3934/mbe.2023474
| [1] | Siyuan Tian, Yinan Hu, Chunmei Yang, Jiahao Yu, Jingyi Liu, Guoyun Xuan, Yansheng Liu, Keshuai Sun, Miao Zhang, Shuoyi Ma, Yulong Shang, Xia Zhou, Ying Han . A novel immune checkpoint-related gene signature for hepatocellular carcinoma to predict clinical outcomes and therapeutic response. Mathematical Biosciences and Engineering, 2022, 19(5): 4719-4736. doi: 10.3934/mbe.2022220 |
| [2] | Xiuxian Zhu, Xianxiong Ma, Chuanqing Wu . A methylomics-correlated nomogram predicts the recurrence free survival risk of kidney renal clear cell carcinoma. Mathematical Biosciences and Engineering, 2021, 18(6): 8559-8576. doi: 10.3934/mbe.2021424 |
| [3] | Yan He, Nannan Cao, Yanan Tian, Xuelin Wang, Qiaohong Xiao, Xiaojuan Tang, Jiaolong Huang, Tingting Zhu, Chunhui Hu, Ying Zhang, Jie Deng, Han Yu, Peng Duan . Development and validation of two redox-related genes associated with prognosis and immune microenvironment in endometrial carcinoma. Mathematical Biosciences and Engineering, 2023, 20(6): 10339-10357. doi: 10.3934/mbe.2023453 |
| [4] | Yuan Yang, Lingshan Zhou, Xi Gou, Guozhi Wu, Ya Zheng, Min Liu, Zhaofeng Chen, Yuping Wang, Rui Ji, Qinghong Guo, Yongning Zhou . Comprehensive analysis to identify DNA damage response-related lncRNA pairs as a prognostic and therapeutic biomarker in gastric cancer. Mathematical Biosciences and Engineering, 2022, 19(1): 595-611. doi: 10.3934/mbe.2022026 |
| [5] | Xiaowei Zhang, Jiayu Tan, Xinyu Zhang, Kritika Pandey, Yuqing Zhong, Guitao Wu, Kejun He . Aggrephagy-related gene signature correlates with survival and tumor-associated macrophages in glioma: Insights from single-cell and bulk RNA sequencing. Mathematical Biosciences and Engineering, 2024, 21(2): 2407-2431. doi: 10.3934/mbe.2024106 |
| [6] | Yong Luo, Xiaopeng Liu, Jingbo Lin, Weide Zhong, Qingbiao Chen . Development and validation of novel inflammatory response-related gene signature to predict prostate cancer recurrence and response to immune checkpoint therapy. Mathematical Biosciences and Engineering, 2022, 19(11): 11345-11366. doi: 10.3934/mbe.2022528 |
| [7] | Wei Niu, Lianping Jiang . A seven-gene prognostic model related to immune checkpoint PD-1 revealing overall survival in patients with lung adenocarcinoma. Mathematical Biosciences and Engineering, 2021, 18(5): 6136-6154. doi: 10.3934/mbe.2021307 |
| [8] | Gianluca D'Antonio, Paul Macklin, Luigi Preziosi . An agent-based model for elasto-plastic mechanical interactions between cells, basement membrane and extracellular matrix. Mathematical Biosciences and Engineering, 2013, 10(1): 75-101. doi: 10.3934/mbe.2013.10.75 |
| [9] | Tongmeng Jiang, Pan Jin, Guoxiu Huang, Shi-Cheng Li . The function of guanylate binding protein 3 (GBP3) in human cancers by pan-cancer bioinformatics. Mathematical Biosciences and Engineering, 2023, 20(5): 9511-9529. doi: 10.3934/mbe.2023418 |
| [10] | Jianpei Hu, Zengnan Mo . Dissection of tumor antigens and immune landscape in clear cell renal cell carcinoma: Preconditions for development and precision medicine of mRNA vaccine. Mathematical Biosciences and Engineering, 2023, 20(2): 2157-2182. doi: 10.3934/mbe.2023100 |
Papillary renal cell carcinoma (PRCC) is a malignant neoplasm of the kidney and is highly interesting due to its increasing incidence. Many studies have shown that the basement membrane (BM) plays an important role in the development of cancer, and structural and functional changes in the BM can be observed in most renal lesions. However, the role of BM in the malignant progression of PRCC and its impact on prognosis has not been fully studied. Therefore, this study aimed to explore the functional and prognostic value of basement membrane-associated genes (BMs) in PRCC patients. We identified differentially expressed BMs between PRCC tumor samples and normal tissue and systematically explored the relevance of BMs to immune infiltration. Moreover, we constructed a risk signature based on these differentially expressed genes (DEGs) using Lasso regression analysis and demonstrated their independence using Cox regression analysis. Finally, we predicted 9 small molecule drugs with the potential to treat PRCC and compared the differences in sensitivity to commonly used chemotherapeutic agents between high and low-risk groups to better target patients for more precise treatment planning. Taken together, our study suggested that BMs might play a crucial role in the development of PRCC, and these results might provide new insights into the treatment of PRCC.
Since the end of 2010, the Central Bank of the Republic of Turkey (CBRT) has designed and implemented a new monetary policy strategy consisting of new policy tools such as unconventional interest rate corridor, differentiated required reserve ratio, and reserve option mechanism to supplement the conventional policy rate.1 In this new strategy, the CBRT adopted weekly repo funding rate as its primary policy rate instead of overnight borrowing rate and let it change within the upper and lower bound of the corridor. More importantly, the CBRT often let the interbank repo rate to deviate from the weekly repo rate which makes that the unconventional interest rate corridor to play a crucial role for the monetary policy framework as compared to its counterparts. Since the CBRT actively uses upper and lower bounds of the corridor (overnight lending rate and overnight borrowing rate, respectively) as an effective policy tool by both changing them at different rates and directions and determining the funding composition of the financial system in this new strategy, there appears an alternative policy rate which is known as the CBRT average funding rate to supplement the weekly repo rate. Empirical findings of Binici et al. (2016) indicated that the policy stance of the CBRT can be best expressed by the CBRT average funding rate and interbank repo rate, which are called as effective rates by the authors, rather than the official policy rates (weekly repo rate, overnight lending rate overnight borrowing rate and late liquidity rate). In this study, we examine the interest rate pass-through (IRPT) from these effective rates to the retail rates. But in order to make a comparison with the findings of Binici et al. (2016), we also took official rates into account in our analysis.2
1 The main reason for designing and implementing a new policy mix was that short-term interest rates may not prevent dangerous build ups of financial risks in terms of current account deficits, credit growth, debt accumulation, and international short-term capital flows although it may meet price stability objectives. For detailed information on the new policy mix, see Akar and Cicek (2015).
2 Apart from Turkey, there are several excellent papers focusing on unconventional monetary policy period around the world (Aristei and Gallo, 2014; Hristov et al., 2014; Apergis and Cooray, 2015; Papadaomu et al., 2018). They provide different and insightful methodologies, approaches and findings about the transmission process on unconventional monetary policy periods. Since the unconventional monetary policy period in Turkey diverges from other countries (starts from 2010), we decided to concentrate for the period of unconventional interest rate corridor.
A faster and more complete relationship between effective policy rates and retail rates reflects the effectiveness of a central bank's monetary policy. While a quicker, symmetric, and complete interest rate pass-through leads to a well-functioning, competitive, and efficient financial system, a weak relationship between effective policy rates and retail rates prevents central banks from achieving and maintaining their targets. Therefore, understanding the main structure of interest rate pass-through will provide better outcomes in terms of monetary policy decisions and improved efficiency.
Many economists have proposed linear models to analyse the effect of policy rates on retail rates. One common assumption characterizes these studies: Policy rate changes affect the retail rates evenly, regardless of whether the change is positive (upward) or negative (downward). However, this approach prevents a detailed inquiry into the transmission mechanism since the policy rates are assumed to affect retail rates symmetrically and linearly. Various reasons, which will be explained in the following section, indicate that the policy rates exhibit asymmetric behaviours on retail rates. Therefore, the non-linear specification of retail rates may be more appropriate than a linear specification. More specifically, in the presence of non-linearity, the response of bank loans interest rates and bank deposits interest rates to a rise in policy rates is more likely to be higher than to a decrease in policy rates. Therefore, many economists also employed non-linear models such as VAR, VEC and Markov-switching methods to capture the asymmetric effect of policy rates on retail rates (Papadamou and Markopoulos, 2018; Papadamou et al., 2018; Hristov et al., 2014; Gaina and Philippas, 2013; Payne and Waters, 2008; Payne, 2006; Humala, 2005). Their findings showed that the aforementioned methods have satisfactory ability to represent asymmetric relations between the variables under investigation.
This research has also focused on the questions of whether there is a long-run relationship between effective policy rates and the retail rates under the period of unconventional interest rate corridor and whether the effective policy rates have an asymmetric effect on retail rates. In order to capture possible long-run relationship and asymmetric behaviour of the variables under investigation, we employed both linear and non-linear autoregression distributed lag (ARDL and NARDL) methods developed by Pesaran et al. (2001) and Shin et al. (2014), respectively.3 NARDL method has some advantages against its counterparts. First, it allows for the asymmetric effect of policy rates on retail rates. The existence of such an asymmetry indicates that the central bank has no complete pass-through impact on retail rates. The main advantage of the model we employed is that the method has a non-restrictive assumption that the variables under examination are integrated to the same order and are suitable even if the sample size is small. Finally, it provides unbiased estimates of the long-run model and valid t-statistics even when some of the regressors are endogenous.
3 For searching asymmetry in the process of interest rate pass through, the NARDL method was previously employed by Apergis and Coorey (2015), Yu et al., (2013), Greenwood-Nimmo et al. (2010).
The data used in the empirical analysis are monthly figures covering 2011:M1 through 2017:M12 and based on policy rates (effective and official policy rates) and retail rates (interest rates for bank commercial loans, bank consumer loans and bank deposits). Our findings indicate that all retail rates are cointegrated with effective policy rates, namely the CBRT average funding rate and interbank repo rates in the long-run. Therefore, the pricing of loans and deposits are driven by the effective policy rates. Turning to the asymmetric behaviours on retail rates, we found that the pass-through differs for decreases and rises in effective policy rates where the retail rates respond faster to policy rate cuts than hikes.
The paper is organized as follows: Section 2 provides a detailed theoretical explanation of asymmetric interest rate pass-through. Section 3 outlines the NARDL framework. Section 4 describes the data and empirical results. Section 5 concludes the paper.
Interest rate pass-through is the degree, speed, and pattern with which banks adjust their retail interest rates to changes in policy interest rates (Cavusoglu, 2010; Yuksel & Ozcan, 2013). Interest rate pass-through takes place in two phases: In the first phase, the central bank provides the liquidity that the banking sector needs from its newly changed policy interest rate and, hence, affects the short-term money market interest rates (Hofmann and Mizen, 2004). Then, the changes in short-term interest rates are transmitted to the long-term interest rates as the expectations about future interest rates change. The more stable the yield curve, the greater is the change in long-term interest rates (Cavusoglu, 2010; Égert et al., 2007). In the second phase, banks adjust their retail interest rates in response to the changes in policy and market interest rates. Since the banking sector depends on money market and central bank sources to a certain extent, changes in these interest rates affect banks' marginal cost of funding and, therefore, they reflect these changes in the credit interest rates they apply to their customers (Égert et al., 2007). Furthermore, bond market interest rates constitute the opportunity cost of credit for the banking sector; therefore, changes in money market interest rates also affect credit interest rates by changing the share of bonds and credits in asset portfolios (Borio and Fritz, 1995; Égert et al., 2007).
Theoretically, under conditions of perfect competition and in the absence of uncertainty, interest rate pass-through is expected to be immediate and complete, that is, perfect (Fuertes et al., 2010; Wang and Lee, 2009). However, empirical studies on the subject have revealed the existence of anomalies. First, retail interest rates are rigid, especially in the short term and the degree and speed of adjustment vary considerably among the countries, depending on the kind of interest rate (Bredin et al., 2002; Aydin, 2007; Heinemann and Schüler, 2006; Sander and Kleimeier, 2004). On the other hand, findings on long-term pass-through in retail interest rates are mixed. Some studies have found that even though retail rates are rigid in the short run, the adjustment is complete in the long run (Cottarelli and Kourelis, 1994; De Bondt, 2005; Hofmann and Mizen, 2004; Karagiannis et al., 2010; Payne, 2006). Others suggested that interest rate pass-through is far from being complete even in the long term (Burgstaller, 2005).
Another kind of anomaly observed in empirical studies is the nonlinear adjustment. Two types of nonlinearity are commonly encountered: The first type is the dependence of level and speed of adjustment on the magnitude of the change in policy interest rates: The greater the deviation from the equilibrium interest rate, the greater the degree and speed of the adjustment in retail rates. (Graeve et al., 2007; Tkacz, 2001).
The second type of nonlinearity is the asymmetric adjustment, which refers to different levels and speeds of adjustment in response to positive and negative changes in policy interest rates. Specifically, Borio and Fritz (1995) found that increases and decreases in policy interest rates of the same magnitude have different effects on retail interest rates. According to Apergis and Cooray (2015), Deger (2012), and Payne and Waters (2000), credit interest rates exhibit downward rigidity or faster upward adjustment and deposit interest rates exhibit upward rigidity or faster downward adjustment. On the other hand, contradictory empirical findings are present in the literature as well. For example, Deger (2012) found upward rigidity in credit interest rates in Bolivia, The Philippines, Malaysia, Dominican Republic, Thailand, and Croatia. Lim (2001) and Karagiannis et al. (2010) found downward rigidity in both credits and deposit interest rates. Finally, Lim (2001) and Gambacorta and Iannotti (2007) reported that even though the adjustment is asymmetric in the short term, the long-term adjustment is symmetric.
The rigidities in retail interest rates of the banking sector that result in these anomalies arise from different factors, such as asymmetric information (Stiglitz and Weis, 1981; Thompson, 2006; Payne, 2006) imperfect competition (Heinemann and Schüler, 2006), switching costs (Cavusoglu, 2010), adjustment costs (Fuertes et al., 2010; Hofmann and Mizen, 2004), long-term customer relations and customer reaction, macroeconomic conditions and bank characteristics (Égert et al., 2007; Égert and MacDonald, 2009).
The empirical literature on interest rate pass-through in Turkey is relatively new and few studies have examined the subject. Aydin (2007) inspected the relationship between the money market interest rate and several types of credit interest rates such as business, housing, consumer, and automobile from June 2001 through September 2005. His results showed that interest rate-pass through are not complete even in the long run. The levels of pass-through for housing credit interest rates are higher than for business interest rates. However, the adjustment speed is higher for business credits. He argued that business credits are riskier than consumer credits and the consumer credit market is more competitive. In a period of fast credit expansion, the level of pass-through in automobile credits was complete. Finally, after the third quarter of 2003, the adjustment speed of credit rates to money market rates increased.
Ucak and Yildirak (2012) examined the relationship between money market interest rates and different types of credit interest rates. Their results showed that business credit interest rates have the complete level of pass-through. Furthermore, business and housing credit interest rates are more sensitive to changes in the market interest rates than others.
Cavusoglu (2010) analysed the relationship between policy interest rates and retail interest rates from January 2002 through December 2009. She found that retail interest rates are rigid in the short term, but deposit interest rates adjust more completely and faster than credit interest rates. Since the policy interest rates decreased continuously over the analysed period, these results are compatible with the banking sector's profit maximization behaviour. On the other hand, credit interest rates are adjusted more completely than deposit interest rates. The reason for this finding is that the credit market is more competitive than the deposit market. Moreover, the level of adjustment for business credit interest rates is lower than that of consumer credit interest rates and higher for business deposit interest rates than for saving deposit interest rates. This means that the asymmetric adjustment problem is more serious for firms than for consumers.
Ozdemir (2009) researched the relationship between retail interest rates and policy interest rates and between retail interest rates and market interest rates for April 2001 through December 2006. His results suggested that interest rate pass-through from policy interest rates is complete in the long term, but credit interest rates are adjusted faster than deposit interest rates in the short term. Consistent with the implicit collusive agreement hypothesis, credit interest rates are more rigid downward, and in accordance with the customer reaction hypothesis, deposit interest rates are again rigid downward. However, he repeated the same analysis by using market interest rates, he did not find any asymmetries.
Yuksel and Ozcan (2013) investigated the relationship between money market interest rates and consumer, automobile, housing, business credits, and deposit interest rates. They found that interest rate pass-through is symmetric for all types of retail interest rates. The average time of convergence to equilibrium is three months. However, deposit interest rates adjust more slowly than credit interest rates.
Yildirim (2013) studied the interest rate pass-through between credit interest rates and money market interest rates for November 2002 through October 2011. He found that credit interest rates adjust faster while market interest rates are increasing than while market interest rates are decreasing. Therefore, there is a downward rigidity in credit interest rates. Even so, the degree of rigidity varies among the types of credit and business credits are the most rigid of all types. To explain this finding, he argued that business credit demand was inelastic since the financial system was still shallow and local firms have limited funding sources.
Binici et al. (2016) investigated the relationship between interest rates of loans/deposits and effective/official policy rates under the unconventional interest rate corridor period. They found that the effective rates are more relevant than official rates for the transmission of monetary policy and interbank repo rate plays the crucial role in determining the rates of loans and deposits. On the asymmetric part, they found evidence in favour of asymmetry that the response of loans/deposits rates to hikes in effective policy rates is higher than to the cuts.
Lastly, Yılmaz et al. (2018) searched for the pass-through speed and the rate of changes regarding the overnight borrowing rate of the CBRT to the bank rates for loans from 2002 to 2014. They employed VAR, cointegration and Granger causality methods and found that the pass-through from overnight interest rates to the bank loan rates is fast and high in the long term, regardless of the deposit and loan types. Additionally, they captured that the pass-through effect from overnight repo rates to the loan rates for household loans are faster in comparison to the commercial loans.
When we look at the previous interest rate pass-through studies regarding the Turkish economy, we see that there are some deficiencies in the literature. Two of them are quite important. First, there is only one paper focusing on unconventional interest rate corridor period which has quite important role for the monetary policy framework. And second, other papers have not employed the methodology we have used in the paper, hence, our paper may provide an opportunity to compare the performances of the methods and findings with previous papers. Therefore, we believe that our paper has potential to fill a gap in the interest rate pass-through literature, especially for the Turkish economy.
The NARDL approach may help us capture possible asymmetric effects of policy rates (prm) variations on retail rates (rrn) [where m indicates late overnight rate (lor), overnight lending rate (olr), weekly repo rate (wrr), the CBRT average funding rate (afr), interbank repo rate (irr) and spread repo rate (srr) while n indicates the rates for commercial loans (lcr), consumer (personal) loans (lpr) and bank deposits (bdr)]. Equation 1 suggests the possible long-run relationship between the policy rates and retail rates.
| rrnt=β0+βm1prmt+εnmt | (1) |
where the regressors of prm are defined such that ∆prtm = ϵtm and εtnm and ϵtm follow the iid process with a zero mean and finite variances. The coefficient of β1m indicates the long-run pass-through coefficient for policy rates which reflects the change in policy rates is transmitted to the banking retail rates in the long-run. Equation 1 can be written as a restricted error correction model (ECM) of Equation 2 if the error terms are present in the data-generating process as
| Δrrnt=α0+ξ(rrnt−1−βm1prmt−1)+p−1∑i=1ϑniΔrrnt−i+k∑j=0δmiΔprmt−j+ηnmt | (2) |
In Equation 2, ∆ indicates the difference operator and
| Δrrnt=α0+αn1rrnt−1+αm2prmt−1+p−1∑i=1ϑniΔrrnt−i+k∑j=0δmiΔprmt−j+ηnmt | (3) |
where
As it is more likely that bank commercial loan rate, bank consumer loan rate and bank deposit rate behave asymmetric regarding a change in policy rates, the linear model shown in Equation 3 may not be adequate to represent the possible asymmetries in the coefficients. To capture possible asymmetries in the model, we use the NARDL developed by Shin et al. (2014). To establish the NARDL model, we first decompose the variables as positive and negative parts:
| prmt=prm0+prm+t+prm−t | (4) |
where prm indicates the policy rates; prtm+ and prtm- are the partial sum process of positive and negative deviations in policy rates, respectively. The partial sum process can be shown as:
| prm+t=t∑i=1Δprm+i=t∑i=1max(Δprmi,0)prm−t=t∑i=1Δprm−i=t∑i=1min(Δprmi,0) | (5) |
Since we expect the interest rates of bank commercial loans, bank consumer loans and bank deposits to have different sensitivity to policy rate rises than policy rate decreases, we may rewrite Equation 1 by adding the positive and negative partial sums of pr:
| rrnt=β0+βm+1prm+t+βm−1prm−t+εnmt | (6) |
Equation 3 also can be rewritten as follows;
| Δrrnt=α0+αn1rrnt−1+αm+2prm+t−1+αm−2prm−t−1+p−1∑i=1ϑiΔrrnt−i+p∑i=0(θm+iΔprm+t−i+γm−iΔprm−t−i)+ηnmt | (7) |
By adding positive and negative changes, we can capture the possible asymmetric effects of policy rates in both the long run and the short run. Note that the testing procedure is the same as in the linear ARDL specification. Based on Equation 7, we seek a long-run relationship via H0:α1 = α2m+ = α2m- = 0 against α1n≠0, α2m+≠0 and α2m-≠0. In addition, the asymmetric long-run multipliers of explanatory variables can be computed as:
| β0=α0−αn1,βm+1=αm+2−αn1,βm−1=αm−2−αn1 |
Regarding the Equation 7, our hypotheses are;
H1: There is a long-run relationship between the policy rates and retail rates which corresponds to reject the null hypothesis of H0:α1n = α2m+ = α2m- = 0 in Equation 7.
H2: There is a long-run symmetry between the policy rates and retail rates which corresponds to accept the null hypothesis of H0:α2m+ = α2m- in Equation 7.
H3: There is a complete long-run pass-through for (ⅰ) positive and (ⅱ) negative changes in policy rates which correspond to accept the null hypothesis of (ⅰ) H0:(α2m+/-α1n) = 1 and (ⅱ) H0:(α2m-/-α1n) = 1 in Equation 7.
H4: There is a short-run symmetry between the policy rates and retail rates which corresponds to accept the null hypothesis of H0:θ0m+ = δ0m- in Equation 7.
H5: There is a short-run relationship between the policy rates and retail rates which corresponds to reject the null hypothesis of H0:θ0m+ = δ0m- = 0 in Equation 7.
The data used in the analysis are monthly figures covering 2011:M1 through 2017:M12. Since we search for the effect of policy rates (prm) on retail rates (rrn), we added policy rates to the model where the m indicates late overnight rate (lor), overnight lending rate (olr), weekly repo rate (wrr), the CBRT average funding rate (afr) and interbank repo rate (irr) while the n indicates the rates for commercial loans (lcr), consumer (personal) loans (lpr) and bank deposits (bdr). Since Binici et al. (2016) indicate that the spread between interbank repo rate and the CBRT average funding rate is an important variable while explaining the monetary policy transmission mechanism, we also search for the effect of spread repo rate (srr) as a policy rate on retail rates. All variables are obtained from the Electronic Data Dissemination System (EVDS) of the CBRT (See Figure 1 and 2).
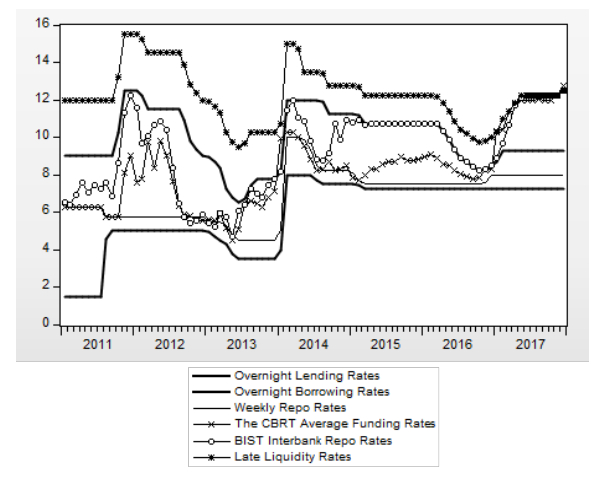 Figure 1. Policy rates and interbank repo rate. Source: CBRT.
Figure 1. Policy rates and interbank repo rate. Source: CBRT.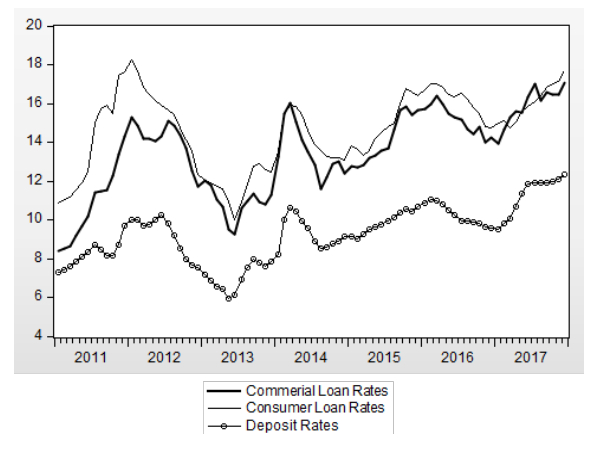 Figure 2. Retail Rates. Source: CBRT.
Figure 2. Retail Rates. Source: CBRT.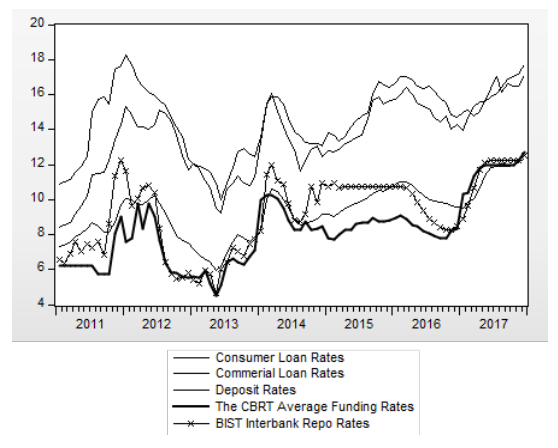 Figure 3. Selected Policy Rates and Retail Rates. Source: CBRT.
Figure 3. Selected Policy Rates and Retail Rates. Source: CBRT.| Mean | Max. | Min. | Std. Dev. | JB | Prob. | Obs. | |
| Retail Rates (Bank Level Variables) | |||||||
| rrlpr | 14.65 | 18.23 | 10.00 | 2.00 | 4.72 | 0.09 | 84 |
| rrlcr | 13.50 | 17.07 | 8.42 | 2.21 | 4.91 | 0.09 | 84 |
| rrbdr | 9.31 | 12.36 | 5.95 | 1.48 | 1.16* | 0.56 | 84 |
| Policy Rates (Short-term Interest Rates) | |||||||
| prlor | 12.24 | 15.50 | 9.50 | 1.52 | 1.61* | 0.45 | 84 |
| prolr | 9.89 | 12.50 | 6.50 | 1.52 | 2.82* | 0.24 | 84 |
| prwrr | 6.92 | 10.00 | 4.50 | 1.40 | 1.40* | 0.50 | 84 |
| probr | 5.86 | 8.00 | 1.50 | 1.94 | 11.45 | 0.00 | 84 |
| prafr | 8.22 | 12.75 | 4.52 | 1.98 | 3.10* | 0.21 | 84 |
| prirr | 9.22 | 12.50 | 4.66 | 2.17 | 5.84 | 0.05 | 84 |
| prsrr | 1.00 | 4.04 | -1.77 | 1.10 | 1.42* | 0.49 | 84 |
| *Note: Indicates that the normality has rejected at 10% level. | |||||||
In this study, we used the augmented Dickey-Fuller (ADF) test to estimate unit root. The results of unit root estimations are presented in Table 2 and indicate that all series follow unit root process.
| Levels | Differences | ||||||
| No intercept, no trend | Intercept, no trend | Interceptand trend | No intercept, no trend | Intercept, no trend | Interceptand trend | ||
| Retail Rates (Bank Level Variables) | |||||||
| rrlpr | 0.4511 | -2.4146 | -2.5710 | ∆rrlpr | -5.6056*** | -5.6431*** | -4.8207*** |
| rrlcr | 0.5168 | -2.5556 | -3.3327* | ∆rrlcr | -5.5980*** | -5.6660*** | -5.6332*** |
| rrbdr | 0.0854 | -2.3887 | -2.9397 | ∆rrbdr | -6.5439*** | -6.5479*** | -6.5073*** |
| Policy Rates (Short-term Interest Rates) | |||||||
| prlor | 0.2348 | -2.6818* | -2.8660 | ∆prlor | -6.7105*** | -6.6695*** | -6.6273*** |
| prolr | 0.3266 | -2.4953 | -2.5273 | ∆prolr | -6.6151*** | -6.5742*** | -6.5491*** |
| prwrr | 0.0559 | -1.8096 | -2.4463 | ∆prwrr | -7.8103*** | -7.7117*** | -7.7240*** |
| probr | 0.3662 | -2.2433 | -2.3116 | ∆probr | -7.8699*** | -7.9270*** | -7.9743*** |
| prafr | 0.7480 | -0.9913 | -2.1267 | ∆prafr | -8.3476*** | -8.3934*** | -8.3866*** |
| prirr | 0.0854 | -2.3887 | -2.9397 | ∆prirr | -6.5439*** | -6.5479*** | -6.5073*** |
| prsrr | -1.7157* | -2.3847 | -2.5435 | ∆prsrr | -12.848*** | -12.769*** | -12.751*** |
| *Note: Reported figures are the Augmented Dickey-Fuller (ADF) test statistics where (***), (**), and (*) indicate rejection of the null hypothesis of a unit root at 1%, 5%, and 10% levels of significance, respectively. The optimal lags were chosen using Schwarz Information Criterion with a maximum lag of 13. | |||||||
The main variables under investigation are the interest rates of commercial loans, consumer loans and bank deposits set by the commercial banks. According to the many authors, the retail rates are driven by the central banks in the long-run. In Turkey, the CBRT has designed a new monetary policy framework where there are several policy rates are actively used by the CBRT. Therefore, the questions of which policy rate has the impact (or stronger impact) on a specific retail rate and whether the response of retail rates to monetary policy decisions is asymmetric in during tightening and easing periods are unclear. Therefore, the aim of our regression analyses is to capture both the specific role and the asymmetry of policy rates in the pricing of retail rates.
In this subsection, we first estimated conventional ARDL models in order to get whether the specific retail rates are cointegrated with a specific policy rate. In order to do that, we first included each policy rates separately to the models as an explanatory variable. Then we interpreted the significance and magnitude of the coefficient of each explanatory variable. Since two policy rates (the CBRT average funding rate and interbank repo rate) gained importance in this new policy framework to reflect the stance of the monetary policy of the CBRT, we then entered the CBRT Fesgrh average funding rate and spread repo rate into the same specification jointly.4 In here, spread repo rate reflects the behaviour of interbank repo rates since spread repo rate is mainly driven by the interbank repo rate.
4 In order to avoid the endogeneity problems that may arise from using interest rate series as the explanatory variables which may have similar patterns, we just use one explanatory variable in the models. Since spread repo rate is the difference between interbank repo rate and the CBRT average funding rate, it does not cause an endogeneity problem when spread repo rate and average funding rate are used explanatory variables in the models. Moreover, the methodology we used in the paper provides unbiased estimates of the long-run model and valid t-statistics even when some of the regressors are endogenous. For detailed information please see: Shin et al., (2014).
After capturing the symmetric long-run cointegration, we then estimated asymmetric ARDL models for each policy rates represented by Equation 7 to search for asymmetry in the interest rate pass-through. After estimating the equation with alternative policy rates, we then applied the Wald test to test the null hypothesis of the asymmetric long-run relationship between the variables under investigation. Wald test results shown in Table 3 indicated that long-run symmetry does not occur for 11 out of 24 alternative models since the H2 statistic values exceed its upper critical value which provides evidence in favour of asymmetry. The details are presented as follows.
| Late Overnight Rate | Overnight Lending Rate | Weekly Repo Rate | The CBRT Average Funding Rate | Interbank Repo Rate | Spread Repo Rate | The CBRT Average Funding Rates and Spread Repo Rate | ||
| prlor | prolr | prwrr | prafr | prirr | prsrr | prafr | prsrr | |
| Dependent Variables | ||||||||
| rrlcr | 0.7717 | 0.3401 | 12.2392*** | 3.3493 | 12.2703*** | 0.4583 | 5.3763*** | 15.4190*** |
| rrlpr | 2.7166 | 2.1288 | 0.3505 | 1.6786 | 17.0857*** | 1.1388 | 3.2973** | 6.0396*** |
| rrbdr | 4.4992** | 3.6890 | 11.5331*** | 0.6654 | 10.0791*** | 10.0703*** | 0.8751 | 0.6640 |
| *Note: (1) The null hypothesis for long-run symmetry is H0:α2m+=α3m-. (2) ***, ** and * indicates the rejection of the null hypothesis at the 1%, 5% and 10% level, respectively. | ||||||||
Commercial Loan Rate
The results of symmetric and asymmetric ARDL analysis for commercial loan rate are given in Table 4. Hypothesis result rows in symmetric ARDL part of Table 4 give information us about the long-run relationship and symmetric behaviour of the variables in the both long- and short-run. Since the Pesaran-Shin-Smith F-test (H1) results (H1 test statistics) exceed their respective upper critical values, we may say that interest rate of commercial loans is separately cointegrated with the CBRT average funding rate and interbank repo rate and jointly cointegrated with the CBRT average funding rate and spread repo rate in the long-run.5 As can be seen from the Table 4, both significance level and magnitude of the coefficient of the interbank repo rate are higher than the CBRT average funding rate (0.1404 versus 0.1219). According to the long-run pass-through (LR-PT) coefficients, we may specifically say that a 1% change in the CBRT average rate or interbank repo rate causes commercial loan rate to change by 0.78% and 0.91%, respectively, in the long-run. For the model in which the long-run relationship is jointly estimated, both the significance level and magnitudes of the coefficients of the CBRT average funding rate and spread repo rate get higher when it is compared to the separately estimated models. Moreover, the magnitude of the coefficient of the CBRT average funding rate becomes higher than the spread repo rate (essentially interbank repo rate) while it was lower in separately estimated models. These findings imply that effective policy rates (namely interbank repo rate and the CBRT average funding rate) have the impact on the interest rate of the commercial loans, but the CBRT average funding rate has the stronger impact than the interbank repo rate in the long-run when they are jointly taken into account. It should be noted that the latter finding is dissimilar to the empirical findings of Binici et al. (2016) where they found that the magnitude of spread rate is higher than the CBRT average funding rate when two variables are jointly considered. The reason might be that their analysis is for capturing the short-term behaviours of the variables under consideration while ours is for the long-run. Since ₺-denominated commercial loans are mostly short-term in Turkey, it is more likely that the banks to price their commercial loans according to the spread repo rates (namely, interbank repo rate) in the short-run. But in the long-run, the CBRT average funding rate may gain importance because it has potential to reflect the stance of monetary policy in both short- and the long-run.
| Late Overnight Rate | Overnight Lending Rate | Weekly Repo Rate | The CBRT Average Funding Rate | Interbank Repo Rate | Spread Repo Rate | The CBRT Average Funding Rates and Spread Repo Rate | ||||
| prlor | prolr | prwrr | prafr | prirr | prsrr | prafr prsrr |
||||
| Symmetric ARDL Results | Estimated Coefficients | |||||||||
| α0 | 0.6391 | 0.5261 | 0.7899* | 1.1633*** | 0.8570** | 0.6677 | 1.3735*** | |||
| [1.1840] | [0.9719] | [1.6420] | [3.0553] | [2.1804] | [1.2918] | [3.1522] | ||||
| α1 | -0.0524* | -0.0412 | -0.0773* | -0.1561*** | -0.1550*** | -0.0361 | -0.2723*** | |||
| [-1.8417] | [-1.1508] | [-1.7913] | [-3.4271] | [-3.7575] | [-0.9648] | [-5.7212] | ||||
| α2m | 0.0136 | 0.0083 | 0.0463 | 0.1219** | 0.1404*** | -0.1016 | 0.2617*** | |||
| [0.3279] | [0.1775] | [0.8634] | [2.3514] | [3.3625] | [-1.6366] | [5.6591] | ||||
| α3m | - | - | - | - | - | - | 0.2138*** | |||
| - | - | - | - | - | [3.6437] | |||||
| LR PT | 0.2595 | 0.2015 | 0.5990 | 0.7809 | 0.9058 | -2.8144 | 0.9611 | |||
| 0.7852 | ||||||||||
| Hypothesis Results | ||||||||||
| H1 | 1.7227 | 0.0662 | 1.6380 | 6.0811*** | 7.5142*** | 1.9850 | 13.5805*** | |||
| H3 | 0.9480 | 0.5537 | 0.5071 | 1.1617 | 0.2367 | 1.1648 | 0.1140 | |||
| 0.9257 | ||||||||||
| H5 | 18.1668*** | 3.1362 | 15.7615*** | 9.1506*** | 11.9508*** | 4.6862** | 6.1690*** | |||
| Diagnostic Tests | ||||||||||
| R2 | 0.3517 | 0.3866 | 0.4237 | 0.3958 | 0.3766 | 0.3391 | 0.5614 | |||
| DW | 1.8948 | 1.5913 | 1.4012 | 1.9681 | 1.9498 | 1.9050 | 2.0175 | |||
| LM | 0.0903 | 0.8150 | 0.5493 | 0.6952 | 0.2163 | 0.7555 | 0.5601 | |||
| ARCH | 0.7971 | 0.6597 | 0.2954 | 0.2673 | 0.2267 | 0.2994 | 0.6684 | |||
| Asymmetric ARDL Results | Estimated Coefficients | prafr is asymmetric | prsrr is asymmetric | |||||||
| α0 | 1.3895*** | 0.2001 | 2.9919*** | 1.1166 | 2.5707*** | 1.1512** | 2.5770*** | 2.0955*** | ||
| [2.5883] | [0.3437] | [4.7284] | [1.5066] | [4.1789] | [2.2189] | [3.9523] | [5.7302] | |||
| α1 | -0.1028 | -0.0263 | -0.2480*** | -0.1398*** | -0.1559*** | -0.0894* | -0.2134*** | -0.3081*** | ||
| [-2.0819] | [-0.5690] | [-5.3671] | [-2.6333] | [-3.3184] | [-1.9185] | [-4.2401] | [-8.1644] | |||
| α2m+ | 0.0326 | 0.0247 | 0.0067 | 0.1008* | 0.2740*** | 0.0415 | 0.2433*** | 0.2856*** | ||
| [0.4930] | [0.3870] | [0.1055] | [1.7554] | [6.2948] | [0.5861] | [4.4293] | [5.9244] | |||
| α2m- | 0.0081 | 0.0074 | -0.1677* | 0.0666 | 0.3314*** | 0.0309 | 0.2722*** | 0.3396*** | ||
| [0.1689] | [0.1434] | [-1.6659] | [0.9722] | [6.3600] | [0.4583] | [4.1523] | [6.6249] | |||
| α3m | - | - | - | - | - | - | 0.2054*** | 0.3837*** | ||
| - | - | - | - | - | - | [3.7042] | [8.5194] | |||
| LR PT+ | 0.3171 | 0.9392 | 0.0270 | 0.7210 | 1.7575 | 0.4642 | 1.1401 | 0.9270 | ||
| LR PT- | 0.0788 | 0.2814 | -0.6762 | 0.4764 | 2.1257 | 0.3456 | 1.2755 | 1.1022 | ||
| LR PT | - | - | - | - | - | - | 0.9625 | 1.2454 | ||
| Hypothesis Results | ||||||||||
| H1 | 2.2552 | 0.1473 | 12.3678*** | 4.6984** | 13.6548*** | 1.4565 | 8.3178*** | 23.4957*** | ||
| H2 | 0.7717 | 0.3401 | 12.2392*** | 3.3493 | 12.2703*** | 0.4583 | 5.3763*** | 15.4190*** | ||
| H3a | 1.5772 | 0.0007 | 14.8815*** | 1.0690 | 3.1389 | 0.4954 | 0.5131 | 0.2015 | ||
| H3b | 4.2584** | 0.1476 | 13.8961*** | 1.8444 | 3.1866 | 0.7563 | 1.0682 | 0.3226 | ||
| H4 | 2.2718 | 2.5955 | 6.0869*** | 7.2922*** | 11.5664*** | - | 8.0668*** | 47.7121*** | ||
| H5 | 20.5590*** | 7.9546*** | 3.1243 | 21.2726*** | 6.7580*** | - | 15.2799*** | 15.6532*** | ||
| Diagnostic Tests | ||||||||||
| R2 | 0.3491 | 0.3618 | 0.5770 | 0.4809 | 0.5458 | 0.0166 | 0.4956 | 0.7654 | ||
| DW | 1.8844 | 1.6931 | 2.0610 | 2.0182 | 1.9810 | 1.1308 | 1.6582 | 2.1151 | ||
| LM | 0.5624 | 0.9177 | 0.9677 | 0.6528 | 0.8735 | 0.0046 | 0.3056 | 0.1630 | ||
| ARCH | 0.5515 | 0.5910 | 0.1947 | 0.5055 | 0.0300 | 0.2127 | 0.7336 | 0.5459 | ||
| (1) m indicates the policy rates (pp superscript: lor, olr, wrr, afr, irr or srr). (2) α2m+ and α2m- indicate the long-run coefficients of rises and decreases in policy rates, respectively. (3) Values in brackets underneath the coefficients are the t-values for the ***1%, **5% and *10%. (4) H1 denotes the Paseran-Shin-Smith F test statistic values under the hypothesis of H0:α1n=αim=0 for k=2 for the symmetric models and H0:α1n=αim+=αim-=0 for k=3 for the asymmetric models and critical values according to Pesaran et. al (2001) are 3.77, 4.35 and 5.61 for the ***10%, **5% and *1%, respectively, where i={2, 3}. (5) H2 denotes the F-test statistic values under the hypothesis of H0:αim+=αim- where i={2, 3}. (6) H3, H3a and H3b denote the F-test statistic values under the hypothesis of (ⅰ) H0:(αim/-α1n)=1 (ⅱ) H0:(αim+/α1n)=1 and (ⅲ) H0:(αim-/α1n)=1, respectively, where i={2, 3}. (7) H4 denotes the F-test statistic values under the hypothesis of H0:θ0m+=δ0m- for asymmetric models. (8) H5 denotes the F-test statistic values under the hypothesis of H0:θ0m=0 for symmetric models and H0:θ0m+=δ0m-=0 for asymmetric models. (9) R2, DW LM and ARCH rows give adjusted R-square, Durbin-Watson, the p-values of a test for autocorrelation up to lag 12 and a test for ARCH effects up to 12 lags, respectively. | ||||||||||
5 As indicated before, the spread repo rate is the difference between the interbank repo rates and the CBRT average funding rates. Since the CBRT average funding rates are level and the spread repo rate is the spread, one may worry about how to interpret the coefficients of each policy rate in absolute terms. Binici, Kara and Özlü (2016) indicated that the coefficient of the spread can be interpreted as the effect of the interbank repo rates since the variation in the spread repo rates is mainly driven by the interbank repo rates over the study period. Therefore, we embraced their approach in our study for interpreting the coefficient.
When one considers whether the LR-PT coefficients (of the significant models according to the H1 test results) equal to one, we may say that the LR-PT is separately complete for the CBRT average funding rate and interbank repo rate, and is jointly complete for the CBRT average funding rate and spread repo rate because the H3 hypothesis cannot be rejected.6 When we concentrate on the short-run pass-through (SR-PT) test results, H5 row indicates that the interest rate of commercial loans shows the immediate response to the changes in all policy rates except for overnight lending rate. Actually, the CBRT average funding rate is weighted average interest rates of the funds provided by the CBRT to the financial system and varies depending on the funding composition choice of the CBRT. Since a change in official policy rates (either weekly repo rate, late overnight rate or overnight lending rate), other things are being equal, will change the CBRT average funding rate, it is consistent that the banks immediately adjust their commercial loan rate when the official policy rates change. It should be noted that these findings are consistent with the findings of Binici et al. (2016) except for overnight lending rate which was insignificant in our results both in the short- and long-run.
6 For the models H1 test statistics are insignificant, we did not interpret whether the LR-PT is complete although the H3 hypotheses are accepted.
Turning to asymmetric ARDL models, Wald test results of H2 hypothesis show that just two policy rates separately have the asymmetric impact on the interest rate of commercial loans: weekly repo rate and interbank repo rate. Additionally, the CBRT average funding rate and spread repo rate also have the asymmetric impact on the interest rate of commercial loans when they are jointly considered in two different asymmetric models, while the CBRT average funding rate does not when it is modelled separately. If we consider H1 and H2 test results together for the CBRT average funding rate in the asymmetric model, we may say that there is a long-run cointegration (since H1 is rejected) between the variables but the cointegration is symmetric; not asymmetric (since H2 is accepted). When we concentrate on the coefficients of the valid asymmetric models, we may see that the interest rate of the commercial loans responses to both positive and the negative changes in interbank repo rate while the coefficients of positive and negative changes of the weekly repo rate are either insignificant or carry the wrong sign. Hence, a 1% rise in interbank repo rate causes commercial loan rate to rise by 1.75% while a 1% decrease led the commercial loan rate to decrease by 2.12% in the long-run. Regarding the LR-PT values of the asymmetric ARDL model for interbank repo rate, H3a and H3b hypotheses indicate the estimated coefficients of positive and negative changes are not equal to one (H3a and H3b are accepted). But since both coefficients are significant, we may say that the LR-PT is over proportionally for the interbank repo rate in the long-run since the coefficients are larger than one.
But the same is not valid when we take the CBRT average funding rate and spread repo rate jointly into account. While estimating these two variables jointly, we assumed one variable is symmetric and the other one is asymmetric. Therefore, we estimated two alternative models. According to these asymmetric models, we captured that a 1% rise in the CBRT average funding rate will increase the rate of commercial loans by 1.14% while a 1% fall will decrease the rate of commercial loans by 1.27% once the spread repo rate is controlled. Similarly, a 1% rise in the spread repo rate (essentially interbank repo rate) will increase the rate of commercial loans by 0.93% while a 1% fall will decrease the rate of commercial loans by 1.10% once the CBRT average funding rate is controlled. The meaning of these finding is that the interest rate of commercial loans shows more response to negative changes than the positive ones, for both the CBRT average funding rate and spread repo rate. That is to say, the response of commercial loan rates to monetary policy is weaker during tightening periods and stronger in easing periods. Another important thing is that the magnitude and the significance level of the coefficients of positive and negative changes of spread repo rate are higher than the CBRT average funding rate. The reason might be that the elasticity of the liquidity demand of the banks for the daily funds is low (the interbank repo facility is in the daily basis) while the elasticity of the liquidity demand for the weekly funds is relatively high (weekly repo facility is in 7 days).
When concentrating on the symmetry in short-run coefficients (H4), one may see that the short-run symmetry is rejected for weekly repo rate, the CBRT average funding rate, interbank repo rate and jointly for the CBRT average funding rate and spread repo rate (for both alternative models), but not for late overnight rate and spread repo rate. Lastly, H5 hypothesis indicates that adjustment process is immediate for all policy rates except for weekly repo rate. If we interpret H4 and H5 hypothesis together, we may say that the interest rate of commercial loans immediately (H5 is rejected), asymmetrically (H4 is rejected) and separately adjust to the changes in the CBRT average funding rate and interbank repo rate, and jointly adjust to the changes in the CBRT average funding rate and spread repo rate.
Consumer Loan Rate
Table 5 represents the results for consumer loan rate. When we focus on the symmetric models, the respective F-test results indicate that interest rate of consumer loans is just separately cointegrated with interbank repo rate and is jointly cointegrated with the CBRT average funding rate and spread repo rate. According to the LR-PT coefficients, we may specifically say that a 1% change in interbank repo rate causes interest rate of the consumer loans to chance by 0.81% in the long-run. As can be seen from the Table 5, we may see that the coefficient of the CBRT average funding rate is insignificant when it is estimated separately. But then becomes significant when it is jointly modelled with spread repo rate. This joint model indicates that the spread repo rate (also interbank repo rate) has greater magnitude and significance than the CBRT average funding rate, that is to say, consumer loans are more sensitive to interbank repo rate than the policy rates since the consumer loans are mostly short-term in nature. It should be noted that the maturity term of the consumer loans is longer than the commercial loans. Therefore, they are less sensitive to the spread repo rate when it is compared to the commercial loans. If we look at the jointly estimated model at Table 4, we can see that both the significance level and the coefficient of spread repo rate are lower in Table 5. Therefore, the finding is consistent with our maturity term interpretation and very similar the findings of Binici et al. (2016). On the other hand, both the significance level and the magnitude of the CBRT repo rate are lower than the spread repo rate in Table 5 where it is adverse in Table 4. Turning to whether the LR-PT coefficients equal to one, we may say that the LR-PT is complete for interbank repo rate (for separately model) and both the CBRT average funding rate and spread repo rate (for joint model) since H3 is not rejected. The H5 hypothesis also indicates that all models show the immediate response to the changes in all policy rates except for spread repo rate in the short-run.
| Late Overnight Rate | Overnight Lending Rate | Weekly Repo Rate | The CBRT Average Funding Rate | Interbank Repo Rate | Spread Repo Rate | The CBRT Average Funding Rates and Spread Repo Rate | ||||
| prlor | prolr | prwrr | prafr | prirr | prsrr | prafr prsrr |
||||
| Symmetric ARDL Results | Estimated Coefficients | |||||||||
| α0 | 1.0062** | 1.0353** | 1.0575** | 1.0960** | 1.0184** | 1.6454*** | 1.2542*** | |||
| [2.0526] | [2.3878] | [2.2791] | [2.4615] | [2.2688] | [2.9195] | [2.8327] | ||||
| α1 | -0.0654** | -0.0583* | -0.0752** | -0.1011*** | -0.1359*** | -0.110*** | -0.1340*** | |||
| [-2.1204] | [-1.7917] | [-2.2960] | [-2.6392] | [-3.3555] | [-2.8512] | [-3.2871] | ||||
| α2m | 0.0004 | -0.0127 | 0.0128 | 0.0515 | 0.1098*** | 0.0152 | 0.0755* | |||
| [0.0095] | [-0.3029] | [0.2801] | [1.2928] | [2.9343] | 0.2496 | [1.8546] | ||||
| α3m | - | - | - | - | - | - | 0.1241** | |||
| - | - | - | - | - | [2.0667] | |||||
| LR PT | 0.0061 | -0.2178 | 0.1702 | 0.5094 | 0.8079 | 0.1382 | 0.5634 | |||
| 0.9261 | ||||||||||
| Hypothesis Results | ||||||||||
| H1 | 2.8482 | 2.7502 | 2.8586 | 3.5763 | 6.0638*** | 4.1500* | 5.9093*** | |||
| H3 | 2.6757 | 2.3703 | 2.0087 | 2.4401 | 0.8140 | 2.5445 | 3.5626 | |||
| 0.0297 | ||||||||||
| H5 | 29.8596*** | 29.5263*** | 11.5691*** | 7.2041*** | 9.6966*** | - | 9.7705*** | |||
| Diagnostic Tests | ||||||||||
| R2 | 0.4299 | 0.4296 | 0.3040 | 0.3084 | 0.3424 | 0.2707 | 0.3365 | |||
| DW | 2.1173 | 2.0515 | 2.0099 | 2.1326 | 2.0916 | 1.9526 | 2.0424 | |||
| LM | 0.1963 | 0.2664 | 0.0221 | 0.1243 | 0.1397 | 0.0614 | 0.3184 | |||
| ARCH | 0.6615 | 0.6058 | 0.9963 | 0.9392 | 0.6161 | 0.7603 | 0.6416 | |||
| Asymmetric ARDL Results | Estimated Coefficients | prafr is asymmetric | prsrr is asymmetric | |||||||
| α0 | 1.8079*** | 1.4155*** | 1.4243*** | 2.0300*** | 2.2359*** | 1.1328** | 2.4801*** | 1.7286*** | ||
| [3.9094] | [2.8596] | [2.8791] | [3.4689] | [4.0563] | [2.3075] | [3.7685] | [3.4403] | |||
| α1 | -0.1202*** | -0.0938*** | -0.0961*** | -0.1453*** | -0.1154*** | -0.0931*** | -0.1802*** | -0.1993*** | ||
| [-3.8008] | [-2.9099] | [-2.9029] | [-3.7078] | [-3.1463] | [-2.5970] | [-3.8868] | [-4.4772] | |||
| α2m+ | 0.0277 | -0.0341 | 0.0151 | 0.1274*** | 0.1907*** | 0.0682 | 0.1727*** | 0.1476*** | ||
| [0.6315] | [-0.7416] | [0.2559] | [2.6098] | [6.5638] | [1.0113] | [3.2324] | [2.4662] | |||
| α2m- | 0.0009 | -0.0603 | -0.0118 | 0.1481*** | 0.2401*** | 0.0561 | 0.2041*** | 0.1861*** | ||
| [0.0252] | [-1.5355] | [-0.1255] | [2.4667] | [6.8049] | [0.8646] | [3.1422] | [2.8655] | |||
| α3m | - | - | - | - | - | - | 0.1465*** | 0.2230*** | ||
| - | - | - | - | - | - | [2.2435**] | [4.0446] | |||
| LR PT+ | 0.2304 | -0.3635 | 0.1571 | 0.8768 | 1.6525 | 0.7325 | 0.9584 | 0.7406 | ||
| LR PT- | 0.0075 | -0.6429 | -0.1228 | 1.0193 | 2.0806 | 0.6026 | 1.1326 | 0.9338 | ||
| LR PT | - | - | - | - | - | - | 0.8130 | 1.1189 | ||
| H1 | 5.9618*** | 5.6779*** | 2.9711 | 4.6247** | 15.5440*** | 2.2288 | 4.3920** | 5.5092*** | ||
| H2 | 2.7166 | 2.1288 | 0.3505 | 1.6786 | 17.0857*** | 1.1388 | 3.2973** | 6.0396*** | ||
| H3a | 5.0377** | 6.3346*** | 1.9875 | 0.2201 | 1.9867 | 0.1529 | 0.0313 | 0.9503 | ||
| H3b | 11.8176*** | 9.6388*** | 1.2875 | 0.0031 | 2.1216 | 0.3528 | 0.1941 | 0.0574 | ||
| H4 | 16.1175*** | 6.7968*** | 4.4578** | 7.5113*** | 24.3757*** | 1.9334 | 3.5298 | 8.9545*** | ||
| H5 | 14.9246*** | 7.0354*** | 7.4986*** | 4.7801** | 12.1897*** | 1.3281 | 3.5298 | 3.2923 | ||
| R2 | 0.6288 | 0.5678 | 0.3379 | 0.3434 | 0.6332 | 0.2097 | 0.2001 | 0.3680 | ||
| DW | 1.9601 | 2.0815 | 2.0119 | 2.0096 | 1.8842 | 2.0306 | 1.2253 | 1.9734 | ||
| LM | 0.2912 | 0.5723 | 0.1079 | 0.1536 | 0.0340 | 0.0731 | 0.0068 | 0.7611 | ||
| ARCH | 0.6786 | 0.7191 | 0.9990 | 0.8916 | 0.9661 | 0.6619 | 0.0638 | 0.6342 | ||
| (1) m indicates the policy rates (pp superscript: lor, olr, wrr, afr, irr or srr). (2) α2m+ and α2m- indicate the long-run coefficients of rises and decreases in policy rates, respectively. (3) Values in brackets underneath the cs foefficients are the t-valueor the ***1%, **5% and *10%. (4) H1 denotes the Paseran-Shin-Smith F test statistic values under the hypothesis of H0:α1n=αim=0 for k=2 for the symmetric models and H0:α1n=αim+=αim-=0 for k=3 for the asymmetric models and critical values according to Pesaran et. al (2001) are 3.77, 4.35 and 5.61 for the ***10%, **5% and *1%, respectively, where i={2, 3}. (5) H2 denotes the F-test statistic values under the hypothesis of H0:αim+=αim- where i={2, 3}. (6) H3, H3a and H3b denote the F-test statistic values under the hypothesis of (ⅰ) H0:(αim/-α1n)=1 (ⅱ) H0:(αim+/α1n)=1 and (ⅲ) H0:(αim-/α1n)=1, respectively, where i={2, 3}. (7) H4 denotes the F-test statistic values under the hypothesis of H0:θ0m+=δ0m- for asymmetric models. (8) H5 denotes the F-test statistic values under the hypothesis of H0:θ0m=0 for symmetric models and H0:θ0m+=δ0m-=0 for asymmetric models. (9) R2, DW LM and ARCH rows give adjusted R-square, Durbin-Watson, the p-values of a test for autocorrelation up to lag 12 and a test for ARCH effects up to 12 lags, respectively. | ||||||||||
Focusing on asymmetric models, H2 test results point out that just interbank repo rate can be described as asymmetric where the interbank repo rate is modelled separately. Additionally, the CBRT average funding rate and spread repo rate have also asymmetric impact on the interest rate of consumer loans when they are jointly considered in two different asymmetric models, while the CBRT average funding rate does not in the separately estimated model. When we concentrate on the coefficients of the valid asymmetric models, we may see that the interest rate of the consumer loans response to both positive and negative changes in interbank repo rate. Detail, a 1% rise in interbank repo rate causes interest rate of the consumer loans to rise by 1.65% while a 1% decrease will lead consumer loan rate to fall by 2.08% in the long-run. Regarding the LR-PT values of the asymmetric model for interbank repo rate, H3a and H3b test results point out that the estimated coefficients do not equal to one which means that the LR-PT is over proportionally. If we focus on jointly estimated models, we see that all coefficients are significant, that is to say, a 1% rise in the CBRT average funding rate will increase the interest rate of consumer loans 0.95% while a 1% fall will decrease by 1.13% once the spread repo rate is controlled. Similarly, a 1% rise in spread repo rate will increase the rate of consumer loans by 0.74% while a 1% fall in it will decrease by 0.93%, once the CBRT average funding rate is controlled. These findings imply that the interest rate of consumer loans show more response to negative changes than the positive ones for both the CBRT average funding rate and spread repo rate. That is to say, the response of consumer loan rates to monetary policy is weaker during tightening periods and stronger in easing periods.
Symmetry test (H4) results of valid asymmetric models for short-run coefficients indicate that the short-run symmetry is accepted for both interbank repo rate and one of the joint models for the spread repo rate is controlled. Lastly, H5 hypothesis indicates that adjustment process is immediate just for interbank repo rate. If we interpret H4 and H5 together, we may say that the interest rate of consumer loans immediately, asymmetrically and separately adjust to the changes in interbank repo rate.
Banking Deposit Rate
The results of conventional and asymmetric ARDL analysis for banking deposit rate are given in Table 6. Regarding the results of the conventional part, H1 row indicates that interest rate of banking deposits is not separately cointegrated with the policy rates, but cointegrated with the CBRT average funding rate and spread repo rate when they are jointly estimated. In this model, the interest rate of spread repo has higher magnitude and significance level than the CBRT average funding rate which is unlikely the findings of Binici et al. (2016). Specifically, a 1% change in spread repo rate and the CBRT average funding rate cause interest rate of banking deposits to change by 1.94% and 1.09, respectively. H3 test statistics indicate that both coefficients are not equal to one, which means the LR-PT is over proportionally in the long-run. Since the H5 test result is rejected, we also say that the adjustment process is immediate for these effective policy rates.
| Late Overnight Rate | Overnight Lending Rate | Weekly Repo Rate | The CBRT Average Funding Rate | Interbank Repo Rate | Spread Repo Rate | The CBRT Average Funding Rates and Spread Repo Rate | |||
| prlor | prolr | prwrr | prafr | prirr | prsrr | prafr prsrr |
|||
| Symmetric ARDL Results | Estimated Coefficients | ||||||||
| α0 | 0.7378*** | 0.1881 | -0.0775 | 0.2450 | 0.0132 | 0.3844* | -0.0884 | ||
| 2.7448 | [0.7511] | [-0.3879] | [1.3892] | [0.0763] | [1.7632] | [-0.5709] | |||
| α1 | -0.0322 | -0.0189 | -0.0523** | -0.0934*** | -0.0978*** | -0.0368 | -0.0669* | ||
| [-1.5899] | [-0.8575] | [-1.9551] | [-2.5553] | [-2.8593] | [-1.5770] | [-1.7124] | |||
| α2m | -0.0333 | 0.0024 | 0.0846*** | 0.0775*** | 0.1005*** | -0.0160 | 0.0730** | ||
| [-1.7447] | [0.1086] | [3.5475] | [2.6757] | [3.8544] | [-0.4876] | [2.3140] | |||
| α3m | - | - | - | - | - | - | 0.1301*** | ||
| - | - | - | - | - | - | [5.7197] | |||
| LR PT | -1.0342 | 0.1270 | 1.6176 | 0.8298 | 1.0276 | -0.4348 | 1.0912 | ||
| 1.9447 | |||||||||
| H1 | 3.5474 | 0.3846 | 6.2955*** | 3.6354 | 7.7312*** | 1.4457 | 12.2059*** | ||
| H3 | 4.4012** | 0.5828 | 0.8745 | 1.2396 | 0.0204 | 2.2452 | 0.1144 | ||
| 0.7977 | |||||||||
| H5 | 4.6632** | 4.2564* | 8.6101*** | 24.2045*** | 13.5851*** | 8.1212*** | 22.4438*** | ||
| R2 | 0.6551 | 0.6343 | 0.7592 | 0.7359 | 0.7478 | 0.4263 | 0.8271 | ||
| DW | 1.8612 | 1.9100 | 1.8588 | 1.9195 | 2.2606 | 1.6593 | 1.6254 | ||
| LM | 0.3588 | 0.7013 | 0.0142 | 0.7554 | 0.7290 | 0.0391 | 0.7318 | ||
| ARCH | 0.7290 | 0.5567 | 0.7859 | 0.9670 | 0.1368 | 0.6861 | 0.6697 | ||
| Asymmetric ARDL Results | prafr is asymmetric | prsrr is asymmetric | |||||||
| α0 | 0.4324** | 0.2989 | 1.0987*** | 0.8518*** | 0.6933*** | -0.1525 | 0.0950 | -0.1013 | |
| [1.9558] | [1.3468] | [3.7934] | [2.7277] | [2.4526] | [-0.6959] | [0.2624] | [-0.5255] | ||
| α1 | -0.0608** | -0.0464 | -0.1365*** | -0.0979*** | -0.0647* | -0.0251 | -0.0472 | -0.0636* | |
| [-2.1060] | [-1.0167] | [-4.2841] | [-2.6694] | [-1.7722] | [-0.8987] | [-1.0772] | [-1.7230] | ||
| α2m+ | 0.0103 | -0.0022 | 0.0089 | 0.0729** | 0.1101*** | 0.0264 | 0.0586* | 0.1206*** | |
| [0.3438] | [-0.0981] | [0.2850] | [2.3078] | [4.9830] | [0.8935] | [1.7477] | [5.7663] | ||
| α2m- | -0.0181 | -0.0240 | -0.0661 | 0.0781** | 0.1286*** | 0.0037 | 0.0507 | 0.1257*** | |
| [-0.8417] | [-1.1718] | [-1.4546] | [2.2311] | [5.4940] | [0.1310] | [1.4007] | [5.5279] | ||
| α3m | - | - | - | - | - | - | 0.0993*** | 0.0887*** | |
| - | - | - | - | - | - | [4.3127] | [2.8816] | ||
| LR PT+ | 0.1694 | -0.0474 | 0.0652 | 0.7446 | 1.7017 | 1.0518 | 1.2415 | 1.8962 | |
| LR PT- | -0.2977 | -0.5172 | -0.4842 | 0.7978 | 1.9876 | 0.1474 | 1.0742 | 1.9764 | |
| LR PT | - | - | - | - | - | - | 2.1038 | 1.3947 | |
| H1 | 3.2163 | 2.3629 | 8.9670*** | 2.4453 | 12.5206*** | 3.9921* | 6.9228*** | 9.5999*** | |
| H2 | 4.4992** | 3.6890 | 11.5331*** | 0.6654 | 10.0791*** | 10.0703*** | 0.8751 | 0.6640 | |
| H3a | 3.6116 | 4.3823** | 19.3011*** | 1.8582 | 5.1872** | 0.0012 | 0.1816 | 0.7607 | |
| H3b | 7.5762*** | 6.3286*** | 18.7915*** | 0.8157 | 7.3644*** | 0.3077 | 0.0195 | 0.8171 | |
| H4 | 0.6261 | - | 5.8924*** | 1.9380 | 7.1633*** | - | 6.8106*** | 0.4586 | |
| H5 | 7.9872*** | - | 23.4619*** | 39.5893*** | 8.8415*** | - | 37.4997*** | 11.6265*** | |
| R2 | 0.7798 | 0.5599 | 0.6741 | 0.7454 | 0.8536 | 0.6545 | 0.8133 | 0.8914 | |
| DW | 1.9076 | 1.6706 | 1.5501 | 1.8348 | 1.8634 | 1.9818 | 1.5103 | 2.1036 | |
| LM | 0.1539 | 0.5227 | 0.0343 | 0.6738 | 0.6243 | 0.0229 | 0.4781 | 0.1693 | |
| ARCH | 0.9935 | 0.7437 | 0.9169 | 0.9892 | 0.4406 | 0.0495 | 0.9938 | 0.3570 | |
| (1) m indicates the policy rates (pp superscript: lor, olr, wrr, afr, irr or srr). (2) α2m+ and α2m- indicate the long-run coefficients of rises and decreases in policy rates, respectively. (3) Values in brackets underneath the coefficients are the t-values for the ***1%, **5% and *10%. (4) H1 denotes the Paseran-Shin-Smith F test statistic values under the hypothesis of H0:α1n=αim=0 for k=2 for the symmetric models and H0:α1n=αim+=αim-=0 for k=3 for the asymmetric models and critical values according to Pesaran et. al (2001) are 3.77, 4.35 and 5.61 for the ***10%, **5% and *1%, respectively, where i={2, 3}. (5) H2 denotes the F-test statistic values under the hypothesis of H0:αim+=αim- where i={2, 3}. (6) H3, H3a and H3b denote the F-test statistic values under the hypothesis of (ⅰ) H0:(αim/-α1n)=1 (ⅱ) H0:(αim+/α1n)=1 and (ⅲ) H0:αim-/α1n=1, respectively, where i={2, 3}. (7) H4 denotes the F-test statistic values under the hypothesis of H0:θ0m+=δ0m- for asymmetric models. (8) H5 denotes the F-test statistic values under the hypothesis of H0:θ0m=0 for symmetric models and H0:θ0m+=δ0m-=0 for asymmetric models. (9) R2, DW LM and ARCH rows give adjusted R-square, Durbin-Watson, the p-values of a test for autocorrelation up to lag 12 and a test for ARCH effects up to 12 lags, respectively. | |||||||||
When focusing on the asymmetry in models, we see that just three models suggest the asymmetry in the coefficients for the long-run cointegration process: weekly repo rate, interbank repo rate and spread repo rate. Although two jointly estimated models indicate long-run cointegration (H1 is rejected), the coefficients do not follow asymmetric behaviour in the models since H2 is accepted. When we focus on the significance level and the magnitudes for the valid asymmetric models, we just see that interbank repo rate plays importance in determining the rate of banking deposits and the LR-PT coefficient equal to one in the long-run. The same model indicates that the interest rate of banking deposits immediately, asymmetrically and separately adjusts to the changes in interbank repo rates and jointly to the changes in both the CBRT average funding rate and spread repo rate in the short-run.
In summary, the results of our symmetric and asymmetric ARDL analysis provide insightful findings. Regarding cointegration, we have found that all retail rates are cointegrated with the interbank repo rate which gained importance in this new policy framework to reflect the stance of the monetary policy of the CBRT. Additionally, we found that the interest rate of commercial loans is also cointegrated with the CBRT average funding rate, the interest rate of consumer loans is cointegrated with the spread repo rate and the interest rate of bank deposits is cointegrated with the weekly repo rate. Regarding completeness of long-run pass through (LR-PT), we just concentrated on the significant models of cointegration tests and found that the long-run pass through is complete for all models under investigation. Turning to the short-run pass through (SR-PT), we reached the conclusion that all retail rates show the immediate response to the changes in all policy rates with just one exception (no short-run relationship between commercial loans and overnight lending rate). On the asymmetric side, we provided evidence in favour of asymmetry between all retail rates and interbank repo rates. We also found that the speed of pass-through differs for decreases and rises for interbank repo rates, and the retail rates respond faster to rate cuts than hikes. These findings imply that the interest rate pass-through is complete in the long-run in Turkey during the period of unconventional interest rate corridor and the pricing of loans and deposits are asymmetrically driven by the effective policy rates.
This study investigates the interest rate pass-through from multiple policy rates to various retail rates for the Turkish economy after the CBRT has designed and implemented a new monetary policy strategy at the end of 2010. By applying both conventional and asymmetric cointegration methodologies, we tested for the long-run relationship between the retail rates and multiple policy rates. Our findings have shown that both the CBRT average funding rate and interbank repo rate jointly play important role in the pass-through process.
Based on the data covering the period of unconventional interest rate corridor, our results from conventional ARDL framework revealed that all retail rates are cointegrated with effective policy rates, namely the CBRT average funding rate and interbank repo rates in the long-run. As the CBRT average funding rate and interbank repo rate jointly considered, both the significance level and magnitudes of the coefficients increase. Therefore, the pricing of loans and deposits are driven by the effective policy rates. For the linear models under investigation, the pass-through is almost complete for all retail rates in the long-run which confirms the effectiveness of monetary policy transmission mechanism. Turning to the asymmetric behaviours on retail rates derived from the asymmetric ARDL models, we found that both loans and deposits are cointegrated again with both the CBRT average funding rate and interbank repo rate. We also found that the pass-through differs for decreases and rises for effective policy rates where the retail rates respond faster to policy rate cuts than hikes. According to the long-run pass-through coefficients, the magnitude of the pass-through is nearly complete on all retail rates when the effective policy rates are considered jointly.
In a nutshell, our results confirm the findings of Binici, Kara and Özlü (2016) that interest rates of the CBRT average funding and interbank repo are the main drivers of the retail rates during the period of unconventional interest rate corridor. Therefore, these two rates have potential to assess the monetary policy stance of the CBRT regardless of the success of monetary policy. Moreover, since these policy rates show asymmetric characteristics during this period, we may understand that the adjustment process differs in case of rises and falls for effective policy rates. But it should critically be noted that, unlike the findings of Binici, Kara and Özlü (2016), the response of retail rates to effective policy rates hikes was found lower than to the cuts in our research.
The authors thank the anonymous referees for their valuable comments and suggestions.
The authors declare no conflict of interest.
| [1] |
G. Courthod, M. Tucci, M. Di Maio, G. V. Scagliotti, Papillary renal cell carcinoma: A review of the current therapeutic landscape, Crit. Rev. Oncol./Hematol., 96 (2015), 100–112. https://doi.org/10.1016/j.critrevonc.2015.05.008 doi: 10.1016/j.critrevonc.2015.05.008

|
| [2] |
N. Mendhiratta, P. Muraki, A. E. Sisk Jr, B. Shuch, Papillary renal cell carcinoma: Review, Urol. Oncol.: Semin. Orig. Invest., 39 (2021), 327–337. https://doi.org/10.1016/j.urolonc.2021.04.013 doi: 10.1016/j.urolonc.2021.04.013

|
| [3] |
J. Cheng, Z. Han, R. Mehra, W. Shao, M. Cheng, Q. Feng, et al., Computational analysis of pathological images enables a better diagnosis of TFE3 Xp11.2 translocation renal cell carcinoma, Nat. Commun., 11 (2020), 1778. https://doi.org/10.1038/s41467-020-15671-5 doi: 10.1038/s41467-020-15671-5

|
| [4] |
S. Steffens, M. Janssen, F. C. Roos, F. Becker, S. Schumacher, C. Seidel, et al., Incidence and long-term prognosis of papillary compared to clear cell renal cell carcinoma-a multicentre study, Eur. J. Cancer, 48 (2012), 2347–2352. https://doi.org/10.1016/j.ejca.2012.05.002 doi: 10.1016/j.ejca.2012.05.002

|
| [5] |
Q. Chen, L. Cheng, Q. Li, The molecular characterization and therapeutic strategies of papillary renal cell carcinoma, Expert Rev. Anticancer Ther., 19 (2019), 169–175. https://doi.org/10.1080/14737140.2019.1548939 doi: 10.1080/14737140.2019.1548939

|
| [6] |
M. de Vries-Brilland, D. F. McDermott, C. Suárez, T. Powles, M. Gross-Goupil, A. Ravaud, et al., Checkpoint inhibitors in metastatic papillary renal cell carcinoma, Cancer Treat. Rev., 99 (2021), 102228. https://doi.org/10.1016/j.ctrv.2021.102228 doi: 10.1016/j.ctrv.2021.102228

|
| [7] |
R. Reuten, S. Zendehroud, M. Nicolau, L. Fleischhauer, A. Laitala, S. Kiderlen, et al., Basement membrane stiffness determines metastases formation, Nat. Mater., 20 (2021), 892–903. https://doi.org/10.1038/s41563-020-00894-0 doi: 10.1038/s41563-020-00894-0

|
| [8] |
S. E. Wilson, A. Torricelli, G. K. Marino, Corneal epithelial basement membrane: Structure, function and regeneration, Exp. Eye Res., 194 (2020), 108002. https://doi.org/10.1016/j.exer.2020.108002 doi: 10.1016/j.exer.2020.108002

|
| [9] |
N. Khalilgharibi, Y. Mao, To form and function: on the role of basement membrane mechanics in tissue development, homeostasis and disease, Open Biol., 11 (2021), 200360. https://doi.org/10.1098/rsob.200360 doi: 10.1098/rsob.200360

|
| [10] |
F. Kai, A. P. Drain, V. M. Weaver, The extracellular matrix modulates the metastatic journey, Dev. Cell, 49 (2019), 332–346. https://doi.org/10.1016/j.devcel.2019.03.026 doi: 10.1016/j.devcel.2019.03.026

|
| [11] |
R. W. Naylor, M. Morais, R. Lennon, Complexities of the glomerular basement membrane, Nat. Rev. Nephrol., 17 (2021), 112–127. https://doi.org/10.1038/s41581-020-0329-y doi: 10.1038/s41581-020-0329-y

|
| [12] |
R. Jayadev, M. Morais, J. M. Ellingford, S. Srinivasan, R. W. Naylor, C. Lawless, et al., A basement membrane discovery pipeline uncovers network complexity, regulators, and human disease associations, Sci. Adv., 8 (2022), 2265. https://doi.org/10.1126/sciadv.abn2265 doi: 10.1126/sciadv.abn2265

|
| [13] |
D. Szklarczyk, A. L. Gable, K. C. Nastou, D. Lyon, R. Kirsch, S. Pyysalo, et al., The STRING database in 2021: customizable protein-protein networks, and functional characterization of user-uploaded gene/measurement sets, Nucleic Acids Res., 49 (2021), 605–612. https://doi.org/10.1093/nar/gkaa1074 doi: 10.1093/nar/gkaa1074

|
| [14] |
D. Szklarczyk, A. L. Gable, D. Lyon, A. Junge, S. Wyder, J. Huerta-Cepas, et al., STRING v11: protein-protein association networks with increased coverage, supporting functional discovery in genome-wide experimental datasets, Nucleic Acids Res., 47 (2019), 607–613. https://doi.org/10.1093/nar/gky1131 doi: 10.1093/nar/gky982

|
| [15] |
D. Warde-Farley, S. L. Donaldson, O. Comes, K. Zuberi, R. Badrawi, P. Chao, et al., The GeneMANIA prediction server: biological network integration for gene prioritization and predicting gene function, Nucleic Acids Res., 38 (2010), 214–220. https://doi.org/10.1093/nar/gkq537 doi: 10.1093/nar/gkq537

|
| [16] |
G. Zhou, O. Soufan, J. Ewald, R. Hancock, N. Basu, J. Xia, NetworkAnalyst 3.0: a visual analytics platform for comprehensive gene expression profiling and meta-analysis, Nucleic Acids Res., 47 (2019), 234–241. https://doi.org/10.1093/nar/gkz240 doi: 10.1093/nar/gkz240

|
| [17] |
L. Danilova, W. J. Ho, Q. Zhu, T. Vithayathil, A. De Jesus-Acosta, N. S. Azad, et al., Programmed cell death Ligand-1 (PD-L1) and CD8 expression profiling identify an immunologic subtype of pancreatic ductal adenocarcinomas with favorable survival, Cancer Immunol. Res., 7 (2019), 886–895. https://doi.org/10.1158/2326-6066.CIR-18-0822 doi: 10.1158/2326-6066.CIR-18-0822

|
| [18] |
T. Li, J. Fan, B. Wang, N. Traugh, Q. Chen, J. S. Liu, et al., TIMER: A web server for comprehensive analysis of tumor-infiltrating immune cells, Cancer Res., 77 (2017), 108–110. https://doi.org/10.1158/0008-5472.CAN-17-0307 doi: 10.1158/1538-7445.AM2017-108

|
| [19] |
B. Li, E. Severson, J. C. Pignon, H. Zhao, T. Li, J. Novak, et al., Comprehensive analyses of tumor immunity: implications for cancer immunotherapy, Genome Biol., 17 (2016), 174. https://doi.org/10.1186/s13059-016-1028-7 doi: 10.1186/s13059-016-1028-7

|
| [20] |
E. Y. Chen, C. M. Tan, Y. Kou, Q. Duan, Z. Wang, G. V. Meirelles, et al., Enrichr: interactive and collaborative HTML5 gene list enrichment analysis tool, BMC Bioinformatics, 14 (2013), 128. https://doi.org/10.1186/1471-2105-14-128 doi: 10.1186/1471-2105-14-128

|
| [21] |
M. V. Kuleshov, M. R. Jones, A. D. Rouillard, N. F. Fernandez, Q. Duan, Z. Wang, et al., Enrichr: a comprehensive gene set enrichment analysis web server 2016 update, Nucleic Acids Res., 44 (2016), 90–97. https://doi.org/10.1093/nar/gkw377 doi: 10.1093/nar/gkw377

|
| [22] |
Z. Xie, A. Bailey, M. V. Kuleshov, D. Clarke, J. E. Evangelista, S. L. Jenkins, et al., Gene set knowledge discovery with enrichr, Curr. Protoc., 1 (2021), 90. https://doi.org/10.1002/cpz1.90 doi: 10.1002/cpz1.90

|
| [23] |
D. S. Chandrashekar, S. K. Karthikeyan, P. K. Korla, H. Patel, A. R. Shovon, M. Athar, et al., UALCAN: An update to the integrated cancer data analysis platform, Neoplasia, 25 (2022), 18–27. https://doi.org/10.1016/j.neo.2022.01.001 doi: 10.1016/j.neo.2022.01.001

|
| [24] |
D. S. Chandrashekar, B. Bashel, S. Balasubramanya, C. J. Creighton, I. Ponce-Rodriguez, B. Chakravarthi, et al., UALCAN: A portal for facilitating tumor subgroup gene expression and survival analyses, Neoplasia, 19 (2017), 649–658. https://doi.org/10.1016/j.neo.2017.05.002 doi: 10.1016/j.neo.2017.05.002

|
| [25] |
F. Chen, Y. Zhang, Y. Şenbabaoğlu, G. Ciriello, L. Yang, E. Reznik, et al., Multilevel genomics-based taxonomy of renal cell carcinoma, Cell Rep., 14 (2016), 2476–2489. https://doi.org/10.1016/j.celrep.2016.02.024 doi: 10.1016/j.celrep.2016.02.024

|
| [26] |
T. Klatte, K. M. Gallagher, L. Afferi, A. Volpe, N. Kroeger, S. Ribback, et al., The VENUSS prognostic model to predict disease recurrence following surgery for non-metastatic papillary renal cell carcinoma: development and evaluation using the ASSURE prospective clinical trial cohort, BMC Med., 17 (2019), 182. https://doi.org/10.1186/s12916-019-1419-1 doi: 10.1186/s12916-019-1419-1

|
| [27] |
Y. Bao, L. Wang, L. Shi, F. Yun, X. Liu, Y. Chen, et al., Transcriptome profiling revealed multiple genes and ECM-receptor interaction pathways that may be associated with breast cancer, Cell. Mol. Biol. Lett., 24 (2019), 38. https://doi.org/10.1186/s11658-019-0162-0 doi: 10.1186/s11658-019-0162-0

|
| [28] |
J. Shen, B. Cao, Y. Wang, C. Ma, Z. Zeng, L. Liu, et al., Hippo component YAP promotes focal adhesion and tumour aggressiveness via transcriptionally activating THBS1/FAK signalling in breast cancer, J. Exp. Clin. Cancer. Res., 37 (2018), 175. https://doi.org/10.1186/s13046-018-0850-z doi: 10.1186/s13046-018-0850-z

|
| [29] |
J. A. Fresno Vara, E. Casado, J. de Castro, P. Cejas, C. Belda-Iniesta, M. González-Barón, PI3K/Akt signalling pathway and cancer, Cancer Treat. Rev., 30 (2004), 193–204. https://doi.org/10.1016/j.ctrv.2003.07.007 doi: 10.1016/j.ctrv.2003.07.007

|
| [30] |
C. Xue, G. Li, J. Lu, L. Li, Crosstalk between circRNAs and the PI3K/AKT signaling pathway in cancer progression, Signal Transduct. Target. Ther., 6 (2021), 400. https://doi.org/10.1038/s41392-021-00788-w doi: 10.1038/s41392-021-00788-w

|
| [31] |
R. Kelwick, I. Desanlis, G. N. Wheeler, D. R. Edwards, The ADAMTS (A Disintegrin and Metalloproteinase with Thrombospondin motifs) family, Genome Biol., 16 (2015), 113. https://doi.org/10.1186/s13059-015-0676-3 doi: 10.1186/s13059-015-0676-3

|
| [32] |
M. M. Gomari, M. Farsimadan, N. Rostami, Z. Mahmoudi, M. Fadaie, I. Farhani, et al., CD44 polymorphisms and its variants, as an inconsistent marker in cancer investigations, Mutat. Res. Rev. Mutat. Res., 787 (2021), 108374. https://doi.org/10.1016/j.mrrev.2021.108374 doi: 10.1016/j.mrrev.2021.108374

|
| [33] |
X. Li, X. Ma, L. Chen, L. Gu, Y. Zhang, F. Zhang, et al., Prognostic value of CD44 expression in renal cell carcinoma: a systematic review and meta-analysis, Sci. Rep., 5 (2015), 13157. https://doi.org/10.1038/srep13157 doi: 10.1038/srep13157

|
| [34] |
Y. Yan, X. Zuo, D. Wei, Concise review: Emerging role of CD44 in cancer stem cells: A promising biomarker and therapeutic target, Stem Cells Transl. Med., 4 (2015), 1033–1043. https://doi.org/10.5966/sctm.2015-0048 doi: 10.5966/sctm.2015-0048

|
| [35] |
A. S. Merseburger, J. Hennenlotter, P. Simon, P. A. Ohneseit, U. Kuehs, S. Kruck, et al., Cathepsin D expression in renal cell cancer-clinical implications, Eur. Urol., 48 (2005), 519–526. https://doi.org/10.1016/j.eururo.2005.03.019 doi: 10.1016/j.eururo.2005.03.019

|
| [36] |
I. Romayor, M. L. García-Vaquero, J. Márquez, B. Arteta, R. Barceló, A. Benedicto, Discoidin domain receptor 2 expression as worse prognostic marker in invasive breast cancer, Breast J., 2022 (2022), 5169405. https://doi.org/10.1155/2022/5169405 doi: 10.1155/2022/5169405

|
| [37] |
M. M. Tu, F. Lee, R. T. Jones, A. K. Kimball, E. Saravia, R. F. Graziano, et al., Targeting DDR2 enhances tumor response to anti-PD-1 immunotherapy, Sci. Adv., 5 (2019), 2437. https://doi.org/10.1126/sciadv.aav2437 doi: 10.1126/sciadv.aav2437

|
| [38] |
A. L. Laccetti, B. Garmezy, L. Xiao, M. Economides, A. Venkatesan, J. Gao, et al., Combination antiangiogenic tyrosine kinase inhibition and anti-PD1 immunotherapy in metastatic renal cell carcinoma: A retrospective analysis of safety, tolerance, and clinical outcomes, Cancer Med., 10 (2021), 2341–2349. https://doi.org/10.1002/cam4.3812 doi: 10.1002/cam4.3812

|
| [39] |
M. M. Watany, N. M. Elmashad, R. Badawi, N. Hawash, Serum FBLN1 and STK31 as biomarkers of colorectal cancer and their ability to noninvasively differentiate colorectal cancer from benign polyps, Clin. Chim. Acta., 483 (2018), 151–155. https://doi.org/10.1016/j.cca.2018.04.038 doi: 10.1016/j.cca.2018.04.038

|
| [40] |
W. Xiao, J. Wang, H. Li, W. Guan, D. Xia, G. Yu, et al., Fibulin-1 is down-regulated through promoter hypermethylation and suppresses renal cell carcinoma progression, J. Urol., 190 (2013), 291–301. https://doi.org/10.1016/j.juro.2013.01.098 doi: 10.1016/j.juro.2013.01.098

|
| [41] |
X. Zhou, S. Liang, Q. Zhan, L. Yang, J. Chi, L. Wang, HSPG2 overexpression independently predicts poor survival in patients with acute myeloid leukemia, Cell Death Dis., 11 (2020), 492. https://doi.org/10.1038/s41419-020-2694-7 doi: 10.1038/s41419-020-2694-7

|
| [42] |
J. W. Wragg, J. P. Finnity, J. A. Anderson, H. J. Ferguson, E. Porfiri, R. I. Bhatt, et al., MCAM and LAMA4 are highly enriched in tumor blood vessels of renal cell carcinoma and predict patient outcome, Cancer Res., 76 (2016), 2314–2326. https://doi.org/10.1158/0008-5472.CAN-15-1364 doi: 10.1158/0008-5472.CAN-15-1364

|
| [43] |
X. Chen, X. Li, X. Hu, F. Jiang, Y. Shen, R. Xu, et al., LUM expression and its prognostic significance in gastric cancer, Front. Oncol., 10 (2020), 605. https://doi.org/10.3389/fonc.2020.00605 doi: 10.3389/fonc.2020.00605

|
| [44] |
K. Y. Ng, Q. T. Shea, T. L. Wong, S. T. Luk, M. Tong, C. M. Lo, et al., Chemotherapy-Enriched THBS2-Deficient cancer stem cells drive hepatocarcinogenesis through matrix softness induced histone H3 modifications, Adv. Sci., 8 (2021), 2002483. https://doi.org/10.1002/advs.202002483 doi: 10.1002/advs.202002483

|
| [45] |
S. Zhang, H. Yang, X. Xiang, L. Liu, H. Huang, G. Tang, THBS2 is closely related to the poor prognosis and immune cell infiltration of gastric cancer, Front. Genet., 13 (2022), 803460. https://doi.org/10.3389/fgene.2022.803460 doi: 10.3389/fgene.2022.803460

|
| [46] |
Y. Shou, Y. Liu, J. Xu, J. Liu, T. Xu, J. Tong, et al., TIMP1 indicates poor prognosis of renal cell carcinoma and accelerates tumorigenesis via EMT signaling pathway, Front. Genet., 13 (2022), 648134. https://doi.org/10.3389/fgene.2022.648134 doi: 10.3389/fgene.2022.648134

|
| [47] |
T. Simon, J. S. Bromberg, Regulation of the immune system by laminins, Trends Immunol., 38 (2017), 858–871. https://doi.org/10.1016/j.it.2017.06.002 doi: 10.1016/j.it.2017.06.002

|
| [48] |
Z. Gong, J. Xie, L. Chen, Q. Tang, Y. Hu, A. Xu, et al., Integrative analysis of TRPV family to prognosis and immune infiltration in renal clear cell carcinoma, Channels, 16 (2022), 84–96. https://doi.org/10.1080/19336950.2022.2058733 doi: 10.1080/19336950.2022.2058733

|
| [49] |
S. Negrier, N. Rioux-Leclercq, C. Ferlay, M. Gross-Goupil, G. Gravis, L. Geoffrois, et al., Axitinib in first-line for patients with metastatic papillary renal cell carcinoma: Results of the multicentre, open-label, single-arm, phase Ⅱ AXIPAP trial, Eur. J. Cancer, 129 (2020), 107–116. https://doi.org/10.1016/j.ejca.2020.02.001 doi: 10.1016/j.ejca.2020.02.001

|
| [50] |
M. S. Gordon, M. Hussey, R. B. Nagle, P. N. Lara Jr, P. C. Mack, J. Dutcher, et al., Phase Ⅱ study of erlotinib in patients with locally advanced or metastatic papillary histology renal cell cancer: SWOG S0317, J. Clin. Oncol., 27 (2009), 5788–5793. https://doi.org/10.1200/JCO.2008.18.8821 doi: 10.1200/JCO.2008.18.8821

|
| [51] |
J. E. Megías-Vericat, D. Martínez-Cuadrón, A. Solana-Altabella, J. L. Poveda, P. Montesinos, Systematic review of pharmacogenetics of ABC and SLC transporter genes in acute myeloid leukemia, Pharmaceutics, 14 (2022), 878. https://doi.org/10.3390/pharmaceutics14040878 doi: 10.3390/pharmaceutics14040878

|
| [52] |
M. Morais, P. Tian, C. Lawless, S. Murtuza-Baker, L. Hopkinson, S. Woods, et al., Kidney organoids recapitulate human basement membrane assembly in health and disease, Elife, 11 (2022), 73486. https://doi.org/10.7554/eLife.73486 doi: 10.7554/eLife.73486

|
| [53] |
S. Mikami, M. Oya, R. Mizuno, T. Kosaka, K. Katsube, Y. Okada, Invasion and metastasis of renal cell carcinoma, Med. Mol. Morphol., 47 (2014), 63–67. https://doi.org/10.1007/s00795-013-0064-6 doi: 10.1007/s00795-013-0064-6

|
| [54] |
Y. Li, H. Liu, H. Yan, J. Xiong, Research advances on targeted-Treg therapies on immune-mediated kidney diseases, Autoimmun. Rev., 22 (2023), 103257. https://doi.org/10.1016/j.autrev.2022.103257 doi: 10.1016/j.autrev.2022.103257

|
 mbe-20-06-474-supplementary.zip mbe-20-06-474-supplementary.zip |
 |
| 1. | Xuezhou Zhang, Baoan Hong, Hongwei Li, Jiahui Zhao, Mingchuan Li, Dechao Wei, Yongxing Wang, Ning Zhang, Basement membrane-related MMP14 predicts poor prognosis and response to immunotherapy in bladder cancer, 2024, 24, 1471-2407, 10.1186/s12885-024-12489-y |
| Mean | Max. | Min. | Std. Dev. | JB | Prob. | Obs. | |
| Retail Rates (Bank Level Variables) | |||||||
| rrlpr | 14.65 | 18.23 | 10.00 | 2.00 | 4.72 | 0.09 | 84 |
| rrlcr | 13.50 | 17.07 | 8.42 | 2.21 | 4.91 | 0.09 | 84 |
| rrbdr | 9.31 | 12.36 | 5.95 | 1.48 | 1.16* | 0.56 | 84 |
| Policy Rates (Short-term Interest Rates) | |||||||
| prlor | 12.24 | 15.50 | 9.50 | 1.52 | 1.61* | 0.45 | 84 |
| prolr | 9.89 | 12.50 | 6.50 | 1.52 | 2.82* | 0.24 | 84 |
| prwrr | 6.92 | 10.00 | 4.50 | 1.40 | 1.40* | 0.50 | 84 |
| probr | 5.86 | 8.00 | 1.50 | 1.94 | 11.45 | 0.00 | 84 |
| prafr | 8.22 | 12.75 | 4.52 | 1.98 | 3.10* | 0.21 | 84 |
| prirr | 9.22 | 12.50 | 4.66 | 2.17 | 5.84 | 0.05 | 84 |
| prsrr | 1.00 | 4.04 | -1.77 | 1.10 | 1.42* | 0.49 | 84 |
| *Note: Indicates that the normality has rejected at 10% level. | |||||||
| Levels | Differences | ||||||
| No intercept, no trend | Intercept, no trend | Interceptand trend | No intercept, no trend | Intercept, no trend | Interceptand trend | ||
| Retail Rates (Bank Level Variables) | |||||||
| rrlpr | 0.4511 | -2.4146 | -2.5710 | ∆rrlpr | -5.6056*** | -5.6431*** | -4.8207*** |
| rrlcr | 0.5168 | -2.5556 | -3.3327* | ∆rrlcr | -5.5980*** | -5.6660*** | -5.6332*** |
| rrbdr | 0.0854 | -2.3887 | -2.9397 | ∆rrbdr | -6.5439*** | -6.5479*** | -6.5073*** |
| Policy Rates (Short-term Interest Rates) | |||||||
| prlor | 0.2348 | -2.6818* | -2.8660 | ∆prlor | -6.7105*** | -6.6695*** | -6.6273*** |
| prolr | 0.3266 | -2.4953 | -2.5273 | ∆prolr | -6.6151*** | -6.5742*** | -6.5491*** |
| prwrr | 0.0559 | -1.8096 | -2.4463 | ∆prwrr | -7.8103*** | -7.7117*** | -7.7240*** |
| probr | 0.3662 | -2.2433 | -2.3116 | ∆probr | -7.8699*** | -7.9270*** | -7.9743*** |
| prafr | 0.7480 | -0.9913 | -2.1267 | ∆prafr | -8.3476*** | -8.3934*** | -8.3866*** |
| prirr | 0.0854 | -2.3887 | -2.9397 | ∆prirr | -6.5439*** | -6.5479*** | -6.5073*** |
| prsrr | -1.7157* | -2.3847 | -2.5435 | ∆prsrr | -12.848*** | -12.769*** | -12.751*** |
| *Note: Reported figures are the Augmented Dickey-Fuller (ADF) test statistics where (***), (**), and (*) indicate rejection of the null hypothesis of a unit root at 1%, 5%, and 10% levels of significance, respectively. The optimal lags were chosen using Schwarz Information Criterion with a maximum lag of 13. | |||||||
| Late Overnight Rate | Overnight Lending Rate | Weekly Repo Rate | The CBRT Average Funding Rate | Interbank Repo Rate | Spread Repo Rate | The CBRT Average Funding Rates and Spread Repo Rate | ||
| prlor | prolr | prwrr | prafr | prirr | prsrr | prafr | prsrr | |
| Dependent Variables | ||||||||
| rrlcr | 0.7717 | 0.3401 | 12.2392*** | 3.3493 | 12.2703*** | 0.4583 | 5.3763*** | 15.4190*** |
| rrlpr | 2.7166 | 2.1288 | 0.3505 | 1.6786 | 17.0857*** | 1.1388 | 3.2973** | 6.0396*** |
| rrbdr | 4.4992** | 3.6890 | 11.5331*** | 0.6654 | 10.0791*** | 10.0703*** | 0.8751 | 0.6640 |
| *Note: (1) The null hypothesis for long-run symmetry is H0:α2m+=α3m-. (2) ***, ** and * indicates the rejection of the null hypothesis at the 1%, 5% and 10% level, respectively. | ||||||||
| Late Overnight Rate | Overnight Lending Rate | Weekly Repo Rate | The CBRT Average Funding Rate | Interbank Repo Rate | Spread Repo Rate | The CBRT Average Funding Rates and Spread Repo Rate | ||||
| prlor | prolr | prwrr | prafr | prirr | prsrr | prafr prsrr |
||||
| Symmetric ARDL Results | Estimated Coefficients | |||||||||
| α0 | 0.6391 | 0.5261 | 0.7899* | 1.1633*** | 0.8570** | 0.6677 | 1.3735*** | |||
| [1.1840] | [0.9719] | [1.6420] | [3.0553] | [2.1804] | [1.2918] | [3.1522] | ||||
| α1 | -0.0524* | -0.0412 | -0.0773* | -0.1561*** | -0.1550*** | -0.0361 | -0.2723*** | |||
| [-1.8417] | [-1.1508] | [-1.7913] | [-3.4271] | [-3.7575] | [-0.9648] | [-5.7212] | ||||
| α2m | 0.0136 | 0.0083 | 0.0463 | 0.1219** | 0.1404*** | -0.1016 | 0.2617*** | |||
| [0.3279] | [0.1775] | [0.8634] | [2.3514] | [3.3625] | [-1.6366] | [5.6591] | ||||
| α3m | - | - | - | - | - | - | 0.2138*** | |||
| - | - | - | - | - | [3.6437] | |||||
| LR PT | 0.2595 | 0.2015 | 0.5990 | 0.7809 | 0.9058 | -2.8144 | 0.9611 | |||
| 0.7852 | ||||||||||
| Hypothesis Results | ||||||||||
| H1 | 1.7227 | 0.0662 | 1.6380 | 6.0811*** | 7.5142*** | 1.9850 | 13.5805*** | |||
| H3 | 0.9480 | 0.5537 | 0.5071 | 1.1617 | 0.2367 | 1.1648 | 0.1140 | |||
| 0.9257 | ||||||||||
| H5 | 18.1668*** | 3.1362 | 15.7615*** | 9.1506*** | 11.9508*** | 4.6862** | 6.1690*** | |||
| Diagnostic Tests | ||||||||||
| R2 | 0.3517 | 0.3866 | 0.4237 | 0.3958 | 0.3766 | 0.3391 | 0.5614 | |||
| DW | 1.8948 | 1.5913 | 1.4012 | 1.9681 | 1.9498 | 1.9050 | 2.0175 | |||
| LM | 0.0903 | 0.8150 | 0.5493 | 0.6952 | 0.2163 | 0.7555 | 0.5601 | |||
| ARCH | 0.7971 | 0.6597 | 0.2954 | 0.2673 | 0.2267 | 0.2994 | 0.6684 | |||
| Asymmetric ARDL Results | Estimated Coefficients | prafr is asymmetric | prsrr is asymmetric | |||||||
| α0 | 1.3895*** | 0.2001 | 2.9919*** | 1.1166 | 2.5707*** | 1.1512** | 2.5770*** | 2.0955*** | ||
| [2.5883] | [0.3437] | [4.7284] | [1.5066] | [4.1789] | [2.2189] | [3.9523] | [5.7302] | |||
| α1 | -0.1028 | -0.0263 | -0.2480*** | -0.1398*** | -0.1559*** | -0.0894* | -0.2134*** | -0.3081*** | ||
| [-2.0819] | [-0.5690] | [-5.3671] | [-2.6333] | [-3.3184] | [-1.9185] | [-4.2401] | [-8.1644] | |||
| α2m+ | 0.0326 | 0.0247 | 0.0067 | 0.1008* | 0.2740*** | 0.0415 | 0.2433*** | 0.2856*** | ||
| [0.4930] | [0.3870] | [0.1055] | [1.7554] | [6.2948] | [0.5861] | [4.4293] | [5.9244] | |||
| α2m- | 0.0081 | 0.0074 | -0.1677* | 0.0666 | 0.3314*** | 0.0309 | 0.2722*** | 0.3396*** | ||
| [0.1689] | [0.1434] | [-1.6659] | [0.9722] | [6.3600] | [0.4583] | [4.1523] | [6.6249] | |||
| α3m | - | - | - | - | - | - | 0.2054*** | 0.3837*** | ||
| - | - | - | - | - | - | [3.7042] | [8.5194] | |||
| LR PT+ | 0.3171 | 0.9392 | 0.0270 | 0.7210 | 1.7575 | 0.4642 | 1.1401 | 0.9270 | ||
| LR PT- | 0.0788 | 0.2814 | -0.6762 | 0.4764 | 2.1257 | 0.3456 | 1.2755 | 1.1022 | ||
| LR PT | - | - | - | - | - | - | 0.9625 | 1.2454 | ||
| Hypothesis Results | ||||||||||
| H1 | 2.2552 | 0.1473 | 12.3678*** | 4.6984** | 13.6548*** | 1.4565 | 8.3178*** | 23.4957*** | ||
| H2 | 0.7717 | 0.3401 | 12.2392*** | 3.3493 | 12.2703*** | 0.4583 | 5.3763*** | 15.4190*** | ||
| H3a | 1.5772 | 0.0007 | 14.8815*** | 1.0690 | 3.1389 | 0.4954 | 0.5131 | 0.2015 | ||
| H3b | 4.2584** | 0.1476 | 13.8961*** | 1.8444 | 3.1866 | 0.7563 | 1.0682 | 0.3226 | ||
| H4 | 2.2718 | 2.5955 | 6.0869*** | 7.2922*** | 11.5664*** | - | 8.0668*** | 47.7121*** | ||
| H5 | 20.5590*** | 7.9546*** | 3.1243 | 21.2726*** | 6.7580*** | - | 15.2799*** | 15.6532*** | ||
| Diagnostic Tests | ||||||||||
| R2 | 0.3491 | 0.3618 | 0.5770 | 0.4809 | 0.5458 | 0.0166 | 0.4956 | 0.7654 | ||
| DW | 1.8844 | 1.6931 | 2.0610 | 2.0182 | 1.9810 | 1.1308 | 1.6582 | 2.1151 | ||
| LM | 0.5624 | 0.9177 | 0.9677 | 0.6528 | 0.8735 | 0.0046 | 0.3056 | 0.1630 | ||
| ARCH | 0.5515 | 0.5910 | 0.1947 | 0.5055 | 0.0300 | 0.2127 | 0.7336 | 0.5459 | ||
| (1) m indicates the policy rates (pp superscript: lor, olr, wrr, afr, irr or srr). (2) α2m+ and α2m- indicate the long-run coefficients of rises and decreases in policy rates, respectively. (3) Values in brackets underneath the coefficients are the t-values for the ***1%, **5% and *10%. (4) H1 denotes the Paseran-Shin-Smith F test statistic values under the hypothesis of H0:α1n=αim=0 for k=2 for the symmetric models and H0:α1n=αim+=αim-=0 for k=3 for the asymmetric models and critical values according to Pesaran et. al (2001) are 3.77, 4.35 and 5.61 for the ***10%, **5% and *1%, respectively, where i={2, 3}. (5) H2 denotes the F-test statistic values under the hypothesis of H0:αim+=αim- where i={2, 3}. (6) H3, H3a and H3b denote the F-test statistic values under the hypothesis of (ⅰ) H0:(αim/-α1n)=1 (ⅱ) H0:(αim+/α1n)=1 and (ⅲ) H0:(αim-/α1n)=1, respectively, where i={2, 3}. (7) H4 denotes the F-test statistic values under the hypothesis of H0:θ0m+=δ0m- for asymmetric models. (8) H5 denotes the F-test statistic values under the hypothesis of H0:θ0m=0 for symmetric models and H0:θ0m+=δ0m-=0 for asymmetric models. (9) R2, DW LM and ARCH rows give adjusted R-square, Durbin-Watson, the p-values of a test for autocorrelation up to lag 12 and a test for ARCH effects up to 12 lags, respectively. | ||||||||||
| Late Overnight Rate | Overnight Lending Rate | Weekly Repo Rate | The CBRT Average Funding Rate | Interbank Repo Rate | Spread Repo Rate | The CBRT Average Funding Rates and Spread Repo Rate | ||||
| prlor | prolr | prwrr | prafr | prirr | prsrr | prafr prsrr |
||||
| Symmetric ARDL Results | Estimated Coefficients | |||||||||
| α0 | 1.0062** | 1.0353** | 1.0575** | 1.0960** | 1.0184** | 1.6454*** | 1.2542*** | |||
| [2.0526] | [2.3878] | [2.2791] | [2.4615] | [2.2688] | [2.9195] | [2.8327] | ||||
| α1 | -0.0654** | -0.0583* | -0.0752** | -0.1011*** | -0.1359*** | -0.110*** | -0.1340*** | |||
| [-2.1204] | [-1.7917] | [-2.2960] | [-2.6392] | [-3.3555] | [-2.8512] | [-3.2871] | ||||
| α2m | 0.0004 | -0.0127 | 0.0128 | 0.0515 | 0.1098*** | 0.0152 | 0.0755* | |||
| [0.0095] | [-0.3029] | [0.2801] | [1.2928] | [2.9343] | 0.2496 | [1.8546] | ||||
| α3m | - | - | - | - | - | - | 0.1241** | |||
| - | - | - | - | - | [2.0667] | |||||
| LR PT | 0.0061 | -0.2178 | 0.1702 | 0.5094 | 0.8079 | 0.1382 | 0.5634 | |||
| 0.9261 | ||||||||||
| Hypothesis Results | ||||||||||
| H1 | 2.8482 | 2.7502 | 2.8586 | 3.5763 | 6.0638*** | 4.1500* | 5.9093*** | |||
| H3 | 2.6757 | 2.3703 | 2.0087 | 2.4401 | 0.8140 | 2.5445 | 3.5626 | |||
| 0.0297 | ||||||||||
| H5 | 29.8596*** | 29.5263*** | 11.5691*** | 7.2041*** | 9.6966*** | - | 9.7705*** | |||
| Diagnostic Tests | ||||||||||
| R2 | 0.4299 | 0.4296 | 0.3040 | 0.3084 | 0.3424 | 0.2707 | 0.3365 | |||
| DW | 2.1173 | 2.0515 | 2.0099 | 2.1326 | 2.0916 | 1.9526 | 2.0424 | |||
| LM | 0.1963 | 0.2664 | 0.0221 | 0.1243 | 0.1397 | 0.0614 | 0.3184 | |||
| ARCH | 0.6615 | 0.6058 | 0.9963 | 0.9392 | 0.6161 | 0.7603 | 0.6416 | |||
| Asymmetric ARDL Results | Estimated Coefficients | prafr is asymmetric | prsrr is asymmetric | |||||||
| α0 | 1.8079*** | 1.4155*** | 1.4243*** | 2.0300*** | 2.2359*** | 1.1328** | 2.4801*** | 1.7286*** | ||
| [3.9094] | [2.8596] | [2.8791] | [3.4689] | [4.0563] | [2.3075] | [3.7685] | [3.4403] | |||
| α1 | -0.1202*** | -0.0938*** | -0.0961*** | -0.1453*** | -0.1154*** | -0.0931*** | -0.1802*** | -0.1993*** | ||
| [-3.8008] | [-2.9099] | [-2.9029] | [-3.7078] | [-3.1463] | [-2.5970] | [-3.8868] | [-4.4772] | |||
| α2m+ | 0.0277 | -0.0341 | 0.0151 | 0.1274*** | 0.1907*** | 0.0682 | 0.1727*** | 0.1476*** | ||
| [0.6315] | [-0.7416] | [0.2559] | [2.6098] | [6.5638] | [1.0113] | [3.2324] | [2.4662] | |||
| α2m- | 0.0009 | -0.0603 | -0.0118 | 0.1481*** | 0.2401*** | 0.0561 | 0.2041*** | 0.1861*** | ||
| [0.0252] | [-1.5355] | [-0.1255] | [2.4667] | [6.8049] | [0.8646] | [3.1422] | [2.8655] | |||
| α3m | - | - | - | - | - | - | 0.1465*** | 0.2230*** | ||
| - | - | - | - | - | - | [2.2435**] | [4.0446] | |||
| LR PT+ | 0.2304 | -0.3635 | 0.1571 | 0.8768 | 1.6525 | 0.7325 | 0.9584 | 0.7406 | ||
| LR PT- | 0.0075 | -0.6429 | -0.1228 | 1.0193 | 2.0806 | 0.6026 | 1.1326 | 0.9338 | ||
| LR PT | - | - | - | - | - | - | 0.8130 | 1.1189 | ||
| H1 | 5.9618*** | 5.6779*** | 2.9711 | 4.6247** | 15.5440*** | 2.2288 | 4.3920** | 5.5092*** | ||
| H2 | 2.7166 | 2.1288 | 0.3505 | 1.6786 | 17.0857*** | 1.1388 | 3.2973** | 6.0396*** | ||
| H3a | 5.0377** | 6.3346*** | 1.9875 | 0.2201 | 1.9867 | 0.1529 | 0.0313 | 0.9503 | ||
| H3b | 11.8176*** | 9.6388*** | 1.2875 | 0.0031 | 2.1216 | 0.3528 | 0.1941 | 0.0574 | ||
| H4 | 16.1175*** | 6.7968*** | 4.4578** | 7.5113*** | 24.3757*** | 1.9334 | 3.5298 | 8.9545*** | ||
| H5 | 14.9246*** | 7.0354*** | 7.4986*** | 4.7801** | 12.1897*** | 1.3281 | 3.5298 | 3.2923 | ||
| R2 | 0.6288 | 0.5678 | 0.3379 | 0.3434 | 0.6332 | 0.2097 | 0.2001 | 0.3680 | ||
| DW | 1.9601 | 2.0815 | 2.0119 | 2.0096 | 1.8842 | 2.0306 | 1.2253 | 1.9734 | ||
| LM | 0.2912 | 0.5723 | 0.1079 | 0.1536 | 0.0340 | 0.0731 | 0.0068 | 0.7611 | ||
| ARCH | 0.6786 | 0.7191 | 0.9990 | 0.8916 | 0.9661 | 0.6619 | 0.0638 | 0.6342 | ||
| (1) m indicates the policy rates (pp superscript: lor, olr, wrr, afr, irr or srr). (2) α2m+ and α2m- indicate the long-run coefficients of rises and decreases in policy rates, respectively. (3) Values in brackets underneath the cs foefficients are the t-valueor the ***1%, **5% and *10%. (4) H1 denotes the Paseran-Shin-Smith F test statistic values under the hypothesis of H0:α1n=αim=0 for k=2 for the symmetric models and H0:α1n=αim+=αim-=0 for k=3 for the asymmetric models and critical values according to Pesaran et. al (2001) are 3.77, 4.35 and 5.61 for the ***10%, **5% and *1%, respectively, where i={2, 3}. (5) H2 denotes the F-test statistic values under the hypothesis of H0:αim+=αim- where i={2, 3}. (6) H3, H3a and H3b denote the F-test statistic values under the hypothesis of (ⅰ) H0:(αim/-α1n)=1 (ⅱ) H0:(αim+/α1n)=1 and (ⅲ) H0:(αim-/α1n)=1, respectively, where i={2, 3}. (7) H4 denotes the F-test statistic values under the hypothesis of H0:θ0m+=δ0m- for asymmetric models. (8) H5 denotes the F-test statistic values under the hypothesis of H0:θ0m=0 for symmetric models and H0:θ0m+=δ0m-=0 for asymmetric models. (9) R2, DW LM and ARCH rows give adjusted R-square, Durbin-Watson, the p-values of a test for autocorrelation up to lag 12 and a test for ARCH effects up to 12 lags, respectively. | ||||||||||
| Late Overnight Rate | Overnight Lending Rate | Weekly Repo Rate | The CBRT Average Funding Rate | Interbank Repo Rate | Spread Repo Rate | The CBRT Average Funding Rates and Spread Repo Rate | |||
| prlor | prolr | prwrr | prafr | prirr | prsrr | prafr prsrr |
|||
| Symmetric ARDL Results | Estimated Coefficients | ||||||||
| α0 | 0.7378*** | 0.1881 | -0.0775 | 0.2450 | 0.0132 | 0.3844* | -0.0884 | ||
| 2.7448 | [0.7511] | [-0.3879] | [1.3892] | [0.0763] | [1.7632] | [-0.5709] | |||
| α1 | -0.0322 | -0.0189 | -0.0523** | -0.0934*** | -0.0978*** | -0.0368 | -0.0669* | ||
| [-1.5899] | [-0.8575] | [-1.9551] | [-2.5553] | [-2.8593] | [-1.5770] | [-1.7124] | |||
| α2m | -0.0333 | 0.0024 | 0.0846*** | 0.0775*** | 0.1005*** | -0.0160 | 0.0730** | ||
| [-1.7447] | [0.1086] | [3.5475] | [2.6757] | [3.8544] | [-0.4876] | [2.3140] | |||
| α3m | - | - | - | - | - | - | 0.1301*** | ||
| - | - | - | - | - | - | [5.7197] | |||
| LR PT | -1.0342 | 0.1270 | 1.6176 | 0.8298 | 1.0276 | -0.4348 | 1.0912 | ||
| 1.9447 | |||||||||
| H1 | 3.5474 | 0.3846 | 6.2955*** | 3.6354 | 7.7312*** | 1.4457 | 12.2059*** | ||
| H3 | 4.4012** | 0.5828 | 0.8745 | 1.2396 | 0.0204 | 2.2452 | 0.1144 | ||
| 0.7977 | |||||||||
| H5 | 4.6632** | 4.2564* | 8.6101*** | 24.2045*** | 13.5851*** | 8.1212*** | 22.4438*** | ||
| R2 | 0.6551 | 0.6343 | 0.7592 | 0.7359 | 0.7478 | 0.4263 | 0.8271 | ||
| DW | 1.8612 | 1.9100 | 1.8588 | 1.9195 | 2.2606 | 1.6593 | 1.6254 | ||
| LM | 0.3588 | 0.7013 | 0.0142 | 0.7554 | 0.7290 | 0.0391 | 0.7318 | ||
| ARCH | 0.7290 | 0.5567 | 0.7859 | 0.9670 | 0.1368 | 0.6861 | 0.6697 | ||
| Asymmetric ARDL Results | prafr is asymmetric | prsrr is asymmetric | |||||||
| α0 | 0.4324** | 0.2989 | 1.0987*** | 0.8518*** | 0.6933*** | -0.1525 | 0.0950 | -0.1013 | |
| [1.9558] | [1.3468] | [3.7934] | [2.7277] | [2.4526] | [-0.6959] | [0.2624] | [-0.5255] | ||
| α1 | -0.0608** | -0.0464 | -0.1365*** | -0.0979*** | -0.0647* | -0.0251 | -0.0472 | -0.0636* | |
| [-2.1060] | [-1.0167] | [-4.2841] | [-2.6694] | [-1.7722] | [-0.8987] | [-1.0772] | [-1.7230] | ||
| α2m+ | 0.0103 | -0.0022 | 0.0089 | 0.0729** | 0.1101*** | 0.0264 | 0.0586* | 0.1206*** | |
| [0.3438] | [-0.0981] | [0.2850] | [2.3078] | [4.9830] | [0.8935] | [1.7477] | [5.7663] | ||
| α2m- | -0.0181 | -0.0240 | -0.0661 | 0.0781** | 0.1286*** | 0.0037 | 0.0507 | 0.1257*** | |
| [-0.8417] | [-1.1718] | [-1.4546] | [2.2311] | [5.4940] | [0.1310] | [1.4007] | [5.5279] | ||
| α3m | - | - | - | - | - | - | 0.0993*** | 0.0887*** | |
| - | - | - | - | - | - | [4.3127] | [2.8816] | ||
| LR PT+ | 0.1694 | -0.0474 | 0.0652 | 0.7446 | 1.7017 | 1.0518 | 1.2415 | 1.8962 | |
| LR PT- | -0.2977 | -0.5172 | -0.4842 | 0.7978 | 1.9876 | 0.1474 | 1.0742 | 1.9764 | |
| LR PT | - | - | - | - | - | - | 2.1038 | 1.3947 | |
| H1 | 3.2163 | 2.3629 | 8.9670*** | 2.4453 | 12.5206*** | 3.9921* | 6.9228*** | 9.5999*** | |
| H2 | 4.4992** | 3.6890 | 11.5331*** | 0.6654 | 10.0791*** | 10.0703*** | 0.8751 | 0.6640 | |
| H3a | 3.6116 | 4.3823** | 19.3011*** | 1.8582 | 5.1872** | 0.0012 | 0.1816 | 0.7607 | |
| H3b | 7.5762*** | 6.3286*** | 18.7915*** | 0.8157 | 7.3644*** | 0.3077 | 0.0195 | 0.8171 | |
| H4 | 0.6261 | - | 5.8924*** | 1.9380 | 7.1633*** | - | 6.8106*** | 0.4586 | |
| H5 | 7.9872*** | - | 23.4619*** | 39.5893*** | 8.8415*** | - | 37.4997*** | 11.6265*** | |
| R2 | 0.7798 | 0.5599 | 0.6741 | 0.7454 | 0.8536 | 0.6545 | 0.8133 | 0.8914 | |
| DW | 1.9076 | 1.6706 | 1.5501 | 1.8348 | 1.8634 | 1.9818 | 1.5103 | 2.1036 | |
| LM | 0.1539 | 0.5227 | 0.0343 | 0.6738 | 0.6243 | 0.0229 | 0.4781 | 0.1693 | |
| ARCH | 0.9935 | 0.7437 | 0.9169 | 0.9892 | 0.4406 | 0.0495 | 0.9938 | 0.3570 | |
| (1) m indicates the policy rates (pp superscript: lor, olr, wrr, afr, irr or srr). (2) α2m+ and α2m- indicate the long-run coefficients of rises and decreases in policy rates, respectively. (3) Values in brackets underneath the coefficients are the t-values for the ***1%, **5% and *10%. (4) H1 denotes the Paseran-Shin-Smith F test statistic values under the hypothesis of H0:α1n=αim=0 for k=2 for the symmetric models and H0:α1n=αim+=αim-=0 for k=3 for the asymmetric models and critical values according to Pesaran et. al (2001) are 3.77, 4.35 and 5.61 for the ***10%, **5% and *1%, respectively, where i={2, 3}. (5) H2 denotes the F-test statistic values under the hypothesis of H0:αim+=αim- where i={2, 3}. (6) H3, H3a and H3b denote the F-test statistic values under the hypothesis of (ⅰ) H0:(αim/-α1n)=1 (ⅱ) H0:(αim+/α1n)=1 and (ⅲ) H0:αim-/α1n=1, respectively, where i={2, 3}. (7) H4 denotes the F-test statistic values under the hypothesis of H0:θ0m+=δ0m- for asymmetric models. (8) H5 denotes the F-test statistic values under the hypothesis of H0:θ0m=0 for symmetric models and H0:θ0m+=δ0m-=0 for asymmetric models. (9) R2, DW LM and ARCH rows give adjusted R-square, Durbin-Watson, the p-values of a test for autocorrelation up to lag 12 and a test for ARCH effects up to 12 lags, respectively. | |||||||||
| Mean | Max. | Min. | Std. Dev. | JB | Prob. | Obs. | |
| Retail Rates (Bank Level Variables) | |||||||
| rrlpr | 14.65 | 18.23 | 10.00 | 2.00 | 4.72 | 0.09 | 84 |
| rrlcr | 13.50 | 17.07 | 8.42 | 2.21 | 4.91 | 0.09 | 84 |
| rrbdr | 9.31 | 12.36 | 5.95 | 1.48 | 1.16* | 0.56 | 84 |
| Policy Rates (Short-term Interest Rates) | |||||||
| prlor | 12.24 | 15.50 | 9.50 | 1.52 | 1.61* | 0.45 | 84 |
| prolr | 9.89 | 12.50 | 6.50 | 1.52 | 2.82* | 0.24 | 84 |
| prwrr | 6.92 | 10.00 | 4.50 | 1.40 | 1.40* | 0.50 | 84 |
| probr | 5.86 | 8.00 | 1.50 | 1.94 | 11.45 | 0.00 | 84 |
| prafr | 8.22 | 12.75 | 4.52 | 1.98 | 3.10* | 0.21 | 84 |
| prirr | 9.22 | 12.50 | 4.66 | 2.17 | 5.84 | 0.05 | 84 |
| prsrr | 1.00 | 4.04 | -1.77 | 1.10 | 1.42* | 0.49 | 84 |
| *Note: Indicates that the normality has rejected at 10% level. | |||||||
| Levels | Differences | ||||||
| No intercept, no trend | Intercept, no trend | Interceptand trend | No intercept, no trend | Intercept, no trend | Interceptand trend | ||
| Retail Rates (Bank Level Variables) | |||||||
| rrlpr | 0.4511 | -2.4146 | -2.5710 | ∆rrlpr | -5.6056*** | -5.6431*** | -4.8207*** |
| rrlcr | 0.5168 | -2.5556 | -3.3327* | ∆rrlcr | -5.5980*** | -5.6660*** | -5.6332*** |
| rrbdr | 0.0854 | -2.3887 | -2.9397 | ∆rrbdr | -6.5439*** | -6.5479*** | -6.5073*** |
| Policy Rates (Short-term Interest Rates) | |||||||
| prlor | 0.2348 | -2.6818* | -2.8660 | ∆prlor | -6.7105*** | -6.6695*** | -6.6273*** |
| prolr | 0.3266 | -2.4953 | -2.5273 | ∆prolr | -6.6151*** | -6.5742*** | -6.5491*** |
| prwrr | 0.0559 | -1.8096 | -2.4463 | ∆prwrr | -7.8103*** | -7.7117*** | -7.7240*** |
| probr | 0.3662 | -2.2433 | -2.3116 | ∆probr | -7.8699*** | -7.9270*** | -7.9743*** |
| prafr | 0.7480 | -0.9913 | -2.1267 | ∆prafr | -8.3476*** | -8.3934*** | -8.3866*** |
| prirr | 0.0854 | -2.3887 | -2.9397 | ∆prirr | -6.5439*** | -6.5479*** | -6.5073*** |
| prsrr | -1.7157* | -2.3847 | -2.5435 | ∆prsrr | -12.848*** | -12.769*** | -12.751*** |
| *Note: Reported figures are the Augmented Dickey-Fuller (ADF) test statistics where (***), (**), and (*) indicate rejection of the null hypothesis of a unit root at 1%, 5%, and 10% levels of significance, respectively. The optimal lags were chosen using Schwarz Information Criterion with a maximum lag of 13. | |||||||
| Late Overnight Rate | Overnight Lending Rate | Weekly Repo Rate | The CBRT Average Funding Rate | Interbank Repo Rate | Spread Repo Rate | The CBRT Average Funding Rates and Spread Repo Rate | ||
| prlor | prolr | prwrr | prafr | prirr | prsrr | prafr | prsrr | |
| Dependent Variables | ||||||||
| rrlcr | 0.7717 | 0.3401 | 12.2392*** | 3.3493 | 12.2703*** | 0.4583 | 5.3763*** | 15.4190*** |
| rrlpr | 2.7166 | 2.1288 | 0.3505 | 1.6786 | 17.0857*** | 1.1388 | 3.2973** | 6.0396*** |
| rrbdr | 4.4992** | 3.6890 | 11.5331*** | 0.6654 | 10.0791*** | 10.0703*** | 0.8751 | 0.6640 |
| *Note: (1) The null hypothesis for long-run symmetry is H0:α2m+=α3m-. (2) ***, ** and * indicates the rejection of the null hypothesis at the 1%, 5% and 10% level, respectively. | ||||||||
| Late Overnight Rate | Overnight Lending Rate | Weekly Repo Rate | The CBRT Average Funding Rate | Interbank Repo Rate | Spread Repo Rate | The CBRT Average Funding Rates and Spread Repo Rate | ||||
| prlor | prolr | prwrr | prafr | prirr | prsrr | prafr prsrr |
||||
| Symmetric ARDL Results | Estimated Coefficients | |||||||||
| α0 | 0.6391 | 0.5261 | 0.7899* | 1.1633*** | 0.8570** | 0.6677 | 1.3735*** | |||
| [1.1840] | [0.9719] | [1.6420] | [3.0553] | [2.1804] | [1.2918] | [3.1522] | ||||
| α1 | -0.0524* | -0.0412 | -0.0773* | -0.1561*** | -0.1550*** | -0.0361 | -0.2723*** | |||
| [-1.8417] | [-1.1508] | [-1.7913] | [-3.4271] | [-3.7575] | [-0.9648] | [-5.7212] | ||||
| α2m | 0.0136 | 0.0083 | 0.0463 | 0.1219** | 0.1404*** | -0.1016 | 0.2617*** | |||
| [0.3279] | [0.1775] | [0.8634] | [2.3514] | [3.3625] | [-1.6366] | [5.6591] | ||||
| α3m | - | - | - | - | - | - | 0.2138*** | |||
| - | - | - | - | - | [3.6437] | |||||
| LR PT | 0.2595 | 0.2015 | 0.5990 | 0.7809 | 0.9058 | -2.8144 | 0.9611 | |||
| 0.7852 | ||||||||||
| Hypothesis Results | ||||||||||
| H1 | 1.7227 | 0.0662 | 1.6380 | 6.0811*** | 7.5142*** | 1.9850 | 13.5805*** | |||
| H3 | 0.9480 | 0.5537 | 0.5071 | 1.1617 | 0.2367 | 1.1648 | 0.1140 | |||
| 0.9257 | ||||||||||
| H5 | 18.1668*** | 3.1362 | 15.7615*** | 9.1506*** | 11.9508*** | 4.6862** | 6.1690*** | |||
| Diagnostic Tests | ||||||||||
| R2 | 0.3517 | 0.3866 | 0.4237 | 0.3958 | 0.3766 | 0.3391 | 0.5614 | |||
| DW | 1.8948 | 1.5913 | 1.4012 | 1.9681 | 1.9498 | 1.9050 | 2.0175 | |||
| LM | 0.0903 | 0.8150 | 0.5493 | 0.6952 | 0.2163 | 0.7555 | 0.5601 | |||
| ARCH | 0.7971 | 0.6597 | 0.2954 | 0.2673 | 0.2267 | 0.2994 | 0.6684 | |||
| Asymmetric ARDL Results | Estimated Coefficients | prafr is asymmetric | prsrr is asymmetric | |||||||
| α0 | 1.3895*** | 0.2001 | 2.9919*** | 1.1166 | 2.5707*** | 1.1512** | 2.5770*** | 2.0955*** | ||
| [2.5883] | [0.3437] | [4.7284] | [1.5066] | [4.1789] | [2.2189] | [3.9523] | [5.7302] | |||
| α1 | -0.1028 | -0.0263 | -0.2480*** | -0.1398*** | -0.1559*** | -0.0894* | -0.2134*** | -0.3081*** | ||
| [-2.0819] | [-0.5690] | [-5.3671] | [-2.6333] | [-3.3184] | [-1.9185] | [-4.2401] | [-8.1644] | |||
| α2m+ | 0.0326 | 0.0247 | 0.0067 | 0.1008* | 0.2740*** | 0.0415 | 0.2433*** | 0.2856*** | ||
| [0.4930] | [0.3870] | [0.1055] | [1.7554] | [6.2948] | [0.5861] | [4.4293] | [5.9244] | |||
| α2m- | 0.0081 | 0.0074 | -0.1677* | 0.0666 | 0.3314*** | 0.0309 | 0.2722*** | 0.3396*** | ||
| [0.1689] | [0.1434] | [-1.6659] | [0.9722] | [6.3600] | [0.4583] | [4.1523] | [6.6249] | |||
| α3m | - | - | - | - | - | - | 0.2054*** | 0.3837*** | ||
| - | - | - | - | - | - | [3.7042] | [8.5194] | |||
| LR PT+ | 0.3171 | 0.9392 | 0.0270 | 0.7210 | 1.7575 | 0.4642 | 1.1401 | 0.9270 | ||
| LR PT- | 0.0788 | 0.2814 | -0.6762 | 0.4764 | 2.1257 | 0.3456 | 1.2755 | 1.1022 | ||
| LR PT | - | - | - | - | - | - | 0.9625 | 1.2454 | ||
| Hypothesis Results | ||||||||||
| H1 | 2.2552 | 0.1473 | 12.3678*** | 4.6984** | 13.6548*** | 1.4565 | 8.3178*** | 23.4957*** | ||
| H2 | 0.7717 | 0.3401 | 12.2392*** | 3.3493 | 12.2703*** | 0.4583 | 5.3763*** | 15.4190*** | ||
| H3a | 1.5772 | 0.0007 | 14.8815*** | 1.0690 | 3.1389 | 0.4954 | 0.5131 | 0.2015 | ||
| H3b | 4.2584** | 0.1476 | 13.8961*** | 1.8444 | 3.1866 | 0.7563 | 1.0682 | 0.3226 | ||
| H4 | 2.2718 | 2.5955 | 6.0869*** | 7.2922*** | 11.5664*** | - | 8.0668*** | 47.7121*** | ||
| H5 | 20.5590*** | 7.9546*** | 3.1243 | 21.2726*** | 6.7580*** | - | 15.2799*** | 15.6532*** | ||
| Diagnostic Tests | ||||||||||
| R2 | 0.3491 | 0.3618 | 0.5770 | 0.4809 | 0.5458 | 0.0166 | 0.4956 | 0.7654 | ||
| DW | 1.8844 | 1.6931 | 2.0610 | 2.0182 | 1.9810 | 1.1308 | 1.6582 | 2.1151 | ||
| LM | 0.5624 | 0.9177 | 0.9677 | 0.6528 | 0.8735 | 0.0046 | 0.3056 | 0.1630 | ||
| ARCH | 0.5515 | 0.5910 | 0.1947 | 0.5055 | 0.0300 | 0.2127 | 0.7336 | 0.5459 | ||
| (1) m indicates the policy rates (pp superscript: lor, olr, wrr, afr, irr or srr). (2) α2m+ and α2m- indicate the long-run coefficients of rises and decreases in policy rates, respectively. (3) Values in brackets underneath the coefficients are the t-values for the ***1%, **5% and *10%. (4) H1 denotes the Paseran-Shin-Smith F test statistic values under the hypothesis of H0:α1n=αim=0 for k=2 for the symmetric models and H0:α1n=αim+=αim-=0 for k=3 for the asymmetric models and critical values according to Pesaran et. al (2001) are 3.77, 4.35 and 5.61 for the ***10%, **5% and *1%, respectively, where i={2, 3}. (5) H2 denotes the F-test statistic values under the hypothesis of H0:αim+=αim- where i={2, 3}. (6) H3, H3a and H3b denote the F-test statistic values under the hypothesis of (ⅰ) H0:(αim/-α1n)=1 (ⅱ) H0:(αim+/α1n)=1 and (ⅲ) H0:(αim-/α1n)=1, respectively, where i={2, 3}. (7) H4 denotes the F-test statistic values under the hypothesis of H0:θ0m+=δ0m- for asymmetric models. (8) H5 denotes the F-test statistic values under the hypothesis of H0:θ0m=0 for symmetric models and H0:θ0m+=δ0m-=0 for asymmetric models. (9) R2, DW LM and ARCH rows give adjusted R-square, Durbin-Watson, the p-values of a test for autocorrelation up to lag 12 and a test for ARCH effects up to 12 lags, respectively. | ||||||||||
| Late Overnight Rate | Overnight Lending Rate | Weekly Repo Rate | The CBRT Average Funding Rate | Interbank Repo Rate | Spread Repo Rate | The CBRT Average Funding Rates and Spread Repo Rate | ||||
| prlor | prolr | prwrr | prafr | prirr | prsrr | prafr prsrr |
||||
| Symmetric ARDL Results | Estimated Coefficients | |||||||||
| α0 | 1.0062** | 1.0353** | 1.0575** | 1.0960** | 1.0184** | 1.6454*** | 1.2542*** | |||
| [2.0526] | [2.3878] | [2.2791] | [2.4615] | [2.2688] | [2.9195] | [2.8327] | ||||
| α1 | -0.0654** | -0.0583* | -0.0752** | -0.1011*** | -0.1359*** | -0.110*** | -0.1340*** | |||
| [-2.1204] | [-1.7917] | [-2.2960] | [-2.6392] | [-3.3555] | [-2.8512] | [-3.2871] | ||||
| α2m | 0.0004 | -0.0127 | 0.0128 | 0.0515 | 0.1098*** | 0.0152 | 0.0755* | |||
| [0.0095] | [-0.3029] | [0.2801] | [1.2928] | [2.9343] | 0.2496 | [1.8546] | ||||
| α3m | - | - | - | - | - | - | 0.1241** | |||
| - | - | - | - | - | [2.0667] | |||||
| LR PT | 0.0061 | -0.2178 | 0.1702 | 0.5094 | 0.8079 | 0.1382 | 0.5634 | |||
| 0.9261 | ||||||||||
| Hypothesis Results | ||||||||||
| H1 | 2.8482 | 2.7502 | 2.8586 | 3.5763 | 6.0638*** | 4.1500* | 5.9093*** | |||
| H3 | 2.6757 | 2.3703 | 2.0087 | 2.4401 | 0.8140 | 2.5445 | 3.5626 | |||
| 0.0297 | ||||||||||
| H5 | 29.8596*** | 29.5263*** | 11.5691*** | 7.2041*** | 9.6966*** | - | 9.7705*** | |||
| Diagnostic Tests | ||||||||||
| R2 | 0.4299 | 0.4296 | 0.3040 | 0.3084 | 0.3424 | 0.2707 | 0.3365 | |||
| DW | 2.1173 | 2.0515 | 2.0099 | 2.1326 | 2.0916 | 1.9526 | 2.0424 | |||
| LM | 0.1963 | 0.2664 | 0.0221 | 0.1243 | 0.1397 | 0.0614 | 0.3184 | |||
| ARCH | 0.6615 | 0.6058 | 0.9963 | 0.9392 | 0.6161 | 0.7603 | 0.6416 | |||
| Asymmetric ARDL Results | Estimated Coefficients | prafr is asymmetric | prsrr is asymmetric | |||||||
| α0 | 1.8079*** | 1.4155*** | 1.4243*** | 2.0300*** | 2.2359*** | 1.1328** | 2.4801*** | 1.7286*** | ||
| [3.9094] | [2.8596] | [2.8791] | [3.4689] | [4.0563] | [2.3075] | [3.7685] | [3.4403] | |||
| α1 | -0.1202*** | -0.0938*** | -0.0961*** | -0.1453*** | -0.1154*** | -0.0931*** | -0.1802*** | -0.1993*** | ||
| [-3.8008] | [-2.9099] | [-2.9029] | [-3.7078] | [-3.1463] | [-2.5970] | [-3.8868] | [-4.4772] | |||
| α2m+ | 0.0277 | -0.0341 | 0.0151 | 0.1274*** | 0.1907*** | 0.0682 | 0.1727*** | 0.1476*** | ||
| [0.6315] | [-0.7416] | [0.2559] | [2.6098] | [6.5638] | [1.0113] | [3.2324] | [2.4662] | |||
| α2m- | 0.0009 | -0.0603 | -0.0118 | 0.1481*** | 0.2401*** | 0.0561 | 0.2041*** | 0.1861*** | ||
| [0.0252] | [-1.5355] | [-0.1255] | [2.4667] | [6.8049] | [0.8646] | [3.1422] | [2.8655] | |||
| α3m | - | - | - | - | - | - | 0.1465*** | 0.2230*** | ||
| - | - | - | - | - | - | [2.2435**] | [4.0446] | |||
| LR PT+ | 0.2304 | -0.3635 | 0.1571 | 0.8768 | 1.6525 | 0.7325 | 0.9584 | 0.7406 | ||
| LR PT- | 0.0075 | -0.6429 | -0.1228 | 1.0193 | 2.0806 | 0.6026 | 1.1326 | 0.9338 | ||
| LR PT | - | - | - | - | - | - | 0.8130 | 1.1189 | ||
| H1 | 5.9618*** | 5.6779*** | 2.9711 | 4.6247** | 15.5440*** | 2.2288 | 4.3920** | 5.5092*** | ||
| H2 | 2.7166 | 2.1288 | 0.3505 | 1.6786 | 17.0857*** | 1.1388 | 3.2973** | 6.0396*** | ||
| H3a | 5.0377** | 6.3346*** | 1.9875 | 0.2201 | 1.9867 | 0.1529 | 0.0313 | 0.9503 | ||
| H3b | 11.8176*** | 9.6388*** | 1.2875 | 0.0031 | 2.1216 | 0.3528 | 0.1941 | 0.0574 | ||
| H4 | 16.1175*** | 6.7968*** | 4.4578** | 7.5113*** | 24.3757*** | 1.9334 | 3.5298 | 8.9545*** | ||
| H5 | 14.9246*** | 7.0354*** | 7.4986*** | 4.7801** | 12.1897*** | 1.3281 | 3.5298 | 3.2923 | ||
| R2 | 0.6288 | 0.5678 | 0.3379 | 0.3434 | 0.6332 | 0.2097 | 0.2001 | 0.3680 | ||
| DW | 1.9601 | 2.0815 | 2.0119 | 2.0096 | 1.8842 | 2.0306 | 1.2253 | 1.9734 | ||
| LM | 0.2912 | 0.5723 | 0.1079 | 0.1536 | 0.0340 | 0.0731 | 0.0068 | 0.7611 | ||
| ARCH | 0.6786 | 0.7191 | 0.9990 | 0.8916 | 0.9661 | 0.6619 | 0.0638 | 0.6342 | ||
| (1) m indicates the policy rates (pp superscript: lor, olr, wrr, afr, irr or srr). (2) α2m+ and α2m- indicate the long-run coefficients of rises and decreases in policy rates, respectively. (3) Values in brackets underneath the cs foefficients are the t-valueor the ***1%, **5% and *10%. (4) H1 denotes the Paseran-Shin-Smith F test statistic values under the hypothesis of H0:α1n=αim=0 for k=2 for the symmetric models and H0:α1n=αim+=αim-=0 for k=3 for the asymmetric models and critical values according to Pesaran et. al (2001) are 3.77, 4.35 and 5.61 for the ***10%, **5% and *1%, respectively, where i={2, 3}. (5) H2 denotes the F-test statistic values under the hypothesis of H0:αim+=αim- where i={2, 3}. (6) H3, H3a and H3b denote the F-test statistic values under the hypothesis of (ⅰ) H0:(αim/-α1n)=1 (ⅱ) H0:(αim+/α1n)=1 and (ⅲ) H0:(αim-/α1n)=1, respectively, where i={2, 3}. (7) H4 denotes the F-test statistic values under the hypothesis of H0:θ0m+=δ0m- for asymmetric models. (8) H5 denotes the F-test statistic values under the hypothesis of H0:θ0m=0 for symmetric models and H0:θ0m+=δ0m-=0 for asymmetric models. (9) R2, DW LM and ARCH rows give adjusted R-square, Durbin-Watson, the p-values of a test for autocorrelation up to lag 12 and a test for ARCH effects up to 12 lags, respectively. | ||||||||||
| Late Overnight Rate | Overnight Lending Rate | Weekly Repo Rate | The CBRT Average Funding Rate | Interbank Repo Rate | Spread Repo Rate | The CBRT Average Funding Rates and Spread Repo Rate | |||
| prlor | prolr | prwrr | prafr | prirr | prsrr | prafr prsrr |
|||
| Symmetric ARDL Results | Estimated Coefficients | ||||||||
| α0 | 0.7378*** | 0.1881 | -0.0775 | 0.2450 | 0.0132 | 0.3844* | -0.0884 | ||
| 2.7448 | [0.7511] | [-0.3879] | [1.3892] | [0.0763] | [1.7632] | [-0.5709] | |||
| α1 | -0.0322 | -0.0189 | -0.0523** | -0.0934*** | -0.0978*** | -0.0368 | -0.0669* | ||
| [-1.5899] | [-0.8575] | [-1.9551] | [-2.5553] | [-2.8593] | [-1.5770] | [-1.7124] | |||
| α2m | -0.0333 | 0.0024 | 0.0846*** | 0.0775*** | 0.1005*** | -0.0160 | 0.0730** | ||
| [-1.7447] | [0.1086] | [3.5475] | [2.6757] | [3.8544] | [-0.4876] | [2.3140] | |||
| α3m | - | - | - | - | - | - | 0.1301*** | ||
| - | - | - | - | - | - | [5.7197] | |||
| LR PT | -1.0342 | 0.1270 | 1.6176 | 0.8298 | 1.0276 | -0.4348 | 1.0912 | ||
| 1.9447 | |||||||||
| H1 | 3.5474 | 0.3846 | 6.2955*** | 3.6354 | 7.7312*** | 1.4457 | 12.2059*** | ||
| H3 | 4.4012** | 0.5828 | 0.8745 | 1.2396 | 0.0204 | 2.2452 | 0.1144 | ||
| 0.7977 | |||||||||
| H5 | 4.6632** | 4.2564* | 8.6101*** | 24.2045*** | 13.5851*** | 8.1212*** | 22.4438*** | ||
| R2 | 0.6551 | 0.6343 | 0.7592 | 0.7359 | 0.7478 | 0.4263 | 0.8271 | ||
| DW | 1.8612 | 1.9100 | 1.8588 | 1.9195 | 2.2606 | 1.6593 | 1.6254 | ||
| LM | 0.3588 | 0.7013 | 0.0142 | 0.7554 | 0.7290 | 0.0391 | 0.7318 | ||
| ARCH | 0.7290 | 0.5567 | 0.7859 | 0.9670 | 0.1368 | 0.6861 | 0.6697 | ||
| Asymmetric ARDL Results | prafr is asymmetric | prsrr is asymmetric | |||||||
| α0 | 0.4324** | 0.2989 | 1.0987*** | 0.8518*** | 0.6933*** | -0.1525 | 0.0950 | -0.1013 | |
| [1.9558] | [1.3468] | [3.7934] | [2.7277] | [2.4526] | [-0.6959] | [0.2624] | [-0.5255] | ||
| α1 | -0.0608** | -0.0464 | -0.1365*** | -0.0979*** | -0.0647* | -0.0251 | -0.0472 | -0.0636* | |
| [-2.1060] | [-1.0167] | [-4.2841] | [-2.6694] | [-1.7722] | [-0.8987] | [-1.0772] | [-1.7230] | ||
| α2m+ | 0.0103 | -0.0022 | 0.0089 | 0.0729** | 0.1101*** | 0.0264 | 0.0586* | 0.1206*** | |
| [0.3438] | [-0.0981] | [0.2850] | [2.3078] | [4.9830] | [0.8935] | [1.7477] | [5.7663] | ||
| α2m- | -0.0181 | -0.0240 | -0.0661 | 0.0781** | 0.1286*** | 0.0037 | 0.0507 | 0.1257*** | |
| [-0.8417] | [-1.1718] | [-1.4546] | [2.2311] | [5.4940] | [0.1310] | [1.4007] | [5.5279] | ||
| α3m | - | - | - | - | - | - | 0.0993*** | 0.0887*** | |
| - | - | - | - | - | - | [4.3127] | [2.8816] | ||
| LR PT+ | 0.1694 | -0.0474 | 0.0652 | 0.7446 | 1.7017 | 1.0518 | 1.2415 | 1.8962 | |
| LR PT- | -0.2977 | -0.5172 | -0.4842 | 0.7978 | 1.9876 | 0.1474 | 1.0742 | 1.9764 | |
| LR PT | - | - | - | - | - | - | 2.1038 | 1.3947 | |
| H1 | 3.2163 | 2.3629 | 8.9670*** | 2.4453 | 12.5206*** | 3.9921* | 6.9228*** | 9.5999*** | |
| H2 | 4.4992** | 3.6890 | 11.5331*** | 0.6654 | 10.0791*** | 10.0703*** | 0.8751 | 0.6640 | |
| H3a | 3.6116 | 4.3823** | 19.3011*** | 1.8582 | 5.1872** | 0.0012 | 0.1816 | 0.7607 | |
| H3b | 7.5762*** | 6.3286*** | 18.7915*** | 0.8157 | 7.3644*** | 0.3077 | 0.0195 | 0.8171 | |
| H4 | 0.6261 | - | 5.8924*** | 1.9380 | 7.1633*** | - | 6.8106*** | 0.4586 | |
| H5 | 7.9872*** | - | 23.4619*** | 39.5893*** | 8.8415*** | - | 37.4997*** | 11.6265*** | |
| R2 | 0.7798 | 0.5599 | 0.6741 | 0.7454 | 0.8536 | 0.6545 | 0.8133 | 0.8914 | |
| DW | 1.9076 | 1.6706 | 1.5501 | 1.8348 | 1.8634 | 1.9818 | 1.5103 | 2.1036 | |
| LM | 0.1539 | 0.5227 | 0.0343 | 0.6738 | 0.6243 | 0.0229 | 0.4781 | 0.1693 | |
| ARCH | 0.9935 | 0.7437 | 0.9169 | 0.9892 | 0.4406 | 0.0495 | 0.9938 | 0.3570 | |
| (1) m indicates the policy rates (pp superscript: lor, olr, wrr, afr, irr or srr). (2) α2m+ and α2m- indicate the long-run coefficients of rises and decreases in policy rates, respectively. (3) Values in brackets underneath the coefficients are the t-values for the ***1%, **5% and *10%. (4) H1 denotes the Paseran-Shin-Smith F test statistic values under the hypothesis of H0:α1n=αim=0 for k=2 for the symmetric models and H0:α1n=αim+=αim-=0 for k=3 for the asymmetric models and critical values according to Pesaran et. al (2001) are 3.77, 4.35 and 5.61 for the ***10%, **5% and *1%, respectively, where i={2, 3}. (5) H2 denotes the F-test statistic values under the hypothesis of H0:αim+=αim- where i={2, 3}. (6) H3, H3a and H3b denote the F-test statistic values under the hypothesis of (ⅰ) H0:(αim/-α1n)=1 (ⅱ) H0:(αim+/α1n)=1 and (ⅲ) H0:αim-/α1n=1, respectively, where i={2, 3}. (7) H4 denotes the F-test statistic values under the hypothesis of H0:θ0m+=δ0m- for asymmetric models. (8) H5 denotes the F-test statistic values under the hypothesis of H0:θ0m=0 for symmetric models and H0:θ0m+=δ0m-=0 for asymmetric models. (9) R2, DW LM and ARCH rows give adjusted R-square, Durbin-Watson, the p-values of a test for autocorrelation up to lag 12 and a test for ARCH effects up to 12 lags, respectively. | |||||||||