Heterogeneity and spillover effects of carbon emission trading on green innovation

1.   Introduction

The continuing global warming caused by the dramatic increase in carbon emissions poses a serious challenge to the natural ecosystems on which humanity depends for its survival and development. Along with the formal entry into force of the Kyoto Protocol ^[1], the carbon emissions trading (CET) market, which promotes greenhouse gas emission reduction by market-based means, has entered a phase of rapid development ^[2]. Among them, the European Union Emissions Trading System (ETS), launched in 2005, is currently the largest market in the world and has become an important tool for managing carbon emission reductions ^[3,4]. CET is the trading of carbon dioxide emission rights as a commodity through the market mechanism. Specifically, the government determines the cap on the total amount of carbon emissions and the initial amount of carbon emission allowances for market participants ^[5,6,7].

As a main carbon emission country, a series of measures and policies on energy efficiency and emissions reduction have been implemented in China. Initially, local governments in China mainly adopted some command-and-control carbon emission reduction measures, such as "power rationing". Although such measures were effective, they seriously disrupted the normal operation of the market. In the face of the dual pressure of carbon emission reduction and the upgrade of industrial structures, the Chinese government began to actively explore the establishment of a CET system. In October 2011, China promulgated "the notice of carbon emission permits trading", approving seven provinces and municipalities—Beijing, Tianjin, Shanghai, Chongqing, Guangdong, Hubei and Shenzhen—to start piloting CET. Since 2013, the above seven provinces and cities, plus Fujian Province, have officially launched the CET pilot. From the real data, the CET system has achieved obvious results. For example, in 2020, the volume of transactions of pilot markets reached 130 million tonnes, with a transaction value of approximately RMB 2 billion. As of December 31, 2020, the cumulative volume of carbon market quotas traded was 445 million tonnes, with a transaction value of RMB 10.431 billion. It can be seen that the carbon market in the pilot areas has acted as a disincentive for carbon emission reduction.

At present, much attention has been paid to the carbon emission reduction effects and green innovation effects of CET policies. Most of the literature recognizes that a market-based CET can not only significantly reduce carbon emissions ^{[8,9,10,11,12]}, but it can also increase carbon efficiency ^[13,14,15] and raise energy utilization efficiency ^[16]. However, research on the impact of CET on green innovation is still controversial. Some studies indicate restraining effects of CET on green technology innovation. An empirical study by Zhang et al. ^[17] at the provincial level suggests that CET inhibits green technology innovation at this stage, but significantly reduces carbon emissions. In addition, there is no relationship between CET policies and green innovation ^[18]. Generally speaking, the controversial findings on the impact of CET on green innovation could be explained by relevant theories. On the one hand, according to the Porter hypothesis, reasonable environmental regulations can stimulate firms to implement green innovation and thus improve their competitiveness, which means that the CET can induce a green innovation compensation effect ^[19,20,21]. On the other hand, it has also been argued that environmental regulation can reduce green innovation by increasing firms' environmental management costs, reducing profit margins and crowding out R&D investments ^[21,22,23]. It can be seen that the ultimate impact of environmental regulation on green innovation depends on the comparison of the input and output of firms on green innovation. Therefore, there is a need to re-evaluate the effects of CET implementation by situation or category.

Although previous studies have mainly explored the effects of CET on green innovation from different perspectives, some heterogeneity perspectives need to be addressed. First, in the process of implementing green innovation in enterprises or research units, different motivations for innovation may produce differentiated forms of green innovation. According to the technical content, difficulty degree and R&D cycle, the green innovation can be divided into substantive and strategic green innovation. Substantive green innovation generally refers to invention patents, which have a higher technological content but are more difficult and have a longer cycle time. In comparison, strategic green innovation generally refers to patented utility model technology, which is at a lower level, but is less difficult and has a shorter cycle time. In fact, during the CET pilot period in China, the market-based mechanisms for environmental protection and regulatory mechanisms, such as carbon information disclosure, have been in the exploratory stage of development. Hence, there may be asymmetric information on carbon emissions between the government and enterprises, which may lead to differences in motivation and, subsequently, to the development of green innovation ^[24]. It is also proved that China's CET has different degrees of inducing effect on the quantity and quality of green innovation ^[25]. Second, different levels of green innovation usually imply regional differences in the inputs, outputs and capabilities of green innovation. In the case of enterprises, when faced with a CET policy, the green R&D investment and innovation behavior of enterprises at different levels of green innovation may differ significantly, leading to different green innovation effects. Third, the heterogeneous effects of the CET on urban green innovation are also reflected in three aspects: the level of regional marketization, the degree of government environmental concern and the degree of fiscal decentralization. As CET is a market-based environmental regulation instrument, the price advantage and bargaining power of regions with different levels of marketization differ, which can lead to different measures being taken by different regions in response to CET. At the same time, as the operation of CET requires a strong rule of law system and strict environmental regulations, the different strengths of environmental enforcement by different governments leads to different possibilities for companies to comply with the CET rules. In addition, the degree of fiscal decentralization varies between local governments, resulting in different levels of financial investment in corporate production and residential emissions management and, hence, different impacts of CET on green innovation. Therefore, under the dual background of environmental protection and industrial transformation, it is of great significance to re-examine the impact of China's CET on green innovation from the perspective of heterogeneous effects.

This paper first studies the impact of CET on different types of green innovation through a multi-period different-in-different (DID) model by taking China's CET pilot policy as a quasi-natural experiment around 2013. On this basis, on the one hand, an unconditional panel quantile DID model is used to examine the heterogeneity and evolutionary characteristics of the marginal effect of CET on green innovation at different levels of green innovation. On the other hand, the heterogeneous impact from the perspective of different external environmental characteristics is discussed from the perspective of grouping regression. Then, the spatial DID model is further employed to examine the spatial spillover effect of CET on green innovation. The main marginal contributions of this paper are as follows.

First, the heterogeneous effects of CET on green innovation in China are discussed in terms of two dimensions: substantive green innovation and strategic green innovation. In the face of CET, different motivations for green innovation lead to different forms of green innovation, but little attention has been paid to the differences in the impact of CET on different forms of green innovation in cities. Therefore, this paper discusses the heterogeneous impact of the CET on substantive and strategic green innovation by taking a sample of prefecture-level cities in China. This helps to reveal whether the policy can promote the quality of green innovation, and it is an important guide to the future reform and improvement of China's CET policy.

Second, this paper further analyzes the effects of heterogeneity of CET on green innovation from the perspectives of different levels of green innovation and different external conditions. On one hand, there is minimal empirical research that distinguishes between different levels of green innovation. However, the drivers of green innovation are multidimensional and dynamic, and discussion without differentiating between levels of innovation is inconsistent with reality and the development of innovation activities. Unconditional panel quantile regressions allow for understanding the marginal impact of CET on green innovation while ensuring accurate model identification and consistent parameter estimation ^[26,27]. Thus, based on an unconditional panel quantile regression model in this empirical study, this technique can effectively uncover the evolutionary characteristics of the significance and magnitude of the marginal effect of the CET pilot on green innovation. On the other hand, this paper analyzes the heterogeneity effect of CET on green innovation from three new perspectives: regional marketization level, government environmental concern and fiscal decentralization degree, which is of great significance for the optimization of the implementation effect of CET.

Third, by using a spatial DID model, the spatial spillover effects of CET on green innovation are explored. CET has been shown to be a key market-based policy instrument for promoting carbon emission reduction and green innovation in pilot regions. However, most studies have ignored the spatial spillover effects of CET. In fact, there is a strong spatial correlation between carbon emissions and environmental regulation. Based on regional demonstration and competition effects, the policy benefits generated by the CET have a spillover effect on green innovation in neighboring provinces. Unlike Liu et al. ^[28], this paper studies the spillover effect of CET on green innovation at the urban spatial level, which helps to objectively and comprehensively assess the policy implementation effect of CET.

The structure of the rest of this paper is arranged as follows. Part 2 is a literature review and theoretical analysis; Part 3 is the empirical strategy, and it includes model setting, sample and data. Part 4 is an analysis of the heterogeneous impact of CET on different types of green innovation, and it includes tests of the implementation effect of CET, benchmark regression analysis and robustness tests. Part 5 is a further discussion, focusing on the heterogeneity at different quartiles, heterogeneity regressions for sub-samples with different external characteristics and spatial spillover effects. Part 6 contains the conclusions and policy recommendations.

2.   Literature review and theoretical analysis

2.1.   Literature review

First of all, since the primary goal of CET implementation is to control greenhouse gas emissions, a large number of studies have been carried out on the carbon emission reduction assessment of CET. Most studies indicate that a CET system can indeed reduce carbon emissions and produce positive policy effects. Typically, from a dynamic perspective, Wang et al. ^[29] pointed out that CET significantly reduces carbon emissions, and that the effect is dynamic and cumulative. At the city level, Dong et al. ^[30] believe that China's CET policies can indirectly affect carbon emissions by changing the innovation capacity and the location choice of local industries. At the industry level, through policy simulation, it has been found that the interdepartmental CET scheme can reduce 17.17 billion tons of carbon dioxide and 19.8% of carbon intensity ^[31]. However, CET pilot policies are not all effective, as its carbon reduction effect is only effective in individual pilot areas ^[32,33].

Second, relevant studies discussed the impact of environmental regulation on technological innovation from different aspects. In theory, the narrow "Porter's hypothesis" holds that flexible environmental regulation can better stimulate enterprise innovation than normative environmental regulation ^[34]. Market-based environmental policy is an indirect and flexible regulation method. In order to achieve the regulation goals, enterprises can freely choose to pay pollutant discharge taxes or reduce pollutant discharge through innovation and other ways ^[35]. Hu et al. ^[36] support that the CET policy can promote both the quantity and quality of innovation, and that the impact on the former is greater than the latter. In addition, the empirical study, based on trading data from seven CET pilot markets in China, has found that both high carbon trading price and high carbon trading price volatility can promote enterprise innovation, which confirms the effectiveness of carbon trading policies in promoting enterprise carbon emission reduction innovation ^[37].

In addition, a lot of studies have focused on the influence of CET on green innovation. From the perspective of micro enterprises, Tian et al. ^[38] pointed out that China's CET can effectively stimulate green technology innovation, and that CET, under different environmental strategies, has a positive impact on enterprise green innovation. Zhu et al. ^[39] found that China's CET pilot increases its low-carbon innovation by 5–10% without crowding out other technological innovations of enterprises. Yang et al. ^[40] pointed out that the CET policy has significantly promoted enterprise green innovation, and that the proportion of enterprise green innovation had increased by 13.43%. Zhang et al. ^[41] showed that China's CET system is effective in terms of green innovation, and that it is better in the market with less competition. Other studies based on the data of China's A-share listed companies also indicate that the implementation of CET pilot projects significantly improve the green innovation output of enterprises in pilot areas ^{[42,43,44,45]}. At the city level, China's CET plays a significant role in promoting green technology innovation in pilot cities. Weng et al. ^[46] holds that CET policy significantly promotes urban green technology innovation, and with every 1 million yuan increase in carbon trading turnover, the number of green invention patents authorized would increase by 119.4. Li et al. ^[47] considered that China's CET pilot has a positive impact on urban green innovation and greatly stimulates urban green innovation closely related to energy conservation and emission reduction, including alternative energy production, transportation, energy conservation, etc. Zhou and Wang ^[48] found that China's ETS policy can significantly promote green technology innovation in pilot cities, and that environmental regulation and development strategies can greatly enhance this positive effect.

However, some studies have also found that CET can inhibit green innovation. Zhang et al. ^[17] showed the CET system to inhibit green innovation at the present stage, although it significantly reduced carbon emissions. Based on the research results of listed companies, Chen et al. ^[49] found that the CET pilot policy significantly reduces the proportion of green patents by about 9.26%. Similarly, Lyu et al. ^[50] found that the CET system will inhibit the development of low-carbon technology innovation in the short term. In addition, the effect of CET on green innovation is not always significant ^[18]. For example, Zhao et al. ^[24] found that CET did not produce a green innovation effect on the whole industry or all manufacturing industries, but it could significantly improve the green innovation of some resource-based industrial enterprises. Yao et al. ^[51] showed that, except Hubei Province, other CET pilots could not promote low-carbon innovation because of the lack of an auction mechanism in the initial quota allocation and a strong regulatory mechanism. Wei et al. ^[52] created a virtual decision-making and trading mechanism. Through the empirical research of 351 thermal power companies, they found that green innovation effects could not be realized in the early stages of China's ETS.

In general, abundant research on the impact of CET on carbon emission and green innovation has been conducted. However, it has not been discussed specifically from the perspective of the heterogeneity of green innovation forms and green innovation levels. In addition, it has also not examined the heterogeneity from the perspective of the external environment, like the level of regional marketization, the degree of government environmental concern and the degree of fiscal decentralization.

2.2.   Theoretical analysis

As a market-based environmental regulation, the CET policy essentially introduces market-based instruments to externalize and make tradable the costs associated with pollution emissions, which promotes corporate autonomy in choosing the costs and benefits of environmental pollution management ^[53]. On one hand, CET helps to improve the expected benefits of green innovation and correct environmental externalities, thus encouraging enterprises' green innovation activities ^[54]. On the other hand, green innovation significantly reduces carbon reduction, as well as the cost of emission reduction, by developing more affordable energy-efficient and emission-reducing technologies ^[55]. Therefore, green innovation is an important way to respond to CET policy and achieve sustainable development.

First, for inefficient companies, if they choose to reduce their production in the face of a market-oriented CET policy, they will lose profits; if they do not, they will have to pay for emission rights ^[56]. In other words, a CET policy not only limits the production activities of less efficient emission control firms, but it also increases their production costs ^[5,57]. This is undoubtedly inconsistent with firms' goal of maximizing profits. Hence, in order to ease the cost pressure of CET, low-efficiency enterprises will carry out green innovation activities. Second, for high-efficiency enterprises that exceed their emission allowances, they need to purchase additional allowances in the carbon trading market to emit the carbon dioxide in the production process. Thus, it increases their costs to a certain extent, thus threatening their product competitiveness and profitability ^[58]. Due to cost-benefit considerations, companies will implement green innovations that not only build cost-saving advantages, but also generate revenue through the sale of surplus allowances. Third, the government often implements complementary policies and measures to incentivize emission-controlled companies to innovate while implementing a CET policy. For example, it offers tax breaks to companies who actively engage in green innovation activities, or subsidies for green innovation activities. In this way, the risk costs for emission-controlling enterprises to carry out relevant innovation activities is reduced ^[59], which in turn promotes R&D investment in green and low-carbon technology innovation for the whole society ^[60]. Fourth, the development and implementation of the CET policy sends an important signal to the market. The signal theory suggests that observability and costliness are two key characteristics of effective signals ^[61,62]. Based on the theory of signaling, the promotion of the CET policy implies that the high-carbon assets of a company are likely to become "liabilities", while the low-carbon assets can only become "expensive" resources for a company's sustainable development. As a result, the expectations of companies regarding the CET policy will influence the implementation of their green innovation activities.

However, the impact of a CET policy on green innovation is qualitatively and quantitatively heterogeneous ^[36], which is reflected in the different types of green innovation. On the one hand, different types of green innovations differ in terms of technology content, difficulty factor and R&D cycle. Compared to substantive green innovations, strategic green innovations are less difficult and have shorter cycles. Therefore, when faced with a CET policy, companies tend to increase their green strategic innovations first. On the other hand, there may be problems such as asymmetric information on carbon emissions between government and enterprises ^[63]. As the cost of environmental regulation rises, companies will prefer strategic innovation in order to obtain government subsidies and tax incentives for environmental protection, while responding to people's call for environmental protection. Therefore, the CET policy has a significant contribution to strategic green innovation, while the impact on substantive green innovation is not significant.

3.   Empirical strategy

3.1.   Empirical model

3.1.1.   Typical DID model

The DID model has been widely used in policy effect evaluation in various fields because it overcomes the endogeneity problem to some extent. The general form of its benchmark model is

where $du$ is the dummy variable of the experimental group and the control group. Generally, it mainly has a 0 or 1 value. Particularly, $du$ = 1 indicates the policy influence for an individual, that is, the experimental group; $du$ = 0 refers to the control group, which indicates that an individual is not affected by the policy implementation. $dt$ is the dummy variable of time, which is directly affected by the implementation of the policy; its value is 0 or 1 before or after the policy implementation, respectively. Therefore, $du*dt$ is the interaction term. α₃ reflects the net effect of the policy implementation ^[64]. The principle of the DID model is shown in Table 1.

In order to accurately identify the causality between CET and green innovation, the CET pilots in Beijing, Tianjin, Shanghai, Chongqing, Guangdong, Hubei and Shenzhen since 2013 were selected as exogenous policy shocks. Among them, Shenzhen, Guangdong and Tianjin launched CET markets in 2013; Beijing, Shanghai, Hubei and Chongqing were officially launched in 2014; additionally, Fujian Province was launched in 2016. Considering the above three batches of these pilot provinces and cities, the multi-period differential model was constructed. Referring to Beck et al. ^[65], the control group covers the cities in the provinces without the pilot, while the experimental group covers the cities with the pilot. Generally, individual effects and time effects are correlated with explanatory variables ^[66,67], so the following two-way fixed effects multi-period DID regression model was also constructed:

where ${gi}_{it}$ represents the green innovation level of city i in year t. The value of the time dummy variable (Time) was set to 1, which is mainly based on the beginning year and subsequent years of the pilot city with CET; the value of the remaining years was set to 0. The value of the group dummy variable (Group) was 1 for the city in a CET pilot area, otherwise, the value was 0. The dummy variable did is directly generated, that is, if a city i is listed as the pilot city of CET in year t, the value of did is 1, otherwise, it is 0. If the CET pilot can promote green innovation, the coefficient α should be significantly positive. control represents a collection of control variables, ${\mu }_{i}$ represents the individual fixed effect, ${\eta }_{t}$ represents the time fixed effect and ${\varepsilon }_{it}$ denotes the random error term.

The ordinary least square (OLS) estimators are inconsistent in the estimation because the individual fixed effects μ_i are correlated with an explanatory variable. Therefore, it is necessary to eliminate the individual fixed effects μ_i through model transformation. Given an individual i, the average result about time on both sides of Eq (2) is

Considering Eq (2) minus Eq (4), the deviation form of the model can be obtained as follows:

In Eq (5), μ_i is canceled; that is, the OLS method can be used to consistently estimate α and β as long as ${{{\rm{ \mathsf{ ε} }}_{it}} - {{{\rm{ \mathsf{\bar ε} }}}_i}}$ is uncorrelated with the explanatory variables after transformation. Considering the possibility of intra-group autocorrelation, each individual was considered as the cluster robust standard error in the estimation.

3.1.2.   PSM-DID model

China's CET pilot areas were determined by local economic development level, environmental pollution and treatment status, which it may lead to heterogeneity bias. In other words, regional objective difference may lead to the non-randomness of the CET policy pilot (quasi-natural experiment), which will make the DID model violate the assumption of a random experiment, thus causing the deviation of the benchmark results. The control group obtained by the propensity score matching (PSM) model tends to be comparable and stable, which makes the identification result of a PSM-DID model more robust ^[68]. Therefore, the PSM method proposed by Rosenbaum and Rubin ^[69] was adopted to solve the problem of the robustness of the conclusion from the DID model.

Take the balance panel data as an example, first, the match variables are divided into ordinary match variables $x_n$ and special class variables $x_s$. It no longer takes the propensity score (ps) value as a single criterion for matching, but as a double criterion for special class variables $x_s$ and ps values. The specific formula is as follows:

where i is an individual in the treatment group of the s class, and j is any individual in the control group. Its essence is to find the individual with the nearest ps value as the matching object under the same category, so as to ensure that both matching parties have the same category.

In order to prevent the control group from changing before and after the impact, the matching relationship between i (treated individuals) and e (matching object) should be ensured to be the same once it matched successfully. For that, all of the matched variables in each section of panel data should conduct logit regression, and the value ps of each individual in each period should also be calculated. The basis for finding the matching object e for the treated individuals i in the control group is as follows:

where t represents the period and T is the total number of periods. That is, the individual with the shortest distance from j to i is the matching object e. Accordingly, the validity of the DID model analysis can be ensured by obtaining the comparable and stable control group.

3.1.3.   Unconditional quantile regression model

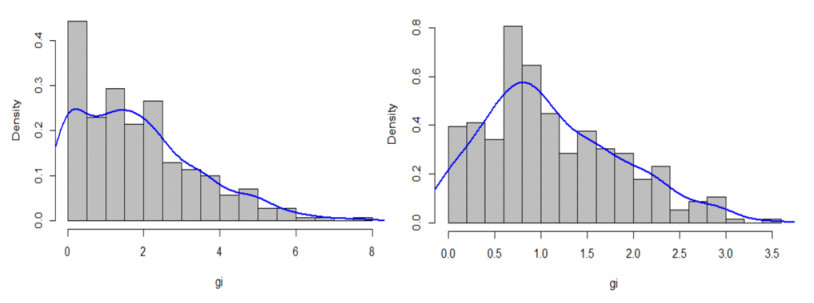
There may be strong spatial heterogeneity in regional green innovation in China, and the impact of CET on green innovation may be significantly different among cities. The regions with low green innovation levels have limited innovation ability and lack the motivation to carry out green innovation, which leads to the weak green innovation effect of CET. Conversely, when the level of green innovation in a region increases to a certain extent, the innovation capability and innovation output effect are greatly enhanced. In this case, the innovation compensation effect of CET is greater than the innovation cost effect. Therefore, in the face of market-oriented environmental regulation, enterprises in this region are more inclined to carry out green innovation. In addition, the statistical distribution characteristics of the number of green patents lead to the limitation of the mean regression model. Figure 1 shows the distribution of the logarithm of green patents (green innovation, gi) in 2008 and 2019, and the solid line is the fitted probability density function. The total number of green patents has an obvious right-skewed distribution, which makes it difficult for the mean regression model to accurately reflect the exact relationship between CET and green innovation.

Quantile regression models can not only accurately describe the influence of explanatory variables on the variation range and conditional distribution shape of explained variables, but they can also more comprehensively describe the complete picture of the conditional distribution of the explained variables. Moreover, they do not make any assumptions about the distribution of random error terms, so the results are not easily affected by extreme values. In addition, unconditional quantile regression (UQR) can not only yield the unconditional quantile partial effect (UQPE) of explanatory variables on explained variables, but it can also effectively avoid the heteroscedasticity problem of data ^[70]. To further test the heterogeneous impact of CET on green innovation at different green innovation levels, UQR was used for verification. The general form of the panel quantile regression model is as follows:

where Y is the explained variable (gi), X is the explanatory variable (did) and $q_{\tau_{i t}}(Y)$ represents the quantile of Y at $\tau_{i t}$, that is, $\tau \in \left({0, 1} \right)$. I_i donates the individual effect.

In the area of quantile estimation, Firpo et al. ^[70] introduced recentered influence functions (RIFs) into quantile regression. Then, the centralized influence function corresponding to the unconditional quantile is expressed as follows:

where $RIF\left({{q_{\rm{ \mathsf{ τ} }}}, y, {F_Y}} \right)$ represents the recentralized influence function of $F_Y$ (the distribution function of Y) corresponding to the τ-quantile; ${{q_{\rm{ \mathsf{ τ} }}}}$ is the unconditional quantile of Y, which satisfies ${F_Y}\left({{q_{\rm{ \mathsf{ τ} }}}} \right) = {\rm{ \mathsf{ τ} }}$; then, ${F_Y}\left(. \right)$ is the density function of Y. Equation (9) is followed by using the iterative method of conditional expectation:

The UQPE of unit translation of X on Y can be obtained by subtracting Eqs (10) and (9), then dividing by Δx and letting it approaching 0:

On the basis of the work of Firpo et al. ^[70], a method was proposed to estimate the UQR effectively in the presence of high-dimensional fixed effects ^[71]. First, we determined the outcome variable in the specified quantile, then determined the density of Y at the quantile and calculated the RIF. Finally, the RIF was used as the explained variable in the panel fixed-effects regression to get the panel UQRE estimator.

3.1.4.   Spatial panel DID model

On the basis of the classical DID model, a spatial expansion form of the differential model was constructed, namely, the spatial differential model (SDID) ^[72]. The general form of the SDID model was constructed as follows in order to explore the spatial spillover effect of CET on green innovation in geographically adjoining cities:

where W is the spatial weight matrix, which is used to reflect the spatial connections between sample individuals. $\rho$ is the spatial self-correlation coefficient for the explained variable; $\beta$ is the spillover effect of the other control variables; λ is the spatial self-correlation coefficient of random error; ${\alpha }_{3}$ is the spillover effect of CET. Equation (12) is the general form of the spatial differential model, which can be divided into different kinds based on whether different coefficients are zero at the same time. The first model can be transformed into a spatial lag model (SLM) from the general model when $\rho \ne 0, \gamma = 0, \delta = 0, \lambda = 0$. The second model is the spatial error model (SEM) when $\rho = 0, \gamma = 0, \delta = 0, \lambda \ne 0$. The third model can be transformed into the spatial Dubin model (SDM) from the general model when $\rho \ne 0, \gamma \ne 0, \delta \ne 0, \lambda = 0$.

Based on the work of Belotti et al. ^[73], quasi-maximum likelihood (QML) estimators are used in the estimation of the spatial models. As its regression coefficient is difficult to explain when considering the spatial correlation in the spatial econometric model, the spatial effect was decomposed into several different effects by referring to the solution of Lesage and Pace ^[74]. Among them, the spatial direct effect refers to the effect of CET in a certain region on local green innovation. The spatial indirect effect is also known as the spatial spillover effect, which is used to measure the impact of CET on green innovation in surrounding areas. The decomposition process for the spatial effect for the SDM is as follows.

According to Lesage and Pace ^[74], the general form of the SDM can be expressed as

where, under certain stable conditions, $(\boldsymbol{I}-\rho \boldsymbol{W})^{-1} = \boldsymbol{I}+\rho \boldsymbol{W}+\rho^2 \boldsymbol{W}^2+\rho^3 \boldsymbol{W}^3+\ldots$.

By taking the SLM under the framework of cross-sectional data (only W^*Y is considered) as an example, the calculation formulas for the direct and indirect effects (spillover effects) can be illustrated as

Suppose that did is denoted by X₀ and green innovation is denoted by Y. While the sample observation value of a city is modified to a certain value when keeping other values of X₀ unchanged, X₁ is denoted as the modified did:

Taking the partial derivative of $E\left(\mathit{\boldsymbol{y}} \right)$ on x, then,

The direct effect is the average value of the diagonal elements of the above matrix. The spillover effect is the average value of the off-diagonal elements of the above matrix. The total effect equals the direct effect plus the spillover effect.

3.2.   Variables and data

First, the sample period was selected from 2008 to 2019. China's CET pilot first started in 2013, and its Ministry of Ecology and Environment issued the "Carbon Emission Trading Management Measures (Trial)" in 2020, which officially started the first implementation cycle of the national carbon market. Then, 279 prefecture-level cities in China were selected as research samples due to the availability and completeness of the data. The explanation of the measurement indicators and data sources of each variable are as follows:

1) Explained variable: green innovation (gi). Based on the definition of Liao et al. ^[75], the level of green innovation was measured from the perspective of the number of green patents granted in cities. The urban green innovation can be divided into two dimensions of substantive green innovation and strategic green innovation, which were respectively measured by the number of green invention patents granted (ginp) and the number of green utility patents granted (gup). Then, the number of two different types of patent grants was increased by 1 and then subjected to logarithmic treatment in order to reduce heteroscedasticity. The resources of the data were taken from the comprehensive combing and screening of patents by the State Intellectual Property Office and Google Patent.

2) Explanatory variable: CET. The market-oriented and low-carbon policy was taken as the representative of the CET policy. Considering the differences in the starting time of each CET pilot, it took the actual pilot year as the standard and set the did value of city i in the year of CET implementation, with subsequent years set as as 1 and other values as 0.

3) Control variables. The first is advanced industrial structure (isa), which focuses on the shift of the industrial center of gravity. It affects green innovation through affecting environmental pollution emission. Referring to the research ^[76], the proportion of the added value of the tertiary industry and the secondary industry was used to measure the advanced industrial structure. The data were taken from the website of the China National Bureau of Statistics. The second one is economic development level (ed), which selects the logarithm of per capita gross regional product of each prefecture-level city as the proxy variable. The third one is economic openness (open). The impact of economic openness on green innovation is uncertain because of the pollution paradise effect with the introduction of foreign capital ^[77], as well as the diffusion of green technology innovation. It applied the proportion of foreign direct investment (FDI) in the gross domestic product (GDP), and its data were taken from China's EPS database. The fourth one is investment in scientific research (R&D), which came from the logarithm of R&D investment within each region ^[78,79,80]. The data were obtained from an EPS database, and some missing data were replaced by scientific expenditure ^[81]. The fifth one is energy consumption intensity (ec), which is expressed as the energy consumption per unit GDP, that is, the total energy consumption GDP ^[82]. The data were taken from the China Energy Statistical Yearbook and China Urban Statistical Yearbook. The total energy consumption was calculated based on the natural gas, coal gas and electricity consumption of the whole society following conversion into tons of standard coal.

4) Grouping variables. The first one is marketization level (mar), which was calculated based on the relevant data for each prefecture-level city according to the indicators of the Gang et al. marketization index ^[83]. The index was composed of 23 indicators from five aspects, each reflecting a specific aspect of marketization, such as the relationship between the government and the market, the development of the non-state economy, the development of the product market, the development of the factor market, the development of the market intermediary organization and the legal system environment. The second one is government environmental concern (gec). Referring to relevant studies ^{[84,85,86,87]}, the urban panel data of the government environmental concern was obtained by crawling and summarizing the annual government work report using crawler technology. There are three steps for its calculation process. In the first step, all sentences containing 44 keywords were selected as "environment-related sentences" according to the government work report of a certain city in a certain year. The 44 keywords were environmental protection, green development, new energy, fog, haze, pollution, energy consumption, pollution, emissions, pollution, ecological environment, ecological protection, ecological damage, water ecology, low carbon, sulfur dioxide, carbon dioxide, PM₁₀ and PM_2.5, chemical oxygen demand, scattered pollution, emission, air, water environment, water security, water quality, green water, black odor, sewage, waste gas, waste residue, environmental violations, environmental crimes, environmental cases, environmental penalties, environmental governance, environmental quality, blue sky, coal burning, green, dust, exhaust gas and volatile organic compounds. The second step was calculating the total numbers in the work report and all of the words numbers in the "environment-related sentence". In the third step, environmental attention is equal to the ratio of the total number of words in the "environmental sentence" to the total number of words in the work report. The third one is fiscal decentralization (fd). Taking the reference of Zhang et al. ^[88], the calculation formula of fiscal decentralization is fd = fdc / (fdc + fdp + fdf); among them, fdc, fdp and fdf represent the per capita fiscal expenditure of the city, provincial and central government, respectively. This index can exclude the impact of population size and the central government on local transfer payments, and the data were taken from the EPS database. The descriptive statistics of variables are shown in Table 2.

4.   Heterogeneous impact of CET on different types of green innovation

4.1.   Result analysis of the benchmark DID model

Based on Eq (2), the estimated results are shown in Table 3. Among the following six columns, (1) and (2) respectively show the impact of CET on green innovation. The column (1) controls the time fixed effects and individual fixed effects, and column (2) adds a series of control variables on the basis of column (1). Similarly, (3) and (4) respectively show the impact of CET on substantive green innovation, and (5) and (6) respectively show the impact of CET on strategic green innovation under different conditions. It can be seen that CET has a significant impact on green innovation. Furthermore, from the perspective of different types of green innovation, in the model without and with control variables, the regression coefficients for green substantive innovation were not significant, while that of strategic innovation were 0.118 and 0.115, which are both significant at 5 and 1% significance levels. These indicate that CET has no significant impact on substantive green innovation, but promotes strategic green innovation significantly. In other words, the impact of CET on green innovation is mainly reflected in strategic innovation. The reason is that enterprises will preferentially choose strategic innovation with small R&D difficulty and short cycles in order to obtain environmental protection subsidies and tax incentives from the government when they are facing rising costs caused by environmental regulations. In addition, the results of the model with and without control variables are consistent, indicating that the model has certain robustness.

4.2.   Robustness test

4.2.1.   Common trend test

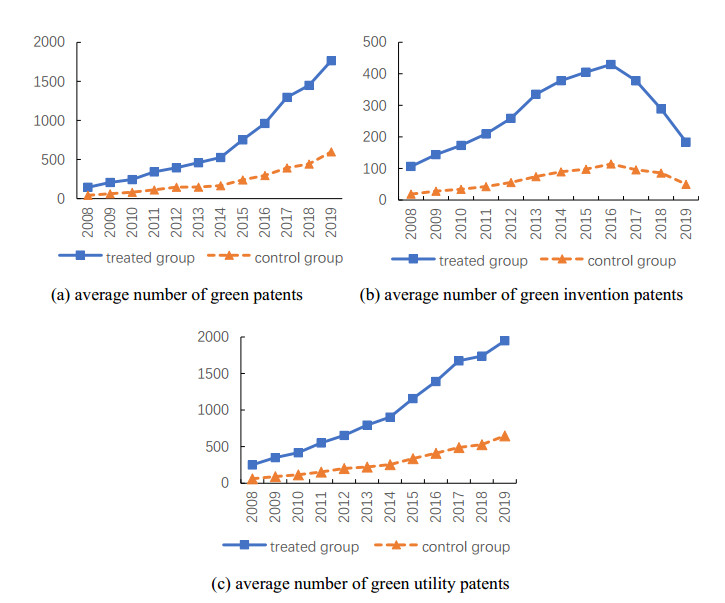
In view of the common trend hypothesis being the premise for the establishment of the DID model, the common trend hypothesis should be tested first. The test methods were comparing the trends of change of the average number of green patents, green invention patents and green utility patents between pilot and non-pilot areas before and after the policy implementation. From Figure 2, the trends of the experimental group and the control group were generally consistent before 2013. It can be further seen that the growth rate of the number of green patents and green utility patents in the experimental group (i.e., CET pilot areas) increased significantly after 2013, while the change is not obvious in the non-pilot areas, which provides a condition for a quasi-natural experimental study. In addition, the growth rate of green invention patents in the experimental group is basically consistent with those of the control group before 2013. This also further supports the conclusion of the baseline regression that indicates that CET has no significant impact on practical green innovation, but has a significant impact on strategic green innovation.

4.2.2.   Test of PSM-DID model

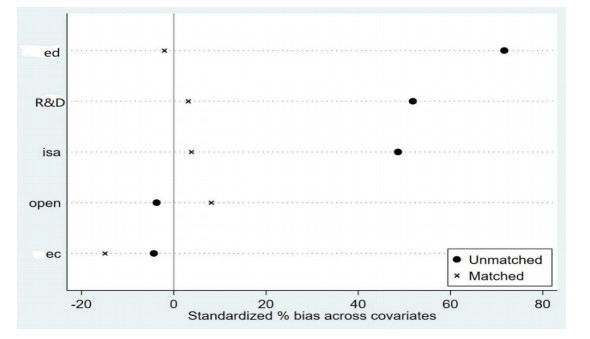
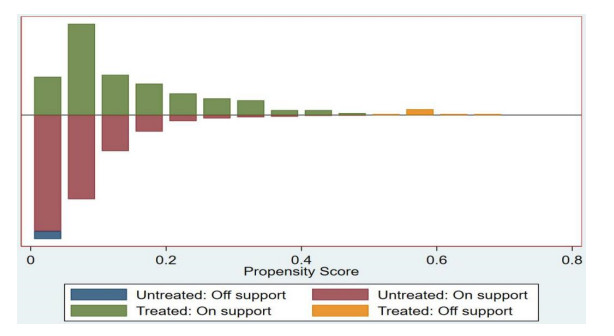
In order to prevent heterogeneity bias in grouping, the samples were re-matched by adopting the PSM method. In the process of PSM, all of the above control variables acted as covariates. Meanwhile, a series of tests were carried out on the validity of the matching grouping results. First of all, the results of covariate testing in Table 4 showed that there was no significant difference in the mean value of covariates between the treatment group and the control group, and that all t-tests of covariates become insignificant after PSM. This indicates that the PSM-DID method is effective, because the distribution of each variable was balanced between these two groups. Second, the deviation test of covariates before and after matching are shown in Figure 3. The matched values all hit 0, indicating that the matching results from PSM were good within 10% standard deviation. The final matching result in Figure 4 reflects that 97 unsuccessful matching samples were deleted and 3251 samples were left.

Furthermore, based on the samples matched by PSM, an intra-group estimation method with robust standard error was adopted to estimate the benchmark DID model. The results are shown in Table 5. In terms of significance, CET has no significant effect on green substantive innovation, while it has a significant promoting effect on green innovation and green strategic innovation, which is consistent with the conclusion of baseline regression. In terms of the regression coefficient size, the results of the PSM-DID model show little difference with the benchmark regression, which proves that the conclusion of the benchmark regression has certain robustness.

4.2.3.   Placebo test

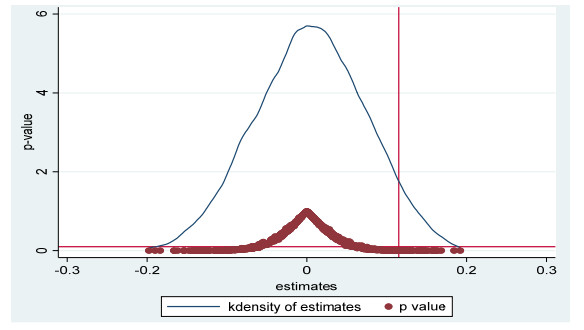
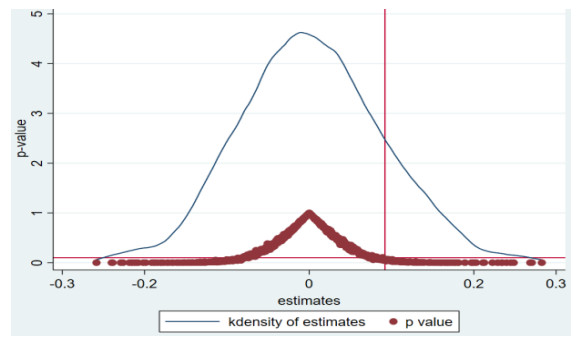
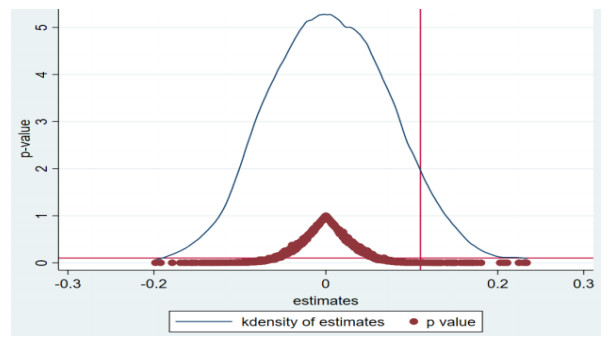
In order to further exclude the differences in green innovation between pilot cities and non-pilot cities due to other factors, a placebo test was conducted by randomly assigning a treatment group and control group ^[89]. The method of random sampling grouping ensures that the previous construction has no impact on green innovation. Specifically, the way of generating random numbers was based on 279 cities randomly generating a corresponding number of treatment groups and control groups. Then, the benchmark regression model of Eq (2) was estimated and repeated 1000 times. The Appendix reports the mean of the regression estimate after 1000 random assignments, as well as the kernel density function of the estimator and its corresponding P-value. The results in the Appendix show that the means of all of the estimated coefficients of did were almost zero, which indicates that the regression results are robust. In addition, the vertical line shows that the coefficient estimates for the policy effect in the three real benchmark regression models were 0.110, 0.092 and 0.115, respectively. Most of the 1000 estimated values were on the left of the real benchmark regression coefficient, which also indicates that the benchmark regression results are robust.

5.   Further discussion

5.1.   Heterogeneity of CET on green innovation under different quantiles

Based on the benchmark regression of Eq (7), the unconditional panel quantile fixed-effects regression models from Firpo et al. ^[90] and Borgen ^[91] were taken as references to test the heterogeneous impact of CET on green innovation at different quantile levels. Table 6 shows the estimation results at the 10–90% quantile level of green innovation. In Table 6, CET has no significant impact on green innovation at the quantile of 10–20%, while it has a significant impact on green innovation at the 30–90% quantile. With the increase of quartiles, the effect of CET on green innovation changes from insignificant to significant. Theoretically, regions with low green innovation levels have insufficient innovation ability and no motivation to carry out green innovation, but are more willing to accept the cost of complying with environmental regulations. Therefore, the green innovation effect of CET is weak. Conversely, when the level of green innovation in a region increases to a certain extent, the innovation capability and innovation output effect will be greatly enhanced. In this case, the innovation compensation effect of CET is greater than the innovation cost effect. Therefore, in the face of market-oriented environmental regulation, enterprises in this region are more inclined to carry out green innovation. At the same time, the government should also take more targeted measures.

5.2.   Heterogeneous impact of CET on green innovation given different external environments

From the above, the effectiveness of CET in promoting green innovation by benchmark regression is proved. However, due to the different external environments in the pilot areas, we questioned whether there is a certain degree of difference in the response of green innovation to the impact of policies under different degrees of marketization, fiscal decentralization and government environmental attention. The analysis of this problem is helpful to further understand the mechanism of CET.

The whole sample was divided according to the level of marketization, the degree of fiscal decentralization and the level of environmental concern of the government from low to high. The first 50% of samples were low marketization, low decentralization or low government attention, while the other 50% of samples were high marketization, high decentralization or high government attention. The benchmark DID model was further used to estimate the heterogeneous effect of CET on green innovation in different samples. The obtained estimation results are shown in Table 7.

From Table 7, the impact of CET on green innovation is heterogeneous in cities with different levels of marketization, fiscal decentralization and government environmental concern. In cities with high marketization, the estimated regression coefficient of did was 0.148, which passes the significance test of 1%. However, in cities with low marketization, the estimated regression coefficient did not pass the significance test. This indicates that CET has a better effect on promoting green innovation in cities with high marketization. The reason for this result is that the promoting effect of CET on green innovation is based on the innovation compensation effect. The revenue or cost that can be saved through green innovation can compensate for the extra cost incurred by environmental regulation; additionally, the development of technological innovation depends on the process of regional marketization. In regions with low marketization, CET has an insufficient incentive and innovation compensation effect on enterprise decision-making. Therefore, CET has no significant impact on green innovation in this region, and vice versa.

Second, in cities with high decentralization, the regression coefficient of did failed to pass the coefficient significance test; however, in cities with low decentralization, the estimated regression coefficient of did was 0.168, which passes the significance test of 1%. It shows that CET has a better effect on promoting green innovation in cities with low fiscal decentralization. The Chinese-style decentralization and the performance evaluation system based on GDP theory tends to make local governments engage in vicious competition for external resources in order to obtain relative competitive advantages. In higher decentralization areas, the efficiency of environmental regulation tools is lower, and the impact on green innovation is less significant. The opposite is not true.

Third, in cities where the government pays high levels of attention to the environment, the estimated regression coefficient of did was 0.244, which passes the significance test of 1%; however, in cities with low government environmental attention, that is not significant. When the environmental concern is low, enterprises with weak social responsibility will not take the initiative to purchase emission rights in the carbon market, nor pay attention to improving the proportion of green innovation when they face low emission or pollution control costs. Therefore, when the government pays less attention to the environment, the impact of CET on green innovation is not significant. When governments pay more attention to the environment, the adverse impact of being subject to "compliance costs" becomes greater, but the compensation effect of innovation increases even more. As a result, companies will increase their share of green innovation. Therefore, when the government pays a high level of attention to the environment, CET can significantly improve green innovation.

5.3.   Spillover effect of CET on green innovation

On the one hand, carbon emissions have negative externalities. On the other hand, technological innovation belongs to public goods, and it has the characteristic of positive externality. Therefore, the impact mechanism of CET on green innovation has a spatial spillover effect. To further explore the spillover effect, a spatial econometric model was implemented in an empirical study. In the construction of the spatial weight matrix, the economic geographical spatial weight matrix in the benchmark spatial panel econometric model was adopted, as it could better reflect the links and differences between different provinces and cities. The weight matrix of economic geographic space was obtained by multiplying the weight matrix of economic distance with the weight matrix of geographical distance. Among them, the spatial weight matrix of geographical distance was constructed based on the actual distance between two places, and the calculation was based on the longitude and latitude of the city. The weight matrix of economic distance was constructed by using the reciprocal difference of the mean per capita GDP among cities from 2008 to 2019. In addition, the results of the Hausman's test show that the fixed-effects model is relatively better than the random-effects model. Therefore, the two-way fixed effects in terms of the individual and time were controlled in the econometric spatial model.

Based on the model (12) and the weight matrix of the economic and geographical distance, the two-way fixed effects of the SDM, SEM and SLM were estimated respectively. The results are shown in Table 8. It can be found that the SDM was the largest in terms of the log likelihood (LogL), which is better than the other two models. Therefore, the empirical results were taken as the final interpretation basis. From column (1) in Table 8, the estimated regression coefficient for the core explanatory variable did was positive and significant at the 5% level, which further verifies that CET promotes the improvement of the urban green innovation level. In addition, the coefficient of W^*did between the spatial weight matrix of the experienced geographical distance and the difference term was positive and significant at the 5% significance level, indicating that CET has a positive spatial spillover effect on green innovation. The reason is that CET not only increases indigenous R&D, but it also accelerates the flow and diffusion of knowledge and information technology across regions. Through the "free-rider" effect and demonstration effect, the green innovation in the surrounding areas is then promoted.

Based on the estimation of the SDM with two-way fixed effects for the time and individual, the partial differential method was used to decompose the spatial effect of green innovation above, and the results are shown in Table 9. The overall promoting effect of CET on green innovation was dominated by the spatial spillover effect and supplemented by the spatial direct effect. First, the spatial direct effect size of CET on green innovation was 0.08, which is significantly positive. Second, the spatial spillover effect of CET on green innovation was 0.238, which is significantly positive at the 5% significance level. In addition, from the proportion of the spatial direct effect and spillover effect, the proportion of the spatial spillover effect of CET accounted for 74.8%, which indicates that the spatial spillover effect is more significant than the direct effect in the overall impact of CET on green innovation. Therefore, this externality should be receive attention in relevant research and policy-making.

6.   Conclusions

Based on the sample data of 279 prefecture-level cities in China from 2008 to 2019, this paper presents a DID identification framework for the study of the heterogeneity effect and spillover effect of CET on green innovation in cities. The main conclusions are as follows.

First, CET has heterogeneous effects on different types of green innovation. On the one hand, the results of benchmark regression show that CET has a significant promoting effect on strategic green innovation, but it has no significant impact on substantive green innovation. That is, the impact of CET on green innovation is mainly reflected in strategic green innovation. On the other hand, the common trend test, PSM-DID model test and placebo test all support the conclusion of benchmark regression. For this reason, enterprises will give priority to strategic innovation activities with low research and development difficulty and a short cycle in order to cope with the rising costs brought by environmental regulation and obtain government subsidies and tax incentives for environmental protection.

Second, at different quantile levels of green innovation, the impact of CET on green innovation is heterogeneous. From the unconditional quantile panel fixed-effects regression results, under the 10–20% quantile of green innovation, CET has no significant impact on green innovation. However, under the 30–90% quantile, CET has a significant impact. That is, with the increase of quantile, the effect of CET on green innovation changes from insignificant to significant. This is because the regions with low green innovation levels have limited innovation ability and a lack of motivation to carry out green innovation, which leads to the weak green innovation effect of CET. Conversely, when the level of green innovation in a region increases to a certain extent, the innovation capability and innovation output effect are greatly enhanced. In this case, the innovation compensation effect of CET is greater than the innovation cost effect. Therefore, in the face of market-oriented environmental regulation, enterprises in this region are more inclined to carry out green innovation.

Third, the impact of CET on green innovation is heterogeneous under different degrees of marketization, fiscal decentralization or government environmental attention. The regression results of grouped samples show that the positive impact of CET on green innovation is significant under the external conditions of a high degree of marketization, low degree of fiscal decentralization or high level of government environmental attention, while it is not significant under the external conditions of a low degree of marketization, high degree of fiscal decentralization or low level of government attention.

Fourth, CET has a positive spillover effect on green innovation, and the spillover effect is more significant than the direct effect. The results of the panel SDM show that the spillover effect of CET on green innovation accounted for 74.8% of the total effect. The reason is that CET not only increases local independent research and development, but it also accelerates the cross-regional flow and diffusion of knowledge and information technology. Through the "free-rider" effect and demonstration effect, green innovation in surrounding areas can be enhanced.

These empirical results have important practical significance for promoting green innovation and realizing low carbon emission reduction. There are some policy suggestions that follow. First, when further improving the operational mechanism of China's CET policy, policymakers should also find ways to guide enterprises to tilt their resources toward substantive green innovation technologies. On the one hand, it should improve the carbon emission information disclosure, mechanisms of carbon market supply and demand, competition and price, so as to guarantee the effective compensation of the cost of green innovation for enterprises. On the other hand, the information symmetry between the government and enterprises in the CET system, environmental subsidies and other environmental regulations should be improved so as to guide enterprises to take the substantial environmental value output as the direction of resource allocation and promote enterprises to be inclined toward substantive green innovation technologies. Second, after the launch of the national carbon emission market, policy tools such as prices, taxes and subsidies should be provided to distinguish enterprises in different cities according to local conditions. Meanwhile, the aim should be to flexibly provide targeted institutional guarantees and economic rewards for the technological innovation of enterprises with different levels of green innovation so as to improve the green innovation effect of the national carbon market. Third, the government should take the differences in the level of marketization, financial system environment and environmental regulation intensity among regions into account and reasonably formulate the total carbon emission target and the inter-regional quota distribution method so as to give full play to the green innovation effect of the national carbon market. Fourth, it should actively promote the spatial spillover effect of CET on green innovation. On the one hand, local governments should establish a sense of regional community, accelerate the free flow of resource elements and strengthen the coordination of carbon emission reduction mechanisms. On the other hand, it should promote the diffusion and dissemination of green innovation technology and improve the conversion rate of green technology in surrounding cities, thus driving the carbon emission reduction of surrounding cities and strengthening the compensation of green innovation.

Acknowledgments

The authors would like to thank the University of South China for sponsoring this research.

Conflict of interest

The authors declare that there is no conflict of interest.

Appendix A