Dynamic analysis of the discrete fractional-order Rulkov neuron map

Gayathri Vivekanandhan; Hamid Reza Abdolmohammadi; Hayder Natiq; Karthikeyan Rajagopal; Sajad Jafari; Hamidreza Namazi; Gayathri Vivekanandhan; Hamid Reza Abdolmohammadi; Hayder Natiq; Karthikeyan Rajagopal; Sajad Jafari; Hamidreza Namazi

doi:10.3934/mbe.2023220

Mathematical Biosciences and Engineering

2023, Volume 20, Issue 3: 4760-4781. doi: 10.3934/mbe.2023220

Previous Article Next Article

Research article Special Issues

Dynamic analysis of the discrete fractional-order Rulkov neuron map

1.
Department of Computerscience Engineering, Chennai Institute of Technology, Chennai 600069, Tamil Nadu, India
2.
Electrical and Computer Engineering Group, Golpayegan College of Engineering, Isfahan University of Technology, Golpayegan, 87717-67498, Iran
3.
Department of Computer Technology Engineering, College of Information Technology, Imam Ja'afar Al-Sadiq University, Baghdad, Iraq
4.
Centre for Nonlinear Systems, Chennai Institute of Technology, Chennai 600069, Tamil Nadu, India
5.
Department of Biomedical Engineering, Amirkabir University of Technology (Tehran polytechnic), Iran
6.
Health Technology Research Institute, Amirkabir University of Technology (Tehran polytechnic), Iran
7.
College of Engineering and Science, Victoria University, Melbourne, Australia
8.
School of Engineering, Monash University, Selangor, Malaysia

Received: 25 November 2022 Revised: 20 December 2022 Accepted: 23 December 2022 Published: 30 December 2022

Human evolution is carried out by two genetic systems based on DNA and another based on the transmission of information through the functions of the nervous system. In computational neuroscience, mathematical neural models are used to describe the biological function of the brain. Discrete-time neural models have received particular attention due to their simple analysis and low computational costs. From the concept of neuroscience, discrete fractional order neuron models incorporate the memory in a dynamic model. This paper introduces the fractional order discrete Rulkov neuron map. The presented model is analyzed dynamically and also in terms of synchronization ability. First, the Rulkov neuron map is examined in terms of phase plane, bifurcation diagram, and Lyapunov exponent. The biological behaviors of the Rulkov neuron map, such as silence, bursting, and chaotic firing, also exist in its discrete fractional-order version. The bifurcation diagrams of the proposed model are investigated under the effect of the neuron model's parameters and the fractional order. The stability regions of the system are theoretically and numerically obtained, and it is shown that increasing the order of the fractional order decreases the stable areas. Finally, the synchronization behavior of two fractional-order models is investigated. The results represent that the fractional-order systems cannot reach complete synchronization.
- discrete fractional-order,
- Rulkov neuron map,
- stability analysis,
- bifurcation,
- synchronization
Citation: Gayathri Vivekanandhan, Hamid Reza Abdolmohammadi, Hayder Natiq, Karthikeyan Rajagopal, Sajad Jafari, Hamidreza Namazi. Dynamic analysis of the discrete fractional-order Rulkov neuron map[J]. Mathematical Biosciences and Engineering, 2023, 20(3): 4760-4781. doi: 10.3934/mbe.2023220

Related Papers:

Abstract

Human evolution is carried out by two genetic systems based on DNA and another based on the transmission of information through the functions of the nervous system. In computational neuroscience, mathematical neural models are used to describe the biological function of the brain. Discrete-time neural models have received particular attention due to their simple analysis and low computational costs. From the concept of neuroscience, discrete fractional order neuron models incorporate the memory in a dynamic model. This paper introduces the fractional order discrete Rulkov neuron map. The presented model is analyzed dynamically and also in terms of synchronization ability. First, the Rulkov neuron map is examined in terms of phase plane, bifurcation diagram, and Lyapunov exponent. The biological behaviors of the Rulkov neuron map, such as silence, bursting, and chaotic firing, also exist in its discrete fractional-order version. The bifurcation diagrams of the proposed model are investigated under the effect of the neuron model's parameters and the fractional order. The stability regions of the system are theoretically and numerically obtained, and it is shown that increasing the order of the fractional order decreases the stable areas. Finally, the synchronization behavior of two fractional-order models is investigated. The results represent that the fractional-order systems cannot reach complete synchronization.

References

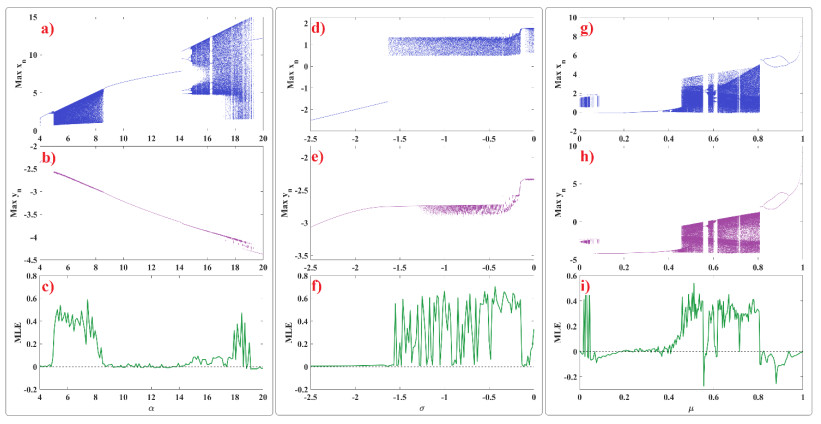
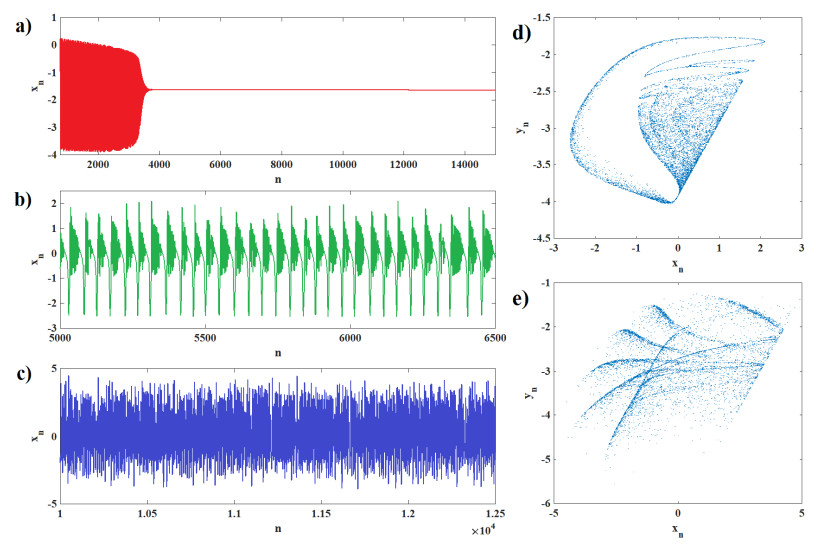
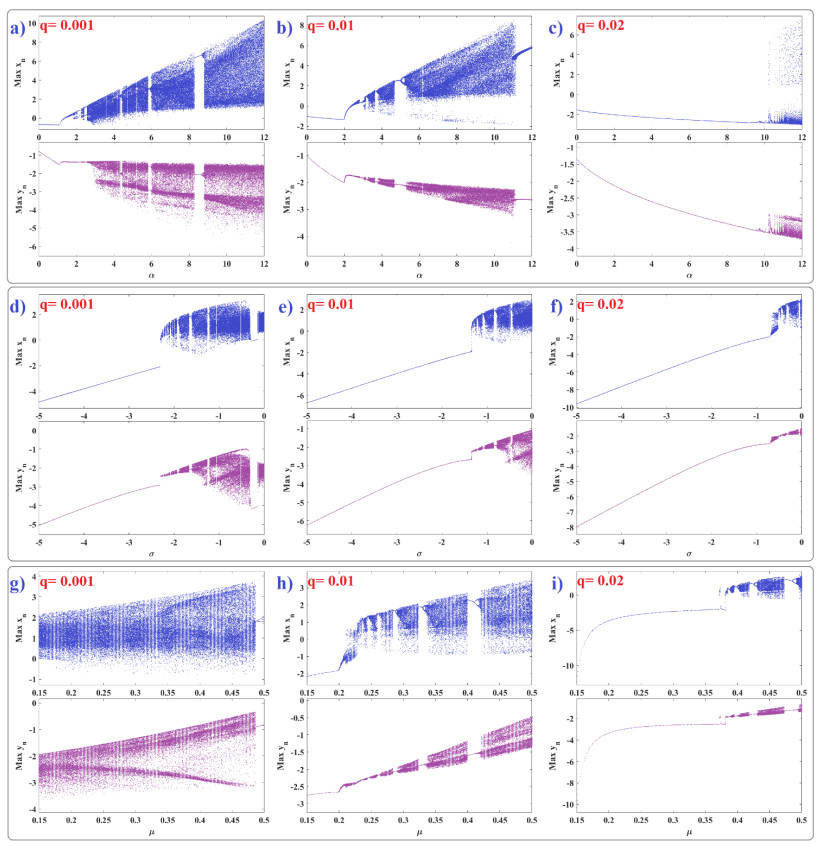
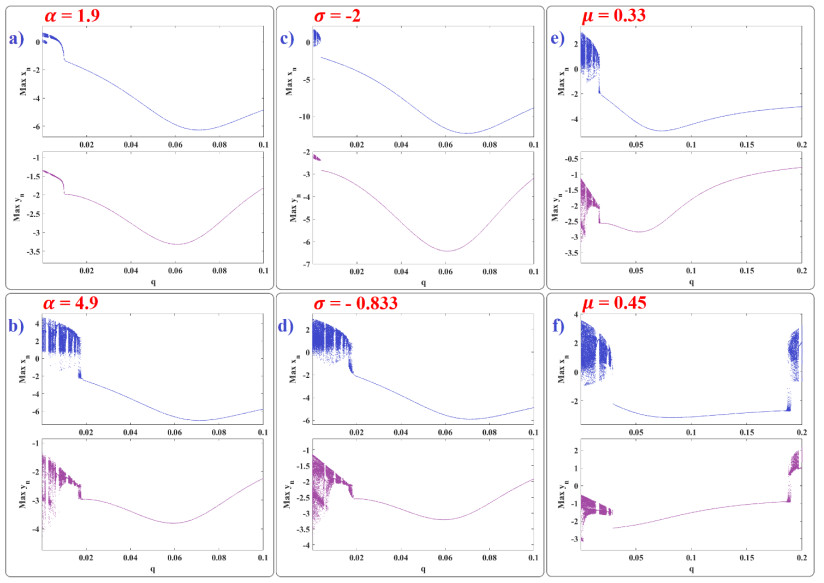
[1]	F. Corinto, A. Torcini, Nonlinear dynamics in computational neuroscience, Springer, 2019. https://doi.org/10.1007/978-3-319-71048-8
[2]	D. Sterratt, B. Graham, A. Gillies, D. Willshaw, Principles of computational modelling in neuroscience, Cambridge University Press, 2011.
[3]	J. F. Tagne, H. C. Edima, Z. T. Njitacke, F. F. Kemwoue, R. N. Mballa, J. Atangana, Bifurcations analysis and experimental study of the dynamics of a thermosensitive neuron conducted simultaneously by photocurrent and thermistance, Eur. Phys. J. Spec. Top, 231 (2022), 993–1004. https://doi.org/10.1140/epjs/s11734-021-00311-w doi: 10.1140/epjs/s11734-021-00311-w
[4]	E. M. Izhikevich, Dynamical systems in neuroscience, MIT press, 2007.
[5]	D. Guo, S. Wu, M. Chen, M. Perc, Y. Zhang, J. Ma, et al., Regulation of irregular neuronal firing by autaptic transmission, Sci. Rep., 6 (2016), 1–14. https://doi.org/10.1038/srep26096 doi: 10.1038/s41598-016-0001-8
[6]	J. Ma, J. Tang, A review for dynamics in neuron and neuronal network, Nonlinear Dyn., 89 (2017), 1569–1578. https://doi.org/10.1007/s11071-017-3565-3 doi: 10.1007/s11071-017-3565-3
[7]	A. Foroutannia, M. Ghasemi, F. Parastesh, S. Jafari, M. Perc, Complete dynamical analysis of a neocortical network model, Nonlinear Dyn., 100 (2020), 2699–2714. https://doi.org/10.1007/s11071-020-05668-6 doi: 10.1007/s11071-020-05668-6
[8]	Q. Xu, X. Tan, D. Zhu, H. Bao, Y. Hu, B. Bao, Bifurcations to bursting and spiking in the Chay neuron and their validation in a digital circuit, Chaos Solit. Fract., 141 (2020), 110353. https://doi.org/10.1016/j.chaos.2020.110353 doi: 10.1016/j.chaos.2020.110353
[9]	A. L. Hodgkin, A. F. Huxley, A quantitative description of membrane current and its application to conduction and excitation in nerve, J. Physiol., 117 (1952), 500. https://doi.org/10.1113%2Fjphysiol.1952.sp004764 doi: 10.1113/jphysiol.1952.sp004764
[10]	R. FitzHugh, Impulses and physiological states in theoretical models of nerve membrane, Biophys. J., 1 (1961), 445–466. https://doi.org/10.1016/S0006-3495(61)86902-6 doi: 10.1016/S0006-3495(61)86902-6
[11]	Z. T. Njitacke, C. N. Takembo, J. Awrejcewicz, H. P. E. Fouda, J. Kengne, Hamilton energy, complex dynamical analysis and information patterns of a new memristive FitzHugh-Nagumo neural network, Chaos Solit. Fract., 160 (2022), 112211. https://doi.org/10.1016/j.chaos.2022.112211 doi: 10.1016/j.chaos.2022.112211
[12]	J. L. Hindmarsh, R. Rose, A model of neuronal bursting using three coupled first order differential equations, Proc. R Soc. London Ser. B, 221 (1984), 87–102. https://doi.org/10.1098/rspb.1984.0024 doi: 10.1098/rspb.1984.0024
[13]	Z. T. Njitacke, J. Awrejcewicz, A. N. K. Telem, T. F. Fozin, J. Kengne, Complex dynamics of coupled neurons through a memristive synapse: extreme multistability and its control with selection of the desired state, IEEE Trans. Circuits Syst. Ⅱ Express Briefs, (2022). https://doi.org/10.1109/TCSII.2022.3172141 doi: 10.1109/TCSII.2022.3172141
[14]	Z. T. Njitacke, T. F. Fozin, S. S. Muni, J. Awrejcewicz, J. Kengne, Energy computation, infinitely coexisting patterns and their control from a Hindmarsh–Rose neuron with memristive autapse: Circuit implementation, AEU Int. J. Electron. Commun., 155 (2022), 154361. https://doi.org/10.1016/j.aeue.2022.154361 doi: 10.1016/j.aeue.2022.154361
[15]	Z. N. Tabekoueng, S. S. Muni, T. F. Fozin, G. D. Leutcho, J. Awrejcewicz, Coexistence of infinitely many patterns and their control in heterogeneous coupled neurons through a multistable memristive synapse, Chaos, 32 (2022), 053114. https://doi.org/10.1063/5.0086182 doi: 10.1063/5.0086182
[16]	B. Ibarz, J. M. Casado, M. A. Sanjuán, Map-based models in neuronal dynamics, Phys. Rep., 501 (2011), 1–74. https://doi.org/10.1016/j.physrep.2010.12.003 doi: 10.1016/j.physrep.2010.12.003
[17]	M. Gosak, M. Milojević, M. Duh, K. Skok, M. Perc, Networks behind the morphology and structural design of living systems, Phys. Life Rev. (2022). https://doi.org/10.1016/j.plrev.2022.03.001 doi: 10.1016/j.plrev.2022.03.001
[18]	S. Majhi, M. Perc, D. Ghosh, Dynamics on higher-order networks: A review, J. R Soc. Interf., 19 (2022), 20220043. https://doi.org/10.1098/rsif.2022.0043 doi: 10.1098/rsif.2022.0043
[19]	M. Perc, Spatial coherence resonance in neuronal media with discrete local dynamics, Chaos Solit. Fract., 31 (2007), 64–69. https://doi.org/10.1016/j.chaos.2005.09.021 doi: 10.1016/j.chaos.2005.09.021
[20]	E. M. Izhikevich, Simple model of spiking neurons, IEEE Trans. Neural Networks, 14 (2003), 1569–1572. https://doi.org/10.1109/TNN.2003.820440 doi: 10.1109/TNN.2003.820440
[21]	J. Nagumo, S. Sato, On a response characteristic of a mathematical neuron model, Kybernetik, 10 (1972), 155–164. https://doi.org/10.1007/BF00290514 doi: 10.1007/BF00290514
[22]	K. Aihara, T. Takabe, M. Toyoda, Chaotic neural networks, Phys. Lett. A, 144 (1990), 333–340. https://doi.org/10.1016/0375-9601(90)90136-C doi: 10.1016/0375-9601(90)90136-C
[23]	F. Pasemann, A simple chaotic neuron, Physica D, 104 (1997), 205–211. https://doi.org/10.1016/S0167-2789(96)00239-4 doi: 10.1016/S0167-2789(96)00239-4
[24]	N. F. Rulkov, Modeling of spiking-bursting neural behavior using two-dimensional map, Phys. Rev. E, 65 (2002), 041922. https://doi.org/10.1103/PhysRevE.65.041922 doi: 10.1103/PhysRevE.65.041922
[25]	N. F. Rulkov, Regularization of synchronized chaotic bursts, Phys. Rev. Lett.., 86 (2001), 183. https://doi.org/10.1103/PhysRevLett.86.183 doi: 10.1103/PhysRevLett.86.183
[26]	M. Mehrabbeik, F. Parastesh, J. Ramadoss, K. Rajagopal, H. Namazi, S. Jafari, Synchronization and chimera states in the network of electrochemically coupled memristive Rulkov neuron maps, Math. Biosci. Eng., 18 (2021), 9394–9409. https://doi.org/10.3934/mbe.2021462 doi: 10.3934/mbe.2021462
[27]	B. Bao, J. Hu, J. Cai, X. Zhang, H. Bao, Memristor-induced mode transitions and extreme multistability in a map-based neuron model, Nonlinear Dyn.. (2022), 1–15. https://doi.org/10.1007/s11071-022-07981-8 doi: 10.1007/s11071-022-07981-8
[28]	K. Li, B. Bao, J. Ma, M. Chen, H. Bao, Synchronization transitions in a discrete memristor-coupled bi-neuron model, Chaos Solit. Fract., 165 (2022), 112861. https://doi.org/10.1016/j.chaos.2022.112861 doi: 10.1016/j.chaos.2022.112861
[29]	H. Sun, H. Cao, Synchronization of two identical and non-identical Rulkov models, Commun. Nonlinear Sci. Numer. Simul., 40 (2016), 15–27. https://doi.org/10.1016/j.cnsns.2016.04.011 doi: 10.1016/j.cnsns.2016.04.011
[30]	I. Franović, V. Miljković, The effects of synaptic time delay on motifs of chemically coupled Rulkov model neurons, Commun. Nonlinear Sci. Numer. Simul., 16 (2011), 623–633. https://doi.org/10.1016/j.cnsns.2010.05.007 doi: 10.1016/j.cnsns.2010.05.007
[31]	S. Rakshit, A. Ray, B. K. Bera, D. Ghosh, Synchronization and firing patterns of coupled Rulkov neuronal map, Nonlinear Dyn., 94 (2018), 785–805. https://doi.org/10.1007/s11071-018-4394-8 doi: 10.1007/s11071-018-4394-8
[32]	A. Wagemakers, M. A. Sanjuán, Electronic circuit implementation of the chaotic Rulkov neuron model, J. Franklin Inst., 350 (2013), 2901–2910. https://doi.org/10.1016/j.jfranklin.2013.01.026 doi: 10.1016/j.jfranklin.2013.01.026
[33]	K. Li, H. Bao, H. Li, J. Ma, Z. Hua, B. Bao, Memristive Rulkov neuron model with magnetic induction effects, IEEE Trans. Ind. Inf., 18 (2021), 1726–1736. https://doi.org/10.1109/TII.2021.3086819 doi: 10.1109/TII.2021.3086819
[34]	L. Cheng, H. Cao, Synchronization dynamics of two heterogeneous chaotic Rulkov neurons with electrical synapses, Int. J. Bifurc. Chaos, 27 (2017), 1730009. https://doi.org/10.1142/S0218127417300099 doi: 10.1142/S0218127417300099
[35]	J. Ma, Biophysical neurons, energy, and synapse controllability: A review, J. Zhejiang Univ. Sci. A, (2022).
[36]	Y. Xie, Z. Yao, J. Ma, Phase synchronization and energy balance between neurons, Front. Inf. Technol. Electron. Eng., (2022), 1–14. https://doi.org/10.1631/FITEE.2100563 doi: 10.1631/FITEE.2100563
[37]	M. Rahimy, Applications of fractional differential equations, Appl. Math. Sci., 4 (2010), 2453–2461.
[38]	L.-L. Huang, G.-C. Wu, D. Baleanu, H.-Y. Wang, Discrete fractional calculus for interval–valued systems, Fuzzy Sets Syst., 404 (2021), 141–158. https://doi.org/10.1016/j.fss.2020.04.008 doi: 10.1016/j.fss.2020.04.008
[39]	F. M. Atici, P. Eloe, Discrete fractional calculus with the nabla operator, Electron. J. Qual. Theory Differ Equ., 2009 (2009), 12, electronic only. https://doi.org/10.14232/ejqtde.2009.4.3
[40]	G. A. Anastassiou, Principles of delta fractional calculus on time scales and inequalities, Math. Comput. Modell., 52 (2010), 556–566. https://doi.org/10.1016/j.mcm.2010.03.055 doi: 10.1016/j.mcm.2010.03.055
[41]	Y. Wang, K. Sun, S. He, H. Wang, Dynamics of fractional-order sinusoidally forced simplified Lorenz system and its synchronization, Eur. Phys. J. Spec. Top, 223 (2014), 1591–1600. https://doi.org/10.1140/epjst/e2014-02181-3 doi: 10.1140/epjst/e2014-02181-3
[42]	K. Rajagopal, A. Karthikeyan, S. Jafari, F. Parastesh, C. Volos, I. Hussain, Wave propagation and spiral wave formation in a Hindmarsh–Rose neuron model with fractional-order threshold memristor synaps, Int. J. Mod. Phys. B, 34 (2020), 2050157. https://doi.org/10.1142/S021797922050157X doi: 10.1142/S021797922050157X
[43]	B. Ramakrishnan, F. Parastesh, S. Jafari, K. Rajagopal, G. Stamov, I. Stamova, Synchronization in a Multiplex Network of Nonidentical Fractional-Order Neurons, Fractal Fract, 6 (2022), 169. https://doi.org/10.3390/fractalfract6030169 doi: 10.3390/fractalfract6030169
[44]	W. M. Ahmad, J. C. Sprott, Chaos in fractional-order autonomous nonlinear systems, Chaos Solit. Fract., 16 (2003), 339–351. https://doi.org/10.1016/S0960-0779(02)00438-1 doi: 10.1016/S0960-0779(02)00438-1
[45]	L. Wang, K. Sun, Y. Peng, S. He, Chaos and complexity in a fractional-order higher-dimensional multicavity chaotic map, Chaos Solit. Fract., 131 (2020), 109488. https://doi.org/10.1016/j.chaos.2019.109488 doi: 10.1016/j.chaos.2019.109488
[46]	Y. Peng, S. He, K. Sun, Chaos in the discrete memristor-based system with fractional-order difference, Results Phys., 24 (2021), 104106. https://doi.org/10.1016/j.rinp.2021.104106 doi: 10.1016/j.rinp.2021.104106
[47]	G.-C. Wu, D. Baleanu, Discrete chaos in fractional delayed logistic maps, Nonlinear Dyn., 80 (2015), 1697–1703. https://doi.org/10.1007/s11071-014-1250-3 doi: 10.1007/s11071-014-1250-3
[48]	A. Elsonbaty, Z. Sabir, R. Ramaswamy, W. Adel, Dynamical analysis of a novel discrete fractional SITRs model for COVID-19, Fractals, (2021), 2140035. https://doi.org/10.1142/S0218348X21400351 doi: 10.1142/S0218348X21400351
[49]	S. Kassim, H. Hamiche, S. Djennoune, M. Bettayeb, A novel secure image transmission scheme based on synchronization of fractional-order discrete-time hyperchaotic systems, Nonlinear Dyn., 88 (2017), 2473–2489. https://doi.org/10.1007/s11071-017-3390-8 doi: 10.1007/s11071-017-3390-8
[50]	M. R. Dar, N. A. Kant, F. A. Khanday, Dynamics and implementation techniques of fractional-order neuron models: A survey, Fract. Order Syst., (2022), 483–511. https://doi.org/10.1016/B978-0-12-824293-3.00017-X doi: 10.1016/B978-0-12-824293-3.00017-X
[51]	D. M. Gash, A. S. Deane, Neuron-based heredity and human evolution, Front. Neurosci., 9 (2015), 209. https://doi.org/10.3389%2Ffnins.2015.00209 doi: 10.3389%2Ffnins.2015.00209
[52]	S. Rakshit, S. Majhi, J. Kurths, D. Ghosh, Neuronal synchronization in long-range time-varying networks, Chaos, 31 (2021), 073129. https://doi.org/10.1063/5.0057276 doi: 10.1063/5.0057276
[53]	Q. Xu, T. Liu, S. Ding, H. Bao, Z. Li, B. Chen, Extreme multistability and phase synchronization in a heterogeneous bi-neuron Rulkov network with memristive electromagnetic induction, J. Cogn. Neurosci., , (2022), 1–12. https://doi.org/10.1007/s11571-022-09866-3 doi: 10.1007/s11571-022-09866-3
[54]	K. Clark, R. F. Squire, Y. Merrikhi, B. Noudoost, Visual attention: Linking prefrontal sources to neuronal and behavioral correlates, Prog. Neurobiol., 132 (2015), 59–80. https://doi.org/10.1016/j.pneurobio.2015.06.006 doi: 10.1016/j.pneurobio.2015.06.006
[55]	J. Ma, J. Tang, A review for dynamics of collective behaviors of network of neurons, Sci. China Technol. Sci., 58 (2015), 2038–2045. https://doi.org/10.1007/s11431-015-5961-6 doi: 10.1007/s11431-015-5961-6
[56]	J. Munkhammar, Chaos in a fractional order logistic map, Fract. Calc. Appl. Anal., 16 (2013), 511–519. https://doi.org/10.2478/s13540-013-0033-8 doi: 10.2478/s13540-013-0033-8
[57]	M.-F. Danca, Puu system of fractional order and its chaos suppression, Symmetry, 12 (2020), 340. https://doi.org/10.3390/sym12030340 doi: 10.3390/sym12030340
[58]	T. Abdeljawad, On Riemann and Caputo fractional differences, Comput. Math. Appl., 62 (2011), 1602–1611. https://doi.org/10.1016/j.camwa.2011.03.036 doi: 10.1016/j.camwa.2011.03.036
[59]	M. T. Holm, The Laplace transform in discrete fractional calculus, Comput. Math. Appl., 62 (2011), 1591–1601. https://doi.org/10.1016/j.camwa.2011.04.019 doi: 10.1016/j.camwa.2011.04.019
[60]	F. Atici, P. Eloe, Initial value problems in discrete fractional calculus, Proc. Am. Math. Soc., 137 (2009), 981–989. https://doi.org/10.1090/S0002-9939-08-09626-3 doi: 10.1090/S0002-9939-08-09626-3
[61]	A. Chen, Y. Chen, Existence of solutions to anti-periodic boundary value problem for nonlinear fractional differential equations with impulses, Adv. Differ. Equat., 2011 (2011), 1–17. https://doi.org/10.1155/2011/915689 doi: 10.1155/2011/915689
[62]	W. Gerstner, W. M. Kistler, Spiking neuron models: Single neurons, populations, plasticity, Cambridge university press, 2002.
[63]	A. Gangopadhyay, D. Mehta, S. Chakrabartty, A spiking neuron and population model based on the growth transform dynamical system, Front. Neurosci., 14 (2020), 425. https://doi.org/10.3389/fnins.2020.00425 doi: 10.3389/fnins.2020.00425
[64]	R. Nickalls, Viete, Descartes and the cubic equation, Math. Gaz., 90 (2006), 203–208. https://doi.org/10.1017/S0025557200179598 doi: 10.1017/S0025557200179598
[65]	J. Čermák, I. Győri, L. Nechvátal, On explicit stability conditions for a linear fractional difference system, Fract. Calc. Appl. Anal., 18 (2015), 651–672. https://doi.org/10.1515/fca-2015-0040 doi: 10.1515/fca-2015-0040
[66]	H. Sun, H. Cao, Complete synchronization of coupled Rulkov neuron networks, Nonlinear Dyn., 84 (2016), 2423–2434. https://doi.org/10.1007/s11071-016-2654-z doi: 10.1007/s11071-016-2654-z
[67]	D. A. Gusnard, M. E. Raichle, Searching for a baseline: Functional imaging and the resting human brain, Nat. Rev. Neurosci., 2 (2001), 685–694. https://doi.org/10.1038/35094500 doi: 10.1038/35094500
[68]	S. G. Horovitz, A. R. Braun, W. S. Carr, D. Picchioni, T. J. Balkin, M. Fukunaga, et al., Decoupling of the brain's default mode network during deep sleep, Proc. Natl. Acad. Sci., 106 (2009), 11376–11381. https://doi.org/10.1073/pnas.0901435106 doi: 10.1073/pnas.0901435106
[69]	K. Rajagopal, S. Panahi, M. Chen, S. Jafari, B. Bao, Suppressing spiral wave turbulence in a simple fractional-order discrete neuron map using impulse triggering, Fractals, 29 (2021), 2140030. https://doi.org/10.1142/S0218348X21400302 doi: 10.1142/S0218348X21400302
[70]	O. Brandibur, E. Kaslik, D. Mozyrska, M. Wyrwas, A Rulkov neuronal model with Caputo fractional variable-order differences of convolution type, Dynam. Syst. Theory Appl., (2019), 227–235. https://doi.org/10.1007/978-3-030-77310-6_20 doi: 10.1007/978-3-030-77310-6_20
[71]	L. J. Liu, Y. H. Qin, Dynamics of discrete memristor-based Rulkov neuron, IEEE Access, 10 (2022), 72051–72056. https://doi.org/10.1109/ACCESS.2022.3188787 doi: 10.1109/ACCESS.2022.3188787
[72]	O. Brandibur, E. Kaslik, D. Mozyrska, M. Wyrwas, Stability of systems of fractional-order difference equations and applications to a Rulkov-type neuronal model, New Trends Nonlinear Dyn., (2020), 305–314. https://doi.org/10.1007/978-3-030-34724-6_31 doi: 10.1007/978-3-030-34724-6_31

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)