A vertically transmitted epidemic model with two state-dependent pulse controls

1.   Introduction

It's well-known that infectious diseases are usually transmitted by virtue of various different mechanisms, for example, by person to person interactions, by insect vectors or via vertical transmission from parents to their unborn offspring as well. Unfortunately but objectively, the modelling dynamics of such disease transmission could be very complicated; and therefore, the development of reasonable strategies for controlling and preventing the spread of these diseases requires much appropriate mathematical analysis ^[1]. Through investigating related documents, we find that many diseases will transfer to new born offspring from an infectious parent, such as hepatitis B, herpes simplex, rubella, tuberculosis and most notoriously AIDS ^[1,2,3,4]. Hence, with the transmission character of these infectious diseases considered, the vertical transmission has important research significance. Over the past few years, the studies of epidemic models in which vertical transmission was involved have become some of the most relevant topics in the mathematical theory of epidemiology ^{[1,2,4,5,6,7,8]} and some of those have largely been motivated by the works of Busenberg and Cooke ^[7,8]. In those works, the transmission of Keystone virus in the mosquito Aedes atlanticus and of Rickettsia rickettsii in the tick Dermacentor andersoni were modeled with vertical transmission being considered, since both of these infections could be transmitted vertically from an infective parent to newborn offspring as well as horizontally via direct or indirect contacts with infected individuals. The work on a vertical infection transmission model has made certain progress; for the latest work on this topic, please refer to ^[9,10].

In recent decades, with the pollution and destruction of the ecological environment or for certain unknown reasons, some viruses that had been controlled or even disappeared in the past have recovered and spread all over the world again. Therefore, the control of infectious diseases still has been relevant in many interdisciplinary fields. Of all known and conventional strategies, the most efficient ways to eliminate or control infectious diseases are still immunization before the onset and effective medical care after the onset. The standard conventional approach is always constant vaccination or uniform treatment, as we can see more details in ^[11]. Nevertheless, when the economic costs and the side effects of the medications are both taken into consideration, particularly for infants, it is obviously both expensive and potentially harmful to implement medications for such a large population coverage. In view of the above reasons, in the actual situation, we naturally prefer to use the impulsive control strategy, which is easier to manipulate, and the relative expense can be reduced to a certain extent.

The theoretical research on pulse control strategy, which was first introduced by Agur and coauthors in ^[1], has become an important topic in mathematical biology and mathematical epidemiology in recent decades, attracting the research interests of many researchers ^{[12,13,14,15,16,17]}. Especially, the theory of an epidemic model concerning vertical transmission with pulse control at fixed times has been deeply investigated ^[18,19]. Song ^[16] discussed an SIR epidemic model with vertical transmission and impulsive vaccination which may undergo inherent oscillation and acquired conditions about the existence and global asymptotic stability of the positive disease-free periodic solution. Liu et al. ^[17] investigated an SIR epidemic model with a saturated infectious force and vertical transmission, and they carried out three different vaccination and treatment strategies. In recent years, Covid-19 has become a global epidemic, and there are also vaccination and treatment strategies against Covid-19 ^[20,21]. By comparing these strategies, they draw the conclusion that PTPVS (Pulse Treatment and Pulse Vaccination Strategies) behaved much better in the elimination and control of the disease than CTPVS (Continuous Treatment and Pulse Vaccination Strategies).

As previously analyzed, notwithstanding that a fixed-time pulse control strategy is widely performed in practice, a considerable portion of data shows that it has some defects, regardless of the effect of the strategy on preventing the spread of certain infectious diseases and the cost of medication, particularly, for the infectious diseases with vertical transmission, such as AIDS, hepatitis B and so on. For example, in the case of large infected population and rehabilitation are extremely urgent, but vaccination and treatment are not performed for it is not the fixed-time. In this regard, a natural idea is to vaccinate and treat when the observed infected population reaches a certain threshold size; in essence, it is based on the state feedback control strategy method. This state pulse is obviously more suitable and reasonable for disease control.

Due to its low cost, high efficiency and practicality, the control strategy with the state-dependent impulsive feedback has demonstrated applications in many seemingly different and widespread fields, especially in science and engineering. Especially, in the ecological surroundings, the control measures (catching, poisoning, releasing the natural predator, harvesting, etc.) are taken only when the amount of species reaches a threshold value, rather than the usual pulse fixed-time control strategy. Many papers have been devoted to the analysis of describing impulsive differential equations models with state-dependent effects. Tang et al. ^[18,19,22], Jiang et al. ^[23,24], Zhao et al. ^[25] and Nie et al. ^[26,27,28] considered various predator-prey models with state-dependent impulsive effects by poisoning the prey or releasing the predator, and they analyzed the existence and the stability of positive order-$k$ ($k\geq3$) period solutions. Particularly, Nie et al. ^[29,30,31] introduced the epidemic model with state-dependent pulse control and considered the existence and stability of positive order-1 or order-2 periodic solutions by using the $Poincar\acute{e}\; map$, the differential inequality and the analogue of the $Poincar\acute{e}$ criterion. Moreover, they showed that there is no positive order-$k$ ($k\geq3$) periodic solutions. For more studies on state-dependent pulse control, we suggest that the readers refer to ^{[32,33,34,35]}.

Motivated by the above considerations and the dynamic behavior of infectious diseases, in this paper, we will consider an SIR model in which vertical transmission and two state-dependent pulse effects are involved. In the next section, we put forward this SIR model and two $Poincar\acute{e}\; maps$, as well as some basic definitions as preliminaries. Next, the foundational dynamic behaviors of our model, including the existence and stability of equilibrium are illustrated. By using the $Poincar\acute{e}\; map$, the analogue of the $Poincar\acute{e}$ criterion and the method of qualitative analysis, the existence and the stability of the positive periodic solution of the SIR model are studied in Section 3. Simulations by virtue of MATLAB are given in Section 4, illustrating the applicability of our main results to the models studied. At last, we give some conclusions and map out directions for future work.

2.   Model formulation and preliminaries

We consider an epidemic in a rather closed environment, for instance, in a university, where the total population almost stays constant in a short period, that is, the natural birth rate equals the mortality rate. In a closed environment, an ordinary SIR epidemic model with vertical transmission is of the following form:

where $\mu$ is the natural birth (and also natural death) rate, $\beta$ is the transmission rate of disease when the susceptible contact the infectious, $\delta(0\leq \delta \leq 1)$ is the proportion of uninfected offspring from infectious mothers, and $\gamma$ is the recovery rate. All these parameters are positive constants. The total population size is normalized to one, i.e., $S(t)$+$I(t)$+$R(t)$ = 1. About the SIR model, there is also some new research. For example, ^[36] discussed Optimal control of the SIR model, which is different from our work, since we will study pulse vaccination and treatment problems.

According to the simple dynamics analysis of the model (2.1), we get the following theorem.

Theorem 2.1. If the basic reproduction number $\Re_{0} = \frac{\beta}{\delta \mu+\gamma} < 1$, then the disease-free equilibrium $P_{0}(1, 0, 0)$ of System (2.1) is globally asymptotically stable. However, for $\Re_{0} > 1$, there exists an unstable disease-free equilibrium $P_{0}$ and an unique endemic equilibrium $P^{*}(S^{*}, I^{*}, R^{*})$, which is globally asymptotically stable, where $S^{*} = \frac{\delta\mu+\gamma}{\beta}, \, I^{*} = \frac{\mu\left(\beta-\delta\mu-\gamma\right)}{\beta(\gamma+\mu)}, \, R^{*} = \frac{\gamma\left(\beta-\delta\mu-\gamma\right)}{\beta(\gamma+\mu)}.$

In practice, considering the impact of the economy and the traits of infectious diseases, a pulse state feedback control strategy for infectious diseases is often proposed, rather than the usual continuous control or fixed-time pulse control strategy. When the amount of infected individuals is few, taking into account secondary actions of the medications, we hope that treatment is taken only for the infectious. On the other hand, when the infectious diseases have outbreaks, thinking about the effective control, we hope both vaccination and treatment are taken. Hereby, the control strategy is based on the following assumptions.

($A_{1}$) When the quantity of infected individuals reaches the first hazardous threshold value $H_{1}$, where $0 < H_{1} < 1-S^{*}$, and the quantity of susceptible $S < S^{*} = \frac{\delta\mu+\gamma}{\beta}$ at the time $t_{i}(H_{1})(i\in N^{+})$, only treatment is taken. The quantities of infectious and recovered suddenly turn to $(1-m)I(t_{i}(H_{1}))$ and $R(t)+mI(t_{i}(H_{1}))$, where $m\in(0, 1)$ is the proportion of the infectious cured at $t_{i}$, which is called the pulse cure rate, respectively.

($A_{2}$) When the quantity of infected individuals reaches the second hazardous threshold value $H_{2}$, where $0 < H_{2} < 1-S^{*}$ and $H_{2} > H_{1}$, and the quantity of susceptibles $S\geq S^{*} = \frac{\delta\mu+\gamma}{\beta}$ at the time $t_{i}(H_{2})(i\in N^{+})$, vaccination and medication are taken. The quantities of susceptible, infectious and recovered abruptly turn to $(1-q)S(t_{i}(H_{2}))$, $(1-p)I(t_{i}(H_{2}))$ and $R(t_{i}(H_{2}))+pI(t_{i}(H_{2}))+qS(t_{i}(H_{2}))$, respectively, where $q, \; p\in(0, 1)$ are the proportions of the susceptible vaccinated and the infectious cured successfully at $t_{i}$, which are called the pulse vaccination rate and the pulse cure rate. According to the practical significance of the integrated control model, the condition: $H_{1} < (1-p)H_{2} < H_{2} < I^{*}$ is always given as such.

According to assumptions $(A_{1})$ and $(A_{2})$, a control model of vertical transmission of disease is proposed, which is described by the following ordinary differential equations with two state-dependent pulse controls:

We assume, throughout this paper, that $\Re_{0} = \frac{\beta}{\delta \mu+\gamma} > 1$. That is to say, System (2.2) without pulse effects has unique globally asymptotically stable equilibrium $P^{*}(S^{*}, I^{*}, R^{*})$. Set $\mathbb{R}_{+} = (0, \; +\infty)$, based on the biological background of System (2.2), and we only need to consider the region

Lemma 2.1. Suppose that $(S, \; I, \; R)$ is a solution of System (2.2) which starts from the point $(S(t_{0}), \; I(t_{0}), \; R(t_{0}))\in \mathbb{R}^{3}_{+}$. Then, $\mathbb{R}^{3}_{+}$ is positively invariant.

Proof. For any initial value $(S(t_{0}), \; I(t_{0}), \; R(t_{0}))\in \mathbb{R}^{3}_{+}$, we discuss all possible cases by the relation of the solution $(S, \; I, \; R)$ to the lines $L_{1}:I = H_{1}$ and $L_{2}:I = H_{2}$, as follows.

Case 1: The solution $(S, \; I, \; R)$ intersects with $L_{1}$ finitely, while it intersects with $L_{2}$ infinitely.

In this case, suppose that the solution $(S, \; I, \; R)$ intersects with $L_{1}:I = H_{1}$ at times $t_{1, i}$, $i = 1, \; 2, \; \cdots\; k, \; k\in N^{+}$, while it intersects with $L_{2}:I = H_{2}$ at times $t_{2, j}$, $j = 1, \; 2, \; \cdots\;$, and $\lim\limits_{j\to\infty}t_{2, j} = \infty$. If the result of Lemma 2.1 was not tenable, we should have a $t^{*} > t_{0}$ such that $min\{S(t^{*}), \; I(t^{*}), \; R(t^{*})\} = 0$, and $S(t) > 0, \; I(t) > 0, \; R(t) > 0$ for all $t_{0} < t < t^{*}$. For this $t^{*}$, there is a positive integer $n(n > k+1)$ such that $t_{2, n-1} < t^{*} < t_{2, n}$. There are three possible cases.

(ⅰ) $I(t^{*}) = 0, \; S(t^{*})\geq 0, \; R(t^{*})\geq 0$. Without loss of generality, we suppose the solution $(S, \; I, \; R)$ initially intersects with $L_{1}$ and then with $L_{2}$. For this case, the result follows from the second, fifth and eighth equations of System (2.2), that

contradicting with $I(t^{*}) = 0$.

(ⅱ) $R(t^{*}) = 0, \; S(t^{*})\geq 0, \; I(t^{*})\geq 0$. For this case, the result follows from the third, sixth and ninth equations of System (2.2), that

contradicting with $R(t^{*}) = 0$.

(ⅱ) $S(t^{*}) = 0, \; I(t^{*})\geq 0, \; R(t^{*})\geq 0$. For this case, from the first and seventh equations of System (2.2), we have

contradicting with $S(t^{*}) = 0$.

Therefore, we have $S(t) > 0, \; I(t) > 0, \; R(t) > 0$ for all $t\geq t_{0}$.

Case 2: The solution $(S, \; I, \; R)$ intersects with $L_{1}$ and $L_{2}$ infinitely.

By an argument similar to the above, it is easy to obtain an identical conclusion. Therefore, it follows that $\mathbb{R}_{+}^{3}$ is a positive invariant set not only for the solution $(S, \; I, \; R)$ that intersects with $L_{1}$ finitely and with $L_{2}$ infinitely but also for the solution $(S, \; I, \; R)$ that intersects with $L_{1}$ and $L_{2}$ infinitely. The proof is complete.

From System (2.2), the third equation is independent of the variables $S$ and $I$, and the total population has a constant size, which is normalized to unity such that

Therefore, the dynamics of System (2.2) are qualitatively equivalent to the dynamics of the system given by

Firstly, in order to obtain some results, we introduce the basic knowledge of the state impulsive differential equations. Consider the state impulsive differential equation:

where $f(x, y)$ and $g(x, y)$ are continuous differential functions defined on $\mathbb{R}^{2}_{+} = \{(x, y):x, y\in(0, \; +\infty)\}$, and $\varphi(x, y)$ is a sufficiently smooth function with $\nabla\varphi\neq0$.

Now, we give the notion of distance between a point and a set. Let $\Gamma$ be an arbitrary set in $\mathbb{R}^{2}_{+}$ and $Y$ be an arbitrary point in $\mathbb{R}^{2}_{+}$. Then, the distance between point $Y$ and $\Gamma$ is denoted by

Let $X = (S, I)$ be any solution of System (2.3) through the point $X_{0} = (S_{0}, I_{0})\in\mathbb{R}_{+}^{2}$. Then, positive trajectory $\Pi(X_{0}, t_{0})$ for $t\geq t_{0}$ is defined by

Definition 2.1. (Orbital stability ^[34]) An orbit $\Pi(x_{0}, t_{0})$ of System (2.4) is said to be orbitally stable if for any given $\varepsilon > 0$, there exists a constant $\delta = \delta(\varepsilon) > 0$ such that for any other solution $x^{*}(t)$ of System (2.4), when $|x^{*}(0)-x_{0}| < \delta$, one has $d(x^{*}(t), \Pi(x_{0}, t_{0})) < \varepsilon$ for all $t > 0$.

Definition 2.2. (Orbital asymptotical stability ^[34]) An orbit $\Pi(x_{0}, t_{0})$ of System (2.4) is said to be orbitally asymptotically stable if it is orbitally stable, and there exists a constant $\eta > 0$ such that for any other solution $x^{*}(t)$ of System (2.4), when $|x^{*}(0)-x_{0}| < \eta$, $\lim\limits_{t\to\infty}d(x^{*}(t), \Pi(x_{0}, t_{0})) = 0$.

Lemma 2.2. (Analogue of $Poincar\acute{e}$ criterion) If the $Floquet \; multiplier$ $\mu$ satisfies $|\mu| < 1$, where

with

and $f, \; g, \; \frac{\partial\xi}{\partial x}, \; \frac{\partial\xi}{\partial y}, \; \frac{\partial\eta}{\partial x}, \; \frac{\partial\eta}{\partial y}, \; \frac{\partial\varphi}{\partial x}$ and $\frac{\partial\varphi}{\partial y}$ are calculated at the point $(\phi(\tau_{j}), \psi(\tau_{j}))$, $f_{+} = f(\phi(\tau_{j}^{+}), \psi(\tau_{j}^{+}))$, $g_{+} = g(\phi(\tau_{j}^{+}), \psi(\tau_{j}^{+}))$ and $\tau_{j}(j\in N)$ is the time of the $j$-$th$ jump, then, $(\phi(\tau_{j}), \psi(\tau_{j}))$ is orbitally asymptotically stable.

Secondly, in order to analyze the dynamics of the System (2.3), we define four cross-sections:

and

For any point $D_{n}(S_{D_{n}}, H_{2})$, suppose that the orbit $\Pi(D_{n}, t_{n})$ starting from the initial point $D_{n}$ intersects set $M_{2}$ infinitely, that is, the orbit $\Pi(D_{n}, t_{n})$ jumps to point $D_{n}^{+}((1-q)S_{n}, (1-p)H_{2})$ on $N_{2}$ due to the impacts of impulses $\triangle S(t) = -qS(t)$ and $\triangle I(t) = -pS(t)$. Further, the orbit $\Pi(D_{n}, t_{n})$ intersects set $M_{1}$ at point $E_{n}(S_{E_{n}}, H_{1})$ and then jumps to $E_{n}^{+}(S_{E_{n}}, (1-m)H_{1})$ due to the impact of impulse $\triangle I(t) = -mS(t)$. Furthermore, the orbit $\Pi(D_{n}, t_{n})$ intersects set $M_{2}$ at point $D_{n+1}(S_{D_{n+1}}, H_{2})$ and then jumps to point $D_{n+1}^{+}((1-q)S_{D_{n+1}}, (1-p)H_{2})$ on $N_{2}$. Then, the orbit $\Pi(D_{n}, t_{n})$ intersects set $M_{1}$ at point $E_{n+1}(S_{E_{n+1}}, H_{1})$ and then jumps to point $E_{n+1}^{+}(S_{D_{n+1}}, (1-m)H_{1})$ on $N_{1}$ again. Repeating this process, we have four impulsive point sequences $\{D_{n}(S_{D_{n}}, H_{2})\}_{n = 1}^{\infty}$, $\{D_{n}^{+}((1-q)S_{D_{n}}, (1-p)H_{2})\}_{n = 1}^{\infty}$ and $\{E_{n}(S_{E_{n}}, H_{1})\}_{n = 1}^{\infty}$, $\{E_{n}^{+}(S_{E_{n}}, (1-m)H_{1})\}_{n = 1}^{\infty}$, where $S_{D_{n+1}}$ and $S_{E_{n+1}}$ are determined by $S_{n}, \; p, \; q, \; m, \; H_{1}, \; H_{2}$, and $n = 1, 2, \cdots$. Thus, we define the $Poincar\acute{e}\; map$ of $M_{2}$ as follows:

Furthermore, if the orbit $\Pi(D_{n}, t_{n})$ does not intersect set $M_{1}$, we defined the $Poincar\acute{e}\; map$ of $M_{2}$ as follows:

On the other hand, for any $S_{D_{n}}$ having a unique $S_{E_{n}}(n = 0, 1, 2, \cdots)$, let

where the mapping $F$ is continuous and invertible. Then, we have $S_{E_{n}} = F(S_{D_{n}})$ and

Let

Then, another $Poincar\acute{e}\; map$ can be obtained for $M_{1}$:

Definition 2.3. (Order-$k$ periodic solution) An orbit $\Pi(D_{n}, t_{n})$ of System (2.3) is said to be order-$k$ periodic if there exists a positive integer $k\geq1$ such that $k$ is the smallest integer for$S_{D_{n+k}} = S_{D_{n}}$.

3.   Existence and stability of periodic solution

The task ahead is to consider System (2.3) under the condition $I < I^{*}$. For definiteness and without loss of generality, we just discuss the case that the orbit $\Pi(K_{0}, t)$ starting from $K_{0}(0, (1-p)H_{2})$ intersects $M_{1}$ at $K_{1}(S_{K_{1}}, H_{1})$ where $S_{K_{1}} < S^{*}$. Then, by the existence and uniqueness theorem of differential equations, there exists a unique point $Q_{0}(S_{Q_{0}}, (1-p)H_{2})$ on $N_{2}$ such that the orbit $\Pi(Q_{0}, t)$ starting from $Q_{0}$ is tangent to $M_{1}$ at point $P(S_{P}, H_{1})$, where $S_{P} = S^{*}$. Therefore, if $(1-q)(1-H_{2}) < S_{Q_{0}}$, then the orbit $\Pi(A_{0}, t)$ where $A_{0}(S_{A_{0}}, I_{A_{0}})$ intersects both set $M_{1}$ and $M_{2}$ infinitely. However, if $\frac{(1-q)(\delta\mu+\gamma)}{\beta} > S_{Q_{0}}$, the orbit $\Pi(A_{0}, t)$ starting from the initial point $A_{0}(S_{A_{0}}, I_{A_{0}})$ will just intersect set $M_{2}$ infinitely, while it will intersect set $M_{1}$ finitely. In this section, we will give some sufficient conditions for the existence and stability of positive periodic solutions in the cases of $(1-q)(1-H_{2}) < S_{Q_{0}}$ and $\frac{(1-q)(\delta\mu+\gamma)}{\beta} > S_{Q_{0}}$, respectively.

3.1.   The case of $(1-q)(1-H_{2}) < S_{Q_{0}}$

Theorem 3.1. For any $m, p\in(0, 1)$, $(1-q)(1-H_{2}) < S_{Q_{0}}$, System (2.3) has a positive order-1 periodic solution.

Proof. Let the point $A_{1}(\alpha_{1}, (1-m)H_{1})$ on $N_{1}$ where $\alpha_{1}$ is sufficiently small with $\alpha_{1} < (1-q)(1-H_{2}) < S_{Q_{0}}$. In view of the geometrical construction of the phase of the System (2.3), the orbit $\Pi(A_{1}, t)$ of the system starting from the initial $A_{1}$ will intersect the impulsive set $M_{2}$ at point $B_{1}(\theta_{1}, H_{2})$, where $\theta_{1} > S^{*}$. Then, $B_{1}$ jumps to the point $B_{1}^{+}((1-q)\theta_{1}, (1-p)H_{2})$ on $N_{2}$ due to the impacts of impulses $\Delta S(t) = -qS(t)$ and $\Delta I(t) = -pI(t)$. Further, the orbit $\Pi(A_{1}, t)$ intersects the impulsive set $M_{1}$ at the point $C_{1}(\gamma_{1}, H_{1})$. At the state $C_{1}$, the orbit $\Pi(A_{1}, t)$ is subjected by impulsive effects to jumping to the point $C_{1}^{+}(\gamma_{1}, (1-m)H_{1})$. Furthermore, the orbit $\Pi(A_{1}, t)$ intersects $M_{2}, \; N_{2}, \; M_{1}, \; N_{1}$ at the points $B_{2}(\theta_{2}, H_{2})$, $B_{2}^{+}((1-q)\theta_{2}, (1-p)H_{2})$, $C_{2}(\gamma_{2}, H_{1})$, $C_{2}^{+}(\gamma_{2}, (1-m)H_{1})$, respectively.

Since $\alpha_{1} < (1-q)(1-H_{2}) < S_{Q_{0}}$, $B_{2}$ is on the left of $B_{1}$. In fact, if $B_{2}$ is on the right of $B_{1}$, then the orbits $\widehat{A_{1}B_{1}}$ and $\widehat{C_{1}^{+}B_{2}}$ intersect at same point $D(S_{0}, I_{0})$. This shows that there are two different solutions which start from the same initial point $D(S_{0}, I_{0})$. This contradicts the uniqueness of solutions for System (2.3). Correspondingly, we have that $B_{2}^{+}$ is on the left of $B_{1}^{+}$. Similarly, $C_{2}$ is on the left of $C_{1}$, and $C_{2}^{+}$ is on the left of $C_{1}^{+}$ due to the impact of impulse $\Delta I(t) = -mI(t)$. Therefore, following from the $Poincar\acute{e}\; map\; (2.5)$ of set $M_{2}$, we have $\theta_{2} = P_{1}(\theta_{1}, m, p, q, H_{1}, H_{2})$, and

On the other hand, the curve $L: \beta SI-\mu I-\gamma I = 0$ intersects set $N_{1}$ at point $E_{0}(\frac{b+\gamma}{\beta}, (1-m)H_{1})$. Then, the orbit $\Pi(E_{0}, t)$ starting from the initial point $E_{0}$ hits the impulsive set $M_{2}$ at point $F_{1}(\theta_{1}, H_{2})$ and then jumps to $F_{1}^{+}((1-q)\theta_{1}, (1-p)H_{2})$ on $N_{2}$. Further, the orbit $\Pi(E_{0}, t)$ hits the set $M_{1}$ at the point $G_{1}(\gamma_{1}, H_{1})$. At the start $G_{1}$, the orbit $\Pi(E_{0}, t)$ is subjected by impulsive effects to jump to the point $G_{1}^{+}(\gamma_{1}, (1-m)H_{1})$. Furthermore, the orbit $\Pi(E_{0}, t)$ intersects the sets $M_{2}, \; N_{2} \; and \; M_{1}, \; N_{1}$ at the points $F_{2}(\theta_{2}, H_{2}), \; F_{2}^{+}((1-q)\theta_{2}, (1-p)H_{2})$ and $G_{2}(\gamma_{2}, H_{1}), \; G_{2}^{+}(\gamma_{2}, (1-m)H_{1})$.

Since $(1-q)(1-h_{2}) < S_{Q_{0}}$, similarly, in view of the geometrical construction of the phase of the system, we obtain that $F_{2}$ is on the right of $F_{1}$, and therefore it follows from the $Poincar\acute{e}\; map$ that $\theta_{2} = P_{1}(\theta_{1}, m, p, q, H_{1}, H_{2})$, and

From the above considerations (3.1) and (3.2), it follows that the $Poincar\acute{e}\; map$ has a fixed point, that is, System (2.3) has a positive order-1 periodic solution. The proof is complete.

Next, about orbital asymptotical stability of a positive order-1 or order-2 periodic solution of System (2.3), we have the following result.

Theorem 3.2. For any $m, \; p\in(0, 1)$, $(1-q)(1-H_{2}) < S_{Q_{0}}$, System (2.3) has a positive order-1 or order-2 periodic solution, which is orbitally asymptotically stable. Furthermore, the System (2.3) has no order-k $(k\geq3)$ periodic solution.

Proof. In view of the geometric construction of the phase space of System (2.3), the orbit which starts from $A_{0}(S_{A_{0}}, (1-m)H_{1})$ will intersect with $M_{1}$ and $M_{2}$ infinitely due to the impacts of impulses for $S$ and $I$.

Suppose the orbit $\Pi(D_{0}, t)$ of System (2.3) starting from the initial point $D_{0}(S_{0}, H_{2})(S_{0}\in(S^{*}, \; 1-H_{2}))$ on $M_{2}$ jumps to point $D_{0}^{+}(\hat{S_{0}}, (1-p)H_{2})$, where $\hat{S_{0}} < S_{Q_{0}}$, due to the condition of $(1-q)(1-H_{2}) < S_{Q_{0}}$ on set $N_{2}$. Afterwards, the orbit $\Pi(D_{0}, t)$ intersects set $M_{1}$ at the point $C_{0}(\gamma_{0}, H_{1})$ and jumps to the point $C_{0}^{+}(\gamma_{0}, (1-m)H_{1})$ on $N_{1}$ due to the impact of impulse $\Delta I\left(t\right) = -mI(t)$, and it then reaches set $M_{2}$ at point $D_{1}(S_{1}, H_{2})$ where $S_{1}\in(S^{*}, \; 1-H_{2})$. Further, the orbit $\Pi(D_{0}, t)$ jumps to point $D_{1}^{+}(\hat{S_{1}}, (1-p)H_{2})$ on $M_{2}$ and intersects set $M_{1}$ at point $C_{1}(\gamma_{1}, H_{1})$, then jumps to point $C_{1}^{+}(\gamma_{1}, (1-m)H_{1})$, and finally reaches set $M_{2}$ again at point $D_{2}(S_{2}, H_{2})$ where $S_{2}\in(S^{*}, \; 1-H_{2})$. Therefore, by the $Poincar\acute{e}\; map$ (2.9) of set $M_{1}$, we have $\gamma_{k+1} = P_{2}(\gamma_{k}, m, p, q, H_{1}, H_{2})$.

On the other hand, under the condition $(1-q)(1-H_{2}) < S_{Q_{0}}$, for any two points $D_{i}(S_{i}, H_{2})$ and $D_{j}(S_{j}, H_{2})$ on set $M_{2}$, where $S_{i}, S_{j}\in(S^{*}, \; 1-H_{2})$ and $S_{i} < S_{j}$. The points $D_{i}((1-q)S_{i}, (1-p)H_{2})$ and $D_{j}((1-q)S_{j}, (1-p)H_{2})$ both are on the left of the point $Q_{0}$. Obviously, from the geometrical construction of the phase space of System (2.3), we have

Now, for $(1-q)(1-H_{2}) < S_{Q_{0}}$ and any $S_{0}\in(S^{*}, 1-H_{2})$, from the $Poincar\acute{e}\; map$ (2.5) of set $M_{2}$, we have $S_{1} = P_{1}(S_{0}, m, p, q, H_{1}, H_{2})$, $S_{2} = P_{1}(S_{1}, m, p, q, H_{1}, H_{2})$ and $S_{k+1} = P_{1}(S_{k}, m, p, q, H_{1}, H_{2})$ $(k = 3, 4, \cdots)$.

According to the relationship between the quantity $S_{0}$ and $S_{1}$, we discuss the periodic solution by three cases 1–3 as follows.

1). If $S_{0} = S_{1}$, then System (2.3) has a positive order-1 periodic solution.

2). If $S_{0}\neq S_{1}$, without loss generality, suppose that $S_{1} < S_{0}$. It follows from (3.3) that $S_{2} > S_{1}$. Furthermore, if $S_{2} = S_{0}$, then System (2.3) has a positive order-1 periodic solution.

3). If $S_{0}\neq S_{1}\neq S_{2}\neq \cdots \neq S_{k-1}$ $(k\geq3)$ and $S_{0} = S_{k}$, then System (2.3) has a positive order-k periodic solution. In fact, this is impossible. Due to the complexity, next, we discuss this general situation in four different small cases (ⅰ)–(ⅳ) by the relationship among $S_{0}$, $S_{1}$ and $S_{2}$, as follows.

Case 1. $S_{0} < S_{1}$. In this case, it follows from (3.3) that $S_{2} < S_{1}$. So, the relation of $S_{0}, \; S_{1}$ and $S_{2}$ is one of the following two small cases (ⅰ) and (ⅱ).

(ⅰ) $S_{2} < S_{0} < S_{1}$.

If $S_{2} < S_{0} < S_{1}$, it follows that $S_{3} > S_{1} > S_{2}$ by (3.3). Repeating this process, we have

$S^{*} < \cdots < S_{2k} < \cdots < S_{4} < S_{2} < S_{0} < S_{1} < S_{3} < \cdots < S_{2k+1} < \cdots < 1-H_{2}$.

(ⅱ) $S_{0} < S_{2} < S_{1}$.

If $S_{0} < S_{2} < S_{1}$, similar to (ⅰ), we have

$S_{0} < S_{2} < S_{4} < \cdots < S_{2k} < \cdots < S_{2k+1} < \cdots < S_{3} < S_{1} < 1-H_{2}$.

Case 2. $S_{0} > S_{1}$. From (3.3) we obtain that $S_{1} < S_{2}$. In this case, the relation of $S_{0}, \; S_{1}$ and $S_{2}$ is one of the following two small cases (ⅲ) and (ⅳ).

(ⅲ) $S_{1} < S_{0} < S_{2}$.

If $S_{1} < S_{0} < S_{2}$, it follows that $S_{3} > S_{1} > S_{2}$ by (3.3). Repeating this process, we have

$S^{*} < \cdots < S_{2k+1} < \cdots < S_{3} < S_{1} < S_{0} < S_{2} < S_{4} < \cdots < S_{2k} < \cdots < 1-H_{2}$.

(ⅳ) $S_{1} < S_{2} < S_{0}$.

If $S_{1} < S_{2} < S_{0}$, similar to (ⅲ), we have

$S_{1} < S_{3} < \cdots < S_{2k+1} < \cdots < S_{2k} < \cdots < S_{4} < S_{2} < S_{0} < 1-H_{2}$.

If there exists a positive order-k $(k\geq3)$ periodic solution in System (2.3), then $S_{0}\neq S_{1}\neq S_{2}\neq \cdots \neq S_{k-1}$ $(k\geq3)$, and $S_{0}\neq S_{k}$, which is contradictory to (ⅰ)–(ⅳ). So, there exist no order-k $(k\geq3)$ periodic solutions in System (2.3) with $(1-q)(1-H_{2}) < S_{Q_{0}}$. Further, it follows from (ⅰ) that $\lim\limits_{n\to\infty}S_{2k+1} = \lambda_{1}$ and $\lim\limits_{n\to\infty}S_{2k} = \lambda_{2}$, where $S^{*} < \lambda_{2} < \lambda_{1} < 1-H_{2}$. Consequently, we have

and

Meanwhile, a similarly conclusion on set $M_{1}$ following from (ⅰ) is that $\lim\limits_{n\to\infty}\gamma_{2k+1} = \xi_{1}$ and $\lim\limits_{n\to\infty}\gamma_{2k} = \xi_{2}$, where $0 < \xi_{2} < \xi_{1} < 1-H_{2}$. By the mapping (2.7), we have $\xi_{1} = F(\lambda_{1})$ and $\xi_{2} = F(\lambda_{2})$. Therefore, by the $Poincar\acute{e}\; map$ (2.9) of set $M_{1}$, we have

and

So, System (2.3) has an orbitally asymptotically stable positive order-2 periodic solution. Similarly, in (ⅱ) and (ⅳ), System (2.3) has an orbitally asymptotically stable positive order-1 periodic solution. In (ⅲ), System (2.3) has an orbitally asymptotically stable positive order-2 periodic solution.

From the above, we know that System (2.3) with $H_{2}\leq \frac{\mu\left (\beta-\delta\mu-\gamma\right)}{\beta(\gamma+\mu)}$ and $(1-q)(1-H_{2}) < S_{Q_{0}}$ has an orbitally asymptotically stable positive order-1 or order-2 periodic solution. The proof is complete.

3.2.   The case of $\frac{(1-q)(\delta\mu+\gamma)}{\beta} > S_{Q_{0}}$

On the dynamic behavior of System (2.3) with $\frac{(1-q)(\delta\mu+\gamma)}{\beta} > S_{Q_{0}}$, we have the following conclusion.

Theorem 3.3. For any $m, p\in(0, 1)$, $\frac{(1-q)(\delta\mu+\gamma)}{\beta} > S_{Q_{0}}$, System (2.3) has a positive order-1 periodic solution.

Proof. The orbit $\Pi(A_{0}, t)$ on $N_{1}$ starting from the initial point $A_{0}(S_{A_{0}}, (1-m)H_{1}))$ where $S_{A_{0}}\in(0, S^{*})$ will intersect set $M_{2}$ at point $C(S_{C}, H_{2})$, where $S^{*} < S_{C}$. Then, it jumps to the point $C_{0}(S_{C_{0}}, (1-p)H_{2})$ on $N_{2}$ due to the impacts of impulses $\Delta S\left(t\right) = -qS(t), \; \Delta I\left(t\right) = -pI(t)$. Moreover, such $\frac{(1-q)(\delta\mu+\gamma)}{\beta} > S_{Q_{0}}$, then $(1-q)S_{C} > S_{Q_{0}}$, coinciding that the orbit $\Pi(C_{0}, t)$ starts from the initial point $C_{0}(S_{C_{0}}, (1-p)H_{2})$, where $S_{C_{0}} > S_{Q_{0}}$. Therefore, let point $C_{0}(S_{C_{0}}, (1-p)H_{2})\in N_{2}$ for sufficiently small $\varepsilon$ with $S_{Q_{0}} < S_{C_{0}} < S_{Q_{0}}+\varepsilon < \frac{(1-q)(\delta\mu+\gamma)}{\beta}$. In view of the geometrical structure of the phase space of System (2.3), the orbit $\Pi(C_{0}, t)$ starting from the initial point $C_{0}$ will intersect the impulsive set $M_{2}$ at the point $C_{1}(S_{C_{1}}, H_{2})$ where $S^{*} < S_{C_{1}}$. At point $C_{1}$, the orbit $\Pi(C_{0}, t)$ jumps to the point $C_{1}^{+}(S_{C_{1}^{+}}, (1-p)H_{2})$ on set $N_{2}$ due to the impacts of impulses $\Delta S\left(t\right) = -qS(t)$ and $\Delta I\left(t\right) = -pI(t)$. Afterwards, since $\frac{(1-q)(\delta\mu+\gamma)}{\beta} > S_{Q_{0}}$, then $S_{C_{1}^{+}} > \frac{(1-q)(\delta\mu+\gamma)}{\beta}$ apparently. Furthermore, the orbit $\Pi(C_{0}, t)$ intersects set $M_{2}$ at point $C_{2}(S_{C_{2}}, H_{2})$ again. Since $S_{Q_{0}} < S_{C_{0}} < \frac{(1-q)(\delta\mu+\gamma)}{\beta}$, then $C_{0}$ is on the left of $C_{1}^{+}$. Finally, from the geometrical structure of the phase space of System (2.3), we obtain that point $C_{2}$ is on the left of $C_{1}$, that is, $S_{C_{2}} < S_{C_{1}}$. In fact, if it does not hold, that is, $S_{C_{2}}\geq S_{C_{1}}$, then $C_{2}$ is on the right of $C_{1}$, or the two points coincide. So, it follows that the orbits $\widehat{C_{0}C_{1}}$ and $\widehat{C_{1}^{+}C_{2}}$ intersect at a point $(\widehat{S}, \widehat{I})$, which contradicts the uniqueness of the solution. Therefore, from the $Poincar\acute{e}\; map$ (2.6), we have $S_{C_{2}} = P_{1}(S_{C_{1}}, p, q, H_{2})$, and

On the other hand, the curve $L:\; \beta SI+\delta\mu I+\gamma I = 0$ intersects section $N_{2}$ at the point $Q(\frac{\delta\mu+\gamma}{\beta}, (1-p)H_{2})$, and $Q$ is on the right of $Q_{0}$. Then, the orbit $\Pi(Q, t)$ starting from the initial point $Q$ intersects set $M_{2}$ at point $Q_{1}(S_{Q_{1}}, H_{2})$ where $S_{Q_{1}} > S^{*}$. Then, it jumps to the point $Q_{1}^{+}(S_{Q_{1}}^{+}, (1-p)H_{2})$ on set $N_{2}$ and finally reaches the point $Q_{2}(S_{Q_{2}}, H_{2})$ on set $M_{2}$ again. If there is a positive constant $q^{*}$ such that $(1-q^{*})S_{Q_{1}} = \frac{\delta\mu+\gamma}{\beta}$, then $Q_{1}^{+}$ coincides with $Q$ for $q = q^{*}\in(0, 1)$, that is, $Q_{1}$ coincides with $Q_{2}$. Otherwise, $Q_{1}^{+}$ is on the left of $Q$ for $(1-q)Q_{1} < \frac{\delta\mu+\gamma}{\beta}$ and is on the right of $Q$ for $(1-q)Q_{1} > \frac{\delta\mu+\gamma}{\beta}$. However, from the geometrical structure of the phase space of System (2.3), $Q_{2}$ is on the right of $Q_{1}$ for any $q\in(0, q^{*})\cup(q^{*}, 1)$.

To sum up, we get, from the above discussions, that

(ⅰ) When $S_{Q_{1}} = S_{Q_{2}}$, System (2.3) has a positive order-1 periodic solution.

(ⅱ) When $S_{Q_{1}} < S_{Q_{2}}$,

By (3.4) and (3.5), it follows that the $Poincar\acute{e}\; map\; (2.6)$ has a fixed point, that is, System (2.3) has a unique positive order-1 periodic solution in the area $\Omega_{1} = \{(S, I)|H_{1} < I < H_{2}\}$. The proof is complete.

Theorem 3.4. For any $m, p\in(0, 1)$, $\frac{(1-q)(\delta\mu+\gamma)}{\beta} > S_{Q_{0}}$, Let $(\phi(t), \; \psi(t))$ is the positive order-1 periodic solution of System (2.3) in the area $\Omega_{1} = \{(S, I)|H_{1} < I\leq H_{2}\}$. If

where

then the periodic solution $(\phi(t), \psi(t))$ is orbitally asymptotically stable.

Proof. Assume that the periodic orbit $\Pi(C_{0}, t)$ starting from the point $C_{0}(\phi_{0}, (1-p)h_{2})$, where $\phi_{0} > S_{Q_{0}}$ moves to the point $C_{1}(\phi(T), \; \psi(T))$ on impulsive set $M_{2}$. Since $\frac{(1-q)(\delta\mu+\gamma)}{\beta} > S_{Q_{0}}$, then $\Pi(C_{0}, T) = C_{1}$, $C_{1}^{+} = C_{0}$, $\phi(T^{+}) = (1-q)\phi(T)$, $\psi(T^{+}) = (1-p)\psi(T)$. Compared with System (2.4), we get

Thus,

and

On the other hand, integrating both sides of the second equation of System (2.3) along the orbit $\widehat{C_{1}^{+}C_{1}}$, we have

Then, by simple calculation, it follows that

By condition (3.6), System (2.3) satisfies all conditions of Lemma 2.2. Therefore the positive order-1 periodic solution $(\phi(t), \psi(t))$ of System (2.3) is orbitally asymptotically stable. This completes the proof.

4.   Numerical simulations

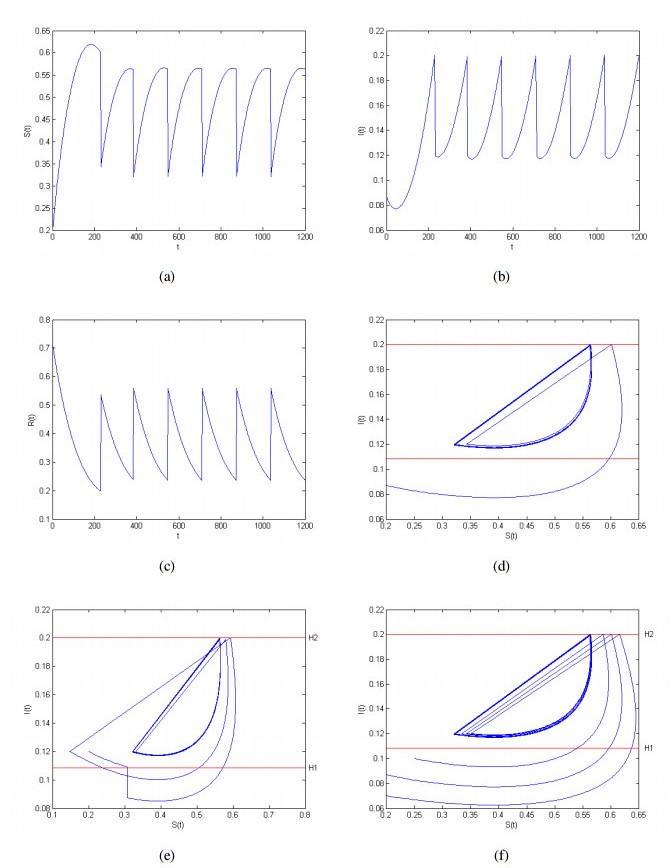
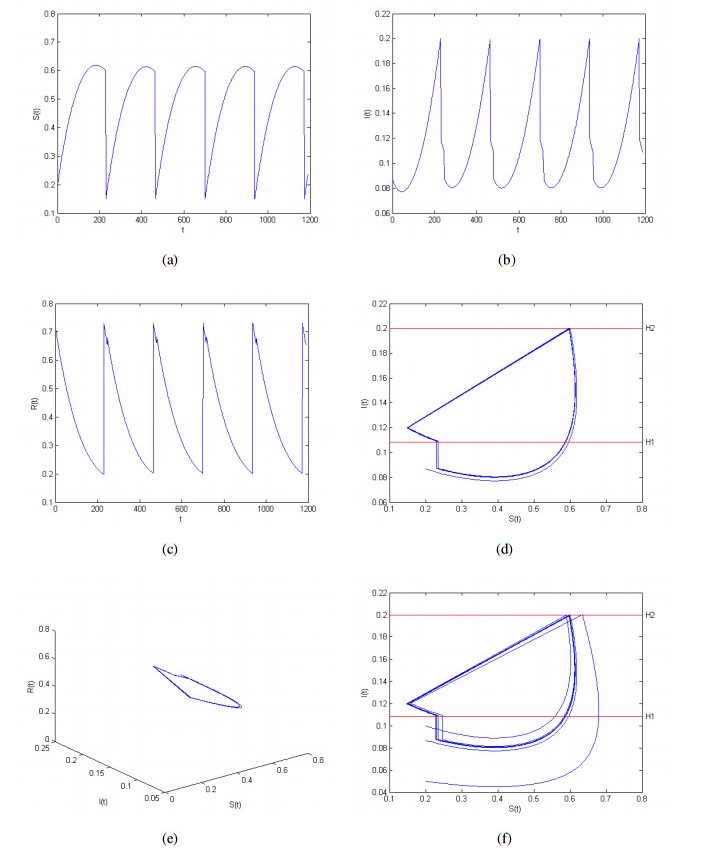
In this section, we test the correctness of our conclusions by numerical simulation. Let $\mu = 0.15, \; \beta = 0.6, \; \delta = 0.9, \; \gamma = 0.1, \; H_{1} = 0.1084, \; H_{2} = 0.2, \; p = 0.4, \; m = 0.2$. By calculation, we obtain that the orbit $\Pi(K_{0}, t)$ starting from $K_{0}(0, 0.12)$ intersects $M_{1}$ at $K_{1}(0.0671, 0.1084)$, where $S_{K_{1}} = 0.0671 < S^{*} = 0.3917$. Therefore, we get $S_{P} = 0.3917, \; P(0.3917, 0.1084)$ and the point $Q_{0}(0.22, 0.12)$ which the orbit $\Pi(Q_{0}, t)$ starting from on $N_{2}$ is also unique confirmed. Then, we consider the following SIR epidemic system with two state-dependent pulse controls:

Obviously, if $R_{0} > 1$, System (4.1) without the pulse effects has a unique endemic equilibrium $(S^{*}, \; I^{*}, \; R^{*}) = (0.3917, 0.365, 0.2433)$ which is globally asymptotically stable.

Case 1. Since $(1-q)(1-h_{2}) < S_{Q_{0}}$, then $q > 0.725$. Let $q = 0.75$, and the initial point is (0.2, 0.08672, 0.71328). According to Theorem 3.1 or Theorem 3.2, we know System (4.1) has a positive order-1 periodic solution (see Figure 1(a)–(c)). Furthermore, the positive order-1 periodic solution is orbitally asymptotically stable and has the asymptotic phase property, which is shown in Figure 1(d). Because $H_{2} < \frac{\mu\left(\beta-\delta\mu-\gamma\right)}{\beta(\gamma+\mu)}$, we also note that system (4.1) always has an orbitally asymptotically stable positive order-1 or order-2 periodic solution (Figure 1(e), (f)). Therefore, infectious disease may be prevented and reduced to a very low level through adjustment of the pulse immunization rate $m, q$, the pulse treatment rate $p$ and the hazardous threshold values $H_{1}$ and $H_{2}$.

Case 2. Since $\frac{(1-q)(\delta\mu+\gamma)}{\beta} > S_{Q_{0}}$, then $q < 0.4383$. Let $q = 0.43$, and the initial point is (0.2, 0.08672, 0.71328). From Theorem 3.3, we know System (4.1) has a unique positive order-1 periodic solution in the area $\Omega_{1} = \{(S, I)|H_{1} < I\leq H_{2}\}$, which is shown in Figure 2(a)–(c). Further, the positive order-1 periodic solution is orbitally asymptotically stable and has the asymptotic phase property (see Figure 2(d)–(f)).

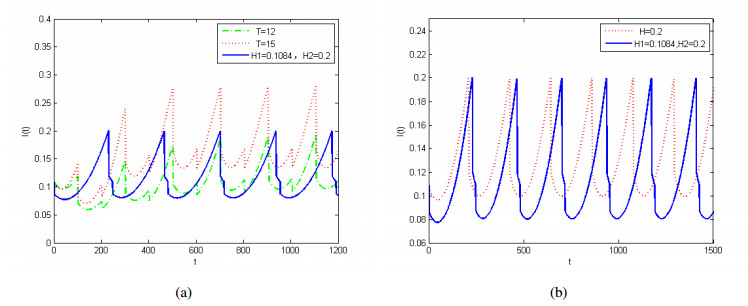
In addition, we compare the state-dependent pulse control strategy and PTPVS. From the numerical simulation, we note that infectious disease could decline quickly to a very low level by two state-dependent pulse controls. This is well explained in Figure 3. Assume that the hazardous threshold is 0.2, and the initial value is $(0.2, 0.1084, 0.6916)$. When the infected group is controlled to within 0.2, the solution tends quickly to a stable periodic solution due to the state feedback control strategies, that is, the disease is completely controlled. However, in order to attain the same goal, the fixed time pulse controls are not efficient (see Figure 3(a)). For the same initial value $(0.2, 0.1084, 0.6916)$, if we take control measures $\Delta I(t) = -0.2H_{1}$ at fixed time $t = \frac{nT}{2}$ and $\Delta S(t) = -0.75S(t), \; \Delta I(t) = -0.4H_{2}$ at fixed time $t = nT$, where $T = 15$ and $n = 1, 2, \cdots,$ the density of infected population can not be controlled under the hazardous threshold 0.2, and hence the disease will be spreading.

Furthermore, if we take control measures with $T = 12$, it slightly frequent than the state-dependent control, but the control cost obviously is higher, and it is difficult to achieve the expected purpose. We also can obtain that the two state-dependent pulse control strategies are more effective than the state-dependent pulse control which is just one time (see Figure 3(b)).

5.   Conclusions and discussion

This paper has formulated an SIR epidemic model with vertical transmission and two state-dependent pulse controls, while the dynamical behaviors have been investigated. Given a basic reproduction, the steady state of System (2.1) without impulsive effects has the disease present. By using the $Poincar\acute{e}\; map$, an analogue of the $Poincar\acute{e}$ criterion and the qualitative analysis method, some sufficient conditions are presented on the existence and the orbital asymptotical stability of a positive order-1 or order-2 periodic solution of System (2.3). This means that we can control the density of infectious disease at a low level over a long period of time by adjusting immune or medicated strength. It reveals the significant role that the pulse vaccination rate plays in System (2.3). When pulse vaccination $q > 1-\frac{\beta S_{Q_{0}}}{\delta\mu+\gamma}$ ($S_{Q_{0}}$ depends on the hazardous threshold value $H_{1}$), the disease period is relatively long, but it is short with $q < 1-\frac{S_{Q_{0}}}{1-H_{2}}$. It is concluded that the two state-dependent pulse control strategies, particularly for an epidemic with vertical transmission, are more feasible, effective and importantly, easily implemented than the state-dependent pulse control which is just one time or the fixed-time pulse control.

In this paper, the incidence rate is assumed to have the form $f(S, I) = \beta SI$, but many investigations have been done to extend this law in order to model the contagion process better. Mainly, the attention has been focused on modeling non-linear dependencies on $S$, such as $\beta S^{p}I, \; \frac{\beta S}{1+\alpha S}I$ and so on. In addition, it is well known that the environment is generally influenced by random factors. Hence the deterministic theory has not meet the needs of the reality of study well. Epidemic models are inevitably affected by environmental white noise, which often plays an important role in the real world, since it can provide an additional degree of realism compared to their deterministic counterparts ^[37,38]. Therefore, compared to our epidemic model, stochastic differential systems are more reasonable and realistic. These works will be left as our future consideration.

Additionally, we notice a phenomen on that when a disease spreads within a community, individuals will acquire knowledge about this disease. It will be more interesting to investigate the memory effect on the dynamics of our model by using the new generalized fractional derivative presented in ^[38] instead of the classical derivative used in (2.3). Therefore, in the future, we can refer to the practice of ^[39,40] to study the memory effect on the dynamics of our model.

Acknowledgments

Thanks for the support from the following fundings: the Natural Science Foundation of Gansu Province, China (No.21JR7RA217, No.20JR5RA460), and National Natural Science Foundation of China (No.1216053). Additionally, we should express appreciation to the two anonymous reviewers whose valuable suggestions improve the quality of our manuscript.

Conflict of interest

The authors declare there is no conflict of interest.