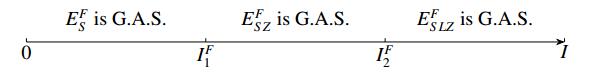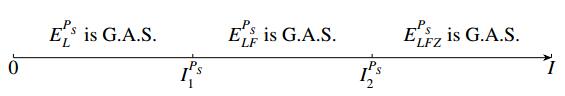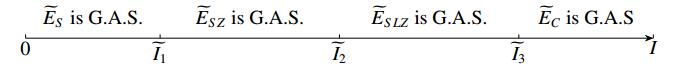Computational analysis of a collaboration network on human-computer interaction in Korea

1.   Introduction

It is important to determine survivors, which ultimately shape an ecosystem. However, answering this fundamental question depends on what we consider in a food web. There are studies on ecosystems that incorporate a different concept, like epidemics ^[10,11] and allelopathy ^[8].

Our work considers a microbial food web in the presence of parasitic fungi (e.g., chytrids). The importance of parasites in food webs has been emphasized in the literature; see ^[5,6,7]. According to a review paper ^[15] by Sommer et al, researchers have only recently considered parasites as one of the main drivers for phytoplankton succession. This review highlights the theory of mycoloop, a food chain conceived by Kagami and her team to explain the transfer of energy from large phytoplankton (Asterionella) to zooplankton (Daphnia) via parasitic fungi ^[1,2,3,4].

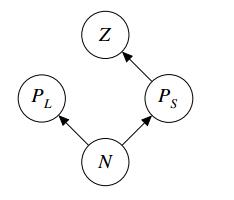
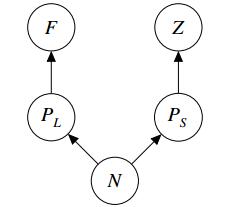
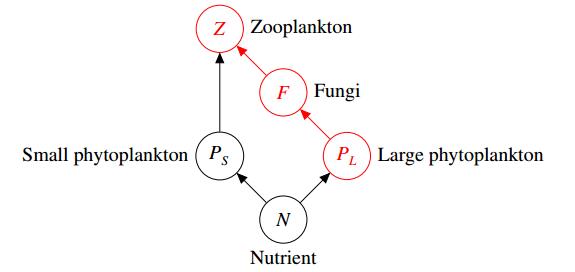
In this paper, we consider the following chemostat model based on Figure 1, where $^\prime = d/dt$.

The parameters of this model are described in Table 1.

Miki, Takimoto and Kagami formulated system (1.1) in their paper ^[9] and performed a local (steady-state) analysis to investigate the roles of parasitic fungi. We assume $I = q N^{(0)}$.

We focus on global dynamics and the limiting behavior of the solution

as $t$ goes to infinity. In particular, we determine initial and parameter conditions for the solution to describe the survival and extinction of species $P_S$, $P_L$, $F$, and $Z$.

Let

It is easy to show the state space $X$ and its interior $int(X)$ are positively invariant.

The rest of this paper is organized as follows. In Section 2, we establish that our model is dissipative, from which the nutrient uniformly persists regardless of the input $I$. In Section 3, we study the boundary dynamics. Notably, we construct a Lyapunov function to determine the basin of attraction. An investigation on the local and global stability of boundary equilibrium points is presented in Section 4. In Section 5, we apply the uniform persistence theory ^[12,13,16] to prove the coexistence of species $P_S$, $P_L$, $F$, $Z$ with $F-Z$ link, i.e., $\gamma >0$. Section 6 deals with the dynamics of system (1.1) with the presence of parasitic fungi, but no $F-Z$ link, i.e., $\gamma = 0$. We conclude the paper with a discussion in Section 7.

2.   Dissipativity and nutrient persistence

First we show that our model system (1.1) is dissipative, as stated in the following theorem.

Theorem 2.1. Each solution of system (1.1) in $X$ satisfies the following inequality:

Proof. Let $c = \displaystyle \frac{1}{\max\{e_P, \frac{f_F}{e_F}\}}$. We introduce the variable

It follows that $u^\prime \leq q\left[{N^{\left( 0 \right)}} - u\right]$. Moreover,

for all $t \geq 0$. Passing the limit supremum to inequality (2.2) as $t\rightarrow\infty$, we get $\limsup_{t\to\infty} u(t) \leq {N^{\left( 0 \right)}}$, which is inequality (2.1).

Theorem 2.2. The nutrient $N$ uniformly persists in $X$.

Proof. Observe that

Hence $N(t) \geq \delta > 0$ for $t\geq T_\epsilon$, where $\displaystyle \delta = \frac{I}{q+\max\left(a_S, a_L\right)\left(N^{(0)}+\epsilon \right)}$. This proves the uniform persistence of $N$ in $X$.

3.   Boundary Dynamics

The ecologically relevant equilibrium points lie in the state space $X$. For our analysis, we focus on boundary equilibrium points, which have at least one zero coordinate. To this end, we let

From ^[14], our basic assumption is

That is, we assume phytoplankton species of small size, $P_S$, is a strong competitor than that of large size, $P_L$.

3.1.   Boundary dynamics in the absence of parasitic fungi

When $F\equiv 0$, system (1.1) becomes

and its food web is shown in Figure 2.

The conditions for the global stability of the equilibrium points of system (3.1) are stated in the next theorem.

Theorem 3.1. Let $(H)$ hold and

For system (3.1), the following statements hold:

(i) If $N^\star < \lambda_S$, then $E_S^F = \left( \lambda_S, N^{(0)} - \lambda_S, 0, 0 \right)$ is globally asymptotically stable (G.A.S.).

(ii) If $\lambda_S < N^\star < \lambda_L$, then $E_{SZ}^F = \left( N^\star, P_S^\star, 0, Z^\star \right)$ is G.A.S., where $\displaystyle Z^\star = \frac{a_SN^\star-q}{b}$.

(iii) If $\lambda_S < \lambda_L < N^\star < \frac{I}{q}$, then $E_{SLZ}^F = \left( \lambda_L, P_S^\star, \widetilde {{P_L}}, \widetilde {Z} \right)$ exists and is G.A.S., where $\displaystyle \widetilde {Z} = \frac{1}{b} \left( a_S\lambda_L - q \right)$ and $\widetilde {{P_L}} = \frac{I}{q} - \lambda_L - \frac{a_S}{ a_L} P_S^\star$.

Proof. The statements are established as follows:

(ⅰ) We introduce the Lyapunov function given by

where $\widehat {{P_S}} = N^{(0)} - \lambda_S$, and $c_{1}, c_{2}, c_{3} > 0$ are to be determined. Then

Choose $c_{1} = 1$, $c_{2} = 1$, $c_{3} = \frac{1}{e_P}$. Since

it follows that

Therefore, LaSalle's invariance principle implies that $E_S^F = \left( \lambda_S, \widehat {{P_S}}, 0, 0 \right)$ is G.A.S.

(ⅱ)Note that $N^\star > \lambda_S$ implies that $Z^\star > 0$. Define the Lyapunov function

We obtain

by using the equivalent expression

Hence, by LaSalle's invariance principle, $E_{SZ}^F = \left( N^\star, P_S^\star, 0, Z^\star \right)$ is G.A.S.

(ⅲ) We construct the following Lyapunov function:

where

From the assumptions that $N_C = \lambda_L > \lambda_S = \frac{q}{a_S}$ and $N^\star > \lambda_L$, we see that $P_L^C >0$ and $Z_C >0$. Thus

We conclude from the invariance principle that $E_{SLZ}^F$ is G.A.S.

As a consequence of the above theorem, we obtain the following equivalent expressions:

Letting $I_1^F = q\left( \lambda_S+P_S^\star \right)$ and $I_2^F = q\left( \lambda_L+\frac{\lambda_L}{\lambda_S}P_S^\star \right)$ with $I_1^F < I_2^F$, we conclude that

(ⅰ) if $0 < I < I_1^F$, then $E_S^F = \left( \lambda_S, \widehat {{P_S}}, 0, 0 \right)$ is G.A.S.

(ⅱ) if $I_1^F < I < I_2^F$, then $E_{SZ}^F = \left( N^\star, P_S^\star, 0, Z^\star \right)$ is G.A.S.

(ⅲ) if $I_2^F < I$, then $E_{SLZ}^F \left( \lambda_L, P_S^\star, \widetilde {{P_L}}, \widetilde {Z} \right)$ is G.A.S.

The global stability of equilibrium points of system (3.1) is depicted in Figure 3.

3.2.   Boundary dynamics in the absence of zooplankton

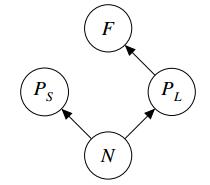
We consider the case that $Z \equiv 0$. Then system (1.1) becomes

and its food web is presented in Figure 4.

From hypothesis $(H)$, we see that $P_S$ is a better competitor for nutrient than $P_L$. Obviously from the fact that parasitic fungi $F$ only consume $P_L$, it follows that $E_S^Z = \left( \lambda_S, \widehat {{P_S}}, 0, 0 \right)$ with $\widehat {{P_S}} = N^{(0)} - \lambda_S$ is G.A.S. Below we state the result without proof.

Theorem 3.2. Under assumption $(H)$, $E_S^Z = \left( \lambda_S, \widehat {{P_S}}, 0, 0 \right)$ is G.A.S. for system (3.2).

3.3.   Boundary dynamics in the absence of phytoplankton species

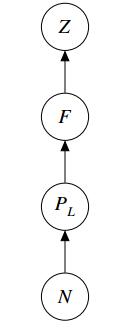
For the case when $P_S \equiv 0$, system (1.1) becomes

with the corresponding food web provided in Figure 5.

Using the same Lyapunov functions $V$ as defined in Theorem 3.1, we can prove Theorem 3.3 stated below. We thus omit the proof.

Theorem 3.3. Let hypothesis $(H): 0 < \lambda_S < \lambda_L < \frac{I}{q}$ hold. Then the solution of system (3.3) satisfies the following statements:

(i) If $0 < I < \lambda_L q\left( 1+\frac{a_L}{f_F\beta } \right)$, then $E_{L}^{P_S} = \left( \lambda_L, N^{(0)}-\lambda_L, 0, 0 \right)$ is G.A.S.

(ii) If $\lambda_L q\left( 1+\frac{a_L}{f_F\beta } \right) < I < \lambda_L\left( 1+\frac{a_L}{f_F\beta } \right)\left( q+\frac{\beta }{e_P\gamma }\left( q+m_Z \right) \right)$, then $E_{LF}^{P_S} = \left( \bar N, \bar L, \bar F, 0 \right)$ is G.A.S. Here $\bar L = \frac{q}{f_F\beta }$, $\bar N = \frac{I}{q+a_L\bar L}$, $\bar F = \frac{a_L\bar N - q}{\beta } > 0$.

(iii) If $I > \lambda_L\left( 1+\frac{a_L}{f_F\beta } \right)\left( q+\frac{\beta }{e_F\gamma }\left( q+m_Z \right) \right)$, then the positive equilibrium G.A.S. He $E_{LFZ}^{P_S} = \left( \widehat N, \widehat {{P_L}}, \widehat F, \widehat Z \right)$ exists and is G.A.S. Here $\widehat F = \frac{q+m_Z}{\gamma e_F}$, $\widehat N = \frac{\beta \widehat F + q}{a_L}$, $\widehat Z = \frac{f_F\beta \widehat {{P_L}} - q}{\gamma } > 0$, $\widehat {{P_L}} = \frac{I-q\widehat N}{a_L\widehat N} > 0$.

Taking $I_1^{P_S} = \lambda_L q\left( 1+\frac{a_L}{f_F\beta } \right)$ and $I_2^{P_S} = \lambda_L\left( 1+\frac{a_L}{f_F\beta } \right)\left( q+\frac{\beta }{e_F\gamma }\left( q+m_Z \right)\right)$, the global stability of equilibrium points of system (3.3) is provided in Figure 6.

4.   Boundary equilibrium points of system (1.1) and their stability

From Section 3, there are seven distinct boundary equilibrium points of system (1.1) listed below :

where

Next we discuss the local asymptotic stability of the boundary equilibrium points in (4.1) with respect to system (1.1). Obviously $E_0$ is unstable under hypothesis $(H)$.

For the stability of $E_S$, let $N^{(0)} < \lambda_S + \frac{q+m_Z}{e_Pb}$. Then

and all of the eigenvalues of the Jacobian matrix of system (1.1) at $E_S$ are negative. Hence $E_S$ is asymptotically stable if $N^{(0)} < \lambda_S + \frac{q+m_Z}{e_Pb}$.

For the stability of $E_{SZ}$, if $N^{(0)} < \lambda_L + \frac{\lambda_L}{\lambda_S}P_S^\star$, then

Thus, if $N^{(0)} < \lambda_L + \frac{\lambda_L}{\lambda_S}P_S^\star$, then $E_{SZ}$ is asymptotically stable.

For the stability of $E_{SLZ}$, consider

Therefore, $E_{SLZ}$ is asymptotically stable if (4.5) holds.

For the stability of $E_L$, let $N^{(0)} < \lambda_L + \frac{q}{f_F\beta }$. Then

We conclude that $E_L$ is unstable in the $P_S$ direction and stable in $F$ and $Z$ directions.

For the stability of $E_{LF}$, the assumption and $\bar F > \frac{q+m_Z}{e_F\gamma }$ imply that

For the stability of $E_{LFZ}$, consider

Hence $E_{LFZ}$ is asymptotically stable if $a_S\widehat N - b\widehat Z - q < 0$.

A summary of the results on the asymptotic stability of boundary equilibrium points of system (1.1) is provided in Table 2.

Now we present some extinction results in the next theorem.

Theorem 4.1. Suppose $f_F \leq \frac{e_P}{e_F}$ holds. Then the following statements hold.

(i) If $N^{(0)} < \lambda_S + \frac{q+m_Z}{e_Pb}$, then $E_S = \left( \lambda_S, N^{(0)}-\lambda_S, 0, 0, 0 \right)$ attracts each point $\left( N, P_S, P_L, F, Z \right) \in \mathbb{R}_+^5$.

(ii) If $\lambda_S + P_S^\star < N^{(0)} < \lambda_L + \frac{\lambda_L}{\lambda_S}P_S^\star$, then $E_{SZ} = \left( N^\star, P_S^\star, 0, 0, Z^\star \right)$ attracts each point $\left( N, P_S, P_L, F, Z \right) \in \mathbb{R}_+^5$.

Proof. (ⅰ) Introduce the Lyapunov function

Choose $c_1 = c_2 = 1$, $c_3 = \frac{e_F}{e_P}$, and $c_4 = \frac{1}{e_P}$. Then

It folows from the invariance principle that $E_S$ is a global attractor.

(ⅱ) Define the Lyapunov function by

Let $c_1 = 1$, $c_2 = 1$, $c_3 = \frac{e_F}{e_P}$, and $c_4 = \frac{1}{e_P}$. Then

By invariance principle, $E_{SZ}$ is a global attractor.

Remark 4.2: From our numerical simulation results, we conjecture that the equilibria $E_S$ and $E_{SZ}$ are G.A.S. even when $f_F > \frac{e_P}{e_F}$.

5.   Uniform persistence of system (1.1) with both parasitic fungi and an $F$-$Z$ link, i.e., $\gamma > 0$

In this section, we determine conditions for the species in system (1.1) to coexist by applying the theory of uniform persistence of Butler, Freedman and Waltman ^[12,13,16]. Since the boundary dynamics for $F \equiv 0$, $Z \equiv 0$, and $P_S \equiv 0$ are discussed in Section 3 and the acyclic conditions are easy to verify, it remains only to verify that $W^{S}\left( {\cal M}_i \right) \cap {\underline{{\rm Int}}} (\mathbb{R}_+^{5}) = \phi$ for each boundary equilibrium ${\cal M}_i$.

Consider the operation diagram in Figure 3 and the case that $I > I_2^F = \lambda_L\left( q+a_LP_S^\star \right)$. From the equation for $F$ in system (1.1), the invasion condition for the boundary equilibrium $E_{SLZ} = \left( \lambda_L, P_S^\star, \widetilde{P_L}, 0 , \widetilde{Z} \right)$ is $\frac{F}{F} > 0$. That is,

where $\widetilde {{P_L}} = \frac{I}{q} - \lambda_L - \frac{a_S}{a_L}P_S^\star > 0$, $\widetilde {Z} = \frac{1}{b}\left( a_S\lambda_L - q \right) > 0$, and $P_S^\star = \frac{q+m_Z}{e_Pb}$ (See 4.2).

Lemma 5.1 below shows that inequality (5.1) is equivalent to

Next, we consider the operation diagram in Figure 6 and the case that

Similarly, the equation for $P_S$ in system (1.1) provides the following invasion condition for the boundary equilibrium $E_{LFZ} = \left( \widehat N, 0, \widehat {{P_L}}, \widehat F, \widehat Z \right)$ :

where $\widehat F = \frac{q+m_Z}{\gamma e_F}$, $\widehat {{P_L}} = \frac{I - q\widehat N}{a_L\widehat N} > 0$, $\widehat Z = \frac{f_F\beta \widehat {{P_L}} - q}{\gamma }$, and $\widehat N = \frac{\beta \widehat F + q}{a_L}$ (See (4.2)).

In Lemma 5.1, we also prove that inequality (5.3) is equivalent to

We state the lemma below.

(i) Inequalities (5.1) and (5.2) are equivalent.

(ii) Inequalities (5.3) and (5.4) are equivalent.

(iii) If $\frac{e_P}{e_F} > f_F$, then $I_3 > I_2$.

Proof. (ⅰ) Equivalence is established by substituting $\widetilde {{P_L}} = \frac{I}{q} - \lambda_L - \frac{a_S}{a_L}P_S^\star$ and $\widetilde {Z} = \frac{1}{b}\left( a_S\lambda_L - q \right)$ into inequality (5.1). We have

This proves (ⅰ).

(ⅱ) First note that $\widehat N = \frac{\beta }{a_L}\widehat F + \lambda_L > \lambda_S$ implies $a_S\widehat N - q > 0$. We have

Using the equalities

we express $I_3$ as

Next, by the equivalence

it follows that $I_2^{P_S} = \lambda_L\left( 1+\frac{a_L}{f_F\beta } \right) \left( q + \beta \widehat F \right) < I_3$. Hence (ii) is established.

(ⅲ) Expanding $I_2$ and $I_3$, we have

and

If $e_Ff_F < e_P$, then $\frac{a_S \lambda_L}{bf_Fe_F} > \frac{a_S \lambda_L}{e_Pb}$. Thus, it is easy to verify that $I_3 - I_2 >0$.

We establish the coexistence of species in the next theorem wherein the proof follows directly from the above lemma.

Theorem 5.2. The following statements hold:

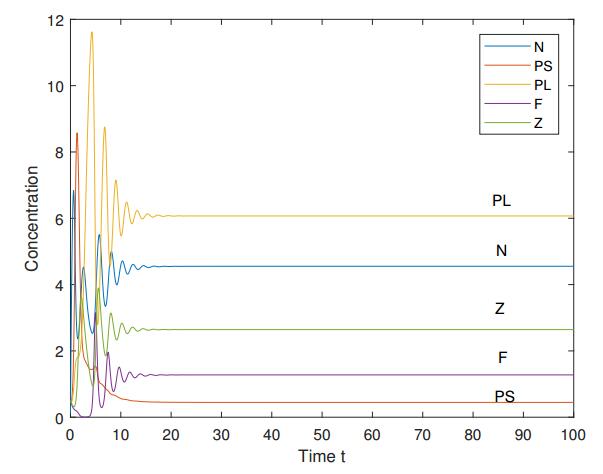
(i) If $I_2 < I < I_3$, then system (1.1) is uniformly persistent and the positive equilibrium is globally asymptotically stable.

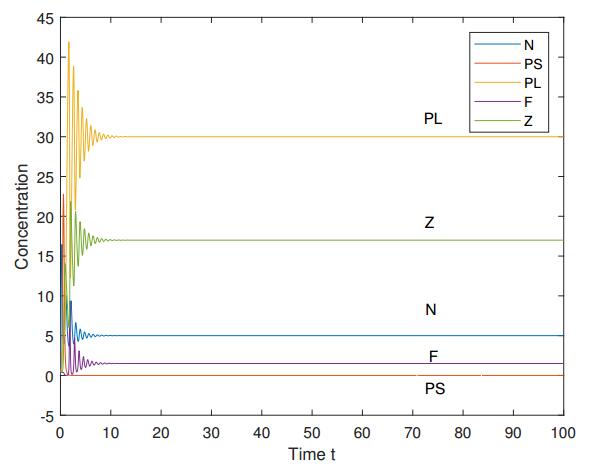
(ii) If $I > I_3$, then $P_S(t) \to 0$ as $t \to \infty$.

Using the parameter values $q = 1$, $a_S = 0.8$, $a_L = 0.5$, $\lambda_s = 1.25$, $\lambda_L = 2$, $b = 1$, $e_P = 0.5$, $e_F = 0.4$, $\beta = 1$, $\gamma = 1$, $f_F = 0.6$, and $m_Z = 0.5$, we have $I_2 = 11.35$ and $I_3 = 66.92$. By setting $I = 20$, we obtain a numerical simulation of statement (ⅰ) as depicted in Figure 7. Letting $I = 80$, a numerical simulation for statement (ⅱ) is shown in Figure 8.

6.   Dynamics with parasitic fungi, but without an $F$-$Z$ link

When $\gamma \equiv 0$, system (1.1) becomes

and its food web is shown in Figure 9.

Theorem 6.1. Let $(H): 0 < \lambda_S < \lambda_L < \frac{I}{q}$ hold.

(i) If $P_S^\star > \widehat {{P_S}}$, then $\widetilde{E}_S = \left( \lambda_S, \widehat {{P_S}}, 0, 0, 0 \right)$ is G.A.S., where $\widehat {{P_S}} = \frac{I-q\lambda_S}{a_S\lambda_S}$ and $P_S^\star = \frac{q+m_Z}{e_Pb}$.

(ii) If $P_S^\star < \widehat {{P_S}}$ and $\lambda_S <N^\star < \lambda_L$, then $\widetilde{E}_{SZ} = \left( N^\star, P_S^\star, 0, 0, Z^\star \right)$ is G.A.S., where $N^\star = \frac{I}{q+a_SP_S^\star}$ and $Z^\star = \frac{a_SN^\star - q}{b}$.

(iii) If $P_S^\star < \widehat {{P_S}}$ and $N_C < \lambda_L < N^\star$, then $\widetilde{E}_{SLZ} = \left( \lambda_L, P_S^\star, P_L^\star, 0, \widehat Z \right)$ is G.A.S., where $P_L^\star = \frac{I - q\lambda_L - a_SP_S^\star\lambda_L}{a_L\lambda_L}$.

(iv) If $P_S^\star < \widehat {{P_S}}$, $N^\star > \lambda_L$, and $N_C > \lambda_L$, then $\widetilde{E}_{C}= \left( N_C, P_S^C, P_L^C, F_C, Z_C \right)$ is G.A.S., where $P_L^C = \frac{q}{f_F\beta }$, $P_S^C = \frac{q+m_Z}{e_Pb} = P_S^\star$, $N_C = \frac{I}{q + a_SP_S^C + a_LP_L^C}$, $Z_C = \frac{a_SN_C - q}{b}$, and $F_C = \frac{a_LN_C - q}{\beta }$.

Let $\widetilde{I}_1 = q\lambda_S + a_SP_S^C\lambda_S$, $\widetilde{I}_2 = q\lambda_L + a_SP_S^C\lambda_L$ and $\widetilde{I}_3 = q \lambda_L + a_SP_S^C\lambda_L + a_LP_L^C\lambda_L$. Then $\widetilde{I}_1 < \widetilde{I}_2 < \widetilde{I}_3$. As a consequence of Theorem 6.1, the following statements hold.

(ⅰ) If $0 < I < \widetilde{I}_1$, then $\widetilde{E}_S$ is G.A.S.

(ⅱ) If $\widetilde{I}_1 < I < \widetilde{I}_2$, then $\widetilde{E}_{SZ}$ is G.A.S.

(ⅲ) If $\widetilde{I}_2 < I < \widetilde{I}_3$, then $\widetilde{E}_{SLZ}$ is G.A.S.

(ⅳ) If $I > \widetilde{I}_3$, then $\widetilde{E}_{C}$ is G.A.S.

The global stability of system (6.1) is given in Figure 10.

Proof. (ⅰ) Note that $\widehat {{P_S}} > P_S^\star \Leftrightarrow N^\star > \lambda_S \Leftrightarrow Z^\star > 0$. We introduce the Lyapunov function

Then

from the assumption $P_S^\star > \widehat {{P_S}}$. Thus $\widetilde{E}_S$ is G.A.S. by invariance principle.

(ⅱ) Note that $\widehat {{P_S}} > P_S^\star$ ensures that $Z^\star > 0$. Introduce the Lyapunov function

Then, by the assumptions $P_S^\star < \widehat {{P_S}}$ and $N^\star < \lambda_L$, we have

Therefore $\widetilde{E}_{SZ}$ is G.A.S. by invariance principle.

(ⅲ) Define the Lyapunov function

Then

Using the assumptions $P_S^\star < \widehat {{P_S}}$ and $N_C < \lambda_L < N^\star$, and the equivalence below

we have $\overset{\bullet}{V} \leq 0$. Hence $\widetilde{E}_{SLS}$ is G.A.S. by invariance principle.

(ⅳ) Observe that the assumptions $P_S^\star < \widehat {{P_S}}$, $N^\star > \lambda_L$, and $N_C > \lambda_L$ imply $\widehat {{P_S}} >0$, $P_L^{*} >0$, and $F_C >0$, respectively. By introducing the Lyapunov function

we obtain

Therefore it follows from invariance principle that $\widetilde{E}_{C}$ is G.A.S.

7.   Discussion

In this paper, we study an aquatic ecosystem with five species : a single nutrient resource $N$ (Phosphorus), the small phytoplankton $P_S$, the large phytoplankton $P_L$, the zooplankton $Z$, and the parasitic fungi $F$. Both $P_S$ and $P_L$ consume $N$. In the food web (see Figure 1), the zooplankton $Z$ only consumes the small phytoplankton $P_S$ but the large phytoplankton $P_L$ is inedible to the zooplankton. In the absence of zooplankton, we assume that the small phytoplankton $P_S$ is a better competitor than the large $P_L$ in the exploitative competition for nutrient. With the presence of parasitic fungi $F$, we consider two cases : the food web with an $F - Z$ link and that without an $F - Z$ link. In Section 3, we first study the boundary dynamics of the food web, i.e., the population dynamics under the assumptions that $F \equiv 0$, $Z \equiv 0$ and $P_S \equiv 0$. We then employ Lyapunov functions to establish the results of global stability as the nutrient input I varies. Section 4 deals with the determination of conditions for the local stability of boundary equilibrium points of system (1.1) and the proofs of several partial results on the extinction of species. In Section 5, with the well understood information of boundary dynamics proven in Section 3, we establish the uniform persistence of the food web. Section 6 is devoted to determine conditions for the global stability of species in the system of food web without an $F - Z$ link.

Now we discuss the role played by parasitic fungi in the coexistence of species in the food web. Recall that, in the absence of parasitic fungi, from Figure 3, coexistence of species occurs when $I>I _2^F$. When parasitic fungi are present in the food web, we consider two cases: one with an $F - Z$ link and another without an $F-Z$ link. In the case without an $F - Z$ link, coexistence of species occurs when $I > \widetilde{I}_3$ (see Theorem 6.1), whereas in the case with an $F - Z$ link, coexistence of species occurs when $I_2<I< I_3$ (see Theorem 5.2). A comparison of the three quantities $I_2^F$, $\widetilde{I}_3$, $I_2$ shows that

where

In view of the above, the best case for the coexistence of species of the food web is when $I > I_2^F$. That is, coexistence of species occurs if there is no parasitic fungus. In the case that parasitic fungus is present and there is no $F-Z$ link, coexistence of species occurs if $I > \widetilde{I}_3$. With the presence of parasitic fungi and an $F-Z$ link, we have coexistence in the parameter region $I_2 < I < I_3$. From our numerical simulation (see Figure 8), we observe that, if $I > I_3$, then the small phytoplankton $P_S$ goes to extinction.

Finally, we note that in ^[9] the authors discuss the role of parasitic fungi in zooplankton biomass at steady states. Their conclusion is that the presence of an $F-Z$ link can benefits large phytoplankton and strengthens competition between small and large phytoplankton reducing material transfer from smaller phytoplankton to zooplankton. While our analysis shows that without $F-Z$ link if $I_1^F < I < I_2^F$ then zooplankton, fungi, small phytoplankton coexist; if $I > I_2^F$, the zooplankton, fungi, small and large phytoplankton coexist (see Figure 3). However, with $F-Z$ link, the system (1.1) is uniformly persistent if $I_2 < I < I_3$ (Theorem 5.2). From the inequality $I_2^F < I_2 < I_3$, it is easier to obtain coexistence when there is no $F-Z$ link.

Acknowledgments

The first author would like to acknowledge the financial support of the Department of Science and Technology-Science Education Institute (DOST-SEI), through the Accelerated Science and Technology Human Resource Development Program-National Science Consortium (ASTHRDP-NSC). The second author acknowledges the support of Ministry of Science and Technology (MOST), Taiwan and National Center of Theoretical Science, Taiwan.

Conflict of interest

The authors declare there is no conflict of interest.