1.
Introduction
The walking system of biped robot is a complex dynamic system with multi variables and strong coupling, which makes the research of robot in different walking environments challenging. Passive dynamic walking (PDW), which was proposed by McGeer [1], provides new ideas for walking dynamics of biped robot. The passive dynamic walking robot can walk stably on a gentle slope without any input. In recent years, most of the research on walking dynamics concerns robots on downhill or flat road, while only little has addressed robots climbing stairs. The results about robot walking dynamics on downhill or flat road are very rich. For example, bifurcations and the chaotic behavior of passive dynamic biped robots were discussed in [2], a combination of feedback linearization and finite-time controllers was used to control the walking posture and the stability of the whole behavior was investigated by analysis of a one-dimensional Poincaré map [3]. However, little is known about the walking dynamics of biped robot climbing stairs. This work focuses on biped robot climbing stairs.
Human walking is a complex mechanical motion powered by the activity of numerous muscles. For humanoid robot, it is necessary to consider what kind of drive to compensate energy loss caused by heel strike and make it walk more stably and effectively in different environments [4,5,6]. Different types of driving forces are added to the ankles of robots to simulate the positive ankle push-off during human walking. For example, Daniel et al. [7] considered a simple model based on spring-mass-running with a compliant ankle joint, Zelik et al. [8] and Chen et al.[9] studied a simple dynamic walking model with feet and series elasticity at the ankle joint. The authors utilized non-instantaneous spring thrust added at the ankle to compensate for collision losses. In recent research, impulsive thrust is considered to provide driving force for robot. This driving force can provide effective power to a compass model on level ground [10,11]. The results of simple two-dimensional (2-D) models with impulsive thrust show that such thrust (ankle push-off) can minimize energy consumption and is a promising driving method for biped robot [12].
In the past, different kinds of robots, such as wheeled robot [13], tracked robot [14], hexapod robot[15] and so on, have been used to investigate walking dynamics of stair ascending. Bipedal robot, which is closer to human behavior, is considered as an important one investigating walking dynamics of stair ascending. A virtual slope method, which regards the stairs as a virtual slope, was proposed to discuss walking trajectory planning on stairs for biped robots [16]. In 1999, Shih et al. designed a 7-DOF biped robot BR-1 with a simplest bipedal structure, which has two variable-length legs for simulating knee joints of human walking and a translatable balance weight in the body for stair climbing[17]. Its walking stability was insured by large feet and carefully controlling the position of the center of gravity. Figliolini et al. developed a biped robot EP-WAR2 with a suitable binary pneumatic actuation and used external control elements like suction cups to ensure equilibrium of the biped while walking or climbing stairs [18]. For the biped robot with multi joints, the complex structure and multi degrees of freedom make the research of walking dynamics more difficult[19,20,21]. Moreover, stair ascending, so far, is still studied for biped robot as challengeable topics. The theoretical analysis of dynamic stability during stair ascending has been still scarcely involved.
In the process of climbing stairs, the leg structure of bipedal robot is required to be flexible enough to avoid the scuffing problem between the bottom of the foot and the stairs. Telescopic legs can successfully complete the movement of ascending stairs, for example, Asano discussed a modified mechanism for a parametric excitation using telescopic legs and considered this biped robot to ascent stairs by utilizing the hybrid actuation effect [22]. A unifying framework to study energy-efficient optimal gaits for a bipedal model with telescopic legs and without elastic elements on different support surfaces such as level ground, sloped or staircase is discussed in [23].
There are many research methods and results on the dynamics of robots walking on slope and level ground. For example, stability of periodic gaits, limit cycle, chaos, and bifurcations of robot walking are well investigated [24,25,26,27], a method of linearization is used to build Poincaré map for PDW [28,29], linear inverted pendulum model is used to discuss biped robots walking [30]. However, the research on the walking of stair climbing biped robot with telescopic legs and impulse thrust is difficult and very challenging at present, and most of the research conclusions are numerical results. Non-smooth system exists widely in the real world and has complex dynamic behavior [31]. The model of ascending stair biped robot with telescopic legs and impulse thrust belongs to the category of non-smooth system and needs to be further investigated theoretically. For an ascending stair biped model, the clear dynamic information, such as the transition during different phase of the stair ascending, the dynamic equation during swing phase and so on, is critical to plan the motion of the robot's two legs. Motivated by these facts, walking dynamics of a ascending stair biped robot with telescopic legs and impulse thrust is discussed in this paper. The research focuses on calculation of torque to ensure robot walking and on theoretical analysis of the existence of periodic gaits.
This paper is organized as follows: In Section 2, a model of ascending stair biped robot with telescopic legs and impulse thrust is proposed. Theoretical analysis of complex walking dynamics of the ascending stair biped model is given in Section 3. Simulation results are given in Section 4 and this paper is concluded in Section 5.
2.
Model description
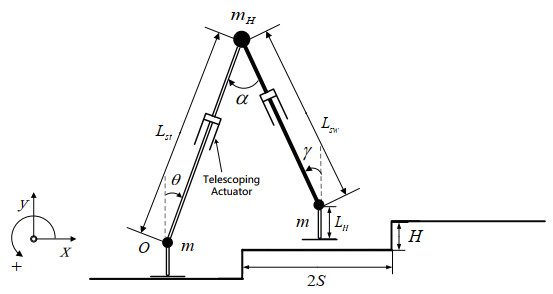
The model of ascending stair biped robot, which contains a hip joint and two rigid legs with massless telescoping actuator, is illustrated in Figure 1. The length of supporting leg is Lst and the length of non-supporting leg is Lsw. For simplicity, we assume that the mass of the biped robot is distributed as three units, namely, ankle joints of two legs (m) and hip joint (mH), where mH≫m. The variable-length legs is set to serve as knee joints for ascending stairs. The variables θ and γ represent the angles of the supporting (stance) and non-supporting (swing) leg relative to the ground of vertical, respectively. The length and height of the stair are 2S and H, respectively. α is the angle between two legs and is given as α=θ−γ.
During swing phase, we assume that the frictional coefficient is large enough to prevent sliding between the stance foot and the floor, and the foot of the stance leg is always on the ground. The robot starts from the initial posture with two feet placed in the middle of the stairs and the stride length of the robot is fixed to 2S. The projection of the hip joint is located at the boundary of the stair. We assume that the process of collision between the swinging legs and the ground is modeled as the collision of two rigid bodies. After the impact, the stance leg abandons the ground without any interaction with the ground.
The remaining joint below the ankle, which is used to keep balance of the robot during ascending and whose mass is ignored, is called the heel of the ascending stair biped. The mass of telescoping actuator is merged into that of ankle joint. The actuator can make the leg stretch to a specific length in a short time, while not generating additional impulse force to make the leg bounce from the ground.
2.1. Four-phase gait
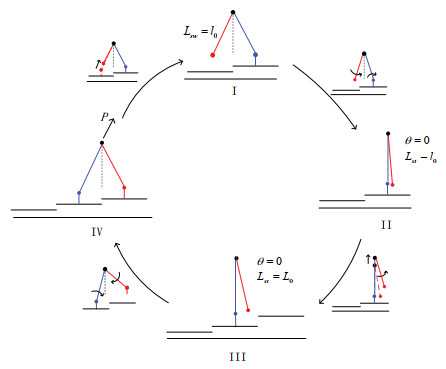
As shown in Figure 2, the four phases separate one step into two continuous phases and two instantaneous process, namely, the swing phase before stretching of the stance leg (Ⅰ and Ⅱ), the instantaneous stretching phase of the stance leg (Ⅱ and Ⅲ), the swing phase after stretching of the stance leg (Ⅲ and Ⅳ), the impact conditions (Ⅳ).
Let q=[θγ] be the vector of generalized coordinates of the ascending stair biped model. The two continuous phases of bipedal robot walking model can be represented by the following nonlinear differential equations according to the Lagrangian dynamics.
where L(q,˙q )=K(q,˙q )−V(q) is the Lagrange equation defined by the kinetic energy (K) and potential energy (V) in the system. Fi is the generalized force applied to the mass points.
At the instantaneous stretching phase of the stance leg and the impact instant with the stair, the state variable of the system undergo two transient variations according to the law of conservation of angular momentum.
The first phase(Ⅰ–Ⅱ). The bipedal robot starts climbing with the initial state, namely, θ=θ0, γ=γ0 and Lst=Lsw=l0. The behavior of this phase is similar to that of swing phase of a simple two link biped. This phase lasts until θ=0 (the stance leg perpendicular to the stair). It follows from (1) that
where M1 is the inertia matrix, C1 includes Coriolis and centrifugal terms, G1 includes gravity forces, B1 is the input matrix, u is the torque vector. They are given as follows.
where ρ=mmH, the torques u1 and u2 are applied to the hip joint and the ankle joints of stance during this phase, respectively.
The second phase (Ⅱ and Ⅲ). The instantaneous phase occurs when the stance leg perpendicular to the stair, which is defined by the following set.
There is no change in the angular momentum just before and after the stretching phase and the length of the stance leg is varied from l0 to L0, where L0 is the maximum leg length. The transition rules at the moment are given as follows.
where the subscripts and represent just after and just before this instantaneous phase, respectively. Se(q)=(Q+1(α))−1Q−1(α) with α=θ−−γ−=θ+−γ+,
and
The third phase (Ⅲ and Ⅳ). The stance leg continues swinging around the ankle joint until the swing leg and the stair are about to collide. Unlike first phase, the two legs are not equal in length in this phase. The dynamics of this phase can be expressed as follows.
where
The forth phase (Ⅳ). In this instantaneous process, in order to let the biped robot have enough energy during the next period gait, we apply impulse force p on the the stance leg, which follows the direction of this leg. Moreover, for avoiding the scuffing problem, the length of the new swing leg is shortened to l0 at the moment of role switch between the two legs, as well as its heel is retracted. The impact phase occurs for the three following mathematical conditions are satisfied.
where Υ2(q,˙q)=dΥ1(q)dt=∂Υ1(q)∂q˙q. Condition (6) ensures that the swing leg reaches the stair, is moving downward, and is in front of the stance leg and the mass points of two legs are 2S apart.
In this impact phase, impulse thrust p along the direction of the stance leg is used to provide the power. Instantaneous collision switching model for bipedal robots with impulse thrust is shown in Figure 3. One can calculate that
It follows from v+=l0˙θ+,v−=L0˙θ− that
According to the momentum theorem, the following algebraic expression is obtained.
The transition of the impact phase can be expressed as follows.
where s33=L0l0cos(α−), s43=(1−L0l0+l0L0)cos(α+)s33, w3=1mHl0sin(α−), and w4=(1−L0l0+l0L0)mHl0sin(α−)cos(α+).
2.2. Impulsive hybrid nonlinear dynamics
Equations (2), (4), (5) and (8) and conditions (3) and (6) represent different parts of the walking dynamics of ascending stair biped model in one step. Thus the complete walking dynamics of the ascending stair biped model can be represented as an impulsive hybrid system consisting of multiple continuous nonlinear differential equations and multiple discrete algebraic mappings.
Let X=(q ˙q)T=(θ γ ˙θ ˙γ)T=(x1 x2 x3 x4)T be the state vector. In view of (2)–(8), the impulsive hybrid system is described as follows.
where
Ω1 and Ω2 denote the state space of the swing phase before and after stretching of the stance leg, respectively.
3.
Dynamical analysis
3.1. Poincaré map
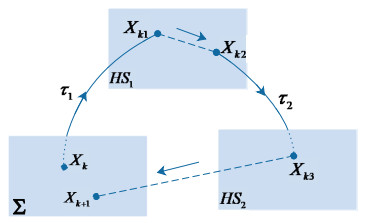
Choose the following hyperplane as the Poincaré section.
Let Xk=(arcsinSl0, −arcsinSL0, x3k, x4k)T be the initial point of X(t), where Xk=X(0)∈Σ.
As shown in Figure 4, the trajectory X(t) starting from Xk reaches the point Xk1= (0, x2k1, x3k1, x4k1)T=X(τ1) at t=τ1, and jumps to Xk2= (0, x2k2, x3k2, x4k2)T=X(τ+1) in the plane HS1, where Xk2=Δ1(Xk1).
The trajectory X(t) reaches the point Xk3= (−arcsinSL0, arcsinSl0, x3k3, x4k3)T in the plane HS2 at t=τ1+ τ2 under the action of torques, where Xk3=X(τ1+ τ2). Then it jumps to Xk+1=(arcsinSl0, −arcsinSL0, x3(k+1), x4(k+1))T in Poincaré section Σ due to the effect of impulse thrust p and role exchange of two legs.
Hence we obtain the following Poincaré map.
However, due to the fact that the impulsive hybrid nonlinear dynamics of the system (9) includes two nonlinear differential equations, it is difficult to obtain explicit expression of τ1, τ2, and solutions to (9), especially to ensure the trajectory X(t) intersects the plane HS2 at t=τ1+ τ2, namely, the two conditions x1(τ1+ τ2)=−arcsinSL0 and x2(τ1+ τ2)=arcsinSL0 hold at the same time. Hence, the Poincaré map (12) can be used for numerically simulation of the complex dynamic behavior of system (9), but not for theoretical analysis of walking dynamics. In order to solve the above problems, we linearize system (9), obtain an explicit map, and discuss the walking dynamics of ascending stair biped robot.
3.2. Linearized system
For simplicity, we denote basic unit ι by ιΔ=√l0g. By dimensionless and linearizing the Eqs (2) and (5) around the equilibrium point q=˙q=O2×2, we have
where u∗i=uil20mH(i=1,2,3), u∗4=u4L20mH, d1=l0L0.
Hence system (9) can be rewritten as
where ˜Δ1(x)=[I2×2O2×2O2×2˜Se(x)]x, ˜Se=[L200−l0L0cos(α)l20]−1[l200−l20cos(α)l20], and the input torques u∗2=e2, and u∗4=e4 are constant.
3.3. Realization of climbing stairs
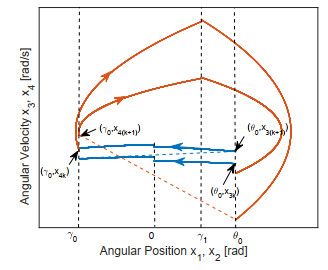
Now set the initial point as A+k=(θ0, γ0, x3k0, x4k0)T, where x4k0=cosα0(1−1d1+d1)x3k0, α0=θ0−γ0, x3k0 represents the initial angular velocity of the kth step of the robot's stance leg. As shown in Figure 5, the trajectory of system (13) starting from A+k reaches the point B−k(0, x2(τ1), x3(τ1), x4(τ1))T in HS1 at t=τ1, and jumps to B+k via the algebraic equation in (13), where
and α1=x1(τ1)−x2(τ1)=−x2(τ1).
For t∈[0,τ1], the solution of (13) is
It follows from T (x(τ1))=x1(τ1)=0 that
For convenient calculation and analysis, assume x2(τ1)=γ1 is constant under the action of unknown torque u∗1 and definite torque u∗2=e2. So we obtain
Suppose that the trajectory reaches the point A−k+1=(γ0, θ0, x3(τ1+τ2), x4(τ1+τ2)) in the plane HS2 at t=τ1+τ2, and jumps to A+k+1. Similarly, for t∈(τ1,τ1+τ2], the solution of (13) is
where
It follows from A−k+1=(γ0, θ0, x3(τ1+τ2), x4(τ1+τ2))T∈HS2 that x1(τ1+τ2)=γ0 and x2(τ1+τ2)=θ0. Hence
Set the values of the torques u∗1 and u∗3 according to conditions (16) and (19). It follows that x1(τ1+τ2)=γ0 and x2(τ1+τ2)=θ0 hold at the same time, which enables two legs to exchange smoothly and ensures the realization of climbing stairs. The following result is obtained.
Proposition 1. Given the values of torque u∗2 and u∗4 in system (13) and set the initial point as A+k=(θ0, γ0, x3k0, x4k0)T, where x4k0=cosα0(1−1d1+d1)x3k0. To ensure the realization of climbing stairs, the torque u∗1 and u∗3 are determined by (16) and (19), respectively. The time of each step is τ1+τ2, where τ1 and τ2 are shown in (15) and (18), respectively.
3.4. Existence of periodic gaits
In the above subsection, A−k+1=(γ0, θ0, x3(τ1+τ2), x4(τ1+τ2))T in the plane HS2. It follows from A−k+1 and X+=Δ2(X−)+g(X−)p (X−∈HS2) that
where x3(τ1+τ2)=−√4gL0Z21+gL0γ20+2γ0e4.
The previous literature considered the constant impulse thrust [10,11], but the change of velocity should be considered in the implementation of impulse thrust. Since the impulse thrust is constrained by control amplitude [32], we consider the following impulse thrust with velocity dependent and amplitude constraint.
where b∈R, c∈R, and |p|≤|b|+|c|.
Together with the points A+k and A+k+1, we obtain the following result.
where Z1=d212√L0g√x23k0−θ20+2θ0e2.
Now consider the following map.
Let the fixed point of map (21) is x3d, then
where Z1=d212√L0g√x23d−θ20+2θ0e2.
One fixed point sd of map (21) corresponds to one periodic gait of (13), which starts from the point A+k=(θ0, γ0, x3d, x4d)T and returns to the point A+k after time τ1d+τ2d under the action of torques u∗1d and u∗3d, where x4d=cosα0(1−1d1+d1)x3d,
In particular, set e2=θ02, e4=−γ02d22 (γ0<0) in (13), where d2=√L0g. It follows from map (21) that
Note that x3d<0 and α0∈(0, π2), the fixed point of map (22) is the solution of equation
Now construct a function σ1(y) as follows.
where c∈(0, +∞).
For y=0,
For y=−π2,
under condition
The function σ1(y) is continuous for y∈[−π2,0]. It follows from
that
So σ1(y) is a monotonically increasing function and there is only one root of equation σ1(y)=0 for b<min{b1, b2}. There is an unique fixed point in map (22) and hence there is an unique periodic gait in system (13) for e2=θ02, e4=−γ02d22 (γ0<0), and b<min{b1, b2}. Thus we obtain the following result.
Proposition 2. Set e2=θ02, e4=−γ02d22 in system (13). There is an unique periodic gait for b<min{b1, b2}, where b1 and b2 are shown in (27) and (28), respectively.
Now expand the range of parameter e4 and discuss existence of periodic solution of system (13). Set e2=θ02, e4∈(γ02d22, 0). The fixed point of map (21) is the solution of the following equation.
Construct function σ2(y) as follows.
where c∈(0, −[−π2+cosα0d1√π2d144+2γ20d22]mHl0sinα0) and α0∈(0, π2).
It follows from e4∈(γ02d22,0) that
and
So σ2(0)>σ1(0)>0.
For y=−π2,
under condition (31) and
It follows from y∈(−π2, 0) and (31) that
and
under condition
σ2(y) is monotonically increasing for y∈(−π2,0).
For y∈(0, +∞), σ′2(y)> 0 under condition 0<b<b4. In view of σ2(0)>0, σ2(y)>0 for y∈(0, +∞).
For y∈(−∞, −π2), we have
and y+cosα0d1√d14y2+2e4γ0+γ20d22 is monotonically increasing, so we obtain
under condition 0<b<b3.
There is only one root of equation σ2(y)=0 for −∞<y<+∞, which means that there is an unique fixed point in map (22) and hence there is an unique periodic gait in system (13) for e2=θ02, e4∈(γ02d22, 0), and 0<b<min{b3,b4}. The following result is obtained.
Proposition 3. Set e2=θ02, e4∈(23d2γ0, 0) in system (13). There is an unique periodic gait for 0<b<min{b3, b4}, where b3 and b4 are shown in (32) and (33), respectively.
3.5. Stability and bifurcation of periodic gaits
As mentioned in the above subsection, one fixed point x3d of map (21) corresponds to one periodic gait of (13). Now we discuss stability of this periodic gait of (13).
In view of (21), the eigenvalue of the fixed point x3d is
where r={1,x3d∈(−2nπ, −(2n−1)π),−1,x3d∈(−(2n−1)π, −2(n−1)π), n∈N. The periodic gait of (13) is stable for |λd|<1.
Proposition 2 shows that system (13) has an unique periodic gait for some conditions. It follows from map (22) that the eigenvalue of the fixed x3d is
This periodic gait is stable for |λd|<1, namely
Note that cosx3d∈(0,1), it follows that
So system (12) has a unique stable period-1 gait for b2−2mHl0sinα0<b<min{b1, b2}.
Let (x3d, b5) be the solution to the following equations.
It follows from (35) that λd=−1 for b=b5. An eigenvalue with -1 is associated with a flip bifurcation. So (x3d, b5) is a candidate for flip bifurcation point in map (22).
Now use the following lemma [27] to discuss the stability and direction of bifurcation of period-1 gait.
Lemma 1. Let fμ:R→R be a one-parameter family of maps such that fμ has a fixed point sd with eigenvalue −1. Assume that the following two conditions hold.
Then, there is a smooth curve of fixed points of fμ passing through (sd,μd), the stability of which changes at (sd,μd). There is also a smooth curve β passing through (sd,μd) so that β∖(sd,μd) is a union of hyperbolic period−2 orbits.
In map (22), if the following condition holds,
at (b5, x3d2), a flip bifurcation occurs at b=b5. System (13) has a stable period-2 gait for b∈(b5, b5+ϵ), where ϵ>0. Consequently, we obtain the following result.
Proposition 4. Set e2=θ02, e4=−γ02d22 in system (13). There is an unique stable periodic gait for b2−2mHl0sinα0<b<min{b1, b2}, where b1 and b2 are shown in (27) and (28), respectively. A flip bifurcation occurs at b=b5 under condition (38) and system (13) has a stable period-2 gait for b∈(b5, b5+ϵ), where ϵ>0 and b5 is the solution to (37).
4.
Simulation results
To discuss the complex dynamics of system (13), the values of some parameters are given in Table Ⅰ.
Now first investigate the existence and stability of period-1 gaits of linearized system (13) with θ0=0.6945 rad, γ0=−0.6351 rad, and c=3.
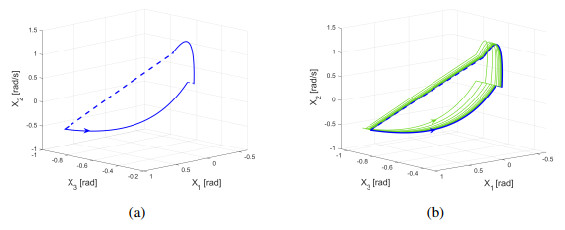
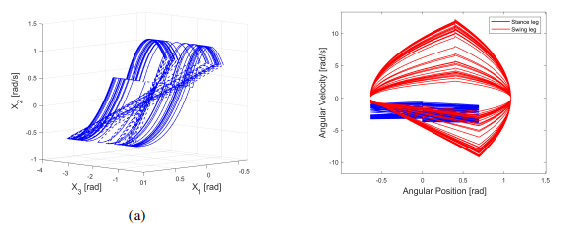
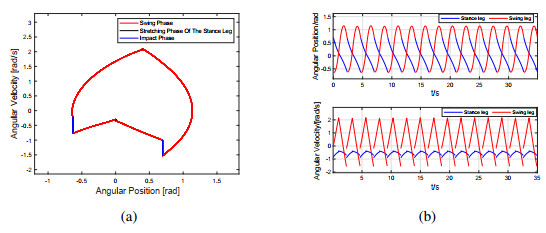
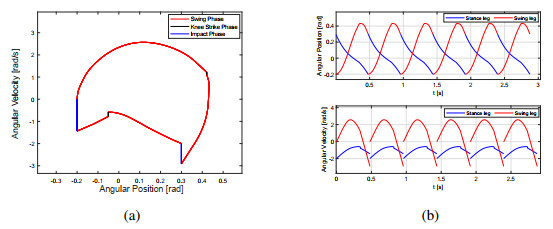
Set u∗2=e2=0.34725,u∗4=e4=0.256, γ1=0.4. It follows from (16), (19), (27) and (28) that u∗1=−0.26, u∗3=−0.12, b1≈9.59, and b2≈8.02, respectively. Set b=4.8, where b<min{b1, b2}. System (13) has a period-1 gait, which starts from the initial point Ad=(0.6945, −0.6351, −0.79, −0.16)T, reaches B−d=(0, 0.4, −0.79, 2.08)T at t=τ1=0.94, jumps to B+d=(0, 0.4, −0.68, 2.14)T, reaches A−d=(−0.6351, 0.6945, −0.71, −1.7)T at t=τ1+τ2=1.918, and jumps to Ad. The portrait in x1−x3 space and time series of xi (i=1,2,3,4) are shown in Figure 6, which is in agreement with Proposition 2.
Set u∗2=e2=0.34725, u∗4=e4=−0.07, where e4∈(23d2γ0, 0). It follows from (16), (19), (32) and (33) that u∗1=−0.275, u∗3=0.24, b3≈2.05, b4≈4.96, respectively. Set γ1=0.9, b=2, where 0<b<min{b3, b4}. As shown as Figure 7, system (13) has a period-1 gait, which is in agreement with Proposition 3.
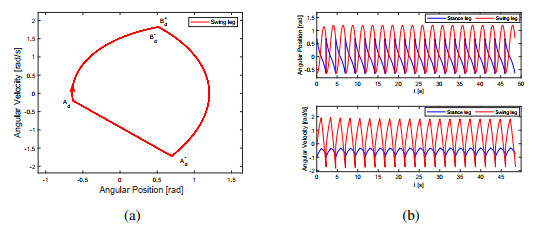
Set b=6.7, γ1=0.4, u∗1=0.298, u∗2=−0.25, u∗3=0.183, u∗4=−0.13. In view of the map (22), we can find x3d1≈−1.1, |λd|<1, and the fixed point Ad=(0.6945, −0.6351, −1.1, −0.23)T by numerical calculation. It's seen from Figure 8(a) that there exists a period-1 gait starting from Ad in system (13). In Figure 8(b), a gait starting from the point (0.6945, −0.6351, −0.97, −0.195)T tends to the period-1 gait with t increasing, which means that the period-1 gait is stable.
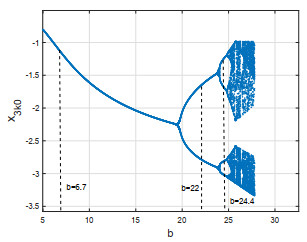
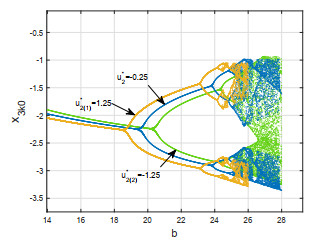
By viewing b as a parameter, the bifurcation diagram, which can well show the dynamic characteristics of system (13) with (θ0,γ0)=(0.6945, −0.6351), c=3, γ1=0.4, u∗2=−0.25, u∗4=−0.13, is shown in Figure 9. A period-2 gait bifurcates from the period-1 gait at b≈19.095 and the period-2 gait is stable for b∈(19.095, 23.752). The numerical results shown in Figures 8 and 9 are in agreement with Proposition 4.
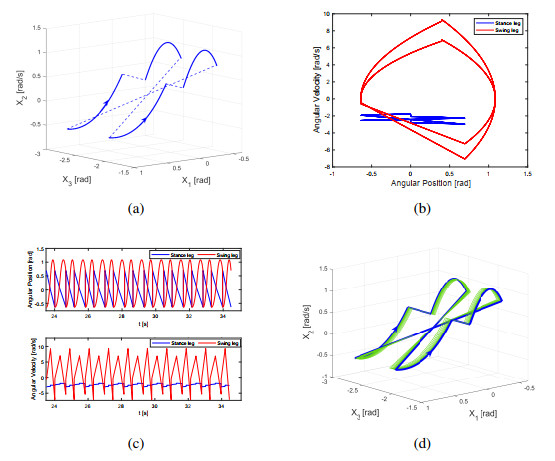
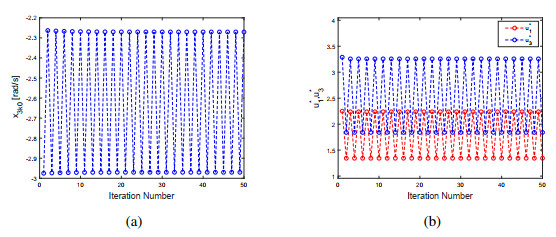
As shown in Figure 10(a)–(c), there exists a stable period-2 gait in system (13) with b=22, c=3, γ1=0.4, u∗2=−0.25, u∗4=−0.13. In Figure 10(d), a gait starting from the point (0.6945, −0.6351, −2.7, −0.547)T tends to the period-1 gait with t increasing, which means that the period-2 gait is stable. The values of x3k0, u∗1, u∗3 of this period-2 gait of iteration number n are given in Figure 11.
Set b=24.4, c=3, γ1=0.4, u∗2=−0.25, u∗4=−0.13. A period-4 gait is given in Figure 12.
Let b=26 in system (13). Figure 13 shows a chaotic portrait of system (13) with c=3, γ1=0.4, u∗2=−0.25, u∗4=−0.13. The numerical results in Figures 10−13 are in agreement with bifurcation diagrams in Figure 9.
Now discuss the effect of torque on bifurcation of system (13). In Figure 9, a period-2 gait bifurcates from the period-1 gait at b≈19.095 for u∗2=−0.25. Set u∗2(1)=1.25 and u∗2(2)=−1.25. It's seen from Figure 14 that the occurrence of bifurcation is delayed to b≈20.324 for u∗2(2)=−1.25 and advanced to b≈18.653 for u∗2(1)=1.25.
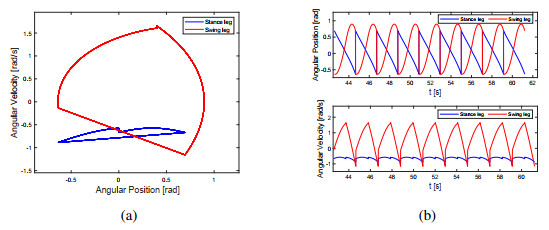
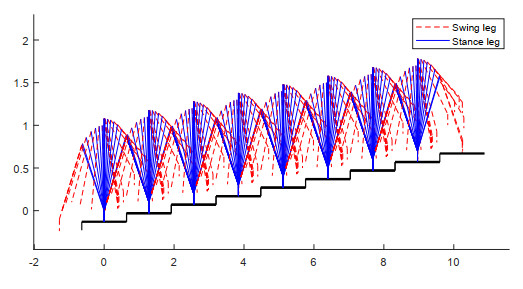
The above numerical results show that the linearized system (13) has complex dynamic behavior. Through the study of linearized system, we can roughly understand the dynamic properties of nonlinear system (9). For b=7.8, c=3, a stable period−1 gait of linearized system (9) is shown in Figure 7. When the parameters b and c are slightly disturbed, nonlinear system (9) still has a stable period−1 gait. Figure 15 shows a stable period-1 gait of nonlinear model for b=8.6, c=3, u1=3.32, u2=−2.5, u3=2.4 and u4=−1.3, where the fixed point is Xd=[qT, ˙qT]T=[0.6945, −0.6351, −1, −0.2037]T. Stick diagram of system (9) in Figure 16 clearly illustrates the process of ascending stairs of this robot.
The model of biped robot with knee joints [33] is more complex than that of straight legs biped robot. Now, we use the impulse thrust (20) to drive a biped robot with knee joints to walk upwards along slope. The walking process of this bipedal robot with knee joints is divided into four stages, namely, the knee-free phase, the knee strike phase, the knee-locked phase and heel strike. The modeling of up sloped bipedal robot with knee joints is shown in Appendix.
Set a1=0.375, a2=0.175, b1=0.125, b2=0.325, ms=0.05, mt=0.5, mh=0.5, ls=0.5, lt=0.5,L=1, u1=3.2, u2=−0.27, u3=0.003 in this dynamic model of up sloped bipedal robot with knee joints. Set b=3.12, c=1 in impulse thrust (20). Figure 17 shows a stable period−1 gait of the up sloped bipedal robot with knee joints. The stick diagram Figure 18 clearly illustrates the process of walking upwards along a slope of this robot.
5.
Conclusions
In this study, telescopic legs and impulse thrust were considered to build a walking model of stair climbing biped robot. The nonlinear ascending stair biped model was linearized and an one-dimensional discrete map was obtained. The conditions for the existence and stability of period-1 gait were obtained by this one-dimensional discrete map. Flip bifurcation was investigated. Numerical simulation, such as phase diagram of period-1 gait, period-2 gait and period-4 gait, the bifurcation diagram, were given in an example.
The relationship among the torques u∗i (i=1,2,3,4) and the initial point (θ0, γ0, x3k0, x4k0)T was investigated through theoretical analysis. We first give the initial point and the torques u∗i (i=2,4), and then calculate the value of u∗i (i=1,3), which enable two legs to exchange smoothly and ensure the realization of climbing stairs.
The parameter b play an important role in the ascending stair biped robot model. Proposition 4 gives the interval (b2−2mHl0sinα0, min{b1, b2}) of parameter b that makes system has a stable period-1 gait in theory. Figure 9 shows that system has a stable period-1 gait for b∈(5, 19.095). We can choose the appropriate value of b such that the stair climbing biped robot walk stably with period-1 gait.
We can adjust the value of torques to broaden the interval of parameter b of the existence of stable period-1 gait. Figure 14 shows that the interval of parameter b of the existence of stable period-1 gait is b∈(5, 18.653), b∈(5, 19.095), and b∈(5, 20.324) for u∗2=1.25, u∗2=−0.25, and u∗2=−1.25, respectively. Obviously, under certain conditions, the larger the value of parameter u∗2, the wider the interval of parameter b for the stair climbing biped robot to walk stably with period-1 gait.
Theoretical analysis and numerical simulation results obtained in this study provide a theoretical basis for stable walking of ascending stair biped robot with periodic gaits.
Acknowledgments
This work is jointly supported by the National Natural Science Foundation of China (11662001), the Science Foundation of Guangxi Province (2018GXNSFAA138177), the Young and Middle-aged Teachers Ability Promotion Project of Guangxi District (2019KY0228), and the Graduate innovation program of Guilin University of Electronic Technology (2021YCXS112).
Conflict of interest
The authors declare there is no conflicts of interest.
Appendix
The description of a up sloped biped robot with knee joints
The model contains a hip joint and two legs with knee joints. The length of each leg is L which is divided into two parts (L=ls+lt), where ls is the distance between the knee and the heel and lt is the distance between the knee and the hip. For simplicity, we assume that the mass of the biped robot is distributed as three units, namely, shanks of two legs (ms), shanks of two legs (mt) and hip joint (mh), where mh≫ms(mh). Shanks and thighs are divided into two parts, ls=a1+b1 and lt=a2+b2, where a1 (resp. b1) is the distance between the sub-mass center ms and the heel (resp. knee), and a2 (resp. b2) is the distance between the sub-mass center mt and the knee(resp. hip). The variables q1, q2 and q3 represent the angles of the stance leg, the swing thigh and the swing shank relative to the ground of vertical, respectively.
Dynamic Model of the up sloped biped robot with knee joints
1) Knee-free phase
The following nonlinear dynamics of the biped robot during the knee-free swinging phases is
where J is the inertia matrix, H includes Coriolis and centrifugal terms, G includes gravity forces,
B3 is the input matrix, u is the torque vector. They are given as follows.
where the torques u1, u2 and u3 are applied to the hip joint, the ankle joints of stance during this phase and the knee of swing leg, respectively.\\
2) Knee strike phase
For the knee strike phase, the collision condition is
At the impact, a conservation of the angular momentum exists and leads to the following expression.
where q+=[q+1q+2]T, q−=[q−1q−2q−3]T, and
3) Knee-locked phase
The moving pattern of this phase is similar to the third phase(Ⅲ-Ⅳ) of the ascending stair biped robot, so the kinetic equation of this phase is similar to Eq (2).
4) Heel strike
For the heel strike phase, the collision condition is given by the following expression:
where φ(φ>0) is the angle of the slope.
In this impact phase, impulse thrust p along the direction of the stance leg is used to provide the power. It follows that
According to the momentum theorem, the following algebraic expression is obtained.









 DownLoad:
DownLoad: