1. Introduction

In human history, over 70 % of the emerging infectious diseases are zoonoses, which mainly originate from animal reservoirs. Zoonotic pathogens can transmit from animals to humans. And about 75 % of these zoonotic pathogens originate from wildlife [28,3,24]. Wildlife, domestic animals and humans construct the network of pathogen transmission crossing the species barrier. Wildlife and domestic animals play important roles in the transmission of zoonotic pathogens, in spite of the fact that we always neglected them before a zoonosis emerging or reemerging [12,4].

No matter how well the science and technology developed in human society, human is just one kind of animals, even though other animals are not equal to humans in living status. The existence of the humans has changed the relationship between humans and animals due to some anthropogenic factors. Humans domesticated wolf, which was the ancestor of dog, for hunting about tens of thousands of years ago. Later, the intimacy between humans and dogs was increased more and more by natural selection or human selection, to be precise. In the meantime rabies virus existed permanently in human life by dog-human interface maintaining, as dogs were the mainly natural reservoirs of them, especially in Asia[24,32].

Animals are divided into wildlife and domestic animals by human selection [24]. Humans can manage domestic animals in their entire life, but they cannot control wildlife at liberty. At the same time, humans can contact with domestic animals sufficiently, but they have few opportunities to get in touch with wildlife except for some special professions, such as forest conservationists and poachers. As wildlife and domestic animals play different roles in human life, the zoonotic pathogen transmissions in wildlife infection, domestic animal infection and human infection would be in different styles [17,27]. Various mathematical models have been established in the study of zoonoses [26,1,16,31,11,29]. For example, Doctor Saenz and his partners discussed the impact of domestic animal-human interface in pathogen transmission [26] and Doctor Allen constructed several types of mathematical models to reflect the pathogen transmission in wildlife [1].

For pathogen transmission in multiple species, the multi-SIR model can be established as the form [1,17]:

$\begin{cases}{{\dot S}_i} = {A_i} - \sum\limits_{j = 1}^n {{\beta _{ji}}{I_j}{S_i}} - {\mu _i}{S_i}, \\ {{\dot I}_i} = \sum\limits_{j = 1}^n {{\beta _{ji}}{I_j}{S_i}} - {\mu _i}{I_i} - {\gamma _i}{I_i} - {\alpha _i}{I_i}, \\ {{\dot R}_i} = {\gamma _i}{I_i} - {\mu _i}{R_i}. \\ \end{cases}$

(1)

$S_i$, $I_i$ and $R_i$ represent the number of susceptibles, infectives, and recovered individuals for species $i$, $i$=1, 2, $\cdots$, $n$. $A_i$ is the birth or immigration rate for species $i$. $\mu_i$ is the natural mortality rate. $\alpha_i$ is the disease-induced mortality rate. $\gamma_i$ is the recovery rate. And $\beta_{ji}$ is the per capita incidence rate from species $j$ to species $i$, which denotes the probability of $I_j$ infecting $S_i$.

The basic reproduction number $R_0$ for model (1) is the spectral radius of ${[R_{0(ji)}]}_{n\times n}$, where ${R_{0(ji)}} = \frac{{{A_i}{\beta _{ji}}}}{{{\mu _i}({\mu _i} + {\gamma _i} + {\alpha _i})}}$ [10]. For $\beta_{ji}\neq 0$, $\forall$ $j,i$, it is difficult to get $R_0$ clearly. So we can take some biological characteristics of wildlife, domestic animals and humans into account to limit the value of $\beta_{j i}$ in order to simplify ${[R_{0(ji)}]}_{n\times n}$.

For wildlife, they are always the origin of animal-borne zoonoses [24,12]. The pathogen transmission from wildlife to humans is often neglected due to geographic distance between them, but the globalization and urbanization has shortened this distance. The linkage between wildlife and humans is established with anthropogenic land expanding[24]. And pathogens parasitized in different species could be transmitted to others crossing species barrier by this linkage. But for emerging zoonoses, wildlife play as the only role of natural reservoirs. The pathogen transmission from domestic animals to wildlife or from humans to wildlife could not cause emerging zoonoses. Because the pathogens parasitized in humans or domestic animals have already existed for a period of time, which could be not defined as an emerging event even if the pathogens might transmit back to humans. For example, Severe Acute Respiratory Syndromes (SARS) is defined as an emerging zoonosis, which originate from Rhinolophus, then transmit via palm civets as intermediate host to humans [8]. But for mycobacterium tuberculosis, taking humans as their reservoirs, it could not give rise to an emerging zoonosis even if it had opportunities to infect other animals [20].

That is to say, for wildlife, the zoonotic pathogens could transmit in them, $\beta_{WW}\neq 0$, but $\beta_{HW}= 0$ and $\beta_{DW}= 0$. Here we classify the hosts into three groups: wildlife, domestic animals and humans. And notation W presents wildlife, D presents domestic animals and H presents humans. In order to simplify the model further, we assume that the zoonotic pathogen transmission could not occur from humans to domestic animals in emerging event. The need of infected people is to have a rest, but not to take care of other animals [24,26]. We assume that if an emerging zoonosis was prevalent in human life, people could be infected from other people without the need of passing by domestic animals, then to humans. So $\beta_{HD}= 0$, but $\beta_{DD}\neq 0$ and $\beta_{WD}\neq 0$.

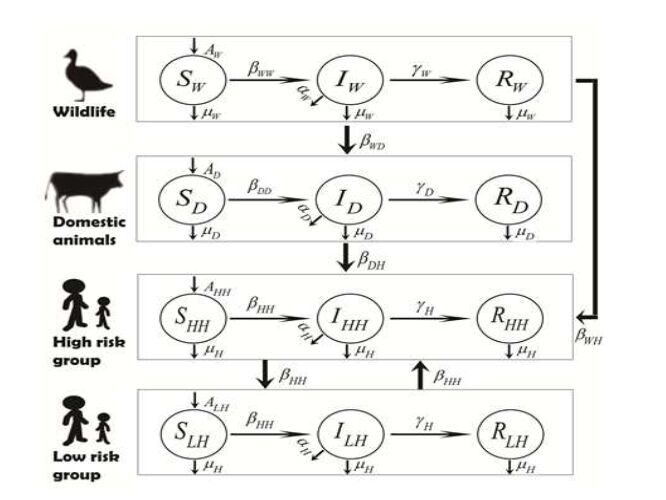
For the relationship between animals and humans, we assume that not all of people could have opportunities to be infected from animals. Live animals are the mainly origin of zoonotic pathogens and only part of people could contact with them including CAFO (Confined Animal Feeding Operation) workers and hunters [26]. We also take the human population heterogeneity into consideration in this paper. The human population is classified into two groups: high risk group and low risk group. High risk group has the opportunities to contact with infected animals sufficiently. But low risk group are the others. That is, high risk group can get pathogens from animals and humans, but low risk group from humans only. The emerging zoonotic pathogen transmission can be described in FIGURE 1.

Emerging zoonotic pathogen transmission from wildlife, to domestic animals, to humans can be described as the model (2).

$S_i$, $I_i$ and $R_i$ represent the number of susceptibles, infectives, and recovered individuals for wildlife with $i=W$, domestic animals with $i=D$, high risk group with $i=HH$ and low risk group with $i=LH$. Ai is the birth or immigration rate for species $i=W$, $D$, $HH$ or $LH$. $\mu_i$, $\gamma_i$, and $\beta_{ji}$ are defined as the same as model (1) with $i=W, D,$ or $H$. Here we assume that recovered individuals could be immune in a period time when a novel zoonosis is emerging.

$\begin{cases} &{{\dot S}_W}{\text{ = }}{A_W} - {\beta _{WW}}{I_W}{S_W} - {\mu _W}{S_W}, \\ &{{\dot I}_W} = {\beta _{WW}}{I_W}{S_W} - ({\mu _W} + {\gamma _W} + {\alpha _W}){I_W}, \\ &{{\dot R}_W} = {\gamma _W}{I_W} - {\mu _W}{R_W}, \\ &{{\dot S}_D} = {{\text{A}}_D} - ({\beta _{WD}}{I_W} + {\beta _{DD}}{I_D}){S_D} - {\mu _D}{S_D}, \\ &{{\dot I}_D} = ({\beta _{WD}}{I_W} + {\beta _{DD}}{I_D}){S_D} - ({\gamma _D} + {\alpha _D} + {\mu _D}){I_D}, \\ &{{\dot R}_D} = {\gamma _D}{I_D} - {\mu _D}{R_D}, \\ &{{\dot S}_{HH}}{\text{ = }}{{\text{A}}_{HH}} - [{\beta _{WH}}{I_W} + {\beta _{DH}}{I_D} + {\beta _{HH}}({I_{HH}} + {I_{LH}})]{S_{HH}} - {\mu _H}{S_{HH}}, \\ &{{\dot I}_{HH}} = [{\beta _{WH}}{I_W} + {\beta _{DH}}{I_D} + {\beta _{HH}}({I_{HH}} + {I_{LH}})]{S_{HH}}\\ & \ \ \ \ \ \ \ \ \ - ({\gamma _H} + {\alpha _H} + {\mu _H}){I_{HH}}, \\ &{{\dot R}_{HH}} = {\gamma _H}{I_{HH}} - {\mu _H}{R_{HH}}, \\ &{{\dot S}_{LH}}{\text{ = }}{{\text{A}}_{LH}} - {\beta _{HH}}({I_{HH}} + {I_{LH}}){S_{LH}} - {\mu _H}{S_{LH}}, \\ &{{\dot I}_{LH}} = {\beta _{HH}}({I_{HH}} + {I_{LH}}){S_{LH}} - ({\gamma _H} + {\alpha _H} + {\mu _H}){I_{LH}}, \\ &{{\dot R}_{LH}} = {\gamma _H}{I_{LH}} - {\mu _H}{R_{LH}}. \\ \end{cases}$

(2)

The basic model has been established to reflect the pathogen transmission from wildlife, to domestic animals, to humans as model (2). Next step, we take the isolation and slaughter strategies into consideration [22,23,8,31,2,25,18]. For wildlife, it is difficult to control them when a zoonosis is emerging. Lethal control, vaccination and fencing (physical barriers) are the primary approaches to limit the number of susceptibles in wildlife. In this paper, we take lethal control and fencing (physical barriers) as the strategies to compare the similar isolation and slaughter strategies in emerging zoonotic pathogen transmission.

$\begin{cases} &{{\dot S}_W}{\text{ = }}{A_W} - {\beta _{WW}}{I_W}{S_W} - ({\mu _W}+{\delta _S}){S_W}, \\ &{{\dot I}_W} = {\beta _{WW}}{I_W}{S_W} - ({\mu _W} + {\gamma _W} + {\alpha _W}+{\delta _I}){I_W}, \\ &{{\dot R}_W} = {\gamma _W}{I_W} - ({\mu _W}+{\delta _R}){R_W}, \\ &{{\dot S}_D} = {{\text{A}}_D} - ((1-\theta _{D}){\beta _{WD}}{I_W} + {\beta _{DD}}{I_D}){S_D} - {\mu _D}{S_D}, \\ &{{\dot I}_D} = ((1-\theta _{D}){\beta _{WD}}{I_W} + {\beta _{DD}}{I_D}){S_D} - ({\gamma _D} + {\alpha _D} + {\mu _D}){I_D}, \\ &{{\dot R}_D} = {\gamma _D}{I_D} - {\mu _D}{R_D}, \\ &{{\dot S}_{HH}}{\text{ = }}{{\text{A}}_{HH}} - [(1-\theta _{H}){\beta _{WH}}{I_W} + {\beta _{DH}}{I_D} + {\beta _{HH}}({I_{HH}} + {I_{LH}})]{S_{HH}} \\ & \ \ \ \ \ \ \ \ \ - {\mu _H}{S_{HH}}, \\ &{{\dot I}_{HH}} = [(1-\theta _{H}){\beta _{WH}}{I_W} + {\beta _{DH}}{I_D} + {\beta _{HH}}({I_{HH}} + {I_{LH}})]{S_{HH}}\\ & \ \ \ \ \ \ \ \ \ - ({\gamma _H} + {\alpha _H} + {\mu _H}){I_{HH}}, \\ &{{\dot R}_{HH}} = {\gamma _H}{I_{HH}} - {\mu _H}{R_{HH}}, \\ &{{\dot S}_{LH}}{\text{ = }}{{\text{A}}_{LH}} - {\beta _{HH}}({I_{HH}} + {I_{LH}}){S_{LH}} - {\mu _H}{S_{LH}}, \\ &{{\dot I}_{LH}} = {\beta _{HH}}({I_{HH}} + {I_{LH}}){S_{LH}} - ({\gamma _H} + {\alpha _H} + {\mu _H}){I_{LH}}, \\ &{{\dot R}_{LH}} = {\gamma _H}{I_{LH}} - {\mu _H}{R_{LH}}. \\ \end{cases}$

(3)

$\delta_s$, $\delta_I$ and $\delta_R$ represent lethal control or slaughter rate of susceptibles, infectives, and recovered individuals in wildlife. $\theta_D$, $\theta_H$ represent effectiveness of fencing (physical barriers), $\theta_D,\theta_H\in[0,1]$. If $\theta_D=1$, $\theta_H=1$, fencing plays the best role in the control of emerging zoonoses. If $\theta_D=0$, $\theta_H=0$, fencing is useless in the control of emerging zoonoses.

For domestic animals, we can manage them in their entire lives. It is no need to slaughter all of the susceptibles in domestic animals. We can quarantine all of the domestic animals, then isolate susceptibles and slaughter infectives.

$\begin{cases} &{{\dot S}_D} = {{\text{A}}_D} - ({\beta _{WD}}{I_W} + {\beta _{DD}}{I_D}){S_D} - {\mu _D}{S_D}, \\ &{{\dot I}_D} = ({\beta _{WD}}{I_W} + {\beta _{DD}}{I_D}){S_D} - ({\gamma _D} + {\alpha _D} + {\mu _D} + {\Delta _I}){I_D}, \\ &{{\dot R}_D} = {\gamma _D}{I_D} - {\mu _D}{R_D}, \\ &{{\dot S}_{HH}}{\text{ = }}{{\text{A}}_{HH}} - [{\beta _{WH}}{I_W} + (1-\Theta _{H}){\beta _{DH}}{I_D} +{\beta _{HH}}({I_{HH}} + {I_{LH}})]{S_{HH}}\\ & \ \ \ \ \ \ \ \ \ - {\mu _H}{S_{HH}}, \\ &{{\dot I}_{HH}} = [{\beta _{WH}}{I_W} + (1-\Theta _{H}){\beta _{DH}}{I_D} + {\beta _{HH}}({I_{HH}} + {I_{LH}})]{S_{HH}}\\ & \ \ \ \ \ \ \ \ \ - ({\gamma _H} + {\alpha _H} + {\mu _H}){I_{HH}}, \\ &{{\dot R}_{HH}} = {\gamma _H}{I_{HH}} - {\mu _H}{R_{HH}}, \\ &{{\dot S}_{LH}}{\text{ = }}{{\text{A}}_{LH}} - {\beta _{HH}}({I_{HH}} + {I_{LH}}){S_{LH}} - {\mu _H}{S_{LH}}, \\ &{{\dot I}_{LH}} = {\beta _{HH}}({I_{HH}} + {I_{LH}}){S_{LH}} - ({\gamma _H} + {\alpha _H} + {\mu _H}){I_{LH}}, \\ &{{\dot R}_{LH}} = {\gamma _H}{I_{LH}} - {\mu _H}{R_{LH}}. \\ \end{cases}$

(4)

$\Delta_I$ represents slaughter rate of infectives in domestic animals. $\Theta_H$ represents effectiveness of isolation, $\Theta_H\in[0,1]$. If $\Theta_H =1$, isolation from susceptible domestic animals play the best role in the control of emerging zoonoses. If $\Theta_H=0$, isolation in domestic animals is useless in the control of emerging zoonoses.

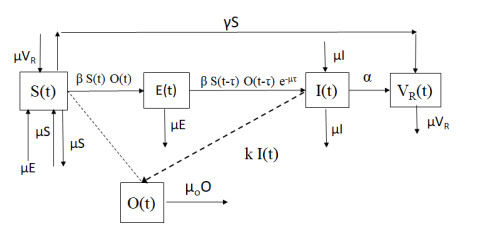
For humans, we could not 'slaughter' anyone no matter how serious they were infected with some kind of zoonoses. The quarantine and isolation may be the best method to limit the pathogen transmission except for vaccination. But the effect of quarantine and isolation strategies in humans are different from animals. For taking isolation strategies in animals, it is the susceptible humans, who are afraid of getting infected, to take the initiative and get away from susceptible animals. So the per capita incidence rate from animals to humans, $\beta_{WH}$ and $\beta_{DH}$, is decreased by $\theta_H$ and $\Theta_H$. But in humans, we quarantine and isolate the infected people to cut off pathogen transmission way. $\beta_{HH}$ would not change at this time, but there is a new compartment O produced, which denotes the isolation compartment [25].

$\begin{cases} &{{\dot S}_{HH}}{\text{ = }}{A_{HH}} - [{\beta _{WH}}{I_W} + {\beta _{DH}}{I_D}+ {\beta _{HH}}({I_{HH}} + {I_{LH}})]{S_{HH}} \\ &\ \ \ \ \ \ \ \ \ - {\mu _H}{S_{HH}} - \varphi (I){S_{HH}} + {\gamma _{H1}}{O_{HH1}}, \\ &{{\dot O}_{HH1}} = \varphi (I){S_{HH}} - {\gamma _{H1}}{O_{HH1}} - {\mu _H}{O_{HH1}}, \\ &{{\dot I}_{HH}} = [{\beta _{WH}}{I_W} + {\beta _{DH}}{I_D} + {\beta _{HH}}({I_{HH}} + {I_{LH}})]{S_{HH}} \\ &\ \ \ \ \ \ \ \ \ - ({\gamma _H} + {\alpha _H} + {\mu _H} + {\sigma}) {I_{HH}}, \\ &{{\dot O}_{HH2}} = \sigma {I_{HH}} - {\gamma _{H2}}{O_{HH2}} - {\mu _H}{O_{HH2}}, \\ &{{\dot R}_{HH}} = {\gamma _H}{I_{HH}} + {\gamma _{H2}}{O_{HH2}} - {\mu _H}{R_{HH}}, \\ &{{\dot S}_{LH}}{\text{ = }}{A_{LH}} - {\beta _{HH}}({I_{HH}} + {I_{LH}}){S_{LH}} - {\mu _H}{S_{LH}} \\ &\ \ \ \ \ \ \ \ \ - \varphi (I){S_{LH}} + {\gamma _{H1}}{O_{LH1}}, \\ &{{\dot O}_{LH1}} = \varphi (I){S_{LH}} - {\gamma _{H1}}{O_{LH1}} - {\mu _H}{O_{LH1}}, \\ &{{\dot I}_{LH}} = {\beta _{HH}}({I_{HH}} + {I_{LH}}){S_{LH}} - ({\gamma _H} + {\alpha _H} + {\mu _H} + \sigma) {I_{LH}}, \\ &{{\dot O}_{LH2}} = \sigma {I_{LH}} - {\gamma _{H2}}{O_{LH2}} - {\mu _H}{O_{LH2}}, \\ &{{\dot R}_{LH}} = {\gamma _H}{I_{LH}} + {\gamma _{H2}}{O_{LH2}} - {\mu _H}{R_{LH}}. \\ \end{cases}$

(5)

$O_{HH1}$ and $O_{HH2}$ represent isolation compartments from susceptibles and infectives in high risk group respectively. $O_{LH1}$ and $O_{LH2}$ represent isolation compartments from susceptibles and infectives in low risk group. Susceptibles enter the $O_{HH1}$ and $O_{LH1}$ classes at the rate of $\varphi(I)S_{HH}$ and $\varphi(I)S_{LH}$, with $\varphi(I)=\rho(I_{HH}+I_{LH})$ [23]. The infectives are isolated at the constant per-capita rate of $\sigma$. $\gamma_{H1}$ is the remove rate from isolation compartment to susceptible compartment.$\gamma_{H2}$ is the remove rate from isolation compartment to recovery individual compartment.

In conclusion, we can get the isolation and slaughter strategies controlling model by (3), (4) and (5) in wildlife, domestic animals and humans as the form:

$\begin{cases} &{{\dot S}_W}{\text{ = }}{A_W} - {\beta _{WW}}{I_W}{S_W} - ({\mu _W} + {\varepsilon _W}{\delta _S}){S_W}, \\ &{{\dot I}_W} = {\beta _{WW}}{I_W}{S_W} - ({\mu _W} + {\gamma _W} + {\alpha _W} + {\varepsilon _W}{\delta _I}){I_W}, \\ &{{\dot R}_W} = {\gamma _W}{I_W} - ({\mu _W} + {\varepsilon _W}{\delta _R}){R_W}, \\ &{{\dot S}_D} = {{\text{A}}_D} - ((1 - {\varepsilon _W}{\theta _D}){\beta _{WD}}{I_W} + {\beta _{DD}}{I_D}){S_D} - {\mu _D}{S_D}, \\ &{{\dot I}_D} = ((1 - {\varepsilon _W}{\theta _D}){\beta _{WD}}{I_W} + {\beta _{DD}}{I_D}){S_D} \\ &\ \ \ \ \ \ \ \ \ - ({\gamma _D} + {\alpha _D} + {\mu _D} + {\varepsilon _D}{\Delta _I}){I_D}, \\ &{{\dot R}_D} = {\gamma _D}{I_D} - {\mu _D}{R_D}, \\ &{{\dot S}_{HH}}{\text{ = }}{A_{HH}} - [(1 - {\varepsilon _W}{\theta _H}){\beta _{WH}}{I_W} + (1 - {\varepsilon _D}{\Theta _H}){\beta _{DH}}{I_D}+ {\beta _{HH}}({I_{HH}} \\ &\ \ \ \ \ \ \ \ \ + {I_{LH}})]{S_{HH}} - {\mu _H}{S_{HH}} - {\varepsilon _H}{\varphi (I)}{S_{HH}} + {\gamma _{H1}}{O_{HH1}}, \\ &{{\dot O}_{HH1}} = {\varepsilon _H}{\varphi (I)}{S_{HH}} - {\gamma _{H1}}{O_{HH1}} - {\mu _H}{O_{HH1}}, \\ &{{\dot I}_{HH}} = [(1 - {\varepsilon _W}{\theta _H}){\beta _{WH}}{I_W} + (1 - {\varepsilon _D}{\Theta _H}){\beta _{DH}}{I_D} \\ &\ \ \ \ \ \ \ \ \ + {\beta _{HH}}({I_{HH}} + {I_{LH}})]{S_{HH}} - ({\gamma _H} + {\alpha _H} + {\mu _H} + {\varepsilon _H}{\sigma}) {I_{HH}}, \\ &{{\dot O}_{HH2}} = {\varepsilon _H}{\sigma} {I_{HH}} - {\gamma _{H2}}{O_{HH2}} - {\mu _H}{O_{HH2}}, \\ &{{\dot R}_{HH}} = {\gamma _H}{I_{HH}} + {\gamma _{H2}}{O_{HH2}} - {\mu _H}{R_{HH}}, \\ &{{\dot S}_{LH}}{\text{ = }}{A_{LH}} - {\beta _{HH}}({I_{HH}} + {I_{LH}}){S_{LH}} - {\mu _H}{S_{LH}} \\ &\ \ \ \ \ \ \ \ \ - {\varepsilon _H}{\varphi (I)}{S_{LH}} + {\gamma _{H1}}{O_{LH1}}, \\ &{{\dot O}_{LH1}} = {\varepsilon _H}{\varphi (I)}{S_{LH}} - {\gamma _{H1}}{O_{LH1}} - {\mu _H}{O_{LH1}}, \\ &{{\dot I}_{LH}} = {\beta _{HH}}({I_{HH}} + {I_{LH}}){S_{LH}} - ({\gamma _H} + {\alpha _H} + {\mu _H} + {\varepsilon _H}{\sigma}) {I_{LH}}, \\ &{{\dot O}_{LH2}} = {\varepsilon _H}{\sigma} {I_{LH}} - {\gamma _{H2}}{O_{LH2}} - {\mu _H}{O_{LH2}}, \\ &{{\dot R}_{LH}} = {\gamma _H}{I_{LH}} + {\gamma _{H2}}{O_{LH2}} - {\mu _H}{R_{LH}}. \\ \end{cases}$

(6)

with Strategy 1,

$\begin{cases} \varepsilon _W = 0, I_{LH} + I_{HH} < I_{WC}\,\\ \varepsilon _W = 1,I_{LH} + I_{HH} \geq I_{WC} \end{cases}$

(7)

Strategy 2,

$\begin{cases} \varepsilon _D = 0, I_{LH} + I_{HH} < I_{DC}\,\\ \varepsilon _D = 1,I_{LH} + I_{HH} \geq I_{DC} \end{cases}$

(8)

Strategy 3,

$\begin{cases} \varepsilon _H = 0, I_{LH} + I_{HH} < I_{HC}\,\\ \varepsilon _H = 1,I_{LH} + I_{HH} \geq I_{HC} \end{cases}$

(9)

The feasible set $\Omega = \{( {S_W}\left( t \right),{\text{ }}{I_W}\left( t \right),{\text{ }}{R_W}\left( t \right),{\text{ }}{S_D}\left( t \right),{\text{ }}{I_D}\left( t \right),{\text{ }}{R_D}\left( t \right), {S_{HH}}\left( t \right),$ ${O_{HH1}}\left( t \right),{\text{ }} {I_{HH}}\left( t \right),{\text{ }}{O_{HH2}}\left( t \right),{\text{ }}{R_{HH}}\left( t \right),{S_{LH}}\left( t \right),{\text{ }}{O_{LH1}}\left( t \right),{\text{ }}{I_{LH}}\left( t \right),{\text{ }}{O_{LH2}}\left( t \right), {R_{LH}}\left( t \right)) \mid S_i(t),I_i(t),R_i(t),O_j(t) \geq 0,$ $0 < N \leq \frac{{{A_W}}}{{{\mu _W}}} + \frac{{{A_D}}}{{{\mu _D}}} + \frac{{{A_{HH}}}}{{{\mu _H}}} + \frac{{{A_{LH}}}}{{{\mu _H}}}, i = W,D,HH,LH, j = HH1,HH2,LH1,LH2 \}$ is the positively invariant with respect to (6).

Total number of wildlife is $N_W=S_W+I_W+R_W$. Total number of domestic animals is $N_D=S_D+I_D+R_D$. Total number of humans is $N_H=S_{HH}+ O_{HH1} +I_{HH}+ O_{HH2}+R_{HH} +S_{LH}+ O_{LH1}+I_{LH}+ O_{LH2}+R_{LH}$. Total number of susceptible humans is $S_H=S_{HH} +S_{LH}$. Total number of infective humans is $I_H=I_{HH} +I_{LH}$. Total number of recovery humans is $R_H=R_{HH} +R_{LH}$. Total number of all is $N=N_W+N_D+N_H$.

It is difficult for us to take any strategies to control emerging zoonoses in first time. Only the infected of numbers of people would cause our attention to take some strategies to control the infectious disease. So it is assumed that if the number of infectives in human including high risk group and low risk group reached a threshold at $I_{WC}, I_{DC}$ or $I_{HC}$, we would take measures as Strategy 1 in wildlife, Strategy 2 in domestic animals or Strategy 3 in humans.

---

2. Stability analysis

With $\varepsilon_W=0, \varepsilon_D=0, \varepsilon_H=0$, we can get (2) before taking any measures in emerging zoonoses. At first, we analyze the equilibrium stability of model (2) [5,14,19,16].

In (2), the wildlife class can be separated as

$\begin{cases}{{\dot S}_W}{\text{ = }}{A_W} - {\beta _{WW}}{I_W}{S_W} - {\mu _W}{S_W}, \\ {{\dot I}_W} = {\beta _{WW}}{I_W}{S_W} - {\mu _W}{I_W} - {\gamma _W}{I_W} - {\alpha _W}{I_W}. \end{cases}$

(10)

We can get the basic reproductive number in wildlife ${R_{0(WW)}} = \frac{{{A_W}{\beta _{WW}}}}{{{\mu _W}({\mu _W} + {\gamma _W} + {\alpha _W})}}$.

The disease-free equilibrium is $E_{0(W)} =(\overline{ S_W},\overline{I_W})=(\frac{A_W}{\mu_W},0)$, the epidemic equilibrium is $E_{(w)}^\ast=(\hat S_W,\hat I_W)=(\frac{\mu_W+\gamma_W+\alpha_W}{\beta_{WW}},\frac{\mu_W}{\beta_{WW}}(\frac{A_W \beta_{WW}}{\mu_{W}(\mu_{W}+\gamma_W+\alpha_W)}-1))$. The number of recovery individuals would not change the stability of the system, so we neglect it in the study of equilibriums.

Theorem 2.1. If $R_{0(WW)} < 1$, the disease-free equilibrium $E_{0(W)}$ in wildlife is stable. If $R_{0(WW)}>1$, the epidemic equilibrium $E_{(W)}^\ast$ in wildlife is stable.

Proof. The next generation matrix of the vector field corresponding to system (10) at $E_{0(W)}$ is

${J_W}({E_{0(W)}}) = \left( {\begin{array}{*{20}{c}} { - {\mu _W}}&{ - {\beta _{WW}}\frac{{{A_W}}}{{{\mu _W}}}} \\ {\text{0}}&{{\beta _{WW}}\frac{{{A_W}}}{{{\mu _W}}} - {\mu _W} - {\gamma _W} - {\alpha _W}} \end{array}} \right)$

If ${R_{0(WW)}} = \frac{{{A_W}{\beta _{WW}}}}{{{\mu _W}({\mu _W} + {\gamma _W} + {\alpha _W})}} < 1$, the eigenvalues of $J_{W}(E_{0(W)})$ are negative and $E_{0(W)}$ is stable.

Similarly, the next generation matrix at $E_{(W)}^\ast$ is

${J_W}(E_{(W)}^*) = \left( {\begin{array}{*{20}{c}} { - {\beta _{WW}}{{\hat I}_W} - {\mu _W}}&{ - {\beta _{WW}}{{\hat S}_W}} \\ {{\beta _{WW}}{{\hat I}_W}}&{{\beta _{WW}}{{\hat S}_W} - {\mu _W} - {\gamma _W} - {\alpha _W}} \end{array}} \right)$

The characteristic equation of ${J_W}(E_{(W)}^*)$ is

$\begin{split}{f_W}(\lambda ) &= {\lambda ^2} + \frac{{{A_W}{\beta _{WW}}}}{{{\mu _W} + {\gamma _W} + {\alpha _W}}}\lambda + {\mu _W}({\mu _W} + {\gamma _W} + {\alpha _W})(\frac{{{A_W}{\beta _{WW}}}}{{{\mu _W}({\mu _W} + {\gamma _W} + {\alpha _W})}} - 1)\\ &= 0 \end{split}$

If ${R_{0(WW)}} = \frac{{{A_W}{\beta _{WW}}}}{{{\mu _W}({\mu _W} + {\gamma _W} + {\alpha _W})}} > 1$, the real parts of eigenvalues of ${J_W}(E_{(W)}^*)$ are negative and $E_{(W)}^\ast$ is stable.

In (2), the wildlife and domestic animals classes can be separated as

$\begin{cases}{{\dot S}_W}{\text{ = }}{A_W} - {\beta _{WW}}{I_W}{S_W} - {\mu _W}{S_W}, \\ {{\dot I}_W} = {\beta _{WW}}{I_W}{S_W} - {\mu _W}{I_W} - {\gamma _W}{I_W} - {\alpha _W}{I_W}, \\ {{\dot S}_D}{\text{ = }}{{\text{A}}_D} - {\beta _{WD}}{I_W}{S_D} - {\beta _{DD}}{I_D}{S_D} - {\mu _D}{S_D}, \\ {{\dot I}_D} = {\beta _{WD}}{I_W}{S_D} + {\beta _{DD}}{I_D}{S_D} - {\gamma _D}{I_D} - {\alpha _D}{I_D} - {\mu _D}{I_D}. \\ \end{cases}$

(11)

We can get the basic reproductive number in domestic animals is ${R_{0(DD)}} = \frac{{{A_D}{\beta _{DD}}}}{{{\mu _D}({\mu _D} + {\gamma _D} + {\alpha _D})}}$.

The disease-free equilibrium is $E_{0(WD)} =(\overline{ S_W},\overline{I_W},\overline{ S_D},\overline{I_D})=(\frac{A_W}{\mu_W},0,\frac{A_D}{\mu_D},0)$, the epidemic equilibrium is

$E_{(WD)}^\ast=(\hat S_W,\hat I_W,\hat S_D,\hat I_D) =(\frac{\mu_W+\gamma_W+\alpha_W}{\beta_{WW}},\frac{\mu_W}{\beta_{WW}}(\frac{A_W \beta_{WW}}{\mu_{W}(\mu_{W}+\gamma_W+\alpha_W)}-1),\hat S_D,\hat I_D)$.

Theorem 2.2. If $R_{0(WW)} < 1$ and $R_{0(DD)} < 1$, the disease-free equilibrium $E_{0(WD)}$ in system (11) is stable. If $R_{0(WW)}>1$, there exists one unique positive epidemic equilibrium $E_{(WD)}^\ast$, and $E_{(WD)}^\ast$ is stable.

Proof. There always exists $E_{0(WD)}$ and the next generation matrix at $E_{0(WD)}$ is

${J_{WD}}({E_{0(WD)}}) = \left( {\begin{array}{*{20}{c}} {{J_W}({E_{0(W)}})}&0 \\ *&{{J_D}({E_{0(D)}})} \end{array}} \right)$

with

${J_D}({E_{0(D)}}) = \left( {\begin{array}{*{20}{c}} { - {\mu _D}}&{ - {\beta _{DD}}\frac{{{A_D}}}{{{\mu _D}}}} \\ {\text{0}}&{{\beta _{DD}}\frac{{{A_D}}}{{{\mu _D}}} - {\mu _D} - {\gamma _D} - {\alpha _D}} \end{array}} \right)$

If ${R_{0(WW)}} = \frac{{{A_W}{\beta _{WW}}}}{{{\mu _W}({\mu _W} + {\gamma _W} + {\alpha _W})}} < 1$ and ${R_{0(DD)}} = \frac{{{A_D}{\beta _{DD}}}}{{{\mu _D}({\mu _D} + {\gamma _D} + {\alpha _D})}} < 1$, the eigenvalues of $J_{WD}(E_{0(WD)})$ are negative and $E_{0(WD)}$ is stable.

In (11), the epidemic equilibrium $E_{(WD)}^*=(\hat S_W,\hat I_W,\hat S_D,\hat I_D)$ satisfies

${A_W} - {\beta _{WW}}{\hat I_W}{\hat S_W} - {\mu _W}{\hat S_W}{\text{ = }}0$

(12)

${\beta _{WW}}{\hat I_W}{\hat S_W} - {\mu _W}{\hat I_W} - {\gamma _W}{\hat I_W} - {\alpha _W}{\hat I_W}{\text{ = }}0$

(13)

${A_D} - {\beta _{WD}}{\hat I_W}{\hat S_D} - {\beta _{DD}}{\hat I_D}{\hat S_D} - {\mu _D}{\hat S_D}{\text{ = }}0$

(14)

${\beta _{WD}}{\hat I_W}{\hat S_D} + {\beta _{DD}}{\hat I_D}{\hat S_D} - {\mu _D}{\hat I_D} - {\gamma _D}{\hat I_D} - {\alpha _D}{\hat I_D}{\text{ = }}0$

(15)

From (12), (13), (14), (15), we can get

${\hat S_W} = \frac{{{\mu _W} + {\gamma _W} + {\alpha _W}}}{{{\beta _{WW}}}}$

${\hat I_W} = \frac{{{\mu _W}}}{{{\beta _{WW}}}}(\frac{{{A_W}{\beta _{WW}}}}{{{\mu _W}({\mu _W} + {\gamma _W} + {\alpha _W})}} - 1)$

$\begin{split}{\hat I_D}&{\text{ = }}\frac{{{\beta _{WD}}{{\hat I}_W}{{\hat S}_D}}}{{{\mu _D} + {\gamma _D} + {\alpha _D} - {\beta _{DD}}{{\hat S}_D}}} \\ &= \frac{{{\beta _{WD}}{{\hat S}_D}}}{{{\mu _D} + {\gamma _D} + {\alpha _D} - {\beta _{DD}}{{\hat S}_D}}} \times \frac{{{\mu _W}}}{{{\beta _{WW}}}}(\frac{{{A_W}{\beta _{WW}}}}{{{\mu _W}({\mu _W} + {\gamma _W} + {\alpha _W})}} - 1) \end{split}$

and

$\hat S_D = \frac{1}{{2{\mu _D}{\beta _{DD}}}} \nonumber [ {{A_D}{\beta _{DD}} + ({\mu _D} + {\gamma _D} + {\alpha _D})({\mu _D} + {\beta _{WD}}{{\hat I}_W})} ] \\ \nonumber - \frac{1}{{2{\mu _D}{\beta _{DD}}}} [ A_D^2\beta _{DD}^2 + 2{A_D}{\beta _{DD}}({\mu _D} + {\gamma _D} + {\alpha _D})({\beta _{WD}}{{\hat I}_W}\\ - {\mu _D}) + {{({\mu _D} + {\gamma _D} + {\alpha _D})}^2}{{({\mu _D} + {\beta _{WD}}{{\hat I}_W})}^2} ]^\frac{1}{2}$

So if $R_{0(WW)}>1$, there exists one unique positive epidemic equilibrium $E_{(WD)}^\ast$.

In fact, for ${\hat S_D}$, ${\hat S_D}$ satisfies

$\begin{split} {g_1}({\hat S_D}) &= {\mu _D}{\beta _{DD}}{\hat S_D}^2 - \left[ {{A_D}{\beta _{DD}} + ({\mu _D} + {\gamma _D} + {\alpha _D})({\mu _D} + {\beta _{WD}}{{\hat I}_W})} \right]{\hat S_D}\\ & + {A_D}({\mu _D} + {\gamma _D} + {\alpha _D}) = 0 \end{split}$

If ${g_1}({\hat S_D}) = 0$, ${\hat S_D}$ always has two positive roots because of $- {A_D}{\beta _{DD}} + ({\mu _D} + {\gamma _D} + {\alpha _D})({\mu _D} + {\beta _{WD}}{\hat I_W}) < 0$, ${A_D}({\mu _D} + {\gamma _D} + {\alpha _D}) > 0$, and the smaller ${\hat S_D}$ and the bigger ${\hat S_D}$ stand on both sides of $\frac{{{\mu _D} + {\gamma _D} + {\alpha _D}}}{{{\beta _{DD}}}}$ for ${g_1}(\frac{{{\mu _D} + {\gamma _D} + {\alpha _D}}}{{{\beta _{DD}}}}) < 0$ and ${\mu _D}{\beta _{DD}} > 0.$

So we choose

$\hat S_D = \frac{1}{{2{\mu _D}{\beta _{DD}}}} \nonumber [ {{A_D}{\beta _{DD}} + ({\mu _D} + {\gamma _D} + {\alpha _D})({\mu _D} + {\beta _{WD}}{{\hat I}_W})} ] \\ \nonumber - \frac{1}{{2{\mu _D}{\beta _{DD}}}} [ A_D^2\beta _{DD}^2 + 2{A_D}{\beta _{DD}}({\mu _D} + {\gamma _D} + {\alpha _D})({\beta _{WD}}{{\hat I}_W}\\- {\mu _D}) + {{({\mu _D} + {\gamma _D} + {\alpha _D})}^2}{{({\mu _D} + {\beta _{WD}}{{\hat I}_W})}^2} ]^\frac{1}{2}$

to guarantee ${\hat I_D} > 0.$

The next generation matrix at $E_{(WD)}^\ast$ is

${J_{WD}}(E_{(WD)}^*) = \left( {\begin{array}{*{20}{c}} {{J_W}(E_{(W)}^*)}&0 \\ *&{{J_D}(E_{(D)}^*)} \end{array}} \right)$

with

${J_D}(E_{(D)}^*) = \left( {\begin{array}{*{20}{c}} { - {\beta _{WD}}{{\hat I}_W} - {\beta _{DD}}{{\hat I}_D} - {\mu _D}}&{ - {\beta _{DD}}{{\hat S}_D}} \\ {{\beta _{WD}}{{\hat I}_W} + {\beta _{DD}}{{\hat I}_D}}&{{\beta _{DD}}{{\hat S}_D} - {\mu _D} - {\gamma _D} - {\alpha _D}} \end{array}} \right)$

The characteristic equation of $J_D(E_{(D)}^\ast)$ is ${f_D}(\lambda ) = {\lambda ^2}{\text{ + (}}\frac{{{A_D}}}{{{{\hat S}_D}}}{\text{ + }}\frac{{{\beta _{WD}}{{\hat I}_W}{{\hat S}_D}}}{{{{\hat I}_D}}}{\text{)}}\lambda + \frac{{{\beta _{WD}}{{\hat I}_W}{A_D}}}{{{{\hat I}_D}}}{\text{ + }}{\beta _{WD}}{\beta _{DD}}{\hat S_D}{\hat I_W}{\text{ + }}{\beta _{DD}}^2{\hat S_D}{\hat I_D} = 0$.

If $E_{(D)}^\ast$ exists, all of the real parts of eigenvalues of $J_D(E_{(D)}^\ast)$ are negative for $\frac{{{A_D}}}{{{{\hat S}_D}}}{\text{ + }}\frac{{{\beta _{WD}}{{\hat I}_W}{{\hat S}_D}}}{{{{\hat I}_D}}} > 0$ and $\frac{{{\beta _{WD}}{{\hat I}_W}{A_D}}}{{{{\hat I}_D}}}{\text{ + }}{\beta _{WD}}{\beta _{DD}}{\hat S_D}{\hat I_W}{\text{ + }}{\beta _{DD}}^2{\hat S_D}{\hat I_D} > 0$.

In conclusion, if ${R_{0(WW)}} = \frac{{{A_W}{\beta _{WW}}}}{{{\mu _W}({\mu _W} + {\gamma _W} + {\alpha _W})}} > 1$, the real parts of eigenvalues of $J_D(E_{(D)}^\ast)$ are negative and $E_{(WD)}^\ast$ is stable.

The human class in (2) can be separated as the form:

$\begin{cases}&{{\dot S}_{HH}}{\text{ = }}{{\text{A}}_{HH}} - {\beta _{WH}}{I_W}{S_{HH}} - {\beta _{DH}}{I_D}{S_{HH}} - {\beta _{HH}}({I_{HH}} + {I_{LH}}){S_{HH}}\\ & \ \ \ \ \ \ \ \ \ - {\mu _H}{S_{HH}}, \\ &{{\dot I}_{HH}} = {\beta _{WH}}{I_W}{S_{HH}} + {\beta _{DH}}{I_D}{S_{HH}} + {\beta _{HH}}({I_{HH}} + {I_{LH}}){S_{HH}} - {\gamma _H}{I_{HH}} \\ &\ \ \ \ \ \ \ \ \ \ - {\alpha _H}{I_{HH}} - {\mu _H}{I_{HH}}, \\ &{{\dot S}_{LH}}{\text{ = }}{{\text{A}}_{LH}} - {\beta _{HH}}({I_{HH}} + {I_{LH}}){S_{LH}} - {\mu _H}{S_{LH}}, \\ &{{\dot I}_{LH}} = {\beta _{HH}}({I_{HH}} + {I_{LH}}){S_{LH}} - {\gamma _H}{I_{LH}} - {\alpha _H}{I_{LH}} - {\mu _H}{I_{LH}}. \\ \end{cases}$

(16)

There always exists disease-free equilibrium $E_{0(WDH)}=(\overline{S_W},\overline{I_W},\overline{S_D},\overline{I_D},\overline{S_{HH}}, \overline{I_{HH}},\overline{S_{LH}},\overline{I_{LH}})=(\frac{A_W}{\mu_W},0,\frac{A_D}{\mu_D},0,\frac{A_{HH}}{\mu_{HH}},0,\frac{A_{LH}}{\mu_{LH}})$ in (2).

The next generation matrix at $E_{0(WDH)}$ is

${J_{WDH}}({E_{0(WDH)}}) = \left( {\begin{array}{*{20}{c}} {{J_W}({E_{0(W)}})}&0&0 \\ *&{{J_D}({E_{0(D)}})}&0 \\ *&*&{{J_H}({E_{0(H)}})} \end{array}} \right)$

with

$\begin{split} &{J_H}({E_{0(H)}})=\\ &\left( {\begin{array}{*{20}{c}} { - {\mu _H}}&{ - {\beta _{HH}}\frac{{{A_{HH}}}}{{{\mu _H}}}}&0&{ - {\beta _{HH}}\frac{{{A_{HH}}}}{{{\mu _H}}}} \\ {\text{0}}&{{\beta _{HH}}\frac{{{A_{HH}}}}{{{\mu _H}}} - {\mu _H} - {\gamma _H} - {\alpha _H}}&0&{{\beta _{HH}}\frac{{{A_{HH}}}}{{{\mu _H}}}} \\ 0&{ - {\beta _{HH}}\frac{{{A_{LH}}}}{{{\mu _H}}}}&{ - {\mu _H}}&{ - {\beta _{HH}}\frac{{{A_{LH}}}}{{{\mu _H}}}} \\ 0&{{\beta _{HH}}\frac{{{A_{LH}}}}{{{\mu _H}}}}&0&{{\beta _{HH}}\frac{{{A_{LH}}}}{{{\mu _H}}} - {\mu _H} - {\gamma _H} - {\alpha _H}} \end{array}} \right)\end{split}$

The characteristic equation of $J_{H}(E_{0(H})$ is

${f_{H1}}(\lambda ) = {(\lambda + {\mu _H})^2}({\lambda ^2} - ({\beta _{HH}}\frac{{{A_{HH}} + {A_{LH}}}}{{{\mu _H}}} - 2{\mu _H} - 2{\gamma _H} - 2{\alpha _H})\lambda - ({\mu _H} + {\gamma _H}\\ + {\alpha _H})({\beta _{HH}}\frac{{{A_{HH}} + {A_{LH}}}}{{{\mu _H}}} - {\mu _H} - {\gamma _H} - {\alpha _H})) = 0$

If there is ${R_{0(H)}} = \frac{{({A_{HH}} + {A_{LH}}){\beta _{HH}}}}{{{\mu _H}({\mu _H} + {\gamma _H} + {\alpha _H})}} < 1$, we have ${\beta _{HH}}\frac{{{A_{HH}} + {A_{LH}}}}{{{\mu _H}}} - 2{\mu _H} - 2{\gamma _H} - 2{\alpha _H} < 0$ and $({\mu _H} + {\gamma _H} + {\alpha _H})({\beta _{HH}}\frac{{{A_{HH}} + {A_{LH}}}}{{{\mu _H}}} - {\mu _H} - {\gamma _H} - {\alpha _H}) < 0$. Then we get all of the real parts of eigenvalues of $J_{H}(E_{0(H)})$ are negative, $E_{0(H)}$ is stable.

At the same time, the spectral radius of $\left[ {\begin{array}{*{20}{c}} {{R_{0(HHHH)}}}&{{R_{0(LHHH)}}} \\ {{R_{0(HHLH)}}}&{{R_{0(LHLH)}}} \end{array}} \right]$ is ${R_{0(H)}} = \frac{{({A_{HH}} + {A_{LH}}){\beta _{HH}}}}{{{\mu _H}({\mu _H} + {\gamma _H} + {\alpha _H})}}$, with ${R_{0(HHHH)}} = {R_{0(LHHH)}} = \frac{{{A_{HH}}{\beta _{HH}}}}{{{\mu _H}({\mu _H} + {\gamma _H} + {\alpha _H})}}$ and ${R_{0(LHLH)}} = {R_{0(HHLH)}} = \frac{{{A_{LH}}{\beta _{HH}}}}{{{\mu _H}({\mu _H} + {\gamma _H} + {\alpha _H})}}$.

Theorem 2.3. If $R_{0(WW)} < 1$, $R_{0(DD)} < 1$ and $R_{0(H)} < 1$, the disease-free equilibrium $E_{0(WDH)}$ in system (2) is stable. If $R_{0(WW)}>1$, there exists epidemic equilibrium $E_{(WDH)}^*$, and $E_{(WDH)}^*$ is stable.

Proof. The next generation matrix at $E_{0(WDH)}$ is

${J_{WDH}}({E_{0(WDH)}}) = \left( {\begin{array}{*{20}{c}} {{J_W}({E_{0(W)}})}&0&0 \\ *&{{J_D}({E_{0(D)}})}&0 \\ *&*&{{J_H}({E_{0(H)}})} \end{array}} \right).$

If $R_{0(WW)} < 1$, $R_{0(DD)} < 1$ and $R_{0(H)} < 1$, all of the real parts of eigenvalues of $J_{WDH}(E_{0(WDH)})$ are negative, then we get the disease-free equilibrium $E_{0(WDH)}$ in system (2) is stable (Theorem 2.1, Theorem 2.2).

Next we prove the existence of epidemic equilibrium $E_{(WDH)}^*$ and the stability of $E_{(WDH)}^*$.

In (16), the epidemic equilibrium $E_{(WDH)}^*=(\hat S_W,\hat I_W,\hat S_D,\hat I_D,\hat S_{HH} ,\hat I_{HH},\hat S_{LH},\\ \hat I_{LH}).$ satisfies

${{\text{A}}_{HH}} - {\beta _{WH}}{\hat I_W}{\hat S_{HH}} - {\beta _{DH}}{\hat I_D}{\hat S_{HH}} - {\beta _{HH}}({\hat I_{HH}} + {\hat I_{LH}}){\hat S_{HH}} - {\mu _H}{\hat S_{HH}}{\text{ = }}0$

(17)

$\begin{split} {\beta _{WH}}{\hat I_W}{\hat S_{HH}} + {\beta _{DH}}{\hat I_D}{\hat S_{HH}} &+ {\beta _{HH}}({\hat I_{HH}} + {\hat I_{LH}}){\hat S_{HH}} - {\gamma _H}{\hat I_{HH}} \\ &- {\alpha _H}{\hat I_{HH}} - {\mu _H}{\hat I_{HH}}{\text{ = }}0\\ \end{split}$

(18)

${{\text{A}}_{LH}} - {\beta _{HH}}({\hat I_{HH}} + {\hat I_{LH}}){\hat S_{LH}} - {\mu _H}{\hat S_{LH}}{\text{ = }}0$

(19)

${\beta _{HH}}({\hat I_{HH}} + {\hat I_{LH}}){\hat S_{LH}} - {\gamma _H}{\hat I_{LH}} - {\alpha _H}{\hat I_{LH}} - {\mu _H}{\hat I_{LH}}{\text{ = }}0$

(20)

From (17) + (19), (18) + (20), we get

$\begin{split} {{\text{A}}_{HH}} + {{\text{A}}_{LH}}- {\beta _{WH}}{\hat I_W}{\hat S_{HH}}& - {\beta _{DH}}{\hat I_D}{\hat S_{HH}} - {\beta _{HH}}({\hat I_{HH}} + {\hat I_{LH}})({\hat S_{HH}} \\ &+ {\hat S_{LH}})- {\mu _H}({\hat S_{HH}} + {\hat S_{LH}}{\text{) = }}0\\ \end{split}$

(21)

$\begin{split} {\beta _{WH}}{\hat I_W}{\hat S_{HH}} +& {\beta _{DH}}{\hat I_D}{\hat S_{HH}} + {\beta _{HH}}({\hat I_{HH}} + {\hat I_{LH}})({\hat S_{HH}} + {\hat S_{LH}}) \\ &- ({\gamma _H} + {\alpha _H} + {\mu _H})({\hat I_{HH}}{\text{ + }}{\hat I_{LH}}{\text{) = }}0\\ \end{split}$

(22)

It is assumed that ${\eta _S} = \frac{{{{\hat S}_{HH}}}}{{{{\hat S}_{HH}} + {{\hat S}_{LH}}}}$ ${\hat S_H} = {\hat S_{HH}} + {\hat S_{LH}}$ and ${\hat I_H} = {\hat I_{HH}} + {\hat I_{LH}}$ with ${\eta _S} \in (0,1).$

Then we have

${{\text{A}}_{HH}} + {{\text{A}}_{LH}} - {\eta _S}{\beta _{WH}}{\hat I_W}{\hat S_H} - {\eta _S}{\beta _{DH}}{\hat I_D}{\hat S_H} - {\beta _{HH}}{\hat I_H}{\hat S_H} - {\mu _H}{\hat S_H}{\text{ = }}0$

(23)

${\eta _S}{\beta _{WH}}{\hat I_W}{\hat S_H} + {\eta _S}{\beta _{DH}}{\hat I_D}{\hat S_H} + {\beta _{HH}}{\hat I_H}{\hat S_H} - ({\gamma _H} + {\alpha _H} + {\mu _H}){\hat I_H}{\text{ = }}0$

(24)

From (23), (24), we can get

${\hat I_H}{\text{ = }}\frac{{{\eta _S}{\beta _{WH}}{{\hat I}_W}{{\hat S}_H} + {\eta _S}{\beta _{DH}}{{\hat I}_D}{{\hat S}_H}}}{{{\gamma _H} + {\alpha _H} + {\mu _H} - {\beta _{HH}}{{\hat S}_H}}}$

and

$\hat S_H = \frac{1}{2 \mu _H \beta _{HH}} \nonumber [ ( A_{HH}+A_{LH})\beta_{HH}+(\gamma _H + \alpha _H +\mu _H) (\mu _H + \eta _S \beta _{WH} {\hat I}_W \\ +\eta _S \beta _{DH} {\hat I}_D) ] \nonumber - \frac{1}{2 \mu _H \beta _{HH}} [ (A_{HH}+A_{LH})^2\beta_{HH}^2 + 2(A_{HH} +A_{LH})\beta_{HH}\\ (\gamma_H + \alpha_H + \mu_H) (\eta _S \beta _{WH} \hat I_W +\eta _S \beta _{DH} \hat I_D -\mu_H) +(\gamma_H + \alpha_H + \mu_H)^2 \nonumber \\ (\mu_H + \eta _S \beta _{WH} \hat I_W +\eta _S \beta _{DH} \hat I_D )^2 ]^\frac{1}{2}$

Similarly to the calculation of Theorem 2.2, we have

$\begin{split} {g_2}({\hat S_H})&= {\mu _H}{\beta _{HH}}{\hat S_H}^2+ {\text{(}}{{\text{A}}_{HH}} + {{\text{A}}_{LH}})({\mu _H} + {\gamma _H} + {\alpha _H}) -[(A_{HH} + A_{LH})\beta_{HH}\\ & { + ({\mu _H} + {\gamma _H} + {\alpha _H})({\mu _H} + {\eta _S}{\beta _{WH}}{{\hat I}_W} + {\eta _S}{\beta _{DH}}{{\hat I}_D})} ]{\hat S_H}\\ &= 0 \\ \end{split}$

So if $R_{0(WW)}>1$, there exists epidemic equilibrium $E_{(WDH)}^*$ in (2). The next generation matrix at $E_{(WDH)}^*$ is

${J_{WDH}}(E_{(WDH)}^*) = \left( {\begin{array}{*{20}{c}} {{J_W}(E_{(W)}^*)}&0&0 \\ *&{{J_D}(E_{(D)}^*)}&0 \\ *&*&{{J_H}(E_{(H)}^*)} \end{array}} \right)$

with

${J_H}(E_{(H)}^*) = \left( {\begin{array}{*{20}{c}} {J_{11} }&{ - {\beta _{HH}}{{\hat S}_{HH}}}&0&{ - {\beta _{HH}}{{\hat S}_{HH}}} \\ {J_{21}}&{J_{22}}&0&{{\beta _{HH}}{{\hat S}_{HH}}} \\ 0&{ - {\beta _{HH}}{{\hat S}_{LH}}}&{J_{33}}&{ - {\beta _{HH}}{{\hat S}_{LH}}} \\ 0&{{\beta _{HH}}{{\hat S}_{LH}}}&{{\beta _{HH}}({{\hat I}_{HH}} + {{\hat I}_{LH}})}&{J_{44}} \end{array}} \right)$

$J_{11}=- {\beta _{WH}}{{\hat I}_W} - {\beta _{DH}}{{\hat I}_D} - {\beta _{HH}}({{\hat I}_{LH}} + {{\hat I}_{LH}}) - {\mu _H}$

$J_{21}={\beta _{WH}}{{\hat I}_W} + {\beta _{DH}}{{\hat I}_D} + {\beta _{HH}}({{\hat I}_{LH}} + {{\hat I}_{LH}})$

$J_{22}={\beta _{HH}}{{\hat S}_{HH}} - {\gamma _H} - {\alpha _H} - {\mu _H}$

$J_{33}=- {\beta _{HH}}({{\hat I}_{HH}} + {{\hat I}_{LH}}) - {\mu _H}$

$J_{44}={\beta _{HH}}{{\hat S}_{LH}} - {\gamma _H} - {\alpha _H} - {\mu _H}$

The characteristic equation of $J_H(E_{(H)}^*)$ is

${f_{H2}}(\lambda ) = {\lambda ^4}{\text{ + }}{a_1}{\lambda ^3} + {a_2}{\lambda ^2}{\text{ + }}{a_3}\lambda {\text{ + }}{a_4} = 0$

with

${a_1} = \frac{{{A_{HH}}}}{{{{\hat S}_{HH}}}} + \frac{{{A_{LH}}}}{{{{\hat S}_{LH}}}} - {\beta _{HH}}({\hat S_{HH}} + {\hat S_{LH}}) + 2({\gamma _H} + {\alpha _H} + {\mu _H}),$

$\begin{split} {a_2} &= (\frac{{{A_{HH}}}}{{{{\hat S}_{HH}}}} + \frac{{{A_{LH}}}}{{{{\hat S}_{LH}}}})({\gamma _H} + {\alpha _H} + {\mu _H}) - {\mu _H}{\beta _{HH}}({{\hat S}_{HH}} + {{\hat S}_{LH}}) \\ &- \beta _{HH}^2{{\hat S}_{HH}}{{\hat S}_{LH}} + (\frac{{{A_{HH}}}}{{{{\hat S}_{HH}}}} + {\beta _{WH}}\frac{{{{\hat I}_W}}}{{{{\hat I}_{HH}}}}{{\hat S}_{HH}} + {\beta _{DH}}\frac{{{{\hat I}_D}}}{{{{\hat I}_{HH}}}}{{\hat S}_{HH}} \\ &+ {\beta _{HH}}\frac{{{{\hat I}_{LH}}}}{{{{\hat I}_{HH}}}}{{\hat S}_{HH}})(\frac{{{A_{LH}}}}{{{{\hat S}_{LH}}}} + {\beta _{HH}}\frac{{{{\hat I}_{HH}}}}{{{{\hat I}_{LH}}}}{{\hat S}_{LH}}), \end{split}$

$\begin{split} {a_3}& = \frac{{{A_{LH}}}}{{{{\hat S}_{LH}}}}(\frac{{{A_{HH}}}}{{{{\hat S}_{HH}}}} + {\gamma _H} + {\alpha _H} + {\mu _H})({\gamma _H} + {\alpha _H} + {\mu _H})\\ &- {\mu _H}{\beta _{HH}}{{\hat S}_{LH}}(\frac{{{A_{HH}}}}{{{{\hat S}_{HH}}}} + {\gamma _H} + {\alpha _H} + {\mu _H}) - {\beta _{HH}}{{\hat S}_{HH}}\frac{{{A_{LH}}}}{{{{\hat S}_{LH}}}}({\gamma _H}\\ &+ {\alpha _H} + {\mu _H}) + \frac{{{A_{HH}}}}{{{{\hat S}_{HH}}}}(\frac{{{A_{LH}}}}{{{{\hat S}_{LH}}}} + {\gamma _H} + {\alpha _H} + {\mu _H})({\gamma _H} + {\alpha _H} + {\mu _H})\\ &- {\mu _H}{\beta _{HH}}{{\hat S}_{HH}}(\frac{{{A_{LH}}}}{{{{\hat S}_{LH}}}} + {\gamma _H} + {\alpha _H} + {\mu _H}) - {\beta _{HH}}{{\hat S}_{LH}}\frac{{{A_{HH}}}}{{{{\hat S}_{HH}}}}({\gamma _H} \\ &+ {\alpha _H} + {\mu _H}), \\ \end{split}$

$\begin{split} {a_4}& = \frac{{{A_{HH}}}}{{{{\hat S}_{HH}}}}\frac{{{A_{LH}}}}{{{{\hat S}_{LH}}}}{({\gamma _H} + {\alpha _H} + {\mu _H})^2} - {\mu _H}{\beta _{HH}}({\hat S_{HH}}\frac{{{A_{LH}}}}{{{{\hat S}_{LH}}}} + {\hat S_{LH}}\frac{{{A_{HH}}}}{{{{\hat S}_{HH}}}})({\gamma _H}\\ & + {\alpha _H} + {\mu _H}) \end{split}$

It is assumed that ${\mu _H} \approx 0$ for $\mu_H$ is much smaller than other parameters. Then we get ${a_1} > 0$ ${a_2} > 0$ ${a_3} > 0$ ${a_4} > 0$ ${b_1} = \frac{{{a_1}{a_2} - {a_3}}}{{{a_1}}} > 0$ and ${c_1} = \frac{{{b_1}{a_3} - {a_1}{a_4}}}{{{b_1}}} > 0 .$ So if $E_{(WDH)}^*$ exists, all of the real parts of eigenvalues of $J_H(E_{(H)}^*)$ are negative according to Routh$-$Hurwitz stability criterion.

In conclusion, if ${R_{0(WW)}} = \frac{{{A_W}{\beta _{WW}}}}{{{\mu _W}({\mu _W} + {\gamma _W} + {\alpha _W})}} > 1$, the real parts of eigenvalues of $J_{WDH}(E_{(WDH)}^*)$ are negative and $E_{(WDH)}^*$ is stable.

From Theorem 2.1, Theorem 2.2 and Theorem 2.3, it is more difficult to satisfy the conditions to control emerging zoonoses with the number of susceptible species increasing. But if there was an epidemic in wildlife with ${R_{0(WW)}} = \frac{{{A_W}{\beta _{WW}}}}{{{\mu _W}({\mu _W} + {\gamma _W} + {\alpha _W})}} > 1,$ emerging zoonoses might be prevalent in humans.

Next we take Strategy 1, Strategy 2 and Strategy 3 into consideration in order to compare the effects of different isolation and slaughter strategies in wildlife, domestic animals and humans on emerging zoonoses.

Strategy 1.

It is assumed that $\delta = {\delta _S} = {\delta _I} = {\delta _R}$ with same slaughter rate in susceptibles, infectives, and recovered individuals in wildlife in order to simply the model (3).

$\begin{cases} &{{\dot S}_W}{\text{ = }}{A_W} - {\beta _{WW}}{I_W}{S_W} - {\mu _W}{S_W} - \delta {S_W}, \\ &{{\dot I}_W} = {\beta _{WW}}{I_W}{S_W} - {\mu _W}{I_W} - {\gamma _W}{I_W} - {\alpha _W}{I_W} - \delta {I_W}, \\ &{{\dot R}_W} = {\gamma _W}{I_W} - {\mu _W}{R_W} - \delta {R_W}, \\ &{{\dot S}_D}{\text{ = }}{{\text{A}}_D} - (1 - {\theta _D}){\beta _{WD}}{I_W}{S_D} - {\beta _{DD}}{I_D}{S_D} - {\mu _D}{S_D}, \\ &{{\dot I}_D} = (1 - {\theta _D}){\beta _{WD}}{I_W}{S_D} + {\beta _{DD}}{I_D}{S_D} - {\gamma _D}{I_D} - {\alpha _D}{I_D} - {\mu _D}{I_D}, \\ &{{\dot R}_D} = {\gamma _D}{I_D} - {\mu _D}{R_D}, \\ &{{\dot S}_{HH}}{\text{ = }}{{\text{A}}_{HH}} - (1 - {\theta _H}){\beta _{WH}}{I_W}{S_{HH}} - {\beta _{DH}}{I_D}{S_{HH}} - {\beta _{HH}}({I_{HH}}\\ &\ \ \ \ \ \ \ \ \ + {I_{LH}}){S_{HH}} - {\mu _H}{S_{HH}},\\ &{{\dot I}_{HH}} = (1 - {\theta _H}){\beta _{WH}}{I_W}{S_{HH}} + {\beta _{DH}}{I_D}{S_{HH}} + {\beta _{HH}}({I_{HH}} + {I_{LH}}){S_{HH}} \\ &\ \ \ \ \ \ \ \ \ - {\gamma _H}{I_{HH}} - {\alpha _H}{I_{HH}} - {\mu _H}{I_{HH}}, \\ &{{\dot R}_{HH}} = {\gamma _H}{I_{HH}} - {\mu _H}{R_{HH}}, \\ &{{\dot S}_{LH}}{\text{ = }}{{\text{A}}_{LH}} - {\beta _{HH}}({I_{HH}} + {I_{LH}}){S_{LH}} - {\mu _H}{S_{LH}}, \\ &{{\dot I}_{LH}} = {\beta _{HH}}({I_{HH}} + {I_{LH}}){S_{LH}} - {\gamma _H}{I_{LH}} - {\alpha _H}{I_{LH}} - {\mu _H}{I_{LH}}, \\ &{{\dot R}_{LH}} = {\gamma _H}{I_{LH}} - {\mu _H}{R_{LH}}. \\ \end{cases}$

(25)

In (25), we get the control reproductive number in wildlife is ${R_{1(WW)}} = \frac{{{A_W}{\beta _{WW}}}}{{({\mu _W} + \delta )}}\\ \frac{1}{({\mu _W} + {\gamma _W} + {\alpha _W} + \delta )}$, the control reproductive number in domestic animals is ${R_{1(DD)}} = \frac{{{A_D}{\beta _{DD}}}}{{{\mu _D}({\mu _D} + {\gamma _D} + {\alpha _D})}}$, the control reproductive number in humans is ${R_{1(H)}} = \frac{{({A_{HH}} + {A_{LH}})}}{{({\mu _H} + {\gamma _H} + {\alpha _H})}} \frac{{\beta _{HH}}}{{\mu _H}}$. The epidemic equilibrium of $I_W$, $I_D$ and $I_H$ are $\hat I_W^1 = \frac{1}{{{\beta _{WW}}}}(\frac{{{A_W}{\beta _{WW}}}}{{{\mu _W} + \delta + {\gamma _W} + {\alpha _W}}} - {\mu _W} - \delta )$, $\hat I_D^1{\text{ = }}\frac{{(1 - {\theta _D}){\beta _{WD}}\hat I_{_W}^1\hat S_{_D}^1}}{{{\mu _D} + {\gamma _D} + {\alpha _D} - {\beta _{DD}}\hat S_{_D}^1}}$ and $\hat I_H^1{\text{ = }}\frac{{(1 - {\theta _H}){\eta _S}{\beta _{WH}}\hat I_W^1\hat S_H^1 + {\eta _S}{\beta _{DH}}\hat I_D^1\hat S_H^1}}{{{\gamma _H} + {\alpha _H} + {\mu _H} - {\beta _{HH}}\hat S_H^1}}$ in strategy 1.

For the epidemic equilibrium of $S_W$, $S_D$ and $S_H$, we get $\hat S_W^1 = \frac{{{\mu _W} + {\gamma _W} + {\alpha _W} + \delta }}{{{\beta _W}}} > {\hat S_W}$, $\hat S_D^1 > {\hat S_D}$ and $\hat S_H^1 > {\hat S_H}$ for ${g_1}(\hat S_D^1) < 0$ and ${g_2}(\hat S_H^1) < 0$.

Theorem 2.4. If $R_{1(WW)} < 1$, $R_{1(DD)} < 1$ and $R_{1(H)} < 1$, the disease-free equilibrium $E_{0(WDH)}^1$ in system (25) is stable. If $R_{1(WW)}>1$, there exists epidemic equilibrium $E_{(WDH)}^{**}$, and $E_{(WDH)}^{**}$ is stable.

Strategy 2.

In (4), we get the control reproductive number in wildlife is ${R_{2(WW)}} = \frac{{A_W}}{{\mu _W}} \frac{{{\beta _{WW}}}}{{({\mu _W} + {\gamma _W} + {\alpha _W})}}$, the control reproductive number in domestic animals is ${R_{2(DD)}}= \frac{{{\beta _{DD}}}}{{({\mu _D} + {\gamma _D} + {\alpha _D} + {\Delta _I})}} \frac{{A_D}}{{\mu _D}}$, the control reproductive number in humans is ${R_{2(H)}} = \frac{{{\beta _{HH}}}}{{{\mu _H}}} \frac{({A_{HH}} + {A_{LH}})}{({\mu _H} + {\gamma _H} + {\alpha _H})}$. The epidemic equilibrium of $I_W$, $I_D$ and $I_H$ are $\hat I_W^2 = \frac{1}{{{\beta _{WW}}}}(- {\mu _W} +\frac{{{A_W}{\beta _{WW}}}}{{{\mu _W} + {\gamma _W} + {\alpha _W}}} ) = {\hat I_W}$, $\hat I_D^2{\text{ = }}\frac{{{\beta _{WD}}\hat I_{_W}^2\hat S_{_D}^2}}{{{\mu _D} + {\gamma _D} + {\alpha _D} + {\Delta _I} - {\beta _{DD}}\hat S_{_D}^2}}$ and $\hat I_H^2{\text{ = }}\frac{1}{{{\gamma _H} + {\alpha _H} + {\mu _H} - {\beta _{HH}}\hat S_H^2}} ({{\eta _S}{\beta _{WH}}\hat I_W^2\hat S_H^2 + (1 - {\Theta _H}){\eta _S}{\beta _{DH}}\hat I_D^2\hat S_H^2})$ in strategy 2.

For the epidemic equilibrium of $S_W$, $S_D$ and $S_H$, we get $\hat S_W^2 = \frac{{{\mu _W} + {\gamma _W} + {\alpha _W}}}{{{\beta _W}}} = {\hat S_W}$, $\hat S_D^2 > {\hat S_D}$ and $\hat S_H^2 > {\hat S_H}$ for ${g_2}(\hat S_H^2) < 0$.

In fact, $\hat S_D^2$ is the smaller root of

$\begin{split} {g_3}(\hat S_D^2)= &{\mu _D}{\beta _{DD}}{(\hat S_D^2)^2} - \left[ {{A_D}{\beta _{DD}} + ({\mu _D} + {\gamma _D} + {\alpha _D} + {\Delta _I})({\mu _D} + {\beta _{WD}}{{\hat I}_W})} \right]\hat S_D^2 \\ &+ {A_D}({\mu _D} + {\gamma _D} + {\alpha _D}+ {\Delta _I})\\ = &0\\ \end{split}$

So we have

$\begin{split} {g_3}({\hat S_D})=& {\mu _D}{\beta _{DD}}{\hat S_D}^2 - \left[ {{A_D}{\beta _{DD}} + ({\mu _D} + {\gamma _D} + {\alpha _D} + {\Delta _I})({\mu _D} + {\beta _{WD}}{{\hat I}_W})} \right]{\hat S_D}\\ & + {A_D}({\mu _D} + {\gamma _D} + {\alpha _D} + {\Delta _I})\\ \end{split}$

If

$\begin{split}{g_1}({\hat S_D})=& {\mu _D}{\beta _{DD}}{\hat S_D}^2 - \left[ {{A_D}{\beta _{DD}} + ({\mu _D} + {\gamma _D} + {\alpha _D})({\mu _D} + {\beta _{WD}}{{\hat I}_W})} \right]{\hat S_D}\\ & + {A_D}({\mu _D} + {\gamma _D} + {\alpha _D})\\ =&0\\ \end{split}$

and

${A_D} - {\beta _{WD}}{\hat I_W}{\hat S_D} - {\beta _{DD}}{\hat I_D}{\hat S_D} - {\mu _D}{\hat S_D}{\text{ = }}0,$

we get

$\begin{split} {g_3}({{\hat S}_D}) =& \left[ {{A_D}{\beta _{DD}} + ({\mu _D} + {\gamma _D} + {\alpha _D})({\mu _D} + {\beta _{WD}}{{\hat I}_W})} \right]{{\hat S}_D} - {A_D}({\mu _D} + {\gamma _D} \\ &+ {\alpha _D}) - \left[ {{A_D}{\beta _{DD}} + ({\mu _D} + {\gamma _D} + {\alpha _D} + {\Delta _I})({\mu _D} + {\beta _{WD}}{{\hat I}_W})} \right]{{\hat S}_D} + {A_D}({\mu _D} \\ &+ {\gamma _D} + {\alpha _D} + {\Delta _I})\\ =&- {\Delta _I}({\mu _D} + {\beta _{WD}}{{\hat I}_W}){{\hat S}_D} + {\Delta _I}{A_D}\\ =&{\Delta _I}{\beta _{DD}}{{\hat I}_D}{{\hat S}_D}\\ >&0. \\ \end{split}$

Then we get $\hat S_D^2 > {\hat S_D}$ with ${\mu _D}{\beta _{DD}} > 0$.

Theorem 2.5. If $R_{2(WW)} < 1$, $R_{2(DD)} < 1$ and $R_{2(H)} < 1$, the disease-free equilibrium $E_{0(WDH)}^2$ in system (4) is stable. If $R_{2(WW)}>1$, there exists epidemic equilibrium $E_{(WDH)}^{***}$, and $E_{(WDH)}^{***}$ is stable.

Strategy 3.

If we took quarantine and isolation strategies in humans only, the impact of wildlife and domestic animals in human epidemic would be never changed comparing to no strategy. So we select the human epidemic model (26) from (5) for further analysis. At the same time, we choose $\varphi (I) = \rho \left( {{I_{HH}} + {\text{ }}{I_{LH}}} \right)$ to simplify the model.

$\begin{cases} &{{\dot S}_{HH}}{\text{ = }}{A_{HH}} - {\beta _{WH}}{I_W}{S_{HH}} - {\beta _{DH}}{I_D}{S_{HH}} - {\beta _{HH}}({I_{HH}} + {I_{LH}}){S_{HH}} \\ &\ \ \ \ \ \ \ {\mu _H}{S_{HH}} - \rho \left( {{I_{HH}} + {\text{ }}{I_{LH}}} \right){S_{HH}} + {\gamma _{H1}}{O_{HH1}}, \\ &{{\dot O}_{HH1}} = \rho \left( {{I_{HH}} + {\text{ }}{I_{LH}}} \right){S_{HH}} - {\gamma _{H1}}{O_{HH1}} - {\mu _H}{O_{HH1}}, \\ &{{\dot I}_{HH}} = {\beta _{WH}}{I_W}{S_{HH}} + {\beta _{DH}}{I_D}{S_{HH}} + {\beta _{HH}}({I_{HH}} + {I_{LH}}){S_{HH}}\\ &\ \ \ \ \ \ \ \ - {\gamma _H}{I_{HH}} - {\alpha _H}{I_{HH}} - {\mu _H}{I_{HH}} - \sigma {I_{HH}}, \\ &{{\dot O}_{HH2}} = \sigma {I_{HH}} - {\gamma _{H2}}{O_{HH2}} - {\mu _H}{O_{HH2}}, \\ &{{\dot S}_{LH}}{\text{ = }}{A_{LH}} - {\beta _{HH}}({I_{HH}} + {I_{LH}}){S_{LH}} - {\mu _H}{S_{LH}} - \rho \left( {{I_{HH}} + {\text{ }}{I_{LH}}} \right){S_{LH}} \\ &\ \ \ \ \ \ \ \ + {\gamma _{H1}}{O_{LH1}}, \\ &{{\dot O}_{LH1}} = \rho \left( {{I_{HH}} + {\text{ }}{I_{LH}}} \right){S_{LH}} - {\gamma _{H1}}{O_{LH1}} - {\mu _H}{O_{LH1}}, \\ &{{\dot I}_{LH}} = {\beta _{HH}}({I_{HH}} + {I_{LH}}){S_{LH}} - {\gamma _H}{I_{LH}} - {\alpha _H}{I_{LH}} - {\mu _H}{I_{LH}} - \sigma {I_{LH}}, \\ &{{\dot O}_{LH2}} = \sigma {I_{LH}} - {\gamma _{H2}}{O_{LH2}} - {\mu _H}{O_{LH2}}. \\ \end{cases}$

(26)

We get the control reproductive number in humans is:

${R_{3(H)}} = \frac{{({A_{HH}} + {A_{LH}}){\beta _{HH}}}}{{{\mu _H}({\mu _H} + {\gamma _H} + {\alpha _H} + \sigma )}}$

Theorem 2.6. If $R_{0(WW)} < 1$, $R_{0(DD)} < 1$ and $R_{3(H)} < 1$, the disease-free equilibrium $E_{0(WDH)}^3$ in system (5) is stable. If $R_{0(WW)}>1$, there exists epidemic equilibrium $E_{(WDH)}^{****}$, and $E_{(WDH)}^{****}$ is stable.

---

3. Numerical simulation

In this section we take avian influenza epidemic in China as an example to analyze the effects of different strategies on emerging zoonoses. Avian influenza is a kind of zoonoses, which have been prevalent in humans since 150 years ago. Avian influenza virus originated from aquatic birds, and it infected domestic birds by sharing watersheds. Humans can be infected by avian influenza virus via infected domestic birds[11,30,6,9]. But for birds, we cannot get the exact parameters to reflect the virus transmission clearly. So we take some similar data to estimate the process of avian influenza virus transmission approximately (TABLE 2).

The number of domestic birds is 4.2 times more than the number of humans in China [7], so we assume that the number of domestic birds is 8400 and the number of humans is 2000 to simplify the calculation. And it is assumed that there are about 1000 wild aquatic birds for no exact data found. And it is assumed that $R_{0(WD)}$ = 0.1$*R_{0(DD)}$, $R_{0(WH)}= 0.1*R_{0(H)}$ and $R_{0(DH)}= 0.1*R_{0(H)}$.

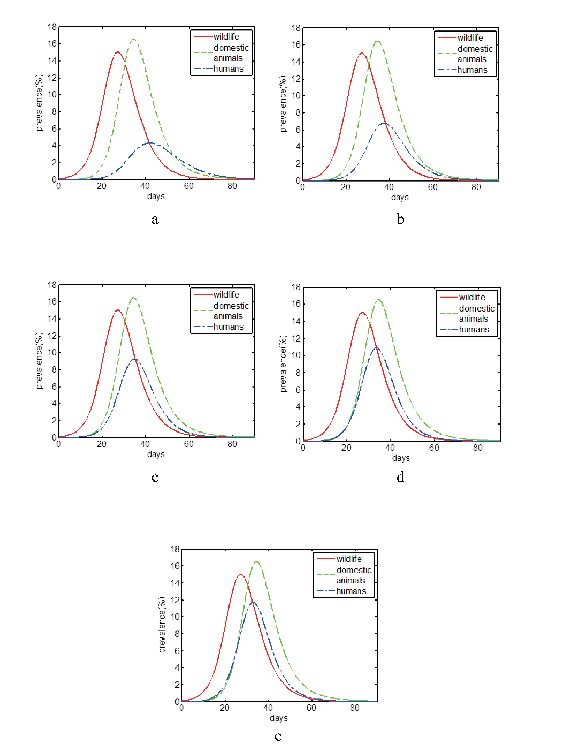
The avian influenza virus transmission has been shown in model (2), which included wildlife, domestic animals, high risk group and low risk group [10,21,13]. For high risk group and low risk group in humans, there may be shown in different proportion in different areas. Less people are needed to take care of live animals in modern farming than tradition. Few people have opportunities to contact with live animals in some areas, which are the potential hosts of some pathogens in emerging zoonoses. But in some other areas, stock raising is the main economy origin of the residents. More people have to look after live animals to help support the family. The proportion of high risk group and low risk group is higher in these areas than others. Here we choose different proportions of high risk group and low risk group, such as 1:9, 1:3, 1:1, 3:1 and 9:1, to reflect emerging avian influenza prevalence in different areas (FIGURE 2).

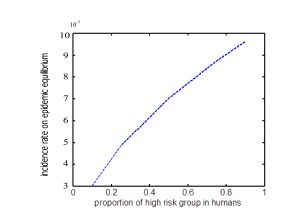
From a to e in FIGURE 2, we get that more and more high proportion of humans are infected in the first 90 days. More people would be infected with higher proportion of them having the opportunity to contact with susceptible animals. From FIGURE 3, we get that the incidence rate on epidemic equilibrium is increasing with higher proportion of high risk group in humans. Although the proportion of high risk group in humans would never change the basic reproductive number, it could impact the final prevalence in humans.

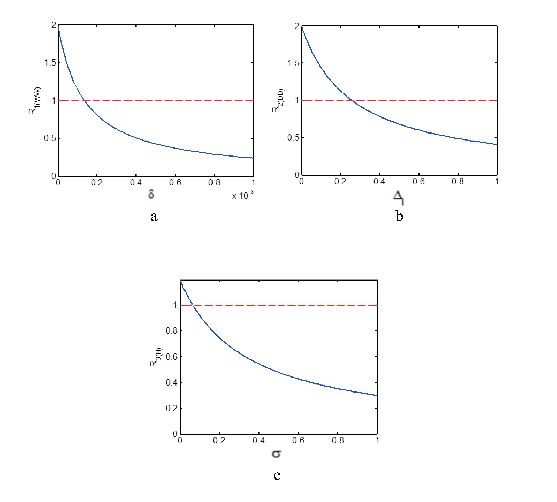
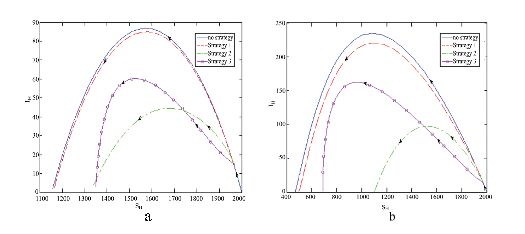
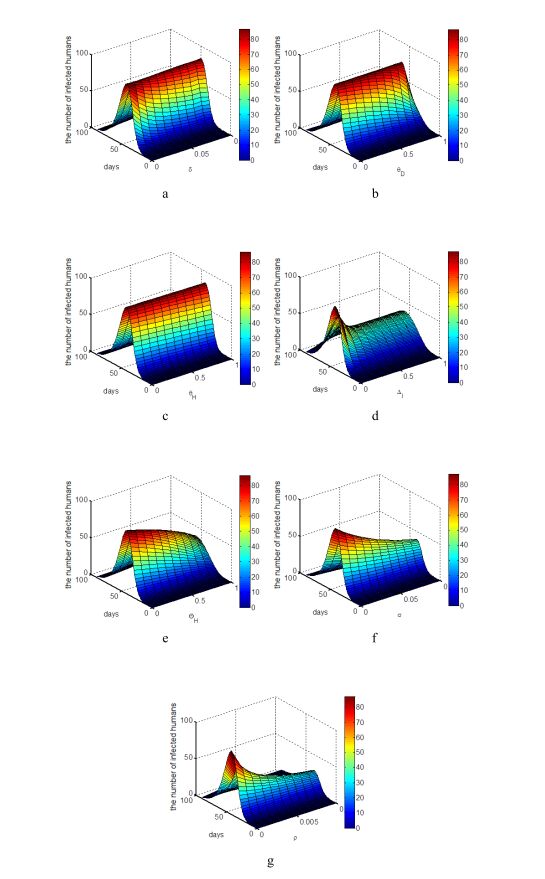
The effects of parameters $\delta, \Delta_I, \sigma$ in Strategy 1, Strategy 2 and Strategy 3 on control reproductive numbers have been shown in FIGURE 4. The existence of parameters $\delta, \Delta_I,$ and $\sigma$ would decrease the value of $R_{1(WW)}, R_{2(DD)}$ and $R_{3(H)}$. If $\delta < 0.142*10^{-3}, \Delta_I < 0.258$ and $\sigma < 0.066, R_{1(WW)}, R_{2(DD)}$ and $R_{3(H)}$ would get the value below threshold to control the zoonoses in wildlife, domestic animals and humans respectively. The effects of Strategy 1, Strategy 2 and Strategy 3 in different areas are shown in FIGURE 5, when ${I_{DC}} = {I_{WC}} = {I_{HC}} = 15 .$ The effects of $\delta, \theta_D, \theta_H, \Delta_I, \Theta_H, \sigma$ and $\rho$ on the number of infected humans in the first 90 days are shown in FIGURE 6.

---

4. Discussion

From Ebola, Hendra, Marburg, SARS to H1N1, H7N9, more and more zoonotic pathogens come into humans. Tens of thousands of people have dead of these zoonoses in the last hundreds of years. Some public health policies have to be established to answer emerging or remerging zoonoses. For different species participating in an emerging zoonosis, different strategies should been taken for controlling. In this paper, we established model (3), model (4) and model (5) to reflect the effects of Strategy 1, Strategy 2 and Strategy3 about isolation and slaughter in emerging zoonoses respectively. Strategy 1 is the controlling measure for wildlife. Strategy 2 is the controlling measure for domestic animals. And Strategy 3 is the controlling measure for humans.

All of the three strategies would change the basic reproductive number to their own control reproductive number. The involvement of Strategy 1, Strategy 2 and Strategy 3 would change the conditions, which determine the zoonoses prevalence or not. At the same time, we conclude that the extinction of zoonoses must satisfy the conditions ensuring all of basic (control) reproductive numbers in different species are less than 1, whether it is taken controlling strategy or not. But if and only if basic (control) reproductive numbers in wildlife is more than 1, the zoonoses might be prevalent in all of the susceptible species.

The stability analysis on models in section 2 reflects the effects of three strategies on control reproductive numbers and equilibriums. In section 3, some numerical simulations show the effects of the three strategies on avian influenza epidemic in different areas in China at beginning. In this paper, we take isolation and slaughter strategies into consideration to study their effects on emerging zoonoses. But the other effective strategies like vaccination are neglected, which could be proposed in a forthcoming paper.

---

Acknowledgments

This work was supported by the National Natural Science Foundation of China (11371048).

---