Dynamics of a stochastic SIRS epidemic model with standard incidence and vaccination

1.   Introduction

Colorectal cancer (CRC), one of the most common malignancies worldwide, ranks the third and fifth leading cause of cancer-related mortality in the United States and China, respectively ^[1]. Despite advances in therapeutic methods, CRC patients with metastasis, recurrence, or drug-resistance still undergo a poor prognosis ^[2]. Therefore, novel therapeutic targets are urgently required to improve the clinical outcome of CRC patients. Besides, reliable novel prognostic models are also needed to make therapeutic methods more feasible.

Pyroptosis is a pro-inflammatory programmed cell death which is activated by inflammasomes in both canonical and noncanonical inflammasome pathways ^[3]. Pyroptotic cells are characterized by cell swelling, plasma membrane lysis, chromatin fragmentation and release of the intracellular proinflammatory contents ^[4]. Pyroptosis is closely related to the malignant progression of tumors. On one hand, pyroptosis can create a tumor-suppressive environment by releasing inflammatory factors ^[4]. Mounting studies reported that various chemical agents function through regulating proptosis in CRC. For example, GW4064 and LPS enhance the chemosensitivity of CRC cells to oxaliplatin via inducing pyroptosis ^[5,6]. In addition, FL118 restrains the growth and metastasis of CRC by inducing NLRP3-ASC-Caspase-1 mediated pyroptosis ^[7]. On the other hand, proptosis also inhibits tumor growth by enhancing anti-tumor immunity ^[8]. Combinations of BRAF inhibitors and MEK inhibitors (BRAFi + MEKi) are FDA-approved to treat -mutant melanoma. Recently, Erkes et al. revealed that BRAFi and MEKi treatment promoted cleavage of gasdermin E (GSDME), a marker of pyroptosis, and induced tumor-associated T cell and activated dendritic cell infiltration ^[9]. Tumor-infiltrating immune cells in the tumor microenvironment significantly contribute to the malignancy progression and prognosis of CRC. Whereas the correlation between immune regulation and pyroptosis in CRC remains elusive. Therefore, it is essential to identify a pyroptosis-related signature to predict prognosis and to indicate immune cell infiltration in CRC. Fortunately, analysis of next-generation sequencing data is a novel method that can quickly identify cancer characteristics and suggest us about the most appropriate therapeutic strategies.

In the present study, we performed a systematic bioinformatics analysis to determine the expression profiles of pyroptosis-related genes (PRGs) and their prognostic significance in CRC. Based on differentially expressed PRGs, we constructed a prognostic model for CRC and classified CRC patients into two clusters with distinct prognosis and immunotherapy potential.

2.   Materials and methods

2.1.   Study design

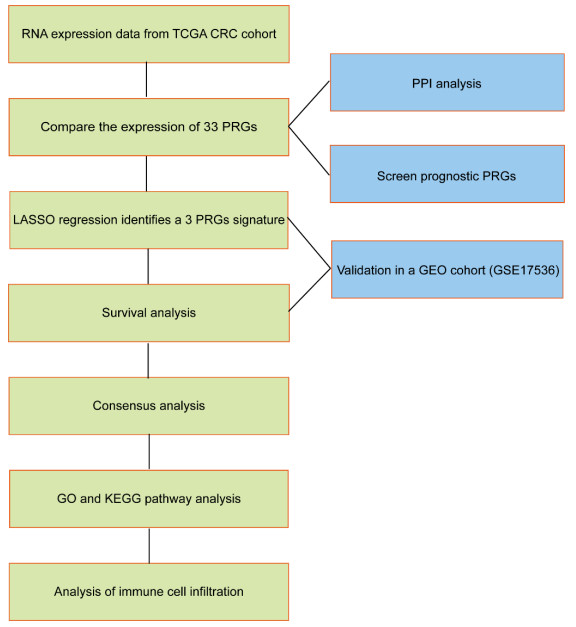
We first downloaded the RNA sequencing data of genes deposited in TCGA CRC cohort and analyzed the expression and interaction of 33 PRGs in CRC tissues. Then we selected three prognostic PRGs and constructed a prognostic model for CRC, which was validated by an independent Gene Expression Omnibus (GEO) cohort (GSE17536) ^[10]. Subsequently, we identified the differentially expressed genes between high-risk score group and low-risk score group and reclassified CRC patients into two novel clusters. Moreover, the differentially expressed genes were further used to conduct GO and KEGG pathway analysis. Finally, the immune cell infiltration between high-risk score group and low-risk score group was analyzed. The flow diagram of this study was shown in Figure 1.

2.2.   Gene expression data and processing

The RNA sequencing data of genes deposited in TCGA CRC cohort and GEO dataset (GSE17536) were downloaded from the University of California Santa Cruz (UCSC) Xena browser (https://xenabrowser.net/datapages/) and GEO database (https://www.ncbi.nlm.nih.gov/geo/). CRC patients without survival information were ignored. 33 pyroptosis-related genes were extracted from prior studies ^[3,11]. In fact, in addition to canonical pyroptosis-related genes, PRGs also contain genes that regulate pyroptosis indirectly, such as ELANE, IL6, and CASP9. For example, GSDMD cleavage and activation in neutrophils was caspase independent and was mediated by ELANE ^[12]. Besides, ineffective formation of the Apaf-1/caspase-9 decreased processing of procaspases-3 and -8 to trigger pyroptosis ^[13]. The differentially expressed PRGs were identified by R package "limma" with a P-value < 0.05.

2.3.   GSEA analysis

The GSEA analysis was used to search for gene sets that are correlated with risk score in CRC. The gene expression data were obtained from the TCGA CRC cohort. CRC tissue samples were clarified into a high expression group and a low expression group according to the median value of risk score. The GSEA tool was implemented to explore the distribution of gene sets in the MSigDB database ^[14]. The gene sets whose |normalized enrichment score (NES)| > 1, normalized p-value < 0.05, and FDR value < 0.25 were identified to be significantly correlated.

2.4.   Enrichment analysis and hub genes selection

Gene ontology (GO) enrichment analysis and Kyoto Encyclopaedia of Genes and Genomes (KEGG) pathway analysis were conducted in the DAVID database (https://david.ncifcrf.gov) ^[15], whose results were represented by a bubble chart using the OmicShare tool, a free online platform for data analysis (http://www.omicshare.com/tools). A protein-protein interaction (PPI) network for PRGs was constructed with the Search Tool for the Retrieval of Interacting Genes (STRING) (https://string-db.org/) database. The top ten hub genes among the PPI network were identified by using the Cytohubba plug-in in Cytoscape.

2.5.   Evaluating immune cell infiltration level in CRC tissues

To investigate the immune infiltration landscape of CRC tissues, the ESTIMATE algorithm was used to assess the immune cell infiltration level according to the expression levels of immune cells-specific marker genes. Marker genes of immune cells were obtained from the bulk transcriptome data of Bindea et al. ^[16]. The immune infiltration analysis was performed with the TIMER2 online tool (http://timer.cistrome.org).

2.6.   Construction of prognostic model

Univariate and multivariate Cox regression analysis were performed to select prognostic PRGs and clinicopathological characteristics. The key PRGs were further used to construct a prognostic model through least absolute shrinkage and selection operator (LASSO) regression using R software.

2.7.   Statistical analysis

Statistical analysis was performed by GraphPad Prism 8.0 (GraphPad Software, USA). Analysis between the two groups were performed using the unbiased Mann-Whitney test. Survival analysis was performed using Kaplan-Meier curves with a log-rank test or Cox proportional hazard model. The Spearman correlation analysis was used to evaluate correlations. P-value < 0.05 was considered statistically significant.

3.   Results

3.1.   Identification of differentially expressed PRGs in CRC tissues

The expression levels of 33 PRGs were compared in CRC tissues and normal tissues, and we identified 32 differentially expressed PRGs in CRC (all p-value < 0.05) among which 20 genes (ELANE, NLRP7, NLRP2, CASP5, GZMA, NLRP6, NLRC4, NLRP3, IL18, TNF, NLRP1, GSDMB, CASP1, PYCARD, CASP9, TIRAP, PRKACA, CASP3, CASP6, and GSDMD) were downregulated while 11 other genes (CASP8, GPX4, NOD1, CASP4, PLCG1, IL1B, IL6, NOD2, GZMB, GSDMA, and GSDMC) were upregulated in CRC tissues (Figure 2A). To explore the interactions of these PRGs, a PPI analysis was conducted with a minimum required interaction score of 0.9 (Figure 2B). Moreover, we determined that NLRP1, IL18, PYCARD, IL1B, CASP1, TNF, NLRC4, CASP4, NOD2, and AIM2 were top 10 hub genes (Figure 2C).

3.2.   Constructing a prognostic model for CRC using differentially expressed PRGs

To generate a prognostic model for CRC, we first performed univariate Cox regression analysis to screen the prognostic PRGs. We identified three significantly differentially expressed PRGs (PRKACA, CASP3, and GPX4) that were significantly correlated with prognosis (Figure 3A). Then PRGs were considered for LASSO regression analysis to generate a prognostic model and three genes were selected according to the optimum λ value (Figure 3B-C). The risk score was determined using the following formula: PRKACA × (0.677) + CASP3 × (-0.438) + GPX4 × (0.641). Based on the median value of risk scores, CRC patients were equally divided into low- and high-risk score groups. The KM plot curve were used to evaluate the performance of three-PRG signature in predicting the outcome of the CRC patients. As shown in Figure 3D, the overall survival between the low- and high-risk groups classified by our prognostic model was significantly different (p = 0.0021). The time-dependent receiver operating characteristic (ROC) analysis showed that the area under the ROC curve (AUC) was 0.705 for 5-year survival (Figure 3E). Moreover, multivariate Cox regression analysis showed that the risk score was an independent prognostic factor of CRC (Table 1). To validate our prognostic model, a total of 177 CRC patients from a Gene Expression Omnibus (GEO) cohort (GSE17536) were utilized. Based on the median risk score identified in the TCGA cohort, 81 CRC patients and 96 CRC patients in the GEO cohort were classified into the high-risk group and the low-risk group, respectively. Kaplan–Meier analysis also indicated a significant difference in the survival rate between the low-and high-risk groups (p = 0.038) (Figure 3F). These results indicated that the three-PRG prognostic model was robust in predicting the outcome of CRC patients.

3.3.   Classifying CRC into two new clusters

To explore genes that influence the risk score of CRC, we determined 1889 differentially expressed genes (DEGs) between high-risk score group and low-risk score group (Figure 4A). Univariate Cox regression analysis showed that 11 DEGs (SUCLG2, RIMKLB, ABCD3, CPT2, MPP2, GABRD, PANX2, CAPN9, ZNF883, MYO16, and CYP46A1) were significantly associated with patient prognosis with p-value < 0.001 (Figure 4B). In addition, most of the 11 DEGs were either positively or negatively correlated with PRGs (PRKACA, CASP3, and GPX4) (Figure 4C). To explore the connections between the pyroptosis-related prognostic model and CRC subtypes, we performed a consensus clustering analysis based on three prognostic PRGs (PRKACA, CASP3, and GPX4) and eleven prognostic DEGs (SUCLG2, RIMKLB, ABCD3, CPT2, MPP2, GABRD, PANX2, CAPN9, ZNF883, MYO16, and CYP46A1) between high-risk score group and low-risk score group by using the R package of Consensus ClusterPlus. The optimal clustering stability (k = 2–9) was determined by the proportion of ambiguous clustering measurements, and k = 2 was identified indicating that the CRC patients could be well divided into two clusters (Figure 4D). Based on the unsupervised clustering, we eventually identified two distinct clusters (Figure 4E). The KM plot curve analysis showed that CRC patients in cluster 2 underwent worse overall survival than those in cluster 1 (p < 0.001) (Figure 4F). Consistently, the risk scores of cluster-2 samples were significantly higher than those of cluster-1 samples (Figure 4G).

3.4.   Functional analysis of the DEGs between two risk score groups in CRC

To further explore the differences in the DEG functions and pathways between the high- and low-risk score groups, GO enrichment analysis and KEGG pathway analysis were then performed. Biological process (BP) analysis indicated that the DEGs were significantly associated with the immune response, inflammatory response, apoptosis process, and pyroptosis (Figure 5A). Molecular function (MF) analysis showed that the DEGs mainly participate in protein binding, cytokine activity, IL6 receptor binding, and TNF receptor binding (Figure 5B). Cellular component (CC) analysis exhibited that the DEGs mainly located at cytosol (Figure 5C). Moreover, KEGG pathway analysis showed that the DEGs were significantly enriched in several vital pathways in cancer, such as TNF signaling pathway and NF-kappa B signaling pathway (Figure 5D).

3.5.   Analysis of the immune activity between two new CRC clusters classified by the prognostic model

Given that the risk scores were significantly associated with immune regulation in CRC and differenced between two new CRC clusters classified by the prognostic model, we investigated the potential connections between immune and two new classified CRC clusters. The GSEA analysis showed that gene signatures of HALLMARK_INFLAMMATORY_RESPONSE, HALLMARK_COMPLEMENT, HALLMARK_INTERFERON_GAMMA_RESPONSE, HALLMARK_INTERFERON_ALPHA_RESPONSE, HALLMARK_IL6_JAK_STAT3_SIGNALING, and HALLMARK_IL2_STAT5_SIGNALING were significantly enriched in cluster 1 samples (Figure 5A). In addition, the immune scores were significantly downregulated in cluster 1 samples compared with cluster 2 samples (Figure 5B). Consistently, the infiltrated levels of immune cells, including T cell follicular helper, Tregs, tumor-associated macrophages (TAMs), myeloid dendritic cell activated, were significantly elevated in cluster 2 samples compared with cluster 1 samples (Figure 5C). Moreover, the immune checkpoint genes (ICGs), including PD-1, PD-L1, and CTLA-4, were significantly upregulated in cluster 2 samples (Figure 6D).

4.   Discussion

Programmed cell death is beneficial to cancer treatment. There are several known cell death types, such as necrosis, apoptosis, and autophagy ^[17]. Pyroptosis is a novel form of programmed cell death triggered by caspase 1/4/5/11 which is activated by several inflammasomes. Caspase-1 is a protease that activates precursors of IL-18 and IL-1β ^[3]. The effect of pyroptosis on cancer development is complex which is dependent of tissues and genetic backgrounds. On one hand, pyroptosis can suppress the initiation and development of tumors and is regarded as a promising cancer therapeutic strategy; on the other hand, multiple signaling pathways and inflammatory factors are released during pyroptosis which forms a cancer promoting environment microenvironment ^[18]. For example, GSDMD and GSDME, two PRGs, were significantly downregulated in gastric cancer ^[19,20], but upregulated in lung cancer ^[21]. In CRC, seven PRGs (NLRP1, NLRP3, AIM2, GSDMA, GSDMC, GSDMD, and GSDME) has been reported to be dysregulated in CRC ^{[20,22,23,24,25]}. However, the expression of other PRGs as well as their connections remained unclear. In this study, we discovered that most PRGs were differentially expressed in CRC compared with normal tissues and NLRP1, IL18, PYCARD, IL1B, CASP1, TNF, NLRC4, CASP4, NOD2, and AIM2 were hub genes among these PRGs.

Molecular signatures associated with distinct clinical outcomes have been excavated in various cancers to improve clinical therapeutic strategies. Based on prognostic genes, LASSO Cox regression analysis was often applied to construct models to predict the overall survival of cancer patients. Previous studies have identified PRGs-related prognostic signatures for gastric cancer ^[26], lung adenocarcinoma ^[27], and ovarian cancer ^[11]. However, the prognostic values of PRGs in CRC have not been reported. In our study, we first constructed a prognostic signature for CRC based on PRGs, which provided more choices for prognosis prediction in CRC. Although PRGs has been used to construct prognostic models for several cancers, the PRGs used in diverse cancers is different ^[11,26,27]. For example, PRGs used in the prognostic model for gastric cancer were GZMB, RBPMS2, CASP1, TAC1, TPM2, and GBP4 ^[26], rather than PRKACA, CASP3, and GPX4 in our model. In addition, the expression of the same PRG in tumors also depends on tissue heterogeneity. So far, our model should be specific for CRC.

Function analysis showed that the DEGs between high- and low-risk score groups mainly enriched in pyroptosis, apoptosis, and immune response in CRC. As tumor develops, apoptosis and pyroptosis may coexist and interact with each other. For instance, three PRGs (CASP3, CASP6, and PLCG1) are also known as essential regulators in apoptotic signaling pathway. Pyroptosis has some similar characteristics with apoptosis such as DNA damage, nuclear condensation, and caspase dependence, whereas it is distinguished from apoptosis by its special morphological features. Generally, apoptosis keeps an intact cell plasma membrane and does not release intracellular contents and does not directly cause inflammatory responses, while pyroptosis shows the opposite characteristics ^[28]. Wang et al. once designed a bioorthogonal system and suggested that pyroptosis-induced inflammation triggers robust anti-tumor immunity and can synergize with checkpoint blockade ^[29]. In this study, based on risk scores, we classified CRC patients into two clusters with distinct prognosis and immunotherapy potential. The KM plot curve analysis showed that CRC patients in cluster 2 underwent worse overall survival than those in cluster 1. Besides, the infiltrated levels of immune cells, such as Tregs and TAMs, were significantly elevated in cluster 2 samples compared with cluster 1 samples. Tregs and TAMs have been reported to suppress antitumor immunity and to be correlated with poor clinical outcomes of CRC patients ^[30,31]. Over the last decade, dramatic advances in cancer treatment through immunotherapy has been authenticated. One promising method to achieve anti-cancer immunity is to block the immune checkpoint pathways ^[32]. Our results showed that the immune checkpoint genes (PD-1, PD-L1, and CTLA-4) were significantly elevated in cluster 2 samples, which suggests that CRC patients in cluster 2 may be more suitable for immune checkpoint blockade treatment.

Indeed, there are several limitations in our study. First, the expression of PRGs in CRC tissues were only examined through analysis of TCGA CRC cohort. They should be further validated by using qRT-PCR analysis of clinical samples. Second, three programmed cell death pathways, including pyroptosis, apoptosis, and necroptosis, play critical roles in the malignancy progression of CRC ^[5,33,34]. Although these pathways have unique characteristics, they utilize common activation mechanisms, including homotypic interactions to form large activation complexes. Recent studies have highlighted mechanistic overlaps and extensive, multifaceted crosstalk between pyroptosis, apoptosis, and necroptosis, which led to the development of the concept of PANoptosis ^[35]. Though there are still many unanswered questions about the mechanistic details of this emerging pathway, the coordinated activation of these pathways through PANoptosis provides an effective backup strategy for a host to circumvent risks, whereby the blockade of an innate immune signaling pathway results in the activation of another pathway ^[36]. Therefore, we plan to construct a prognostic model for CRC based on PANoptosis-related genes in our subsequent study. Finally, with the development of pyroptosis research, other new PRGs may be identified. Therefore, it is necessary to update the prognostic model for CRC to improve its accuracy and prediction value.

5.   Conclusion

In summary, we first identified a PRGs-related prognostic model for CRC, according to which CRC patients can be classified into two clusters with distinct prognosis and immunotherapy potential.

Acknowledgements

We acknowledge TCGA and GEO databases for providing their platforms and contributors for uploading their meaningful datasets.

Conflict of interest

The authors have no conflict of interest.