A hybrid ant colony algorithm for the winner determination problem

Jun Wu; Mingjie Fan; Yang Liu; Yupeng Zhou; Nan Yang; Minghao Yin; Jun Wu; Mingjie Fan; Yang Liu; Yupeng Zhou; Nan Yang; Minghao Yin

doi:10.3934/mbe.2022148

Mathematical Biosciences and Engineering

2022, Volume 19, Issue 3: 3202-3222. doi: 10.3934/mbe.2022148

Previous Article Next Article

Research article Special Issues

A hybrid ant colony algorithm for the winner determination problem

1.
Information Science and Technology, Northeast Normal University, Changchun, China
2.
School of Science, Beijing University of Posts and Telecommunications, Bejing, China
3.
CHEARI Certification & Testing Co., Ltd., Beijing, China
4.
Key Laboratory of Applied Statistics of MOE, Northeast Normal University, Changchun, China

Academic Editor: William Guo

Received: 31 August 2021 Revised: 27 December 2021 Accepted: 13 January 2022 Published: 20 January 2022

Combinatorial auction is an important type of market mechanism, which can help bidders to bid on the combination of items more efficiently. The winner determination problem (WDP) is one of the most challenging research topics on the combinatorial auction, which has been proven to be NP-hard. It has more attention from researchers in recent years and has a wide range of real-world applications. To solve the winner determination problem effectively, this paper proposes a hybrid ant colony algorithm called DHS-ACO, which combines an effective local search for exploitation and an ant colony algorithm for exploration, with two effective strategies. One is a hash tabu search strategy adopted to reduce the cycling problem in the local search procedure. Another is a deep scoring strategy which is introduced to consider the profound effects of the local operators. The experimental results on a broad range of benchmarks show that DHS-ACO outperforms the existing algorithms.
- ant colony algorithm,
- local search,
- combinatorial auction,
- winner determination problem,
- tabu search
Citation: Jun Wu, Mingjie Fan, Yang Liu, Yupeng Zhou, Nan Yang, Minghao Yin. A hybrid ant colony algorithm for the winner determination problem[J]. Mathematical Biosciences and Engineering, 2022, 19(3): 3202-3222. doi: 10.3934/mbe.2022148

Related Papers:

Abstract

Combinatorial auction is an important type of market mechanism, which can help bidders to bid on the combination of items more efficiently. The winner determination problem (WDP) is one of the most challenging research topics on the combinatorial auction, which has been proven to be NP-hard. It has more attention from researchers in recent years and has a wide range of real-world applications. To solve the winner determination problem effectively, this paper proposes a hybrid ant colony algorithm called DHS-ACO, which combines an effective local search for exploitation and an ant colony algorithm for exploration, with two effective strategies. One is a hash tabu search strategy adopted to reduce the cycling problem in the local search procedure. Another is a deep scoring strategy which is introduced to consider the profound effects of the local operators. The experimental results on a broad range of benchmarks show that DHS-ACO outperforms the existing algorithms.

References

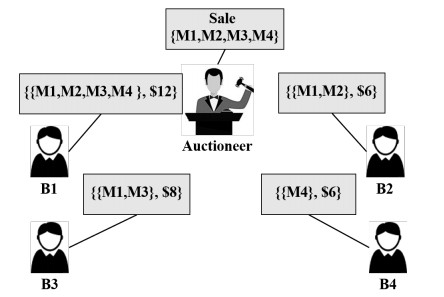
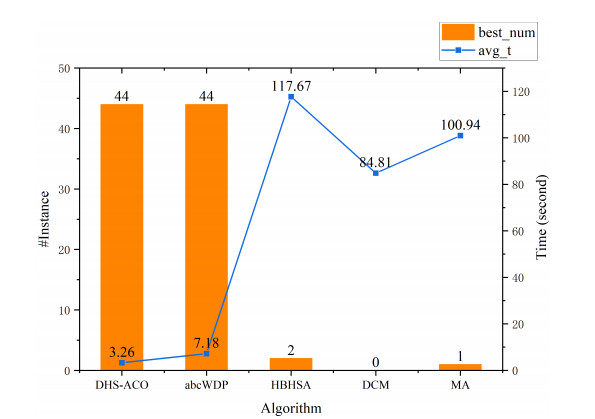
[1]	S. J. Rassenti, V. L. Smith, R. L. Bulfin, A combinatorial auction mechanism for airport time slot allocation, Bell J. Econ., 13 (1982), 402–417. https://doi.org/10.2307/3003463 doi: 10.2307/3003463
[2]	K. Xu, Y. Zhang, X. Shi, H. Wang, Y. Wang, M. Shen, Online combinatorial double auction for mobile cloud computing markets, in IEEE 33rd International Performance Computing and Communications Conference, (2014), 1–8. https://doi.org/10.1109/PCCC.2014.7017103
[3]	T. G. Chetan, M. Jenamani, S. P. Sarmah, Two-stage multi-attribute auction mechanism for price discovery and winner determination, Trans. Eng. Manage., 66 (2019), 112–126. https://doi.org/10.1109/TEM.2018.2810510 doi: 10.1109/TEM.2018.2810510
[4]	S. Wang, S. Qu, M. Goh, M. Wahab, H. Zhou, Integrated multi-stage decision-making for winner determination problem in online multi-attribute reverse auctions under uncertainty, Int. J. Fuzzy Syst., 22 (2019), 2354–2372. https://doi.org/10.1007/s40815-019-00757-0 doi: 10.1007/s40815-019-00757-0
[5]	W. Fontanini, P. A. Ferreira, A game-theoretic approach for the web services scheduling problem, Expert Syst. Appl., 41 (2014), 4743–4751. https://doi.org/10.1016/j.eswa.2014.02.016 doi: 10.1016/j.eswa.2014.02.016
[6]	D. H. Kim, S. A. Kazmi, A. Ndikumana, A. Manzoor, W. Saad, C. S. Hong, et al., Distributed radio slice allocation in wireless network virtualization: matching theory meets auctions, IEEE Access, 8 (2020), 494–732. https://doi.org/10.1109/ACCESS.2020.2987753 doi: 10.1109/ACCESS.2020.2987753
[7]	A. K. Ray, M. Jenamani, P. K. Mohapatra, Supplier behavior modeling and winner determination using parallel mdp, Expert Syst. Appl., 38 (2011), 4689–4697. https://doi.org/10.1016/j.eswa.2010.08.044 doi: 10.1016/j.eswa.2010.08.044
[8]	S. De Vries, R. V. Vohra, Combinatorial auctions: a survey, INFORMS J. Comput., 15 (2003), 284–309. https://doi.org/10.1287/ijoc.15.3.284.16077 doi: 10.1287/ijoc.15.3.284.16077
[9]	M. Rekik, S. Mellouli, Reputation-based winner determination problem for combinatorial transportation procurement auctions, J. Oper. Res. Soc., 63 (2012), 1400–1409. https://doi.org/10.1057/jors.2011.108 doi: 10.1057/jors.2011.108
[10]	W. Zhong, K. Xie, Y. Liu, C. Yang, S. Xie, Multi-resource allocation of shared energy storage: a distributed combinatorial auction approach, IEEE Trans. Smart Grid, 11 (2020), 4105–4115. https://doi.org/10.1109/TSG.2020.2986468 doi: 10.1109/TSG.2020.2986468
[11]	M. H. Rothkopf, A. Pekeč, R. M. Harstad, Computationally manageable combinational auctions, Manag. Sci., 44 (1998), 1131–1147. https://doi.org/10.1287/mnsc.44.8.1131 doi: 10.1287/mnsc.44.8.1131
[12]	X. Li, S. Ma, Multi-objective memetic search algorithm for multi-objective permutation flow shop scheduling problem, IEEE Access, 4 (2016), 2154–2165. https://doi.org/10.1109/ACCESS.2016.2565622 doi: 10.1109/ACCESS.2016.2565622
[13]	Z. Lu, Y. Zhou, J. K. Hao, A hybrid evolutionary algorithm for the clique partitioning problem, IEEE Trans. Cybernetics, (2021).
[14]	M. Aïder, O. Gacem, M. Hifi, A hybrid population-based algorithm for the bi-objective quadratic multiple knapsack problem, Expert Syst. Appl., 191 (2022), 116238. https://doi.org/10.1016/j.eswa.2021.116238 doi: 10.1016/j.eswa.2021.116238
[15]	Q. Zhou, J. K. Hao, Q. Wu, A hybrid evolutionary search for the generalized quadratic multiple knapsack problem, Eur. J. Oper. Res., 296 (2022), 88–803. https://doi.org/10.1016/j.ejor.2021.04.001 doi: 10.1016/j.ejor.2021.04.001
[16]	X. Li, X. Zhang, M. Yin, J. Wang, A genetic algorithm for the distributed assembly permutation flowshop scheduling problem, in 2015 IEEE Congress on Evolutionary Computation (CEC), (2015), 3096–3101. https://doi.org/10.1109/CEC.2015.7257275
[17]	Y. Zhou, X. Liu, S. Hu, Y. Wang, M. Yin, Combining max-min ant system with effective local search for solving the maximum set k-covering problem, Knowl. Based Syst., 239 (2021), 108000. https://doi.org/10.1016/j.knosys.2021.108000 doi: 10.1016/j.knosys.2021.108000
[18]	Ș. Öztürk, R. Ahmad, N. Akhtar, Variants of artificial bee colony algorithm and its applications in medical image processing, Appl. Soft Comput., 97 (2020), 106799. https://doi.org/10.1016/j.asoc.2020.106799 doi: 10.1016/j.asoc.2020.106799
[19]	M. Dorigo, L. M. Gambardella, Ant colony system: a cooperative learning approach to the traveling salesman problem, IEEE Trans. Evol. Comput., 1 (1997), 53–66. https://doi.org/10.1109/4235.585892 doi: 10.1109/4235.585892
[20]	X. Zhang, X. Li, J. Wang, Local search algorithm with path relinking for single batch-processing machine scheduling problem, Neural Comput. Appl., 28 (2017), 313–326. https://doi.org/10.1007/s00521-016-2339-z doi: 10.1007/s00521-016-2339-z
[21]	M. Li, J. K. Hao, Q. Wu, Learning-driven feasible and infeasible tabu search for airport gate assignment, Eur. J. Oper. Res., 2021 (2021). https://doi.org/10.1016/j.ejor.2021.12.019 doi: 10.1016/j.ejor.2021.12.019
[22]	Z. Lu, J. K. Hao, U. Benlic, D. Lesaint, Iterated multilevel simulated annealing for large-scale graph conductance minimization, Inform. Sci., 572 (2021), 182–199. https://doi.org/10.1016/j.ins.2021.04.102 doi: 10.1016/j.ins.2021.04.102
[23]	F. Glover, Tabu search-part i, ORSA J. Comput., 1 (1989), 190–206. https://doi.org/10.1287/ijoc.1.3.190 doi: 10.1287/ijoc.1.3.190
[24]	Y. Zhou, J. Li, Y. Liu, S. Lv, Y. Lai, J. Wang, Improved memetic algorithm for solving the minimum weight vertex independent dominating set, Mathematics, 8 (2020), 1155. https://doi.org/10.3390/math8071155 doi: 10.3390/math8071155
[25]	P. V. Silvestrin, M. Ritt, An iterated tabu search for the multi-compartment vehicle routing problem, Comput. & Oper. Res., 81 (2017), 192–202. https://doi.org/10.1016/j.cor.2016.12.023 doi: 10.1016/j.cor.2016.12.023
[26]	L. Xing, Y. Liu, H. Li, C. C. Wu, W. C. Lin, X. Chen, A novel tabu search algorithm for multi-agv routing problem, Mathematics, 8 (2020), 279. https://doi.org/10.3390/math8020279 doi: 10.3390/math8020279
[27]	B. Vangerven, D. R. Goossens, F. C. Spieksma, Winner determination in geometrical combinatorial auctions, Eur. J. Oper. Res., 258 (2017), 254–263. https://doi.org/10.1016/j.ejor.2016.08.037 doi: 10.1016/j.ejor.2016.08.037
[28]	M. Kaleta, Network winner determination problem, Arch. Control Sci., 28 (2018). https://doi.org/10.24425/119077 doi: 10.24425/119077
[29]	N. Remli, A. Amrouss, I. El Hallaoui, M. Rekik, A robust optimization approach for the winner determination problem with uncertainty on shipment volumes and carriers' capacity, Trans. Res. Part B: Meth., 123 (2019), 127–148. https://doi.org/10.1016/j.trb.2019.03.017 doi: 10.1016/j.trb.2019.03.017
[30]	X. Qian, S. C. Fang, M. Huang, X. Wang, Winner determination of loss-averse buyers with incomplete information in multiattribute reverse auctions for clean energy device procurement, Energy, 177 (2019), 276–292. https://doi.org/10.1016/j.energy.2019.04.072 doi: 10.1016/j.energy.2019.04.072
[31]	X. Qian, F. T. Chan, M. Yin, Q. Zhang, M. Huang, X. Fu, A two-stage stochastic winner determination model integrating a hybrid mitigation strategy for transportation service procurement auctions, Comput. Ind. Eng., 149 (2020), 106703. https://doi.org/10.1016/j.cie.2020.106703 doi: 10.1016/j.cie.2020.106703
[32]	C. W. Lee, W. P. Wong, J. Ignatius, A. Rahman, M. L. Tseng, Winner determination problem in multiple automated guided vehicle considering cost and flexibility, Comput. Ind. Eng., 142 (2020), 106337. https://doi.org/10.1016/j.cie.2020.106337 doi: 10.1016/j.cie.2020.106337
[33]	Y. Fujishima, K. Leyton-Brown, Y. Shoham, Taming the computational complexity of combinatorial auctions: Optimal and approximate approaches, in IJCAI, 99 (1999), 548–553.
[34]	N. Nisan, Bidding and allocation in combinatorial auctions, in Proceedings of the 2nd ACM Conference on Electronic Commerce, (2000), 1–12. https://doi.org/10.1145/352871.352872
[35]	K. Leyton-Brown, Y. Shoham, M. Tennenholtz, An algorithm for multi-unit combinatorial auctions, in Aaai/iaai, (2000), 56–61.
[36]	T. Sandholm, S. Suri, Bob: Improved winner determination in combinatorial auctions and generalizations, Artif. Intell., 145 (2003), 33–58. https://doi.org/10.1016/S0004-3702(03)00015-8 doi: 10.1016/S0004-3702(03)00015-8
[37]	O. Günlük, L. Ladányi, S. De Vries, A branch-and-price algorithm and new test problems for spectrum auctions, Manag. Sci., 51 (2005), 391–406. https://doi.org/10.1287/mnsc.1040.0332 doi: 10.1287/mnsc.1040.0332
[38]	L. F. Escudero, M. Landete, A. Marín, A branch-and-cut algorithm for the winner determination problem, Decis. Support Syst., 46 (2009), 649–659. https://doi.org/10.1016/j.dss.2008.10.009 doi: 10.1016/j.dss.2008.10.009
[39]	H. H. Hoos, C. Boutilier, Solving combinatorial auctions using stochastic local search, in Aaai/iaai, (2000), 22–29.
[40]	Y. Guo, A. Lim, B. Rodrigues, Y. Zhu, Heuristics for a bidding problem, Comput. Oper. Res., 33 (2006), 2179–2188.
[41]	D. Boughaci, B. Benhamou, H. Drias, Stochastic local search for the optimal winner determination problem in combinatorial auctions, in International Conference on Principles and Practice of Constraint Programming, Springer, (2008), 593–597.
[42]	N. Wang, D. Wang, Model and algorithm of winner determination problem in multi-item e-procurement with variable quantities, in The 26th Chinese Control and Decision Conference (2014 CCDC), (2014), 5364–5367. https://doi.org/10.1109/CCDC.2014.6852222
[43]	M. B. Dowlatshahi, V. Derhami, Winner determination in combinatorial auctions using hybrid ant colony optimization and multi-neighborhood local search, J. AI Data Min., 5 (2017), 169–181.
[44]	D. Boughaci, B. Benhamou, H. Drias, A memetic algorithm for the optimal winner determination problem, Soft Comput., 13 (2009), 905. https://doi.org/10.1007/s00500-008-0355-3 doi: 10.1007/s00500-008-0355-3
[45]	H. Zhang, S. Cai, C. Luo, M. Yin, An efficient local search algorithm for the winner determination problem, J. Heuristics, 23 (2017), 367–396. https://doi.org/10.1007/s10732-017-9344-y doi: 10.1007/s10732-017-9344-y
[46]	G. Lin, W. Zhu, M. M. Ali, An effective discrete dynamic convexized method for solving the winner determination problem, J. Comb. Optim., 32 (2016), 563–593. https://doi.org/10.1007/s10878-015-9883-9 doi: 10.1007/s10878-015-9883-9
[47]	G. Lin, Z. Li, A hybrid binary harmony search algorithm for solving the winner determination problem, Int. J. Innovative Comput. Appl., 10 (2019), 59–68. https://doi.org/10.1504/IJICA.2019.100547 doi: 10.1504/IJICA.2019.100547
[48]	H. C. Lau, Y. G. Goh, An intelligent brokering system to support multi-agent web-based 4/sup th/-party logistics, in 14th IEEE International Conference on Tools with Artificial Intelligence, (2002), 154–161.
[49]	K. Leyton-Brown, M. Pearson, Y. Shoham, Towards a universal test suite for combinatorial auction algorithms, in Proceedings of the 2nd ACM Conference on Electronic Commerce, (2000), 66–76. https://doi.org/10.1145/352871.352879
[50]	M. López-Ibáñez, J. Dubois-Lacoste, L. P. Cáceres, M. Birattari, and T. Stützle, The irace package: Iterated racing for automatic algorithm configuration, Oper. Res. Perspect., 3 (2016), 43–58. https://doi.org/10.1016/j.orp.2016.09.002 doi: 10.1016/j.orp.2016.09.002

Reader Comments

Your name:*

Email:*
© 2022 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)