An integrated optimization mode for multi-type aircraft flight scheduling and routing problem

1.   Introduction

Flight scheduling (FS) and aircraft routing (AR) present the two-core task of daily airline management. FS is aimed to obtain a series of flight trips from their origins at departure times to destinations at arrival times, while AR is used to arrange several airplanes located at different airports to cover all flight trips. If the integrated operation of FS and AR is neglected, aircraft flight scheduling plans based on an unreasonable fixed timetable would require a larger fleet of airplanes. The output of FS being the input of AR in the interactive process of FS and AR preparation, such integration will significantly reduce operation costs ^[1,2]. Therefore, it is necessary to find their optimal relationship in the integrated FS and AR (IFSAR), in order to pursue the optimal global solution.

In the process of developing the IFSAR plan, each airline's aircraft routing schedule (solution of AR) is up to its own discretion, but the timetable of each flight line (solution of FS) is jointly determined by the airlines and the civil aviation administration. The airlines will expect to choose a flight time of maximum load rates in pursuit of more profit. If the civil aviation administration determines that this time is within the feasible time window for an aircraft taking off or landing at an airport and passing through an air route related to air traffic control (which depends on weather conditions and military aspects), this flight is allowed. Otherwise, airlines will need to repeatedly submit the flight timetable before it is approved by the civil aviation authority. However, IFSAR with consideration of the interactions between flexible time window, schedule and load rate is less studied.

Another major motivation of this paper is to address the IFSAR with multi-type aircraft. In the conventional IFSAR, each flight trip with its own particular aircraft type can only be covered by the respective aircraft-type plane. In the proposed model, flight trip via a small airplane can be alternatively covered by a larger one. Compared to IFSAR with a single aircraft type, the proposed model may reduce the aircraft fleet in the case where the supply and demand of different types of aircrafts are not balanced in time and space. However, to the best of the authors' knowledge, no IFSAR with multi-type aircraft has been comprehensively analyzed yet.

The main contribution of this study is the development of an optimization framework for IFSAR with multiple aircraft type and flexible time window. The study focused on the following critical research tasks: 1) Coordination of FS and AR to reveal optimal relation between flexible schedule, load rate and operation cost; 2) development of a two-stage heuristic model based on ant colony optimization (ACO) algorithm to efficiently yield the acceptable solution. Finally, a real-world case study is used to illustrate the validity of the proposed method.

The remainder of the paper is organized as follows. Section 2 summarizes the research status of IFSAR. The optimization framework of IFSAR and its mathematical formulation are described in Section 3. Section 4 presents a two-stage heuristic model based on the ACO algorithm. A real-world case is examined to prove the validity of the proposed model and algorithm in Section 5, and some concluding remarks are given in Section 6.

2.   Review of literature

In recent years, flight scheduling (FS) and aircraft routing (AR) are two key decision problems in airline planning processes. Although they are typically solved sequentially and independently, integration of some of these solutions in airline planning can further enforce decision consistency and achieve significant savings ^[3]. These integrated models are classified into leg-based methods and itinerary-based methods, where the former ones are well-justified for small- and medium-sized airline companies with a single flight leg, while the latter ones are more applicable for large airline companies with several flight legs ^[4,5].

In FS, a profitable flight schedule is optimized to find optimal relation between aircraft utilization, airline revenue generation, and passenger convenience ^[6]. There are a variety of FSs, involving various objectives, constraints and solution methods ^[7,8]. Most of these studies assume that static O/D traffic are inputs to the model, resulting in flight delay. However, the demand is highly uncertain especially 10–12 weeks prior to the departure date of a flight. Compared to static FS, dynamic model reschedules a partial change of flights to meet short-term demand changes, which could improve flight schedule punctuality ^[2,9,10,11]. AR was firstly proposed for network flow methods by Simpson as early as in 1969 ^[12] and extended by Daskin and Panayotopoulos ^[13] in a hub-and-spoke-network, in order to build an integer-programming model. In recent years, such integration of AR with extensions of FS, fleet assignment (FA) and crew scheduling (CS) has caused widespread concern in the academic community. The integrated model of AR and FS was firstly proposed by Desaulniers et al. ^[14] to formulate a set partitioning model and a multi-commodity network flow model, and also extended by Salazar-Gonzalez ^[15] with extensions in CS, and by Cacchiani and Salazar-Gonzalez ^[16] to abide by specific rules to obtain both aircraft and crew routes.

Since the input of AR is derived from scheduled flight departure and arrival times in FS, many works aimed at finding a robust AR scheme with consideration of delay propagation in FS were conducted, e. g. ^{[17,18,19,20]}. These works mainly minimized the occurrence and the amount of flight delay in aircraft routing and/or flight retiming based on historical delay data. Due to the complexity of the problem solved independently, several authors ^[21,22,23] presented some IFSAR models to avoid some shortcomings of these studies. In particular, Sherali et al. ^[21] studied an IFSAR model with the extension of FA. Jamili ^[22] extended this work by considering uncertain travel time. Gürkan et al. ^[23] presented a leg-based IFSAR model with consideration of fuel and CO₂ emission costs. Besides, Faust et al. ^[24] studied an IFSAR model with consideration of maintenance problems. However, the above-mentioned IFSAR studies were based on the deterministic demand. To reduce the loss of operation profit related to the demand variability and disruptions, Kenan et al. ^[18] further accounted for the demand uncertainty in the IFSAR model. The solution algorithms include the branch-and-price-and-cut algorithm ^[19], iterative heuristic approach ^[20,25], row-and-column generation approach ^[26], and integrated scenario-based heuristic approach ^[27].

The above brief survey of available FS & AR & IFSAR models and their solution methods made it possible to identify the shortlist of issues that require a more in-depth analysis:

1) Although a variety of FSs & ARs were elaborated in several studies, only a few of them took into account a feasible time for an aircraft's take-off and landing at airports and ban time for a plane passing through a certain air route. Similarly, a few of them consider each flight trip with its own special aircraft type being covered by itself or a larger plane.

2) The basic assumption of conventional FSs is given flight timetabling that is the output for ARs. It implies a neglect of the integrated operation of FS (guide the airline choice of the most profitable departure time of flight trip by taking fares and seats into account) and AR (guide transits from selected flight trips to an aircraft of a particular type).

3) IFSAR, as an extension of the classic vehicle routing problem (VRP), is also a nondeterministic polynomial time (NP) hard problem, which implies that the exact algorithm cannot find a feasible solution at the acceptable time. Hence, an efficient heuristic algorithm needs to be designed to solve such a problem.

3.   Methodology

3.1.   Research framework

An airline operates a set of flight trips belonging to different aircraft routes between some airports. Each flight trip with certain travel time is covered by an aircraft from an origin at departure time to the destination at arrival time. Many different types of airplanes are initially located at the docked airports, so any flight trip via a particular aircraft type can be covered by the latter or a larger plane. The aim of multi-aircraft-type IFSAR is to simultaneously determine the departure time of each flight trip and assign a set of airplanes located at different airports to perform all flight trips. The departure and arrival time of each flight trip must be within a flexible time window in its aircraft's route and origin/destination airports, related to air traffic control. If two adjacent flight trips are covered by the airplane, the arrival time of the previous flight trip plus airplane's maintenance time should not exceed the departure time of the next flight trip, except for the case where the origin airport of the former trip coincides with the destination airport of the latter one. In view of aircraft maintenance and the required leisure time of pilots, an aircraft can perform at least two flight trips, in which origin airport of the first flight trip is the same as the destination airport of the last one. To reveal the optimal relationship between FS and AR to maximize the operational efficiency and passenger sales revenues, an integrated mixed-integer programming model was elaborated to pursue the optimal global value.

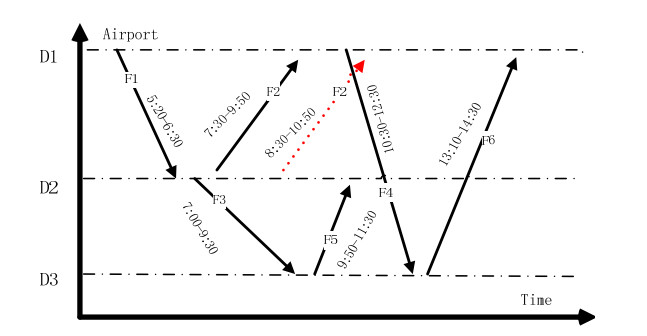
Figure 1 provides a detailed description of the proposed method. There are six flight trips (F1–F6) between three airports (A1–A3). The aircraft type for the first two flight trips is T1, while that of the last four flight trips is T2. In this example, the optimization process yields a trip timetable and two aircraft routes as follows. A T1 aircraft is illustrated by a solid line F1-F2-F4-F6, and a T2 aircraft is illustrated by a solid line F3-F5. The arrival and departure times are 5:20–6:30, 7:30–9:50, 7:00–9:30, 10:30–12:30, 9:50–11:30 and 13:10–14:30, respectively. If departure time of F2 is delayed by an hour in a fixed timetable, the original T1 aircraft can't continue to run the remaining two flights, and a new T2 aircraft is illustrated by a solid line F4-F6. Obviously, traditional FS, being independent of AR, need more than one T2 aircraft, which further proves the validity of our model. Similarly, traditional AR with single aircraft type is worse than our model. Our objective is to find an aircraft flight timetabling and scheduling plan that would simultaneously minimize the weighted operation costs for the fleet of airplanes and the total idle and running time for each flight trips covered by different aircraft, as well as maximize the total passenger sales revenues for all flight trips. To ensure that this approach fits well with the actual situations, the following assumptions are made:

Figure 1.  Graphical representation of the IAFTSP problem solution.

DownLoad: Full-Size Img PowerPoint

(1) Each flight trip is provided by one airplane, which cannot cover two flight trips at the same time.

(2) According to air traffic control, each airport has its own flexible time window for flight trips to take off or land, which can be given in advance. Similarly, a plane running flight trip must pass through the air route in fixed time windows.

(3) Passenger sales revenues of each flight trip are related to its departure time, which determines the number of passengers and fares at the time. Through the big data analysis of airline operations, a simple linear piecewise function describing this relationship can be obtained.

(4) The travel time of each flight trip is a certain value, which is independent of weather conditions, traffic control, etc.

3.2.   Model formulation

3.2.1.   Notations

To facilitate the model elaboration, all definitions and notations used hereafter are summarized in Table 1.

Table 1.  Parameters and variables in the proposed model.

Indices
$i, j$	Flight trip index
0	Virtual flight
$h$	Time section
$r$	Air route
$k$	Aircraft index
$t$	Aircraft type index
$d$	Airport index
Sets
F	Set of trips
T	Set of aircraft types
D	Set of airports
$H$	Set of time sections
${R}_{i}$	Set of air routes related to trip $i$
${K}_{d}^{t}$	Set of aircraft belonging to the particular type $t$ located at airport $d$
Parameters
${sp}_{i}$	Starting (origin) airport of trip $i$
${dp}_{i}$	Ending (destination) airport of trip $i$
${T}_{i}$	Total travel time of trip $i$
${T}_{ir}$	Travel time for the aircraft flight from the origin airport of trip $i$ to the origin of air route $r$
${b}_{i}$	The capacity related to the particular aircraft type for trip $i$
$p\left({st}_{i}\right)$	Number of passengers' demand for trip $i$ at its departure time
${B}_{t}$	The capacity related to aircraft type $t$
${T}_{s}$	Minimum safe time
$D{T}_{d}^{Lh}$	The earliest departure time of a plane at the airport $d$ during time section h
$D{T}_{d}^{Uh}$	The latest departure time of a plane at the airport $d$ during time section h
$A{T}_{d}^{Lh}$	The earliest arrival time of a plane at the airport $d$ during time section h
$A{T}_{d}^{Uh}$	The latest arrival time of a plane at the airport $d$ during time section h
$P{T}_{r}^{Lh}$	The earliest time of a plane passing through the air route $r$ during time section h
$P{T}_{r}^{Uh}$	The latest time of a plane passing through the air route $r$ during time section h
$\theta$	Minimum load rate of an aircraft
${c}_{t}^{1}$	Fixed cost of aircraft type $t$
${c}_{t}^{2}$	Cost of idle time RMB/hour
${c}_{t}^{3}$	Operational cost RMB/hour
$M$	A very large fixed value
Decision variables
${x}_{ij}^{k}$	Whether trip $i$ precedes trip j on aircraft k or not
${y}_{i}^{k}$	Whether trip $i$ is covered by the aircraft k or not
${st}_{i}$	The departure time of trip $i$
${et}_{i}$	The arrival time of trip $i$, i.e., ${st}_{i}+{T}_{i}={et}_{i}$
${U}_{ik}$	An auxiliary (real) variable for sub-tour elimination constraint in aircraft k

---

 | Show Table

DownLoad: CSV

3.2.2.   Problem formulation

The problem under study can be formulated as the following mixed-integer program (MIP), which requires minimization of

which is subject to:

In the above formulation, the primary objective function is given by Eq (1), which includes three terms: The first term deals with a fixed cost of flight fleet, the second one involves operation cost as the total mileage cost of designed routes; while the third one is related to the loss cost of the total idle time for adjacent flight trips covered by an aircraft. The secondary objective function in Eq (2) aims at maximizing the total number of transported passengers in all flight trips. Constraints (3) and (4) guarantee that each flight trip must be assigned to an aircraft of the same type or a larger one. Constraint (5) ensures that the load factor of an aircraft exceeds a certain value. Constraints (6) and (7) imply that all flight trips served by the aircraft should have the same incoming and outgoing arcs. Constraint (8) is used for the sub-tour elimination in the aircraft routing. Constraints (9) and (10) guarantee that the arrival airport of the former is the same as departure airport of the latter, while the arrival time of the former plus aircraft's maintenance time should not exceed the departure time of the latter if adjacent flight trips are covered by the same aircraft. Constraint (11) guarantees that each plane leaves the base airport and eventually returns to the base airport. Constraints (12) and (13) guarantee that a particular type of aircraft firstly leaves the docked airport, then performs a sequence of flight trips and eventually returns to the docked airport. Constraints (14) and (15) ensure that departure and arrival times of each flight trip are within a flexible time window in its origin/destination airport. Constraint (16) grants that time of a plane passing through the air route is within its flexible time window.

The proposed mixed-integer model is used to solve the extended classic VRP. Noteworthy that this is also a nondeterministic polynomial time (NP) hard problem, which cannot be solved by any exact method at an acceptable running time, especially for large-scale cases. To improve the computation efficiency, this study further proposes an ant colony optimization-based two-stage heuristic algorithm to yield meta-optimal solutions in a reasonable amount of time.

4.   The heuristic solution methodology

The ant colony optimization (ACO) principle proposed by Dorigo in 1997 envisages searching for an optimal path in the graph based on the behavior of ants seeking a path between their colony and source of food. Ants navigate from nest to food source, move at random, and deposit pheromone on their path, while the shortest path is discovered by the maximal amount of pheromone trails left by ants who used this path ^[28].

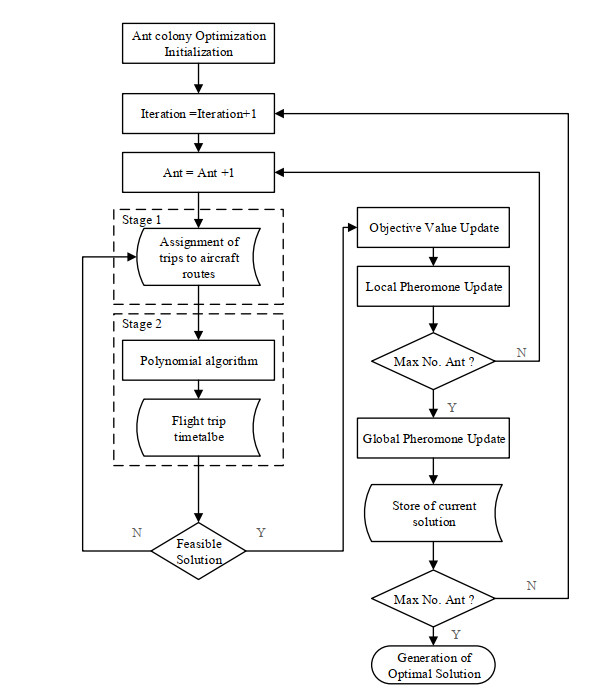
In this section, an ACO-based two-stage heuristic algorithm is designed to realize the proposed model. At the first stage, we assign all flight trips to a set of airplanes initially located at different base airport routes by satisfying each flight trip with its own particular aircraft type being covered by itself or a larger plane. Then, the flight timetable containing the arrival and departure times of each flight trip is scheduled based on the principle of maximizing the total passenger sales revenues for all flight trips at the second stage. Technically, the whole structure is constructed using the ant colony optimization, in which a polynomial algorithm is further embedded for implementing the second stage, as shown in Figure 2.

Figure 2.  The ACO algorithm flowchart.

DownLoad: Full-Size Img PowerPoint

4.1.   Stage Ⅰ: Trip assignment to aircraft routes

At the first stage, we aim to assign all flight trips to different aircraft routes considering network constraint trajectories. For this purpose, we adopt ACO, in which imaginary ants are placed at the docked airport (aircraft's route origin), and then they will visit the whole trip set for assigning flight trips to routes. The required steps of the proposed algorithm are listed in Table 2.

Table 2.  Algorithm for assigning flight trips to aircraft routes.

Step 1. Initialization. 1) Basic parameters: Number of ants, number of routes, and the maximal number of iterations 2) Pheromone ${\rm{ \mathsf{ τ} }}_{ij}\left(0\right)$ and pheromone increment $∆{\rm{ \mathsf{ τ} }}_{ij}\left(0\right)$between each arc (i, j) (In our case, pheromone ${\rm{ \mathsf{ τ} }}_{ij}$ represents the desirability of trip j preceding trip i on the route k), in which ${\rm{ \mathsf{ τ} }}_{ij}\left(0\right)$ and $∆{\rm{ \mathsf{ τ} }}_{ij}\left(0\right)$will be initialized to a constant value and zero, respectively;
Step 2. Network preparation. 1) A sequence of trips by their pre-defined departure time windows, i.e., ${st}_{i}\in [P{T}_{r}^{Lh}-{T}_{ir}, P{T}_{r}^{Uh}-{T}_{ir}]$; 2) Place of M ants at the earliest trip;
Step 3. Generation of candidate routes' set, allowed, for trip i, in which: $allowed=\left\{k\right|{et}_{\psi \left(k\right)}+{T}_{s}\le {st}_{i}\wedge {dp}_{\psi \left(k\right)}={sp}_{i}, \forall k\in K\}$, where $\psi \left(k\right)$ represents the trip proceeding trip i on route k;
Step 4. Selection of route k from the set, allowed, to visit trip i, where we use a pseudo-random-proportional-based transition rule. A random variable, q, which is uniformly distributed within the interval from 0 to 1, is initialized to compare with a pre-defined parameter ${q}_{0}\in \left(\mathrm{0, 1}\right]$. The route k serving trip i is determined by $\mathrm{arg}\underset{k\in \mathit{allowed}}{\mathrm{max}}\left\{{\rm{ \mathsf{ τ} }}_{\psi \left(k\right)i}\right(t){\left[{\eta }_{ik}\right]}^{\beta }\}$ where $q\le {q}_{0}$; otherwise, it will follow the probability function ${p}_{ik}^{m}=\frac{{\rm{ \mathsf{ τ} }}_{\psi \left(l\right)i}^{\alpha }\left(t\right){{\eta }_{ik}}^{\beta }}{\sum _{lϵallowed}{\rm{ \mathsf{ τ} }}_{\psi \left(l\right)i}^{\alpha }\left(t\right){{\eta }_{il}}^{\beta }}$ to decide, which ant (plane) will visit trip i. Note that α and β represent the relative effects of the pheromone trail and heuristic information, respectively, while ${\eta }_{ik}=1/$(${st}_{i}-{et}_{\psi \left(k\right)}-{T}_{s}+0.01)$ means the cost of route k visiting trip i.
Step 5. Repeat steps 3 and 4 until all trips are successfully assigned.

---

 | Show Table

DownLoad: CSV

4.2.   Stage Ⅱ: Service time schedule

Stage Ⅰ has assigned trips to routes, as well as determined the sequence of each route visiting its trips. Stage Ⅱ will be activated to schedule a timetable in a feasible departure time window with the account of the airline revenue maximization. Note that both the route design and air traffic control determine a feasible departure time window. A polynomial algorithm is implemented at this stage, while its detailed procedures are listed in Table 3.

Table 3.  Algorithm for flight timetable for each trip.

Step 1. For route k, calculation of departure time window of each trip via Eq (15), ${st}_{i}\in [P{T}_{r}^{Lh}-{T}_{ir}, P{T}_{r}^{Uh}-{T}_{ir}]$.
Step 2. For route k and trip j linked with trip i; 1) Obtaining of departure time window of trip j, since it is equal to $[P{T}_{r}^{Lh}-{T}_{ir}+{T}_{i}+{T}_{s}, P{T}_{r}^{Uh}-{T}_{ir}+{T}_{i}+{T}_{s}]\cap [P{T}_{r}^{Lh}-{T}_{jr}, P{T}_{r}^{Uh}-{T}_{jr}]\ne \varnothing$ 2) Generation of the threshold for the departure time of each flight trip i with its origin airport's flexible working time via Eqs (13) and (14), which belongs to $[D{T}_{d}^{Lh}, D{T}_{d}^{Uh}]\cap [A{T}_{d}^{Lh}-{T}_{i}, A{T}_{d}^{Uh}-{T}_{i}]\ne \varnothing$; 3) A search of all possible departure times within the threshold of trip i to target the one with the maximization of ${\sum }_{\forall i\in \mathrm{F}}p\left({st}_{i}\right)$, ${st}_{i}\in [P{T}_{r}^{Lh}-{T}_{ir}+{T}_{i}+{T}_{s}, P{T}_{r}^{Uh}-{T}_{ir}+{T}_{i}+{T}_{s}]\cap [P{T}_{r}^{Lh}-{T}_{jr}, P{T}_{r}^{Uh}-{T}_{jr}]\cap [D{T}_{d}^{Lh}, D{T}_{d}^{Uh}]\cap [A{T}_{d}^{Lh}-{T}_{i}, A{T}_{d}^{Uh}-{T}_{i}]$;
Step 3. Repeat step 2 until the departure times of all trips in each route are scheduled.

---

 | Show Table

DownLoad: CSV

Feasibility of the initial solution generated by one ant through stages Ⅰ and Ⅱ will be checked, and the objective value will be updated, in case that the solution is feasible for the proposed model. Subsequently, the local pheromone amount data will keep updating until all ants are used in one iteration. The best solution obtained from the current iteration will be stored to update the global pheromone data until reaching the maximal number of iterations. Once all iterations run out, the optimal solution will be generated and stored.

5.   The numerical test example

5.1.   Example description

In this section, a real example of small- to a medium-sized airline in China, consisting of 32 flight trips (F1–F32) between eleven airports (D1–D11), and two types of aircraft for these trips (T1 and T2), is used to illustrate the applicability of the proposed model and algorithm. The departure and arrival times, starting and ending airport, aircraft type, and feasible departure time window of each flight trip are listed in Table 4. Obviously, the departure time of each trip must satisfy the flexible time window in its aircraft's route and origin/destination airports. The key parameters used in the case study are given as follows:

Table 4.  Basic information on flight trips.

Trip No.	Origin/destination	Flexible departure time window	Flight time (min)	Aircraft type
F1	D1- > D2	6:30–7:30	60	T1
F2	D2- > D1	12:30–14:00	90	T1
F3	D1- > D2	7:00–9:00	120	T1
F4	D2- > D1	12:00–14:00	70	T1
F5	D1- > D3	19:00–20:30	60	T2
F6	D3- > D1	17:00–18:00	60	T2
F7	D8- > D4	11:00–13:00	80	T2
F8	D4- > D1	7:00–8:00	90	T2
F9	D1- > D5	11:00–12:30	90	T2
F10	D5- > D1	8:00–9:30	120	T2
F11	D1- > D6	7:00–9:00	120	T1
F12	D6- > D5	5:00–6:00	60	T1
F13	D1- > D2	6:00–6:30	60	T1
F14	D7- > D1	7:00–8:30	80	T1
F15	D8- > D9	6:30–8:00	60	T2
F16	D9- > D7	5:00–6:30	60	T2
F17	D8- > D10	18:00–19:00	150	T1
F18	D10- > D8	22:00–23:00	70	T1
F19	D8- > D1	6:00–7:30	60	T2
F20	D11- > D1	5:00–6:30	60	T2
F21	D6- > D9	12:00–14:00	80	T1
F22	D9- > D8	10:00–11:00	60	T1
F23	D9- > D11	14:00–16:00	90	T2
F24	D11- > D8	7:30–9:00	150	T2
F25	D8- > D9	11:00–13:00	90	T1
F26	D9- > D8	8:00–10:00	90	T1
F27	D1- > D2	11:00–12:30	60	T1
F28	D2- > D1	8:00–10:00	80	T1
F29	D1- > D2	9:00–11:00	60	T2
F30	D2- > D1	8:00–9:30	90	T2
F31	D1- > D3	9:30–11:00	120	T2
F32	D3- > D1	11:00–12:30	70	T2

---

 | Show Table

DownLoad: CSV

●  Fixed cost of aircraft type $t$:${ c}_{T1}^{1}$ = 10000 RMB/plane and ${c}_{T2}^{1}$ = 11000 RMB/plane.

●  The idle time cost of aircraft type $t$:${ c}_{T1}^{2}$ = 1.7 RMB/min and ${c}_{T2}^{2}$ = 2.5 RMB/min.

●  The operational cost of aircraft type $t$:${c}_{T1}^{3}$ = 1.9 RMB/min and ${c}_{T2}^{3}$ = 3 RMB/min.

●  Capacity related to aircraft type $t$:${B}_{T1}$ = 150 persons and ${B}_{T2}$ = 200 persons.

●  Minimum load rate:$\theta$ = 0.7.

●  Minimum safe time:${ T}_{s}$ = 30 min.

5.2.   Results

Table 5 describes the optimal aircraft route and timetable, which include the departure time, assigned aircraft type, and load rate of each flight trip. Two T1 planes (each carrying up to 150 passengers) and nine T2 planes (each carrying up to 200 passengers) were required for covering 32 trips. The total ideal time of 2795 minutes and running time of 2660 minutes were obtained. A total of 133,648 RMB was spent, in order to transport 5035 passengers by these planes, which amounted to 26.55 RMB per capita. Taking route A2 as an example, a T2 aircraft will leave the base airport D11, cover flight trips F20, F1, F30, and F5 and complete its flights at the base airport D3. The flight trip F1 with the T1 plane could be covered by a larger plane T2, which would pick up 140 passengers at 7:05. In this case, the plane load rate was 140/200 = 0.7. Before performing flight trip F1, it will stay at the airport for the expected ideal time of about 60 min.

Table 5.  Routing and scheduling plan of each plane.

Aircraft No.	Aircrafttype	The sequence of flight trips covered by each plane	Running time (min)	Ideal time (min)	Operation cost (RMB)
A1	T2	D6 - F12 (5:10,150, 0.75) - F10 (8:50,200, 1) -F32 (12:05,200, 1) - F6 (17:45,180, 0.9) - D1	310	737.5	13774
A2	T2	D11 - F20 (5:05,140, 0.7) - F1 (7:05,140, 0.7) - F30 (8:55,150, 0.75) - F5 (20:10,160, 0.8) - D3	270	575	13248
A3	T2	D9 - F16 (5:30,160, 0.8) - F14 (8:15,150, 0.75) -F27 (11:55,150, 0.75) - D2	200	165	12013
A4	T1	D1 - F13 (6:05,140, 0.93) - F2 (13:10,150, 1) - D1	150	325	10838
A5	T2	D8 - F19 (6:30,160, 0.8) - F31 (10:15,180, 0.9) - D3	180	127.5	11859
A6	T2	D4 - F8 (7:55,160, 0.8) - F29 (10:00,180, 0.9) - F4 (13:10,140, 0.7) - D1	220	145	12023
A7	T2	D1 - F3 (7:15,140, 0.7) - F28 (9:35,150, 0.75) - F9 (12:15,180, 0.9) - D5	290	20	11920
A8	T2	D8 - F15 (7:15,160, 0.8) - F22 (10:40,150, 0.75) - F17 (18:20,150, 0.75) - F18 (22:40,150, 0.75) - D8	340	535	13358
A9	T1	D1 - F11 (7:25,135, 0.9) - F21 (12:45,150, 1) - D9	200	160	10652
A10	T2	D11 - F24 (8:15,160, 0.8) - F7 (12:15,170, 0.85) - D4	230	50	11815
A11	T2	D9 - F26 (9:05,150, 0.85) - F25 (12:15,140, 0.7) - F23 (15:40,160, 0.8) - D11	270	135	12148
		TOTAL:	2660	2795	133648

---

 | Show Table

DownLoad: CSV

Furthermore, the proposed model (AFSRP with multi-type aircraft) has some advantages over the AFSRP with a single aircraft type, which are shown in Table 6. The operation costs defined via the proposed model will be reduced by 26.2%. However, the total number of transported persons via the proposed model will be lower by 5.8% than that determined via the conventional one. This is due to the fact that the flight trip covered by a particular aircraft type increases both the number of needed airplanes and the total idle time for two adjacent flight trips covered by the same airplane. In the case where the departure time of the timetable is more flexible, the airline may schedule flights at a time when more passengers are willing to travel. As shown above, the increase in operation costs is fully compensated by the decrease in fixed cost for fleets, which proves that the proposed model feasibility.

Table 6.  Comparative analysis of the proposed and conventional models.

Scenario	Number ofT1 planes	Number ofT2 planes	Total running time (min)	Total ideal time (min)	Number of passengers	Operation costs (RMB)
Proposed model	2	9	2660	2795	5035	133,648
Conventional model	8	8	2660	3157.5	5345	181,057
Difference, %	−75	12.5	0	−11.5	5.8	−26.2

---

 | Show Table

DownLoad: CSV

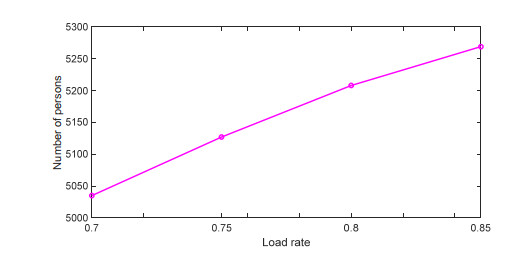
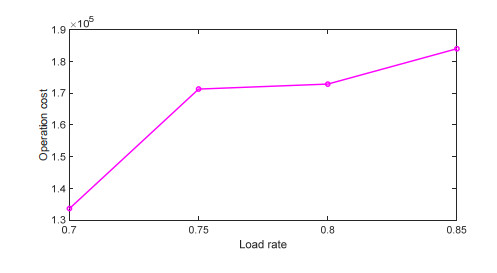
Figures 3 and 4 illustrate how the changes in the load rate affect a trade-off between the operation cost and the number of transported persons. As the load rate $\beta$ gradually increases from 0.7 to 0.85, both of them are also increased. The reason is that higher load rates lead to more restrictions on the flexible choice of timetables, aiming at scheduling flights at a time when more passengers are willing to travel. In this case, the fleet size cannot be saved by fine-tuning the schedule. The increase in fleet size was accompanied by a rise in the ideal time. Hence, operation costs would also grow.

Figure 3.  The load rate effect on the number of transported persons.

DownLoad: Full-Size Img PowerPoint

Figure 4.  The load rate effect on operation costs.

DownLoad: Full-Size Img PowerPoint

6.   Conclusions

This paper presents an integrated optimization framework for IAFTSP with multiple aircraft type to reveal the relationship between temporal and spatial distributions of flight trips, the number of airplanes firstly distributed in the base airports, flight timetabling and scheduling plan. In contrast to available approaches, the proposed one envisages the following two innovations: (ⅰ) It simultaneously coordinates an interactive process of determining the departure times of all flight trips and assigns them to different airplanes, and (ⅱ) it adopts a two-stage heuristic algorithm based on ACO to efficiently yield the acceptable solution. A case study is used to validate the feasibility and applicability of the proposed framework. Results show that operation costs estimated via the proposed model will be reduced by 26.2%, while the total number of transported persons will be increased by 5.8%, as compared to the conventional model. With an increase in the plane load rate, both operation costs and number of transported persons are slightly increased.

Noteworthy is that, in this study, each flight trip was allocated a certain travel time, which neglected random perturbations and respective changes in the travel time. To this end, robust solutions of IAFTSP with random travel time and the related failure recovery are the two major issues in day-to-day operations. Therefore, extending the IAFTSP to the simultaneous determination of delayed times of some flight trips or canceled ones, and the assignment of uncertain flight trips to airplanes in the follow-up studies is quite expedient.

Acknowledgements

This study was financially supported by the Humanities and Social Sciences Foundation of the Ministry of Education of China (20YJCZH176); the central college basic scientific research operating expenses fund in civil aviation university of China (3122020079).

Conflict of interests

The authors declare there is no conflict of interest.