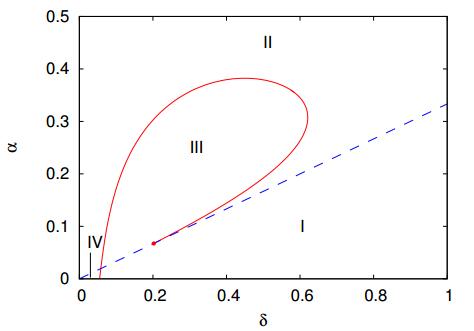
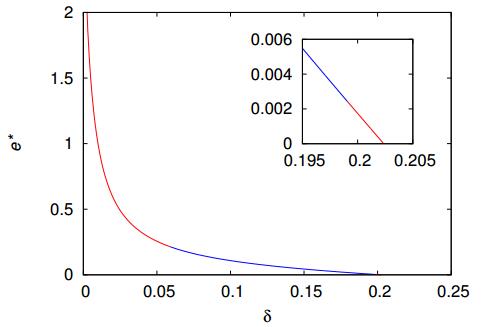
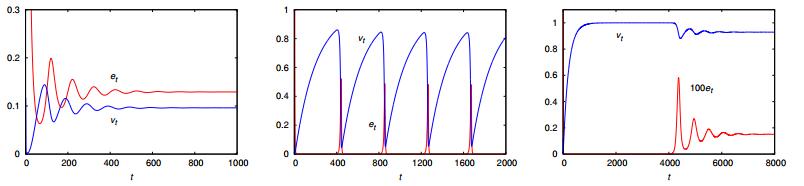
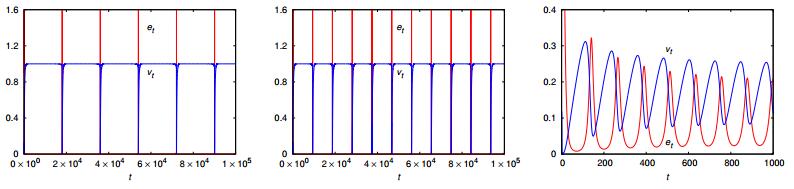
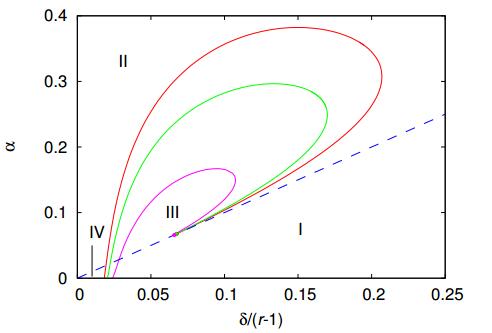
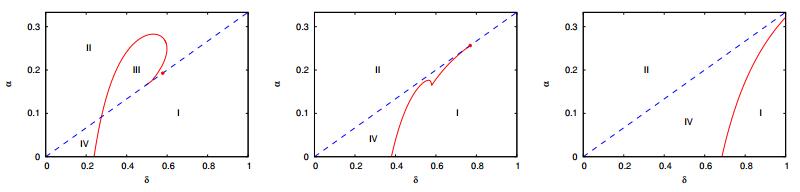
Overpopulation and environmental degradation due to inadequate resource-use are outcomes of human's ecosystem engineering that has profoundly modified the world's landscape. Despite the age-old concern that unchecked population and economic growth may be unsustainable, the prospect of societal collapse remains contentious today. Contrasting with the usual approach to modeling human-nature interactions, which are based on the Lotka-Volterra predator-prey model with humans as the predators and nature as the prey, here we address this issue using a discrete-time population dynamics model of ecosystem engineers. The growth of the population of engineers is modeled by the Beverton-Holt equation with a density-dependent carrying capacity that is proportional to the number of usable habitats. These habitats (e.g., farms) are the products of the work of the individuals on the virgin habitats (e.g., native forests), hence the denomination engineers of ecosystems to those agents. The human-made habitats decay into degraded habitats, which eventually regenerate into virgin habitats. For slow regeneration resources, we find that the dynamics is dominated by rounds of prosperity and collapse, in which the population reaches vanishing small densities. However, increase of the efficiency of the engineers to explore the resources eliminates the dangerous oscillatory patterns of feast and famine and leads to a stable equilibrium that balances population growth and resource availability. This finding supports the viewpoint of growth optimists that technological progress may avoid collapse.
1.
Introduction
The novel coronavirus (COVID-19) disease has developed rapidly in the United States of America and around the world. It has led many nations and localities to reassess their preparedness in case of disease outbreaks. Many phases of the disease have been noticed where the count of COVID-19 cases and related deaths are characterized as too high to continue daily normal activities. There are locations where the severe outbreak has led to drastic decisions and complete shutdowns except for essential services. Some cities have implemented partial shutdowns. The phases of the shutdowns are related to the geographical locations of outbreaks. The latter cannot be ignored in any modeling scheme as they may shed light on the count effects and dynamics of the disease over time and its transmission. Such models will help in the monitoring and prediction of the disease.
In this paper, we make use of a statistical Bayesian approach [1,2,3]. In such Bayesian approach, where the inherent spatio-temporal structure is modeled, the random effects are autocorrelated. We will use the CARBayesST statistical package in R for the inferential statistical analysis. The CARBayesST statistical package allows spatio-temporal areal unit modeling with conditional autoregressive priors. This is the first dedicated software package in R for this purpose. This software package is very flexible in the sense that it allows the researcher to fit a wide range of models, focusing on different aspects of space-time modeling. The CARBayesST statistical package can be used to estimate the overall space and time trends. It can be used to identify clusters.
The data of interest include the total COVID-19 case counts in the state of Virginia, as reported by the Johns Hopkins University (JHU) website (https://coronavirus.jhu.edu/map.html). The type of real and temporal unit data relates to 93 counties in the state of Virginia. Specifically, the random response variable of interest is the daily COVID-19 case counts in these 93 counties. The 93 counties are considered to have non-overlapping areal units. Realizations of the random response and the case counts for the 93 counties have been considered for 490 consecutive days, beginning from January 22, 2020. The total cases of COVID-19 in the state of Virginia, as reported from the JHU, are a type of summary measure. Many authors have used summary measures in analyzing areal and temporal unit data. For example, the total yield in sectors in an agricultural field trial was considered by Besag and Higdon [4]. Choi and Lawson [5] considered the total number of individuals suffering from chronic obstructive pulmonary disease in counties of the US state of Georgia.
The manuscript describes a novel setting for the application of statistical methods in COVID-19 spread and management, with the aim to identify clusters [6,7,8]. This will allow public health officials and decision makers to take timely and effective preventive measures. Our motivation for modeling this spatio-temporal data is to estimate the effect of risk factor(s) on the random response variable. Land area (size of the county) and population density were among the list of potential significant risk factors. Another motivation is to identify clusters and areal units that exhibit elevated values for the response variable, i.e., areas where an elevated risk of the disease is present, such as elderly nursing facilities. These values give an idea of clustering or dispersion, i.e., spatial autocorrelation [9,10]. Linking the changes in the total case counts of the disease to local counties with executive orders will play a key role in dealing with the spread. The dynamic progression with the availability of high-quality data stands as a novel indicator for public health and surveillance. To measure the global spatial autocorrelation in the random response variable of interest, we calculate Moran's I statistic [11] and graph the Moran's I statistic over time. A variety of disease mapping methods from simulated to real data, in the context of goodness-of-fit, have been considered [12,13,14,15]. They have applied the Moran's I statistic to the Pearson residuals from the model fit. To explain differences based on locations, a simple global Moran's value cannot explain the whole growth. As such, [16] proposed to partition the global Moran value into a sum of local indices of spatial association (LISA); the individual Moran values show local trends that are not shared globally.
A zero-inflated Poisson autoregressive model and zero-inflated negative binomial autoregressive model of the COVID-19 data in Ghana have been proposed by Tawiah et al. [17]. Their paper investigated the trend of daily count of COVID-19 deaths in Ghana. Chang et al. [18] have introduced a metapopulation susceptible-exposed-infectious-removed (SEIR) model. This model integrates dynamic mobility networks to simulate the spread of COVID-19 in ten of the largest metropolitan areas in the USA. The mobility networks considered are derived from mobile phone data. Comess et al. [19] have considered testing problems in the context of pooled testing during the COVID-19 pandemic. They have discussed the need of integrating field sampling information with statistical modeling. This integration is to optimize pooled testing procedures. The Institute for Health Metrics and Evaluation (IHME) COVID-19 Forecasting Team [20] has considered COVID-19 case counts and mortality data from February 1, 2020, to September 21, 2020. The SEIR model was used to predict possible trajectories of severe COVID-19 infections and the effects of non-pharmaceutical interventions from September 22, 2020, through February 28, 2021, in the US. Moreover, Moreau [21] studied the COVID-19 outbreak in Brazil in the context of the Weibull distribution model. Their SIR model did not fit well in the COVID-19 context data. The susceptible, infected and recovery compartments that are needed in this disease dynamic are difficult to obtain. Likewise, an extension of the SIR model includes the exposed compartment (SEIR). As mentioned in Tolles and Luong [22], alternative models become more reliable in drawing informed public policy. Their model was used to forecast COVID-19 cases, in scenarios based on the daily number of new deaths as a function of time. Finally, Woolf et al. [23] used a Poisson regression model for the mortality data from March to August 2020 and predicted the number of deaths attributed to COVID-19 in USA in 2020.
Bayesian conditional autoregressive (CAR) models and approaches offer innovative and computational routines that can be adjusted and applied to longitudinal data. One more feature of CAR models is that they allow an update of the prior information in fitting present data and building predictions about the future. Bayesian models evaluate procedures over repeated samplings. In this paper, we use the Bayesian approach, where the inherent spatio-temporal structure is modeled using a set of random effects. This approach is widely used in the modeling of disease data [24]. Conditional autoregressive priors and spatio-temporal extensions have been typically assigned to these models to capture spatial and temporal autocorrelations [4,25]. The model proposed by Knorr-Held [26] provided an ANOVA style decomposition of the data into overall spatial trends, temporal trends and spacetime interaction. While frequentist models have been popular in the literature, the main challenges faced are related to the model accuracy estimates and the design matrix experiment. The idea is presented under the likelihood principle as described in Boedeker [27]. Giudici et al. [28] have considered a class of birth process called self-exciting point in their research to measure the spread in space and time (spatio-temporal network model). They also considered covariates, such as spatio-temporal mobility, and sociodemographic factors (vaccination, policy). The parameters of the model were estimated using the maximum likelihood method via an expectation maximization (EM) algorithm. Giudici et al. [29] proposed a Bayesian time-dependent Poisson autoregressive model. They have considered varying non-pharmaceutical interventions (NPIs) implemented by most countries as their explanatory variables. Paez et al. [30] investigated the influence of environmental factors, such as temperature, humidity and sunshine, on the COVID-19 pandemic in Spain. They have used a seemingly unrelated regressions (SUR) approach and reported results from a spatio-temporal model. The manuscript by De Angelis et al. [31] describes the spatio-temporal spread of COVID-19 from a highway transportation network that dictates mobility. Park et al. [32] proposed a spatio-temporal model using a Dirichlet process mixture model. Aggregated data may not always accurately capture the fine-scale spatial heterogeneity of disease transmission, and this can lead to biased decisions by decision-makers and public health officials. Inaccurate models and unreliable preliminary data can also have significant impacts on decision-making, as seen in the examples provided by Bizzarri et al. [33] and by Guenther et al. [34]. In Bizzarri et al. [33], the unreliable preliminary data, as well as inaccurate models, significantly affected the political decisions of the Italian administration. Another example in Guenther et al. [34] documents a superspreader event in Germany in a meat processing plant. Modeling such an event requires accounting for the precise plant location information, and aggregated data may miss such crucial local information. To address these challenges, it is important to collect and analyze data at specified spatial and temporal scales. Our paper proposes another model to complement the literature. In the Bayesian context, the main challenges are related to prior selection and possible non-robustness of the estimates. Data from the state of Virginia are given consideration, where the area is partitioned into counties. Spatial dependence among the counties is captured by looking at the neighborhood matrix, denoted by W, of closeness distance. Moran measures of spatial correlations are computed. We apply the Poisson count process to provide a method of relating count time series and spatial covariates by specifying different kernels in the W matrix of the measure of proximity.
The manuscript is organized as follows. In Section 2, we provide a description of the data set. We propose preliminary analyses in Section 3. The CARBayes statistical modeling is described in Section 4. In Section 5, Moran's statistic of spatial dependence and spatial analysis are presented. The findings are discussed in Section 6. The conclusion is provided in Section 7.
2.
The data set
Data on total COVID-19 case counts from January 22, 2020, to May 25, 2021, were collected using the R package called "covid19.analytics". Total case counts were accounted for each day, and there was a total of 490 days per county. The aggregate data are also available under the US Centers for Disease Control and Prevention (US CDC). Given the association between population size and COVID-19, data on time in days and area sizes were collected as covariates. Daily counts based on a particular day (starting Monday, January 22) over the time were collected, for a total of 490 daily counts for each county.
3.
Preliminary analyses
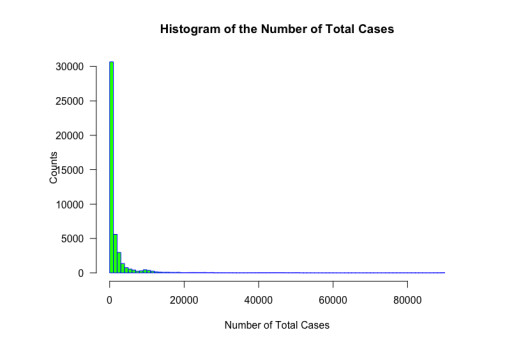
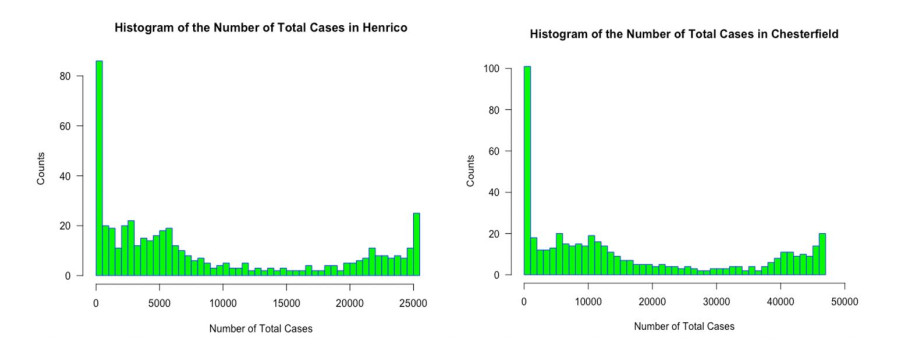
This type of spatial data has an inherent spatio-temporal autocorrelation. Modeling the spatial autocorrelation and the temporal autocorrelation is important to accurately model and classify the growth of total case counts. So, by looking at the overall trend, it is difficult to classify the growth of total case counts without advanced statistical models. From a single time point of cases, no conclusion can be drawn about the trends or the growth of total cases over time. The histogram of total cases in the county of Henrico and its neighbor Chesterfield County reveal trends that are unforeseen. Nearby counties are not necessarily alike. The histogram of the county of Henrico can reach values that are almost twice those of the neighboring county of Chesterfield. See Figure 1.
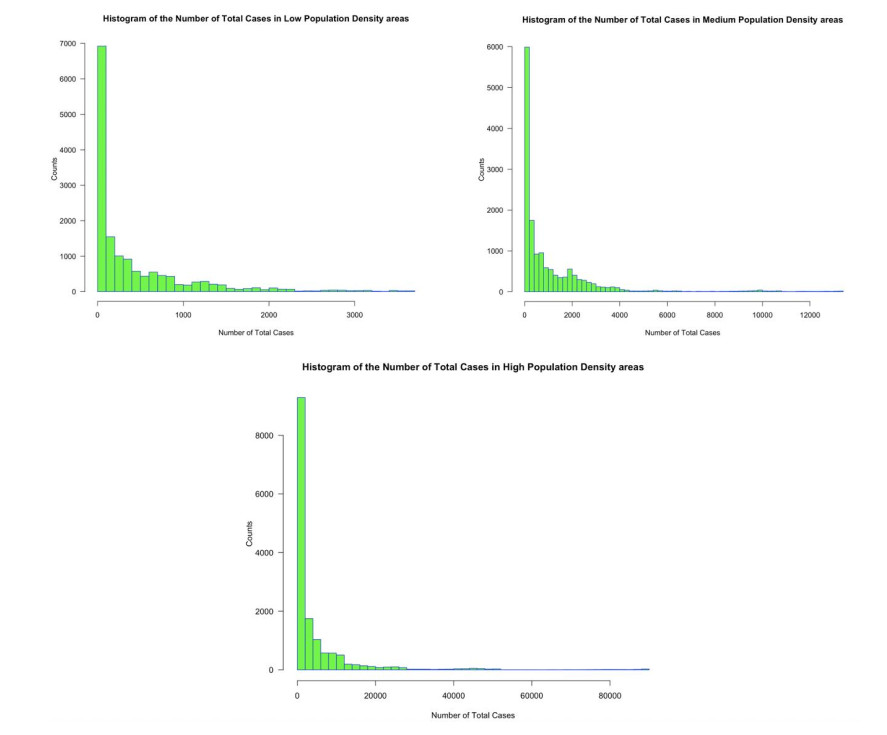
For example, the county of Henrico has higher counts of total cases than Richmond, although Richmond is the capital city in terms of population size and resources. The histogram of the total number of cases shown in Figure 2 is now broken up into three other figures (Figure 3) based on the population density. The population density was obtained by dividing the 2019 population (in thousands) by land area (in square miles). Three categories low (5.3-47.1), medium (47.7-96.5) and high (102.8-9118.4) were generated. The tails of those histograms are heavier for medium- and high-density areas, where we observed the highest number of total cases. We also plotted the data for total cases per county.
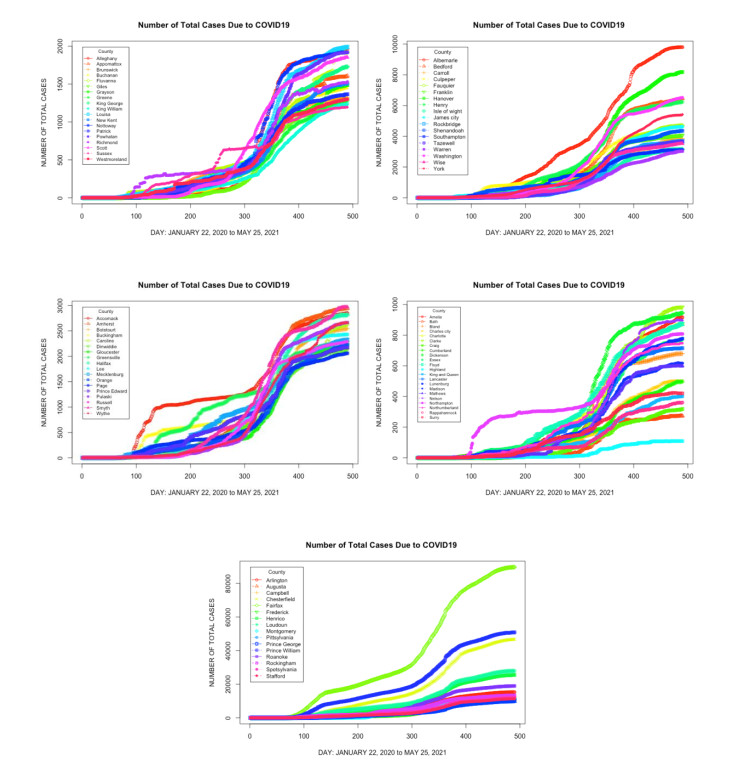
The progression of COVID-19 cases is not accurately tied to the population size in the counties of Virginia. Figures 3 and 4 of the number of cases in high, medium and low-density areas have similar shapes. Such results show the complex temporal variation where the feature inputs are still not well understood. Day and land area are used in our analysis. The range of the total number of cases in Figure 4 changes from 1000 total cases (Amelia) to 2000 total cases (Allegany) to 3000 (Accomack) to 10000 (Albemarle) and 80000 (Arlington). Understanding the spatial dependence of the dataset becomes challenging. So, a simple model is not enough to understand the trends in total case counts in the state. An alternate approach is to look at Moran's spatio-temporal values along with Bayesian analysis methods. The first gives a measure of spatial correlation, an indication of hot spots and a sense of dependence. The second is obtained after running the CARBayes model.
4.
CARBayes statistical modeling
The 93 counties in the state of Virginia, as non-overlapping areal units, are considered the study region. The data are available for each areal unit for 490 consecutive time periods. Here, we are considering 93 counties (K=93) and 490 consecutive days (N=490) from January 22, 2020, to May 25, 2021.
Let Ykt be the number of people who are infected with COVID-19 in the kth county at day t.
We consider p (in our case p=2) known covariates (day and area).
Let xkt=(xkt1,xkt2,..,xktp), k=1,2,…,K and t=1,2,…,N. xkt is a vector of p known covariates for kth county and day t.
The most generalized form of the model that we consider is [35]
where β=(β1,β2,..,βp) is a vector of covariate regression parameters. β is assumed to be a multivariate normal prior with mean μβ and covariance matrix Σβ. The prior parameters can be chosen by the user. The ψkt term in the linear model is a latent component term to encompass areal unit k and time t. The ψkt term will account for the spatio-temporally autocorrelated random effects. ν2 represents the variance of the data.
The complete descriptions of these spatio-temporally autocorrelated random effects and offset terms are as follows:
We use
The spatio-temporal structure that we consider is the model ST.CARar [36]. This spatio-temporal structure consists of a multivariate first order autoregressive process with a spatially correlated precision matrix. The precision matrix is the inverse of the covariance matrix [37,38]. The precise definition of the spatio-temporal structure is as follows:
where ϕt=(ϕ1t,…,ϕkt,…,ϕKt) is a vector of random effects for time t(t=1,…,N). ϕt will evolve over time via a multivariate autoregressive process. Here, we are using the precision matrix (Q(W,ρs)) proposed by [39]. The parameter τ2 controls the overall variability of ϕ1. ρs and ρT represent the spatial and temporal correlations, respectively. The algebraic definition of the precision matrix is as follows:
where the vector 1 is the K×1 vector of ones, and K is the K×K identity matrix. W is called the symmetric non-negative K×K neighborhood, weight or adjacency matrix.
wkj can be described as the spatial closeness between the counties Sk and Sj, for k=1,…,K and j=1,…,K.
The specific model from Eq (1) that we consider in this paper is
for k=1,…,K,t=1,…,N, where Ykt Poisson(μkt), where μkt is the mean for the k th county at time t.
5.
Moran's statistic
The Moran values can indicate spatial similarities and dissimilarities in the progression of the disease. We use the Moran values as a comparative tool for the CARBayes model. Although the assumptions under Moran values may not be met, they provide a basic validation of the results in the Bayesian context [40]. We compare the performance of the CARBayes model and the change in Moran values over time using the spatial weight matrix. This matrix, denoted as W, links the counties' geographical distance. It is the same as the adjacency matrix described in Section 4.
Moran's statistic (referred to as Moran's I) [11] is defined as
where
W is the symmetric non-negative K×K neighborhood, weight or adjacency matrix.
yi is the total number of people infected with COVID-19 in the ith county, i=1…K,
and −y=∑Ki=1yiK.
Positive spatial autocorrelation occurs when similar counts cluster around the same geographical area. Negative spatial autocorrelation occurs when dissimilar counts arise next to each other in the same geographical area. This helps to understand relationships of the observed counts from one county to another and validate if the observations are independent. We are using Moran's statistic to understand the spatial trends of the COVID-19 cases in Virginia.
6.
Statistical findings
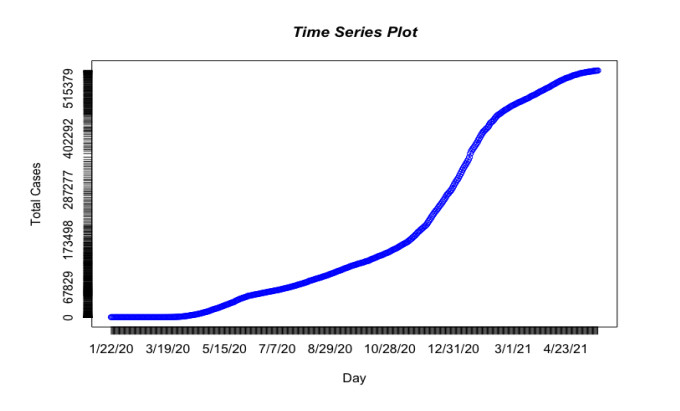
The total case count keeps increasing but at different rates over time, as shown in Figure 5. Covid-19 case counts in different locations cannot be assumed to be independent. If there is some dependence, the Moran value, Eq (4), can lead us to the cluster structure. We develop an accurate classifier of the coefficient and the covariance matrix by analyzing the system as a whole. Other predictors, such as the number of intensive care unit beds available (hospitalization counts) or the population size and density in that area, could have been used.
The analysis is challenging because the measurements are not independent, and clustering is present. We use the linear mixed model to incorporate the temporal trends and patterns under non-normal data with varying intercepts and slope models. Parameters are estimated under CARBayes using conditional auto-regressive priors under Markov Chain Monte Carlo (MCMC) simulations. Slightly similar variations of the models were also considered. An offset was added to allow the Poisson response in a predicted simple linear (or equivalently log linear) regression. This model is known as the quasi-Poisson log linear model, which provides the statistics associated with the day and land area estimates as 0.0024 and -0.00004, respectively (Table 1). They are both significant at the 0.05 level. The signs indicate the spread of total case counts and the pervasive nature of the virus transmission and of people in that area at that time. The case count increases per day but decreases as the location area gets larger. The model is described in the formula of Eq (1).
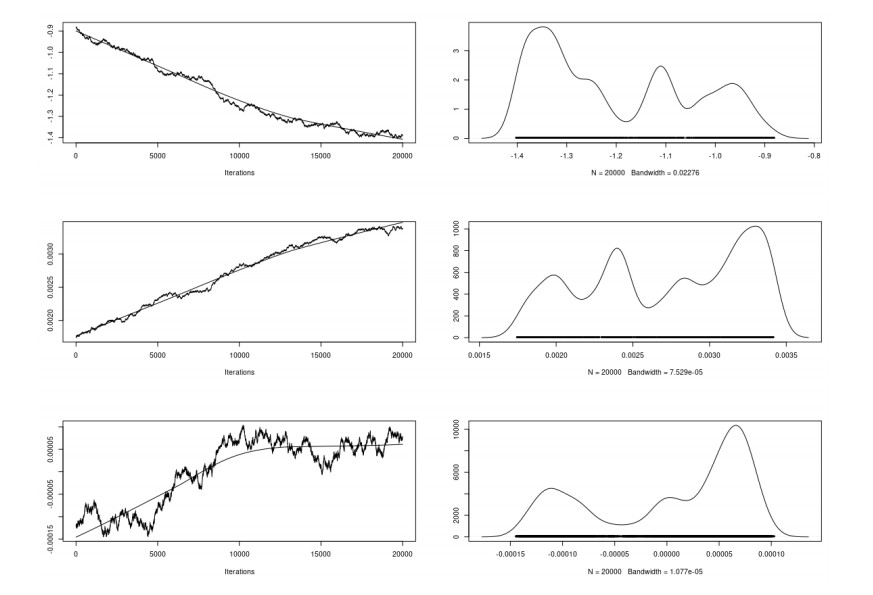
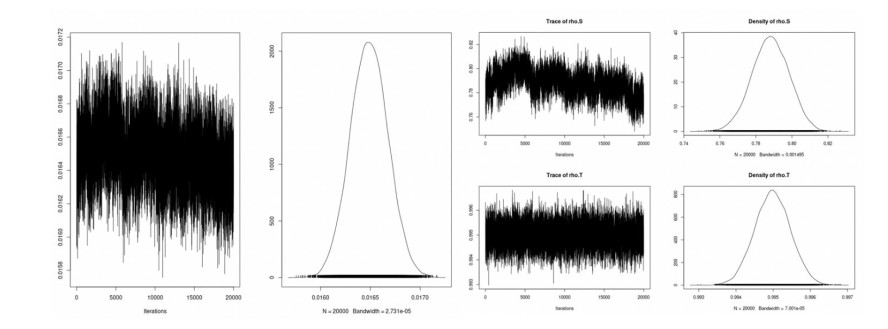
The trace plots (history plots) and the density plots' MCMC convergence of the parameters associated with intercept, day and land area are represented for the model in Figure 6, respectively. Figure 6 shows the monitoring plots and kernel density estimates for the parameters β0, β1, β2 and produced by the CARBayes model Eqs (2) and (3). We ran three independent Gibbs sample chains, and we picked the model chain with the lowest deviance information criterion (DIC). See [41]. The corresponding estimated effective number of parameters (p.d) and its corresponding estimated log of marginal predictive likelihood (LMPL) are also reported. The plots are based on 440, 000 iterations, with 40, 000 first points removed as burning points and a thinning rate of 20 indicative of 40, 000 posterior estimates. Although the convergence is difficult to achieve, as the density plots of the parameters in Figure 6 indicate, it highlights the evolution of the disease as a function of time. No one single distribution function can estimate the parameters of the model. Rather, a mixture of distributions will be a good measure of performance of the variables. The value of the DIC was about 370, 566. The trace plots of the densities (Figure 7) show that the autocorrelation between the successive collected data cannot be ignored. The values of spatial and temporal correlations (rho.S and rho.T) are about 0.7933 and 0.9950.
The proposed model was also evaluated based on the Geweke diagnostic values. The values of the posterior quantities' median scores, the comparisons between the first 2.5% and last 97.5% of the chain quantiles, along with the effective length of the chain are displayed in Table 2. The results in Table 2 reveal that the estimates of the parameters and the autocorrelation are all significant. The spatial dependencies are also all significant. The posterior 95% credible intervals do not contain zero. The exponential of the median for day and land area is 1.0027 and 0.9999, respectively. These values suggest a relative risk increase of cases by 0.27% additional total cases per day, whereas the corresponding relative risk for a one square mile increase in area size is decreased by 0.01%. Thus, we found that the spread of the disease is increasing with time, and decreasing the area size is also related to the spread of the disease.
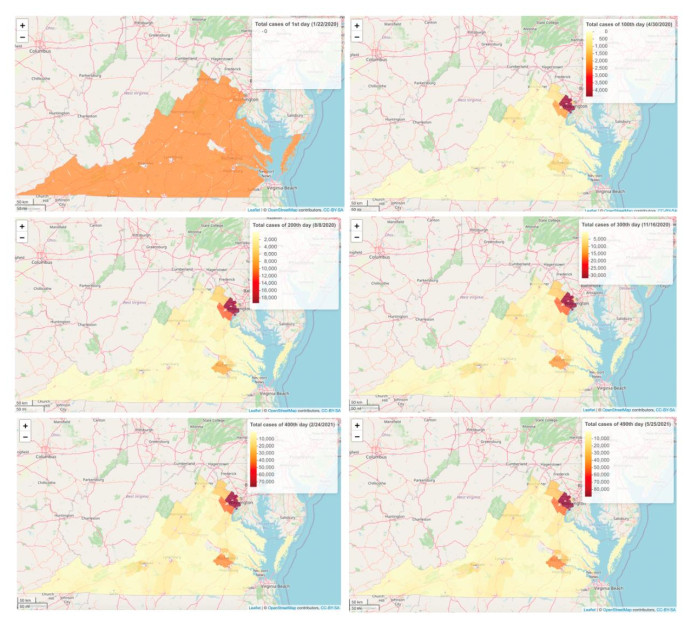
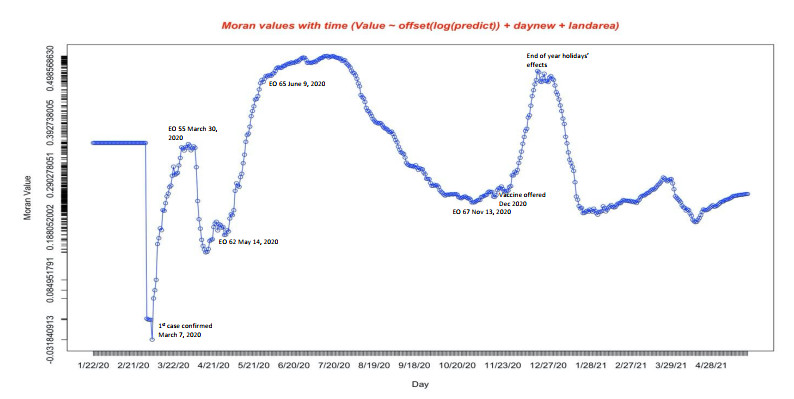
The total cases may vary substantially based on geographical location and time. Based on the structure results using Bar and Wells [42], most sampling locations can be pooled into one cluster (Figure 8). This shows the significance of the spatial correlation and the growth of the total number of cases in the region as a whole. Such results can help to guide healthcare regulations. The results in Figure 8 show that the total cases cannot be discretized and confirm that there is no spatial cluster, and in fact the spread is for the whole region. In Figure 9, the spread is visualized, where the red shows the highest counts of cases at six selected times between January 22, 2020, and May 25, 2021. The scales are changed over the six time points to highlight the counties with high counts of total cases of COVID-19. The pattern can be associated to the Governor's executive orders (EO), as shown in the graph of the Moran values (Figure 10).
The values of Moran's statistic that are significantly below, equal to or above −1(K−1)=−192=−0.01087 imply that there is a negative, zero or positive spatial autocorrelation, respectively [43].
Almost all our computed Moran values are greater than -0.01087 (Figure 10). This shows that there is a positive spatial correlation. There is an inherent relationship between total cases and the predictive variables (day and area). Geographical distance plays a main factor in the COVID-19 cases in short time periods, as mentioned in [44]. We can also see that the Moran values closely connect with the EOs and "end of year effects."
7.
Conclusions
This paper models the progression of the coronavirus (COVID-19) pandemic in 93 counties in the state of Virginia. The daily count data related to the total cases of COVID-19 in these 93 counties are analyzed. The statistical framework of spatio-temporal context with conditional autoregressive (CAR) modeling has been used from the R package CARBayesST for the descriptive and inferential statistical analysis. The Moran statistic values have also been computed to compare spatial properties of the total cases of COVID-19. The results confirm the relationship of the total cases of COVID-19 in space and time. The total cases at a specific time point are impacted by and linked to the Governor's executive orders. We show the connection of the Moran values in state decisions via the plot of the Moran values. With our proposed outlook, we have shown that the Bayesian approach is a solid approach for the modeling of the total cases of COVID-19 in space and time. This is quite novel in the literature of COVID-19 data.
The research literature and applications for spatio-temporal modeling of total cases of COVID-19 are expanding. As new statistical techniques for spatio-temporal modeling develop, the properties of such geostatistical models will be tested and validated. Future work will include conditional and multivariate space-time models that have efficient and tractable computational capabilities.
We have considered two covariates (time and location) in our research. Adding more covariates, such as the number of hospitalizations each day for each county or the intensive or critical care units availability related to COVID-19 in the respective counties, may be useful to understand the disease progression. Also, changing the covariance structure may be considered in future studies.
Acknowledgments
The authors (N.D., H.A.J. and B.D.G.) are grateful for the resources provided by the ODU Advanced Computing Core and grant support from the ODU Research Foundation.
Conflicts of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: