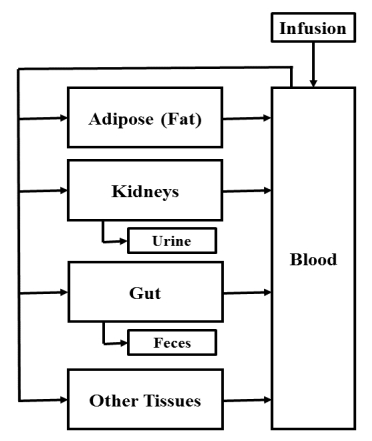
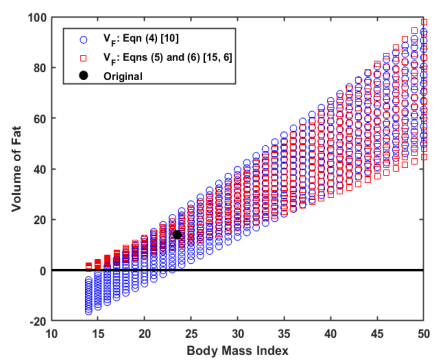
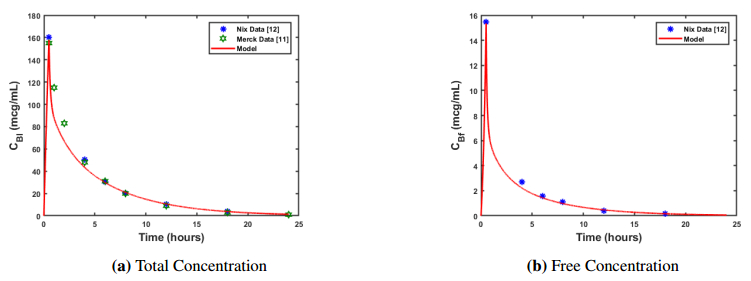
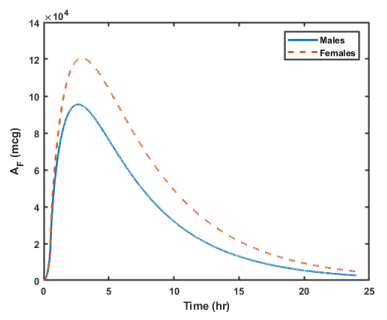
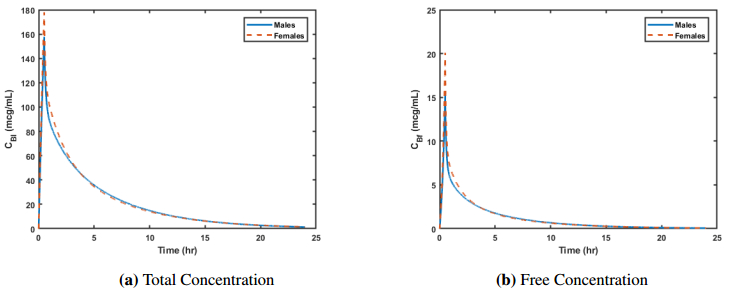
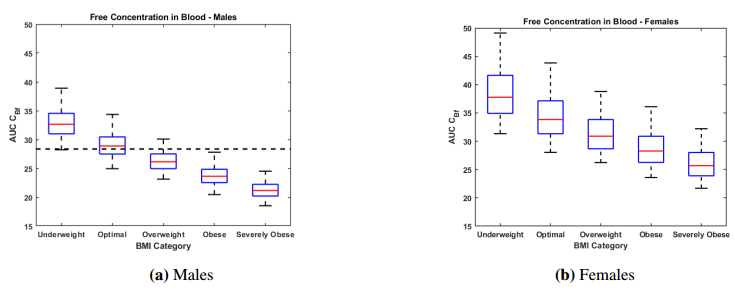
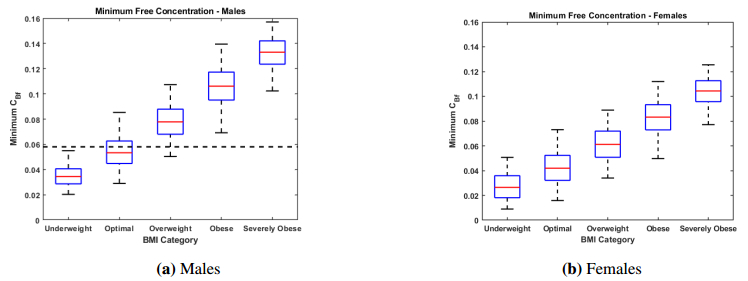
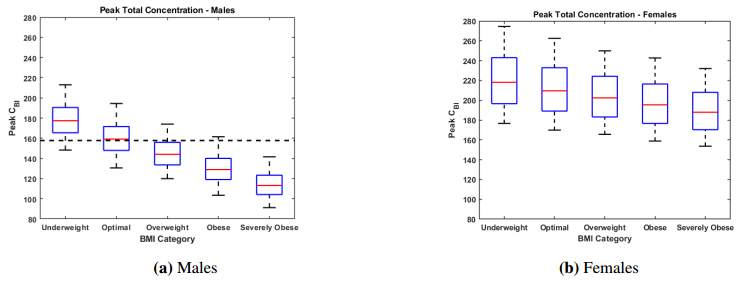
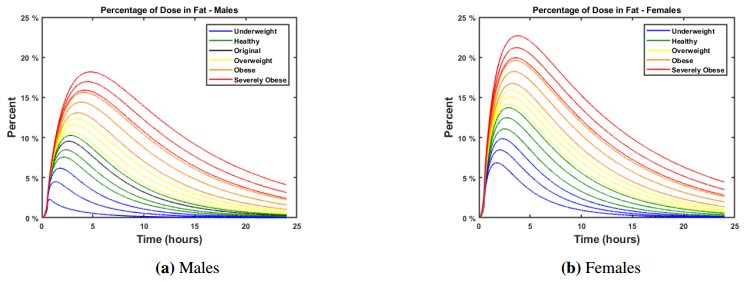
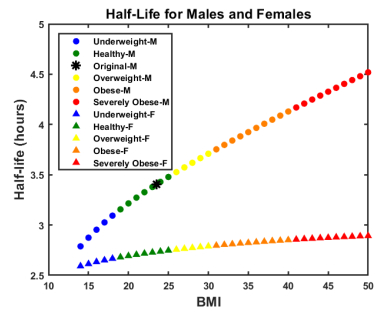
Ertapenem is an antibiotic commonly used to treat a broad spectrum of infections and is part of a broader class of antibiotics called carbapenems. Unlike other carbapenems, ertapenem has a longer half-life and thus only has to be administered once a day. Previously, a physiologically-based pharmacokinetic (PBPK) model was developed to investigate the uptake, distribution, and elimination of ertapenem following a single one gram dose in normal height, normal weight males. Due to the absorption properties of ertapenem, the amount of fat in the body can influence how the drug binds, how quickly the drug passes through the body, and thus how effective the drug might be. Thus, we have revised the model so that it is applicable to males and females of differing body mass index (BMI). Simulations were performed to consider the distribution of the antibiotic in males and females with varying body mass indexes. These results could help to determine if there is a need for altered dosing regimens in the future.
1.
Introduction
The COVID-19 pandemic influenced the way of living of everyone around the globe. A particularly affected group were the people who were living transnational mobile lives. An explanation given by Nasar Meer and Leslie Villegas says that the pandemic "brought the movement of people to a halt as individual states and whole regional blocs have introduced travel restrictions" [1]. Different is the situation of low-skilled migrants—the return "home" for many of them happened not because of personal will and desire, but rather forcefully, due to measures imposed by different states and job loss. One example is how "the Qatari authorities deported Nepali citizens back to Nepal, while the UAE threatened South Asian countries that future labor migration would be jeopardized if they refused to take back their citizens" [2]. "Oftentimes, departing workers lost salaries that were not yet paid or had to leave their belongings behind" [3]. The entry and possibility to stay in different countries were not self-evident either. Under the pandemic circumstances, on one hand, "citizens have been allowed to return to their own country", but on the other, mainly "temporary residents, their family members, international students, and visitors or distant family members of citizens—have been banned from entry. The rationale of these decisions has relied on a balancing act between a health risk, on one hand, and membership and solidarity, on the other" [3].
Uncertainty was felt by all people, yet the ones in highly qualified jobs had secured more privileges, compared to the migrant workers in precarious situations. Returning to their country of origin for many migrant workers happened unexpectedly, having to leave without any preparation. "Seasonal workers from Romania, Poland, and Bulgaria who work in farms and food plants in Germany, Austria, and the UK had to return to their origin countries in March, while in early summer they were asked to return to the destination countries as much-needed agricultural labor [4]. Highly-skilled migrants were also influenced by the pandemic and some of them started reconsidering their possible return plans. The imminent danger of a "job loss" or a "lack of permanent residency" in the host countries led migrants to feel insecure [5]. Thus, both highly qualified mobile specialists, as well as low-skilled migrant workers, found challenges in continuing their regular transnational way of living.
The Bulgarian case of highly qualified mobile Bulgarians living abroad and their potential return intentions are analyzed in this context. On 23 March 2020, only 10 days after the announced state of emergency in Bulgaria, titles of newspapers claimed huge numbers of returns, such as "23 000 only for the last 24 hours", quoting publicly announced data given by prof. Ventzislav Mutafchiiski, the head of the Operation office coordinating the COVID-19 crisis in Bulgaria [6]. A study called "The Grand Return. Covid-19 and remigration to Bulgaria", done in October-November 2020 through an online survey on Facebook and some in-depth interviews, reveals government data of more than 550,000 Bulgarian citizens registered entering Bulgaria by air and land, excluding the entry through the Bulgarian-Greece border, for the period March-May 2020 [7]. The two main reasons for the return given within this survey are "to be close to family and relatives" and "because of job loss". The study also describes the group of highly qualified specialists who have settled abroad as the most difficult to bring back to Bulgaria [7].
2.
Materials and methods
The focus of this article are 11 highly qualified mobile Bulgarians who lived in different countries around the world at the time of the interviews—in Europe (Germany (1), Malta (1), the Netherlands (1), Sweden (1), United Kingdom (2) and beyond (USA (3), Canada (1), Qatar (1)). The time span of their lives abroad was from 4 to 22 years, as some of them lived in another foreign country prior to the one they were currently living in. Two of them have already become citizens of the country of destination and hold dual citizenship. Three are in procedures to acquire citizenship or have permanent residency status. Two live in another European Union member state and say that Bulgarian citizenship is enough for them for the time being in terms of mobility and local status. The age of the respondents ranges from the early 30s up to mid-40s. The common denominator for all these Bulgarians is that they are highly qualified. I use the term "highly qualified" instead of "highly skilled" because the specific characteristic to which I pay attention is they have completed a university degree in their country of origin (Bulgaria), in the destination country, or in another country where they have lived before going to the country where they were currently residing. The respondents for the study have different backgrounds and are currently employed in different sectors (academia, IT, tax, pharmaceutics, library, research and PR). One of the respondents is completing a second MA program after years of working abroad to broaden her expertise in the sphere of education. Three of the respondents are male, and eight are female. Six of the respondents have families and children and five of them are single. Two years after studying, in April-May 2020, one of them is back in Bulgaria, one is back to their previous destination (UK), one is in the process of changing the destination, moving to a previous one (UK) and eight of them are currently (beginning of 2023) living where they were living two years ago.
Researching different aspects of highly qualified migration and mobility of Bulgarian citizens abroad [8,9], the pandemic of COVID-19, and the lockdowns all around the world provoked me to address a number of highly qualified Bulgarians and explore the impact of the pandemic on their professional trajectories and possible intentions to return to Bulgaria and how they feel in the country of destination in regard to the measures taken. This article will focus only on the latter as the first aspect is elaborated earlier [10]. To aspire to deep and meaningful conversations and sincere answers, the people I talked with I knew from before and I have already established trustworthy connections, based on personal or professional encounters. The relationships with my respondents have evolved with different dynamics over time, have started face-to-face and continued online due to the distance in the places of current living. The interviews were conducted online, in most cases as a natural way of continuing the ongoing conversation or reconnecting over time. It was done upon consent mainly through Messenger, WhatsApp and Skype and this is how our normal interactions were happening as well. In some cases, communication could be described as regular, in others, approaching the person was happening over a longer period of time. Besides the online interviews, to a certain extent, in this particular timeframe, I was doing online ethnography, especially through Facebook, if there were posts connected to COVID-19 and how the people handled the situation. However, these posts are rather used as context and are not analyzed intentionally. In terms of the general method, the small research I did within these first days of the COVID-19 situation relates also to what is described by John Postill as remote ethnography with the major difference that in his particular case, remote fieldwork is contextualized "as a safer way of conducting research in conflict-ridden or otherwise hazardous locations" [11]. COVID-19 pandemic and its contagious spread are categorized as dangerous and insecure as well. In elaborating his research regarding the method, Postill steps upon the work of Patty A. Gray, writing that she "argues that there is nothing new about remote anthropology itself. The novelty lies in the fact that anthropologists can now access remote sites in real-time through social media" [11]. This is particularly one of the unique aspects of this particular research—gathering data in an impossible situation (COVID-19 and lockdowns) through the means of the Internet, social media and online technologies. Thus, for the study, I did single or multiple virtual/online interviews with some of the respondents, and with others, also exchanged many messages besides the interviews; with most of them, the communication still continues. The interviews last between one and two hours and are all recorded upon ethical consideration, explanation and personal consent since a limitation could be seen in the fact that the author personally knows all the respondents. This fact might cause blurring the interpretations or anticipating a certain direction. That is why comparing and referring to other studies in the field was necessary in that regard. The recruiting strategy consisted of a short explanation of the research idea and questions aimed at reaching Bulgarian respondents in a variety of destinations within the European Union and beyond. The conducted interviews included highly qualified specialists of other origins and nationalities as well (Moroccan, Turkish, German, etc.), but the focus of this particular article is on the people of Bulgarian origin only. The originality of the article derives from the research design and timing, this is a qualitative study, although small in number, done with a specific group of respondents, highly qualified mobile Bulgarians, in a particular timeframe—immediately after the beginning of strict restrictions in Europe and beyond.
As stated by Russell King and Katie Kuschminder in their introduction article to the "Handbook of Return Migration", "Cassarino's seminal 2004 article remains the key statement on theorizing return migration. It offers a concise overview of how return can be re-thought through the application of several of migration's existing theoretical frames—neoclassical economics, the new economics of labour migration, structuralism, transnationalism and social network theory" [12]. Through all these theoretical lenses, elaborated by Jean-Pierre Cassarino [13], return actually happens due to different personal, social, economic and/or structural reasons. The case in point with return intentions is that in some of the cases (as for the majority of my respondents) it does not. A deeper understanding of the process of return is given by the aspiration-ability framework, proposed by J. Carling [14], where the return is seen as a two-step process, the first one of which, the aspiration, is crucial for the actual happening of the return, that is further explained by King and Kuschminder as not possible "in forced or unplanned migration" [12]. COVID-19 pandemic and the lockdowns because of it could be analyzed as forced and unplanned situations. Additionally, when studying the return intentions of this particular group of Bulgarian citizens, living in different countries throughout Europe and beyond, the core motive to make a move in a certain direction (or stay) within a crisis situation could be seen as the relation of the person to both the country of origin and the country of destination, and to what extent they make the person feel safe and secure. Thus, the social network theory could be applied where maintaining strong linkages (personal, emotional, professional and material) with both their "home" and "host" country—are in focus and "act as conduits for the decision to return." [12]. However, this micro level of secure social ties lies within a larger context, linking how the governments of the countries of destination manage the COVID-19 situation, compared to the country of origin. In this regard, the Bulgarian government took restrictive measures at the beginning to reduce the spread of COVID-19, including "quarantine/blocking, travel bans, social distancing, school closures and closure of public places" [15]. A state of emergency throughout the country was declared by the Bulgarian government on 13 March 2020 and later extended until 13 May 2020. The measures were communicated badly to the public with everyday news reporting the number of deaths, and the number of people who got infected without actual planning on what should be done and measures that could calm people down and show stability.
This situation was additionally strengthened by the fact that politically at the beginning of 2020 Bulgaria was facing a difficult situation. The grumble against the third mandate or more than a decade of rule by the Prime Minister Boyko Borisov and his Citizens for European Development of Bulgaria (GERB) party was rising. The party, although pro-European, is connected with widespread corruption and the fact that the opposition was not strong enough to change the political situation, compared to more emerging nationalist voices, served as a red light and a push factor for many highly qualified Bulgarians.
3.
Results and discussion
In this context, when asked how COVID-19 influenced their decision to continue living in their country of destination and whether some intentions appeared to return to Bulgaria, the quick predominant answer for most of the mobile Bulgarians within the interviewed group was: visits—yes, return—no. However, it should be also noted that return intentions are not a predictor of actual returning. One of the respondents explains that he lives "here" and "there", he has dual citizenship and spends the year between Bulgaria and Sweden. Other two of the respondents think and have intentions to visit Bulgaria, temporarily, while they are not expected to work from their offices, they see it as an opportunity to come to Bulgaria and work remotely for some period from here. In one of the cases, the return is seen as a temporary option with the argument to spend more time with the family during the pandemic, exactly because of having the possibility to work remotely. The respondent that considers moving for a period of time explains: "I am now considering exactly this possibility—whether go back to Bulgaria just for two months, I work from home now, we won't go back to the office by the end of September and I do not see any need to stay in London. I do not see the point of generally going back to Bulgaria, but for some time, to be together with my family, yes. Especially with this situation now, I would like to spend more time with my parents and grandparents and to communicate more with them. I could work from home and be in Bulgaria and have some interviews with my relatives as well, for my personal projects. I do not actually know what to do, whether to go or not. At the same time, I am afraid of flying—whether I could catch the virus and is it good for my family to go back, because I do not want to put my family at risk and this stops me for the time being".
There is more uncertainty in the case of highly qualified respondents who are in the early stage of their professional development. The respondent who is studying for a MA and approaching the end of the student visa explains "My internship is finishing in September and after that, I do not know what will happen and whether I could continue working for this company or I have to find another job".
None of the respondents have lost their jobs because of the pandemic and most of them feel safer and more secure where they are currently living. Two of the respondents were considering moving internationally, which was not an option at the time of the interviews due to the closure of the borders, and the general economic impact of COVID-19 on the labor market. Thus, COVID-19 is seen by several respondents as a limitation to their professional development to move internationally. A respondent who was considering professional development in academia, applying for a PhD position in Canada, and having passed all selection rounds received a negative answer because the new academic year was currently closed for international students due to the COVID-19 situation. A study by Lucia Nalbandian and Anna Triandafyllidou [16] explains that, workwise, Canada temporarily stopped processing work permit or permanent residency applications from March until the end of June 2020.
Another respondent who was considering moving internationally from Europe to the USA explains: "COVID-19 is limiting me because I cannot apply to all the places I wanted to. My initial plan was to try to find something new in the USA, but at the moment the economy in the States is going down along with the fact that they are not that open to foreigners. I would like to live in a bigger city. My manager said that I could continue working in the same institute, for the administration office, but this is not creative enough for me and this is not an option".
It could be concluded that for the highly qualified in search of further professional development, the pandemic situation served as a current stopper in regard to postponed job interviews or no possibility to go globally, but cannot be considered a trigger to move back to Bulgaria.
A study by Eugenia Markova and Russell King regarding the strong effects of the pandemic, particularly in the UK, explains: "On the one hand, the pandemic resulted in unemployment and loss of income for many EU migrants engaged in sectors hit hard by the new restrictions on working, such as agriculture and factory work. On the other hand, bans and strict controls on international travel restricted their ability to return home or lead mobile, transnational lives" [17]. Although conducted before COVID-19 and with a focus on migration intention because of Brexit, this research is of interest for my article, because it lays the grounds for comparison of the intentions to return as researching Bulgarian emigrants in the UK through a combined quantitative and qualitative research. The authors assume "that those who are doing well in the UK labor market, advancing their economic well-being and careers to a level that would not have been possible had they stayed in Bulgaria, would be less likely to want to return to their home country" [17]. From their quantitative online survey with 360 respondents, Markova and King find out that the following key factors are affecting the return: "(1) length of time in the UK (positively correlated with intention to stay); (2) skill level (the higher skilled being more likely to stay); and (3) perception of discrimination (those thinking they are discriminated through being Bulgarian are more likely to express an intention to leave the UK) [17]. The authors conclude that some of their respondents were pushed to return by a combination of Brexit and COVID-19, however, they found out that these are not the main elements of their return decision. More determinant are the pull factors of family obligations, nostalgia and quality of life considerations, including friendships, cost of living, food and the weather [17].
Thus, the findings of the current research, with a particular focus on the highly qualified Bulgarians living in different countries, complement and confirm the ones of Markova and King [17]. The mobile Bulgarians who live abroad for longer periods, who have settled, have prestigious jobs and families and do not experience personal discrimination, rather prefer to stay and do not have particular return intentions. Another study done in 2021 also reinforces the conclusion that: "the tendency to return is high among Bulgarians abroad, however, higher for low-skilled than for high-skilled Bulgarian migrants" [18]. To illustrate the discussion, I have synthesized three figures explaining three models of return intentions at the beginning of COVID-19 pandemic among highly qualified mobile Bulgarians living abroad: the mobile international student, the mobile dual citizen and the mobile European citizen.
● The mobile international student: I prefer to stay here but I have to leave soon because my visa ends and there are not many opportunities currently.
The figure of the mobile international student is represented by a young woman in her early 30s who arrived in the USA in August 2019 with a Fulbright scholarship to acquire her second MA in Education, at Teachers' College in New York. Before that, she lived in Oxford (UK) and has been living outside Bulgaria since 2014. "I came here to study, the first two months were very hard, gaps between my expectations and my aspirations, purely academically what was on offer, what was happening, where I was". She describes herself in an uncertain situation due to the fact that most of her friends and colleagues left the USA, but for her, returning to Bulgaria was not an option. She explains: "I had 2–3 days where I was thinking should I stay or should I go, I was thinking which is the better decision for me, and I decided to stay". A shock for her was when she had to change her dormitory because of the spread of the virus and how it was announced: "All the communication started over our spring break, I had mild symptoms of the virus, here they don't test you, besides you're alone, in a new place, you have to orient yourself, take care of yourself, this stress, because on Thursday they tell you how next Friday you have to move out, and a lot of friends left, in general moving was a big shock. And I still can't believe it happened just over a month ago".
Loneliness and uncertainty are the two predominant feelings described: "I'm trying to look ahead, but this looking ahead is very difficult, I'm looking for a job to stay here, and I still want to do an internship in the summer, which is complicated because a lot of institutions have canceled them. I'm also looking to be more practical because I'm looking to wrap things up. I'm not allowed to stay here after the end of August 2020. At the moment I don't know, I have bigger plans for my dissertation, but the simple things here are very complicated, I'm applying for PhDs, and I've been accepted to a place but without funding".
When asked about a possible return to Bulgaria, the answer is firm and negative: "Oh my God, how am I going to get back to Bulgaria, I haven't lived in Bulgaria since 2014, I might have had two stays of a month, a month and a half between things. I'm looking for a job because of the visa, as a Fulbright fellow I cannot think about anything long-term until I've been 2 years in Bulgaria". Partially this negative opinion comes from the news: "Everything I read from Bulgaria is extremely stressful. I am aware that I am saying this from the position of an absolutely privileged person thousands of miles away and it is extremely worrying that this is happening. It would be extremely difficult to enclose myself in a bubble, my family is outside Sofia and I'm aware of the realities outside Sofia and it's not going to be bearable for me this time, I think a lot of people's bubbles in Sofia are going to burst sooner or later too, and I can't bring myself to do that right now, I don't think I'm at the stage to accept that challenge in Bulgaria, and I don't know". However difficult the situation is, coping with COVID-19 in Bulgaria is not seen as an option.
I summed up this figure as the one of preferred stay in the long run but with no choice and urge to leave soon because of a visa that ends, besides the fact that there are not many opportunities currently because COVID-19 froze the future prospects of highly qualified mobile Bulgarians also in regard to developing professionally where they wanted to stay. This is a case where the stay is wanted, but not possible.
● The mobile dual citizen: I live here and there, I want to go there now, but I am stuck here.
The second figure is represented by a male artist in his mid-40s who lives and works in-between Bulgaria and Sweden for the last 15 years. The pandemic finds him in Sweden, just before he was supposed to go on a trip to India. He feels stuck, "the situation is where it gets you, you remain there", and at the time of the interview, he prefers to go back to Bulgaria, where he predominantly lived for the last several years. He has dual citizenship in both Bulgaria and Sweden.
"I'm lately half here, half there. I'm mostly in Bulgaria now, but I only work outside. In Bulgaria, I find it very difficult aesthetically. It's like there's no environment, the environment, in general, doesn't energize me, it stops me, it tightens me up, it's better here (Sweden) to work, but maybe I'll move to new places". When it comes to work projects, he explains that for him it is better in Sweden: "Here, the idea unfolds in full. In Bulgaria, it's all very difficult. They encourage you and trust you to do what you do, but there are no resources. Bulgaria has an extremely low level of fulfilling things".
Regarding the COVID-19 situation in Sweden, he feels rather relaxed: "there are no measures, here it is all personal responsibility. The other extreme in a way. You can't have more than 50 people in one place. There are no flights. What distances you are reflected in the expressions in people's eyes. They feel uncomfortable if you approach them in the street. But when you walk in the streets, children are playing". He is currently in Stockholm, but before that, he was living in the countryside, in his friend's house who accommodated him there. "I wanted to go to India now for 4–5 weeks, but couldn't. Now I want to go back to Bulgaria, but the flights are either expensive or are 35 hours long. It is good that these people accepted me to live with them. Strange situation. Professionally, it is lucky for me, that's what I had in spring as projects are going on and keep happening. What's supposed to be happening in the fall, and I am not sure how we're going to proceed, and a show in Tallinn where we were supposed to start rehearsals in mid-May, and there's no word on it. A friend called to do an operetta in Varna, but now you can't go anywhere, so things are a bit forced".
This is a case where the stay is forced and leaving is currently not possible. This is the only respondent from the group who during the summer of 2020 actually returned to Bulgaria. In this particular case, the return decision was thought of and considered before the COVID-19 situation and was catalyzed by it. However, immediately after the mobility measures in Europe were taken down, commuting in-between Bulgaria and Sweden by this respondent started again and continues.
● The mobile European citizen: I am staying here, Bulgaria was not an option before, and neither is now.
The third figure is represented by a male in his early 40s who has been living in the Netherlands since 2009. He teaches European studies in Maastricht, feels well as a European citizen, and with his tenure position at the university, feels well-established and recognized. He has been married to a Dutch citizen since 2018 and can become a Dutch citizen himself. However, this is not a priority for him. Being an associate professor in European studies and international relations and having a permanent position in the academic circles is a milestone for him. Before that, he lived in the UK for more than 3 years, where he obtained his PhD. When making the move from the United Kingdom to the Netherlands in 2008, he says that Bulgaria was not an option then, and it is not an option now, especially in the academic sphere. The international professional sphere makes him very happy and teaching is fulfilling. The COVID-19 situation did not change his negative intentions of return, as he felt secure and safe for the following reasons: "From the years I've lived here, I've developed a certain trust in the institutions here, and for me, that's like a guaranteed line that I can compare with societies that I have lived in and I know that the institutions here and the people, the majority of them, treat each other with trust and discipline. In that sense, the measures that are applied here and the way the whole society reacts, I am rather impressed. Also, rather than putting me in a panic because there was a peak, there was no big panic, and I did not watch the news in Dutch either, which might help me, but I live with someone who is Dutch and has a Dutch family, I have Dutch friends, and I felt by them that there was no panic". What caused stress in his situation was transferring his teaching online: "In the very beginning, there was a small moment of stress when we realized we had to go completely online and literally had to do so in one weekend. I had to learn how Zoom works, I even paid for it in the beginning with my own money and made my first account so I could have a two-hour session instead of the 45 min free version. However, the session consisted of constant dialogue with the program director of the master's program, who immediately contacted all the course coordinators, because the crisis caught me right in the last third of a course that I was coordinating, i.e. I developed this course and I am the main teacher in it. In one weekend, I had to transfer everything online, and had to contact the students". A higher level of stress was to combine his work and parental activities: "The hardest part of combining the two—preparing for current research and having a child in the house—is hard. Now it's OK to teach online, I'm glad I learned, which is a positive. I decided to play an instrument every day to get better and write music, which I started doing. I learned other skills as well. As a temperament, I like to stay at my place, so it was not a big transition for me to stay home". The bottom line to handling the COVID-19 situation peacefully in his opinion in the Netherlands was how measures were communicated, setting deadlines and what should be achieved by when and how people should react and support the process. This provided clarity from one side and affected people indirectly because they were trying to achieve it. With this particular figure, the model of stability and security is shown, where the stay is wanted and provides all that is needed.
4.
Conclusions
This virtual ethnographic study, exploring the motivations for a potential return and how the Bulgarians abroad observe and feel the COVID-19 situation in their current country of destination, leads to several interpretations, which are complemented and reinforced by other studies. It could be concluded that most of the highly qualified mobile Bulgarian citizens who settled abroad, have prestigious professions and feel secure regarding measures taken by the national and local governments where they live, have no intention to return to Bulgaria. In particular cases, the ones who can work remotely consider visits, shorter or longer, depending on their working situation. However, it should be noted that intentions are not preconditioning for actual return. In all cases, as mobility is a primary feature of the transnational mobile way of living, it can be concluded that the closure of borders suspended already initiated plans, connected to international travel, for some of the interviewees. These were mobilities connected with either professional or educational development. The COVID-19 situation changed the labor conditions and labor market, not only for the low-skilled professions but for the high-skilled ones as well. In regard to education, some international PhD programs were closed for a certain period for international students, as is the example of one of my respondents. COVID-19 prevented plans of a transnational career move for another interviewee. The three figures presented aim to illustrate the complexity and uncertainty in return intentions and mobility possibilities among the highly qualified Bulgarians, synthesizing the models when a stay is wanted, but not possible in the long term perspective; when leave is wanted, but not currently possible; as well as when the stay is wanted and possible.
Acknowledgments
No funding is received by the author for the presented study. The author wants to express her gratitude to the two reviewers for their valuable comments and recommendations.
Conflict of interest
The author declares no conflicts of interest in this paper.













 DownLoad:
DownLoad: