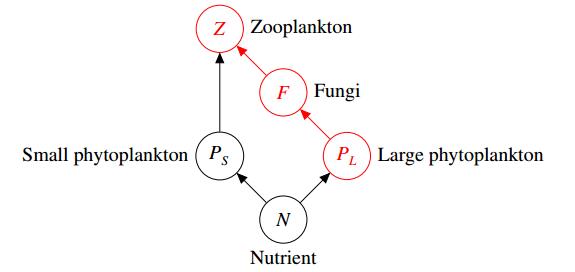
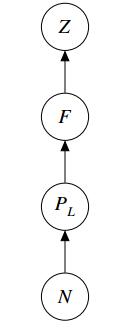
It is recently known that parasites provide a better picture of an ecosystem, gaining attention in theoretical ecology. Parasitic fungi belong to a food chain between zooplankton and inedible phytoplankton, called mycoloop. We consider a chemostat model that incorporates a single mycoloop, and analyze the limiting behavior of solutions, adding to previous work on steady-state analysis. By way of persistence theory, we establish that a given species survives depending on the food web configuration and the nutrient level. Moreover, we conclude that the model predicts coexistence under bounded nutrient levels.
1.
Introduction
Throughout this article, let Cm×n stand for the set of all m×n matrices over the field of complex numbers; A∗ stands for the conjugate transpose of A∈Cm×n; r(A) stands for the rank of A∈Cm×n; Im stands for the identity matrix of order m and [A,B] stands for a columnwise partitioned matrix consisting of two submatrices A and B. We introduce the concept of generalized inverses of a matrix. For an A∈Cm×n, the Moore–Penrose generalized inverse of A is defined to be the unique matrix X∈Cn×m that satisfies the four Penrose equations:
A matrix X∈Cn×m is called an {i,…,j}-generalized inverse of A∈Cm×n, denoted by A(i,…,j), if it satisfies the ith, …,jth matrix equations in (1.1). Notice that solutions of each of the four equations in (1.1) are not necessarily unique. Hence, the set of all {i,…,j}-generalized inverses of the matrix A is usually denoted by the symbol {A(i,…,j)}. There are altogether 15 sorts of {i,…,j}-generalized inverses of A by the above definition, but the following
are usually called the eight commonly-used types of generalized inverses of A in the literature. Admittedly, the Moore–Penrose generalized inverse of a matrix is a natural extension of the standard inverse of an invertible matrix, which has become one of the basic and classic concepts in matrix theory and its applications due to its usefulness in dealing with singular matrices. For more basic results and facts concerning generalized inverses of matrices and their properties, we refer the reader to the three references [1,2,3].
Let us consider the following two general matrix equalities:
where it is assumed that A1, A2, …, Ak+1, B1, B2, …, Bk, C1, C2, …, Ck and A and D are matrices of appropriate sizes. Clearly, (1.3) and (1.4) are generalizations of various concrete matrix equalities that involve mixed operations of ordinary sums and products of several matrices and their generalized inverses. For the sake of exposition, let us take the following two well-known examples:
which are called the parallel sum of matrices and the reverse-order law for generalized inverses of multiple matrix products, respectively. As demonstrated in Lemma 2.2 below, generalized inverses of a matrix can be written as certain linear and bilinear matrix expressions involving two arbitrary matrices. Hence, the two matrix equalities in (1.3) and (1.4) can be equivalently represented as two kinds of linear and nonlinear matrix equations involving multiple arbitrary matrices (variable matrices).
As we know, in algebra theory, or a given algebraic expression or equality that involves variable entries, algebraists can propose many kinds of questions relevant to its properties and performances, but of particular interest regarding the expression or equality is to determine explicit conditions under which the expression is invariant with respect to the variable entries or the equality holds for some/all values of the variable entries included. In view of this consideration, it is natural to ask the questions related to determining necessary and sufficient conditions for the matrix equalities in the context of (1.3) and (1.4) to hold respectively for some/all of the generalized inverses of the matrices in them. In fact, this sort of research problems were proposed and investigated by lots of authors focused generalized inverses of matrices and its various applications [4,5,6,7]. Prompted by this kind of work, the present author and his collaborators considered a selection of linear and nonlinear matrix expressions or matrix equalities that involve one or more arbitrary matrices, established a fundamental theory related to the invariance properties of different types of linear and nonlinear matrix expressions and presented their essential utilizations in the characterizations of many kinds of matrix equalities that involve algebraic operations of generalized inverses of matrices [8,9,10,11,12,13,14]. Particularly in two recent papers [15,16], the present author considered (1.4) for {1}-generalized inverses of matrices of B1, B2, …, Bk with k=2,3, deriving different types of identifying conditions under which the given matrix equalities always hold with respect to all possible {1}-generalized inverses of the given matrices by using a diversity of precise rank equalities associated with certain specified block matrices that are constructed from the given matrices in (1.4). Obviously, characterization problems of (1.3) and (1.4) involve lots of difficult and divisive issues because they are quite inclusive for various possible choices of {i,…,j}-generalized inverses of the given matrices, thus, there exist many concrete cases of (1.3) and (1.4) that we need to give further deep explorations.
As an ongoing study of the above algebraic equality characterization problems on matrices, the main objective of this article is to consider several cases of the matrix equalities in (1.3) and (1.4) for the mixed combinations of {1}- and {1,2}-generalized inverses of matrices with k=2,3, and to give identifying conditions under which these algebraic matrix equalities always hold by using a series of ordinary but skillful calculations of ranks of matrices. The rest of this paper is organized in five sections. In Section 2, the present author introduces a sequence of well-known or existing basic formulas, facts and results related to ranks, ranges and generalized inverses of matrices that we shall utilize in the derivations of our main results regarding (1.3) and (1.4). In Section 3, the author derives necessary and sufficient conditions for the matrix equalities in (1.3) to hold with mixed combinations of {1}- and {1,2}-generalized inverses of matrices for k=2,3 by means of the elementary but the powerful block matrix representation method (BMRM) and the matrix rank method (MRM). In Section 4, the author gives identifying conditions for the matrix equalities in (1.4) to always hold with mixed combinations of {1}- and {1,2}-generalized inverses of matrices for k=2,3. In Section 5, the author presents a variety of parallel conclusions related to several kinds of algebraic matrix equalities that involve different mixed algebraic operations of given matrices and their weighted {1}- and {1,2}-generalized inverses. An application is presented in Section 6 for a matrix equality involving generalized inverses of a 2×2 block matrix. Concluding remarks are given in Section 7.
2.
Some preliminaries
In this section, the author presents some well-known or existing results and conclusions regarding a two-sided linear matrix equation, the general expressions of generalized inverses of a matrix, as well as some equalities and inequalities associated with ranks of block matrices, which we shall adopt as fundamental and feasible matrix analysis tools in the examinations of the algebraic matrix equality problems described in Section 1.
Lemma 2.1 ([17]). Let
be a two-sided linear matrix equation, where A∈Cm×n, B∈Cp×q and C∈Cm×q are given. Then, the following four statements are equivalent:
(a) Equation (2.1) is solvable for X.
(b) R(A)⊇R(C) and R(B∗)⊇R(C∗).
(c) r[A,C]=r(A) and r[BC]=r(B).
(d) AA†CB†B=C.
In this case, the general solution of (2.1) can be written in the following parametric expression
where FA=In−A†A, EB=Ip−BB† and U,V∈Cn×p are arbitrary matrices. Particularly, (2.1) holds for all matrices X∈Cn×p if and only if
Lemma 2.2 ([17]). Let A∈Cm×n. Then, the general expressions of A(1) and A(1,2) can be written as
where EA=Im−AA†, FA=In−A†A and U,V∈Cn×m are arbitrary.
Recall a simple fact in linear algebra that a matrix is null if and only if its rank is zero. As a direct consequence of this fact, we see that two matrices A and B of the same size are equal if and only if the matrix rank equality r(A−B)=0 holds. In other words, these obvious two equivalent statements connect the matrix equality A=B alternatively to the matrix rank equality r(A−B)=0. In view of this assertion, we can see that if certain nontrivial analytical formulas for calculating the rank of A−B are obtained, then we can directly employ them to reveal essential connections between the two matrices. Of course, the usefulness of this proposed methodology is based on the fact that we can precisely calculate ranks of matrix expressions by using elementary operations of matrices. As a matter of fact, algebraists realized that numerous matrix rank formulas can be established in reasonable ways, while these matrix rank formulas have been recognized as powerful tools to construct, characterize and understand hidden structures and properties of various algebraic matrix expressions and matrix equalities.
Lemma 2.3 ([18]). Let A∈Cm×n,B∈Cm×k and C∈Cl×n. Then,
Lemma 2.4 ([19,20]). Let A∈Cm×n, B∈Cm×k, C∈Cl×n and D∈Cl×k be given. Then,
Therefore,
3.
Additive matrix equalities that involve two generalized inverses
The cases of the matrix equalities in (1.3) for k=2 and {1}- and {1,2}-generalized inverses of B1 and B2 are given by
where A1∈Cm×p1, B1∈Cq1×p1, C1∈Cq1×n, A2∈Cm×p2, B2∈Cq2×p2, C2∈Cq2×n and D∈Cm×n. In this section, we first give conditions under which the four matrix equalities in (3.1)–(3.4) always hold for all {1}- and {1,2}-generalized inverses of B1 and B2.
Theorem 3.1. Let A1, B1, C1, A2, B2, C2 and D be as given in (3.1). Then, the following three statements are equivalent:
(a) Equation (3.1) holds for all B(1)1 and B(1)2.
(b) A1B(1)1C1+A2B(1)2C2 is invariant with respect to all B(1)1 and B(1)2 and A1B†1C1+A2B†2C2=D holds.
(c) Any one of the following 9 conditions holds:
(i) A1=0, A2=0 and D=0.
(ii) A1=0, C2=0 and D=0.
(iii) C1=0, A2=0 and D=0.
(iv) C1=0, C2=0 and D=0.
(v) A1=0 and r[B2C2A2D]=r(B2).
(vi) C1=0 and r[B2C2A2D]=r(B2).
(vii) A2=0 and r[B1C1A1D]=r(B1).
(viii) C2=0 and r[B1C1A1D]=r(B1).
(ix) r[B10C10B2C2A1A2D]=r(B1)+r(B2).
Proof. By (2.10), we first obtain that (2.10) holds for all generalized inverses B(1)1 if and only if
Subsequently, we see from (2.10) that the first equality in (3.5) holds for all generalized inverses B(1)2 if and only if
as required for (i), (ii) and (v) in (c). Meanwhile by (2.10), the second equality in (3.5) holds for all generalized inverses B(1)2 if and only if
as required for (iii), (iv) and (vi) in (c). Further, by (2.8),
Hence, the third equality in (3.5) holds for all generalized inverses B(1)2 if and only if
Also by (2.6) and (2.7), we see that
Combining the rank inequalities with the first two equalities in (3.9) yields (vii) and (viii) in (c). The third rank inequality in (3.9) is just (ix) in (c).
It can be seen from the nine conditions in Theorem 3.1(c) that if the matrices Ai≠0 and Ci≠0 in (3.1) for i=1,2, then (3.1) holds for all B(1)1 and B(1)2 if and only if Condition (ix) in Theorem 3.1(c) holds. This special fact brings convenience of using the assertions in Theorem 3.1.
By a similar approach, we can show that the following two theorems hold, and we omit the details of their proofs.
Theorem 3.2. Let A1, B1, C1, A2, B2, C2 and D be as given in (3.3). Then, the following three statements are equivalent:
(a) Equation (3.2) holds for all B(1,2)1 and B(1)2.
(b) A1B(1,2)1C1+A2B(1)2C2 is invariant with respect to all B(1,2)1 and B(1)2 and A1B†1C1+A2B†2C2=D holds.
(c) Any one of the following 12 conditions holds:
(i) A1=0, A2=0 and D=0.
(ii) A1=0, C2=0 and D=0.
(iii) B1=0, A2=0 and D=0.
(iv) B1=0, C2=0 and D=0.
(v) C1=0, A2=0 and D=0.
(vi) C1=0, C2=0 and D=0.
(vii) A1=0 and r[B2C2A2D]=r(B2).
(viii) B1=0 and r[B2C2A2D]=r(B2).
(ix) C1=0 and r[B2C2A2D]=r(B2).
(x) A2=0 and r[B1C1A1D]=r(B1).
(xi) C2=0 and r[B1C1A1D]=r(B1).
(xii) r[B10C10B2C2A1A2D]=r(B1)+r(B2).
In particular, assume that the matrices Ai≠0 and Ci≠0 in (3.4) for i=1,2. Then (3.3) holds for all B(1,2)1 and B(1)2 if and only if Condition (xii) in (c) holds.
Theorem 3.3. Let A1, B1, C1, A2, B2, C2 and D be as given in (3.4). Then, the following three statements are equivalent:
(a) Equation (3.4) holds for all B(1,2)1 and B(1,2)2.
(b) A1B(1,2)1C1+A2B(1,2)2C2 is invariant with respect to all B(1,2)1 and B(1,2)2 and A1B†1C1+A2B†2C2=D holds.
(c) Any one of the following 16 conditions holds:
(i) A1=0, A2=0 and D=0.
(ii) A1=0, B2=0 and D=0.
(iii) A1=0, C2=0 and D=0.
(vi) B1=0, A2=0 and D=0.
(v) B1=0, B2=0 and D=0.
(vi) B1=0, C2=0 and D=0.
(vii) C1=0, A2=0 and D=0.
(viii) C1=0, B2=0 and D=0.
(ix) C1=0, C2=0 and D=0.
(x) A1=0 and r[B2C2A2D]=r(B2).
(xi) B1=0 and r[B2C2A2D]=r(B2).
(xii) C1=0 and r[B2C2A2D]=r(B2).
(xiii) A2=0 and r[B1C1A1D]=r(B1).
(xiv) B2=0 and r[B1C1A1D]=r(B1).
(xv) C2=0 and r[B1C1A1D]=r(B1).
(xvi) r[B10C10B2C2A1A2D]=r(B1)+r(B2).
In particular, assume that the matrices Ai≠0 and Ci≠0 in (3.4) for i=1,2. Then (3.4) holds for all B(1,2)1 and B(1,2)2 if and only if Condition (xvi) in (c) holds.
The case of (1.3) for k=3 is given by
where A1∈Cm×p1, B1∈Cq1×p1, C1∈Cq1×n, A2∈Cm×p2, B2∈Cq2×p2, C2∈Cq2×n, A3∈Cm×p3, B3∈Cq3×p3, C3∈Cq3×n and D∈Cm×n. Clearly, there are eight possible expressions in (3.10) for {1}- and {1,2}-generalized inverses of B1, B2 and B3. In the remaining part of this section, we only give two groups of conditions under which (3.10) always holds for all {1}- and {1,2}-generalized inverses of B1, B2 and B3. It is easy to see that, if any one Ai and Ci in (3.10) is zero for i=1,2,3, (3.10) reduces to two-term cases on the left-hand side. So, we assume that Ai≠0 and Ci≠0 in (3.10) for i=1,2,3 without loss of generality.
Theorem 3.4. Let Ai, Bi, Ci and D be as given in (3.10) and assume that Ai≠0 and Ci≠0 for i=1,2,3. Then, the following three statements are equivalent:
(a) A1B(1)1C1+A2B(1)2C2+A3B(1)3C3=D holds for all B(1)1, B(1)2 and B(1)3.
(b) A1B(1)1C1+A2B(1)2C2+A3B(1)3C3 is invariant with respect to all B(1)1, B(1)2 and B(1)3 and A1B†1C1+A2B†2C2+A3B†3C3=D holds.
(c) r[B100C10B20C200B3C3A1A2A3D]=r(B1)+r(B2)+r(B3).
Proof. Rewriting A1B(1)1C1+A2B(1)2C2+A3B(1)3C3=D as A1B(1)1C1+A2B(1)2C2=D−A3B(1)3C3 and applying Theorem 3.1(c), we obtain that it holds for all B(1)1 and B(1)2 if and only if r[B10C10B2C2A1A2D−A3B(1)3C3]=r(B1)+r(B2). Consequently, applying (2.8) and (2.10) to the matrix equality yields (c).
By a similar approach, we can show the following result, so we omit the details of its proof.
Theorem 3.5. Let Ai, Bi, Ci and D be as given in (3.10) and assume that Ai≠0, Bi≠0 and Ci≠0 for i=1,2,3. Then, the following three statements are equivalent:
(a) A1B(1,2)1C1+A2B(1,2)2C2+A3B(1,2)3C3=D holds for all B(1,2)1, B(1,2)2 and B(1,2)3.
(b) A1B(1,2)1C1+A2B(1,2)2C2+A3B(1,2)3C3 is invariant with respect to all B(1,2)1, B(1,2)2 and B(1,2)3 and A1B†1C1+A2B†2C2+A3B†3C3=D holds.
(c) r[B100C10B20C200B3C3A1A2A3D]=r(B1)+r(B2)+r(B3).
By induction, we are able to derive the following result.
Theorem 3.6. Assume that Ai≠0, Bi≠0 and Ci≠0 in (1.3) are for i=1,2,…,k. Then, (1.3) holds for all mixed combinations of {1}- and {1,2}-generalized inverses of B1,B2,…,Bk if and only if
4.
Matrix equalities that involve mixed products of two generalized inverses
The cases of the matrix equalities in (1.4) for k=2 and {1}- and {1,2}-generalized inverses of B1 and B2 are given by
where A1∈Cm1×m2, B1∈Cm3×m2, A2∈Cm3×m4, B2∈Cm5×m4, A3∈Cm5×m6 and A∈Cm1×m6. Particularly, the case of (4.1) for {1}-generalized inverses of B1 and B2 was studied in [11,15], and the following results were obtained.
Theorem 4.1 ([11,15]). Let A1, B1, A2, B2, A3 and A be as given in (4.1). Then, the following three statements are equivalent:
(a) Equation (4.1) holds for all B(1)1 and B(1)2.
(b) A1B(1)1A2B(1)2A3 is invariant with respect to B(1)1 and B(1)2 and A1B†1A2B†2A3=A holds.
(c) Any one of the following 6 conditions holds:
(i) A=0 and A1=0.
(ii) A=0 and A2=0.
(iii) A=0 and A3=0.
(iv) A=0 and r[0A1A2B1]=r(B1).
(v) A=0 and r[0A2A3B2]=r(B2).
(vi) r[−A0A10A2B1A3B20]=r[A2B1B20]=r(B1)+r(B2).
In what follows, we give the results on the other three cases for {1}- and {1,2}-generalized inverses of B1 and B2 in (4.1).
Theorem 4.2. Let A1, B1, A2, B2, A3 and A be as given in (4.2). Then, the following three statements are equivalent:
(a) Equation (4.2) holds for all B(1)1 and B(1,2)2.
(b) A1B(1)1A2B(1,2)2A3 is invariant with respect to all B(1)1 and B(1,2)2 and A1B†1A2B†2A3=A holds.
(c) Any one of the following 7 conditions holds:
(i) A=0 and A1=0.
(ii) A=0 and A2=0.
(iii) A=0 and B2=0.
(iv) A=0 and A3=0.
(v) A=0 and r[0A1A2B1]=r(B1).
(vi) A=0 and r[0A2A3B2]=r(B2).
(vii) r[−A0A10A2B1A3B20]=r[A2B1B20]=r(B1)+r(B2).
Proof. The equivalence of (a) and (b) follows from the definition of the Moore–Penrose inverse of a matrix and its uniqueness.
By Lemma 4.1(c), we first see that the product A1B(1)1A2B(1,2)2A3=A holds for all generalized inverses B(1)1 if and only if any one of the following three conditions holds:
(i) A=0 and A1=0.
(ii) A=0 and A2B(1,2)2A3=0.
(iii) r[AA1A2B(1,2)2A3B1]=r(B1).
Consequently, we derive the conditions under which (ii) and (iii) hold, respectively. By (2.11), the equality A2B(1,2)2A3=0 in (ii) of the above three conditions holds for all generalized inverses B(1,2)2 if and only if
holds. So, the above condition (ii) is equivalent to (ii), (iii), (iv) and (vi) in (c). By (2.9),
Hence, the rank equality in (iii) of the above three conditions holds for all generalized inverses B(1,2)2 if and only if
By (2.7),
holds. Combining it with the first equality in (4.6) leads to r(A)=r(B2)=0; thus, the first equality in (4.6) is equivalent to (iii) in (c). By (2.6) and (2.7),
holds. Combining it with the second equality in (4.6) leads to A=0 and r[0A1A2B1]=r(B1); thus, the second equality in (4.6) is equivalent to (v) in (c). By (2.7),
holds. Combining it with the third equality in (4.6) leads to A=0 and A3=0; thus the third equality in (4.6) is involved in (iv) in (c). The rank equality in (4.7) is equivalent to (vii) in (c).
We also declare that the following theorems can be shown by a similar approach, so the details of the proofs are omitted.
Theorem 4.3. Let A1, B1, A2, B2, A3 and A be as given in (4.4). Then, the following three statements are equivalent:
(a) Equation (4.4) holds for all B(1,2)1 and B(1,2)2.
(b) A1B(1,2)1A2B(1,2)2A3 is invariant with respect to all B(1,2)1 and B(1,2)2 and A1B†1A2B†2A3=A holds.
(c) Any one of the following 8 conditions holds:
(i) A=0 and A1=0.
(ii) A=0 and B1=0.
(iii) A=0 and A2=0.
(iv) A=0 and B2=0.
(v) A=0 and A3=0.
(vi) A=0 and r[0A1A2B1]=r(B1).
(vii) A=0 and r[0A2A3B2]=r(B2).
(viii) r[−A0A10A2B1A3B20]=r[A2B1B20]=r(B1)+r(B2).
The case of (1.4) for k=3 is given by
where A1∈Cm1×m2, B1∈Cm3×m2, A2∈Cm3×m4, B2∈Cm5×m4, A3∈Cm5×m6, B3∈Cm7×m6, A4∈Cm7×m8 and A∈Cm1×m8. Particularly, the case of (4.8) for {1}-generalized inverses of B1, B2 and B3 was studied in [16], and the following results were obtained.
Theorem 4.4 ([16]). Let A1, B1, A2, B2, A3, B3, A4 and A be as given in (4.8). Then, the following three statements are equivalent:
(a) A1B(1)1A2B(1)2A3B(1)3A4=A holds for all B(1)1, B(1)2 and B(1)3.
(b) A1B(1)1A2B(1)2A3B(1)3A4 is invariant with respect to all B(1)1, B(1)2 and B(1)3 and A1B†1A2B†2A3B†3A4=A holds.
(c) Any one of the following 10 conditions holds:
(i) A=0 and A1=0.
(ii) A=0 and A2=0.
(iii) A=0 and A3=0.
(iv) A=0 and A4=0.
(v) A=0 and r[0A1A2B1]=r(B1).
(vi) A=0 and r[0A2A3B2]=r(B2).
(vii) A=0 and r[0A3A4B3]=r(B3).
(viii) A=0 and r[00A10A2B1A3B20]=r[A2B1B20]=r(B1)+r(B2).
(ix) A=0 and r[00A20A3B2A4B30]=r[A3B2B30]=r(B2)+r(B3).
(x) r[A00A100A2B10A3B20A4B300]=r[0A2B1A3B20B300]=r(B1)+r(B2)+r(B3).
For the other seven matrix equalities in (4.8) with mixed combinations of {1}- and {1,2}-generalized inverses of matrices, we have the following results.
Theorem 4.5. Let A1, B1, A2, B2, A3, B3, A4 and A be as given in (4.8). Then, the following three statements are equivalent:
(a) A1B(1)1A2B(1)2A3B(1,2)3A4=A holds for all B(1)1, B(1)2 and B(1,2)3.
(b) A1B(1)1A2B(1)2A3B(1,2)3A4 is invariant with respect to all B(1)1, B(1)2 and B(1,2)3 and A1B†1A2B†2A3B†3A4=A holds.
(c) Any one of the following 11 conditions holds:
(i) A=0 and A1=0.
(ii) A=0 and A2=0.
(iii) A=0 and A3=0.
(iii) A=0 and B3=0.
(v) A=0 and A4=0.
(vi) A=0 and r[0A1A2B1]=r(B1).
(vii) A=0 and r[0A2A3B2]=r(B2).
(viii) A=0 and r[0A3A4B3]=r(B3).
(ix) A=0 and r[00A10A2B1A3B20]=r[A2B1B20]=r(B1)+r(B2).
(x) A=0 and r[00A20A3B2A4B30]=r[A3B2B30]=r(B2)+r(B3).
(xi) r[A00A100A2B10A3B20A4B300]=r[0A2B1A3B20B300]=r(B1)+r(B2)+r(B3).
Proof. The equivalence of (a) and (b) follows from the definition of the Moore–Penrose inverse of a matrix and its uniqueness.
By Lemma 4.1(c), we first see that the matrix equality A1B(1)1A2B(1)2A3B(1,2)3A4=A holds for all generalized inverses B(1)1 and B(1)2 if and only if any one of the following 6 conditions holds:
(i) A=0 and A1=0.
(ii) A=0 and A2=0.
(iii) A=0 and A3B(1,2)3A4=0.
(iv) A=0 and r[0A1A2B1]=r(B1).
(v) A=0 and r[0A2A3B(1,2)3A4B2]=r(B2).
(vi) r[−A0A10A2B1A3B(1,2)3A4B20]=r[A2B1B20]=r(B1)+r(B2).
We next derive the conditions under which (iii), (v) and (vi) hold, respectively. By (2.10), the equality A3B(1,2)3A4=0 in (iii) of the above 6 conditions holds for all generalized inverses B(1,2)3 if and only if
holds. By (2.8),
So, the rank equality r[0A2A3B(1,2)3A4B2]=r(B2) in (v) of the above 6 conditions holds for all B(1,2)3 if and only if
or
where the first and third rank equalities in (4.10) mean that B3=0 and A4=0 by noting that r[A2B2]≥r(B2). By (2.9),
Hence, the rank equality in (vi) of the above 6 conditions holds for all B(1,2)3 if and only if
Note from (2.6) and (2.7) that the following four groups of matrix rank inequalities
hold. Combining (4.14) with the first equality in (4.12) leads to
This condition, however, is included in (4.9). Combining (4.15) with the second equality in (4.12) leads to
Combining (4.16) and (4.17) with the first equality in (4.13) leads to
Combining the conditions in (i), (ii) and (iv) of the proof with (4.12)–(4.20) leads to the 11 statements in (c).
The following 6 theorems can be established by a similar approach; therefore, the details of the proofs are omitted.
Theorem 4.6. Let A1, B1, A2, B2, A3, B3, A4 and A be as given in (4.8). Then, the following three statements are equivalent:
(a) A1B(1,2)1A2B(1,2)2A3B(1)3A4=A holds for all B(1,2)1, B(1,2)2 and B(1)3.
(b) A1B(1,2)1A2B(1,2)2A3B(1)3A4 is invariant with respect to all B(1,2)1, B(1,2)2 and B(1)3 and A1B†1A2B†2A3B†3A4=A holds.
(c) Any one of the following 12 conditions holds:
(i) A=0 and A1=0.
(ii) A=0 and B1=0.
(iii) A=0 and A2=0.
(iv) A=0 and B2=0.
(v) A=0 and A3=0.
(vi) A=0 and A4=0.
(vii) A=0 and r[0A1A2B1]=r(B1).
(viii) A=0 and r[0A2A3B2]=r(B2).
(ix) A=0 and r[0A3A4B3]=r(B3).
(x) A=0 and r[00A10A2B1A3B20]=r[A2B1B20]=r(B1)+r(B2).
(xi) A=0 and r[00A20A3B2A4B30]=r[A3B2B30]=r(B2)+r(B3).
(xii) r[A00A100A2B10A3B20A4B300]=r[0A2B1A3B20B300]=r(B1)+r(B2)+r(B3).
Theorem 4.7. Let A1, B1, A2, B2, A3, B3, A4 and A be as given in (4.8). Then, the following three statements are equivalent:
(a) A1B(1,2)1A2B(1,2)2A3B(1,2)3A4=A holds for all B(1,2)1, B(1,2)2 and B(1,2)3.
(b)A1B(1,2)1A2B(1,2)2A3B(1,2)3A4 is invariant with respect to all B(1,2)1, B(1,2)2 and B(1,2)3 and A1B†1A2B†2A3B†3A4=A holds.
(c) Any one of the following 13 conditions holds:
(i) A=0 and A1=0.
(ii) A=0 and B1=0.
(iii) A=0 and A2=0.
(iv) A=0 and B2=0.
(v) A=0 and A3=0.
(vi) A=0 and B3=0.
(vii) A=0 and A4=0.
(viii) A=0 and r[0A1A2B1]=r(B1).
(ix) A=0 and r[0A2A3B2]=r(B2).
(x) A=0 and r[0A3A4B3]=r(B3).
(xi) A=0 and r[00A10A2B1A3B20]=r[A2B1B20]=r(B1)+r(B2).
(xii) A=0 and r[00A20A3B2A4B30]=r[A3B2B30]=r(B2)+r(B3).
(xiii) r[A00A100A2B10A3B20A4B300]=r[0A2B1A3B20B300]=r(B1)+r(B2)+r(B3).
5.
Matrix equalities that involve mixed products of two or three weighted {1}- and {1,2}-inverses
In addition to the classical definition in (1.1), some other weighted generalized inverses of a matrix can be defined from common solutions of given matrix equations derived from theory and applied points of view, alternatively there are many approaches and discussions concerning different kinds of weighted generalized inverses of matrices in the literature. Here, we mention such an example of weighted generalized inverses: given three matrices A∈Cm×n, P∈Cp×m and Q∈Cn×q, A is said to be weighted Moore–Penrose invertible with respect to the two matrices (P,Q) if and only if there exists a matrix X∈Cq×p that satisfies the following four matrix equations
In this case, the matrix X is denoted by X=A(†,P,Q). In addition, a matrix X is said to be a {i,…,j,P,Q}-generalized inverse of A, denoted by A(i,…,j,P,Q), if it satisfies the ith, …,jth matrix equations in (5.1), while the set of all {i,…,j,P,Q}-generalized inverses of the matrix A is, as usual, denoted by {A(i,…,j,P,Q)}.
Concerning the existence of X satisfying (5.1) and the corresponding expressions of X, we have the following results.
Lemma 5.1. Let A∈Cm×n, P∈Cp×m and Q∈Cn×q. Then, A is weighted Moore–Penrose invertible with respect to the two matrices (P,Q) if and only if the two range equalities R((PA)∗)=R(A∗) and R(AQ)=R(A) hold, or equivalently, the matrix rank equality r(PAQ)=r(A) holds. In such a case, the matrix equality
always holds. In particular, the general expressions of A(1,P,Q) and A(1,2,P,Q) are given by
and the following matrix equalities
hold, where G,H∈Cq×p are two arbitrary matrices.
Proof. By Lemma 2.1, the first equation in (5.1) is solvable for the matrix X if and only if R(AQ)⊇R(A) and R((PA)∗)⊇R(A∗) hold, both of which are equivalent to the matrix range equalities R((PA)∗)=R(A∗) and R(AQ)=R(A), or equivalently, the matrix rank equality r(PAQ)=r(A). In this case, the first equation in (5.1) is equivalent to PAQXPAQ=PAQ. In this case, we obtain (5.3) and (5.4) from Lemma 2.2.
Analogous to (4.8), it is possible to formulate four additive matrix equalities that involve weighted {1}- and {1,2}-generalized inverses as follows:
where A1∈Cm×q1, P1∈Cp1×s1, B1∈Cs1×t1, Q1∈Ct1×q1, C1∈Cp1×n, A2∈Cm×q2, P2∈Cp2×s2, B2∈Cs2×t2, Q2∈Ct2×q2, C2∈Cp2×n and D∈Cm×n are given.
Theorem 5.2. Assume that B(1,P1,Q1)1 and B(1,P2,Q2)2 exist. Then, the following three statements are equivalent:
(a) Equation (5.9) holds for all B(1,P1,Q1)1 and B(1,P2,Q2)2.
(b) A1B(1,P1,Q1)1C1+A2B(1,P2,Q2)2C2 is invariant with respect to all B(1,P1,Q1)1 and B(1,P2,Q2)2 and A1(P1B1Q1)†C1+A2(P2B2Q2)†C2=D holds.
(c) Any one of the following 9 conditions holds:
(i) A1=0, A2=0 and D=0.
(ii) A1=0, C2=0 and D=0.
(iii) C1=0, A2=0 and D=0.
(iv) C1=0, C2=0 and D=0.
(v) A1=0 and r[P2B2Q2C2A2D]=r(B2).
(vi) C1=0 and r[P2B2Q2C2A2D]=r(B2).
(vii) A2=0 and r[P1B1Q1C1A1D]=r(B1).
(viii) C2=0 and r[P1B1Q1C1A1D]=r(B1).
(ix) r[P1B1Q10C10P2B2Q2C2A1A2D]=r(B1)+r(B2).
Proof. By (5.3), the matrix equality in (5.9) is equivalent to
In this case, applying Theorem 3.1 to the matrix equality yields the results in (a), (b) and (c).
The following theorems can be shown by a similar approach.
Theorem 5.3. Assume that B(1,P1,Q1)1 and B(1,P2,Q2)2 exist. Then, the following three statements are equivalent:
(a) Equation (5.10) holds for all B(1,2,P1,Q1)1 and B(1,P1,Q1)2.
(b) A1B(1,2,P1,Q1)1C1+A2B(1,P2,Q2)2C2 is invariant with respect to all B(1,2,P1,Q1)1 and B(1,P2,Q2)2 and A1(P1B1Q1)†C1+A2(P2B2Q2)†C2=D holds.
(c) Any one of the following 12 conditions holds:
(i) A1=0, A2=0 and D=0.
(ii) A1=0, C2=0 and D=0.
(iii) B1=0, A2=0 and D=0.
(iv) B1=0, C2=0 and D=0.
(v) C1=0, A2=0 and D=0.
(vi) C1=0, C2=0 and D=0.
(vii) A1=0 and r[P2B2Q2C2A2D]=r(B2).
(viii) B1=0 and r[P2B2Q2C2A2D]=r(B2).
(ix) C1=0 and r[P2B2Q2C2A2D]=r(B2).
(x) A2=0 and r[P1B1Q1C1A1D]=r(B1).
(xi) C2=0 and r[P1B1Q1C1A1D]=r(B1).
(xii) r[P1B1Q10C10P2B2Q2C2A1A2D]=r(B1)+r(B2).
Theorem 5.4. Assume that B(1,P1,Q1)1 and B(1,P2,Q2)2 exist. Then, the following three statements are equivalent:
(a) Equation (5.12) holds for all B(1,2,P1,Q1)1 and B(1,2,P1,Q1)2.
(b) A1B(1,2,P1,Q1)1C1+A2B(1,2,P2,Q2)2C2 is invariant with respect to all B(1,2,P1,Q1)1 and B(1,2,P2,Q2)2 and A1(P1B1Q1)†C1+A2(P2B2Q2)†C2=D holds.
(b) Any one of the following 16 conditions holds:
(i) A1=0, A2=0 and D=0.
(ii) A1=0, B2=0 and D=0.
(iii) A1=0, C2=0 and D=0.
(vi) B1=0, A2=0 and D=0.
(v) B1=0, B2=0 and D=0.
(vi) B1=0, C2=0 and D=0.
(vii) C1=0, A2=0 and D=0.
(viii) C1=0, B2=0 and D=0.
(ix) C1=0, C2=0 and D=0.
(x) A1=0 and r[P2B2Q2C2A2D]=r(B2).
(xi) B1=0 and r[P2B2Q2C2A2D]=r(B2).
(xii) C1=0 and r[P2B2Q2C2A2D]=r(B2).
(xiii) A2=0 and r[P1B1Q1C1A1D]=r(B1).
(xiv) B2=0 and r[P1B1Q1C1A1D]=r(B1).
(xv) C2=0 and r[P1B1Q1C1A1D]=r(B1).
(xvi) r[P1B1Q10C10P2B2Q2C2A1A2D]=r(B1)+r(B2).
Analogous to (1.4), it is possible to formulate some matrix equalities that involve alternative products of matrices and their weighted {1}- and {1,2}-generalized inverses. In what follows, we present a sequence of extensions of the results in the preceding sections to matrix equalities that involve mixed products of two or three weighted {1}- and {1,2}-inverses. In particular, we are able to construct four matrix equalities that involves weighted {1}- and {1,2}-generalized inverses as follows:
where A1∈Cm1×m2, P1∈Cm3×q1, B1∈Cq1×p1, Q1∈Cp1×m2, A2∈Cm3×m4, P2∈Cm5×q2, B2∈Cq2×p2, Q2∈Cp2×m4, A3∈Cm5×m6 and A∈Cm1×m6.
Theorem 5.5. Assume that B(1,P1,Q1)1 and B(1,P2,Q2)2 exist. Then, the following three statements are equivalent:
(a) Equation (5.13) holds for all B(1,P1,Q1)1 and B(1,P2,Q2)2.
(b) A1B(1,P1,Q1)1A2B(1,P2,Q2)2A3 is invariant with respect to all B(1,P1,Q1)1 and B(1,P2,Q2)2 and A1(P1B1Q1)†A2(P2B2Q2)†A3=A holds.
(c) Any one of the following 6 conditions holds:
(i) A=0 and A1=0.
(ii) A=0 and A2=0.
(iii) A=0 and A3=0.
(iv) A=0 and r[0A1A2P1B1Q1]=r(B1).
(v) A=0 and r[0A2A3P2B2Q2]=r(B2).
(vi) r[−A0A10A2P1B1Q1A3P2B2Q20]=r[A2P1B1Q1P2B2Q20]=r(B1)+r(B2).
Proof. Under the given assumptions, we obtain from (5.3) that A1B(1,P1,Q1)1A2B(1,P2,Q2)2A3=A is equivalent to
In this case, applying Theorem 4.1 to the matrix equality yields the results in (a), (b) and (c).
By a similar approach, we obtain the following three groups of results from Theorems 4.2 and 4.3.
Theorem 5.6. Assume that B(1,P1,Q1)1 and B(1,P2,Q2)2 exist. Then, the following three statements are equivalent:
(a) Equation (5.14) holds for all B(1,2,P2,Q2)1 and B(1,P2,Q2)2.
(b) A1B(1,2,P2,Q2)1A2B(1,P2,Q2)2A3 is invariant with respect to all B(1,2,P2,Q2)1 and B(1,P2,Q2)2 and A1(P1B1Q1)†A2(P2B2Q2)†A3=A holds.
(c) Any one of the following 7 conditions holds:
(i) A=0 and A1=0.
(ii) A=0 and B1=0.
(iii) A=0 and A2=0.
(iv) A=0 and A3=0.
(v) A=0 and r[0A1A2P1B1Q1]=r(B1).
(vi) A=0 and r[0A2A3P2B2Q2]=r(B2).
(vii) r[−A0A10A2P1B1Q1A3P2B2Q20]=r[A2P1B1Q1P2B2Q20]=r(B1)+r(B2).
Theorem 5.7. Assume that B(1,P1,Q1)1 and B(1,P2,Q2)2 exist. Then, the following three statements are equivalent:
(a) Equation (5.16) holds for all B(1,2,P1,Q1)1 and B(1,2,P2,Q2)2.
(b) A1B(1,2,P1,Q1)1A2B(1,2,P2,Q2)2A3 is invariant with respect to all B(1,2,P1,Q1)1 and B(1,2,P2,Q2)2 and A1(P1B1Q1)†A2(P2B2Q2)†A3=A holds.
(c) Any one of the following 8 conditions holds:
(i) A=0 and A1=0.
(ii) A=0 and B1=0.
(iii) A=0 and A2=0.
(iv) A=0 and B2=0.
(v) A=0 and A3=0.
(vi) A=0 and r[0A1A2P1B1Q1]=r(B1).
(vii) A=0 and r[0A2A3P2B2Q2]=r(B2).
(viii) r[−A0A10A2P1B1Q1A3P2B2Q20]=r[A2P1B1Q1P2B2Q20]=r(B1)+r(B2).
Finally, we present extensions of Theorems 4.4 and 4.7 to matrix equalities that involve mixed products of three weighted {1}- and {1,2}-inverses. Let
Then, the matrix product A1B(1,P1,Q1)1A2B(1,P2,Q2)2A3B(1,P3,Q3)3A4 is defined accordingly, and we have the following results.
Theorem 5.8. Given the matrices in (5.17)–(5.19) and A∈Cm1×m8, and assume that B(1,P1,Q1)1, B(1,P2,Q2)2 and B(1,P3,Q3)3 exist. Then, the following three statements are equivalent:
(a) A1B(1,P1,Q1)1A2B(1,P2,Q2)2A3B(1,P3,Q3)3A4=A holds for all B(1,P1,Q1)1, B(1,P2,Q2)2 and B(1,P3,Q3)3.
(b) A1B(1,P1,Q1)1A2B(1,P2,Q2)2A3B(1,P3,Q3)3A4 is invariant with respect to all B(1,P1,Q1)1, B(1,P2,Q2)2 and B(1,P3,Q3)3 and A1(P1B1Q1)†A2(P2B2Q2)†A3(P3B3Q3)†A4=A holds.
(c) Any one of the following 10 conditions holds:
(i) A=0 and A1=0.
(ii) A=0 and A2=0.
(iii) A=0 and A3=0.
(iv) A=0 and A4=0.
(v) A=0 and r[0A1A2P1B1Q1]=r(B1).
(vi) A=0 and r[0A2A3P2B2Q2]=r(B2).
(vii) A=0 and r[0A3A4P3B3Q3]=r(B3).
(viii) A=0 and r[00A10A2P1B1Q1A3P2B2Q20]=r[A2P1B1Q1P2B2Q20]=r(B1)+r(B2).
(ix) A=0 and r[00A20A3P2B2Q2A4P3B3Q30]=r[A3P2B2Q2P3B3Q30]=r(B2)+r(B3).
(x) r[A00A100A2P1B1Q10A3P2B2Q20A4P3B3Q300]=r[0A2P1B1Q1A3P2B2Q20P3B3Q300]=r(B1)+r(B2)+r(B3).
Theorem 5.9. Given the assumptions in (5.17)–(5.19) and A∈Cm1×m8, assume that B(1,P1,Q1)1, B(1,P2,Q2)2 and B(1,P3,Q3)3 exist. Then, the following three statements are equivalent:
(a) A1B(1,2,P1,Q1)1A2B(1,2,P2,Q2)2A3B(1,2,P3,Q3)3A4=A holds for all B(1,2,P1,Q1)1, B(1,2,P2,Q2)2 and B(1,2,P3,Q3)3.
(b) A1B(1,2,P1,Q1)1A2B(1,2,P2,Q2)2A3B(1,2,P3,Q3)3A4 is invariant with respect to all B(1,2,P1,Q1)1, B(1,2,P2,Q2)2 and B(1,2,P3,Q3)3 and A1(P1B1Q1)†A2(P2B2Q2)†A3(P3B3Q3)†A4=A holds.
(c) Any one of the following 13 conditions holds:
(i) A=0 and A1=0.
(ii) A=0 and B1=0.
(iii) A=0 and A2=0.
(iv) A=0 and B2=0.
(v) A=0 and A3=0.
(vi) A=0 and B3=0.
(vii) A=0 and A4=0.
(viii) A=0 and r[0A1A2P1B1Q1]=r(B1).
(ix) A=0 and r[0A2A3P2B2Q2]=r(B2).
(x) A=0 and r[0A3A4P3B3Q3]=r(B3).
(xi) A=0 and r[00A10A2P1B1Q1A3P2B2Q20]=r[A2P1B1Q1P2B2Q20]=r(B1)+r(B2).
(xii) A=0 and r[00A20A3P2B2Q2A4P3B3Q30]=r[A3P2B2Q2P3B3Q30]=r(B2)+r(B3).
(xiii) r[A00A100A2P1B1Q10A3P2B2Q20A4P3B3Q300]=r[0A2P1B1Q1A3P2B2Q20P3B3Q300]=r(B1)+r(B2)+r(B3).
6.
An application
There exist many concrete matrix equalities, as described in (1.5) and (1.6), that can be represented in the forms of (1.3) and (1.4). As an application, we consider in this section the following partitioned matrix:
where A∈Cm1×n1, B∈Cm1×n2, C∈Cm2×n1 and D∈Cm2×n2. Given such a partitioned matrix, we are able to construct a special matrix equality
for the generalized inverses. Because generalized inverses of matrices are not necessarily unique, (6.1) can be divided into the following four cases:
It is a tedious work to characterize these four matrix set relations for different choices of the generalized inverses. In what follows, we only consider a special case of the first matrix set inclusion in (6.3). By definition, the first matrix set inclusion in (6.3) holds for {1}-inverses of the matrices if and only if
holds for all A(1), B(1), C(1) and D(1), which in turn can be represented in the form
where P1=[AC], P2=[BD], Q1=[A,B] and Q2=[C,D]. In this case, we are able to find from Theorem 3.6 the following result.
Theorem 6.1. Let Pi and Qi be as given in (6.5) and assume that Pi≠0 and Qi≠0 for i=1,2. Then, (6.4) holds for all A(1), B(1), C(1) and D(1) if and only if
or equivalently,
7.
Conclusions
We investigated the two sorts of general matrix equalities in (1.3) and (1.4) that involve ordinary sum and product operations of matrices and their generalized inverses, and we obtained a variety of necessary and sufficient conditions for them to hold. It can be seen that the corresponding results and facts are fairly easy to understand and utilize within the common discipline of matrix theory and generalized inverses of matrices since they were explicitly derived through various common algebraic calculations of matrices and their generalized inverses, as well as the skillful employments of the elementary but powerful BMRM and MRM.
In addition to the work related to {1}- and {1,2}-generalized inverses of matrices, it would be of interest to consider other {i,…,j}-generalized inverses of the matrices in the two matrix equalities in (1.3) and (1.4); yet, it is not difficult to see that we can easily extend them by induction to general matrix equalities through certain special block matrices that are constructed from the given matrices in the equalities. Finally, we conclude that this study will reveal numerous novel and intrinsic properties and performances of matrix expressions and matrix equalities that are encountered in the theory of generalized inverses. We also believe that these results and facts will provide enough supports to approach various concrete matrix equality problems from theoretical and applied points of view.
Use of AI tools declaration
The author declares that he has not used artificial intelligence tools in the creation of this article.
Acknowledgments
The author would like to express his sincere thanks to the handling editor and three anonymous reviewers for their helpful comments and suggestions.
Conflict of interest
The author declares that there is no conflict of interest.












 DownLoad:
DownLoad: