Optimal control for HIV treatment

1.   Introduction

After three decades, HIV/AIDS still remains a public health threat, especially in developing countries. The World Health Organization (WHO) estimates that globally about 35 million people have already lost their lives due to AIDS, and in 2015, there were 36.7 million people living with HIV, with 2.3 million new infections and 1.1 million AIDS-related deaths ^[32].

Once a person becomes infected, the WHO defines five clinical stages as the infection progresses ^[39]. The acute stage is in the first few months following the initial introduction of the virus into the body. This stage is asymptomatic with no significant immunosuppression ($\text{CD4 count} >500\ \text{cells mm}^{-3}$) and a spike in virus titre. Stage Ⅰ is also asymptomatic with no significant immunosuppression but unlike the acute stage, it is characterized by a low viral load. Stage Ⅱ is symptomatic: the infected person exhibits moderate weight loss amongst other symptoms and mild immunosuppression ($350 < \text{CD4 count} < 499\ \text{cells mm}^{-3}$). Stage Ⅲ is also symptomatic and is characterized by advanced immunosuppression ($200 < \text{CD4 count} < 349\ \text{cells mm}^{-3}$). Stage Ⅳ is the AIDS phase, where the infected person exhibits HIV wasting syndrome, amongst other symptoms, and severe immunosuppression (CD4 $<$200$\frac{\mathrm{cells}}{\mathrm{mm}^{3}}$). This classification based on clinical symptoms is advantageous because it allows for areas with limited laboratory facilities to estimate HIV disease progression and aid in the management of HIV/AIDS patients (e.g., when to start treatment).

In terms of transmissibility, due to the high viral loads, the acute stage is characterized by high rates of transmission. The infected person then goes through a phase (Stages Ⅰ & Ⅱ) where the viral load is lower leading to lower transmission. Without treatment this person moves to Stages Ⅲ & Ⅳ, which is characterized by high transmission rates due to high viral loads ^[4,23,24]. A study of transmission involving a cohort of stable partnerships between heterosexuals in Rakai, Uganda quantified the relative transmissibility of HIV by stage of infection ^[36]. The probability of transmission per coital act in the acute stage was estimated to be 8-10 times higher than during asymptomatic (Stages Ⅰ & Ⅱ). In the last 2 years before death (Stages Ⅲ & Ⅳ), the probability of transmission per coital act was estimated to be 4-8 times higher than during asymptomatic infection.

Antiretroviral therapy (ART) are drugs that target the HIV life cycle with the aim of halting HIV replication and restoring immune function, thus slowing the progression to AIDS ^[7,34]. Apart from traditional role of preventing progression to AIDS, ART has an additional benefit of substantially reducing the infectiousness of infected people leading to reduced transmission ^[3,5]. In 2011, the HIV Prevention Trials Network (HPTN) reported in their HPTN 052 trial that early ART reduces HIV transmission amongst serodiscordant couples by 96% ^[11]. Thanks to the HPTN 052 trial and other studies on the benefits of treatment, the WHO in June 2013 released new guidelines on the use of ART for treating and preventing HIV infection, recommending treatment to infected people with $\text{CD4 count} >500\ \text{cells mm}^{-3}$, i.e. from Stage Ⅱ, thus broadening the spectrum of people eligible for initiation of ART ^[40].

Health authorities worldwide are faced with limited resources and must find economical ways to administer ART. In this study, we used optimal control theory to determine time-dependent treatment strategies that maximize the effectiveness of population-scale interventions.The strategies are the level of ART allocation to people in the different disease stages. We measured the effectiveness by total infection-years, new infections, AIDS-related deaths and cost, and separately found the strategies that optimize each of them.

Optimal control theory, which was developed by Pontryagin and his co-workers in the late 1950s ^[29], has been applied to many areas including economics, management, engineering, biology, physiology and medicine ^{[1,19,21,22,41]}. Indeed, optimal control theory has been used to study HIV treatment both at the cellular level ^[8,18,20] and at the level of individual patients ^[16,28]. All these optimal control models include an assumption for a quadratic cost of the controls in the objective function to simplify the solution process. Akin to a few other studies ^[6,12,27], our model does not make such an assumption and we also impose a constraint on the total drugs available each year.

In this paper, we first introduce our transmission model that captures the 5 stages of HIV/AIDS infection and incorporates three controls for treatment in Stages Ⅱ, Ⅲ & Ⅳ. We then define the objective functions and the optimal control problem and follow that by an analysis of the optimal controls. Finally, we present some numerical solutions for the South African HIV epidemic and discuss the results.

2.   Methods

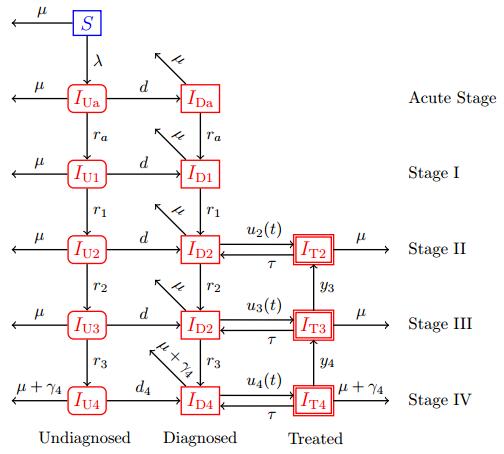
We adopted an HIV model originally developed to study the importance of promoting HIV testing for preventing secondary transmission (Figure 1) ^[38]. The model is for an adult heterosexual population and stratifies the population by HIV status, diagnosis and treatment. People are either susceptible or infected, and then the infected population is divided into 5 classes based on the WHO HIV/AIDS staging system: acute and Stages Ⅰ-Ⅳ. Each of the 5 stages is further divided in 3 levels: those who are infected but unaware of their HIV status (Undiagnosed), those who have been diagnosed but are not yet on treatment (Diagnosed) and those on treatment (Treated). To reflect current WHO guidelines on treatment, a fraction of diagnosed people are on treatment in Stages Ⅱ, Ⅲ & Ⅳ.

People enter the model as susceptible ($S$) with a recruitment rate $b$ and leave either through natural death ($\mu$) or death due to AIDS or HIV-related symptoms ($\gamma_{4}$). Once infected, people move from the susceptible class to the undiagnosed acute infection class ($I_{\mathrm{Ua}}$). From here, people get tested at rate $d$ and move into the diagnosed acute infection class ($I_{\mathrm{Da}}$). Likewise, in Stages Ⅰ, Ⅱ & Ⅲ, undiagnosed people are tested at the same rate $d$. Undiagnosed people in Stage Ⅳ are generally very sick and will already have shown signs of AIDS so, their testing rate $d_4$ is considerably higher than $d$. People in the untreated ($I_{\mathrm{U}i}$) and diagnosed ($I_{\mathrm{D}i}$) classes progress at rate $r_i$ into the next infection stage, for $i = \{\mathrm{a}, 1, 2, 3\}$. It is difficult to diagnose someone in the acute State of infection, however, being that the unit of testing rate is per year, the number of diagnoses in the acute stage will be mitigated by the brief period infected people spend in the acute stage. We assumed that the the testing rate $d$, for the acute Stage and Stages Ⅰ-Ⅲ is equal to the national testing rate and is not symptom dependent.

A proportion of the diagnosed people in Stages Ⅱ, Ⅲ & Ⅳ begin treatment at rates $u_2(t)$, $u_3(t)$ and $u_4(t)$, moving into $I_{\mathrm{T2}}$, $I_{\mathrm{T3}}$ and $I_{\mathrm{T4}}$, respectively. The treatment rates $u_i(t)$ are functions of the controls $U_{i}(t)$, which will be described below. Treated people in Stage Ⅱ ($I_{\mathrm{T2}}$) stay in that class because their immune system does not deteriorate. Treated people in Stage Ⅲ ($I_{\mathrm{T3}}$) transition back to Stage Ⅱ ($I_{\mathrm{T2}}$) at rate $y_3$ due to improvement of their immune system. Likewise, treated people in Stage Ⅳ ($I_{\mathrm{T4}}$) transition back to Stage Ⅲ ($I_{\mathrm{T3}}$) at rate $y_4$. Treatment failure rates $\tau$ might be stage dependent, however due to a lack of data on this we assumed it to be the same in all of the stages.

New infections occur from unprotected sexual contact between susceptible people and infected people. People in Stage Ⅳ ($I_{\mathrm{U4}}$, $I_{\mathrm{D4}}$ and $I_{\mathrm{T4}}$) have full-blown AIDS, thus we assumed that they are too ill to engage in sexual activity. Treatment reduces the probability of transmission by $\alpha$, which we take to be $96\%$ ^[11]. There is also evidence to suggest that individuals who know their HIV status change their sexual behavior (i.e. adopt safer-sex practices), leading to lower transmission ^[25]. The reduction in transmission from individuals that know their infection status is $\xi$. The force of infection, $\lambda$, is the sum over the force of infection by stage:

with

and

The HIV model is given by the system of differential equations

2.1.   Optimal control problem formulation

The control variables $U_{2}(t)$, $U_{3}(t)$, $U_{4}(t)$ are the total number of people targeted to be on treatment in each of the designated Stages Ⅱ, Ⅲ & Ⅳ at each time. The controls ($U_{i}(t)$) are assumed to be bounded and Lebesgue integrable. From these treatment targets, the flows of people into treatment per unit time were taken to be

where $I_{Ti}$ is the total number of people currently on treatment in Stage $i$, $i \in \{\mathrm{II}, \mathrm{III}, \mathrm{IV}\}$. $r_\text{max}$ is the rate of enrolling people on treatment per drug available per untreated person with units $[\text{time}]^{-1}[\text{drugs}]^{-1}$ ^[2]. The total treatment is constraint by $\nu$, where is the total number of drugs available,

We seek to minimize four different objectives: total infection-year, new infections, deaths due to AIDS, and total cost.

Total infection-years: Total infection-years is the sum of the number of all the infected people (undiagnosed, diagnosed, or treated) in all stages at each time, integrated over the time period,

where ($N_{\mathrm{I}}$) is the sum:

New infections: The total number of new infections is the sum of the rates of new infections arising from contact of susceptible people with infected people integrated over the time period,

where ($N_{\mathrm{NI}}$) is the rate of new infection,

Deaths due to AIDS: The total AIDS-related deaths ($N_{\mathrm{D}}$) is the sum of infected people dying from AIDS-related diseases. Our assumption that AIDS-related deaths only occur in Stage Ⅳ means that this is the sum of infected people in Stage Ⅳ dying from AIDS,

$N_{\mathrm{D}}$ is simply the number of people infected in Stage Ⅳ at each time multiplied by the disease induced deaths rate $\gamma_{4}$,

Total cost The total cost ($N_{\mathrm{C}}$) consists of cost of infections, cost of deaths, and cost of treatment. The disease cost per year, which includes monetary equivalent loss of the infected people, such as lost productivity etc., is average cost of disease per person per year multiplied by the total number of people infected,

The cost per year of deaths is the the cost per death multiplied by the number of deaths per year,

The treatment cost per year is the cost per person per year multiplied by the number of people treated,

where the number of people treated ($N_{T}$) is the sum of all people in the treatment class,

The cost objective is discounted sum of these costs, integrated over the time period:

The total cost is discounted at rate $r$, representing the rate a policymaker is willing to pay as trade-off for the cost today versus future cost ^[13].

For ease of analysis, we can define system 4 compactly as

with $X = (S, I_{\mathrm{Ua}}, I_{\mathrm{U1}}, I_{\mathrm{U2}}, I_{\mathrm{U3}}, I_{\mathrm{U4}}, I_{\mathrm{Da}}, I_{\mathrm{D1}}, I_{\mathrm{D2}}, I_{\mathrm{D3}}, I_{\mathrm{D4}}, I_{\mathrm{T2}}, I_{\mathrm{T3}}, I_{\mathrm{T4}})$.

The optimal control problem is

2.2.   Analysis of optimal controls

If we define the integrand of our objective function by $f_{k}(t, X)$ and $g(t, X, U)$ is the right-hand side of the system of differential equations, then the Hamiltonian is

Pontryagin's Maximum Principle ^[29] converts the optimal control problem into a problem of minimizing the Hamiltonian point-wise with respect to $U_2$, $U_3$ and $U_4$. See 4 for a detailed characterization of the optimal control problem.

We can characterize the optimal controls as

where $H(x)$ is the Heaviside function,

The optimal controls are bounded by the number of total drugs available (i.e. $0 \leq U_{i} \leq \nu_{i}$) where $\nu_{2}$, $\nu_{3}$ and $\nu_{4}$ are the total number of drugs allocated to $U_{2}$, $U_{3}$ and $U_{4}$ respectively at each time point. From (6),

Applying these bounds to the controls we obtain

and

Note that in the numerical results, the singular case (when $\frac{\partial \mathcal{H}}{\partial U_{i}} = 0$ on a set of positive measure) does not occur and we can restrict our attention to the bang-bang controls above. We also expect that at all time points $[0, T]$ either $U_2^{*}(t) + U_3^{*}(t) + U_4^{*}(t) = 0$ or $U_2^{*}(t) + U_3^{*}(t) + U_4^{*}(t) = \nu$.

Due to the convexity of the integrand of $J$ with respect to $U_2$, $U_3$ and $U_4$; the priori boundedness and the Lipschitz property with respect to the state variables, the existence of optimal controls with the constraint $U_2 + U_3 +U_4 \leq \nu$ follows as a result of minimizing sequences which converge weakly in $L^2(0, T)$ to an optimal triple (which is an extension of the results of Clayton et al. ^[9] and Fleming et al. ^[14]).

2.3.   Numerical simulations

With an initial guess for the control variables $U_2$, $U_3$ and $U_4$, we solve the state equations (4) forward in time. Using the solutions of the state equations together with the transversality conditions (30), we solve the adjoint equations (43) backward in time. The control is updated after each iteration using the new values of state and adjoint variables put into the optimality conditions (21), and the process is repeated. Iteration is stopped when the difference between successive iteration meet a predetermined tolerance.

We implemented a numerical algorithm originally developed in Wang ^[35]. The steps of algorithm are as follows:

1. Divide the time $[0, T]$ into $W$ subintervals.

2. We start with an initial guess of the controls $U_2^{0}$, $U_3^{0}$ and $U_4^{0}$.

3. Obtain the state variables $X_{i}$ by integrating the state equation (4) from $0$ to $T$ using the controls $U_2^{i}$, $U_3^{i}$ and $U_4^{i}$ and initial condition $X^{i}(t_0) = X^{i}_0$.

4. Integrate the adjoint equations (43) backward in time (from $T$ to $0$) to obtain the adjoint variables $\theta^{i}$, using $X^{i}$, $U^{i}_2$, $U^{i}_3$ and $U^{i}_4$.

5. Stop the algorithm if $\epsilon_\text{rel}\|P_{i}\|+ \|P_{i+1}-P_{i}\| \leq \epsilon_\text{abs}$ for $P \in \{X, U, \theta\}$, where $\epsilon_\text{abs}$ and $\epsilon_\text{rel}$ are predetermined absolute and relative errors, respectively.

6. If step 5 is not satisfied, adjust the control functions, by replacing $U^{i}$ with $U^{i+1}$. $U^{i+1}$ is calculated by the Newton-Raphson method: $U^{i+1}(t_{k}) = U^{i}(t_{k})-\Delta\frac{\partial \mathcal{H}^{i}}{\partial U}(t_{k})$, $k \in \{0, 1, 2, {\ldots}, W-1\}$ and $\Delta$ being the step size ($\frac{\partial \mathcal{H}}{\partial U}$ is from 21). We developed a line-search method to find the step size $\Delta$ that minimizes $J$ for each iteration.

7. Return to step 3.

2.4.   Parameterization

Our model is initialized for the beginning of the year 2014 ($t = 0$), although we used demographic data from 2012, the date of the last South African National HIV Prevalence, Incidence and Behavior Survey ^[30]. We parameterized our model with demographic data from South Africa because of the availability of excellent demographic statistics. If $N_{0}$ is initial total adult (ages 15+) population size, then using prevalence ($\phi$) we determined the infected and the susceptible populations, i.e.

The initial total infected population in each stage was determined by proportion of time a person spends in that Stage. If $N_{\mathrm{Ia}}$, $N_{\mathrm{I1}}$, $N_{\mathrm{I2}}$, $N_{\mathrm{I3}}$ and $N_{\mathrm{I4}}$ represent the total population in the acute, Ⅰ, Ⅱ, Ⅱ and Ⅳ stages respectively, then

The acute stage is very short which means generally it is not enough time for an infected person to be diagnosed, so we assumed that the initial diagnosed population in the acute stage is zero. For the remaining stages, $76.3\%$ of the infected population were considered diagnosed ^[17] and of the diagnosed, $42\%$ are on treatment ^[33]. The initial conditions are summarized in Table 2.

2.5.   Sensitivity

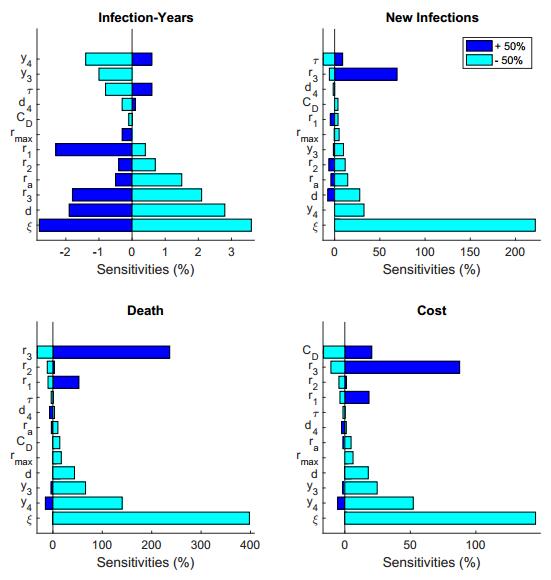
To evaluate the sensitivity of our results to parameter uncertainty, we computed the infection-years, new infections deaths and cost arising from a 50% increase and 50% decrease in the default parameters: Regression rates ($y_{3}$, $y_{4}$), Testing rates ($d$, $d_{4}$), Rate of progression between disease stages ($r_{a}$, $r_{1}$, $r_{2}$, $r_{3}$), Rate of treatment failure ($\tau$), Rate of enrolling people on treatment ($r_{\max}$), Cost of Death ($C_{\mathrm{D}}$) and Percentage reduction in transmission from individuals that know their HIV status ($\xi$).

3.   Results

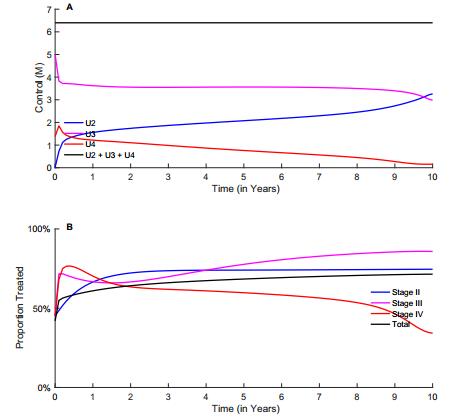
he initial drug availability was assumed to be that which is needed to treat 6.4 million people at any given time, which is enough drugs to treat all of the initial infected population. We simulated our model to determine the levels of treatment that minimize each of the four objectives over a 10-year period. The optimal strategies that minimize infection-years and new infections are similar to each other, and the optimal strategies that minimize death and cost are similar to one another.

To minimize infection-years, the optimal strategy emphasizes early treatment, starting off in the first few months with a sharp decrease in the number of people being treated in Stage Ⅲ from about 5 million to 3.7 million. The decrease in treatment in Stage Ⅲ corresponds with a sharp increases in treatment in Stages Ⅱ & Ⅳ. After this initial dynamics, treatment in Stage Ⅲ stabilizes and a steady decline in treatment of people in Stage Ⅳ with a corresponding increase of treatment in Stage Ⅱ is observed (Figure 2A). The optimal strategy prescribes an initial scale-up of treatment in Stage Ⅱ, Ⅲ and Ⅳ from 42% to about 56%, 69% and 75% respectively. After the initial scale-up, a decrease in the proportion of people treated in Stage Ⅳ and an increase in treatment of Stage Ⅲ is observed (Figure 2B). Treatment of people in Stage Ⅱ increases steadily from 42% and stabilizes at 75% after the second year. Total treatment coverage also increases rapidly from the current coverage of 42% to about 70% and is maintained at about 70% throughout the period.

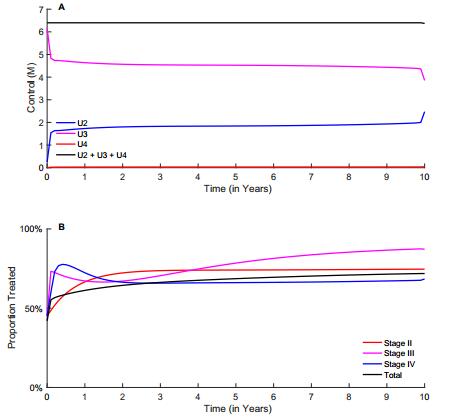
The optimal strategy to minimize new infections also emphasizes early treatment, beginning with a increase in the number of people being treated in Stage Ⅱ within the first year and a steady increase afterwards. The steady increase in treatment in Stage Ⅱ correspond with decreases in Stage Ⅳ. Very few (20,000) people in Stages Ⅳ are being treated. In terms of proportions, the optimal strategy to minimize new infections is similar to that which minimizes infection-years. The initial decrease in the proportion of treatment in Stage Ⅳ when minimizing both infection-years and new infections is not observed here (Figure 3B).

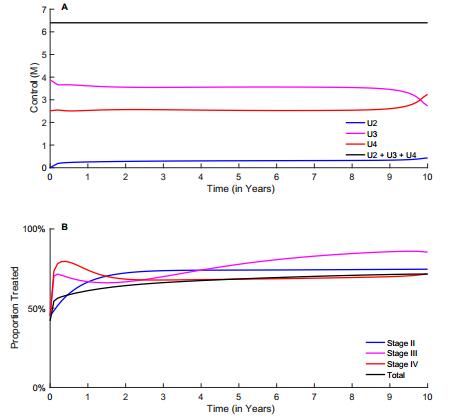
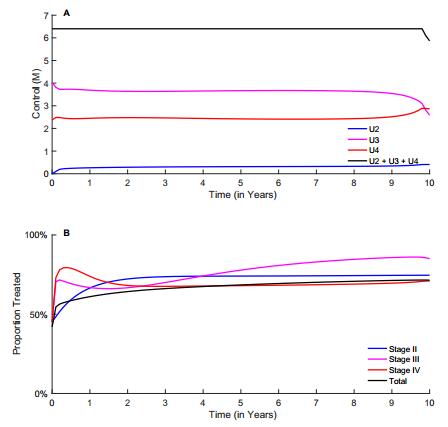
The optimal treatment strategies to minimize deaths and cost are to administer late treatment (i.e., treatment to Stages Ⅲ & Ⅳ) with treatment in Stage Ⅲ being the most favorable (Figures 4A and 5A). An initial scale-up in proportions of people on treatment in all three stages is observed, followed by a decrease in Stage Ⅳ (Figures 4B and 5B). The initial decrease in the proportion of treatment in Stage Ⅳ when minimizing both infection-years and new infections is not observed here.

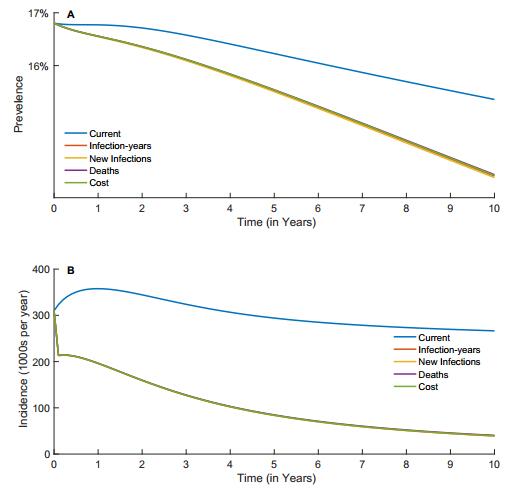
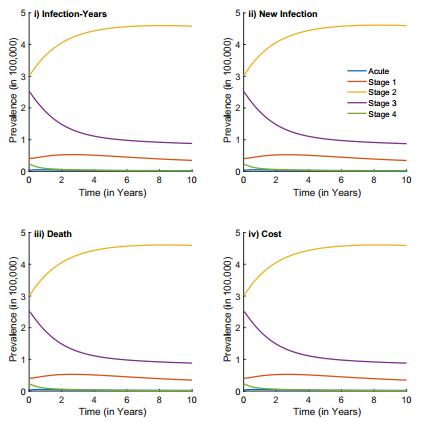
Over the 10-year period, all four optimal strategies resulted in lower prevalence and incidence than the current treatment strategy. Under the current treatment strategy which is a fixed 42% treatment across all three stages at all times, prevalence decreases from from 16.8% to 15.4% and annual incidence from 300,000 to 266,500 in 10 years. The optimal treatment strategies that minimize all four outcomes reduces prevalence from 16.8% to 13.9% (Figure 7A) and annual incidence from 300,000 to about 4,000 (Figure 7B).

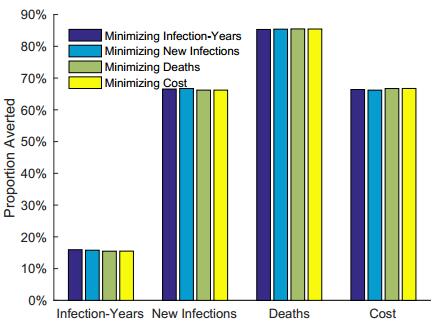
As expected, each of the optimal treatment strategies minimizes its own objective (Figure 8). Deaths are most impacted by the interventions: 85% of the deaths that would occur using the current treatment strategy can be averted by the optimal strategy. Infection-years are the least impacted: only 15% of the infection-years can be averted.

The reduction in transmission from individuals that know their HIV status parameter ($\xi$) is the most sensitive parameter for all four objectives. A 50% increase/decrease in the default value of $\xi$ leads to an increase/decrease of 147-400% in the new infection, deaths and cost and 2.8-3% increase/decrease infection-years (Figure 6). New infection, deaths and cost are sensitive to perturbations in rate of Progression from Stage Ⅲ to Stage Ⅳ ($r_{3}$) and Regression rate from Stage Ⅳ to Stage Ⅲ ($y_{4}$): A 50 % increase/decrease in the value of $r_{3}$ corresponds to an increase/decrease of 69-237% in new infection, deaths and cost while the same perturbation in $y_{4}$ leads to an increase/decrease of 52-140% in deaths and cost (Figure 6). All the other parameters were not very sensitive to perturbation (Figure 6).

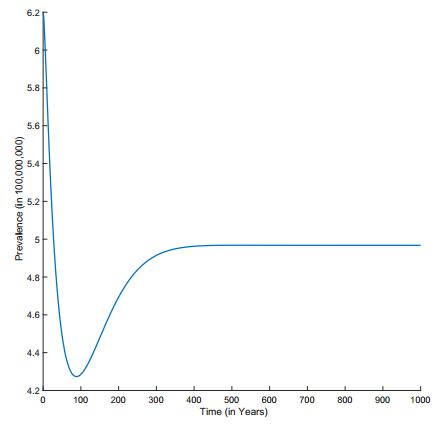
Finally, in the absence of optimal controls, our assumed initial conditions indicate that the dynamics of infected population will reach an equilibrium in about 350 years (Figure 9). For reference, we provide a graph of the population dynamics of each disease stages under the various optimal control strategy (Figure 10).

4.   Discussion

In this paper, we considered the of optimal use of drugs by disease stage to minimize the impact of HIV on the population. Time-dependent optimal control strategies that minimize four objectives, new infection, infection-years, deaths and cost, were presented. Treatment in Stages Ⅱ, Ⅲ and Ⅳ, consistent with the WHO recommendations, were considered.

Our simulations indicated that to minimize infection-years and new infections, emphasis should be placed on treatment in the earlier stages, while to minimize cost and death, the emphasis should be on treating people in Stages Ⅲ & Ⅳ. Our numerical simulations illustrate the effectiveness of adopting each treatment strategy to allow policy makers to learn how much savings they will gain.

The optimal treatment strategy to minimize new infections allocates very little treatment in Stage Ⅳ, driven by our assumption that people in Stage Ⅳ are too weak to engage in sexual activity. The optimal treatment strategies to minimize deaths and cost also place emphasis on treatment in Stage Ⅲ to prevent infected people from progressing to Stage Ⅳ where they die from AIDS. The similarity of treatment for death and cost is because the cost associated with deaths is very high relative to the other costs, thus minimizing deaths is also minimizing cost.

Our results indicated modest reduction of HIV prevalence from the use of the optimal treatment strategies. The modest reduction of HIV prevalence should be expected because a drastic reduction of HIV-related deaths will lead to relatively large numbers of people living with HIV in the population. The use of the optimal treatment strategies however, leads to a substantial reduction in HIV annual incidence, from 300,000 to about 4,000. For comparison, the annual HIV incidence of the adult population (15–49) in South Africa in 2016 was 270,000 ^[32].

The reduction in transmission from individuals that know their HIV status ($\xi$), Rate of progression from Stage Ⅲ to Stage Ⅳ ($r_{3}$) and Regression rate from Stage Ⅳ to Stage Ⅲ ($y_{4}$) are the most sensitive to perturbations. This has implication for HIV control, e.g., HIV prevention programs could lead to increase in $\xi$ from safer sexual habits, thus substantially reducing infections, deaths and cost. $r_{3}$ and $y_{4}$ are related to treatment: promoting treatment of infected population will lead to a reduction in $r_{3}$ and adherence to treatment will lead to an increase in $y_{4}$ leading to substantial gains.

The choice of the best time horizon for our problem was a challenge. A longer time horizon better represents the scale of changes on several generations of HIV infections e.g. reducing transmission. Policymakers however, often prefer a shorter time horizon to answer questions of what can be done immediately to control the epidemic. We therefore believe a 10-year horizon problem is a good compromise. It is important to give more weight in the objective function to earlier rather than later control, so we therefore discounted cost by a rate of 3% ^[37].

We ran our model to equilibrium to determine if the population dynamics observed in our results are dominated by the dynamics of the model towards its equilibrium, by the optimal controls or a mix of these two effects. In the absence of controls, it takes more than three centuries for the infected population dynamics to attain an equilibrium. This is far greater than the 10-year time horizon for our analysis: it is therefore safe to assume that dynamics observed in our results are most likely due to the optimal controls.

In addition to improving their health directly, treatment of infected people is known to reduce their ability to transmit the virus to uninfected people. Policy makers, especially in limited-resource settings, continually seek better ways of harnessing the benefits of treatment. We hope that the results of this modeling study, despite its necessary simplification, can help guide policy decisions.

Acknowledgments

The authors wish to acknowledge Dr. Suzanne Lenhart of the National Institute for Mathematical and Biological Synthesis (NIMBioS) for her guidance on our methods. We also wish to thank Oregon State University for funding for this study.

Conflict of interest

The authors declare there is no conflict of interest.

Appendix: Analysis of optimal control

Given optimal controls ($U_2^{*}, U_3^{*}, U_4^{*}$) and the corresponding state solutions

$X^{*} = (I_{\mathrm{Ua}}^{*}$, $I_{\mathrm{U1}}^{*}, I_{\mathrm{U2}}^{*}$, $I_{\mathrm{U3}}^{*}$, $I_{\mathrm{U4}}^{*}$, $I_{\mathrm{Da}}^{*}$, $I_{\mathrm{D1}}^{*}$, $I_{\mathrm{D2}}^{*}$, $I_{\mathrm{D3}}^{*}$, $I_{\mathrm{D4}}^{*}$, $I_{\mathrm{T2}}^{*}$, $I_{\mathrm{T3}}^{*}$, $I_{\mathrm{T4}}^{*})$ from solving the state system (4), there exist adjoint variables $\theta$ that satisfy the adjoint equations

with the transversality condition

The optimal control characterization holds,

and

To analyze all four objective functions at once, we can rewrite (29) as

for $i = 1, 2, 3, {\ldots}, 14$ and $k \in \{{\mathrm{I}}, {\mathrm{NI}}, {\mathrm{D}}, {\mathrm{C}}\}$. The partial derivative of the objective functions $\frac{\partial f_{j}}{\partial X_{i}}(t, S, I, U)$ are

where

$\psi(t, U)$ collects all the terms with the control variables $U_{i}$ in the Hamiltonian,

This has derivatives

so that

The parts of the partial derivative of the terms in the adjoint equation arising from the right hand side of the system of differential equations minus all the controls terms $\theta^{T} \frac{\partial \ell}{\partial I_{i}}(t, X)$ is

where