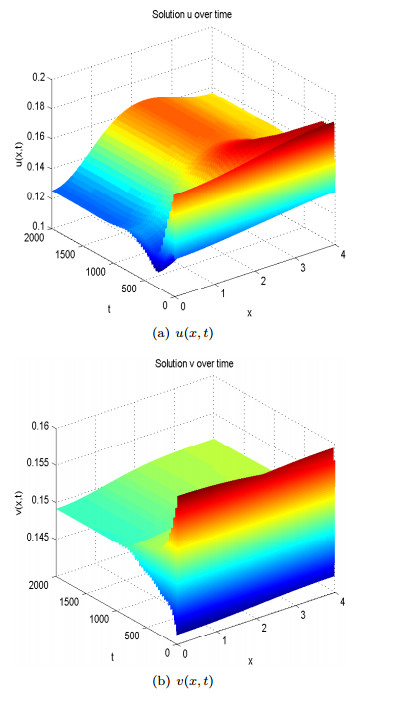
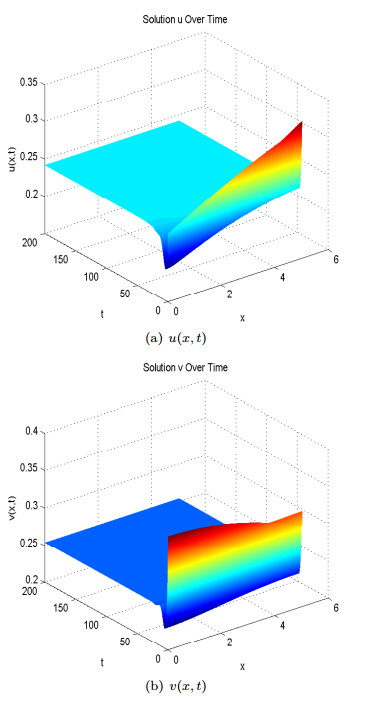
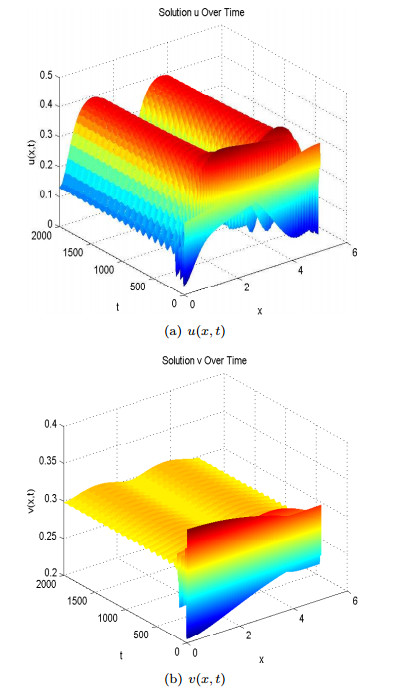
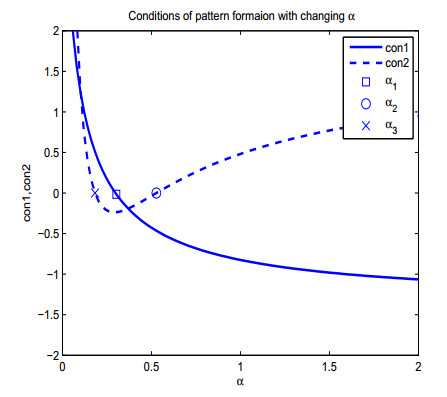
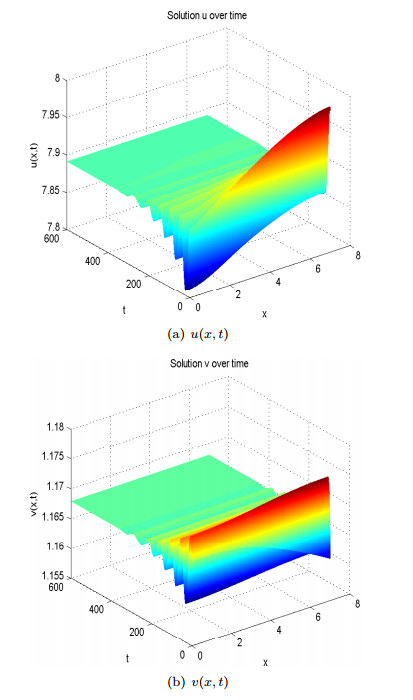
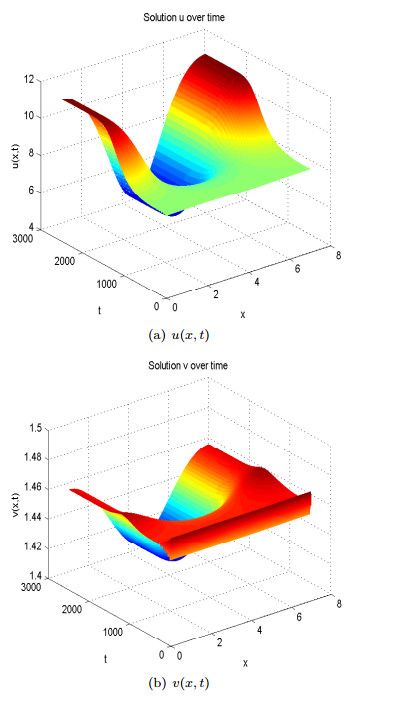
We propose and analyse a reaction-diffusion-advection predator-prey model in which we assume that predators move randomly but prey avoid predation by perceiving a repulsion along predator density gradient. Based on recent experimental evidence that anti-predator behaviors alone lead to a 40% reduction on prey reproduction rate, we also incorporate the cost of anti-predator responses into the local reaction terms in the model. Sufficient and necessary conditions of spatial pattern formation are obtained for various functional responses between prey and predators. By mathematical and numerical analyses, we find that small prey sensitivity to predation risk may lead to pattern formation if the Holling type Ⅱ functional response or the Beddington-DeAngelis functional response is adopted while large cost of anti-predator behaviors homogenises the system by excluding pattern formation. However, the ratio-dependent functional response gives an opposite result where large predator-taxis may lead to pattern formation but small cost of anti-predator behaviors inhibits the emergence of spatial heterogeneous solutions.
1.
Introduction
Oil pollution is a critical environmental challenge that severely impacts marine ecosystems, coastal areas, public health, and economic activities. According to a 2024 report, ten major oil spills from tankers occurred globally, with six incidents involving oil leaks exceeding 700 tons, highlighting the urgent need for effective remediation strategies [1]. Common spilled oil types comprise crude oil (35%), diesel (20%), marine fuel oil (10%), gasoline (8%), and condensate (3%) [2]. Various approaches have been applied to tackle oil pollution, including in situ burning, chemical dispersants, bioremediation, and physical methods such as skimming and adsorption [3]. Among these, adsorption is widely regarded as one of the most efficient and practical techniques due to its operational simplicity, cost-effectiveness, and environmental friendliness [4]. Notably, naturally derived adsorbents offer significant advantages in marine oil spill remediation due to their biocompatibility, recoverability, and effective reusability [5].
Cellulose aerogels have emerged as promising adsorbents due to their ultra-porous structure, low density, and excellent biodegradability. These materials typically possess specific surface areas ranging from 10 to 975 m2/g, porosities between 84.0% and 99.9%, and bulk densities as low as 0.0005 g/cm3 [6]. Compared to silica and synthetic polymer aerogels, cellulose aerogels offer enhanced compressive strength (5.2 kPa to 16.67 MPa) and superior environmental compatibility [6]. Recent studies have explored biomass-derived aerogels from recycled paper [7], wheat straw [8], water hyacinth [9], coffee grounds [10], sugarcane bagasse [11], coconut fiber [12], banana peel [13], and textile waste [14]. Crosslinking agents such as polyamide epichlorohydrin (PAE) [9], Kymene 557H [7], polyvinyl alcohol (PVA) [15], and alkyl ketene dimer (AKD) [11] are commonly used to enhance structural integrity.
Despite these advancements, the development of biodegradable, cost-effective, and high-performance oil adsorbents remains a pressing challenge. This study introduces a novel cellulose aerogel synthesized from RP waste—a sustainable solution that addresses both marine oil pollution and agricultural residue management. The aerogel exhibits high porosity and biodegradability, making it a strong candidate for diesel oil adsorption. Its adsorption behavior is thoroughly evaluated using kinetic, isotherm, and thermodynamic models. The novelty of this work lies in the utilization of an underused biomass resource, the optimization of structural properties, and a comprehensive performance assessment under varying conditions. The findings support its potential for scalable and eco-friendly applications in oil spill remediation.
The materials and methods employed in this study are described in detail in the following section.
2.
Materials and methods
2.1. Materials
The primary material used in this study were cellulose fibers extracted from RP, following the procedure described by Nguyen et al. [16]. Specifically, fibers were obtained from RP via a two-step chemical treatment. In the first step, lignin was removed through delignification using sodium chlorite (NaClO2) in the presence of acetic acid (CH3COOH), resulting in the formation of holocellulose. This step involved sequential reagent addition under controlled temperature conditions (60 ℃), followed by extended soaking to ensure complete delignification. In the second step, the holocellulose underwent alkaline treatment with 17.5% sodium hydroxide (NaOH) to remove hemicellulose and isolate cellulose. The reaction mixture was then neutralized with 10% CH3COOH, thoroughly rinsed with distilled water, and oven-dried at 80 ℃. The resulting cellulose exhibited high purity and was deemed suitable for aerogel fabrication. The selected test oil is diesel oil (DO) 0.05S, with a density ranging from 820 to 860 kg/m3 at 15 ℃. The chemicals used in the study include sodium sulfate anhydrous (Na2SO4) and 98% sulfuric acid (H2SO4), both sourced from Xilong, China. The crosslinking agent employed is PVA. Additionally, other chemicals such as acetic acid (CH3COOH), sodium hydroxide (NaOH), and sodium chlorite (NaClO2) with a purity of 80% were also used, all originating from China.
2.2. Preparation of hydrophobic cellulose aerogels
Cellulose fibers were mixed with deionized water for 1 h to form a homogeneous suspension [17]. A 5% PVA solution was then dispersed into the mixture to achieve the cellulose fiber and PVA concentrations as determined by the findings of Nguyen et al. [16], presented in Table 1. The resulting mixture was subsequently sonicated using a Hielscher ultrasonic homogenizer. The solution was then frozen at -4 ℃ for 24 h before being subjected to freeze-drying for 48 h using a vacuum freeze dryer [18]. The aerogel samples were further crosslinked and structured into a three-dimensional network by annealing at 120 ℃ for 3 h [19]. The hydrophobic modification of the aerogel was carried out by coating its surface with methyltrimethoxysilane (MTMS) via chemical vapor deposition. This process involved placing the aerogel samples inside a large glass chamber containing an open glass vial prefilled with 5 mL of MTMS. The glass chamber was sealed and incubated at 80 ℃ for 3 h. Finally, excess MTMS was removed by placing the glass chamber in a fume hood for 30 min [20]. The cellulose aerogel synthesized from RP in this study is denoted as RP aerogel.
2.3. Characterization of cellulose aerogels
The morphology of the aerogel was analyzed using a scanning electron microscope (SEM, JSM-IT500 InTouchScope™). Functional groups were identified via Fourier-transform infrared spectroscopy (FTIR, Agilent Cary 630). The specific Brunauer–Emmett–Teller (BET) surface area, pore volume, and average pore diameter were measured using nitrogen adsorption-desorption analysis (Micromeritics® TriStar Ⅱ Plus Version 3.03). The water contact angle (WCA) was determined using an optical contact angle measuring device (OCA 20, model ES, DataPhysics, Germany) with an 8 µL water droplet, followed by analysis using specialized software.
The apparent density (ρa, g/cm3) of the aerogel was calculated as the ratio of its mass (m, g) to its volume (v, cm3), as expressed in Eq 1 [21]. Meanwhile, the porosity (Φ, %) was determined based on the apparent density of the aerogel (ρa, g/cm3) and the average density (ρb, g/cm3) of cellulose fibers (ρcellulose = 1.224 g/cm3 [16]) and PVA (ρPVA = 1.3 g/cm3, sourced from Merck), following Eq 2 [21].
2.4. Methods for evaluating oil adsorption efficiency
In this study, the amount of oil adsorbed per gram of material at equilibrium (qe, g/g) and at any given time (qt, g/g) was determined based on the change in oil concentration in the solution before and after the adsorption process. The oil removal efficiency (H, %) reflects the material's oil treatment capability and is calculated based on the difference between the initial and equilibrium oil concentrations [22]:
where Co is the initial oil concentration (g/L), Ce is the oil concentration at equilibrium (g/L), Ct is the oil concentration at a specific time (g/L), V is the solution volume (mL), and M is the mass of the adsorbent used (g).
2.5. Adsorption isotherm modeling for oil/water mixtures
In this study, four common isotherm models (Langmuir, Freundlich, Temkin, and Dubinin–Radushkevich) were employed to describe the equilibrium adsorption data of diesel oil in water at various initial concentrations (5, 10, 15, 20, 25, 30, and 35 g/L [23]). The investigation was conducted at an absolute temperature of 298 K under constant pH conditions.
2.6. Adsorption kinetics study of oil/water mixture on aerogel
To investigate the adsorption kinetics of oil on the aerogel, the samples were exposed to the oil/water mixture, and the adsorption capacity was determined at time intervals of 2, 5, 10, 30, 60, 90,120,180,240, and 300 min [24]. The kinetic constants k1 and k2 were determined using the pseudo-first-order and pseudo-second-order kinetic models, respectively [25].
2.7. Investigation of the influence of environmental factors
To evaluate the influence of environmental factors on the adsorption capacity and oil/water separation efficiency of the aerogel, experiments were conducted under varying pH conditions (3–11) [26], salinity levels (0‰, 5‰, 12‰, 25‰, and 35‰) [26], and water temperatures (15–55 ℃) [26].
3.
Results and discussion
3.1. Characteristics of aerogels
3.1.1. Morphology and structure of the aerogel
As shown in Figure 1, the aerogel was synthesized from cellulose fibers extracted from RP, PVA (as a crosslinking agent), and deionized water (an environmentally friendly solvent). In this study, PVA acts as a physical crosslinker by forming hydrogen bonds with the abundant hydroxyl groups present on the cellulose chains. These non-covalent interactions create an interconnected three-dimensional polymer network, which enhances the mechanical stability and porosity of the composite, thereby improving its oil adsorption performance. The resulting product exhibited the characteristic white color of cellulose, a porous structure, and an ultra-lightweight nature [16].
SEM images (Figure 2) reveal that the aerogel exhibits an open porous network structure with large voids and no distinct microscopic arrangement. This indicates that cellulose fibers self-assemble through hydrogen bonding, forming a three-dimensional porous structure [27]. This unique structure imparts key properties to the aerogel, including sound and thermal insulation, efficient adsorption, and high mechanical strength [11,28,29].
Table 2 presents the density, porosity, and surface area of the synthesized aerogel under the conditions specified in Table 1. The aerogel exhibits a density of 0.027 ± 0.002 g/cm3, which falls within the range of other aerogels, such as those derived from raw pineapple leaf fibers (0.013–0.033 g/cm3) [30] and wastepaper and banana peels (0.0235–0.0297 g/cm3). This density is lower than that of aerogels derived from rice straw (0.05–0.06 g/cm3) [28], sugarcane bagasse (0.0473 g/cm3) [11], and synthetic cellulose aerogels (0.040 g/cm3) [31], but higher than aerogels from waste wool fibers (0.004–0.023 g/cm3) [24].
The aerogel exhibits a porosity of 98.15% ± 0.17%, which is comparable to aerogels from waste wool fibers (97.73%–99.63%) [24], pineapple leaf fibers (96.98%–98.85%) [18], corn stalks (98.13%) [32], and wastepaper combined with banana peels (97.87%–98.37%) [13]. This value is higher than that of hybrid aerogels from coffee grounds and cotton fibers (92%–95%) [10], sugarcane bagasse (95.9%) [11], and coconut fibers (94.2%–96.7%) [12], but lower than that of aerogels derived from Eichhornia crassipes (>99.6%) [9] and raw pineapple leaf fibers (~99%) [30].
Additionally, Table 2 shows that the BET surface area of the RP aerogel is 7.56 ± 0.07 m2/g, while the cumulative pore volume determined by the BJH adsorption method is 0.0025 cm3/g, and the average pore diameter (4 V/A) is 20.8 Å (2.08 nm). According to Lang et al. [33], a larger pore volume can enhance oil absorption capacity; however, if the pore size is excessively large, the surface tension of the liquid may be insufficient to retain the oil, leading to reduced adsorption efficiency. The surface area of RP aerogels is higher than that of aerogels derived from pineapple leaf waste (5.60 m2/g) [29].
3.1.2. Hydrophobic and FTIR analysis of aerogels
The MTMS-coated RP aerogels exhibit excellent superhydrophobicity, with a WCA of up to 152.7° (Figure 3). The MTMS coating forms a stable Si–O–Si cross-linked network via chemical bonding during the chemical vapor deposition process [34]. The WCA is influenced by the functional groups on the aerogel surface, particularly hydroxyl groups, which facilitate the silanization process. This exceptional hydrophobicity enables the RP aerogels to float on water, highlighting its potential application in oil spill remediation. The superhydrophobic nature of the aerogel is confirmed by the presence of methyl groups (–Si–O–CH3–) from the MTMS solution [35]. The WCA of the RP aerogel is higher than that of several other hydrophobic aerogels, such as pineapple leaf fiber aerogel (146.1°) [18], waste wool fiber aerogel (138°) [24], recycled paper aerogel (143–145°) [31], corn stalk aerogel (130.5°) [32], and hybrid coffee-cotton aerogel (139°) [10]. However, it is lower than water hyacinth stem aerogel (154.8°) [9] and rice straw aerogel (151 ± 7°) [36]. Based on the WCA classification [37], RP aerogels are categorized as superhydrophobic (150° < θ < 180°), demonstrating their high potential for waterproofing and oil separation applications.
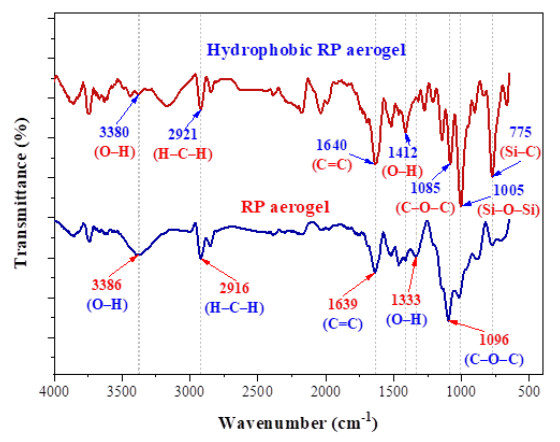
To evaluate the surface alteration of RP aerogels, Fourier-transform infrared spectroscopy (FTIR) analysis was conducted on both uncoated RP aerogels and MTMS-coated RP aerogels (Figure 4).
FTIR analysis was conducted to compare the surface modifications between RP aerogels and hydrophobic RP aerogels (Figure 4). The results indicate that both RP aerogels and their hydrophobic counterpart exhibit characteristic absorption bands of cellulose. Specifically, the presence of PVA in the aerogel structure is confirmed by a broad absorption band at 3386 and 3380 cm-1, which corresponds to hydrogen bonding (O–H) interactions [38]. The bands at 2921 and 2916 cm-1 are attributed to the stretching vibrations of the H–C–H bond in alkyl (CH2) groups from PVA and cellulose [24]. The C = C stretching vibrations (benzene rings) are observed at 1640 and 1639 cm-1 [39], while the bending vibrations of the O–H group (alcohol) appear at 1412 and 1333 cm-1 [40]. The characteristic C–O–C stretching vibrations are detected at 1096 and 1085 cm-1 [18]. Notably, after MTMS coating, the hydrophobic RP aerogels exhibit two additional peaks: A new peak at 1005 cm-1, characteristic of the Si–O–Si bond [21], and another peak at 775 cm-1, corresponding to the Si–C bond [41]. These spectral changes confirm the formation of a Si–O–Si network via the chemical vapor deposition process of MTMS [34]. The silanization process replaces the hydroxyl (–OH) groups with –O–Si–(CH3)3 functional groups, significantly enhancing the hydrophobicity of the aerogel [18].
Table 3 provides a comprehensive summary of the functional groups identified in the chemical composition of RP aerogels. In addition to the characteristic functional groups, including hydrogen bonding (O–H), H–C–H bonds in alkyl (CH2) groups, C = C stretching vibrations (benzene rings), O–H groups (alcohols), and C–O–C stretching vibrations, the hydrophobic RP aerogels further exhibit the formation of Si–O–Si and Si–C bonds. These bonds, introduced via the chemical vapor deposition of MTMS, significantly enhance the hydrophobicity and structural stability of the aerogels.
3.2. Investigation of factors affecting oil adsorption equilibrium
The adsorption performance of RP aerogels in the oil/water system was comprehensively evaluated under various environmental conditions. Specifically, the study focused on the effects of pH, oil concentration, contact time, water temperature, and salinity to determine the practical applicability of this material.
3.2.1. Effect of pH
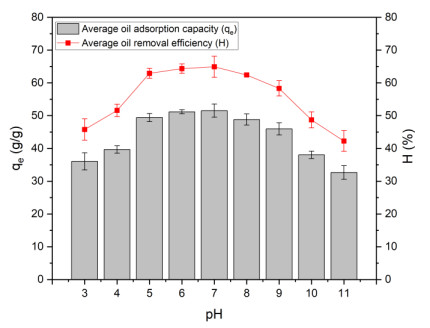
Figure 5 illustrates the effect of pH on the oil adsorption capacity of RP aerogels. The results indicate that the adsorption capacity increases as pH rises from 3 to 5, reaching a maximum of 51.5306 g/g at pH 7, and then gradually declines as pH exceeds 8, with a sharp decrease at pH 10 (38.0366 g/g) and pH 11 (32.6494 g/g). ANOVA analysis confirms a statistically significant difference between pH levels below 5 and above 8, while no significant variation is observed in the pH range of 5–8. This variation may be attributed to the surface charge of cellulose aerogels [26]. In an acidic environment, the positively charged aerogel surface interacts with negatively charged oil molecules, facilitating demulsification; however, excessive H+ ions may compete with oil molecules, reducing adsorption efficiency. At neutral pH, the balance among hydrophobic interactions, Van der Waals forces, and hydrogen bonding optimizes oil adsorption. In alkaline conditions, the aerogel surface becomes negatively charged due to the presence of hydroxyl (−OH) groups, leading to electrostatic repulsion with oil molecules and a subsequent decline in adsorption performance. Furthermore, at pH 10–11, the saponification reaction between NaOH and oil reduces the available oil for adsorption [44]. The influence of pH on the interaction behavior between cellulose aerogels and oil is summarized in Table 4. These findings are consistent with previous studies on carboxymethylated cellulose nanofibril (CNF) aerogels [45] and CNF-SP aerogels [26]. Based on these results, an optimal pH of 7 will be applied in subsequent experiments to evaluate the effect of oil concentration on the adsorption process of the aerogel.
3.2.2. Effect of initial oil concentration and adsorption isotherm
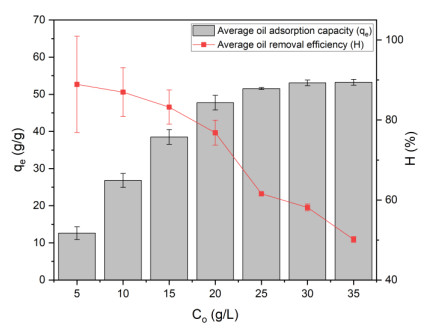
The initial oil concentration plays a crucial role in the adsorption kinetics and thermodynamics, influencing saturation levels, oil diffusion rates into the porous structure, and removal efficiency [46]. The experimental results (Figure 6) indicate that the removal efficiency reaches 88.90% at an initial oil concentration of 5 g/L but declines to 50.14% as the concentration increases to 35 g/L, due to the limited availability of adsorption sites. The adsorption capacity increases with oil concentration, particularly from 12.6064 ± 1.7067 g/g at 5 g/L to 51.5398 ± 0.2490 g/g at 25 g/L. At low concentrations, the excess of available adsorption sites facilitates effective oil adhesion. However, when the concentration exceeds 25 g/L, rapid saturation occurs, slowing the adsorption rate and leading to an insignificant increase from 51.5398 ± 0.2490 g/g at 25 g/L to 53.2324 ± 0.7880 g/g at 35 g/L.
ANOVA analysis confirms a statistically significant difference between concentrations ranging from 5 to 25 g/L, whereas no significant variation is observed at higher concentrations. Therefore, 25 g/L is identified as the optimal initial oil concentration for subsequent studies on the effect of contact time on the oil adsorption process of RP aerogels.
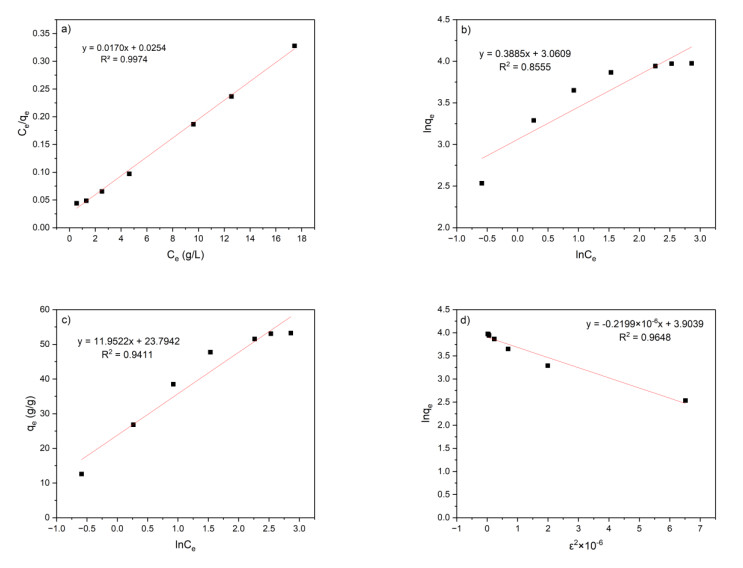
Figure 7 presents the adsorption isotherms of RP aerogels fitted to the Langmuir, Freundlich, Temkin, and Dubinin–Radushkevich models. The parameters and correlation coefficients (R2) of these four adsorption isotherm models are summarized in Table 5.
A comparison of the correlation coefficients (R2) of all models in Table 5 reveals that the oil adsorption process of RP aerogels follows the Langmuir isotherm model, with an R2 value of 0.9974. This demonstrates that the Langmuir model provides the best fit for describing the oil adsorption behavior of RP aerogels. As established, the Langmuir model assumes that adsorption occurs as a monolayer, with all adsorption sites on the aerogel surface being homogeneous and exhibiting uniform binding affinity between molecules. Furthermore, the strong agreement between the experimental data and the Langmuir model suggests the absence of interactions between adsorbed molecules, meaning the adsorption process is independent of whether neighboring sites are occupied [47]. The adhesion of oil onto the aerogel surface primarily occurs due to intramolecular interactions and Van der Waals forces [48]. The adsorption mechanism in this model consists of three main steps: (ⅰ) Diffusion of adsorbate ions or residues to the outer surface of the adsorbent; (ⅱ) diffusion into the porous structure of the adsorbent; and (ⅲ) adsorption of the adsorbate residues onto the inner surface of the adsorbent [49]. The maximum oil adsorption capacity of the RP aerogel, as determined by the Langmuir model, was 58.82 g/g, comparable to that of water hyacinth-based aerogels (52.03–58.82 g/g) [50] and superior to many other cellulose-based aerogels reported in the literature. For instance, office paper-derived cellulose aerogels exhibited adsorption capacities of 29.07 g/g for biodiesel and 26.26 g/g for marine diesel oil [51]; regenerated pomelo peel aerogels reached 49.8 g/g for crude oil [21]; and pineapple leaf-derived aerogels achieved 37.9 g/g for engine oil [18]. These findings underscore the high potential of RP aerogels for practical applications in oil spill remediation.
Table 6 presents the equilibrium parameter (RL) values at 25 ℃ for the Langmuir isotherm model. The RL values for RP aerogels range from 0.0409 to 0.2301. Since the RL values fall within the range of 0 < RL < 1, the adsorption process is considered favorable [52], indicating that the adsorbent material exhibits strong adhesion to the adsorbate and the adsorption process occurs efficiently.
Based on the Freundlich isotherm model, the adsorption process is considered physical when the Freundlich constant n > 1 [53]. Additionally, a value of 0 < 1/n < 1 indicates a heterogeneous surface and a favorable adsorption process [54]. According to the Dubinin–Radushkevich (D–R) model, the mean free energy of adsorption (E) can be used to determine the adsorption mechanism: if 8 < E < 16 kJ/mol, the process is predominantly chemisorption, whereas if E < 8 kJ/mol, it is primarily physisorption [52]. The calculated results from the D–R model indicate that the mean free energy of RP aerogels is 1.5079 kJ/mol, which is significantly lower than 8 kJ/mol. This confirms that the oil adsorption process of RP aerogels is primarily governed by physisorption, where Van der Waals forces play a crucial role in retaining oil molecules on the aerogel surface.
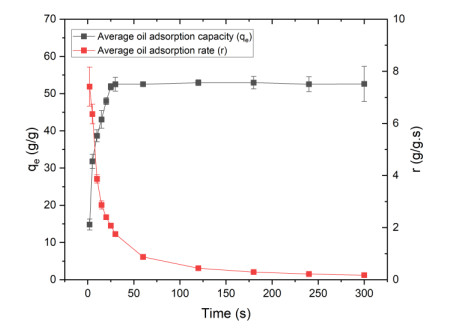
3.2.3. Effect of contact time and adsorption kinetics
Time is a crucial factor influencing the adsorption process; therefore, determining the adsorption rate is essential for designing and evaluating the performance of adsorbent materials in oil treatment [36]. To clarify this effect, the study investigated the oil adsorption capacity of cellulose aerogels over a time range of 2–300 s. The results provide insights into adsorption kinetics, allowing for the optimization of contact time to enhance oil removal efficiency. Detailed findings are presented in Figure 8. RP aerogels exhibited a rapid adsorption rate within the first 10 s, averaging 3.8668 g/g·s with an adsorption capacity of 38.6676 ± 1.5978 g/g. Adsorption equilibrium was reached after 25 s (51.8283 ± 0.8650 g/g), indicating a strong affinity of the material for diesel oil. In the initial stage, active sites on the aerogel surface remained largely unoccupied, facilitating rapid adsorption. As the surface became gradually saturated, competition among oil molecules reduced the adsorption rate until equilibrium was achieved. Additionally, the low viscosity of diesel oil allowed it to penetrate easily into the aerogel's porous structure, resulting in a fast and efficient adsorption process [36,55]. Compared to previous studies, the adsorption rate of RP aerogels within the first 10 s aligns with the findings of the previous studies [56,57], but the equilibrium time (25 s) is shorter than that reported by Phuong [58], where the material required 30 s to reach saturation. RP aerogels also exhibited a faster adsorption rate than WPBP aerogels (35 s) [13] and the aerogel studied by Feng et al. [56] (30 s). However, compared to the findings of Shi et al. [21], where equilibrium was reached in under 20 s, RP aerogels displayed a slower adsorption rate. This material also had a lower adsorption rate than PF/CF composite aerogels, which reached equilibrium in just 20 s [57].
ANOVA analysis indicated no significant difference in adsorption capacity after 25 s of contact time. Therefore, this duration was selected as the optimal time for developing the adsorption kinetic equations and conducting subsequent experiments.
Figure 9 illustrates that the RP aerogels exhibited a rapid adsorption rate within the first 10 seconds, after which they became completely saturated with diesel oil.
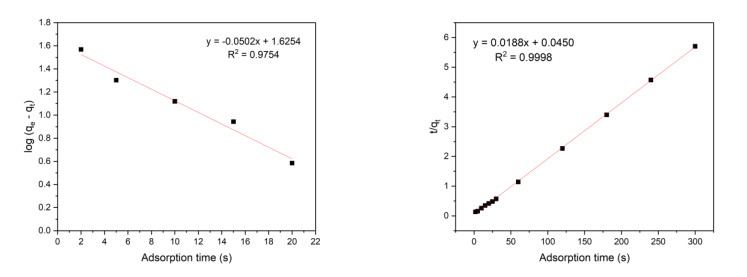
The pseudo-first-order and pseudo-second-order kinetic equations for RP aerogels are presented in Figure 10.
The adsorption kinetic parameters of RP aerogels are summarized and presented in Table 7.
The pseudo-first-order and pseudo-second-order kinetic equations of RP aerogels are presented in Figure 10, with the kinetic parameters summarized in Table 7. These two kinetic models were applied to describe the oil adsorption process of the aerogel. The results indicate that the pseudo-second-order model provides a better fit for describing the adsorption kinetics of RP aerogels, as evidenced by the correlation coefficient R2 (Table 7). Specifically, the pseudo-second-order equation exhibits the highest correlation coefficient (R2 = 0.9998), with an adsorption capacity of 53.1915 g/g. This suggests that the oil adsorption process of RP aerogels follows a second-order kinetic model, which involves two main stages: (ⅰ) Boundary layer diffusion and (ⅱ) pore diffusion [58]. These findings are also consistent with the study by Feng et al. [56].
3.2.4. Effect of salinity
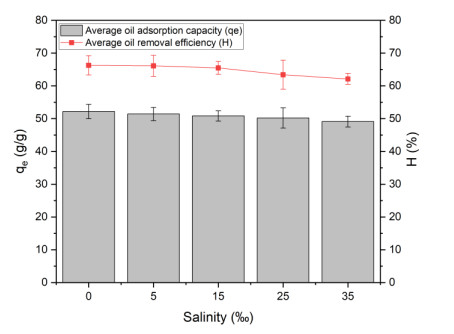
Various physicochemical parameters, such as temperature and salinity, can influence the spread rate of oil spills in a natural water body [2]. In this study, the oil adsorption capacity of the aerogel was evaluated under different salinity levels: 0‰, 5‰, 15‰, 25‰, and 35‰. These salinity levels were selected based on real-world conditions, representing freshwater (0‰), estuarine water (5‰), offshore environments (25‰), and seawater (35‰). The results are presented in Figure 11.
Experimental results indicate that the oil adsorption capacity of RP aerogels slightly decreases with increasing salinity. Specifically, at 0‰ salinity, the adsorption capacity reached 52.1700 g/g, whereas at the highest tested salinity level (35‰), it decreased to 49.0989 g/g. However, the difference in adsorption capacity across salinity levels is minimal, and statistical analysis confirms no significant variation among the tested salinity levels. A similar decreasing trend was observed in oil removal efficiency, which declined from 66.26% (0‰) to 62.12% (35‰). Overall, despite the slight reduction in oil adsorption capacity and removal efficiency, RP aerogels maintain stable oil adsorption performance in seawater and brackish water environments. This highlights their high potential for real-world applications in marine oil spill remediation, making them suitable for deployment in various saline aquatic ecosystems.
The slight decrease in oil adsorption capacity and removal efficiency with increasing salinity can be attributed to the influence of salt ions on the surface charge of the aerogel [59], which alters the interactions between the material and oil. In high-salinity environments, Na+ and Cl- ions can adhere to the aerogel surface, modifying its surface charge. This may reduce the attractive forces between the aerogel and oil molecules, especially if the adsorption process relies on electrostatic interactions or van der Waals forces. Additionally, these ions may compete with oil molecules for adsorption sites on the aerogel surface, further decreasing overall adsorption efficiency. Moreover, some adsorption sites that would otherwise accommodate oil molecules may be occupied by Cl- ions, thereby reducing the aerogel's oil adsorption capacity [26]. This result is consistent with the findings of Wang et al. [26], in which CNF-SP aerogel also demonstrated high and stable oil adsorption efficiency. However, increasing the salinity from 0‰ to 35‰ resulted in a slight decrease in oil adsorption capacity from 29.44 to 28.17 g/g.
3.2.5. Effect of water temperature and thermodynamic study of adsorption
The effect of temperature on the adsorption of oil molecules by the aerogel describes the relationship between temperature and the concentration of oil molecules adsorbed onto the adsorbent at the optimal contact time. The results are presented in Figure 12.
Experimental results indicate that the oil adsorption capacity of RP aerogels is significantly influenced by water temperature. At lower temperatures (5–15 ℃), the adsorption capacity increased from 51.3203 to 53.8498 g/g, reaching its maximum at 15 ℃. This trend can be attributed to the higher viscosity of oil at lower temperatures, which enhances its interaction with the aerogel surface. Additionally, the porous structure of the aerogel remains stable, facilitating efficient oil retention. However, as the temperature increased to 25–35 ℃, the adsorption capacity gradually declined, dropping to 43.1449 g/g at 35 ℃. This decrease may result from the weakening of Van der Waals forces between the oil and aerogel, along with the lower viscosity of oil, making it more prone to flowing out of the porous structure. A more pronounced reduction was observed at higher temperatures (45–55 ℃), with the adsorption capacity decreasing to 33.9115 g/g at 55 ℃. This could be due to oil evaporation, reducing the amount of oil available for adsorption, as well as reduced capillary action in high-temperature conditions. Similarly, the adsorption efficiency (%) decreased from 65.34% at 5 ℃ to 43.54% at 55 ℃, with the highest efficiency recorded at 15 ℃ (69.32%), indicating that this is the optimal temperature for RP aerogel performance. Overall, RP aerogels perform most efficiently within the temperature range of 5–25 ℃, with peak adsorption at 15 ℃. At temperatures above 35 ℃, oil retention decreases sharply, suggesting that high temperatures are unfavorable for the oil adsorption process of RP aerogels.
Experimental results indicate that temperature plays a crucial role in the oil adsorption capacity of the aerogel. At lower temperatures, oil exhibits higher viscosity, which helps maintain strong interactions with the aerogel surface while preserving the stability of its porous structure, thereby enhancing oil retention efficiency. However, at excessively low temperatures (around 5 ℃), the high viscosity hinders oil diffusion into the aerogel's pores, reducing adsorption capacity [60]. As the temperature increases from 5 to 15 ℃, the viscosity of the oil decreases, allowing it to penetrate deeper into the aerogel's porous network, leading to an improved adsorption capacity that peaks at an optimal temperature [44,61]. However, when the temperature continues to rise (within the range of 25–55 ℃), the oil becomes excessively diluted, weakening its adhesion to the aerogel surface and pore walls, resulting in a decline in oil retention capacity [60]. Additionally, the increased desorption rate at higher temperatures reduces the amount of oil retained within the material, thereby lowering oil recovery efficiency [62,63,64]. Furthermore, oil evaporation at elevated temperatures may further decrease the available oil for adsorption, while capillary action within the material becomes less effective.
Other experimental studies have confirmed this trend. For instance, research by Mahmoud et al. [65] demonstrated that when the temperature increased from 28 to 50 ℃, the oil removal rate dropped from 88% to 24%, while the adsorption capacity declined from 1.60 to 1.21 g/g due to the accelerated oil release from the pores. Similarly, a study on cotton fibers [66] also reported a significant decrease in oil adsorption capacity and removal efficiency when the temperature exceeded 20 ℃. In the case of CNF-SP aerogel, the adsorption capacity remained high (29.44–29.77 g/g) in the temperature range of 0–25 ℃; however, at 35 and 45 ℃, the adsorption capacity decreased to 26.96 and 20.19 g/g, respectively. Notably, when the temperature exceeded 50 ℃, the 3D structure of the aerogel was severely affected, leading to a substantial decline in oil adsorption efficiency [26].
To describe the spontaneity of the adsorption process through thermodynamic parameters, the temperature varied from 278 to 328 K. As shown in Table 8, ΔG > 0 at all temperatures (5–55 ℃), indicating that the oil adsorption process does not occur spontaneously and requires an external interaction to proceed. However, this does not imply that adsorption ceases entirely, as the exothermic nature of the process still facilitates adsorption (ΔH < 0) [67]. These interactions may include hydrophobic interactions, Van der Waals forces, capillary effects, and the porous characteristics of the aerogel, which contribute to maintaining an effective adsorption process.
The increase in ΔG with temperature (from 14.25 kJ/mol at 5 ℃ to 16.82 kJ/mol at 55 ℃) suggests that adsorption becomes less favorable at higher temperatures. This can be attributed to the weakening of interactions between oil molecules and the aerogel surface at elevated temperatures, as well as the increased kinetic energy of oil molecules, making them less likely to adhere to the material [68]. The negative enthalpy change (ΔH < 0, -16.34 kJ/mol) confirms that the adsorption of oil onto cellulose aerogel is an exothermic process [68], meaning that energy is released during adsorption. This further implies that the adsorption efficiency decreases with increasing temperature. Additionally, since ΔH is below 40 kJ/mol, the adsorption process is classified as physical adsorption [69], a finding consistent with previous studies [70].
Although ΔG > 0, the negative enthalpy change (ΔH < 0) still facilitates oil adsorption, allowing the process to occur without the need for external stimuli such as catalysts, electric fields, or magnetic fields [67]. This perspective aligns with the study [71], which states that adsorption can still proceed even when ΔG > 0. Furthermore, the negative entropy change (ΔS < 0, -51.32 J/mol.K) indicates that the system becomes more ordered after oil adsorption [72], meaning that once the oil molecules adhere to the aerogel surface, the overall disorder of the system decreases. This observation is consistent with physical adsorption, where oil molecules are immobilized on the material's surface. Given the negative values of both ΔH and ΔS, the adsorption process is more favorable at lower temperatures and less efficient as temperature increases.
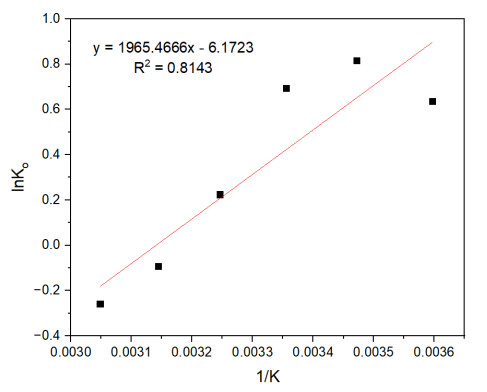
Figure 13 shows the linear relationship between lnKo and 1/T for the adsorption of oil onto aerogels. The fitted line follows the equation y = 1965.4666x – 6.1723 with a coefficient of determination R2 = 0.8143, indicating a good correlation. This plot is used to estimate the thermodynamic parameters related to the adsorption process, such as the enthalpy change (ΔH) and entropy change (ΔS), which are presented in Table 8.
3.3. Mechanism analysis of oil removal by cellulose aerogels
The oil adsorption process of cellulose aerogels was investigated through two kinetic models, four isotherm models, and material characterization before and after adsorption (including FT-IR spectra and energy-dispersive X-ray spectroscopy) [58]. The oil removal mechanism of cellulose aerogels involves a combination of both absorption and adsorption processes. During absorption, oil droplets penetrate the internal pores of the aerogel via capillary forces. The physical properties of the oil, such as viscosity and density, significantly influence the absorption efficiency [73]. In contrast, adsorption occurs only on the surface of the pores without penetration into the aerogel matrix [74], where intermolecular forces such as Van der Waals interactions, hydrogen bonding, and hydrophobic interactions play a dominant role [75]. The hydrophobic nature of the aerogel surface promotes preferential affinity for non-polar diesel molecules, enabling effective oil capture. Simultaneously, van der Waals forces facilitate physical interactions between the aerogel matrix and diesel compounds, enhancing adsorption stability. Moreover, hydrogen bonding between cellulose and PVA contributes to the structural integrity and porosity of the aerogel, indirectly supporting oil uptake by maintaining the three-dimensional network architecture. These synergistic effects account for the material's high adsorption efficiency, as further confirmed by kinetic, isotherm, and thermodynamic modeling.
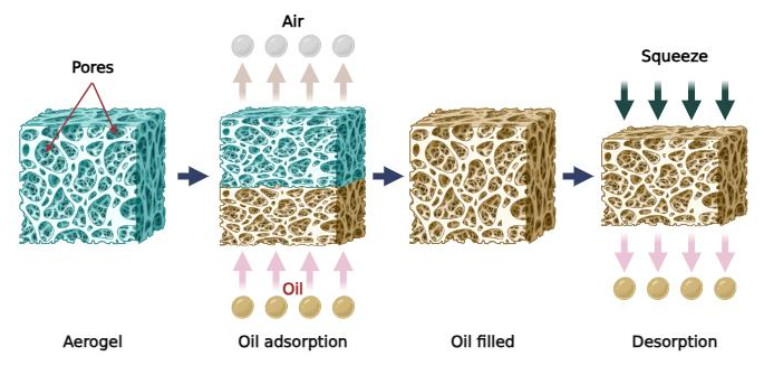
Cellulose aerogels possess a highly porous structure (97.88% ± 0.19%), providing numerous available adsorption sites for diesel oil molecules. SEM images reveal that the aerogel structure consists of interwoven cellulose fibers, forming interconnected pores filled with air. These fibers naturally self-organize through hydrogen bonding, resulting in a three-dimensional porous network [27]. This structural feature enhances the aerogel's oil adsorption capacity [11,28,29]. With a low density (0.027 ± 0.002 g/cm3), cellulose aerogels can float on the water surface, facilitating efficient oil recovery from water bodies. The adsorption process follows an upward direction from the submerged portion of the aerogel to the top surface (Figure 14) [76].
Figure 14 describes the oil adsorption and desorption mechanism of RP aerogels. Initially, the aerogel possesses a porous structure with voids filled with air. When exposed to diesel oil, oil molecules are adsorbed onto the surface and absorbed into the internal pores through capillary forces, while the air inside is simultaneously displaced. This process leads to the formation of oil-saturated aerogel. Subsequently, by applying compression, the adsorbed oil is released from the aerogel structure. This mechanism involves a combination of physical adsorption (driven by Van der Waals forces and hydrophobic interactions) and capillary absorption, ensuring efficient oil removal.
The adsorption isotherm study revealed that the oil adsorption process of RP aerogels follows the Langmuir model, with correlation coefficients (R2) of 0.9974. This indicates that adsorption occurs as a monolayer on homogeneous adsorption sites [47]. Furthermore, the good fit with the Langmuir model suggests no interaction between the adsorbed oil molecules, meaning that the adsorption process is independent of whether neighboring sites are already occupied [47]. The adhesion of oil onto the aerogel surface primarily occurs through Van der Waals forces and intramolecular interactions [48]. The adsorption process follows three main stages: (ⅰ) Diffusion of oil molecules onto the external surface of the aerogel, (ⅱ) penetration into internal pores, and (ⅲ) adsorption onto the internal surface of the aerogel [49].
Additionally, the Langmuir equilibrium parameter (RL) at 25 ℃ ranged from 0.0409 to 0.2301. Since these values fall within the range of 0 < RL < 1, the adsorption process is considered favorable [52], indicating strong adhesion between the adsorbent and the adsorbate, leading to effective adsorption. The Freundlich isotherm constant (n) was greater than 1, confirming that oil adsorption primarily occurs via physisorption [53]. Similarly, the mean free energy calculated from the Dubinin–Radushkevich model was 1.5079 kJ/mol, which is below 8 kJ/mol. This further confirms that the adsorption mechanism of both aerogel types is predominantly physisorption, with Van der Waals forces playing a crucial role [52]. During adsorption, the oil displaces the air inside the aerogel pores, transitioning the aerogel from an air-filled to an oil-filled state.
For adsorption kinetics, the study demonstrated that the pseudo-second-order model was the most suitable for describing the oil adsorption process of aerogels. This conclusion was supported by the high correlation coefficient (R2 = 0.9998). The adsorption capacity of the aerogels reached 53.1915 g/g, indicating that the oil adsorption process follows a second-order kinetic model, which consists of two primary stages: (ⅰ) Boundary-layer diffusion and (ⅱ) capillary diffusion [58].
In the initial stage, the oil adsorption rate increased rapidly within the first 10 s due to the availability of numerous adsorption sites on the aerogel surface. In the intermediate stage, the adsorption rate gradually decreased as these sites became saturated with oil molecules, leading to increased competition among them. Finally, as the equilibrium was reached, the adsorption rate significantly slowed down. The study of adsorption kinetics provides crucial insights into the adsorption rate and mechanism, facilitating the optimization of aerogel materials to enhance oil remediation efficiency.
4.
Conclusions
In this study, a biodegradable cellulose aerogel was successfully synthesized from RP waste and evaluated for its diesel oil adsorption performance. The RP aerogels exhibited ultralow density, high porosity, and excellent hydrophobicity, demonstrating significant potential for oil spill remediation. Adsorption experiments revealed a maximum adsorption capacity of 58.8235 g/g under optimal conditions: pH 7, oil concentration of 25 g/L, adsorption time of 25 s, salinity range of 0‰–35‰, and temperature range of 25–35 ℃. The results indicate that variations in salinity had an insignificant effect on adsorption efficiency, confirming the aerogel's stability in marine environments. Adsorption isotherm analysis showed that the Langmuir model best described the equilibrium data (R2 = 0.9974, RL values at 25 ℃ ranging from 0.0409 to 0.2301), indicating monolayer adsorption on a homogeneous surface. Kinetic analysis confirmed that the adsorption process followed the pseudo-second-order model (R2 = 0.9998), suggesting that both boundary-layer diffusion and capillary diffusion controlled the process. The oil adsorption mechanism of the RP aerogels was primarily governed by Van der Waals forces, hydrogen bonding, and hydrophobic interactions, which played a crucial role in retaining oil molecules on the material surface. Overall, this study demonstrates that cellulose aerogels derived from agricultural waste are highly efficient and eco-friendly oil adsorbents, with great potential for oil spill cleanup and wastewater treatment. These findings provide a valuable foundation for further research on optimization, scale-up production, and reusability assessment of the material under real-world conditions.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This research was fully funded by the HUTECH Institute of High Technology, HUTECH University under grant number 2025.12.ĐTSĐH. Nguyen Trinh Trong was funded by the PhD Scholarship Programme of Vingroup Innovation Foundation (VINIF), code VINIF.2024.TS.118.
Defining and developing the research idea and research framework: N.T.V., B.L.H.; Collecting data and literature, data analysis and synthesis: N.T.T.; Methodology: N.T.V., N.T.T.; Experimental research: T.T.N.; Writing–original draft: N.T.T.; Writing–review & editing–Preparation: N.T.V., B.L.H., N.T.T. All authors have read and approved the final version of the manuscript for publication.
Conflict of interest
All authors declare no conflict of interest in this paper.









 DownLoad:
DownLoad: