Combining robust state estimation with nonlinear model predictive control to regulate the acute inflammatory response to pathogen

1.   Introduction

Jackson ^[25] introduced quantum calculus. Then, it was later developed by Al-Salam who started fitting the concept of $ q $–fractional calculus ^[7]. Agarwal continued studying certain $ q $–fractional integrals and derivatives ^[3]. Furthermore, some researchers have also studied $ q $–difference equations (for more details, see ^{[1,2,5,6,8,9,15,23,24,26,27,33,39,40]}). On the one hand, fractional differential equations have gained a considerable importance due to their applications in various fields of sciences, such as physics, mechanics, chemistry, and engineering (see ^{[17,18,19,20,21]}). In ^[22], El-Sayed discussed a class of nonlinear functional differential equations of arbitrary orders, and Lakshmikantham ^[30] initiated the basic theory for fractional functional differential equations.

In 1996, Delbosco et al. investigated $ \mathbb{D}^{\beta} u(t) = \hslash(t, u) $ with initial condition: $ u(a) = \eta $, where $ a > 0 $, $ \eta\in \mathbb{R} $ and $ \beta \in J : = (0, 1) $ ^[16]. In 2005, Bai et al. presented the boundary problem:

under conditions: $ u(0) = u(1) = 0 $, where $ t \in J $, $ 0 < \beta \leq 2 $, and $ \mathbb{D}_0^{\beta} $ is the Riemann-Liouville standard derivative ^[11]. In 2008, Qiu et al. studied the equation with conditions: $ u(0) = u'(1) = u''(1) = 0 $, where $ t\in J $, $ 2 < \beta < 3 $, $ \mathbb{D}_{0^+}^{\beta} $ is the Caputo derivative and $ h: \bar{J} \times [0, \infty) \to [0, \infty) $, here $ \bar{J}: = [0, 1] $, is such that $ \lim_{t \to 0^+} h (t, .) = \infty $ ^[34]. In 2010, Agarwal et al. considered the singular fractional Dirichlet problem:

with the boundary value condition: $ u(0) = u(1) = 0 $, where $ \beta \in (1, 2] $, $ \gamma > 0 $, $ \beta - \gamma \geq 1 $, $ h \in {\rm{Car}}(\bar{J} \times (0, \infty) \times \mathbb{R}) $, $ h $ is positive and singular at $ t = 0 $, and $ \mathbb{D} $ is the usual Riemann-Liouville derivative ^[4]. In 2012, Cabada et al. investigated the existence of positive solution for the following nonlinear fractional differential equation:

where $ 0 < t < 1 $, $ 2 < \beta < 3 $ and $ h : \bar{J} \times [0, \infty) \to [0, \infty) $ is a continuous function ^[13]. In 2014, Li reviewed the problem:

for each $ t \in J $, under conditions: $ u(0) = u'(0) = 0 $ and $ u'(1) = {}^C \mathbb{D}^{\beta} u(1) $, where $ \beta \in (2, 3) $, $ \gamma \in J $, $ h : (0, 1] \times \mathbb{R}^2 \to \mathbb{R} $ is continuous function that may be singular at $ t = 0 $, $ {}^C \mathbb{D}^\beta $ is the standard Caputo derivative ^[31]. In 2016, the fractional integro-differential equation

under conditions $ u'(0) = u(\eta) $, $ u(1) = \int_0^{\nu} u(\xi) \, \mathrm{d}\xi $ and $ u^{(i)}(0) = 0 $ for $ i = 2, \dots, [\gamma] - 1 $ was investigated, where $ t \in J $, $ \gamma \in [2, 3) $, $ u \in \bar{\mathcal{B}} = C^{1}(\bar{J}) $, $ \alpha, \eta, \nu \in J $, $ \beta > 1 $ and $ h: \bar{J} \times \mathbb{R}^4 \to \mathbb{R} $ is a function such that $ h (t, ., ., ., .) $ is singular at some point $ t \in \bar{J} $ ^[44]. In 2017, Shabibi et al. studied the singular fractional integro-differential equation:

where $ \mu(u(t)) = \int_0^t f(\xi) u(\xi) \, \mathrm{d}\xi, $ under boundary conditions: $ u(0) = u'(0) $ and $ u(1) = {}^C \mathbb{D}^{\gamma} u(t) $, where $ t \in J $, $ u \in \bar{\mathcal{B}} $, $ \beta > 2 $, $ 0 < \gamma, a < 1 $, $ f \in \bar{\mathcal{L}} = L_1(\bar{J}) $, $ \| f \|_1 = m $, $ h(t, u_1, u_2, u_3, u_4) $ is singular at some points $ t \in \bar{J} $ and $ {}^C \mathbb{D}^\beta $ is the Caputo fractional derivative ^[45]. In 2020, Samei considered the singular system of $ q $–differential equations:

with conditions: $ u(0) = v(0) = 0 $, $ u^{(i)} (0) = v^{(i)} (0) = 0 $, for $ i = 2, \dots, n-1 $ and

where $ \mathbb{D}_q^{\alpha_j } $ is the $ q $–derivative of fractional order $ \alpha_j $, $ \alpha_j \in (n, n+1] $ with $ n \geq 3 $, $ \mathbb{I}_q^{ \gamma_j} $ is the $ q $–integral of fractional order $ \gamma_j $, $ \gamma_j \geq 1 $, $ g_j \in C (E) $, $ g_j $ are singular at $ t = 0 $ and satisfy the local Carathéodory condition on $ E = (0, 1] \times (0, \infty) \times (0, \infty) $, and $ w_j \in \bar{ \mathcal{L}} $ are non-negative such that

for $ j = 1, 2 $ ^[37]. Also, Liang et al. ^[32] investigated a nonlinear problem of regular and singular fractional $ q $–differential equation:

with conditions: $ u(0) = c_1 u(1) $, $ u'(0) = c_2 {}^c \mathbb{D}_q^{\beta} u (1) $ and $ u^{(k)}(0) = 0 $ for all $ 2\leq k \leq n-1 $, here $ n-1 < \alpha < n $ with $ n \geq 3 $, $ \beta, q, c_1\in J $, $ 0 < c_2 < \Gamma_q (2- \beta) $, function $ h $ is a $ L^\kappa $-Carathéodory and $ h(t, u_1, u_2, u_3) $ may be singular. Similarly, some related results have been obtained in ^[28,36,38]. Dassios et al. used a generalized system of differential equations of fractional order:

to incorporate memory into an electricity market model by constructing the fractional-order dynamical model, studying its solutions, and providing the closed formulas of solutions, where $ \frac{{\mathrm d} \lambda (t)}{{\mathrm d} t} $, $ \lambda (t) $ are the marginal electricity price and electricity price, respectively, $ \omega^{\rm{ref}} $ represents the reference frequency, $ \omega_{Col} (t) $ represents the frequency of the Col, that is, $ \omega^{\rm{ref}}-\omega_{Col} (t) $ is the deviation frequency of the CoI with respect to the reference frequency, $ T_\lambda $ is the time constant, $ H_d $ is the deviation with respect to a perfect tracking integrator, and for a low-pass filter, it is $ H_d = 1 $, and $ K_E $ can be used as feedback gain ^[14].

Using the ideas from these works, we investigate the existence of solutions for the following nonlinear pointwise defined fractional $ q $–integro-differential equation:

for $ q \in J $, under boundary conditions: $ \int_0^{b } u(r) \, \mathrm{d}r = 0 $, $ u'(1) = u(a) $ and $ u^{(j)} (0) = 0 $ for $ j\geq 2 $, here $ \alpha \geq 2 $, $ a, b, \beta \in J $, $ \varphi : \bar{\mathcal{B}} \to \bar{\mathcal{B}} $ is a map such that

for some non-negative real numbers $ c_1 $ and $ c_2 $ belonging to $ [0, \infty) $ and all $ u_1, u_2 \in \bar{\mathcal{B}} $, where $ \mathbb{D}^\alpha_q $ and $ \mathbb{D}^\beta_q $ are the Caputo fractional $ q $–derivatives of order $ \alpha $ and $ \beta $, respectively, which are defined in (2.11), and $ w \in \bar{ \mathcal{L}} $ is singular at some points $ t \in \bar{J} $.

In fact, the non-constant real-valued function $ u $ on the interval $ I = [a, b] $ is said to be singular on $ I $, if it is continuous, and there exists a set $ S \subseteq I $ of measure $ 0 $ such that for all $ t $ outside of $ S $, $ u' (t) $ exists, and it is zero, that is, the derivative of $ u $ vanish almost everywhere. We say that, $ \mathbb{D}_q^{\alpha} u(t) + g(t) = 0 $ is a pointwise defined equation on $ \bar{J} $ if there exists set $ S \subset \bar{J} $ such that the measure of $ S^c $ is zero, and the equation holds on $ S $ ^[44].

In Section 2, we recall some essential definitions of Caputo fractional $ q $–derivative. Section 3 contains our main results of this work, while an example is presented to support the validity of our obtained results. An application with some needed algorithms for the problems are given in Section 4. In Section 5, conclusion is presented.

2.   Basic definitions for the problem

Throughout the paper, we apply the notations of time scales calculus ^[12]. The Caputo fractional $ q $–derivative is considered here on

for all $ \aleph \in \mathbb{N} $, $ \mathrm{s}_0 \in \mathbb{R} $ and $ q \in J $. If there is no confusion concerning $ \mathrm{s}_0 $, we denote $ \mathbb{T}_{\mathrm{s}_0} $ by $ \mathbb{T} $. Let $ p \in \mathbb{R} $. Let us define $ [p]_{q} = (1 - q^{p}) (1 - q)^{-1} $ ^[25]. The $ q $–factorial function $ (\mathrm{v} - \mathrm{w})_{q}^{(\aleph)} $ with $ \aleph \in \mathbb{N}_0 $ is defined by

and $ (\mathrm{v} - \mathrm{w})_{q}^{(0)} = 1 $, where $ \mathbb{N}_0 : = \{ 0, 1, 2, 3, \dots \} $ ^[2]. Also, for $ \sigma \in \mathbb{R} $, we have:

In ^[10], the authors proved that $ (v - w)_q^{(\sigma+\nu)} = (v - w)_{q}^{(\sigma)} (v - q^\sigma w)_{q}^{(\nu)} $ and

for each $ \mathrm{v}, \mathrm{w} \in \mathbb{R} $. If $ w = 0 $, then it is clear that $ v^{(\sigma)} = v^\sigma $. The $ q $–Gamma function is given by

where $ v \in \mathbb{R} \backslash \{\cdots, -2, -1, 0\} $ ^[25]. In fact, by using (2.2), we have

Note that, $ \Gamma_q (v+1) = [v]_q \Gamma_q (v) $ ^[10]HY__HY, Lemma 1]. For a function $ u : \mathbb{T} \to \mathbb{R} $, the $ q $–derivative of $ u $, is

for all $ t \in \mathbb{T} \setminus \{0\} $, and $ \mathbb{D}_q [u](0) = \lim_{t \to 0} \mathbb{D}_q [u](t) $ ^[2]. Also, the higher order $ q $–derivative of the function $ u $ is defined by $ \mathbb{D}_q^n [u](t) = \mathbb{D}_q \left[ \mathbb{D}_q^{ n-1} [u]\right](t) $, for all $ n \geq 1 $, where $ \mathbb{D}_q^0 [u](t) = u(t) $ ^[2]. In fact,

for $ t \in \mathbb{T}\setminus \{0\} $ ^[9].

Remark 2.1. By using Eq $(2.1)$, we can change Eq $(2.5)$ into the following:

The $ q $–integral of the function $ u $ is defined by

for $ 0 \leq t \leq b $, provided that the series is absolutely convergent ^[2]. If $ a $ is in $ [0, b] $, then

whenever the series converges. The operator $ \mathbb{I}_q^n $ is given by $ \mathbb{I}_q^0 [u](t) = u(t) $ and

for $ n \geq 1 $ and $ u \in C([ 0, b]) $ ^[2]. It has been proven that

whenever the function $ u $ is continuous at $ t = 0 $ ^[2]. The fractional Riemann-Liouville type $ q $–integral of the function $ u $ is defined by

for $ t \in \bar{J} $ and $ \sigma > 0 $ ^[9,23].

Remark 2.2. By using Eqs $(2.2)$, $(2.3)$ and $(2.7)$, we obtain:

Therefore, we have:

The Caputo fractional $ q $–derivative of the function $ u $ is defined by

for $ t \in \bar{J} $ and $ \sigma > 0 $ ^[23,35]. It has been proven that

where $ \sigma, \nu \geq 0 $ ^[23]. Also,

where $ \sigma > 0 $ and $ n \geq 1 $ ^[23].

Remark 2.3. From Eq $(2.3)$, Remark 2.1, and Eq $(2.10)$ in Remark 2.2, we obtain:

Thus, we have:

The authors in ^[41] presented all algorithms and MATLAB code's lines to simplify $ q $–factorial functions $ (v -w)_q^{(n)} $, $ (v -w)_q^{(\sigma)} $, $ \Gamma_{q}(v) $, $ \mathbb{I}_q [u](t) $, and some necessary equations.

Lemma 2.4. ^[27,29] For $ \sigma > 0 $, the general solution of the fractional $ q $–differential equation $ {}^C \mathbb{D}^\sigma u(t) = 0 $ is given by $ u(t) = \sum_{i = 0}^{n-1} e_i t^i $, where $ e_i \in \mathbb{R} $ for $ i = 0, 1, 2, \dots, n-1 $ and $ n = [\sigma ] + 1 $ here $ [\sigma] $ denotes the integer part of the real number $ \sigma $.

We use the three norms: $ \|u\| = \sup_{t \in \bar{J}} |u(t)| $,

and $ \|u\|_1 = \int_{\bar{J}} |u(\xi)|\, {\mathrm d}\xi $ in $ \bar{\mathcal{A}} = C(\bar{J}) $, $ \bar{\mathcal{B}} = C^{1}(\bar{J}) $, and $ \bar{\mathcal{L}} = L_1(\bar{J}) $, respectively. Let $ \Psi $ be the family of nondecreasing functions $ \mathtt{ψ} : [0, \infty) \to [0, \infty) $ such that $ \sum_{n = 1}^{\infty} \mathtt{ψ}^{n}(t) < \infty $, for all $ t > 0 $. Let $ T : \mathcal{X} \to \mathcal{X} $ and $ \alpha : \mathcal{X} \times \mathcal{X} \to (0, \infty) $. $ T $ is called an $ \alpha $-admissible mapping if $ \alpha(u_1, u_2) \geq 1 $ implies that $ \alpha(T(u_1), T(u_2)) \geq 1 $ for each $ u_1, u_2 $ in $ \mathcal{X} $.

Definition 2.5. ^[42] Let $ (\mathcal{X}, \rho) $ be a metric space, where $ \mathtt{ψ} \in \Psi $ and $ \alpha : \mathcal{X}^2 \to [0, \infty) $ is a map. A self-map $ T $ defined on $ \mathcal{X} $ is called an $ \alpha $-$ \mathtt{ψ} $-contraction whenever

for each $ u_1, u_2 \in \mathcal{X} $.

Lemma 2.6. ^[42]Let $ (\mathcal{X}, \rho) $ be a complete metric space and $ T : \mathcal{X} \to \mathcal{X} $ be a continuous, $ \alpha- $admissible and $ \alpha $–$ \mathtt{ψ} $–contraction, then $ T $ has a fixed point whenever there exists $ u_{0} \in \mathcal{X} $ such that $ \alpha(u_{0}, T (u_{0})) \geq 1 $.

Lemma 2.7. ^[43,46]If $ x \in \bar{\mathcal{A}} \cap \bar{\mathcal{L}} $ with $ \mathbb{D}_q^{\alpha} x\in \mathcal{A} \cap \mathcal{L} $, then

where $ [\alpha]\leq n < [\alpha] +1 $, and $ c_i $ is some real number.

3.   Main results

Let us first prove the following essential lemma:

Lemma 3.1. Suppose that $ \alpha \geq 2 $, $ q \in J $ and $ g\in \bar{\mathcal{L}} $. The solution of the boundary value problem: $ \mathbb{D}_q^{\alpha} u(t) = g(t) $ with boundary conditions is expressed as:

is

on a time scale $ \mathbb{T}_{t_0} $ where $ G_q(t, s) $ is expressed as:

whenever $ 0\leq s \leq t \leq 1 $,

whenever $ 0 \leq t \leq s \leq 1 $. Also

and

Proof. Consider the problem: $ \mathbb{D}_q^{\alpha} u(t) = g(t) $. Using Lemma 2.7, it is deduced that $ u(t) = - \mathbb{I}_q^\alpha g(t) + c_0 + c_1 t $, where $ c_0 $, $ c_1 $ are some real numbers, and $ \mathbb{I}_q^\alpha $ is Riemann-Liouville type $ q $–integral of order $ \alpha $. Hence, $ u'(t) = - \mathbb{I}_q^{\alpha -1} g(t) + c_1 $ where $ \mathbb{I}_q^{\alpha -1} $ is a fractional Riemann-Liouville type $ q $–integral of order $ \alpha -1 $. By applying condition $ u'(1) = u(a) $, we get:

and so $ c_0 = - \mathbb{I}_q^{\alpha -1} g(1) + \mathbb{I}_q^\alpha g(a) + (1- a) c_{1} $. one can easily check that

Since $ \int_0^{b} u(r) \, \mathrm{d} r = 0 $, we get:

Thus,

and so

Hence,

Now, some easy evaluations show us that $ u(t) = \int_0^1 G_q(t, s) g(s) \, \mathrm{d}_qs $.

Remark 3.2. Note that, the mappings $ G_q(t, s) $ and $ \frac{ \partial G_q(t, s)}{\partial t} $ are continuous with respect to $ t $. Let $ w $ be a map on $ \bar{J} \times \bar{\mathcal{B}}^2 $ such that $ w $ is singular at some points of $ \bar{J} $. Let us define the function $ \Theta_u : \bar{\mathcal{B}} \to \bar{\mathcal{B}} $ by

for all $ t\in \bar{J} $, where $ \mathbb{I}_q^\alpha $ is the fractional Riemann-Liouville $ q $–integral of order $ \alpha $ which is defined in $(2.9)$, and $ \mathbb{D}^\beta_q $ is the Caputo fractional $ q $–derivative of order $ \beta $ which is defined in $(2.11)$. Then, by taking the first order derivative related to $ t $, we have:

Obviously, the singular pointwise defined Eq $(1.1)$ has a solution iff the map $ \Theta_u $ has a fixed point.

Now, we give our main result as follows:

Theorem 3.3. Assume that $ \alpha\geq 2 $, $ [\alpha] = n-1 $, $ a, b, q\in J $, $ f \in \bar{\mathcal{L}} $ with $ \|f\|_1 = m $, $ \varphi : \bar{\mathcal{B}} \to \mathbb{R} $ is such that

for some $ c_1, c_2 \in [0, \infty) $. Let $ \Omega : \bar{J} \times \bar{\mathcal{B}}^{5} \to \mathbb{R} $ be a mapping which is singular on some points $ \bar{J} $ and

for all $ u_1, u_2, v_1, v_2 \in \bar{\mathcal{B}} $ and almost all $ t \in \bar{J} $, where $ k_0 $ is a natural number, $ \mu_i :\bar{J} \to \mathbb{R}^+ $, $ \hat{\mu}_i \in \bar{\mathcal{L}} $,

$ \Omega_{i}: \bar{\mathcal{B}}^5 \to \mathbb{R}^+ $ is a nondecreasing mapping with respect to all components with

as $ \nu \to 0^+ $ for some $ \gamma_i > 0 $, $ p_i \in \mathbb{R}^+ $ with $ 1 \leq i \leq k_0 $. Suppose that

for all $ (u_1, \dots, u_5) \in \bar{\mathcal{B}}^5 $ and almost all $ t \in \bar{J} $, where $ h: \bar{J} \to \mathbb{R}^+ $, $ \hat{h} \in \bar{ \mathcal{L}} $, $ T : \bar{ \mathcal{B}}^5 \to \mathbb{R^+} $ is a nondecreasing mapping respect all their components such that

where$ \tau = \left(\ell \| \hat{h}\|_1 M_{ \alpha, a, b} \right)^{-1} $,

$ \mu(a, b) $ define by Eq $(3.4)$ in Lemma 3.1 and

If

then the pointwise defined Eq $(1.1)$ under boundary conditions: $ u^{(j)} (0) = 0 $ for $ j\geq 2 $, $ \int_{0}^{b} u({r}) \, {\mathrm d}{r} = 0 $ and $ u'(1) = u({a}) $ has a solution.

Proof. Let $ u, v \in \bar{\mathcal{B}} $. Then, we get:

Since $ \mathbb{D}_q^{\beta} u(t) = \mathbb{I}_q^{1- \beta} u'(t) $ for $ \beta \in J $, we have

and so

Thus, by considering $ \xi = \|u - v\|_{*} $, we have:

This implies that

Assume that $ u, v \in \bar{\mathcal{B}} $. Then, we get:

Hence,

and so

If

then

Let $ 0 < \varepsilon \leq 1 $ be given. Since

for $ 1 \leq i \leq k_0 $, $ \exists \; \delta_i = \delta_i(\varepsilon) $ such that $ \nu \in (0, \delta_i] $ implies

and so $ \Omega_i(\nu, \nu, \nu, \nu, \nu)/ \nu^{\gamma_i} < \varepsilon + p_i $. This consequents

We take $ \delta = \min \{ \delta_1, \dots, \delta_{k_0}, \varepsilon \} $. In this case, $ \nu \in (0, \delta] $ implies

for all $ 1\leq i \leq k_0 $. By using (3.6), we obtain:

At present, by applying (3.5) and (3.7), we obtain:

Now, we consider: $ \gamma = \min \{\gamma_1, \cdots, \gamma_{k_0} \} $. Hence,

Therefore, this implies that $ \Theta $ is continuous. Since

there is $ \varepsilon_1 > 0 $ such that

Let

Then, we have:

and so for each $ \varepsilon > 0 $ there exists $ \delta(\epsilon) > 0 $ such that $ \nu \in (0, \delta(\varepsilon)] $ implies

Hence, $ 0 \leq T(\ell \nu, \dots, \ell \nu) < (\lambda + \varepsilon) \ell \nu $ and

Since $ \lambda \in [0, \tau) $, choose $ \varepsilon_0 > 0 $ such that $ \lambda + \varepsilon_0 < \tau $. Assume that

Then, $ \eta \leq \eta_0 $ implies $ 0 \leq T(\ell \eta, \dots, \ell \eta) < (\lambda + \varepsilon_0) \ell \eta $. Since

there exists $ \eta_1 > 0 $ such that $ \nu \in (0, \eta_1] $ implies

for $ i = 1, \dots, k_0 $. Let $ \eta = \min \{\eta_0, \frac{\eta_1}{ 2}, \frac{1}{2} \} $ and

Define $ \alpha: \bar{\mathcal{B}}^2 \to \mathbb{R} $ by

Assume that $ u, v \in \bar{\mathcal{B}} $ be given. If $ \alpha(u, v) \geq 1 $, then for every $ t \in \bar{J} $, we have:

Therefore,

Also,

Indeed,

Hence, $ \|\Theta_u\|_{*} \leq \eta $ and so $ \Theta_u \in E $. Using a similar proof, we can show that $ \Theta_v \in E $. This implies $ \alpha(\Theta_u, \Theta_v) \geq 1 $ and so $ \Theta_u $ is $ \alpha $-admissible. It is obvious that, $ E \neq \emptyset $. Choose $ u_0 \in E $. Hence, $ \Theta_{u_0} \in E $, and so $ \alpha(u_0, \Theta_{u_0}) \geq 1 $. Let $ u, v \in E $. Then,

where $ \xi = \|u-v\|_{*} $. Also using (3.5), we have

Now, by using (3.8), we conclude that

where $ \gamma = \min \{\gamma_1, \dots, \gamma_{k_0} \} $. We take:

Note that, $ \eta \in [0, 1) $. Define the map $ \mathtt{ψ} : [0, \infty) \to \mathbb{R}^{+} $ by

Then, $ \mathtt{ψ} $ is nondecreasing and

for $ 0\leq t < 1 $. Also, we obtain

for $ t \in [1, \infty) $. Thus, $ \sum_{i = 1}^{\infty} \mathtt{ψ}^{i}(t) $ is a convergent series for all $ t \geq 0 $ and so $ \mathtt{ψ} \in \Psi $. Also, we have

If $ u \notin E $ or $ v \notin E $, then the last inequality holds obviously. This shows that

for all $ u, v \in \bar{\mathcal{B}} $. Now, Lemma 2.6 implies that $ \Theta $ has a fixed point that is the solution for problem (1.1).

4.   An illustrative example with application

The following illustrative example is given to support the validity of our main results. A computational method is provided here to test the proposed problem (1.1). Linear motion is commonly basic among all other motions. From the 1st law of Newton's motion, objects that are not experiencing any net force will continue to move in a straight line with a constant velocity until they are subjected to a net force.

Example 4.1. We consider a constrained motion of a particle along a straight line restrained by two linear springs with equal spring constant (stiffness coefficient) under external force and fractional damping along the $ t $-axis (Figure 1).

We consider the pointwise defined equation:

where

$ \eta $ is constant and $ L $ is the unstretched length of the spring. We change Eq $(4.1)$ into a form of the problem $(1.1)$ as follows:

with boundary conditions:

Also

Take $ \alpha = \frac{5}{2}\geq 2 $, $ \beta = \frac{1}{2}\in J $, $ a = \frac{1}{4}\in J $, $ b = \frac{1}{3} \in J $, $ k_0 = 1 $, $ \gamma_1 = 1 $, $ \mu_1 (t) = h(t) = \frac{1}{\theta (t) } $, $ c_1 = \frac{1}{3} $, $ c_2 = \frac{2}{3} $, $ f(\xi) = \frac{u(\xi)}{\sqrt{\xi} } $, $ \varphi(x) = \sin(x) $ and

Then, we get:

$ \mu_1, h \in L^1 $, $ m = \|h\|_1 = 2 $,

$ T, \Omega_1 $ are non-negative and non-decreasing with respect to $ u_1, \dots, u_5 $,

We put:

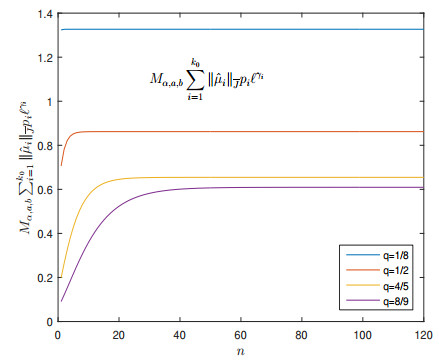
Table 1 shows the values of $ \Lambda_1 $ and $ \Lambda_2 $ for $ q = \left\{\frac{1}{8}, \frac{1}{2}, \frac{4}{5}, \frac{8}{9} \right\} $. We can see that

for $ q = $ $ \frac{1}{8} $, $ \frac{1}{2} $, $ \frac{4}{5} $ and $ \frac{8}{9} $, respectively. Thus, by using the numerical results, we obtain:

whenever $ q = \frac{1}{8} $,

whenever $ q = \frac{1}{2} $,

whenever $ q = \frac{4}{5} $ and

whenever $ q = \frac{8}{9} $. Also, we can check that

and for all $ q \in J $

Table 2 shows numerical results for different values of $ q\in J $. Figure 2 shows the curve of these results. Now, according to the obtained results, Theorem 3.3 implies that problem $(4.2)$ has a solution.

5.   Conclusions

The multi-singular pointwise defined fractional $ q $–integro-differential equation has been successfully investigated in this work. The investigation of this particular equation provides us with a powerful tool in modeling most scientific phenomena without the need to remove most parameters which have an essential role in the physical interpretation of the studied phenomena. Multi-singular pointwise defined fractional $ q $–integro-differential equation (1.1) has been studied on a time scale under some boundary conditions. An application that describes the motion of a particle in the plane has been provided in this work to support our results' validity and applicability in the fields of physics and engineering.

Acknowledgments

The first author was supported by Bu-Ali Sina University.

Conflict of interest

The authors declare that they have no competing interests.