A study of the process of pharmacokinetics-pharmacodynamics (PKPD) of antibiotics and their interaction with bacteria during peritoneal dialysis associated peritonitis (PDAP) is presented. We propose a mathematical model describing the evolution of bacteria population in the presence of antibiotics for different peritoneal dialysis regimens. Using the model along with experimental data, clinical parameters, and physiological values, we compute variations in PD fluid distributions, drug concentrations, and number of bacteria in peritoneal and extra-peritoneal cavities. Scheduling algorithms for the PD exchanges that minimize bacteria count are investigated.
1.
Introduction
In [1], we proposed and studied the following predator-prey reaction-diffusion system, which incorporates a hunting cooperation functional response and prey-taxis:
Here, $ u(t, x) $ and $ v(t, x) $ represent the population densities of prey and predators, respectively, at time $ t $ and spatial location $ x \in \Omega $. The spatial domain $ \Omega \subseteq \mathbb{R}^N $, where $ N \geq 1 $, is bounded and has a smooth boundary, denoted by $ \partial \Omega $. Furthermore, $ n(x) $ denotes the outward unit normal vector on $ \partial \Omega $, and $ \partial_n = \partial / \partial n $. In this system, $ \tau > 0 $ is the constant diffusion rate of the prey species, and the term $ -\chi \nabla \cdot (q(v) \nabla u) $ stands for (repulsive) prey-taxis, where $ q(v) $ is the sensitivity function and $ \chi > 0 $ is the chemotaxis coefficient. Furthermore, the function $ g(u) $ characterizes the intrinsic growth rate of the prey population, while $ f(u, v) $ represents the functional response, indicating the rate at which predators hunt and consume their prey. The constant $ \beta > 0 $ denotes the conversion rate associated with predation, and $ \gamma(v) $ indicates the net growth rate of predators in the absence of prey. Finally, the initial data $ u_0 $ and $ v_0 $ are assumed to satisfy
Ecologically, the constant diffusion rate $ \tau $ quantifies the random dispersal of the prey species throughout the domain $ \Omega $. However, due to the prey-taxis term, predators tend to move in the direction opposite to the increasing prey density gradient, resulting in a scenario in which prey exhibit a group defense strategy against predators (e.g., see [2,3]). An example of such a predator-prey interaction involving group defense through the prey-taxis mechanism, as described in (1.1), can be found in [4]. Furthermore, it is biologically realistic for predators to exhibit a limited response when prey densities are low (see [5,6]). Accordingly, the sensitivity function of predators, represented as $ q(v) $, is expected to be bounded. The intrinsic growth rate of the prey population, denoted as $ g(u) $, is typically influenced by resource limitations and is often expressed as follows:
where $ r $ and $ K $ are positive constants. Regarding the capturing rate, the functional response $ f(u, v) $ generally increases with prey density. In ecosystems with cooperative hunting, higher predator densities enhance the capture rate; however, interference among predators (see [7]) limits this effect. Consequently, $ f(u, v) $ increases with both predator and prey densities, but remains bounded. Representative forms of hunting-cooperation functional responses (e.g., see [1,7,8,9,10,11,12,13]) include
where $ a $, $ e_0 $, $ h_0 $, and $ C $ are positive constants (for their biological meanings, see [7,8,12,13,14]). The net growth rate of predators, denoted as $ \gamma(v) $, may be influenced by the predator death rate or by intraspecific competition. Accordingly, prototype forms for $ \gamma $ are provided by
where $ M_{\gamma} $ and $ \gamma_* $ are positive constants representing the intrinsic death rate and the intraspecific competition rate, respectively. To incorporate these ecological backgrounds in the functions $ g $, $ f $, $ \gamma $, and $ q $ [1], assumed that there exist positive constants $ K $, $ M_g $, $ M_f $, $ M_{\gamma} $, and $ M_q $ such that the following general hypotheses are satisfied:
(H1) $ g \in C^1 ([0, \infty), \mathbb{R}) $, $ g(0) \geq 0 $, $ g(K) = 0 $, $ 0 < g(u)\leq M_g $ for all $ 0 < u < K $, while $ g(u) < 0 $ for any $ u > K $.
(H2) $ f \in C^1 ([0, \infty)^2, [0, \infty)) $, $ f(u, 0) \geq 0 $, $ f(0, v) = 0 $, $ f_u (u, v) > 0 $, and $ f_v (u, v) > 0 $ for any $ u $, $ v > 0 $, and $ f(u, v) \leq M_f $ for all $ u $, $ v \geq 0 $.
(H3) $ \gamma \in C^1 ([0, \infty), [0, \infty)) $, $ \gamma(0) = 0 $, $ \gamma^{\prime} (0) = M_{\gamma} $, $ \gamma(v) \geq M_{\gamma} v $, and $ \gamma^{\prime} (v) > 0 $ for any $ v \geq 0 $.
(H4) $ q \in C^1 ([0, \infty), [0, \infty)) $, $ q(0) = 0 $, and $ q(v) \leq M_q v $ for all $ v \geq 0 $.
Under these assumptions, in [1], we established the global existence of classical solutions to system (1.1) for all $ N \geq 1 $ when the chemotaxis coefficient $ \chi $ is sufficiently small. To achieve this, we employed Amann's local existence theorem [15,16], along with various estimates for the diffusion semigroup and the Gagliardo-Nirenberg inequality (e.g., [17,18,19,20]). Furthermore, we derived a weighted integral estimate using a new weight function, which subsequently yielded an explicit upper bound for $ \chi $ ensuring the existence of bounded solutions.
Not only for Keller–Segel chemotaxis models without reaction terms but also for predator-prey models with prey-taxis, the global existence and boundedness of solutions have been established under either a technical truncation assumption (see [21,22,23]) or a smallness assumption on the prey-taxis coefficient (see [1,24]). Such assumptions are often employed to prevent population overcrowding. The global existence of solutions to PDEs with chemotaxis terms has recently emerged as one of the most actively studied topics in biological mathematics. Our earlier results in [1] align with this trend. In particular, for studies on predator-prey models incorporating prey-taxis, we refer the reader to [1,18,24] and the references therein. This raises a fundamental question: Can global existence of solutions be ensured without imposing any restrictive assumptions? In addressing this, several notable results have demonstrated global existence for all $ \chi > 0 $, without requiring smallness or truncation conditions (e.g., see [4,18,25,26,27,28,29]).
In [25], a prey-taxis system with the ratio-dependent functional response $ (\frac{ u}{u+av}) v $ (for a contant $ a > 0 $) was studied for all $ \chi \geq 0 $ and $ N \geq 1 $. The key inequality $ (\frac{ 1}{u+av}) v \leq \frac{1}{a} $ played a crucial role in obtaining the desired result. The models in [4,26,28,29] incorporate Lotka–Volterra-type interactions among species. In [18], the authors considered a prey-dependent functional response $ f(u) $ satisfying the Holling type-Ⅱ condition, combined with a logistic-type source in the predator equation. They established the global existence of classical solutions for all $ \chi > 0 $, but only for the case $ N = 2 $. Meanwhile, [27] addressed a chemotaxis model in one spatial dimension ($ N = 1 $). These studies collectively highlight that, in ensuring global existence of solutions for prey-taxis models with arbitrary $ \chi > 0 $, the structure of the functional response plays a crucial role. In particular, when attempting to apply an entropy-like equality (cf. [30]) as was done in [18] to our system (1.1) with a functional response $ f(u, v) $ satisfying (H2), one encounters difficulties. This is due to the fact that $ f $ depends on both $ u $ and $ v $, and the quantity $ \frac{f(u, v)}{u} $ is not necessarily bounded. These aspects impose certain limitations on the applicability of various theoretical approaches, including entropy-based methods. In this context, the analysis of prey-taxis models with functional responses satisfying (H2) presents a certain level of novelty. To overcome the associated difficulties and eliminate the need for a smallness condition on the prey-taxis sensitivity coefficient $ \chi $, we begin our study under structural assumptions that incorporate both a logistic-type source and a one-dimensional spatial setting. These assumptions allow for sufficient analytical control, facilitating the derivation of the required a priori estimates.
We note that the question of whether similar results can be obtained without such restrictions (e.g., in higher dimensions or without a logistic source) remains largely open. As seen in the works cited above, the global existence and boundedness of solutions to prey-taxis predator-prey systems is a topic of active ongoing research. Taken together, these studies suggest that either the spatial dimension $ N $ or the presence of a logistic source plays an essential role in the derivation of key estimates, particularly those involving the Gagliardo–Nirenberg inequality. Motivated by this, we study global existence and boundedness in a one-dimensional model with a suitably structured logistic source. In particular, we focus on the impact of the predator growth term and explore whether a refined assumption on $ \gamma(v) $ can enhance the analysis in the one-dimensional case. To this end, we replace assumption (H3) with the following, more stringent condition:
(H3*) $ \gamma \in C^1 ([0, \infty), [0, \infty)) $, $ \gamma(0) = 0 $, $ \gamma^{\prime} (0) = M_{\gamma} $, $ \gamma(v) \geq M_{\gamma} v + \gamma_* v^{\alpha} $, and $ \gamma^{\prime} (v) > 0 $ for some $ \alpha > 1 $ and all $ v \geq 0 $.
We note that the term $ \gamma_* v^{\alpha} $ in (H3*) contributes a self-limiting mechanism to the predator equation. While not logistic in the classical algebraic sense (e.g., of the form $ v(1-v) $), this higher-order damping term serves a similar ecological role by suppressing unbounded population growth at high densities. For this reason, we refer to it as a logistic-type source in the biological modeling. Additionally, prey-taxis predator-prey models featuring similar generalized logistic sources can be found in [29] (see also [28]).
Having established the motivation for incorporating (H3*) into our analysis, we now turn to the main objective of this paper. As a continuation of the discussion presented in Remark 2.2 of [1], we aim to prove the global existence and boundedness of solutions to system (1.1) for any $ \chi > 0 $ in the one-dimensional case (i.e., $ N = 1 $). Accordingly, we present our main result for system (1.1) as follows.
Theorem 1.1. Assume that assumptions (H1), (H2), (H3*), and (H4) hold and that $ N = 1 $. Let $ u_0 $, $ v_0 \in W^{1, p}(\Omega) $ for some $ p > 1 $, where $ u_0 $, $ v_0 \geq 0 \, (\not\equiv 0) $ in $ {\Omega} $. Then, system (1.1) admits a unique, nonnegative, and global classical solution $ (u, v) $, which satisfies the properties
and $ u > 0 $ in $ (0, \infty) \times \overline{\Omega} $. Moreover, the solution is bounded in the sense that there exists a constant $ C > 0 $, independent of $ t $, such that
Having established the global existence and boundedness of classical solutions in one dimension through Theorem 1.1, we now turn our attention to the steady states of (1.1). In particular, an important question arises in the context of reaction-diffusion predator-prey systems with prey-taxis: under what conditions can spatial patterns emerge in the steady-state regime? This phenomenon, commonly referred to as pattern formation, is of great biological and mathematical interest (see, for instance, [4,9,26,31,32,33,34]). In the context of system (1.1), the presence of prey-taxis and nonlinear interactions through cooperative hunting and logistic-type regulation can induce instabilities in constant steady states, potentially leading to the emergence of spatially nonhomogeneous solutions. Such phenomena are often studied via bifurcation theory (e.g., [26,32,33,34]), particularly when investigating how variations in parameters such as the prey-taxis sensitivity $ \chi $ influence the structure of steady states. Motivated by this, we analyze the associated steady-state elliptic system, which governs the equilibrium configurations of parabolic system (1.1). By employing global bifurcation theory, we rigorously demonstrate the existence of nonconstant positive steady states bifurcating from spatially homogeneous equilibria. A key element of this analysis is the derivation of a priori estimates for the steady-state solutions, which are essential for controlling the global bifurcation branches and ensuring the applicability of the theory.
As the second main result of this paper, we present a result on the global bifurcation of positive solutions to the following elliptic system, which corresponds to the steady states of (1.1):
The bifurcation branch emanates from a positive constant steady state of the system. Accordingly, we first ensure the existence of such a constant solution by referring to [1, Theorem 2.3].
Proposition 1.2. Assume that assumptions (H1), (H2), (H3*), and (H4) hold. Assume, additionally, that
(H1b) $ g^{\prime}(K) < 0 $ and $ g^{\prime} (0) > 0 $ hold when $ g(0) = 0 $; $ g^{\prime}(K) < 0 $ holds when $ g(0) > 0 $.
Let
Then (1.1) has at least one steady state of constant coexistence if either one of the following is fulfilled:
For convenience in stating the following theorem, we now prepare the following notations: Let
be all eigenvalues of the problem $ -\phi_{xx} = \mu \phi $ in $ \Omega $ and $ \partial_n \phi = 0 $ on $ \partial \Omega $. Additionally, let $ \phi_i $ denote the normalized eigenfunction corresponding to $ \mu_i $ for $ i\geq 0 $. In particular, when $ \Omega = (0, L) $, we know that $ \mu_i = (\frac{i \pi}{L})^2 $ and $ \phi_i = \cos \frac{i \pi x}{L} $. Furthermore, when (1.2) possesses a positive constant solution $ (u_*, v_*) $, we let
where
Theorem 1.3. Assume that assumptions (H1), (H2), (H3*), (H4), and (H1b) hold and that $ N = 1 $. Furthermore, suppose that $ q \in C^2 ([0, \infty), \mathbb{R}) $, and that one of the conditions in (1.3) is satisfied. Assume additionally that
(H5) $ \mathcal{H}^{\prime} (u_*)\neq 0 $ for all positive constant solutions $ (u_*, v_*) $ of (1.2).
Let
such that
Then the following results hold:
(i) There exists a positive constant $ \epsilon $ such that nonconstant positive solutions of (1.2) lie on a smooth curve
near $ (u_*, v_*) $ at $ \chi = \chi_i^* $, where $ \chi_i (s) $ is a continuous function such that $ \chi (0) = \chi_i^* $, $ u(s) = u_* +s \mathcal{F}_v^* \phi_i (x) +s {\overline{\phi}}_i (s) $, and $ v(s) = v_* +s (\tau \mu_i -\mathcal{F}_u^*) \phi_i (x) +s {\overline{\psi}}_i (s) $ for some smooth functions $ {\overline{\phi}}_i (s) $ and $ {\overline{\psi}}_i (s) $ satisfying $ {\overline{\phi}}_i (0) = {\overline{\psi}}_i (0) = 0 $.
(ii) The curve $ \Gamma_i $ is contained in a global branch $ C_i $ of positive solutions of (1.2). Moreover, either $ C_i $ joins $ (\chi_j^*, u_*, v_*) $ with $ i \neq j $, or $ C_i $ joins to $ \infty $ in $ \chi $.
The following is a brief overview of the paper's structure. In Section 2, we present several preliminary results that are essential for the proof of Theorem 1.1. These include a local existence theorem for system (1.1) and various estimates related to its solutions. In particular, to establish $ L^{\infty} $-estimates for $ v $, we employ the Moser-type iteration method [35] as one of our primary analytical tools. Subsequently, we apply all the previously derived results to complete the proof of Theorem 1.1. Next, using global bifurcation theory [36], we prove the second main result, Theorem 1.3, which establishes that a nonconstant positive solution branch of (1.2) bifurcates from a positive constant equilibrium. As a preliminary step in this analysis, we derive a priori estimates for positive solutions to (1.2).
2.
The proof of the main theorems
The first part of this section is devoted to the proof of Theorem 1.1. To begin, we present a result obtained from [1] stating that (1.1) admits a local classical solution. This can be proven using Amann's local existence results [15,16] (e.g., see [18,24,37] for similar applications).
Lemma 2.1. Assume that (H1), (H2), (H3*), and (H4) hold, and suppose $ u_0 $, $ v_0 \in W^{1, p}(\Omega) $ with some $ p > N $, where $ u_0 $, $ v_0 \geq 0 $ and $ u_0 $, $ v_0 \not\equiv 0 $ in $ {\Omega} $. Then, there exists a maximal-existence-time $ T_{\max} \in (0, \infty] $ such that system (1.1) has a unique classical solution $ (u, v) $, where $ u $, $ v $ are nonnegative functions satisfying $ u, v \in C([0, T_{max}); W^{1, p} (\Omega))\cap C^{2, 1} ((0, T_{\max}) \times {\overline{\Omega}}) $. Moreover, the criterion for extensibility holds:
When $ (u(t, x), v(t, x)) $ is a solution of system (1.1), [1] established an $ L^{\infty} $-norm bound of $ u $ by applying both the comparison principle and the strong maximum principle, as well as an $ L^{1} $-norm bound of $ v $ through elementary integral calculations and the ODE comparison principle. We now restate these results as follows.
Lemma 2.2. Assume that the assumptions given in Lemma 2.1 are satisfied. Then,
Moreover, for any $ t\geq 0 $,
where $ |\Omega| : = {\int}_{\Omega} dx $.
Next, we present some well-known estimates for the diffusion-semigroup subject to homogeneous Neumann boundary conditions; e.g., see [1, Lemma 3.5]. For further details, see [38,39]. For $ 0 < \theta < 1 $, the operator $ (-\tau \Delta +1)^{\theta} $, defined on a dense domain, is the closed fractional powers of the sectorial operator $ -\tau \Delta +1 $ in $ L^p (\Omega) $ for $ p\in (1, \infty) $.
Lemma 2.3. Let $ p $, $ q $, $ \theta $, and $ m $ be constants.
(i) If
then there exists a constant $ C_1 > 0 $ such that for all $ \phi \in \mathit{\text{Dom}}((-\tau \Delta +1)^{\theta}) $,
(ii) If $ 1\leq p \leq q < \infty $ and $ 0 < \theta < 1 $, then there are two constants $ C_2 > 0 $ and $ \alpha_1 > 0 $ such that for all $ \phi \in L^p (\Omega) $, the so-called $ L^p - L^q $ estimate
holds, where $ t > 0 $ and the associated heat semigroup $ (e^{t \tau \Delta})_{t \geq 0} $ maps $ L^p (\Omega) $ into $ \mathit{\text{Dom}}((-\tau \Delta +1)^{\theta}) $.
Now, using the two preceding lemmas, we additionally derive a priori estimates for solutions of (1.1).
Lemma 2.4. Assume that the assumptions in Lemma 2.1 hold and that $ N = 1 $. Then, for any $ p > 1 $, there exists a positive constant $ C = C(p) $ such that
Proof. We begin by choosing an $ \eta \in (0, T_{\max}) $. Note that all constants $ C_i > 0 $ and $ \alpha_i > 0 $ introduced below are fixed and will be used without further specification.
From the representation formulation of the first equation in system (1.1), one can obtain that for $ (t, x) \in (0, T_{\max})\times \Omega $,
where
We choose a
Applying Lemma 2.3(ⅰ) to (2.1) and then using the triangle inequality, one has that
According to Lemma 2.3(ⅱ) and the assumption on $ u_0 $, we obtain that
Moreover, by using assumptions (H1) and (H2) and applying Lemmas 2.2 and 2.3(ⅱ), we deduce that
Here, the last inequality follows from elementary integral calculus due to the fact that $ \theta +\frac{1}{2} -\frac{1}{2p} < 1 $, and $ C_6 $ is independent of $ t $ but depends on $ p $. Thus, by applying (2.3) and (2.4) in (2.2), we see that for all $ t \in (\eta, T_{\max}) $,
Combining this result with the assumption on $ u_0 $ for sufficiently small $ \eta $, we obtain the desired conclusion, thereby completing the proof. □
Lemma 2.5. Assume that the assumptions in Lemma 2.1 hold and that $ N = 1 $. Then, for each $ p > 2 $, there exists a positive constant $ C = C(p) $ such that
Proof. Multiplying the second equation of system (1.1) by $ v^{p-1} $ and integrating the resulting equation on $ \Omega $, and then applying integration by parts, we can derive
By inserting the simple facts that
into (2.5), we can immediately obtain that
Furthermore, applying assumptions (H2)–(H4) to (2.6), we deduce that the right-hand side of (2.6) is bounded above as follows:
By setting
and sequentially applying Hölder's inequality with exponents $ m $ and $ \frac{m}{m-1} $, Lemma 2.4, and Hölder's inequality with exponents $ \frac{2(m-1)}{m-2} $ and $ \frac{2(m-1)}{m} $, it is easy to see that the following holds:
where $ C_1 $ is a positive constant depending on $ m $. After choosing an $ \epsilon $ to satisfy
and incorporating the previously obtained inequality into (2.7), followed by applying Young's inequality, we obtain that
Since $ \alpha > 1 $, it is clear that $ \frac{p-1+\alpha}{p} > 1 $. Thus, we also note that Young's inequality with exponents $ \frac{p-1+\alpha}{p} $ and $ \frac{p-1+\alpha}{\alpha-1} $ implies that
for a fixed constant $ \delta > 0 $ chosen to satisfy
This leads to the following inequality:
Finally, applying Hölder's inequality with exponents $ \frac{p-1+\alpha}{p} $ and $ \frac{p-1+\alpha}{\alpha -1} $ yields the inequality
Substituting this into (2.9) and setting $ y(t) = {\int}_{\Omega} v^p dx $, we eventually obtain that
for all $ t \in (0, T_{\max}) $. Using the fact that $ \frac{p-1+\alpha}{p} > 1 $, we apply an ODE comparison argument to deduce from (2.10) that there exists a positive constant $ C_3 = C_3 (p) $ such that $ y(t) \leq C_3 $ for all $ t \in (0, T_{\max}) $. Thus, the proof is complete. □
When $ N \geq 2 $, inequality (2.8) cannot be derived. In fact, Lemma 2.4 is no longer applicable in this case. This highlights the essential role of the one-dimensional setting ($ N = 1 $) in our analysis.
Using Lemma 2.5, we obtain the following improved result compared to Lemma 2.4.
Lemma 2.6. Assume that the assumptions given in Lemma 2.1 hold and that $ N = 1 $. Then, there exists a positive constant $ C $ such that
Proof. We first choose an $ \eta \in (0, T_{\max}) $. As demonstrated in the proof of Lemma 2.4, we will use the constants $ C_i $ and $ \alpha_i $ mentioned below without explicit reference; all of these constants are positive and independent of $ t $.
For fixed
applying Lemma 2.3(ⅰ) to (2.1), we derive that
As in (2.3), we derive that $ B_1 (t) \leq C_2 \eta^{-\theta} $ holds for all $ t \in (\eta, T_{\max}) $. Additionally, by applying assumptions (H1) and (H2) along with Lemmas 2.2, 2.3(ii), and 2.5, we obtain the following result analogous to (2.4):
Therefore, as in the final part of the proof of Lemma 2.4, we conclude that our claim is valid. □
We now need to establish the $ L^{\infty} $-estimate of $ v $, for which the following Gagliardo-Ladyzhenskaya-Nirenberg inequality (see [42, p. 63]) is required.
Lemma 2.7. Let $ \Omega $ be a bounded domain in $ \mathbb{R}^N $ with a smooth boundary. Then, for all $ \phi \in H^{1}(\Omega) $, there exists a constant $ C = C(N, \Omega) > 0 $ such that
where $ \overline{\phi} = \frac{1}{|\Omega|} {\int}_{\Omega} \phi dx $.
Lemma 2.8. Assume that the assumptions stated in Lemma 2.1 are satisfied and that $ N = 1 $. Then, there exists a positive constant $ C $ such that
Proof. We begin with the following inequality, which is obtained directly by applying assumptions (H2) and (H4) to (2.6) for $ p > 2 $:
The remaining steps follow from standard Moser-type iteration arguments (see, e.g., [4,26,35,40]). For completeness, the full proof is provided in the Appendix. □
We are now finally prepared to prove our main result, Theorem 1.1.
Proof of Theorem 1.1. First, we note from Lemma 2.2 that $ u > 0 $ for all $ t > 0 $. From Lemma 2.1, we see that system (1.1) possesses a classical and local-in-time solution $ (u, v) $ on $ [0, T_{\max}) $. Hence, together with Lemmas 2.6 and 2.8, the extensibility-criterion presented in Lemma 2.1 enables us to conclude $ T_{\max} = \infty $. This completes the proof. □
We now consider the bifurcation of nonconstant positive steady-state solutions of system (1.2). To begin, we derive a priori estimates for the positive solutions of (1.2).
Lemma 2.9. Assume that (H1), (H2), (H3*), and (H4) hold. Let $ (u, v) $ be a positive solution of (1.2). Then there exists a positive constant $ C $ such that
Proof. By directly applying the maximum principle to the first equation in (1.2), we can immediately see that $ \max_{\overline\Omega} u \leq K $.
From the result obtained by integrating the equations in (1.2) over $ \Omega $, we can readily derive the following:
which, together with (H1) and (H3*), implies that
For any $ k > 0 $, multiplying the second equation of system (1.2) by $ v^k $ and integrating the resulting equation on $ \Omega $, and then applying integration by parts, we can derive
By inserting the simple fact that
into (2.13) and using assumptions (H2) and (H4), we can obtain that
Similarly, by multiplying the first equation of system (1.2) by $ \Phi(v) = {\int}_0^v s^{k-1} q(s)ds $, integrating the resulting equation over $ \Omega $, and applying integration by parts, we obtain the following:
Then, using (2.14), (2.15), assumptions (H2) and (H4), and the result obtained by applying our first finding $ \max_{\overline\Omega} u \leq K $ to $ g(u) $ satisfying (H1), we arrive at the following:
Applying Hölder's inequality with exponents $ \frac{\alpha}{\alpha-1}: = \theta $ and $ \alpha $, and then using (2.12), we can deduce that
where $ C_1 $ is a positive constant independent of $ k $. In particular, for $ 1 < k+1 < (k+1)\theta $, Hölder's inequality gives that
Moreover, since $ N = 1 \leq 2 $, the Sobolev inequality implies that for any $ m > 1 $,
where $ C_2 $ is a positive constant independent of $ k $. We now apply (2.17)–(2.19), which together yield
where
Using (2.20) with $ k $ such that $ k+1 = \theta m^{i} $ for $ i \in \mathbb{N} \cup \{0\} $, we obtain
If we set $ m = \theta^2 $, then the above becomes
Similarly, using (2.20) with $ k $ such that $ k+1 = \theta^2 m^{i} $ for $ i \in \mathbb{N} \cup \{0\} $, we obtain
If we set $ m = \theta^2 $, then the above becomes
By iteratively using the inequalities in (2.21) and (2.22), we are finally led to the following:
where
for a positive constant $ S > 1 $ determined by the definition of $ C_5 (k) $.
Taking the limit as $ n \rightarrow \infty $ in (2.23) gives
Consequently, by using (2.12) together with the following inequality to this estimate,
which is obtained via Hölder's inequality, we can complete this proof. □
By combining the above result that all positive solutions $ (u, v) $ of (1.2) are bounded in $ L^{\infty}(\Omega)\, \times \, L^{\infty}(\Omega) $ with the $ L^p $-theory of elliptic equations, the Schauder estimates, and the Sobolev embedding theorem, we can conclude that $ u $, $ v \in C^{2, \beta} $ for some $ \beta \in (0, 1) $ (e.g., see [9,31]).
With respect to (1.2), we will obtain a nonconstant positive solution branch that bifurcates from the positive constant equilibrium $ (u_*, v_*) $ (if it exists), under the assumptions of Theorem 1.3. Let $ \chi $ be a bifurcation parameter and assume that all other coefficients are fixed. For $ p > N = 1 $, we define Banach spaces $ X $ and $ Y $ as
Furthermore, we set a mapping $ \mathcal{A}: \mathbb{R} \times X \times X \rightarrow Y \times Y $ by
where $ \mathcal{F}(u, v) $ and $ \mathcal{G}(u, v) $ were defined before Theorem 1.3. It is obvious that $ \mathcal{A} $ is continuously differentiable in an open set in $ \mathbb{R} \times X \times X $, and that $ \mathcal{A} (\chi, u_*, v_*) = 0 $ for all $ \chi \in \mathbb{R} $, where $ (u_*, v_*) $ is a positive constant steady state of (1.2). It follows that the Fréchet derivative of $ \mathcal{A} $ at $ (\chi, u_0, v_0) \in \mathbb{R} \, \times X \times X $ is given by
where
In particular, when $ (u_0, v_0) = (u_*, v_*) $ (provided that the positive constant solution $ (u_*, v_*) $ exists), a straightforward computation yields
We now identify potential bifurcation values of $ \chi $. To find possible bifurcation points corresponding to values of $ \chi $, we consider the linearized problem $ D_{(u, v)} \mathcal{A} (\chi, u_*, v_*) (u, v) = 0 $ and examine whether it admits a nontrivial solution. Using the eigenfunction expansions $ u = \sum a_i \phi_i $ and $ v = \sum b_i \phi_i $ in this problem, we can derive the following:
We see that the linearized problem has nontrivial solutions if and only if
that is to say, $ \chi = \chi_i^* $ for $ i \in \mathbb{N} $, where $ \chi_i^* $ was defined in Theorem 1.3. Here, the case $ i = 0 $ can be readily excluded, since assumptions (H4) and (H5) imply that
A detailed verification of this computation can be found in the proof of [1, Theorem 2.7].
Lemma 2.10. Suppose that all assumptions of Theorem 1.3 hold. Then $ \dim N(D_{(u, v)} \mathcal{A} (\chi_i^*, u_*, v_*)) = 1 $.
Proof. Suppose $ (\phi, \psi) \in N(D_{(u, v)} \mathcal{A} (\chi_i^*, u_*, v_*)) $. Then as in the previous discussions, using the eigenfunction expansions of $ \phi $ and $ \psi $, we see that $ B_i (\chi_i^*) (a_i \ b_i)^T = 0 $, since the definition of $ \chi_i^* $ gives (2.25). Thus, a direct calculation shows that
Moreover, we observe that
Thus, the assumption given in Theorem 1.3 ensures that $ \chi_i^* \neq \chi_j^* $ for $ i \neq j $. Hence, the assertion holds, as $ \mu_i $ is a simple eigenvalue. □
Lemma 2.11. Suppose that all assumptions of Theorem 1.3 hold. Then $ {{codim}} R(D_{(u, v)} \mathcal{A} (\chi_i^*, u_*, v_*)) = 1 $.
Proof. Consider the adjoint operator of $ D_{(u, v)} \mathcal{A} (\chi_i^*, u_*, v_*) $:
Following the same method as in the proof of Lemma 2.10, we obtain
Suppose $ (\overline \phi, \overline \psi) \in R(D_{(u, v)} \mathcal{A} (\chi_i^*, u_*, v_*)) $. Then there exists $ (\phi, \psi) \in Z $ such that
where $ Z $ is a complement of $ \mbox{span} \{\Phi^* \} $ in $ X \times X $. We easily see that
Thus,
gives $ \mbox{codim} R(D_{(u, v)} \mathcal{A} (\chi_i^*, u_*, v_*)) = 1 $. □
Lemma 2.12. Suppose that all assumptions of Theorem 1.3 hold. Then $ D_{(u, v)\chi} \mathcal{A} (\chi_i^*, u_*, v_*))\Phi \not \in R(D_{(u, v)} \mathcal{A} (\chi_i^*, u_*, v_*)) $, where $ \Phi \in N(D_{(u, v)} \mathcal{A} (\chi_i^*, u_*, v_*)) $.
Proof. Suppose that $ D_{(u, v)\chi} \mathcal{A} (\chi_i^*, u_*, v_*))\Phi \in R(D_{(u, v)} \mathcal{A} (\chi_i^*, u_*, v_*)) $. Then, it is obvious from (2.26)–(2.28) that
and
which is a contradiction. □
We are now finally prepared to prove our main result, Theorem 1.3.
Proof of Theorem 1.3. By virtue of Lemmas 2.10–2.12, the first result follows from the local bifurcation theorem [41].
For the global bifurcation analysis, we consider the interval $ \chi \in (0, \infty) $. In view of the implicit function theorem, the linearization around the trivial solution $ (0, 0) $ and the semi-trial solution $ (K, 0) $ of system (1.2) shows that any solutions bifurcating from $ (0, 0) $ or $ (K, 0) $ are not positive near the bifurcation points. Thus, the positive solution branches cannot be joined to $ (0, 0) $ or $ (K, 0) $. According to the global bifurcation theory [36], one of the following two alternatives must be satisfied:
(ⅰ) $ C_i $ is unbounded in $ (0, \infty) \times X \times X $;
(ⅱ) $ C_i $ meets a point $ (\chi_j^*, u_*, v_*) $ with $ i \neq j $.
We know from Lemma 2.9 that any positive solution $ (u, v) $ to (1.2) is bounded in $ L^{\infty} (\Omega) \times L^{\infty} (\Omega) $. Furthermore, from the discussion presented below Lemma 2.9, $ (u, v) $ is also bounded in $ X \times X $. Therefore, the global branch $ C_i $ is bounded in $ X \times X $, which implies that $ C_i $ must be unbounded in the $ \chi $-direction; that is, $ C_i $ joins to $ \infty $ in $ \chi $. □
3.
Conclusions
In this paper, building upon the considerations outlined above and motivated by Remark 2.2 in [1], we established the global existence and boundedness of classical solutions to system (1.1) in the one-dimensional case (i.e., $ N = 1 $) for arbitrary positive prey-taxis coefficients $ \chi > 0 $. To achieve this result, we introduced a stronger logistic assumption on the predator growth term, denoted as (H3*). This assumption plays a central role in providing sufficient control over population densities, thereby preventing population overcrowding without imposing the restrictive truncation or smallness conditions previously required.
Our analysis relied on deriving a priori estimates through a careful combination of the Moser-type iteration method, weighted integral estimates, and precise applications of the Gagliardo-Ladyzhenskaya-Nirenberg inequality. In particular, the logistic source introduced by condition (H3*), especially through the exponent $ \alpha > 1 $, was essential in ensuring the boundedness of all positive steady states for arbitrary values of $ \chi > 0 $. This boundedness property played a crucial role in enabling the application of global bifurcation theory in the steady-state analysis.
In the latter part of the paper, we applied global bifurcation theory to establish the existence of nonconstant positive steady states, thereby providing a rigorous basis for pattern formation in the model. Such spatial patterns, induced by prey-taxis and cooperative hunting effects, offer insight into how local interactions and movement mechanisms can generate heterogeneous population distributions even in homogeneous environments.
Our results extend and complement the existing literature, particularly the discussions in Remark 2.2 of [1], and confirm the conditions under which population densities remain controlled in one-dimensional predator-prey models with prey-taxis. For future research, an important and challenging direction will be to explore whether similar global existence and boundedness results can be achieved in higher-dimensional scenarios (i.e., $ N \geq 2 $) or in the absence of logistic source terms, thereby broadening the class of predator-prey models for which global existence can be established.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The authors would like to express their sincere appreciation to the associate editor and the anonymous reviewers for their valuable suggestions, which encouraged the addition of bifurcation analysis and contributed to enhancing the manuscript. The first author (K. Ryu) was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. NRF-2021R1A2C1095325).
Conflict of interest
The authors declare there are no conflicts of interest.
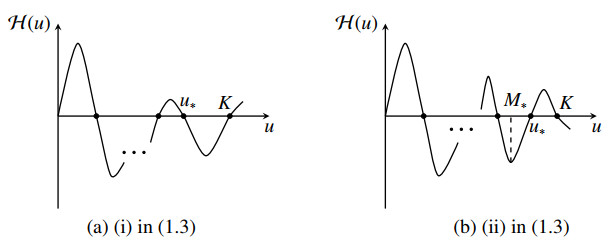









 DownLoad:
DownLoad:


