1. Introduction
Coals are the raw materials for energy production through combustion at power plants and for technological application. Efficiency of coals utilization depends on their structure and properties. As it was shown in review book [1], performance of power production highly relies on coals calorific value, Carbon, Hydrogen, Oxygen, Sulphur and ash contents. As for coals technological properties in coke production, they are determined primarily by rank, caking and coking ability, volatiles yield, ash and Sulphur contents, as well as petrographic composition. As for gasification, coals utilization efficiency is mainly defined by their reactivity with respect to oxidizing agents.
It is well known that coals oxidation at weathering in coalbeds, during storage and transportation leads to energetical and technological quality loss [2]. Namely, coals oxidation leads to decrease of calorific capacity, caking and coking ability, increase of volatiles yield, etc. Coals oxidation is assumed to be the primary reason of appearance of spontaneous combustion hazards [3].
On the other hand, preventive mild oxidation is used for enhancing the coals gasification processes [4] and other aims. These methods are used for obtaining new products with high sorption potential [5,6,7], increase of humic and other organic active water-soluble acids yield [7,8,9], structure characterization [7,9], etc.
A comprehensive review on methods of coals mild oxidation was shown in [7]. One of them is ozonating [7,10,11,12]. Ozone as oxidizing agent involves high rate of oxidation due to high reactivity of O3 molecules as compared with oxygen ones [13]. Currently, ozonating of carbonaceous materials and coals is applied for different aims. The most common one is characterization of carbonaceous filters for ozone removal from indoor air and aircraft cabins [14,15,16]. At the same time, ozone is widely used for controlled modification of surface of different carbonaceous materials for obtaining the ones with desirable properties, for example, increased sorption activity (see e.g., [10,17]). Coals modification by ozone leads to alteration of their chemical composition such as carbon contents decrease (up to 40% mass), increase of oxygen-containing functional groups [18,19], along with, in some cases, to coal matter destruction and fine dust formation [19]. Coals ozonating also leads to significant increase of humic acids yield along with obtaining new products with lower molecular weight [11,12,18]. Ozone could be used for characterization of coals structure as it was shown in [20]. Ozone treatment is applied for attempts of characterization of carbonaceous materials activity e.g., in [21] authors introduced some regression equations for connecting ozone decomposition rate with coefficients describing activity of lignin surface.
Necessity of construction of efficient filtering materials for ozone removal requires characterization of materials activity to ozone decomposition. The following values are being calculated such as the rate of ozone molecules removal and coefficient of ozone decomposition (or the so-called uptake coefficient) γ [22]. In [23] authors presented γ values for different materials (all calculated for the so-called stationary mode of materials interaction with ozone) and mentioned that they highly depend on the experiments conditions such as humidity, temperature, gas pressure, etc. The efficiency of characterization of materials ability for ozone removal by γ coefficients is undoubtable. On the other hand, when it is necessary to characterize alteration of materials activity and properties due to interaction with ozone, γ coefficients determined for the stationary mode are not enough. And it is required to derive γ coefficients and related parameters not only at the stationary, but also the non-stationary modes, because the latter is supposed to characterize the primary stages of surface changes including oxidation or ozone (oxygen) sorption [24,25].
In the view of above, the aim of the current work is to develop means for characterization of coals activity and changes of their properties at interaction with ozone. To this end, a model was proposed for kinetic parameters evaluation considering that coals activity changes at interaction with ozone. The model was applied at data obtained by experiments of ozonating of finely grinded coals. Ozone concentration in such experiments did not exceed 250 µg/m3 which only 2.5 times higher than the WHO recommended maximal average (throughout 8 hours) concentration of ozone in atmospheric air [26]. Such ozone concentration is comparable with the ones observed near areas of forest and peat fires [27]. Three coals samples were used in this work. These coals differ by their nature, rank, organic matter composition and tendency to oxidation.
2. Materials and Method
2.1. Coals samples characteristics
The representative samples of coals were selected from different deposits of the Russian Federation. By the degree of carbon contents growth, the current sample set contains three coals representing their main types: lignite #1, bituminous coal #2 and anthracite #3. Some characteristics of coals samples are shown in Table 1. The aforementioned coals were used in the large sample set used in a series of works dedicated to derivation of indices characterizing coals tendency to oxidation [28,29,30,31]. The detailed description of the aforementioned samples set was shown in paper [28], where the current numbers of samples correspond to the ones listed in article by the following:
#1: Lignite 4, #2: Bituminous coal 7, #3: Anthracite 15.
Table 1. Characteristics of coals samples [28].
| Sample # |
Type |
Vitrinite reflectance index Ror |
Proximate analysis, % mass |
Ultimate analysis, % mass (on dry, ash-free basis) |
Atomic H/C ratio, at |
| Wa |
Ad |
Vdaf |
C |
H |
N |
| 1 |
Lignite |
0.33 |
14.93 |
13.35 |
41.91 |
73.94 |
4.93 |
2.25 |
0.7945 |
| 2 |
Bituminous |
0.50 |
3.1 |
15.3 |
38.8 |
76.39 |
5.15 |
2.23 |
0.8091 |
| 3 |
Anthracite |
3.58 |
1.2 |
4.3 |
3.5 |
92.34 |
1.61 |
1.15 |
0.2098 |
| In Table 1 Wa: moisture, Ad: ash (on dry basis), Vdaf: volatile matter (on dry, ash free basis). |
Coals samples were selected and prepared for experiments in accordance with the standard procedures. Grinded coals samples (with particle diameter not exceeding 200 µm) were conditioned to air-dry state and stored in air-tight containers to exclude their oxidation prior to ozonating tests.
2.2. Experimental installation and description of experiments
Experimental installation and procedure was previously fully described in [13]. Reaction chamber in the installation was a fluoroplastic filter holder with diameter 1.2 cm. Ozone concentration in gas (air) flow was 250 µg/m3 produced by GS-24 commercial generator with ozone specified concentration error of 5% and linear air flow rate of 1 cm/s. GS-24 generator was also a source of pure air—"zero gas" with ozone concentration not exceeding 0.3 µg/m3. Humidity of "zero-gas" was 10–12%. Concentration of ozone at the outlet of reaction chamber was fixed by sensor ozone analyzer [32,33]. Relative error of ozone concentration measurements did not exceed 5% [13].
Prior to experiments, coals were removed from air-tight containers, thoroughly stirred and representative samples were chosen. Each of coal samples' weight was 0.04 ± 0.001 g. The samples were placed to the reaction chamber between layers of passivated (with respect to ozone) fine-fibers filter (the so-called layer-base). Passivation procedure was also in detail presented in [13]. Coals sample height was 0.5–0.65 mm. After samples loading, the experimental installation was kept in "zero-gas" flow for 2 hrs., after which the ozone generation was switched on. Time-length of samples ozonating was 16–18 hours. The measurements results were stored in data files with help of special software.
3. Results and Discussion
3.1. Ozone concentration curves after passing the coals samples
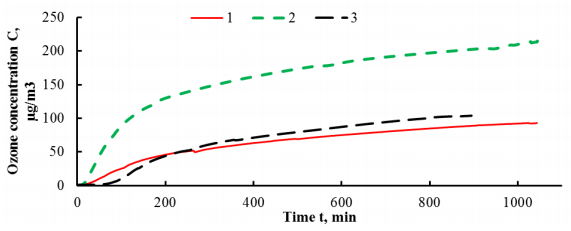
Figure 1 demonstrates curves of ozone concentration at the reaction chamber outlet for all the considered samples.
Comparison of curves of ozone concentration at the outlet of the coal samples reveals that at bituminous coal 2 ozone is less being decomposed than at lignite 1 and anthracite 3. Moreover, the latter samples have qualitatively similar curves of ozone concentration at outlet, especially at the quasi-stationary mode that was achieved for both of coals after approximately 250 minutes of experiment initiation. The latter may lead to a conclusion that activity of coals will be similar when characterized at the stationary mode. But at the same time, in this case we are dealing with coals whose properties, rank and even tendency to oxidation are completely opposite. Namely, coal #1 is lignite with low carbon contents and high value of H/C ratio connected with the aromaticity degree of structure fa by inverse linear relationship [34,35,36], whereas anthracite #3 has very high value of carbon contents and a very low H/C ratio (Table 1). Moreover, in accordance with the known concepts on structure and properties of coals, lignites and anthracites could be considered as principally dissimilar materials [1].
3.2. Kinetic model of ozone decomposition
Assume that ozone molecules decomposition at surface (active sites) is governed by the first-order reaction. Then one may write an equation characterizing ozone interaction with material surface, namely, one-dimensional equation of convective transport with chemical reaction:
|
$
\varepsilon \frac{{\partial c}}{{\partial t}} + u\frac{{\partial c}}{{\partial z}} = - kc
$
|
(1)
|
where с is the ozone concentration, ε is porosity, u is the flow velocity (related to the entire section of the layer), k is a constant of quasi-homogenous reaction, t is time, z is coordinate varying along filter height ($0 < z < L$), and L is the filter height. The time derivative could be neglected in accordance with experimental conditions. Constant of quasi-homogenous reaction k is not entirely a constant but is dependent on time and position along filter length $k = k(z, t)$. The final equation in quasi-stationary approximation could be written as:
|
$
u\frac{{\partial \,c(z,t)}}{{\partial \,z}} = - k(z,t)\,c(z,t)
$
|
(2)
|
To find solution to such equation, it is necessary to use some assumptions regarding the kinetics of deactivation determining dependence of local filter activity $k(z, t)\, $ on time. It is natural to propose that the local rate of filter deactivation is proportional to ozone decomposition rate, and the following kinetic equation for $k(z, t)\, $ might be written as:
|
$
\frac{{\partial \,k(z,t)}}{{\partial \,t}} = - ak(z,t)c(z,t)
$
|
where parameter a denotes a proportionality coefficient characterizing deactivation rate of surface active sites. As the concentration of ozone at filter inlet is constant ($c(0, t) = {c_0}$), solution for $c(z, t)$ is:
|
$
c(z,t) = {c_0}\exp ( - {K_z}(t))
$
|
(3)
|
where ${K_z}(t) = \frac{1}{u}\int\limits_0^z {k(z', t)} \, dz'$, and the subsequent equation for its evaluation is:
|
$
\frac{{\partial {K_z}(t)}}{{\partial \,t}} = - \frac{a}{u}\int\limits_0^z {k(z',t)\,c(z',t)\,dz'}
$
|
Simple transformations could lead to the following:
|
$
\frac{{\partial {K_z}(t)}}{{\partial \,t}} = - a{c_0}(1 - \exp ( - {K_z}(t)))
$
|
On using dimensionless variable $\tau = a{c_0}t$, we could finally come to equation
|
$
\frac{{\partial {K_z}(\tau )}}{{\partial \tau }} = - (1 - \exp ( - {K_z}(\tau ))),
$
|
and its solution
|
$
{K_z}(\tau ) = \ln \left[ {\,1 - \exp ({K_{z0}}) - \exp (\tau )} \right] - \tau ,
$
|
where ${K_{z0}} = {K_z}(0) = {k_0}{\theta _z}$, ${k_0} = k(z, 0)$, ${\theta _z} = z/u$-is time of the flow passing through the filter layer of (0, z)-height.
The expression for dimensionless ozone concentration at filter outlet ${{\tilde c}_L} = c(L, t)/{c_0}$ is:
|
$
{{\tilde c}_L}(\tau ) = \frac{1}{{1 + \exp ( - \tau )(\exp ({K_{L0}}) - 1)}}
$
|
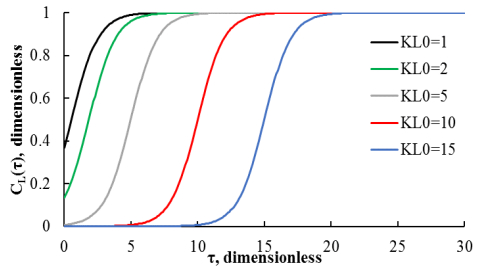
Ozone concentration at filter outlet is primarily dependent on only one parameter ${K_{L0}}$, i.e. initial filter activity, whereas constant a is included in the dimensionless time τ and determines time scale of t during which the filter deactivation is occurring.
Figure 2 demonstrates some dependencies of the dimensionless concentration ${{\tilde c}_L} = c(L, t)/{c_0}$ on time and parameter ${K_{L0}}$.
Figure 2 clearly demonstrates that the aforementioned method is not sufficient for full characterization of the experimentally derived ozone concentration curves for coals (see Figure 1), especially considering the fact that all the coals never allowed ozone to be fully passing through. This could be reasoned by either unknown dependence of proportionality factor a on time or existence of different types of active sites at filter surface with different rates of deactivation. To support the latter assumption, Figure 1 could be considered where it is clearly seen that activity of coals changes with at least two different rates, which is described by at least two different inclination angles of curves (before 200–250 minutes and after, from the initiation of experiments). Then it is possible to assume that there exist at least two types of active sites. They both deactivate at interaction with ozone, but with sufficiently different rate of deactivation. Then let us introduce a model that considers these two types of active sites. Equation (2) could be rewritten as
|
$
u\frac{{\partial c}}{{\partial z}} = - \left[ {{k_1}(z,t) + {k_2}(z,t)} \right]c\left( {z,t} \right),
$
|
(4)
|
where ${{k_1}(z, t)}$ and ${{k_2}(z, t)}$ are constants of quasi-homogenous reaction of ozone decomposition at active sites of type 1 and 2, respectively.
Assuming that the first and second types of active sites deactivate proportionally to ozone decomposition rate, for each ${{k_1}(z, t)}$ and ${{k_2}(z, t)}$ one may write equations (5)
|
$
\frac{{\partial \,{k_i}(z,t)}}{{\partial \,t}} = - {a_i}{k_i}(z,t)c(z,t),i = \mathit{1},\mathit{2},
$
|
(5)
|
where ${a_i}$ are proportionality factors characterizing deactivation rates of active sites of type 1 and 2.
The initial and boundary conditions for equations (4), (5) are expressed by equalities (6)
|
$
c\left( {0,t} \right) = {c_0},\;c\left( {z,0} \right) = 0,\;{k_i}\left( {z,0} \right) = {k_{i0}},\;\;\;\;i = 1,2,
$
|
(6)
|
where ${c_0}$ is inlet concentration, ${k_{i0}}$ are initial values of quasi-homogenous constants corresponding to active sites of type 1 and 2 interacting with ozone. Note that ${{k_1}(z, t)}$ and ${{k_2}(z, t)}$ also depend on experimental conditions, such as porosity $\varepsilon $ of sample.
Application of the proposed model assumes solving of problem (4), (5) with conditions (6) and fitting of experimentally obtained dependencies of concentration c at the filter (sample, coal) outlet.
In addition, the following integral characteristic of filter activity could be used as shown in (7):
|
$
{K_L}(t) = \frac{1}{u}\int\limits_0^L {\left( {{k_1}(z',t) + {k_2}(z',t)} \right)} dz'.
$
|
(7)
|
${K_L}(t)$ could be considered as an integral activity of coal to ozone decomposition at current time t. Analogously to (3), parameter ${K_L}(0)$ could be of a particular interest because it characterizes the total initial activity of coal to ozone.
It should be especially pointed out that the proposed model does not allow characterization of mechanisms of active sites interaction with ozone (whether it is chemisorption, or oxidative destruction, etc.), but only their deactivation and its rate.
3.3. Application of kinetic model for experiments results processing and characterization of coals activity to ozone
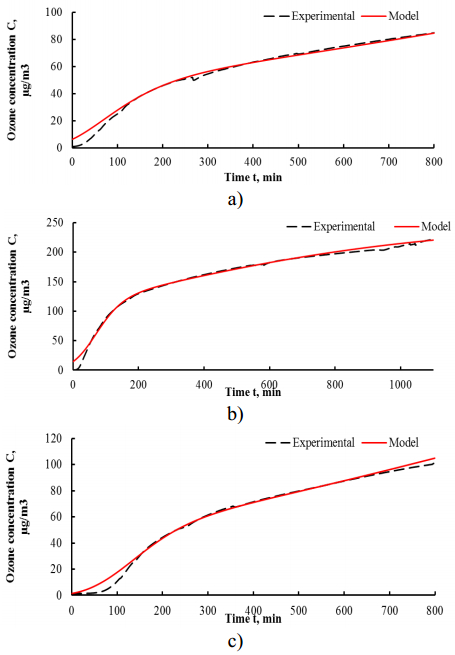
Figure 3 shows results on fitting of experimental outlet ozone concentration curves by model. The range of ${{k_1}(z, t)}$ and ${{k_2}(z, t)}$ parameters choice is justified by the experimental conditions and results, along with the model itself. The average fitting error did not exceed 5% for the whole range of experimental ozone outlet concentration curves.
It could be observed in Figure 3 that the curves of outlet concentrations derived by the model well define the experimental ones.
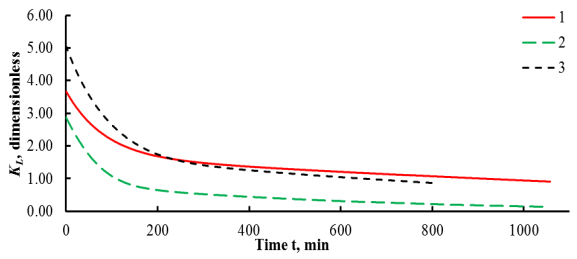
Figure 4 demonstrates graphs of changing of coals integral activity ${K_L}(t)$ with time (calculated in accordance with equality (6)).
It could be seen from Figure 4 that all the coals lose their integral activity to ozone. As a result, each of the samples reached mode when there is observed almost no changing of ${K_L}(t)$ at interaction with ozone. For samples #1 and #3 (lignite and anthracite, correspondingly), the remaining activity is higher than for bituminous coal #2.
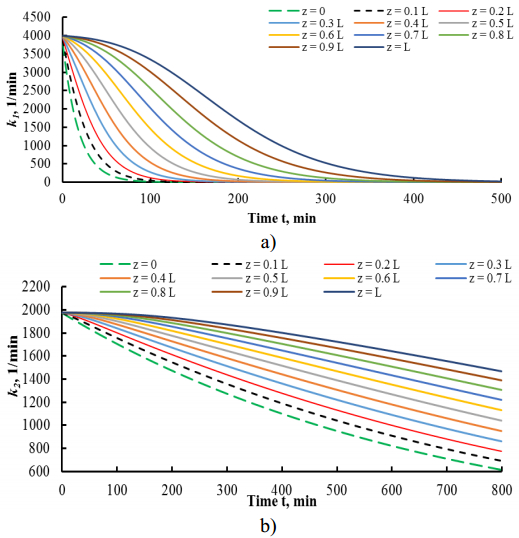
Figure 5 demonstrates dependencies of ${{k_1}(z, t)}$ and ${{k_2}(z, t)}$ on time and location within the anthracite #3 sample. For the other coals these dependencies were similar. According to Figure 5, as it was previously suggested by model introduction, coals activity changes not only with time, but it also depends on position in filter layer, even considering the relative small height of it during the experiments. Deactivation of active sites of the second type is much slower than for active sites of the first type, which is defined by rates a1 and a2. Moreover, active sites of type 1 are being reduced to zero during 500 minutes for anthracite #3, in 470 minutes for lignite #1 and in 290 minutes for bituminous coal #2. These time values were found for ${{k_1}(z, t)}$ at z = L, whereas for z-coordinate less than L these intervals were much lower (see Figure 5a). As for active sites of type 2, for each coal, they never exhausted throughout the whole time-interval of experiments.
Table 2 shows values of parameters used for model fitting of outlet concentrations of ozone after interaction with coals samples, as well as ${K_L}(0)$ characterizing coals initial activity.
Table 2. Results of kinetic parameters evaluation.
| Sample # and type |
k10, 1/min |
k20, 1/min |
a1, × 10–4, m3·µg–1 min–1 |
a2, × 10–6, m3·µg–1 min–1 |
${K_L}(0)$ |
| 1 Lignite |
2400 |
1980 |
1.80 |
4.00 |
3.65 |
| 2 Bituminous coal |
2500 |
942 |
1.60 |
8.20 |
2.87 |
| 3 Anthracite |
4000 |
1976 |
2.20 |
5.84 |
4.98 |
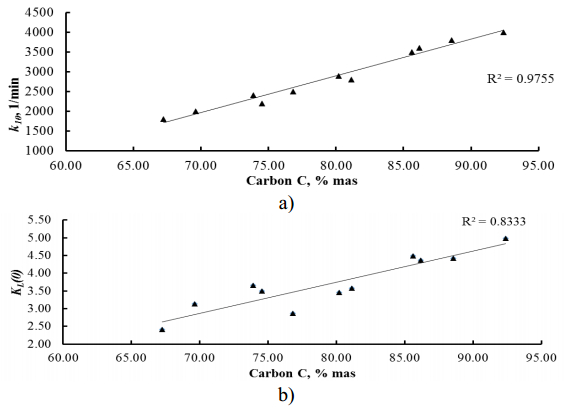
It could be seen from table 2 that the initial value of k20 for all the considered coals is lower than k10. It preliminarily could be observed that unlike k20, parameters k10 depend on coals rank, namely, with coal rank increase from lignite to anthracite, these values increase. Therefore, initial activity of sites of type 1 depend on rank. Moreover, the initial integral activity of coals ${K_L}(0)$ also increase with rank. To support this, we applied the model for calculation of the aforementioned kinetic parameters at selection of coals studied in [13]. Correlations between k10, ${K_L}(0)$ and carbon mass share in coals are shown in Figure 6 revealing strong linear dependence on rank.
It could be noticed that correlations shown in Figure 6 are in good agreement with data on coals microporosity increase with rank (from lignites to anthracites) [37,38]. Therefore, it could be assumed that activity of sites of type 1 (prone to rapid deactivation) strongly depends on microporosity level in coal structure.
On the other hand, it was noticed that the total porosity of coals does not have a pronounced proportional dependence on rank. It is more likely to be polynomial of the second degree as shown in [39,40] with sharp decrease from lignites to low-volatile bituminous coals (reasoned by decrease of macropores amount) and a consequent sharp increase from low-volatile bituminous coals to anthracites (reasoned by significant growth of micropores share in structure). Also, as it was shown in [37], the values of specific surface area of coals have similar polynomial shaped dependence on rank. Therefore, it might be observed that parameters k10 and ${K_L}(0)$ do not have strong correlation with the coals specific area. On the other hand, it should be again mentioned that the proposed model does not allow to separate the mechanisms of active sites deactivation. As well as the fact that their nature is also not known. But, as anthracite #3 and lignite #1 could be referred to dissimilar materials, it could be assumed, that the active sites for two of them have different nature and mechanisms of ozone decomposition at interaction. Therefore, oxidation mechanisms of low-and high-rank coals should be considered as different ones. In order to separate these mechanisms, the additional investigations and experiments should be promoted for analysis of changes in structure and chemical composition of coals after ozonating. For example, it was shown in [20] that ozone treatment of coals of different rank leads to opposite changes in chemical structure for low-and high-rank coals, i.e. reduction of functional groups for low-rank coals and, on the contrary, increase for high-rank ones. This is also in an agreement with the research on coals behavior at oxidation at elevated temperatures by thermogravimetric analysis [28] revealing that bituminous coals and anthracite are more prone to oxygen sorption whereas lignites and peat tend to oxidative destruction of the matter.
4. Conclusion
In this work, a model was proposed for evaluation of kinetic parameters describing coals activity to ozone. The model accounts for alteration of coals surface properties at interaction with ozone (i.e., its deactivation). Considering that experimental data suggests at least two surface deactivation rates, two types of active sites were introduced.
The proposed kinetic parameters characterize coals activity to ozone (local and integral) and active sites deactivation rates. While experimental curves of ozone concentration at outlet suggested that activity of anthracite and lignite coal was similar, application of model allowed to separate them. It was shown that the highest activity to ozone decomposition was found for anthracite (4.98), and the lowest—for lignites (2.40). This was in a good agreement with known data on microporosity of coals of different rank with its decrease from anthracites to lignites. The first type of introduced active sites, characterized by relatively high deactivation rate, revealed its strong dependence on micropores share in structure.
Unfortunately, at the moment, the proposed model does not allow revealing the mechanisms of coals interaction with ozone and/or oxygen. In order to fully explain coals reactivity to oxygen-based agents (including ozone), it is necessary to set up additional experiments to analyze changes within surface structure and chemical composition of coals after interaction with ozone. This also might be used further to find relations between coals oxidation and their tendency to destruction.
Acknowledgments
The research was supported by the Russian Science Foundation (grant #16-17-10217).
Conflict of Interest
All authors declare no conflict of interest in this paper.









 DownLoad:
DownLoad: