Nurshuak-Tolkynay-Myrzakulov system: integrability, geometry and solutions

1.   Introduction

Nonlinear differential equations (NDEs) play an important fundamental role not only in mathematics and physics, but also in other fields of science in describing nonlinear natural phenomena and processes. The theories and practical applications of NDEs have led to the need to develop methods for solving and investigating such equations for more than two centuries. This led to the discovery of the method of the inverse scattering transform (IST) in 1967. It is now rather developed, well established, and well known as soliton theory ^[1,2,3]. The main representatives of soliton theory born more than half a century ago, namely the Korteweg-de Friese equation, the nonlinear Schrödinger equation, the sine-Gordan equation, and the Heisenberg model, have become more popular due to the clarity with which they explain a wide range of complex physical phenomena and display dynamical regularities using localized wave solutions ^[4,5]. Integrable multidimensional extensions of soliton models have attracted considerable interest not only in theoretical and mathematical physics, but also in otsher sections of nonlinear sciences ^[6,7,8]. The methods of their investigation have also been extended. Thus, in ^[9], the (2+1)-dimensional nonlinear damped Klein-Gordon equation is studied using the classical method of Lie symmetry. Closed wave solutions of the (4+1)-dimensional fractional Davy-Stewartson-Kadomtsev-Petviashvili equation are studied using the modified auxiliary equation method and the method of elliptic Jacobi functions in ^[10]. The running solution of the generalized Zakharov system is obtained in ^[11]. The authors of ^[12,13,14] devote their research to equations with fractional order derivatives, which, in turn, provide a more general framework for modeling systems with nonlocality, memory, and anomalous behavior. In the recent work of the authors ^[15], integrable systems with self-consistent potentials were proposed. The works of the authors ^[16,17,18] are devoted to the study of integrable systems mentioned in ^[15]. One of the representatives of nonlinear Lax integrable equations (admitting a Lax pair with a non zero spectral parameter) is the Nurshuak-Tolkynay-Myrzakulov (NTM) system ^[15]. This system belongs to the theory of solitons and describes the dynamic interaction of different fields, where nonlinear effects lead to the formation of stable waves that are capable of propagating over large distances without changing their shape. The purpose of this paper is to give a geometric interpretation of the NTM system and to construct its soliton solutions. The task of establishing a geometric connection between the NTM system and the equation of motion of spatial curves is accomplished by applying the Serret-Frenet equation for curvature and torsion, which describes the properties of curves and surfaces in differential geometry. In it, curvature defines how a curve or surface is curved in space, and torsion is related to how a curve twists around its axis ^[19,20,21]. These geometric characteristics can be related to the physical properties described by the NTM equation. One-soliton solutions of the NTM system are obtained using the traveling wave method ^[22,23,24], which allows the efficient derivation of exact solutions in explicit form without resorting to the time-consuming analytical techniques typical of the classical methods of soliton theory.

This paper is organized as follows: Section 2 presents the NTM equation, its various reductions, and their Lax representations (LRs). The geometric formulation of this equation in terms of space curves is presented in Section 3. In Section 4, soliton solutions of the NTM equation are obtained. We discuss and draw conclusions from our results in Section 5.

2.   Nurshuak-Tolkynay-Myrzakulov equation

In this paper, the object of study is a previously unstudied system of nonlinear equations called the NTM system. The authors present, for the first time, a geometrical interpretation of this system. In particular, a method of finding the Lax pair for this nonlinear system based on the equation of motion of spatial curves is proposed.

The NTM equation has the form

where $q(x, t)$ and $r(x, t)$ are complex functions.

The corresponding Lax representation of Eqs (2.1)–(2.4) are given by

where

Here

The compatibility condition of the systems (2.5) and (2.6)

gives the NTM equations (2.1)–(2.4).

Next, we present some special cases of the NTM equations (2.1)–(2.4).

3.   Reductions of the NTM equation

The NTM equations (2.1)–(2.4) admit some exact integrable reductions, such as the following cases: $r = \epsilon\bar{q}$, $r = \nu$, and $r = \epsilon q$, where $\epsilon = \pm 1$.

3.1.   Case 1: NTM-I equation

First, we consider the reduction $r = \epsilon \bar{q}$, where $\epsilon = \pm 1$. Then the NTME equations (2.1)–(2.4) take the form

3.2.   Case 2: NTM-II equation

Let $q(x, t)$ be a complex function. We now consider the reduction $r = \epsilon q$, where $\epsilon = \pm 1$. Then the NTME equations (2.1)–(2.4) take the form

Now we present the case when $q(x, t)$ is a real function and the reduction $r = \epsilon q$, where $\epsilon = \pm 1$. Then the NTM equations (2.1)–(2.4) will take the same form as in the case when $q(x, t)$ is a complex function.

3.3.   Case 3: NTM-III equation

Let $q(x, t)$ be a real function and assume the reduction $r = \nu$, where $\nu$ is a constant. Then the NTM equations (2.1)–(2.4) take the form

Finally, we note that the NTM-III equations (3.4)–(3.6) can be rewritten in the following equivalent forms:

or

where $\mu_{j}$ represents constants. Note that for the NTM-III equation, the $q(x, t)$ is a real function.

All the special cases of the NTM equations (2.1)–(2.4) above admit Lax pairs.

4.   Integrable motion of space curves induced by the NTM equation

The aim of this section is to present the geometric formulation of the NTM equation in terms of curves and to find its geometrical equivalent counterpart.

We start from the differential geometry of space curves ^[25,26,27]. In this section, we consider the integrable motion of space curves induced by the NTM equation. As usual, we use a smooth space curve ${\bf \gamma} (x, t): [0, X] \times [0, T] \rightarrow R^{3}$ in $R^{3}$. Let $x$ be the arc length of the curve at each time $t$. In differential geometry, such a curve is given by the Serret-Frenet (SF) equation. The SF equation and its temporal counterpart look like

where ${\bf e}_{j}$ represents the unit tangent vector $(j = 1)$, the principal normal vector $(j = 2)$, and the binormal vector $(j = 3)$ which are given by ${\bf e}_{1} = {\bf \gamma}_{x}, \quad {\bf e}_{2} = \frac{{\bf \gamma}_{xx}}{|{\bf \gamma}_{xx}|}, \quad$and$\quad {\bf e}_{3} = {\bf e}_{1}\times {\bf e}_{2},$ respectively. Here, $\times$ means the vector product. In this case

where $\tau$, $\kappa_{1}, \kappa_{2}$ are the torsion, geodesic curvature, and normal curvature of the curve, respectively; $\omega_{j}$ are some functions. Here, we must note that in the standard case, $\tau, \kappa_{j}, \omega_{j}$ are some real functions of $(x, t)$. However, in this paper, we assume that, in general, these functions are complex.

Theorem 1. If the elements of the matrices $U, V \in su(2)$ are related to the elements of the matrices $C, D \in so(3)$ of the SF in Eq (4.1) in the form

and

then the matrices $U, V$ are the Lax pair of the NTM system (2.1)–(2.4) in the case where $\lambda = 0$.

Proof. We underline $L_{j}$ are basic elements of $so(3)$ algebra and have the forms

They satisfy the following commutation relations:

Further, we also need the basic elements of algebra $su(2)$

where the Pauli matrices have the form

These elements satisfy the following conditions

Note that the Pauli matrices obey the following commutation relations:

or

The well-known isomorphism between the Lie algebras $su(2)$ and $so(3)$ implies the following correspondence between their basic elements $L_{j}\leftrightarrow e_{j}$. Using this isomorphism, let us construct the following two matrices:

Hence, we obtain

The compatibility condition of the Eq (4.1) reads as

or, in elements

Now, we suggest that the functions $\kappa_{1}, \kappa_{2}, \tau, \omega_{1}, \omega_{2}, \omega_{3}$ have the forms

and

respectively. Here, $\lambda$ is a complex constant, and $r, q, v, w$ are some functions of $(x, t)$. In the case when $\lambda = 0$, Eqs (4.5)–(4.8) take the forms

and

Substituting the expressions (4.9)–(4.12) into Eqs (4.2)–(4.4) give us the following equations for the functions $r, q, v, w$:

It is well-known that this is the NTM equation.

Thus, the SF equation for curvature and torsion (4.1) depends on the functions $r, q, v$, and $w$, which are solutions of the NTM equation. Parametrization of curvature and torsion through these functions shows that changes in the dynamics described by the NTM equation directly affect the geometric properties of curves and surfaces. □

5.   Analytic solutions of the NTM equation

As an integrable equation, the NTM equation has all ingredients of integrable systems like Lax representation, conservation laws, bi-Hamiltonian structure, soliton solutions, and so on ^[28,29,30]. In particular, it admits the N-soliton solutions. In this section, we want to find the 1-soliton solution of the NTM equation. Namely, we will look for the 1-soliton solution of the following NTM-I equations (3.1)–(3.3):

To find soliton solutions, we use the following complex transformation:

where

and $\alpha, \beta, \nu, \gamma, y_0, \theta_0$ are some real constants. We have

Hence, we obtain

where $v_{0}$ and $w_{0}$ are some constants. Below, we assume that $v_{0} = w_{0} = 0$. Inserting Eqs (5.4)–(5.13) into Eq (5.1) and splitting the real and imaginary parts yields

or

Differentiating Eq (5.15), we obtain

Comparing Eqs (5.14) and (5.16), we obtain the following constraints for real constants of the solutions:

Hence, we get

Note that we have four $\alpha, \beta, \nu, \gamma$ real constants of the solutions. We can define one of them via the last algebraic equations. The other constants remain free.

Let us rewrite Eq (5.15) as

where

Thus, the system of NTM-I equations (5.1)–(5.3) has been reduced to a second-order nonlinear differential equation represented as (5.17). In the following subsections, different types of analytic solutions of the NTM-I equations (5.1)–(5.3) obtained under different conditions of the constant coefficients $a_1, a_2, a_3$ of Eq (5.17) are found.

5.1.   The 1-soliton solution

The 1-soliton solution of the NTM-I equations (5.1)–(5.3) is as follows:

where $k$ is some constant, which is expressed by the four constants $\alpha, \beta, \nu, \gamma$ as

Figures 1–3 present the plots of the obtained solution of the NTM-I equations (5.1)–(5.3) for traveling waves that have steady speeds and shapes, where the velocity is $V = -\frac \nu \beta$.

5.2.   Elliptic solutions

To find the elliptic solutions, let us rewrite Eq (5.17) as

where

Let us rewrite this equation as

where

So that we have

Equation (5.18) has the following solution:

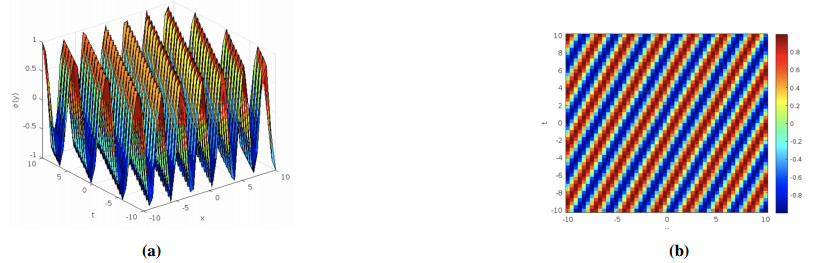
where $sn(y, m)$ is the Jacobi elliptic function. We can rewrite this solution in terms of the Weierstrass elliptic function $\phi(y)$$=$$\pm \sqrt{\frac{e_{1}-e_{3}}{\wp(y)-e_{3}}}$, where $e_1$$=$$\wp\left(\frac {\omega_1} 2\right)\text{ and } e_3 = \wp\left(\frac {\omega_1+\omega_2} 2\right).$ If $m = 0$ and $m = 1$, we obtain particular solutions, specifically, the periodic and kink, respectively. This is the elliptic soliton solution. In Figure 4, we plot this solution for the parameters $\epsilon = -1$, $\alpha = 0.2$, $\beta = 0.2$, $\nu = 0.3,$ and $\gamma = 0.3$.

5.3.   Periodic solution

In the case when $m = 0$, we get the periodic solution via Eq (5.19)

This is the periodic soliton solution. In Figure 5, we plot this solution for the parameters $\epsilon = -1$, $\alpha = 2, \:\beta = 1, \:\gamma = 1, \: \mu = -1$, and $m = 0$.

5.4.   Kink solution

In the case when $m = 1$, we get the kink solution via Eq (5.19)

This is the kink soliton solution. In Figure 6, we plot this solution for the parameters $\epsilon = -1$, $\alpha = 2$, $\beta = 0.5, \:\gamma = 1, \: \mu = -1$, and $m = 1$.

5.5.   Rational solution

It is not difficult to verify that the Eq (5.18) has the following rational solution:

where $k$ is a real constant. This is the rational soliton solution. In Figure 7, we plot this solution for the parameters $\epsilon = -1$, $\alpha = 0.2, \:\beta = 0.2, \:\nu = 0.3,$ and $\:\gamma = 0.3$.

In the present work, the one-soliton solutions of the NTM system are obtained using the traveling wave method. The advantage of this approach is the possibility of obtaining the one-soliton solution of integrable systems in explicit form without the need for complex analytical methods.

6.   Conclusions

In conclusion, we note that the integrability of nonlinear partial differential equations is an important topic that combines both theoretical and practical aspects, and plays a key role in understanding and describing complex dynamic systems.

It is known that the SF equation for curvature and torsion describes the properties of curves and surfaces in differential geometry. Thus, curvature determines how a curve or surface is curved in space, and torsion is related to how the curve twists around its axis. These geometric characteristics can be related to the physical properties described by the NTM equation.

Both types of equations (NTM and SF equations) exhibit nonlinear interactions. In the NTM equation, the nonlinear terms can be related to changes in curvature and torsion, indicating that the dynamics of solitons can affect the geometry of space.

Thus, the NTM system not only describes the dynamics of waves, but also allows us to understand how these waves interact with the geometry of space, which is an important aspect of many physical processes.

In this paper, we propose a method of constructing a Lax pair for a system of nonlinear partial differential equations based on consideration of the equation of motion of a spatial curve. The key link between these two lines of research is the isomorphism between the Lie algebras $so(3)$ and $su(2)$.

The NTM system (2.1)–(2.4) is integrable in the sense of Lax, which guarantees the existence of n-soliton solutions. In this paper, one-soliton solutions are obtained by means of traveling waves, but this method turns out to be insufficient for constructing multidimensional or n-soliton solutions. To obtain more general solutions of the NTM system (2.1)–(2.4), classical methods of soliton theory, such as Hirota's direct method, the Darboux transform, and other approaches based on the integrable structure of the system, can be applied in the future.

Author contributions

The formulation of the problems and the derivation of integrable reductions of the equation in the study were carried out by R. Myrzakulov; G. Nugmanova and A. Azhikhan contributed to establishing the connection between the NTM and SF equations. Exact solutions of the equations were found by A. Myrzakul.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

We would like to thank the anonymous reviewers for their valuable comments and suggestions, which significantly improved the manuscript.

This work was supported by the Ministry of Science and Higher Education of the Republic of Kazakhstan, Grant No. AP22683222.

Conflict of interest

The authors declare no conflict of interest.