1.
Introduction
Image denoising, an essential task in low-level image processing, aims to recover valuable edges from noisy images [1,2,3]. Moreover, the quality of denoising methods significantly affects the performance of downstream tasks, such as classification, semantic segmentation, and target identification [4,5,6]. Thus, image denoising holds important practical value [7].
The field of image denoising has experienced notable advancements in the last few years [8], driven by the continuous development of advanced denoising techniques [9,10]. Deep learning-based approaches provide target-driven yet powerful means for image denoising tasks comparing with traditional non-learning methods [11]. Specifically, these denoisers use a set of training samples to recover the clean counterpart x of the input noisy images y as well as learning the nonlinear mapping fθ(y):y→x with to-be-learned parameters [12]. These supervised denoising methods require large quantities of paired image (noisy/clean) data for training, presenting significant challenges in terms of data collection and annotations. [13,14].
Currently, self-supervised denoisers without pre-collected paired data has become an enormous hotspot [15,16,17]. These methods follow two basic statistical assumptions: (1) the noise is independent and mean-zero; (2) the signals are not pixel-wise independent.
In blind spot denoising (BSD), the blind-spot-driven loss is to measure the blind-noisy difference, as shown in Eq (1.1)
where dcfθ(y;Ωm)=fθ(Ωm(y))−ˆy is the uniform loss of image content, ||⋅||2Ωm=||(1−Ωm)⊙⋅||22 is utilized to signify that the loss is calculated solely over the masked pixels, and ˆy=(I−Ωm)(y) with the identity operator I(⋅); Ωm(⋅) represents a masking operator where the masked pixel is set as zero. For self-supervised learning-based denoisers, fθ indicates self-supervised blind-spot networks.
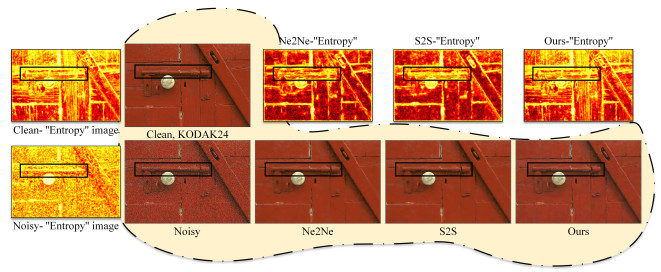
Blind-spot denoisers, employing random masking strategies, have acquired popularity in the field of image processing when clean image annotations or additional images are not required. Nevertheless, their performance is usually worse than the self-supervised methods with multiple images, let alone supervised denoisers [18]. Besides, the loss of the edge-aware information directly influences the quality of image denoising compared with those trivial contents of images, particularly for scenarios featuring high levels of diverse noises as shown in Figure 1.
In this paper, we present a novel self-supervised denoising framework, designated as Blind2Grad, to concurrently address the recovery challenges of multiple details and high-level noisy images. We introduce a dual mask mechanism that functions as a blind spot within the asymmetric networks, facilitating denoising effectively through zero-shot. To optimize the decoder of the asymmetric denoising networks, we adopt the threshold-based standout module to precisely retain the prior value of the gradient features, thereby maximizing the capacity of our proposed network to preserve edge information. Furthermore, we construct a gradient-regularized loss that incorporates the uniform loss to strike a balance of the information between the detailed and flat areas of the image. We utilize the potential attributes of Bayesian probability to demonstrate the relationship between the gradient-regularized loss and supervised loss, theoretically guaranteeing that Blind2Grad can maximize the retention of image edge information during denoising.
In summary, the main contributions of our work are as follows:
● We propose a novel idea for modifying the mask generation of BSD, which is not randomly sampled. Instead, the dual mask mechanism based on Euclidean distance is introduced herein, and the information of the flat area of the image is integrated to effectively preserve the crucial image texture in the denoising process, thereby enhancing the quality of the entire denoised image.
● We introduce a new framework called Blind2Grad (B2G), to enhance the accuracy of the double mask mechanism in capturing overlooked details within a rolling framework. In addition, the framework combines the gradient-regularized loss and the T-Standout model (Threshold-based Standout), which can improve the preservation of detailed gradient information.
● Theoretically, we demonstrate that our loss function can converge to the supervised loss under certain probabilistic conditions. In combination with the global convergence property of the stable game, we can infer the convergence relationship between our proposed loss and the supervised loss. Our framework exhibits outstanding performance on both synthetic and real datasets.
The remainder of this paper is structured as follows: Section 2 undertakes a review of the related work. Section 3 puts forward our approach, which primarily encompasses the dual mask mechanism and the B2G framework. We conduct a theoretical study of the proposed loss as shown in Section 4. Section 5 showcases denoising experiments under diverse noise levels and compares the efficacy of proposed B2G with other typical self-supervised denoising methods. Finally, Section 6 draws conclusions and deliberates on future work.
2.
Related work
2.1. Non-learning or learning with paired images
Denoising approaches initially originated from non-learning approaches, which are highly effective image processing techniques that can be divided as either filter-based [19] or model-based [20]. Model-based denoising approaches have surpassed filter-based approaches in terms of sophistication and effectiveness as the approaches have developed [21]. Nevertheless, these approaches might struggle to handle noise that does not conform to their handcrafted priors [22].
In the recent ten years, the advent of deep learning technology has led to a significant shift in the mainstream strategies of network-based denoising. For supervised denoising, convolutional neural networks (CNNs) trained with plenty of image pairs (noisy/clean) and have become the dominant technique [23,24,25]. However, supervised learning-based denoisers depend on a great number of noisy-clean image pairs for training.
2.2. Self-supervised learning with multiple images
One of the elegant methods known as Noise2Noise (N2N) emerged, using multiple noisy observations of identical scenes for training a deep denoising model [26]. By hypothesizing that the noise components are independent and of zero mean, minimizing the loss of the N2N method yields the same solution as the supervised training with ℓ2-loss. Nevertheless, it is not always feasible to sample two independent noises for the same scene, which brings limitations to applications. Similarly, the Neighbor2Neighbor (Ne2Ne) method was proposed to acquire paired images via sub-sampling the noisy images for training [27]. Nevertheless, the sub-sampling strategy may compromise the integrity of image structures, resulting in an excessive level of smoothing. Noisy-As-Clean [28] and Noisier2Noise [29] introduce attached noise during the training of denoiser. Nevertheless, their practicability is limited due to the assumption of known noise distribution.
2.3. Self-supervised learning with zero-shot
On the one hand, as a pioneer in the field of self-supervised denoising approaches with zero-shot, Ulyanov et al., [30] put forward a deep image prior (DIP) approach for training the denoising network. On the other hand, existing blind-spot denoisers employ well-designed masking schemes wherein the neural network learns to fill in pixel gaps in the noisy images. For instance, Noise2Void (N2V) [31] and Noise2Self (N2S) [32] adopt the uniform pixel selection (UPS) strategy to constitute a particular mask, which is designed to prevent identity transformation. To improve its performance, this basic masking scheme is further refined by Self2Self (S2S) with the dropout skill [33]. Subsequently, Noise2Fast (N2F) [34] introduces a novel "checker-board" mask which is a down-sampling strategy that removes one half of all pixels in a checkerboard pattern. In addition, Zero-Shot Noise2Noise (ZS-N2N) [35] utilizes a lightweight network with regularized loss to achieve cost-effective noise reduction.
However, blind-spot denoisers may lose valuable structures (e.g., edges) while randomly masking pixels in single noisy image, thereby resulting in degraded noise canceling performance. The authors of Blind2Unblind (B2U) [36] and Masked Pretraining Inference (MPI) [37] have observed such weak points of blind-spot driven networks. Nevertheless, compared to other trivial points, the pixels that lie on valuable image structures should be directly emphasized while training blind-spot denoisers.
3.
Proposed method
In this section, we first explain the motivation and strategy distribution of the dual mask mechanism. Besides, we establish a B2G framework based on gradient-regularized loss and the T-standout model to further enhance the deployment of our proposed mask. Finally, we present the B2G training strategy and its computational complexity.
3.1. Dual mask mechanism
As shown on the first page, during the process of converting sensor analog electrical signals into output digital signals, noise reduction methods are employed for this purpose. However, the majority of the current zero-shot methods suffer from the problem of detail loss due to the randomness of the masks, which subsequently degrades the quality of denoised images. Therefore, it is essential to explore a new mask to complement the valuable details of the denoised image.
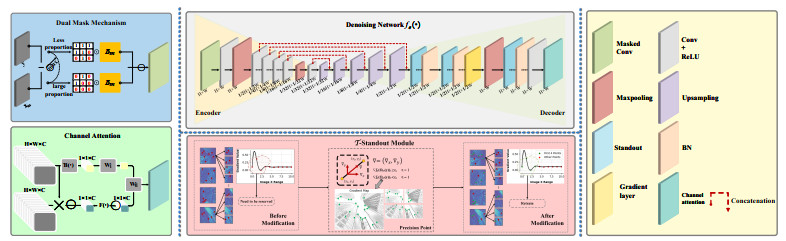
Given a clean image, we could initially observe the diverse manifestations of details and flatness via entropy, as depicted in Figure 2. If the random masking strategy (i.e., used in "S2S") is employed, it will be discovered that the outcomes presented in the penultimate column deviate significantly from the clean image in terms of detail restoration. This indicates that the random strategy is prone to losing valuable detail information, which prompts us to contemplate whether, instead of utilizing a random approach, we utilize conditional masking, that is, masking the flat and texture regions to varying degrees, thereby enabling the combination of more detail information with a certain degree of flat content for the prediction of the denoised image. Thus, a dual mask mechanism is selected. Specifically, a conditional masked convolution layer based on the random mask is introduced, as depicted in the blue box in Figure 3. The significance of the double mask mechanism is also affirmed in the results presented in the last column of Figure 2.
For the dual mask mechanism, we have still used Bernoulli sampling for the first mask (preserving the content of the flat area), and select the conditional allocation based on Euclidean distance for the second mask, while maintaining the final mask rate at 25%. The specific dual mask mechanism is depicted on the left side of Figure 3. Given a medium clean image, denoted as xm, where the noise has been eliminated but the details are blurred, we compute the pixel difference between the noisy y and xm, as presented in formula (3.1):
where variable "i'' represents the pixel value, and the threshold εg is used to distinguish between the texture area and the flat area of the image.
Since noise has less impact on areas with substantial gradient changes as opposed to flat areas, the entropy graph in Figure 2 still indicates that there is still detailed information in the noisy image. Furthermore, the more distinct the detailed information of the denoised image itself is, the more prominent the performance becomes. We have utilized a binary indexed transform to obtain the indices Ii:={in}Nn=1 of the details that need to be preserved, i.e., in=1 if εg≥Gmax; otherwise in=0, with εg<Gmax.
To achieve the deployment of the dual mask mechanism, it is necessary to retain the pixel values encompassing detail information for variable in=1, concurrently enhancing the masking ratio of variable in=0. Subsequently, in the second conditional sampling based on Euclidean distance, we initially calculate the masking quantity corresponding to the Bernoulli sampling Bm as depicted in Eq (3.2).
where IIi and IIIi represent the first and second layers in the dual mask mechanism, with IIci=1−IIi. Our ultimate objective is to diminish the nonzero IBm, denoted as IB−m; concurrently, augment the proportion of IBcm, designated as IBc,+m. Thus, the final double masking mechanism is expressed as:
What is requisite is that we propose a dual mask mechanism Ωm as a mask strategy for the blind spot denoising network, which can effectively retain the significant detail information of the denoised image to a certain extent. However, selecting the optimal value εg also demands the continuous enhancement of the clarity of xm. Therefore, in the subsequent section, we will introduce a novel loop framework B2G to generate high-quality xm, thereby obtaining the optimal εg for better discrimination of the texture and flatness of the image.
3.2. Blind2Grad framework
Since the excessive number of symbol definitions is to be presented in this chapter, a symbol summary table is provided initially (Table 1). Our proposed framework B2G is a recurrent strategy founded on the collaborative operation of gradient-regularized loss, T-standout, and the channel attention mechanism, which is capable of further precisely guiding the generation of Ωm and preserving the significant details of the denoised image.
3.2.1. Gradient-regularized loss
To complement valuable structural details to the restored images, we believe that a blind spot denoiser should be learned by masking pairs not only in the color space as normal does, but also in the edge detail space of the image. In consequence, a loss of gradient is established to measure the gradient deviation between the whole denoised image (i.e., fθ(y)) and the recovered one from its masked instances (i.e., fθ(Ωm(y))), that is,
It is reasonable to minimize the loss of Eq (3.4) to expect that the structural information of the recovered image of Ωm(y) should not be deviated too much in comparison with the one with global details. In this way, image details that are lost due to the masking schemes can be properly supplemented.
Although compared to other pixels, image detail information is crucial for understanding what a graph is; it occupies a rather limited portion of the overall region, such that gradient minimization alone is not sufficient. Thus, we desire to propose a loss that considers both gradient and color differences, with a predetermined parameter ω as the balancing of the two terms. Besides, in order to avoid the case that dcfθ(y;Ωm)=−dgfθ(y;Ωm)≠0, the loss is proposed as:
where the i-th element of ~dcfθ(y;Ωm)/~dgfθ(y;Ωm) denotes the absolute value of the i-th element of dcfθ(y;Ωm)/dgfθ(y;Ωm).
Specifically, we concretely formulate the Eq (3.5) as:
where the dcifθ(y;Ωm) and dgifθ(y;Ωm) are the i-th elements of dcfθ(y;Ωm) and dgfθ(y;Ωm), respectively.
There are theoretically two cases of dcifθ(y;Ωm) in Eq (3.6), that is, dcifθ(y;Ωm)≥0 or dcifθ(y;Ωm)<0. Nevertheless, it is an impossible situation of dcifθ(y;Ωm)<0 since the complete original information will be preserved through fθ. Meanwhile, the pixels of ˆy are less than that of Ωm(y).
With dcifθ(y;Ωm)≥0, there are two cases of dgifθ(y;Ωm), i.e., dgifθ(y;Ωm)≥0 or dgifθ(y;Ωm)<0. Similarly, due to the pixels contained in Ωm(y) being less than that of y, the detail-preserving network will not cause the case of dgifθ(y;Ωm)<0. The results confirm that only the case of dcifθ(y;Ωm)≥0 and dgifθ(y;Ωm)≥0 is a real possibility.
Therefore, we desire to propose our framework by minimizing a gradient-regularized loss, i.e.,
Hypothesize that θ∗ is an optimal solution of Eq (3.7), and the f∗θ is the corresponding denoising network with θ∗. Then, we denote an x∗ as: x∗=f∗θ(Ωm(y))+ωdgf∗θ(y;Ωm). If ω→∞ exists, working out the Eq (3.7) will bring about dgf∗θ(y;Ωm)→0 and f∗θ(y0)=f∗θ(Ωm(y0)) in turn. By denoting the unmasked pixels of Ωm(y) as y0, that is, y0∈y∩Ωm(y), we have f∗θ(y0)=f∗θ(Ωm(y0)). Then, from the theorem of functional continuity, there holds limω→∞x∗=f∗θ(Ωm(y))=f∗θ(y) with the given noisy y. Thus, it is revealed that our gradient-regularized loss is in a position to preserve structural details while restoring the clean image.
It is indeed worthwhile to note that there are two potential conditions: when minimizing the gradient-regularized loss, the dcifθ(y;Ωm)≥0 and dgifθ(y;Ωm)≥0 should be covered. Furthermore, instead of adding those direct constraints, our objective is to minimize the gradient-regularized loss by restricting dcfθ(y;Ωm)=0, forming the optimization as
Our design accentuates the gradient-based loss term dgfθ(y;Ωm), which directly focuses on image edge structures. The incorporation of the color consistency term dcfθ(y;Ωm) serves a secondary function: it aids in maintaining the equilibrium between textured regions and flat areas within the reconstructed image. Therefore, we introduce the constraint dcfθ(y;Ωm)=0 as a penalized regularization term with a penalty parameter γ. The term dcfθ(⋅) is designed primarily to supplement color consistency in flat regions and should not dominate the optimization. In addition, the final optimization model for learning our B2G framework is formulated as
We employ Eq (3.9) as the loss function of the entire B2G framework. The specific procedure can be observed as shown in Figure 4. Regarding Ωm, we initially adopt the Bernoulli sampling approach as Ω1, and subsequently obtain the corresponding x1=fθ(y)1 after the first network cycle. Hence, given a denoised image y, when m>1, our proposed B2G can be characterized as:
3.2.2. T-standout and channel attention
For the dropout, it merely randomly discards certain neurons, preventing them from participating in the calculation during the current training round. This method reduces overfitting while augmenting the quantity of training samples.
However, there exists a risk of losing detailed information in the process of random discarding. Hence, we have developed a new T-standout strategy in the decoder, as depicted in the pink box diagram in Figure 3. Instead of randomly discarding neurons, the gradient threshold strategy is used to reselect the discarded neurons. Specifically, the discarded neurons can be represented as {fθ(Ωm)0,fθ(Ωm)1,…,fθ(Ωm)i}, i.e., denoised image is randomly divided into any combination. We set the threshold ϵs, the weight {η0,η1,…,ηj}, and {η0,η1,…,ηj}⊂{0,1}. such that
exists herein. That is, when ηj=1, the corresponding neuron fθ(Ωm(y))i cannot be discarded, thereby further increasing the quantity of training samples and replenishing the detailed information of the image once again.
On the other hand, to leverage the interdependence between feature channels, a channel attention mechanism is introduced, as shown on the left side of Figure 3. To capture the complete channel dependence from the collective information of the denoised image fθ(Ωm(y)), we opt to introduce gating with a sigmoid function mechanism:
where B(⋅)=1/(H×W)∑Hi=1∑Wi=1fθ(Ωm(y)(i,j), F(⋅) represents the sigmoid gating function [38].
3.3. Network architecture and training scheme
Our B2G network employs an encoder-decoder architecture with a specialized T-Standout Module for gradient-aware processing. Based on the architectural diagram as shown in Figure 3, we present a comprehensive description of each component:
The encoder model follows a progressive downsampling strategy to efficiently extract hierarchical features. (1) Input Processing: The network accepts a noisy input image of the size H∗W; (2)Masked Convolution: Used for initial feature extraction with noise-aware processing; (3) Feature Extraction Path: The encoder consists of multiple stages with precise dimensional transformations; (4) Initial masked convolution at full resolution (H∗W) maxpooling operation reducing dimensions to H/2∗W/2.
Subsequent convolutional blocks with progressive downsampling through the following resolutions:
Each convolutional block incorporates convolution (Conv) + rectified linear unit (ReLU) operations as indicated in our architecture diagram.
Furthermore, the decoder implements a symmetric upsampling path with specialized components for feature refinement: Progressive Upsampling: Starting from the bottleneck features, the decoder gradually restores spatial dimensions:
Each upsampling block utilizes dedicated upsampling operations as shown in Figure 3. (1) Upsampling operations to increase spatial resolution Batch Normalization (BN) for training stability and improved convergence; (2) Gradient layer for edge-aware processing and structural preservation; (3) Channel attention mechanism to emphasize important feature channels concatenation operations (indicated by red dashed lines in our diagram) to merge features from different processing stages.
The decoder concludes with operations that restore the original H∗W resolution, producing the denoised output with preserved structural details. Besides, a key innovation in our architecture is the T-Standout Module, which operates on intermediate features to enhance gradient preservation. The module incorporates a retrain component to further refine the processed features, ensuring optimal gradient preservation.
Moreover, we provide a quick summary of our proposed Blind2Grad training procedure in Algorithm 1. Specifically, we train the asymmetric denoising networks, with the gradient-regularized loss to achieve the goal of preserving detail while denoising.
The main computational complexity of our B2G arises from the dual mask machine (Ωm) and T-standout module. Specifically, for the T-standout module, it is combined with standout, and its complexity O(h(Γ((H×(W−1))+((H−1)×W))g)) is mainly related to the image resolution H×W, where Γ and h represent the number of iterations and layers of the neural network, respectively. Additionally, for the dual mask Ωm(⋅), its complexity mainly comes from Eq (3.1), and O(h(Γ(H×W)εg)) involves gathering the characteristics of Euclidean distance. Then, the whole complexity is obtained by
where M(H−1,W−1;Γ)g=Γ((H×(W−1))+((H−1)×W))g, M(H,W;Γ)εg=Γ(H×W)εg.
4.
Theoretical analysis
For being self-contained, we will provide necessary assumptions and propositions in Section 4.1 before presenting our main theoretical results.
4.1. Necessary preliminaries
For denoising with our proposed self-supervised blind-spot denoising networks, it is necessary to prevent the training from learning into the identity mapping. Nevertheless, it is necessary to assume that the denoising function fθ(y)J should be J-invariant[32], as claimed below.
Assumption 1 (J-invariant). Our proposed denoising function fθ(y)J is assumed to be J-invariant, meaning that the value of fθ(y)J does not depend on yJ for all J∈J, where J is a partition of the dimensions {1,…,m}; fθ(y)J and yJ denote the values of fθ(y) and y on J, respectively[39].
Definition 1. We have fθ(y):{i∈y:i∈[0,255]} as the support set of y. Hence, the state set encompassing the support of the Ωm(y) is defined as fθ(Ωm(y))={Ωm(y)∈∑m=Mm=1Ωm(y):fθ(Ωm(y))⊆fθ(y)}, along with fθ(y)=∑m=Mm=1fθ(Ωm(y)) as the state set containing the support of the Ωm(y). At this juncture, a distance-like function dΩm:Ωm(y)→R can be defined, which satisfies:
where x∗i=f∗θ(y), and both x∗ and fθ(y) conform to the normal distribution of N(0,1).
We present two necessary propositions for proving the main theorem as follows.
Proposition 1. Supposing that there exists a constant s∈[c,d] for the function f(yjx,yjy) with yjx∈[a,b] and yjy∈[c,d], then for every ε>0, there has a δ>0, such that
for all f(yjx)∈[a,b] and f(yjy)∈(s−δ,s+δ).
Then, E(f(yj))=∫bayjf(yj)dyj is also continuous on [a,b] or [c,d].
Given the continuity of E(f(yj)), it lays the conditional basis for the derivation of Proposition 1.
Proposition 2. Supposing that f(yjx,yjy) and its derived function are continuous on [a,b]×[c,d], then with Proposition 1, we have that I(yj)=∫baf(yj)dyj has a continuous derived function I′(yj) on [a,b] or [c,d]; meanwhile,
4.2. Main results
With the above given assumption and propositions, we will first provide a required corollary of the gradient operator we considered in our B2G network. For smooth reading, we leave all the detailed proofs in the Supplementary material.
Corollary 1. Assume that the f(Ωm(y)) and f(y) are unbiased estimators of ˆx, that is, E[f(Ωm(y))|ˆx]=ˆx and E[f(y)|ˆx]=ˆx, where ˆx=(I−Ωm)(x). By supposing that f(Ωm(y)) and f(y) are continuous on closed rectangles, then we have
With the Corollary 1, we could derive the main theorem of our B2G.
Theorem 1. Let J be a fixed partition of the dimensions of the input y∈Rd, and let J∈J denote any subset of dimensions. Consider a family of subspace projections Ωm:Rd→Rd′, and assume the following conditions:
● (i) The estimator f(Ωm(y))J and f(y)J as unbiased estimators of the true target ˆxJ on each subspace J, i.e.,
● (ii) The function f(⋅) is assumed to be J-invariant, meaning f(y)J only depends on yJ, i.e., for all y, y′ such that yJ=y′J, we have f(y)J=f(y′)J.
● (iii) The function f(⋅) is also continuous on a compact subset of Rd.
Then, the following decomposition holds:
Proof. The proof is derived from the application of the expectation-variance decomposition to the denoiser.
First, we use the identity:
where f(⋅)J is the optimal denoiser under the invariance and unbiasedness assumptions. The cross-term vanishes in expectation due to assumption (ⅰ). Then, using the linearity of expectation and the independence of residual terms, the expression reduces to the desired decomposition, separating the estimation error from the self-supervised loss.
□
Theorem 2. Let fθ denote a denoising function, and suppose that the output fθ(Ωm(y)) lies in the interior of a probability simplex Dx∗. Define a game Dx∗(x) over strategy space Vfθ where each dimension i corresponds to a player with payoff given by the log-likelihood logfθ(Ωm(y))i. Assume:
● (i) Dx∗(x) is a strictly stable population game.
● (ii) There exists a unique Nash equilibrium x⋆∈Dx∗(x) representing the optimal denoising result.
● (iii) The dynamics of Vfθ follow a potential game with concave potential function dΩm(⋅).
● (iiii) The evolution of player strategies is governed by the replicator dynamic system Vfθ:
Then the optimal denoising output x⋆ is the unique global asymptotically stable equilibrium of the dynamics Vfθ, and any initial distribution x∈Dx∗ converges to x⋆ under the dynamics.
Proof. Let Dx⋆(x)=∑i∈Ωm(y)x⋆ilogx⋆ixi denote the Kullback-Leibler divergence from x to the equilibrium x⋆. This is a convex Lyapunov function for the replicator dynamics Vfθ. By Jensen's inequality and the concavity of the payoff (log-likelihood), we have Dx⋆(x)≥0, and equality only if x=x⋆. Along the replicator dynamic, the time derivative satisfies:
by strict stability of the game.
Thus, Dx⋆(x) decreases over time and converges to zero. Therefore, x⋆ is globally asymptotically stable. □
As a consequence, the main results of the Theorems 1 and 2 claim that the gradient-regularized loss of our self-supervised denoiser has an equivalence relationship with the loss of a supervised denoising network. Besides, Figure 5 also reveals that our loss function possesses convergence consistency.
5.
Experimental results
In this section, we initially provide detailed descriptions of the experimental setups. Afterward, the method is evaluated by synthetic denoising and real-world denoising, with state-of-the-art methods including self-supervised denoisers with zero-shot or multiple images and a traditional training-free model. Furthermore, ablation studies are conducted to demonstrate the effectiveness of our proposed dual mask mechanism, gradient-regularized loss, T−standout model.
5.1. Experimental
5.1.1. Setup
We take advantage of the B2G architecture with the 1/2H×1/2W gradient convolution layer that is added third from the bottom of the network. Additionally, the kernel size for all the convolution layers is set to 3×3, and the corresponding stride and length of zero paddling are set as 2 throughout the whole experiment. The hyperparameter of each ReLU is set up to 0.1, and the probability of Bernoulli sampling is set up to 0.25. Specifically, our approach randomly selects 75% of pixel values to roughly estimate the remaining 25% in the whole noisy image. We utilize Adam optimizer with an initial learning rate of 2×10−5 for synthetic denoising experiments, and 10−5 for the real-world denoising experiments in different RGB spaces. Furthermore, we introduce a gradient convolutional layer of the size 1/2H×1/2W stacked with standout, calling it 40 times to get the final results during the training process. As for the gradient-regularized parameter ω and the penalty parameter γ used to balance the constraint of the dcfθ(y;Ω), we set ω = 0.8, γ = 0.5 for the RGB synthetic denoising, and ω = 0.5, γ = 0.5 for the real-world denoising.
5.1.2. Datasets for denoising
We have evaluated our proposed B2G on the nine different datasets, including RGB synthetic images (i.e., Set9[30], KODAK24[40], Set14[41], CBSD68[42], BSD300[42], Urban100[43]), generated handwritten Chinese character images (HˊanZi[32]), grey scale natural image (BSD68[42]), and physically captured 3D microscopy dataset (Planaria[44]). In addition, we validate our proposed B2G on images with different sizes and types, with different types and levels of noises, to demonstrate the effectiveness and robustness of the proposed framework. Moreover, the Planaria dataset measures the effectiveness of our approach from the perspective of biological cells. Furthermore, we consider four levels of noise for the synthetic image denoising: (1) Gaussian noise with σ = 25, 50, 75,100 for Set9, HˊanZi, and Urban100, (2) Gaussian noise with σ = 25, 50 for KODAK24, CBSD68, Set14, and BSD300, (3) Gaussian noise with σ = 25 and 50 for the BSD68 dataset, (4) Poisson noise with λ = 30, 50 for the Planaria, and (5) the real-world denoising task the SIDD [45] dataset. Furthermore, we also conduct comparisons on the PolyU [46] and CC [47] datasets for the real-world denoising as detailed in the supplementary materials*.
*Detailed results are provided in the supplementary material.
5.2. Synthetic Denoising
5.2.1. Gaussian Denoising
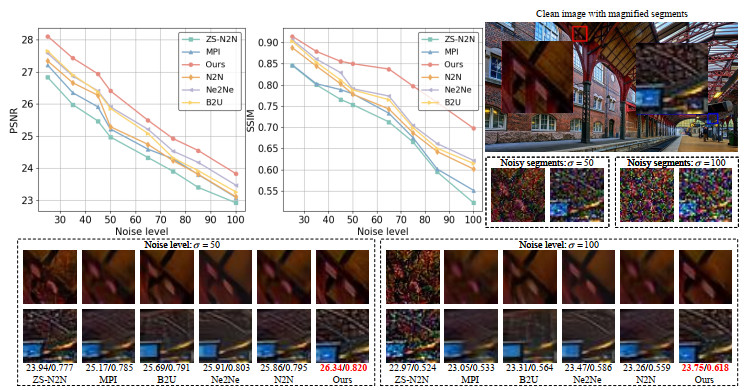
We also implement experiments for removing noise of zero-mean additive Gaussian. As indicated in Tables 2 and 3, our approach significantly outperforms the traditional denoising approach BM3D and all the benchmark self-supervised denoising approaches with zero-shot, including DIP, N2S, S2S, B2U, IDDP, ZS-N2N, and MPI. Although our proposed B2G can exhibit lower quantitative results than the approaches (such as Ne2Ne and N2N) on a few datasets, this can be mainly attributed to the fact that the Ne2Ne and N2N utilize more image content information through the use of image pairs, whereas our method only relies on single noisy images. Furthermore, while evaluating the overall quantitative effects, our method gains comparable performance.
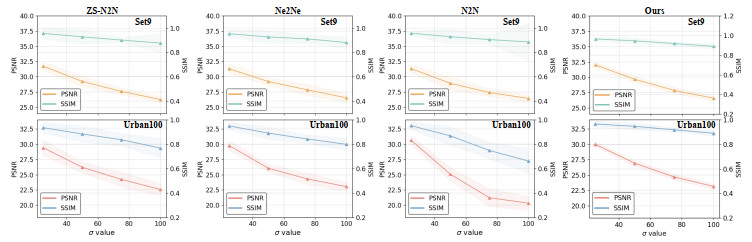
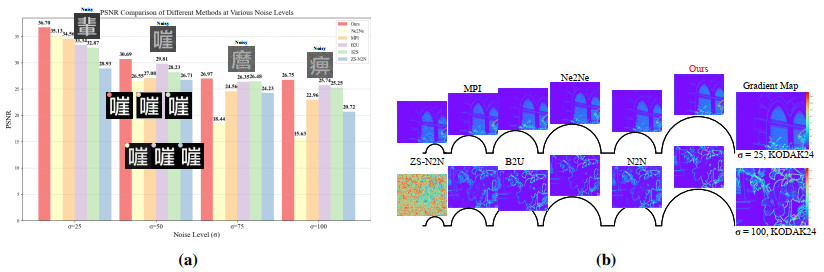
In Figure 6, we plotted the minimum-to-maximum range of the quantitative indicators for ZS-N2N, Ne2Ne, N2N, and our approach with various noise levels. From the results, we can observe that the approach maintains a stable state across different noise levels and different noisy images. Our approach shows commendably even under high noise levels, demonstrating the effectiveness of our proposed gradient-regularized loss.
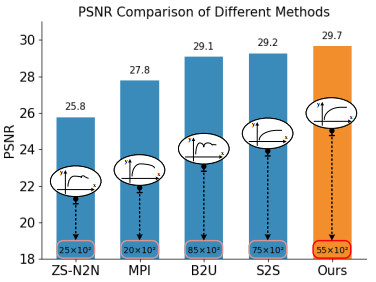
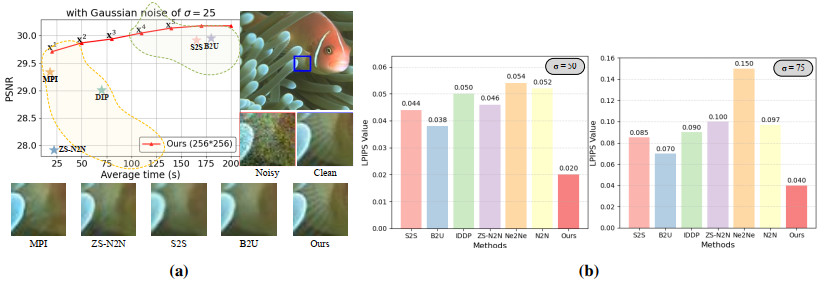
Due to the implementation of our B2G strategy, the average denoising time for a single image might surpass that of other state-of-the-art approaches. We provide a comparison in Figure 7 (a) on the time consumption with other self-supervised denoisers in zero-shot, i.e., DIP [30], S2S [32], B2U [36], ZS-N2N [35], and MPI [37]. In the curve graph provided in Figure 7 (a), existing methods can be roughly divided into two groups, namely, DIP, ZS-N2N, and MPI belonging to the first group, and S2S and B2U falling under the second group. The former approaches need a shorter time but yield relatively lower PSNR values, while the latter ones demand more time for achieving much better results. We also provide the PSNR values and corresponding time for each 3000 iteration in our B2G strategy. It is apparent that employing only 6000 iterations can yield PSNR values comparable to those obtained by other approaches, while also requiring almost the least computational time. Additionally, in comparison to a specific existing method, we establish a fixed iteration to generate much better results within a comparable time (as circled by shadow areas). Thus, the time consumption problem associated with our proposed approach is no need to be concerned.
Furthermore, Figures 8–10 also provide detailed comparisons of the denoising results of compared approaches at different noise levels. B2G exhibits outstanding capability of image detail restoration as shown in Figure 8 (b) surpassing the performance of other evaluated approaches under high noise conditions. The fluctuation of the curve in the Figure 8 (b) can further demonstrate that the method we proposed exhibits the greatest fluctuation (that is, it is most similar to the gradient map of the clean image). Compared to denoising methods with zero-shot, our B2G demonstrates a relatively stronger ability to restore lost details caused by the randomness of masks. In addition, we also introduce a novel indicator, LPIPS, to assess the similarity of human eye cognition, as shown in Figure 7 (b). As is evident from Figure 7 (b), regardless of whether the noise level is 50 or 75, our LPIPS indicator remains the lowest. From this viewpoint, it demonstrates that our proposed B2G approach holds an absolute superiority in human eye cognition.
5.2.2. Poisson denoising
We then premeditate Poisson noise, which can be utilized to model photon noise in most imaging sensors. Similarly, the Poisson noise is also in accordance with the zero-mean assumption adopted in this paper. We added the Poisson noise with determined levels to the ground truth for the Planaria dataset, and the results are presented in Table 4. Although our SSIM metric is the same as the N2N, our PSNR is 0.29 dB higher. Furthermore, we achieved excellent visual results in terms of recovering details, as shown in Figure 11 for λ=30 and λ=50. This demonstrates the superiority of B2G for removing Poisson noise.
5.3. Real-world denoising
Confronting real-world denoising, we introduced a dilated convolution with the aim of disrupting the spatial correlation of real-world noise, and the network architecture is provided in the supplementary material. Table 5 indicates the quality scores for quantitative comparisons on the real-world dataset (SIDD [45]). Besides, we add comparisons with supervised approaches (named as plug-and-play (PnP) [25] and deep generalized unfolding network (DGUNet+) [49]), where the denoising network parameters of DGUNet+ in all stages vary and it is more appropriate for handling real-world noise. Although our approach is disadvantaged in comparison with DGUNet+ on sRGB images, it achieves superior results compared to the state-of-the-art MASH (i.e., excels over other zero-shot approaches), both on sRGB and raw-RGB images. For the AP-BSN [50] and LG-BPN [51] approaches, we utilize these methods from [52] to directly denoise a single image. Table 5 comprehensively indicates the quality scores of quantitative comparisons on real-world denoising. In addition, the quality comparison provided in Figure 12 shows our advantage in effective denoising in real-world scenarios. Thus, our approach is adept at real-world denoising, offering a robust solution for image quality enhancement.
5.4. Ablation studies
In this section, we conduct comprehensive ablation studies on using dual mask mechanism with T-standout, the penalty parameter γ, and the gradient-regularized parameter ω, on the Set9 dataset under the metrics of PSNR/SSIM.
5.4.1. Different mask strategies
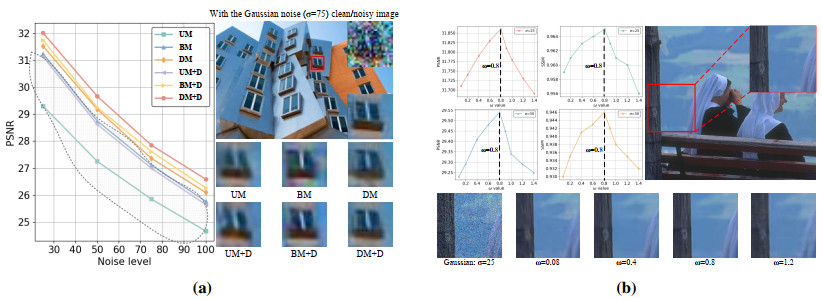
To assess the efficacy of the dual mask mechanism (DM) under different noise levels, we contrast it with the uniform pixel selection method (UM) and Bernoulli sampling (BM) advocated in N2S [32] and S2S [33]. In addition, we validate the adaptability of the T-standout module when applied to different masking mechanisms. Here, we explicitly define the D: = T-standout module, which is used to enhance feature selection by preserving informative neurons. Figure 13 (a) depicts the performance of employing different mask strategies while maintaining detail loss. From the Figure 13 (a), it can be observed that our proposed dual mask mechanism "DM" significantly surpasses "BM" and "UM" in all four noise patterns. The "DM+D" (ours) exhibits superior performance when combined with T-standout, and "UM+D" (i.e., the gray curve area in Figure 13 (a)) is severely restrained. These visual results on the right side of Figure 13(a) further illustrate the detailed preservation advantages brought by the "DM", especially when integrated with T-Standout.
5.4.2. Parameter ω
The gradient-regularized parameter ω is used to make up the common shortcoming of information loss caused by the masking schemes. As depicted in Figure 13 (b), with the increase of ω, the trend of PSNR shows an initial increase followed by the decrease after reaching the maximum value. Therefore, we set ω=0.8 as our experimental configuration in this research. In addition, it seems the gradient-regularized parameter ω is more sensitive than the adjustable parameter γ. Nevetheless, with respect to the two cases with Gaussian noise, for example, setting the ω within the interval of [0.2,1.0] is acceptable for superior performance than all the other BSD networks, which indicates the effectiveness of our gradient-regularized loss.
5.4.3. Parameter ϵs, ϵg
To assess the robustness and sensitivity of the dual mask mechanism and T-standout module, an ablation study is carried out by modulating the threshold parameters ϵs and ϵg. These parameters respectively govern the selection of neurons with high detail pixel significance and high gradient significance. Multiple values of ϵs and ϵg are tested, where ϵs,ϵg∈{15,25,40,55,70,85,100}.
As depicted in Figure 14, the results clearly illustrate that when ϵs=25, the optimal denoising performance in terms of PSNR and SSIM is attained. This value effectively strikes a balance between preserving crucial detailed information and preventing redundancy. In addition, when ϵg=40, it yields the optimal performance by safeguarding the most informative gradient-aware features while avoiding noise amplification. These findings not only validate the robustness of our design decisions but also provide valuable guidance for the practical selection of threshold values.
5.4.4. Parameter γ
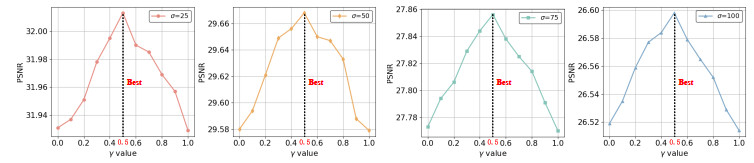
The flexible penalty parameter γ is used to supplement background content information. In Figure 15, it is verified that the denoising performance exhibits a trend of initially increasing and subsequently decreasing with respect to different noise levels. It is noticed that when γ = 0.5, PSNR reaches the optimal score, which more strongly confirms the role of the regularization term in constraining the overall loss function and enhancing the numerical efficacy. Thus, we set γ = 0.5 throughout the experiments in this paper.
6.
Conclusions
We present B2G, a novel self-supervised denoising framework designed to enhance edge restoration using dual mask denoisers. The framework employs a gradient-regularized loss function in conjunction with T-standout to train the denoising network in a zero-shot manner. Simultaneously, the framework continuously updates the dual mask mechanism within an iterative loop, guaranteeing that valuable details are maintained throughout the denoising process. B2G employs a zero-shot way to offer a denoising framework that saves more training data. We validate the performance of our B2G across various noise-related tasks and demonstrate its robust capability in processing images with high noise levels. Therefore, our proposed B2G provides an efficient solution for image denoising, particularly in applications involving images with significant noise.
Author contributions
Bolin Song: Conceptualization, Methodology, Writing original draft, Resources; Zhenhao Shuai: Formal analysis, Supervision, Investigation; Yuanyuan Si: Data curation, Software, Project administration; Ke Li: Funding acquisition, Visualization, Writing review & editing.
Use of Generative-AI tools declaration
The authors declare that they have not used Artificial Intelligence (Al) tools in the creation of this article.
Acknowledgments
This research is supported in part by the National Natural Science Foundation of China (Nos. 62176036, 62102059), the Natural Science Foundation of Liaoning Province (No. 2023-MS-126), and the Fundamental Research Funds for the Central Universities (No. 3132023523).
Conflict of interest
All authors declare no conflicts of interest in this paper.










 DownLoad:
DownLoad: