A review of spatial scan statistics for survival data

1.   Introduction

In epidemiology, the detection of spatial clusters enables the identification of geographical areas presenting an abnormally high (or low) risk. Spatial scan statistics are a well-known method for objectively detecting spatial clusters, and providing an indication of their statistical significance.

In the context of health data, spatial scan statistics based on Poisson and Bernoulli models have been proposed by Kulldorff and Nagarwalla ^[1] and Kulldorff ^[2]. From observed cases and at-risk populations, these can be used, for example, to detect geographical areas where the risk of having or dying from a disease is higher than elsewhere.

A spatial scan statistic based on an ordinal model has also been proposed by Jung et al. ^[3] and enables the detection of spatial clusters in which the stages of patients suffering from a disease are more severe than elsewhere.

Researchers may also be interested in detecting areas where the time to an event of interest (typically death or recovery from a disease) is higher or lower than elsewhere. In this case, the data observed is not a number of cases and a number of people at risk, but for each individual, a time to the event of interest. However, some individuals may never experience the event during the study, in which case they are said to be censored.

This article provides a review of the literature on spatial scan statistics methods for survival data. Section 2 introduces the general principle of spatial scan statistics, while Section 3 presents the different methods proposed in the literature for survival data. Section 4 explains how to adjust cluster detection on covariates and illustrates the approaches on the $\mathtt{LeukSurv}$ dataset. Finally, Section 5 concludes the article.

2.   Spatial scan statistics

Let $s_1, \dots, s_K$ be $K$ nonoverlapping spatial locations of an observation domain $\mathcal{S} \subset \mathbb{R}^2$. Spatial scan statistics aim at detecting spatial clusters in which the distribution of the observed data is different than elsewhere, as well as determining their statistical significance. More precisely, they consider the following test hypotheses:

These test hypotheses can be expressed more explicitly, depending on the type of data and model considered. They will be clarified for each survival data model in the following.

The spatial scan statistic approach is a two-stage process. The first stage is the scanning step. It consists in determining the most likely cluster (MLC) from a set of potential clusters $\mathcal{W}$. Here, we will consider the set of circular clusters containing between 1 and 50% of observations, but it should be noted that other approaches exist, especially elliptical clusters ^[4], graph-based ^[5] or arbitrarily-shaped clusters ^[6,7]. Next, a concentration index is computed for each potential cluster $w \in \mathcal{W}$. It compares the distribution within the potential cluster with that outside, so that the greater the difference, the higher the concentration index. Finally, the spatial scan statistic $\Lambda$ is defined as the maximum of the concentration index over $\mathcal{W}$, and the MLC is the potential cluster for which this maximum is reached.

The second step is to assess the statistical significance of the MLC. Since the distribution of the spatial scan statistic is generally impossible to determine under $\mathcal{H}_0$, two Monte Carlo approaches are commonly used: (ⅰ) $M$ permutations of the data are generated, and the scan statistic $\Lambda^{(m)}$ is calculated on each permuted dataset $m \in \{1, \dots, M\}$ ^[8,9,10]; (ⅱ) if the distribution of the data is known under $\mathcal{H}_0$, $M$ datasets are generated under $\mathcal{H}_0$, and the scan statistic is calculated on each generated dataset ^[1,2,3]. In both approaches, the p-value is then estimated by

3.   Spatial scan statistics for survival data

In the context of spatial survival data, spatial scan statistics allow researchers to identify risk or protective factors related to a study event. The test hypotheses are the following:

We can also define the alternative hypothesis $\mathcal{H}_1^{(w)}$ associated with a potential cluster $w$ as

Then, $\mathcal{H}_1 = \underset{w \in \mathcal{W}}{\bigcup} \mathcal{H}_1^{(w)}$.

Let $i_1^{(1)}, \dots, i_{N_1}^{(1)}, \dots, i_1^{(K)}, \dots, i_{N_K}^{(K)}$ be the observed individuals in $s_1, \dots, s_K$, where $i_n^{(k)}$ corresponds to the $n^\text{th}$ individual in spatial unit $s_k$. For each individual $i_n^{(k)}$, we observe survival data consisting of an observed delay $T_{i_n^{(k)}}$ and a censoring indicator $\delta_{i_n^{(k)}}$ (equal to 1 if $T_{i_n^{(k)}}$ corresponds to the true delay until the event, 0 otherwise, which corresponds to censoring). In the following, we only consider right-censoring (assuming that the event of interest could not have occurred before the beginning of the study). Censoring is assumed to be uninformative, and the event times are assumed to be independent of the censoring times.

This section presents the different scan statistics for survival data proposed in the literature, as well as their limitations.

3.1.   Parametric models

Several parametric approaches have been proposed in the literature. Huang et al. ^[11] first proposed a scan statistic assuming that the true (but not necessarily observed) survival times $Y_{i_n^{(k)}}$ follow an exponential model. The test hypotheses can be rewritten as

The alternative hypothesis associated with a potential cluster $w$ is then

Next, the log-likelihood under $\mathcal{H}_0$ is

which is maximized when $\hat{\theta} = \dfrac{ \sum\limits_{k = 1}^K \sum\limits_{n = 1}^{N_k} T_{i_n^{(k)}} }{ \sum\limits_{k = 1}^K \sum\limits_{n = 1}^{N_k} \delta_{i_n^{(k)}} }$, and the log-likelihood under $\mathcal{H}_1^{(w)}$ is defined as

which is maximized when $\hat{\theta}_w = \dfrac{ \sum\limits_{i_n^{(k)}, s_k \in w} T_{i_n^{(k)}} }{ \sum\limits_{i_n^{(k)}, s_k \in w} \delta_{i_n^{(k)}} }$ and $\hat{\theta}_{w^\mathtt{C}} = \dfrac{ \sum\limits_{i_n^{(k)}, s_k \in w^\mathtt{C}} T_{i_n^{(k)}} }{ \sum\limits_{i_n^{(k)}, s_k \in w^\mathtt{C}} \delta_{i_n^{(k)}} }$.

Then the spatial scan statistic is defined as

However, the exponential distribution is somewhat too simplistic in reality, since it assumes a constant hazard rate over time. An alternative parametric model is the Weibull model, which allows for increasing or decreasing hazard rate over time. Bhatt and Tiwari ^[12] proposed a scan statistic in this context, where the test hypotheses can be rewritten as

The log-likelihood under $\mathcal{H}_0$ is

which is maximized when $\hat{\theta} = \dfrac{ \sum\limits_{k = 1}^K \sum\limits_{n = 1}^{N_k} T_{i_n^{(k)}}^{\hat{\alpha}} }{ \sum\limits_{k = 1}^K \sum\limits_{n = 1}^{N_k} \delta_{i_n^{(k)}} }$, and the log-likelihood under $\mathcal{H}_1^{(w)}$ is defined as

which is maximized when $\hat{\theta}_w = \dfrac{ \sum\limits_{i_n^{(k)}, s_k \in w} T_{i_n^{(k)}}^{\hat{\alpha}_w} }{ \sum\limits_{i_n^{(k)}, s_k \in w} \delta_{i_n^{(k)}} }$ and $\hat{\theta}_{w^\mathtt{C}} = \dfrac{ \sum\limits_{i_n^{(k)}, s_k \in w^\mathtt{C}} T_{i_n^{(k)}}^{\hat{\alpha}_{w^\mathtt{C}} }}{ \sum\limits_{i_n^{(k)}, s_k \in w^\mathtt{C}} \delta_{i_n^{(k)}} }$.

For $\alpha, \alpha_w$ and $\alpha_{w^\mathtt{C}}$, the expressions of the maximum likelihood estimators are more complicated, and, since $\hat{\alpha}, \hat{\alpha}_w$ and $\hat{\alpha}_{w^\mathtt{C}}$ appear in the formulas of $\hat{\theta}, \hat{\theta}_w$ and $\hat{\theta}_{w^\mathtt{C}}$, we can in practice use an optimization algorithm to estimate all the parameters.

Finally, the spatial scan statistic is

These models have been generalized by Bhatt and Tiwari ^[13] to any density function for the $Y_{i_n^{(k)}}$ of the form

where $a, b, c > 0$ are known and $\gamma$ is to be estimated from the data.

In this context, the test hypotheses are

$\gamma, \gamma_w$ and $\gamma_{w^\mathtt{C}}$ can be estimated as in previous models using the maximum likelihood estimators and then the scan statistic is

It should be noted that if $a = b = c = 1$, this approach is equivalent to the exponential model; if $a = 1$ and $b = c$, it results in a Weibull model; and if $a = b = 1$ and $c = 2$, it is equivalent to a Rayleigh model.

More recently, Usman and Rosychuk ^[14] proposed an approach based on a log-Weibull distribution and considering the following test hypotheses:

The log-likelihoods under $\mathcal{H}_0$ and under $\mathcal{H}_1^{(w)}$ are, respectively,

and

And the spatial scan statistic is

Once the spatial scan statistic $\Lambda \in \{\Lambda^{\text{exp}}, \Lambda^{\text{Wei}}, \Lambda^{\text{gen}}, \Lambda^\text{log-Wei} \}$ is computed, the MLC is defined as the potential cluster of $\mathcal{W}$ corresponding to this maximum. The statistical significance of the MLC is then determined using a Monte Carlo procedure with permutations of the individuals (that is, the $(T_{i_n^{(k)}}, \delta_{i_n^{(k)}})$).

Although these approaches are based on conventional models for survival data, they remain parametric and are therefore less flexible than nonparametric or semiparametric approaches. Thus, a method based on a Cox model has been developed by Cook et al. ^[15].

3.2.   Cox model

Cook et al. ^[15] proposed a spatial scan statistic based on a Cox model, which presents the advantage of not assuming a distribution for the data.

They considered the following Cox model on the hazard function $\lambda$ for a potential cluster $w$:

In the context of cluster detection, the test hypotheses are

In this context, the partial log-likelihood under $\mathcal{H}_1^{(w)}$ is

In order to test $\mathcal{H}_0: \alpha_w = 0$ vs. $\mathcal{H}_1^{(w)}: \alpha_w \neq 0$, Cook et al. ^[15] proposed to use the score statistic defined as

where $U(\alpha_w) = \dfrac{\partial \ell_{\mathcal{H}_1^{(w)}}(\alpha_w)}{\partial \alpha_w}$ and $I(\alpha_w) = - \mathbb{E}\left(\dfrac{\partial U(\alpha_w)}{\partial \alpha_w} \right)$. We obtain

and the spatial scan statistic and the MLC are defined as $\Lambda^\text{Cox} = \underset{w \in \mathcal{W}}{\max} \ |LR^{(w)}|$ and $\text{MLC}^\text{Cox} = \underset{w \in \mathcal{W}}{\arg\max} \ |LR^{(w)}|$, respectively.

Finally, the statistical significance of the MLC is determined as previously, by permuting the individuals (that is, the $(T_{i_n^{(k)}}, \delta_{i_n^{(k)}})$).

The spatial scan statistics described until now make the conventional assumption of independence of the observations. However, this assumption is very strong and rather unrealistic in practice, since the spatial nature of the observations leads to potential spatial autocorrelation, as specified by Tobler's first law of geography ^[16]. Moreover, for confidentiality reasons, survival data are often only available on an aggregated spatial level. Thus, we can distinguish two phenomena: (i) the survival times of individuals located in the same spatial unit may be correlated (intra-spatial unit correlation), for example, due to similar healthcare supply, and (ii) there may be the presence of spatial dependence at the level of spatial units. Thus, Frévent et al. ^[17] proposed a spatial scan statistic based on a Cox model with spatially correlated shared frailties. This takes into account both of the above-mentioned phenomena.

3.3.   Cox model with spatially correlated shared frailties

Frévent et al. ^[17] considered the following Cox model with shared frailties:

where $\varphi_1, \dots, \varphi_K$ are the shared frailties associated with the spatial locations $s_1, \dots, s_K$, respectively, and include the cluster effect.

Thus, Frévent et al. ^[17] decomposed the frailties into two terms:

The test hypotheses can be written as

The shared frailties allow us to take into account the potential intra-spatial unit correlation. To take into account the potential spatial dependence between the spatial units, a spatial model, namely the conditional autoregressive (CAR) model, is assumed on the $X_k$:

where $\rho \in [0, 1]$ is the spatial dependence parameter, and $w_{k, l} = 1$ if $s_k$ and $s_l$ share a common boundary and 0 if not. It should be noted that if $\rho$ is assumed to be 0, then the model takes into account the intra-spatial unit correlation but not spatial dependence.

The proposed method is decomposed into two stages. The first one consists in estimating the $\varphi_k$ and $\rho$. To this end, Frévent et al. ^[17] proposed to estimate the $\varphi_k$ and $\rho$ under $\mathcal{H}_0$ and under each alternative hypothesis $\mathcal{H}_1^{(w)}$, and then to extract the estimates $\{\varphi_1^*, \dots, \varphi_K^*, \rho^*\}$ associated with the "best model" according to the Bayes factor criterion, i.e., under $\mathcal{H}_0$ if the Bayes factors comparing the models under each $\mathcal{H}_1^{(w)}$ to the model under $\mathcal{H}_0$ never exceed 30, and the model under $\mathcal{H}_1^{(w)}$ associated with the highest Bayes factor otherwise.

Next, the second stage consists in computing a scan statistic on the $\varphi_k^*$. At this stage, the test hypotheses can be rewritten on $\mathit{\boldsymbol{\varphi}}^* = (\varphi_1^*, \dots, \varphi_K^*)^\top$ as

where $\mathbb{1}, \mathbb{1}_w$ and $\mathbb{1}_{w^\mathtt{C}}$ correspond, respectively, to the column vector composed only of 1, the column vector composed of 1 for the locations in $w$ and 0 otherwise, and the column vector composed of 1 for the locations outside $w$ and 0 otherwise. $A$ is a squared matrix that results in the variance-covariance structure of the CAR model (see ^[17] for more details).

Then, the spatial scan statistic and the MLC are defined as

and

respectively, where

and

Since the distribution of the $\varphi_k^*$ is known, Frévent et al. ^[17] generates $M$ datasets of the $\varphi_k^*$ under $\mathcal{H}_0$ to estimate the p-value associated with the MLC. It should be noted that using permutations of the $\varphi_k^*$ is not possible here, as this would alter the spatial dependence of the data.

4.   Including covariates in the models

In many applications it may be relevant to adjust cluster detection on covariates such as the age of individuals. Thus, this section presents the adjustment procedure proposed by the authors.

4.1.   Including covariates in the parametric approaches

For the exponential model, Huang et al. ^[11] considered the following model to adjust for $p$ covariates $Z^{(1)}, \dots, Z^{(p)}$:

where $\varepsilon_{i_n^{(k)}}$ is an error term with density function $f_{\varepsilon}(e) = \exp{(e)} \exp{[-\exp{(e)}]}$. $\beta_0, \dots, \beta_p$ can be estimated from the $(T_{i_n^{(k)}}, \delta_{i_n^{(k)}})$ using an exponential regression. Next, the observed times are adjusted as

where $\mu_j = \underset{i_n^{(k)}}{\min} \ Z^{(j)}_{i_n^{(k)}}$. Finally, the spatial scan statistic is applied on the $(T_{i_n^{(k)}}^\text{adj}, \delta_{i_n^{(k)}})$.

For the approaches based on the Weibull model, its generalization, or the log-Weibull model, the authors did not propose any adjustment on the covariates.

4.2.   Including covariates in the Cox-based approaches

When the models can directly include covariates, the conventional approach for adjusting cluster detection on covariates in spatial scan statistics is to fit the model under $\mathcal{H}_0$, in order to make the effect of covariates independent of the potential cluster.

In the presence of covariates, the Cox model considered by Cook et al. ^[15] is as follows:

Thus, the score statistic is now expressed as

with

and

The spatial scan statistic is still defined as $\Lambda^\text{Cox} = \underset{w \in \mathcal{W}}{\max} \ |LR^{(w)\text{cov}}(\hat{\beta}_1, \dots, \hat{\beta}_p)|$.

The adjustment on covariates is performed similarly in the approach based on shared frailties. Frévent et al. ^[17] considered the following Cox model: for an individual $i_n^{(k)}$ within spatial unit $s_k$,

$\beta_1, \dots, \beta_p$ are estimated under $\mathcal{H}_0$ and fixed to these values in the models under each alternative hypothesis $\mathcal{H}_1^{(w)}$. Next, the estimates $\{\varphi_1^*, \dots, \varphi_K^*, \rho^*\}$ of $\{\varphi_1, \dots, \varphi_K, \rho\}$ retained are those obtained with the "best model" according to the Bayes factor criterion, and the scan step is performed on them, as described above.

4.3.   Application to the $\mathtt{LeukSurv}$ dataset

In this section, we illustrate the covariate adjustment procedure on the $\mathtt{LeukSurv}$ dataset studied by Henderson et al. ^[18] and available in the $\textsf{R}$ package $\textsf{spBayesSurv}$.

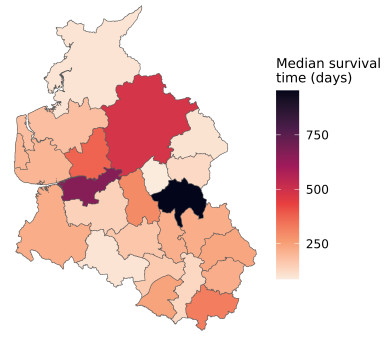
The dataset consists of 1,043 patients with acute myeloid leukemia within 24 districts in northwest England. For each patient, the survival time in days, status (dead or censored), age, sex, white blood cell count at diagnosis (wbc, truncated at 500), Townsend score (tpi, higher values indicate less affluent areas), and district of residence are available. The median survival times are presented in Figure 1.

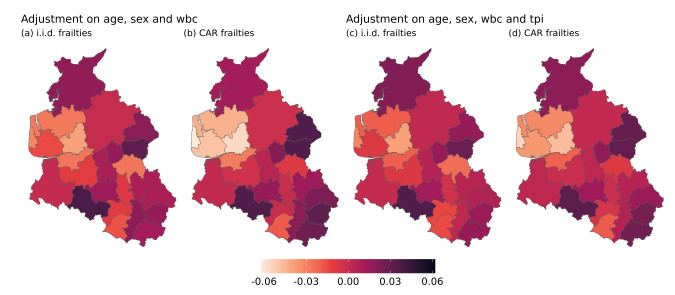
We applied the exponential scan statistic as well as the Cox-based approach with and without shared frailties, using the adjustment procedure described above. Cluster detection was first adjusted on age, sex and wbc at diagnosis, and then we also adjusted the clusters on the Townsend score. The estimated frailties are presented in Figure 2.

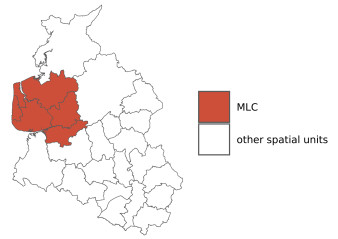
The MLC, presented in Figure 3, is the same for all four models (exponential, Cox without and with i.i.d. or CAR frailties) and both adjustments considered. Tables 1 and 2, respectively, describe the MLC and its statistical significance for the four models and the two covariate adjustments. Similarly to Frévent et al. ^[17], the hazard ratio in Table 2 was estimated in a conventional Cox model adjusted for the covariates.

Although the MLC is identical whatever the method, it should be noted that when we take into account the correlation of observations (with the i.i.d. and the CAR shared frailties approaches), the MLC becomes less statistically significant. When the Townsend score is included in the adjustment, the cluster is no longer statistically significant with these two models (see Table 2).

5.   Conclusions

This article presents a review of the literature on scan statistics for survival data. The first approach developed is based on an exponential model. This has the disadvantage of assuming a constant hazard rate over time, which is rather simplistic. The parametric approaches developed later avoid this problem, as does the approach based on the Cox model, which is even more flexible. However, these scan statistics assume the strong and rather unrealistic, albeit popular, hypothesis of independence of the observations. A more recent approach that does not require this assumption and takes account of the potential correlation, in the data is then presented.

Most applications of spatial scan statistics for survival data require the adjustment of cluster detection on covariates. This is therefore also detailed and illustrated on the $\mathtt{LeukSurv}$ dataset.

Several drawbacks to the current spatial scan statistics approaches can be mentioned. The estimation of the p-value associated with the MLC is carried out using Monte Carlo simulations as the distribution of the spatial scan statistic is intractable under $\mathcal{H}_0$. This leads to high computation times, which limit the practical application on large datasets. A solution is to approximate the p-value using the method proposed by ^[19]. Briefly, this approach consists in estimating the p-value accurately from only a small number of Monte Carlo simulations. Further work would involve obtaining the distribution of the scan statistic under $\mathcal{H}_0$.

Moreover, in practice, it is sometimes necessary to detect secondary clusters, i.e., other clusters that are also statistically significant. Several approaches have been suggested in the literature. For example, Kulldorff ^[2] proposed to perform statistical inference on the other potential clusters in exactly the same way as for the MLC, while other authors suggest removing the MLC from the data ^[20], before repeating the scan procedure. However, these approaches do not maintain the type I error. This is a challenging subject that requires further work.

Use of Generative-AI tools declaration

The author declare that she has not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The author is grateful to the reviewers for their helpful comments, which improved the quality of the paper. The author would also like to thank Sophie Dabo-Niang and Michaël Genin, thanks to whom she developed an expertise in spatial scan statistics during her PhD.

Conflict of interest

The author declares no conflict of interest in this paper