1.
Introduction
Nonlinear partial differential equations (NLPDEs) provide a fundamental framework for analyzing stability and dynamic behaviors. They are crucial for modeling complex physical systems, such as turbulence in fluid dynamics, wave propagation in optical fibers, and chaotic behavior in mechanical systems[1,2,3]. To thoroughly investigate various physical phenomena, including electromagnetic fields, fluid dynamics, heat transfer, mechanical waves, neural networks, and optical fiber communications, these equations are indispensable [4,5,6]. Many natural processes exhibit inherent nonlinearity, making linear models insufficient for accurate representation. Therefore, it is essential to take nonlinear effects into account to describe the behavior of such systems properly [7,8,9].
Recently, significant progress has been made in obtaining exact solutions to nonlinear partial differential equations (NLPDEs), and there is growing interest in developing innovative methods. Methods such as the Jacobi-elliptic method [2,3,12], Hirota bilinear method [13,14,15], Lie symmetry method [4,17], modified extended tanh-function, exp−(ϕ(ξ)) expansion methods [6], extended hyperbolic function and modified Kudryashov methods [7,9,20], tanh-coth method [22,23,24], Laplace transform method [25,26], new extended auxiliary equation method [27,28], generalized (G′/G)-expansion method [29], extended trial equation method [30], modified auxiliary equation method and the Sardar sub-equation method [31], extended Sinh-Gordon expansion method [32], IBSEF method [33], new extended FAN sub-equation method [34], Darboux transform method [35], and improved modified Sardar sub-equation method [36], bilinear neural network method [37], bilinear residual network method [38], and neural network-based symbolic calculation approach [39] have emerged as powerful tools for solving these complex equations. These approaches have provided new insights into nonlinear systems' analytical structure and expanded the possibilities for modeling and understanding intricate physical phenomena.
To understand the fundamental properties and dynamic behavior of physical systems, it is important to study nonlinear partial differential equations (NLPDEs). Our comprehension of the structure and general dynamics of the systems these equations describe is improved when we are able to find exact solutions. Additionally, allowing more knowledge of the behavior of these physical mechanisms, such as the ones utilized in bifurcation analysis, these solutions also disclose the mathematical structure of the equations [40,41,42]. For the purpose of effectively illustrating the dynamic characteristics of phenomena and analyzing their complexity, this understanding is important.
One of the most fundamental features of nonlinear systems is chaotic behavior. Chaos, with regard to [43,44,45], is the sensitivity of a system's dynamics to novel scenarios, where small changes to the initial state may lead to quite different results. In various fields, including fluid dynamics, electrical circuits, biological systems, and weather forecasting, the study of chaotic behavior has significant implications[46,47]. In fluid dynamics, chaotic dynamics play a role in understanding turbulence (see [48,49,50] for an overview of chaotic effects). At the same time, in atmospheric modeling, they establish limitations on long-term weather forecasts.
The analysis of chaotic systems plays a crucial role in advancing our understanding of the instability inherent in physical phenomena while also offering practical applications across various fields. This data is essential for financial mathematics for predicting economic changes, biological modeling to fully understand the transmission of illnesses, and engineering to ensure system stability and safety. For a complete understanding of the dynamic features of these systems, a detailed analysis of precise solutions and nonlinear effects, such as chaotic behavior [51,52], is essential.
The following are the classical integrable representations of the Kairat-Ⅱ and Kairat-Ⅹ equations, respectively [36,53,54]:
and
The limited research reported in the literature on these models has driven ongoing, in-depth investigations to uncover new solutions applicable to various physical and engineering contexts. For instance, in [55], dark, singular, combined solitons, and kink-type solitons for the Kairat-Ⅱ equation have been derived. On the other hand, [56] presents an extensive review of the Kairat-Ⅱ equation, obtaining solutions with closed-form by applying of symmetry reduction approaches. Also, sensitivity analysis built on the Hamiltonian system structure is the main the focus of this work.
Further, traveling wave solutions are generated using the analytical Paul-Painlevé method, with the graphical behavior of these solutions illustrated. An extensive set of local conservation laws is presented through conservation law multipliers. Furthermore, in [57], the solutions for the Kairat-Ⅹ equation are derived in trigonometric, exponential, and rational forms, encompassing periodic wave solitons, mixed bright-dark solitons, kink wave solitons, bright and dark peakon solitons, anti-kink wave solutions, bright solitons, dark solitons, and solitary wave structures.
In this study, we obtain novel exact solutions for the newly developed combined Kairat-Ⅱ-Ⅹ equation, which integrates the characteristics of the Kairat-Ⅱ and Kairat-Ⅹ equations, expressed as [58]:
where κ,α,β,τ, and ρ are non-zero real constants representing, respectively, the effects of inertia or wave speed, dispersion, higher-order dispersion, nonlinear interactions, and restoring forces or system stiffness. This equation plays a role in modeling nonlinear wave dynamics, especially in high-energy settings in plasma physics.
The goal of this study is to obtain exact solutions of the Eq (1.3) using two different analytical methods, namely the modified extended tanh-function (METHF) and (m+1Φ′) expansion methods, and to investigate the bifurcation analysis based on the Hamiltonian structure, as well as to study the periodic, quasi-periodic, and chaotic behaviors of the perturbed system. This study seeks to explore energy analysis in the scenario of sensitivity effects by analyzing developments in the system's potential, kinetic, and total energy elements under many different parameter settings. Our research shows that these variables impact energy components and effect the difference between stable and chaotic behavior. This illustrates how energy disturbances and chaotic dynamics are related, and how sensitive the system is to initial conditions in complex structures with dynamic processes.
The structure of the paper is as follows: Section 2 provides a description of the techniques. Section 3 shows that the steps are applied. The dynamic analysis is the main subject of Section 4. Section 5 highlights the connection between bifurcation theory, applications, and exact solutions. Section 6, the study's result, discusses the implications for researching nonlinear systems and for analyzing its results.
2.
Structural analysis of the suggested methods
2.1. Modified extended tanh-function (METHF) method
To demonstrate the fundamental principle of this approach[59], consider the specific partial differential equation (PDE) expressed as
In this equation, f(x,y,z,…,t) represents a function, and P denotes a polynomial incorporating nonlinear terms in the partial derivatives. By using the transformation
Eq (2.1) is converted into the ordinary differential equation (ODE)
Assume the solution to Eq (2.3) is given by
Here, ϕ(ς) satisfies the Riccati equation
where λ is a constant to be determined later. As shown below, Eq (2.5) admits several solutions:
For λ<0, G(ς) is given by
When λ>0, G(ς) takes the form
If λ=0, G(ς) reduces to
The positive integer M in Eq (2.4) is determined by balancing the highest-order derivatives with the nonlinear terms. Using symbolic computation, the coefficients Ar and Br are derived by substituting Eqs (2.4) and (2.5) into Eq (2.3). Collecting terms with identical powers of Gr for r=0,1,2,…,M and setting each to zero provides the unknown constants. By substituting these constants into Eq (2.4), we obtain exact solutions for Eq (2.1).
2.2. The (m+1Φ′)- expansion method
Assume that the solution of Eq (2.1) can be expressed as a finite power series in the following form, in accordance with the approach in [60],
where Ai, i=−M,...,−2,1,0,1,2,…,M and m are nonzero scalars. Owing to the principles of balance, one can find the value of M. Φ′ satisfies the following differential equation:
Putting Eq (2.7) into Eq (2.3) and then collecting all terms with the same order of the (m+1Φ′(ς))i, the system of algebraic equations for Ai(i=−M,..,−2,1,0,1,2,…,M), λ, μ, and m is obtained. As a result, we solve the obtained system to find the value of Ai(i=−M,−2,1,0,1,2,…,M), and inserting them into Eq (2.7), we can find the exact solution of Eq (2.1).
3.
Application of the proposed methods
To obtain the exact solutions of the proposed equation, it is necessary to reduce the governing equation to an ordinary differential equation (ODE) form. This reduction not only facilitates the direct determination of exact solutions, but also clarifies the fundamental structure of the system. For this purpose, we apply the following transformation:
where ω is the wave speed. Substituting Eq (3.1) into Eq (1.3), we obtain
If the transformation v′(ς)=χ(ς) is applied, Eq (3.2) reduces to the following form:
3.1. The METHF method
In this section, various novel exact solutions for the current Eq (1.3), derived using the METHF method, are presented.
By applying the balancing principles between χ(ς)2 and χ″(ς) in Eq (3.3), we obtain 2M=M+2, which gives M=2 as given in Eq (2.4). From Eq (2.4), the following result is obtained:
where G(ς) satisfies Eq (2.5). Substituting Eqs (3.4) and (2.5) into Eq (3.3) results in a polynomial expressed in terms of powers of G(ς). We then organize terms with similar powers and equate each corresponding coefficient to zero. This procedure yields the following system of algebraic equations:
The results presented below were obtained by solving this system.
Result 1a.
Result 1b.
Result 1a consists of three cases:
Case 1a. For λ<0,
Case 1b. For λ>0,
Case 1c. For λ=0,
Result 1b consists of three cases:
Case 2a. For λ<0,
or
Case 2b. For λ>0,
or
Case 2c. For λ=0, it gives the solution f3(x,t).
3.2. The (m+1Φ′)- expansion method
According to the balancing rule for Eq (3.3), this results in M=2. Therefore, Eq (2.7) becomes
Following the inclusion of Eq (3.12), an algebraic system of equations is formed as follows:
By solving this system, the following results are obtained.
Result 2a.
The solution obtained for Result 2a is presented as follows:
Result 2b.
The solution obtained for Result 2b is presented as follows:
Result 2c.
The solution derived for Result 2c is presented as follows:
where Δ=(−α+√(α−β(λ+2μm)2)2−4κρ+β(λ+2μm)2).
Result 2d.
The solution obtained for Result 2d is presented as follows:
where Δ=(−α+√(α−β(λ+2μm)2)2−4κρ+β(λ+2μm)2).
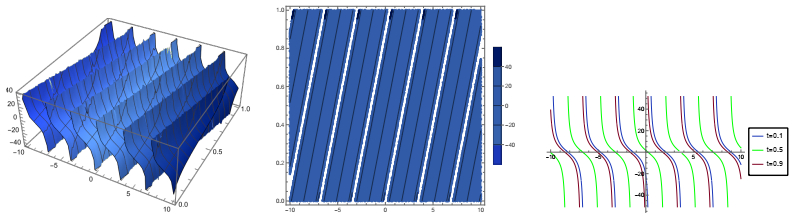
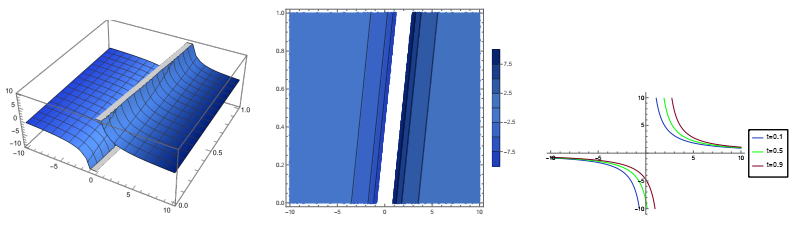
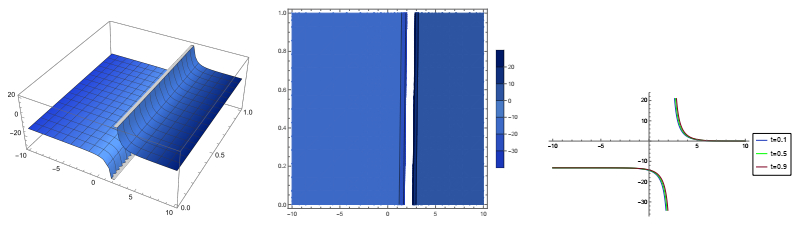
This section presents the results through graphical representations and offers detailed explanations for the corresponding solutions. Figures 1 to 3 illustrate the application of the modified extended tanh-function method, while Figure 4 demonstrates the use of the (m+1Φ′)-expansion method.
Remark 1. For M=2,
● the parameters in Figure 1 are selected as: λ=−0.21;α=−0.23;β=−0.44;κ=1;ρ=0.18;τ=−0.9,
● the parameters in Figure 2 are selected as: λ=0.21;α=−0.23;β=−0.44;κ=0.31;ρ=0.18;τ=−0.3,
● the parameters in Figure 3 are selected as: λ=0;α=0.55;β=0.44;κ=0.31;ρ=−0.18;τ=0.3,
● the parameters in Figure 4 are selected as: λ=1;α=0.33;β=0.6;κ=−1;ρ=0.33;τ=0.3;m=0.5;μ=0.1.
4.
Investigating dynamic behaviors in the proposed model
In classical mechanics, the Galilean transformation provides a foundational approach for connecting coordinates between two inertial reference frames. It is beneficial in scenarios where the relative speed between these frames is significantly less than the speed of light, allowing for accurate analysis in non-relativistic regimes. This transformation simplifies the equations of motion by preserving the independence of space and time, which is essential for modeling systems where relativistic influences are minimal.
By applying the Galilean transformation to the proposed model (3.3), we can thoroughly explore the dynamic behaviors without the complications introduced by relativistic effects. Specifically, this transformation isolates the core dynamical elements of the system, enhancing our understanding of equilibrium points, stability, and possible bifurcations. Consequently, it reveals the intrinsic properties of the system, making it easier to examine behavior across various parameter spaces. Therefore, based on this approach, we obtain the following dynamical system, which enables a detailed investigation of solution interactions and stability across different initial conditions and parameter variations:
where F1=τβ and F2=ρ−αω+κω2βω,(β≠0).
This dynamical system allows for a thorough investigation of its behavior under various parameter values and initial conditions. The terms F1 and F2 are especially significant, as they influence stability and equilibrium. Specifically, F1 introduces a nonlinear interaction with χ(ς), while F2 adds a linear influence that directs the system's overall behavior.
The stability and progression of solutions concerning ς can vary significantly depending on parameter values. We can gain deeper insights into the system's dynamic structure by analyzing equilibrium points and bifurcations across a range of F1 and F2 values. This approach clarifies the conditions for stability and reveals how the system behaves across different parameter regimes.
4.1. Bifurcation analysis
In classical mechanics, the Hamiltonian often represents the overall energy of a system, combining both kinetic and potential energy contributions. The Hamiltonian function for this particular system is defined as:
The expression ψ22 denotes the system's kinetic energy, where ψ plays a role analogous to velocity or momentum in classical mechanics. Conversely, the terms F13χ3−F22χ2 represent the potential energy, depending on χ, and shaping the potential landscape that governs the system's dynamics over time.
A key consideration is that the constant ℏ should only replace the Hamiltonian if it directly represents the system's total energy. In this framework, the Hamiltonian perfectly depicts the energy, encompassing kinetic and potential components.
To find the equilibrium points, we solve the following system:
The system's equilibrium positions, represented by (Λi), are as follows:
Theorem 2. [47,48,49,50] If F1≠0, then:
● When J(χ,ψ)<0, (4.1) exhibits a saddle point.
● When J(χ,ψ)>0, (4.1) exhibits a center point.
● When J(χ,ψ)=0, (4.1) presents a cuspid point.
Proof. To analyze the stability of these equilibrium points, we compute the Jacobian matrix of the system. The Jacobian matrix J(χ,ψ) is derived from the partial derivatives of the system's equations and provides insights into the local behavior near each equilibrium point. The sign of the determinant of the Jacobian matrix dictates the nature of each equilibrium point. Thus, the Jacobian matrix of the equilibrium point Λi (i=1,2.) of system (4.1) is
By adjusting the parameters F1 and F2, the system's dynamic behavior can be examined in various regimes.
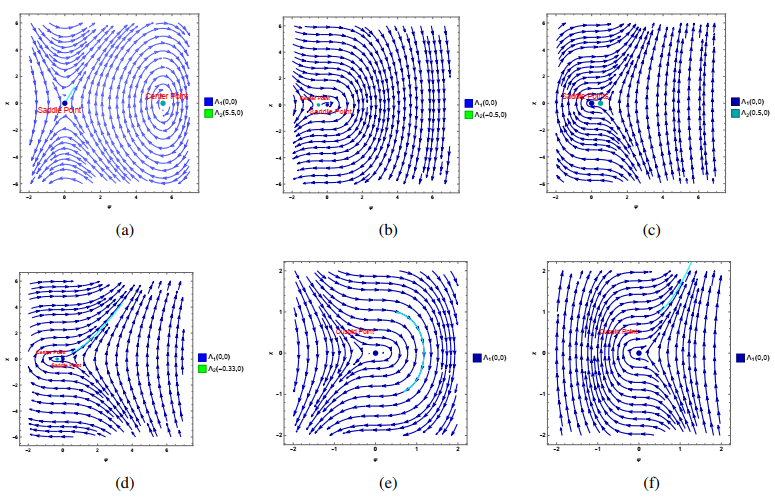
● For F1>0 and F2>0, assigning specific values to the parameters α=2,β=1,κ=3,ρ=3,τ=1, and ω=2, we obtain F1=1 and F2=5.5. The system has two equilibrium points: Λ1=(0,0)andΛ2=(F2F1,0)=(5.5,0). As a result of J(0,0)<0, the equilibrium point Λ1=(0,0) is determined to be a saddle point. Similarly, since J(Λ2)>0, the equilibrium point Λ2=(5.5,0) is classified as a center point. This distinction is shown in Figure 5(a).
● For the condition F1>0 and F2<0, with the parameters α=3, β=1, κ=1, ρ=1, τ=1, and ω=2, and given the values F1=1 and F2=−0.5, the system exhibits two equilibrium points. The first equilibrium point, Λ1=(0,0), is identified as a saddle point because J(Λ1)<0. The second equilibrium point is Λ2=(F2F1,0)=(−0.5,0). Since J(Λ2)>0, this equilibrium is classified as a center point, as shown in Figure 5(b).
● For the condition F1<0 and F2<0, with the parameters α=3, β=1, κ=1, ρ=1, τ=−2, and ω=2, and given the values F1=−2 and F2=−0.5, the system exhibits two equilibrium points. The first equilibrium point, Λ1=(0,0), is identified as a saddle point because J(Λ1)<0. The second equilibrium point is Λ2=(F2F1,0)=(0.5,0). Since J(Λ2)>0, this equilibrium is classified as a center point, as shown in Figure 5(c).
● When F1<0 and F2>0, with the parameters α=1, β=5, κ=1, ρ=1, τ=−3, and ω=1, and given the values F1=−0.6 and F2=0.2, the system exhibits two equilibrium points. The first equilibrium point, Λ1=(0,0), is identified as a saddle point, as J(Λ1)<0. The second equilibrium point is Λ2=(F2F1,0)=(−13,0). Since J(Λ2)>0, this equilibrium is classified as a center point, as illustrated in Figure 5(d).
● When the parameters are α=3, β=1, κ=1, ρ=2, τ=1, and ω=1, with values F1=1 and F2=0, the system displays a single cuspid point at cuspid point=(0,0), as seen in Figure 5(e).
● When the parameters are α=3, β=1, κ=1, ρ=2, τ=−3, and ω=1, with values F1=−3 and F2=0, the system reveals a unique cuspid point at cuspid point=(0,0). This single cuspid point is shown in Figure 5(f) and highlights a critical configuration of the system, marking a distinctive boundary where dynamic behaviors converge.
□
4.2. Discovering patterns that are chaotic in the dynamical system
In this subsection, by considering a perturbed term in the resulting dynamical system, the existence of chaotic behaviors is investigated by analyzing some 2D, 3D, Poincaré map, and time series graphs. To start, consider the following dynamical system:
Here, F3 and ϑ correspond to the amplitude and frequency of the external force perturbation, respectively.
To understand the perturbed system's dynamics comprehensively, we employ various numerical techniques, such as phase portraits, time series, and Poincaré sections. Due to the complex parameter space in system (4.5), evaluating each parameter's effect individually presents a challenge. Therefore, we fix certain parameters and focus our analysis on specific initial conditions. After assessing the system's general dynamic behavior, we examine the specific effects of F3 and ϑ more closely. This approach deepens our insight into how parameter variations influence the system's dynamic properties, revealing the potential for chaotic behavior.
The following figures provide a detailed illustration of how the system evolves under varying initial conditions and parameter adjustments, revealing the diverse trajectories the system can follow in response to these changes. These visuals demonstrate the system's capacity to exhibit dynamic behaviors under different configurations.
Remark 3.
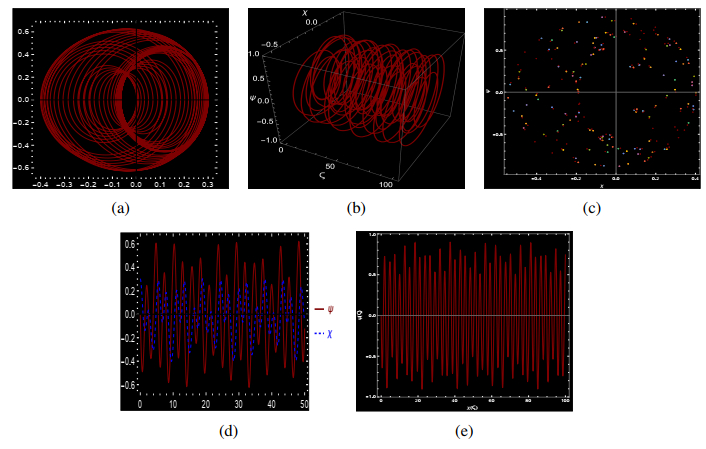
● Figure 6 illustrates the behavior of the system with the parameters F1=3, F2=−5.5, F3=0.7, and ϑ=1. Under these conditions, the system predominantly exhibits quasi-periodic behavior, characterized by complex and interwoven structures that suggest a transition toward chaotic dynamics. The lack of strictly repeating trajectories emphasizes the system's high sensitivity to initial conditions. Over time, irregular oscillations and non-linear interactions contribute to increasing instability. Additionally, external perturbations, such as F3cos(ϑς), further amplify fluctuations, driving the system closer to chaos.
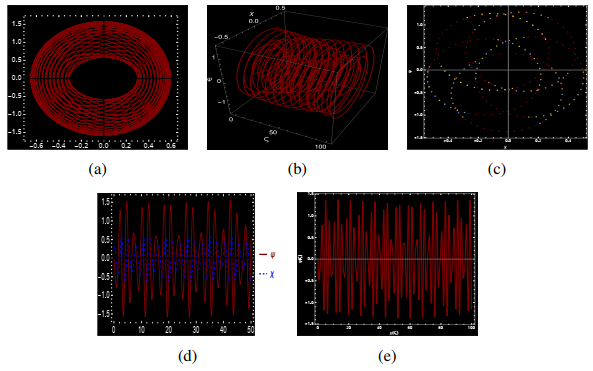
● Figure 7 shows the system's behavior with the parameters F1=1, F2=−5.5, F3=0.7, and ϑ=π. In this instance, the system exhibits quasi-periodic behavior with early signs of instability. As the trajectories gradually diverge from their regular paths, the system begins to show potential for chaotic transitions. Although it remains predominantly quasi-periodic, perturbations introduce slight irregularities, nudging the system toward a more unpredictable state. This is reflected in the non-periodicity of the time series of ψ and its irregular amplitude variations.
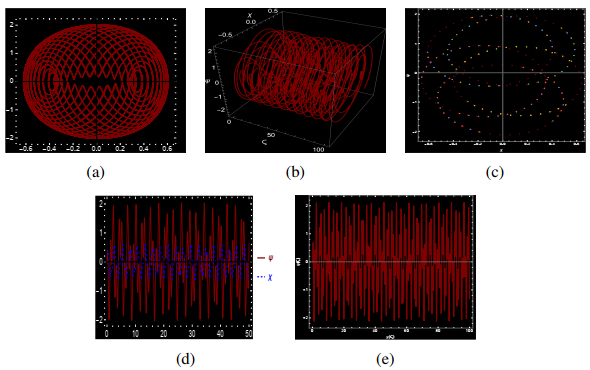
● Figure 8 depicts the system's behavior with the parameters F1=1, F2=−5.5, F3=5, and ϑ=2π. In this case, the system displays quasi-periodic behavior with mild instability. The trajectories retain their structure but are highly sensitive to initial conditions. While the motion does not fully become chaotic, there is instability that could eventually lead to chaotic dynamics. The external perturbations cause irregular oscillations in ψ, leading to significant deviations from periodic behavior, suggesting a transition toward chaos. Nonetheless, the system has not fully entered a chaotic regime and remains in a state of quasi-periodic motion, edging closer to chaos.
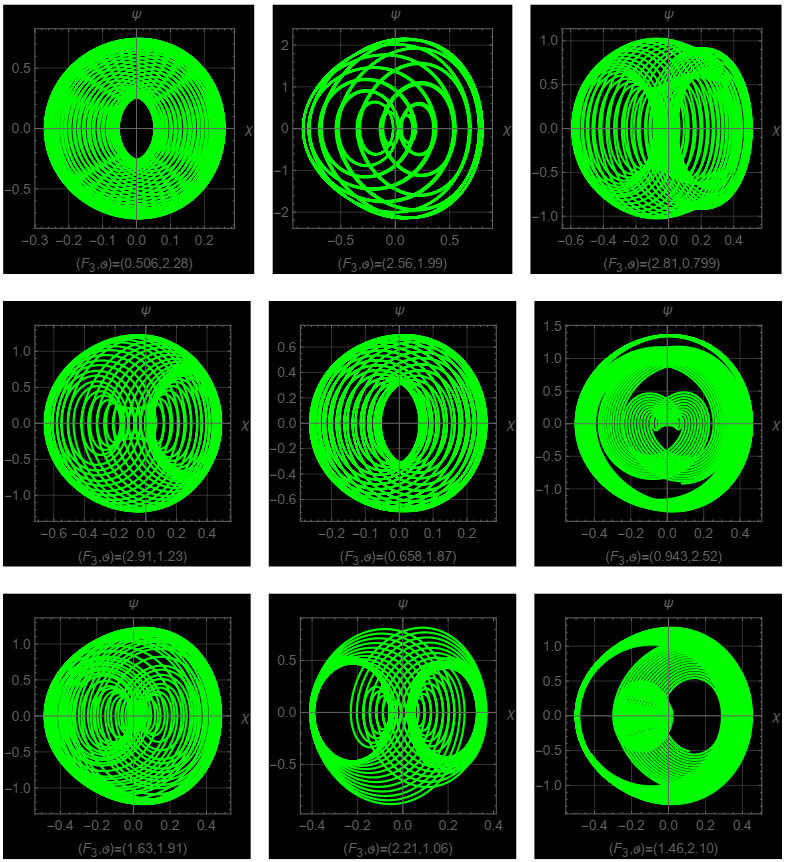
● Figure 9 displays phase portraits of the system with fixed parameters F1=3, F2=−10, F3=1.9, and ϑ=2 for varying initial conditions of χ(0) and ψ(0). These portraits demonstrate the system's strong responsiveness to minor variations in initial conditions. Each subplot highlights unique trajectories that emerge from different starting values, emphasizing the diverse manifestations of chaotic behavior within the system. This variety of paths illustrates how nonlinear dynamics lead to distinct and complex responses in different regions of phase space. Small initial variations rapidly expand over time, resulting in unpredictable and intricate patterns that reflect the system's inherent unpredictability and irregularity in its long-term evolution.
● Figure 10 illustrates the phase portraits of the system under fixed parameters F1=3, F2=−10, showing the impact of varying F3 and ϑ: At lower values of F3 (e.g., F3=0.5,1.2), the phase portraits display more regular, closed-loop structures, indicating quasi-periodic behavior. As F3 increases (e.g., F3=2.1,4.6), the trajectories become more complex, suggesting a transition towards chaotic dynamics. Similarly, lower ϑ values (e.g., ϑ=0.7,1.2) allow the system to synchronize with the external perturbation, resulting in regular trajectories. In contrast, higher values of ϑ (e.g., ϑ=1.9, 2.1) disrupt this synchronization, producing intricate structures indicative of quasi-periodic or chaotic behavior. These findings underscore the system's sensitivity to perturbation parameters, where variations in F3 or ϑ can push the system into chaotic regimes.
4.3. Energy analysis
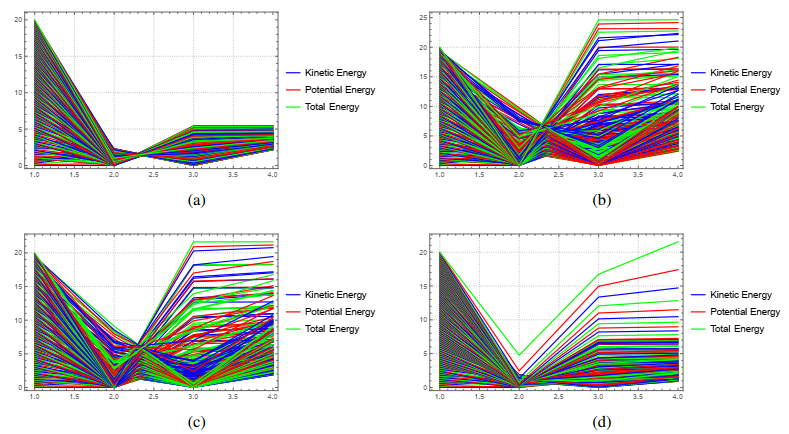
In this section, we investigated the influence of various parameters on the energy components (kinetic, potential, and total energy) within system (4.5). The analysis focuses on the evolution of these energy components under differing conditions, revealing insights into whether the system exhibits chaotic, unstable, or stable behavior. Each case is examined in detail below:
Remark 4.
● For the first set of parameters, where F1=3, F2=−10, F3=0.35, and ϑ=1, the system demonstrated relatively stable behavior. The energy fluctuations were noticeable, especially in the time range between 2 and 3, where a clear minimum in energy levels was observed. This indicates that the system reached a point where potential energy was at its lowest and kinetic energy was at its peak. Under these conditions, the system appears to maintain its overall stability despite regions of potential instability, likely due to the lower ϑ value that limits the influence of external forcing. This behavior is illustrated in Figure 11(a).
● In the second case, where F1=3, F2=−10, F3=0.35, and ϑ=π, the system exhibited a more chaotic structure. Energy fluctuations became significantly more irregular, showing a distinct increase in complexity. Particularly in the 2-3 time interval, the interactions between potential and kinetic energy revealed a region of instability where the energy exchange was highly unpredictable. An increase in ϑ intensified the external forcing, making the system highly reactive to its starting conditions and propelling it towards chaotic dynamics.
This is depicted in Figure 11(b).
● In the third scenario, where F1=−3, F2=−10, F3=0.35, and ϑ=π, the system displayed the most chaotic behavior among the three cases. The fluctuations in energy were the most erratic, with noticeable increases in both kinetic and potential energy variations. The negative value of F1 significantly destabilized the system's potential energy landscape, causing more abrupt transitions between energy states. This setup highlights how a negative F1 disrupts the balance between kinetic and potential energy, leading to a highly unpredictable energy profile that aligns with chaotic characteristics. This chaotic behavior is shown in Figure 11(c).
● In the fourth scenario, where F1=5, F2=−7, F3=1, and ϑ=π6, the system displayed a unique combination of stability and instability. The energy fluctuations were more gradual than in the previous cases, but distinct irregularities were still observed, particularly in the 2-3 time range. The increase in F1 and the adjustment of ϑ to a lower value (π6) created a scenario where the system balanced between order and chaos. This behavior, where the total energy gradually diverges from potential and kinetic energies, suggests the presence of a subtle chaotic influence under the influence of a moderate external force. This behavior is illustrated in Figure 11(d).
Remark 5. Overall, the analysis reveals that the parameters F1, F2, F3, and ϑ significantly influence the system's behavior. Specifically, positive and negative values of F1 dictate the nature of potential energy transitions. A negative F1 intensifies the irregularities in energy fluctuations, leading to chaotic tendencies. Changes in ϑ affect the system's response to external forcing. A higher value of ϑ introduces stronger oscillatory effects, which can destabilize the system and lead to chaotic dynamics. The interactions between F3 and ϑ determine the system's sensitivity to initial conditions. As ϑ increases, the tendency for chaotic behavior rises, emphasizing the role of external forcing in system stability. In the fourth case, with F1=5, F2=−7, F3=1, and ϑ=π6, the system exhibited a delicate balance between order and chaos. The moderate values of F3 and ϑ created a situation where energy fluctuations were less severe, but distinct irregularities were still present, particularly between 2 and 3 in the time domain. This highlights that even moderate external forcing can lead to complex behavior when combined with appropriate system parameters.
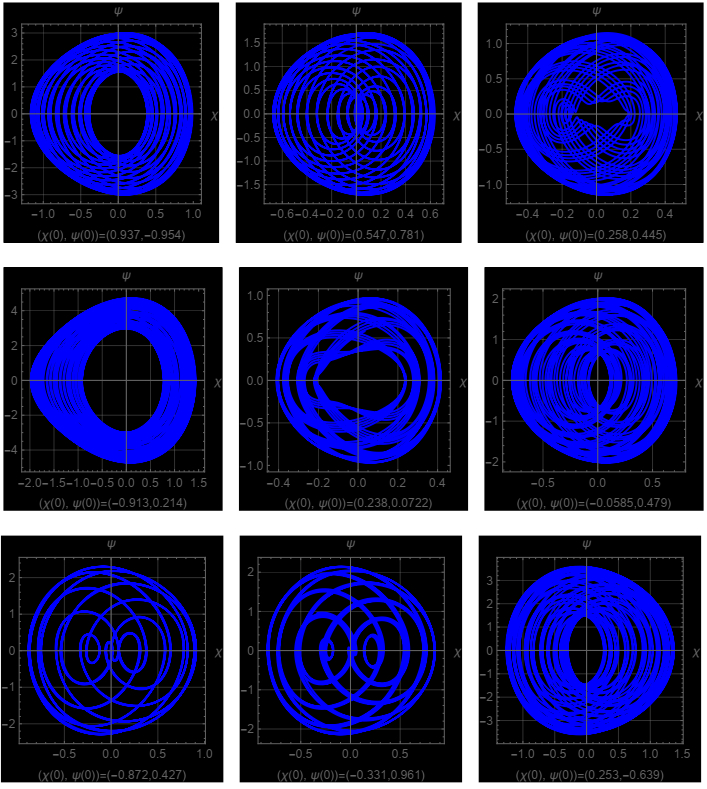
4.4. Sensitivity analysis
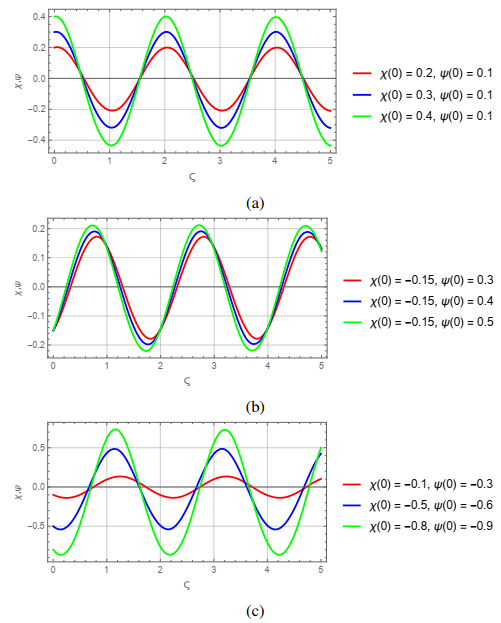
Sensitivity analysis is an essential tool for understanding the responses of dynamic systems to variations in parameters. Such analyses reveal the effects of specific parameters on system behavior, providing in-depth insights into stability and control. In particularly complex systems, even small parameter changes can lead to significant alterations in dynamics. This study will examine the sensitivity of the dynamic system represented by (4.1), aiming to uncover insights into how the system behaves under various conditions. Consequently, a better understanding of the impacts of parameters on the system will be achieved, offering critical information for its control.
The parameters are specified as: F1=3, F2=−10, \ τ=3, β=1, ω=2, α=3, κ=1, and ρ=−10. The initial conditions for the system are provided below:
(a) χ(0)=0.2, ψ(0)=0.1; χ(0)=0.3, ψ(ξ)=0.1; χ(0)=0.4, ψ(0)=0.1.
(b) χ(0)=0.15, ψ(0)=0.3; χ(0)=0.15, ψ(0)=0.4; χ(0)=0.15, ψ(0)=0.5.
(c) χ(0)=−0.1, ψ(ξ)=−0.3; χ(0)=−0.5, ψ(ξ)=−0.6; χ(0)=−0.8, ψ(0)=−0.9.
Remark 6. The sensitivity analysis of the dynamical system (4.6) shows that initial values χ(0) and ψ(0) significantly affect the amplitude and phase of oscillations. In Figure 12(a), lower initial values result in smaller amplitude and more regular oscillations, while in Figures 12(b, c), higher initial values lead to increased amplitude and more pronounced phase shifts. This indicates a nonlinear response of the system to higher initial energy levels. Although the system maintains its fundamental oscillatory behavior, controlling initial conditions is essential to achieve the desired amplitude levels. Physically, this behavior reflects the system's tendency to amplify oscillations with larger initial inputs, which could be critical in applications requiring stability.
5.
Exact solutions and bifurcation: their role in real phenomena
To demonstrate the relationship between exact solutions and bifurcation behavior in real systems, Table 1 provides a comparative summary of various analytical methods. The table presents the types of solutions obtained by each method, their connection to bifurcation structures, and their implications in practical applications. Furthermore, it demonstrates how patterns such as periodicity, chaos, or quasi-periodicity emerge under varying system parameters, providing valuable insights into real-world applications, including plasma physics, mechanical vibration systems, and atmospheric phenomena.
6.
Conclusions
In this study, two analytical methods are applied for analyzing the wave solutions and perform bifurcation analysis of a nonlinear physical system known as the combined Kairat-Ⅱ-Ⅹ NLPE. To achieve exact solutions to the model, the METFM and (m+1Φ′)-expansion method are used. Consequently, several novel singular, hyperbolic, and trigonometric solutions are obtained. The exact solutions presented here are not available in the existing literature. Moreover, the comparison of exact solutions with bifurcation analysis and chaotic structures clearly demonstrates the reliability and high accuracy of the proposed methods.
The bifurcation analysis addresses the system's stability, while the research findings reveal several periodic, quasi-chaotic, and quasi-periodic systems, highlighting the innovative nature of this work. Chaotic, quasi-periodic, and periodic behaviors are investigated using tools such as phase portraits, time series, and the Poincaré map. These analyses indicate the system's high sensitivity to external perturbations and the development of chaotic dynamic structures. In the energy analysis subsection, the study investigates how kinetic and potential energies change over time and how these energies affect the overall system dynamics.
This work has expanded the theoretical framework of the combined Kairat-Ⅱ-Ⅹ equation by revealing the interplay between bifurcation structures, energy dynamics, and sensitivity to initial conditions. This approach provides a solid foundation for practical applications in wave modeling and stability analysis. The proposed methods and analyses have significant potential for both theoretical and practical applications. Future research may build on these findings through numerical simulations and experimental validations, offering new possibilities for more effective modeling and management of nonlinear systems. Additionally, integrating analytical methods with machine learning techniques could enhance the accuracy and computational efficiency of high-dimensional NLPDEs.
Author contributions
Ulviye Demirbilek: Conceptualization, Methodology, Software, Writing-original draft, Formal analysis, Supervision. Ali H. Tedjani: Editing, Supervision. Aly R. Seadawy: Formal Analysis, Editing, Supervision. All authors have read and approved the final version of the manuscript for publication.
Use of Generative-AI tools declaration
The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2502).
Conflict of interest
The authors declare that they have no conflicts of interest.









 DownLoad:
DownLoad: