1.
Introduction
Distributions with heavy right tail are commonly used to model data in various areas of knowledge in which extreme observations generally occur, including environmental studies, geosciences, hydrology, actuarial sciences, economics, finance, product reliability assessment, and income distribution analysis. These datasets tend to be positive with positive asymmetry and heavy right tail (see [1]). Distributions with positive support and these characteristics are usually used to model such data. Areas where heavy-tailed distributions are applicable include engineering, physics, and finance; for other fields, we refer the reader to [2] and its references.
A frequently used distribution in statistical modeling is the Pareto model (see book by Arnold [3]), named after economist Vilfredo Pareto. A random variable X follows a Pareto distribution when its probability density function (pdf) is given by:
where α>0 is the scale parameter and β>0 the shape parameter. We denote this by X∼Pareto(α,β). The corresponding cumulative distribution function (cdf) is:
Johnson et al. [4] classify several types of Pareto distributions, referring to the above model as Pareto Type Ⅰ. Beyond this standard form, various extensions have been proposed in the literature. For instance, Pickands [5] examines the generalized Pareto distribution for making statistical inferences about the upper tail of a distribution. Choulakian and Stephens [6] develop goodness-of-fit tests for this generalized model, while Davison and Smith [7] apply it to hydrological data, analyzing river-flow exceedances over 35 years.
As a further extension, Gupta et al. [8] introduce a family of distributions by raising any positive support CDF to a positive power. A special case arises when using the Pareto cdf (1.2), leading to the exponentiated Pareto (EP) distribution. A random variable X follows an EP distribution if its pdf is defined as:
where α>0 is the scale parameter and β,γ>0 are the shape parameters. This model, denoted X∼ EP(α,β,γ), was first studied by Stoppa [9] (see also [10]), and is a particular case of the family studied by Gupta et al. [8]. Another generalization is the beta-Pareto distribution introduced by Akinsete et al. [11], and Boumaraf et al. [12] perform several optimization methods on the beta-Pareto distribution. For a comprehensive review of Pareto models (see Arnold's book [3]).
Andrews and Mallows [13] conducted research on normal distribution scale mixtures, resulting in the creation of a class of heavy-tailed distributions (including notable examples like Student's t-distribution). These distribution families are extensively applied in robust statistical analysis for symmetrical datasets.
A scale mixture distribution is formed by combining a base probability density with a scaling distribution. The mathematical representation of this mixture takes the form:
where fZ|U=u is the conditional distribution of the random variable Z given U=u, while κ(u) represents a positive function of the random variable U with density function fU, which influences the scale of the random variable Z. A particularly noteworthy case is the Slash distribution (see [4]), where Z|U=u∼N(0,κ(u)), U∼Uniform(0,1) and κ(u)=u1/q. This family's theoretical properties, inferential methods, and extensions have been extensively studied by Rogers and Tukey [14] and Mosteller and Tukey [15], while maximum likelihood (ML) estimation of its location and scale parameters are addressed in [16,17,18]. The same idea has been applied when the conditional distribution is with positive support, for example, to extend the Birnbaum-Saunders distribution (see [19]), and to extend the generalized half-normal distribution (see [20]).
The beta function (B) plays a fundamental role in this paper. It is defined as:
where a>0, b>0, and Γ(⋅) denotes the gamma function. A random variable Y follows a beta distribution with parameters a and b if its pdf is given by:
where a>0 and b>0.
The incomplete beta function, denoted by B(y;a,b), is defined as:
where a>0 and b>0. A related function is the regularized incomplete beta function, Iy(a,b), expressed as Iy(a,b)=B(y;a,b)/B(a,b).
Also used in this paper is the Gauss hypergeometric function (see [21]); it is denoted by 2F1, and is given by
where a,b,c>0 and c>b.
Lerch transcendent function (Φ), is also used in this paper, and can be expressed as:
where a>0, s>0 and z>−1.
A random variable X follows a G distribution with parameters σ and α when its density function is expressed as:
with scale parameter σ>0, shape parameter 0<α<1, and ¯α=1−α. The notation X∼G(σ,α) indicates this distribution, which possesses these key characteristics:
a) The G distribution is unimodal, its mode located at zero.
b) For Y∼Beta(1−α,α), the transformed variable σY1−Y follows a G(σ,α) distribution.
c) The cdf of X is expressed as:
where y=xσ+x and Iy(⋅,⋅) is the regularised incomplete beta function.
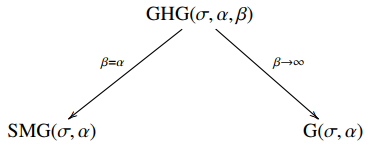
This distribution was first introduced by Gleser [22] and later studied by Olmos et al. [23]. More recently, Olmos et al. [24] proposed a scale mixture of the G and Beta distributions, naming it scale mixture of Gleser (SMG) distribution. They show that the SMG distribution exhibits a heavy right tail, making it a viable alternative to other heavy-tailed distributions such as the Pareto distribution.
A random variable X follows a SMG distribution with parameters σ and α when its density function is:
where σ>0 represents the scale parameter and 0<α<1 the shape parameter. We denote this by X∼SMG(σ,α).
The main motivation of this work is to extend the study of the G distribution by pursuing the following objectives. First, we aim to introduce the GHG distribution, generated from a scale mixture of the G and Beta distributions, similar to how the SMG distribution was derived. Notably, both the SMG and G distributions emerge as special cases of the GHG distribution. Second, we conduct a comprehensive study of the GHG distribution, demonstrating its applicability as an alternative model for actuarial data (e.g., insurance claims, income, and expenses) and hydrological data (e.g., flood peak exceedances), among other fields.
The article is organized as follows: In Section 2, we give a representation and the density of the extension of the G distribution, and its basic properties. In Section 3, we carry out an inference by the ML method, with a simulation study and the Fisher information matrix. Section 4 contains two applications to real data. In Section 5, we offer some conclusions.
2.
New density and properties
In this section, we present the mathematical representation, pdf, key properties, and graphical illustrations of the GHG distribution.
2.1. Density function
The pdf of the GHG distribution is formally defined below, including several special cases.
Definition 2.1. Let Z∼GHG(σ,α,β). Then, the pdf of Z is given by
where σ>0 represents the scale parameter, 0<α<1 and β>0 are shape parameters and 2F1 is the Gauss hypergeometric function.
Remark 1. It is verified as the following:
(1) If β<α, then the GHG distribution can be written as
(2) If β=α, the SMG(σ,α) distribution is obtained, introduced by Olmos et al. [24].
(3) If zσ<1 y using the Lerch transcendent function we obtain
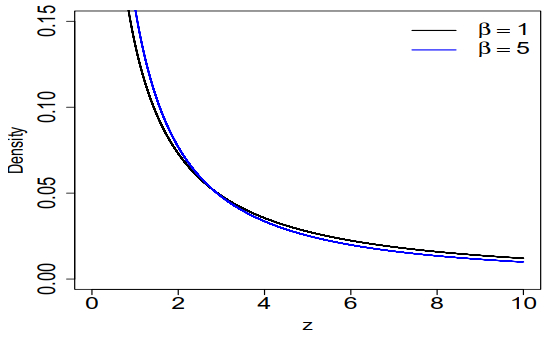
Figure 1 displays the density plots of the GHG distribution for σ=1, α=0.5 and two values of β, while Table 1 presents the values of P(Z>z) for various values of z in the distributions mentioned. It can be seen that the right tail of the GHG distribution is heavier as the value of parameter β decreases.
2.2. Properties
In this subsection, we show some properties of the GHG distribution.
Proposition 2.1. Let Z|U=u∼G(σu−1,α) and U∼Beta(β,1) then Z∼GHG(σ,α,β).
Proof. Proceeding straight to the integral calculation, we obtain:
The result follows from applying (1.7). □
Proposition 2.2. Let X∼G(1,α) and Y∼Beta(β,1) be independent random variables. Then, Z=σXY∼GHG(σ,α,β).
Proof. Using the stochastic representation Z=σXY and applying the Jacobian transformation, we obtain the desired distribution. □
Proposition 2.3. Let Z∼GHG(σ,α,β). If β→∞ then Z converges in law to a random variable Z∼G(σ,α).
Proof. Let Z∼GHG(σ,α,β). Then, by the representation given in Proposition 2.2, we have that Z=σXY. First, we study the probability convergence of Y.
When Y∼Beta(β,1), we have that E[(Y−1)2]=2(β+1)(β+2), if β→∞, then E[(Y−1)2]=2(β+1)(β+2)→0; this implies that YP→1. Applying Slutsky's Lemma (see the book by Lehmann [25]), we obtain the result. □
Remark 2. The result of Proposition 2.1 shows that this distribution arises from a scale mixture of the G and Beta distributions, while Proposition 2.3 indicates that when β→∞ in the GHG distribution, the G distribution is obtained. Figure 2 shows the relationship between the three distributions; we observe that the GHG distribution contains the SMG and G distributions as particular cases.
Proposition 2.4. Let Z∼GHG(σ,α,β). Then, the cdf of Z is given by
where σ>0, 0<α<1, β>0, y=zσ+z and Iy(,) is the regularised incomplete beta function.
Proof. Applying the definition of the cdf directly, we obtain
Hence by integrating by parts and considering u=∫vzσ0w−α1+wdw, we obtain the result. □
Corollary 2.1. Let Z∼GHG(σ,α,β), the survival function ¯FX(t) defined by ¯FX(t)=1−FX(t), is given by
The hazard function h(t), is defined by h(t)=fX(t)¯FX(t), for a random variable GHG is given by
where y=tσ+t.
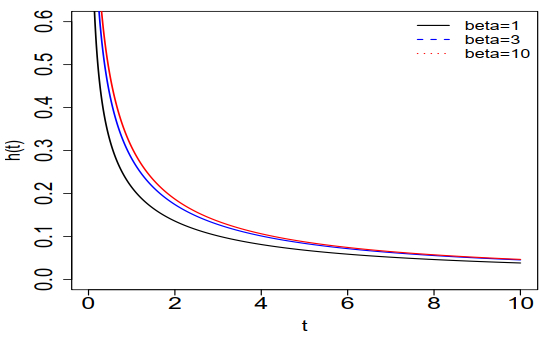
Figure 3 displays the hazard rate function's behavior for varying β parameters, with σ fixed at 1 and α at 0.5.
In the simulation study and in parameter estimation by the ML method, we considered the GHG distribution with only two parameters, i.e., modifying Proposition 2.1 as follows: Z|U=u∼G(u−1,α) and U∼Beta(β,1), and the following pdf of the random variable Z is the result.
where β>0 and 0<α<1 are shape parameters. This reduction in the parametric space aims to obtain a two-parameter distribution that serves as an alternative to the Pareto distribution and other two-parameter heavy right-tailed distributions. The random variable U considers parameter β, which influences the scale in the G distribution since it is where the mixing takes place. When including parameter σ, we observe that it can lead to an overestimation of β for small sample sizes.
For generating random numbers from the GHG model, two approaches are available: Algorithm 1 uses Proposition 2.1 and the composition method (see [26]), whereas Algorithm 2 employs the representation from Proposition 2.2.
Proposition 2.5. Let T∼GHG(β,α). Then, the hazard function of T is decreasing for all t>0.
Proof. Applying item b) of Glaser's Theorem [27], we defined the function:
where f(t) is the pdf given in (2.5). Their first derivative and sign are:
This completes the proof by Glaser's Theorem. □
The following Proposition shows that no moments exist for the GHG distribution; this is quite common in heavy-tailed distributions.
Proposition 2.6. For the random variable Z∼GHG(β,α), the r-th moments does not exist when r≥α.
Proof. We begin with the change of variable t=zw and apply integrating by parts with u=∫z0tβ−α1+tdt. This yields:
The left-hand side expression vanishes for r<β and does not exist when r≥β. As demonstrated in Proposition 1(e) of Olmos et al. [23], the right-hand integral diverges. Consequently, the expression diverges, proving that the r-th moments of Z∼GHG(β,α) do not exist. □
Remark 3. By Proposition 2.2, the existence of the r-th moment of Z reduces to that of X, which does not exist (see Olmos et al. [23]).
2.3. Tail of the distribution
In approximate terms, heavy-tailed distributions are those whose tails decay at a slower than exponential rate. The exponential distribution is regarded as the limit between heavy and light tails. In the areas of knowledge where they are applied, for example in finance and actuarial sciences, the data are positive and have a heavy right tail. The Pareto distribution has been widely used to model financial datasets, but in many cases, it does not provide a good fit. New distributions with heavy right tail are therefore of interest. Such models are crucial for representing losses in insurance, reinsurance, and catastrophic risk. Formally, a distribution of probability with cdf F(x), on the real line, is said to have a heavy right tail (see [28]) if limsupx→∞(−log(¯FX(x))/x)=0.
Regular variation theory plays a fundamental role in extreme value analysis (see for example [29,30,31,32], etc.). This concept is formalized as follows:
Definition 2.2. A distribution function is called regular varying at infinity with index −β (where β≥0) if:
Here, β is termed the tail index.
The GHG distribution exhibits this important property:
Proposition 2.7. The survival function of Z∼GHG(β,α), has regularly varying tails.
Proof. Applying the above definition and L'Hospital's Rule, we have that
and taking into account that β>0 the result follows.
□
As the GHG distribution is of regularly varying tails, it is therefore heavy-tailed (see [29]).
3.
Inference
In this section, we describe ML estimation for the GHG model and include a simulation study assessing the ML estimators' behavior.
3.1. ML estimation
Let z1,…,zn be a random sample from the GHG(β,α) distribution. The log-likelihood is given by:
where c(β,α)=nlog(β)−nlog(¯α+β)−nlog(Γ(¯α))−nlog(Γ(α)).
By equating the first partial derivatives (w.r.t. each parameter) to zero, we obtain the following system of equations:
where ψ(⋅) is the digamma function. From (3.2) and (3.3) we derive:
The ML estimator for α (ˆα) is obtained by numerically solving:
The estimator ˆα corresponds to the solution of Eq (3.5), which when substituted into (3.4) yields ˆβ. Equation (3.5) can be solved using numerical methods such as the Newton-Raphson algorithm. Alternatively, both estimates can be obtained by directly maximizing the log-likelihood surface defined in (3.1) using the optim subroutine in the R software package [33].
3.2. Fisher's information matrix
For a random variable Z∼GHG(β,α), the log-likelihood function corresponding to a single observation z of Z and parameter vector $θθ$=(β,α) is expressed as:
The Appendix contains derivations of both first and second partial derivatives of this log-likelihood function. The Fisher information matrix, denoted I_{F}(\cdot) , for the G distribution takes the form:
where \psi'(\cdot) is the trigamma function and \eta_{ij} = E\left(\frac{\kappa_{0}\Phi\left(-Z, i, \kappa_{0}\right)}{\, _{2}F_{1}\left(1, \kappa_{0}, \kappa_{1};-Z\right)}\right)^j are calculated numerically.
For large samples, the ML estimator \widehat{\boldsymbol{\theta}} is asymptotically normal bivariate:
Consequently, the asymptotic variance of \hat{\boldsymbol{\theta}} equals the inverse of I_{F}(\boldsymbol{\theta}) . In practice, since the parameters are typically unknown, we employ the observed information matrix with ML-estimated parameters.
3.3. Simulation study
To examine the behavior of estimation by ML, we conducted a simulation study to assess the performance of the estimation method for the \beta and \alpha parameters of the GHG distribution. Using Algorithm 2 given in Subsection 2.2 to generate random numbers from the GHG distribution, the simulation analysis was performed by generating 1000 samples of sizes n = 20, 100 and 300 from the GHG distribution. Table 2 shows the empirical bias (Bias), medium bias (MBias), mean of the standard errors (SE), and root of the empirical mean squared error (RMSE). As shown in Table 2, the estimation performance improves as n increases.
4.
Applications with real data
In this section, we analyze two real-data applications, comparing the fits of several distributions against the GHG distribution. Model selection is performed using four information criteria: AIC (Akaike Information Criterion; [34]), BIC (Bayesian Information Criterion; [35]), CAIC (Consistent AIC; [36]) and HQIC (Hannan-Quinn Information Criterion; [37]). These criteria are defined as: \mbox{AIC} = -2\hat{\ell}(\cdot)+2p , \mbox{BIC} = -2\hat{\ell}(\cdot)+\log(n)p , \mbox{CAIC} = -2\hat{\ell}(\cdot)+(\log(n)+1)p = BIC +p , and \mbox{HQIC} = -2\hat{\ell}(\cdot)+2\log(\log(n))p , where p denotes the number of parameters in the model.
4.1. Application to exceedances of flood peak data
The data correspond to the exceedances of flood peaks (in m^3/s ) of the Wheaton River near Carcross in Yukon Territory, Canada. The data consist of 72 exceedances for the years 1958-1984, rounded to one decimal place (see [6,11,38]), and are listed in Table 3. Table 4 presents descriptive statistics, including the sample skewness coefficient (CS) and kurtosis coefficient (CK). We compare the fits of the EP and Pareto distributions, with the fit of the GHG distribution with two parameters given in (2.5).
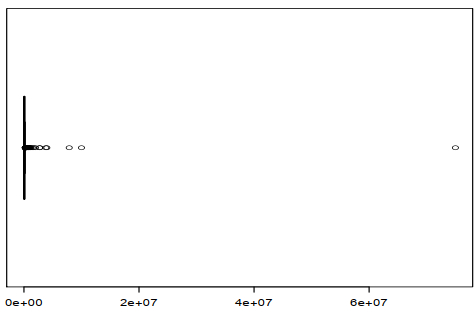
The box plot in Figure 4 shows one very extreme datum. This outlier makes the right tail heavier. While most data points cluster around 10 flood peak exceedances ( m^3/s ), there is one notable outlier at 64 exceedances ( m^3/s ).
Table 5 presents the ML estimates for the GHG, EP, and Pareto model parameters, along with their corresponding AIC, BIC, CAIC, and HQIC values.
The GHG model demonstrates superior fit to the data, as evidenced by its consistently lower AIC, BIC, CAIC, and HQIC values compared to both EP and Pareto models.
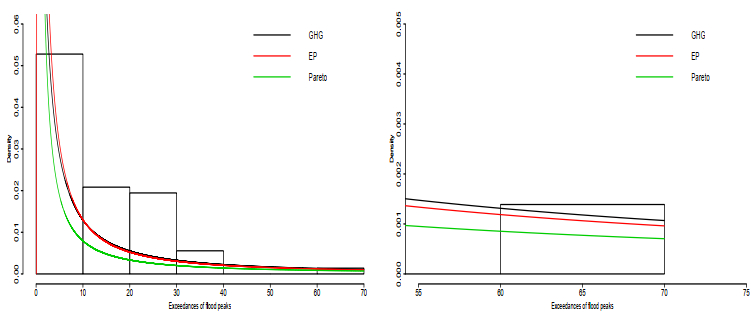
In Figure 5, the left side displays the histogram of the data along with the curves of the respective fitted distributions. It is evident that the GHG distribution provides a better fit for the exceedances of flood peak data compared to the EP and Pareto distributions. On the right side, there is a zoomed-in view of the right tail of the histogram, which more conclusively demonstrates that the GHG distribution concentrates more probability in the right tail than the other two distributions for this data set.
4.2. Application to income data
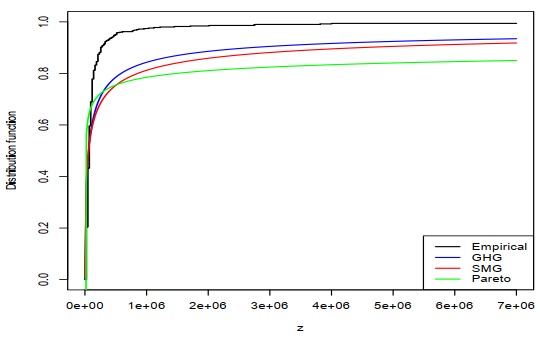
The dataset used in this application comes from the Survey of Consumer Finances (SCF), a nationally representative sample containing extensive information on assets, liabilities, income, and demographic characteristics of respondents (potential U.S. customers). We analyzed a random sample of 500 income-positive U.S. households interviewed in the 2004 survey. The variable of interest is each household's annual income in US dollars. The data can be accessed from the Federal Reserve's webpage: https://www.federalreserve.gov/econres/scfindex.htm. Descriptive statistics for these data are presented in Table 6. We compared the fits of the SMG and Pareto distributions with that of the three-parameter GHG distribution given in (2.1).
Figure 6 displays a boxplot revealing several extreme values. These outliers create a heavy right tail in the distribution. Notably, while most observations cluster around 5,400 (representing typical household income), there is an extreme value of 75 million in family income.
Table 7 presents the ML estimates for the parameters and log-likelihood values of the GHG, SMG, and Pareto models. Table 8 displays the corresponding values for the AIC, BIC, CAIC, and HQIC criteria for each model.
We observed that the GHG model yields the lowest values for the AIC, BIC, CAIC, and HQIC criteria, indicating that it provides a better fit to the data compared to both the SMG and Pareto models.
Figure 7 shows the empirical cdf with estimated GHG, SMG, and Pareto cdf's, which also shows a favorable agreement between the GHG model and the income data.
5.
Conclusions
In this work, we introduce a new heavy-tailed distribution through a scale mixture extension of the G distribution, combining it with the Beta distribution to create the GHG model. We study some properties, perform parameter estimation by the ML method, and show two applications to real data. The GHG distribution contains the G and SMG distributions as special cases. This is of interest, since it can be used in actuarial sciences and related fields. The GHG model is a viable alternative for fitting data with extreme observations. Some other properties of the GHG model are:
● The GHG distribution exhibits a heavy right tail.
● The GHG distribution has two representations, as presented in Propositions 2.1 and 2.2.
● The pdf, cdf, and hazard function have explicit forms expressed through known special functions, such as the Gauss hypergeometric function.
● The hazards function is monotonically decreasing, which provides information about the distribution's tail behavior (specifically, its heavy right tail; see [28]).
● In the first application, we demonstrate that the GHG distribution effectively models flood peak exceedance data, outperforming two well-known distributions: the EP and Pareto distributions.
● In the second application, we show that the three-parameter GHG distribution provides a good fit for income data, surpassing the SMG and Pareto distributions.
● A more comprehensive estimation study of the GHG distribution's three parameters will be addressed in future work, where we will analyze the effects and limitations of the \sigma and \beta parameters in the ML estimation method.
Author contributions
Conceptualization: N.M. Olmos and E. Gómez-Déniz; methodology: N.M. Olmos and E. Gómez-Déniz; software: N.M. Olmos and E. Gómez-Déniz; validation: N.M. Olmos, E. Gómez-Déniz, and O. Venegas; formal analysis: N.M. Olmos and O. Venegas; investigation: E. Gómez-Déniz and N.M. Olmos; writing---original draft preparation: N.M. Olmos and E. Gómez-Déniz; writing---review and editing: O. Venegas and E. Gómez-Déniz. All authors have read and approved the final version of the manuscript for publication.
Use of Generative-AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
EGD was partially funded by grant PID2021-127989OB-I00 (Ministerio de Economía y Competitividad, Spain) and by grant TUR-RETOS2022-075 (Ministerio de Industria, Comercio y Turismo).
Conflict of interest
Prof. Emilio Gómez-Déniz is the Guest Editor of special issue "Advances in Probability Distributions and Social Science Statistics" for AIMS Mathematics. Prof. Emilio Gómez-Déniz was not involved in the editorial review and the decision to publish this article.
The authors declare no conflicts of interest.
Appendix
The first-order partial derivatives of \ell(\boldsymbol{\theta}) with respect to \boldsymbol{\theta} are given by:
The second-order partial derivatives of l({\bf{$ \pmb{\mathsf{ θ}}$ }}) with respect to \boldsymbol{\theta} are given by:
where \kappa_{i} = \overline{\alpha}+\beta+i , \psi(\cdot) and \psi'(\cdot) are the digamma and trigamma functions, respectively.









 DownLoad:
DownLoad: