Local bifurcation analysis of an accelerating beam subjected to two frequency parametric excitations

1.   Introduction

Axially moving systems are commonly observed in many engineering applications such as paper sheets, textile fibers, robot arms, magnetic tapes, conveyor belts, band saw blades, and aerial cable tramways. These components can be modeled as axially moving strings, beams, and plates ^[1,2,3]. One important problem in axially moving mechanical systems is the abrupt occurrence of instability. Consequently, it is essential to investigate the stability characteristics and bifurcation behaviors in axially moving dynamical systems for the design of the system parameters.

Extensive research has been conducted on the nonlinear dynamical behaviors of beams. As an example of early studies, stability and bifurcation phenomenon of a shallow curved beam were discussed by Öz and Pakdemirli ^[4], in which the multiple scales method was employed and two-to-one internal resonance conditions between arbitrary pairs of vibration modes were studied. Applying the differential transform method, Ozgumus and Kaya ^[5,6] conducted a comprehensive vibration analysis of both the doubly tapered Euler-Bernoulli beam and rotating tapered Timoshenko beam. Recently, a sufficient condition for exponential stability was established by Apalara et al.^[7], depending on the equality of wave velocities within the system. In addition, the stability and vibration behaviors of axially moving beams have also been investigated by some researchers. Sze et al. ^[8] formulated the incremental harmonic balance method to analyze the nonlinear vibration of an axially moving beam with internal resonance between the first two transverse modes. Employing the Galerkin method, Yang and Chen ^[9] investigated the bifurcation phenomena and chaotic behaviors of an axially accelerating viscoelastic beam constituted by the Kelvin-Voigt model. The nonlinear dynamical behaviors were systematically studied through numerical analysis employing the Poincare map, the phase portrait, and computation of the largest Lyapunov exponent. An and Su ^[10] utilized the generalized integral transform technique to investigate the dynamic response of clamped axially moving beams. Comparative analysis of the vibration displacement at multiple longitudinal positions along the beam revealed excellent convergence behaviors. Later, Rajasekaran ^[11] adopted the differential transformation-based dynamic stiffness method to analyze the buckling and vibration behaviors of axially functionally graded tapered Euler and Timoshenko beams with different boundary conditions. Zhang et al. ^[12] used the Fourier expansion-based differential quadrature method to investigate the transverse nonlinear vibrations of an axially accelerating viscoelastic beam. Yan et al. ^[13] applied the Galerkin method to investigate the steady-state periodic response and the bifurcation and chaos of an axially accelerating viscoelastic Timoshenko beam with parametric excitation. Tang et al. ^[14] investigated the nonlinear steady-state oscillating response, stability, and bifurcation behaviors of a simply supported moving beam. The method of multiple scales was directly used to derive the solvability conditions, and the coupled effects of viscoelastic and viscous damping parameters on the dynamical behaviors were analyzed in detail. Recently, the stability and nonlinear vibration characteristics of axially moving beams have also been considered in a series of papers ^{[15,16,17,18]}.

2.   Related work

In ^[19], Sahoo et al. analyzed the nonlinear transverse vibration of an axially moving beam subjected to two frequency excitations by means of the multiple scales method. The frequency response plots and amplitude curves were obtained and the stability and bifurcation phenomenon were evaluated using a continuation algorithm. Numerical results were presented to show the complex nonlinear phenomena of the axially moving beam. However, the local dynamical behaviors of this system have not been studied analytically. In addition, there exist only few studies concerned with the stability and bifurcation of axially moving beams. In order to effectively suppress or eliminate large nonlinear vibrations of axially moving beams, it is imperative to advance the theoretical analysis on axially moving beam models, analyze the complex dynamical behaviors, explore the stability regions of the initial equilibrium point, investigate the bifurcation curves for the occurrence of static bifurcation and Hopf bifurcation, and conduct comprehensive research on the impact of key system parameters, so as to ensure the stability and controllability of the axially moving beams. The present work is therefore motivated to examine stability and bifurcation behaviors of the axially moving beam considered by Sahoo et al. ^[19]. In this paper, both analytical and numerical methods are employed to investigate the stability and bifurcation behaviors of the axially moving beam. Simultaneous principal parametric resonance as well as combination parametric resonance with 3:1 internal resonance is considered. According to the types of the degenerated equilibrium points, three different situations will be discussed and analyzed in detail. The normal forms of the differential equations are obtained by using the symbolic computation language Maple. The approach combines the normal form theory and center manifold theory into one step to achieve the closed-form expressions. Stability conditions for the steady state solutions and transition curves are also derived by using the normal form theory and the stability and bifurcation theory. Furthermore, numerical solutions are presented, which confirm the analytical predictions.

This paper is divided as follows: In Section 3, the equations of motion for an axially moving beam subjected to two frequency excitations are given, and the stability conditions for the steady state solutions are established explicitly. A detailed study of the dynamical behaviors of the system is carried out in Section 4. Conclusions are drawn in Section 5.

3.   Formulations of the problem

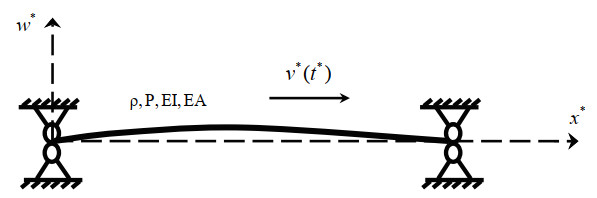
This paper is concerned with the nonlinear dynamical behaviors of a uniform horizontal beam traveling with a harmonically varying velocity. The model is illustrated in Figure 1^[19].

The nonlinear integro-partial differential equation of the beam is provided as follows ^[19]:

and the associated boundary conditions are

See ^[19] for the explanation of all system parameters.

3.1.   Assumptions and parameters

The time dependent velocity is supposed in the following form:

where $v_0^*$, $v_0^*{\eta _n}\, (n = 1, 2)$ and $\Omega _n^*\, (n = 1, 2)$ stand for the mean velocity, the amplitudes, and the frequencies of the harmonically varying velocity components, respectively.

The following are the non-dimensional transformations of the variables and parameters:

and the equation of motion of the beam in non-dimensional form is obtained as ^[19]

with the associated boundary conditions

where ${v_f}$ and ${v_l}$ mean the non-dimensional flexural stiffness and the non-dimensional longitudinal stiffness of the beam. $\mu$ and $\alpha$ represent coefficients of the non-dimensional viscous (external) damping and the non-dimensional material (internal) damping, respectively.

In order to derive the governing equations of motion, the following assumptions of the parameters and variables are introduced: (1) ${v_0}{\eta _n} = \varepsilon {v_n}\, (n = 1, 2)$; (2) for the case of a small amplitude of motion, $w = \sqrt \varepsilon {w^\# }$, where $\varepsilon \ll 1$; (3) simultaneous principal parametric resonance of the first mode (${\Omega _1} \approx 2{\omega _1}$) and combination parametric resonance of the first two modes (${\Omega _2} \approx \omega {}_1 + {\omega _2}$) with 3:1 internal resonance (${\omega _2} \approx 3{\omega _1}$) are considered. It is supposed that the responses in higher modes die down owing to the presence of damping and the Coriolis term in the equation of motion. Therefore, the first two modes will result in the long term system response. In this case, the relations are: ${\Omega _1} \approx 2{\omega _1}$, ${\Omega _2} \approx {\omega_1} + {\omega _2}$, and ${\omega _2} \approx 3{\omega _1}$.

3.2.   Method of analysis

Based on the aforementioned assumptions, the axial speed is obtained as

Removing the superscript "#" for convenience leads to the weakly nonlinear equation as ^[19]

Putting Eq (3.7) into Eq (3.8), the equation of motion can be obtained as follows:

and the boundary conditions are

Applying the multiple scales method, the following expression can be obtained:

where ${T_0} = t$, ${T_1} = \varepsilon t$. Denoting the differential operators as

leads to the following expression:

Substituting Eqs (3.11) and (3.12) into Eqs (3.9) and (3.10), the following equations can be obtained:

The solution of Eq (3.13) can be written as

where ${\phi _n}$ means the complex mode shapes, ${\omega _n}$ denotes the natural frequencies, and $cc$ is the complex conjugate.

In addition, Eq (3.15) can be replaced with

The frequency detuning parameters ${\sigma _1}$, ${\sigma _2}$, and ${\sigma _3}$ are introduced with the following relations:

Substituting Eqs (3.14) and (3.15) into Eq (3.9), two complex variable modulation equations are obtained as follows ^[19]:

where the dot denotes the differentiation with respect to $T_1$, and $s_i$, $g_i$, $K_i$, $C_i$, and $e_i$ are nonlinear interaction coefficients. The over bar signifies a complex conjugate.

Employing the Cartesian transformation for ${A_n}\, (n = 1, 2)$, we have

where ${x_i} \; ({T_1})\, (i = 1, 2, 3, 4)$ are real functions of $T_1$. ${\lambda _1} = 0.5{\sigma _2}$ and ${\lambda _2} = 1.5{\sigma _2} - {\sigma _1}$. Substituting Eq (3.19) into Eq (3.18) leads to the following modulation equations ^[19]:

where

${C_{iR}}$, ${C_{iI}}$, ${e_{iR}}$, ${e_{iI}}$, ${K_{1R}}$, ${K_{1I}}$ are the real and imaginary parts of ${C_i}$, ${e_i}$, and ${K_i}$ presented in the Appendix. All the other coefficients and the nonlinear functions $Nf_1^i\, (i = 1, 2, 3, 4)$ are also summarized in the Appendix.

The Jacobian matrix of Eq (3.20) at the initial equilibrium solutions (E.S.) $x_i = 0 \ (i = 1, 2, 3, 4)$ is as follows:

from which the characteristic polynomial can be obtained:

where

and $h_i(\mu_1, \mu_2, \alpha_1, \alpha_2, \beta_1, \beta_2, k_{21}, k_{22}, k_{31}, k_{32}, k_{81}, k_{82}, k_{91}, k_{92})\, (i = 2, 3, 4)$ are complicated functions provided in the Appendix.

According to the Hurwitz criterion, the stability conditions for $x_i = 0$ $(i = 1, 2, 3, 4)$ can be obtained as follows

If the conditions in Eq (3.24) are violated, the equilibrium solutions may become unstable and then lead to the occurrence of bifurcation. A detailed discussion of codimension-two bifurcations will be carried out in the following section.

4.   Stability and bifurcation analysis

In ^[19], Sahoo et al. analyzed the nonlinear transverse vibration of an axially moving beam using the continuation algorithm. For different control parameters $\mu$, $\alpha$, $\nu_1$, $\nu_2$, $\sigma_1$, and $\sigma_2$, numerical results were presented to show the complex nonlinear phenomena of the axially moving beam, and the stability and bifurcation of the equilibrium solution were simultaneously evaluated. However, the stability and bifurcation behaviors of the steady state solutions have not been studied analytically. This study is therefore motivated to investigate the local dynamical behaviors of the axially moving beam both analytically and numerically. The stability regions of the initial equilibrium point and the explicit expressions of the critical bifurcation curves will be discussed in the following analysis.

As we know, damping has a significant influence on dynamical behaviors of the system, so this section mainly focuses on the stability and bifurcation analysis of the two important parameters ${\mu _1}$ and ${\mu _2}$, which can be expressed in terms of ${\mu}$, $\alpha$, ${C_{iR}}$, and ${e_{iR}}$ ($i = 1, 2$). It can be divided into three parts based on the type of degenerate equilibrium points, and the eigenvalues of the characteristic polynomial (3.22) include the following three cases:

Case (1) ${\lambda _1} = {\lambda _2} = 0$, ${\lambda _3} = -1$, ${\lambda _4} = - 3$, which means that $b_1 = 4$, $b_2 = 3$, and $b_3 = b_4 = 0$.

Case (2) ${\lambda _1} = 0$, ${\lambda _{2, 3}} = \pm 2i$, ${\lambda _4} = - 2$, and $b_1 = 2$, $b_2 = 4$, $b_3 = 8$, $b_4 = 0$.

Case (3) ${\lambda _{1, 2}} = \pm \sqrt 3 i$, ${\lambda _{3, 4}} = \pm \sqrt 5 i$, and $b_2 = 8$, $b_1 = b_3 = 0$, $b_4 = 15$.

4.1.   The case of a double zero and two negative eigenvalues

For case (1), the system parameters can be determined by Eq (3.23) as

${\mu _1} = - 2$, ${\mu _2} = 0$, ${\alpha _1} = \frac{5}{2}$, ${\alpha _2} = 4$, ${\beta _1} = \frac{{11}}{2}$, ${\beta _2} = {k_{21}} = {k_{22}} = {k_{31}} = {k_{32}} = {k_{82}} = {k_{92}} = 1$, ${k_{81}} = 2$,

${k_{91}} = 2$, ${a_{01}} = {a_{02}} = {a_{03}} = {a_{04}} = {a_{05}} = {a_{06}} = 1$, ${b_{01}} = {b_{02}} = {b_{03}} = {b_{04}} = {b_{05}} = {b_{06}} = 1$.

Choosing ${\mu _1}$ and ${\mu _2}$ as the perturbation parameters, and letting ${\mu _1} = -2+{\varsigma _1}$, ${\mu _2} = {\varsigma _2}$, Eq (3.22) becomes

where

The stability conditions for $x_i = 0$ $(i = 1, 2, 3, 4)$ are

i.e.,

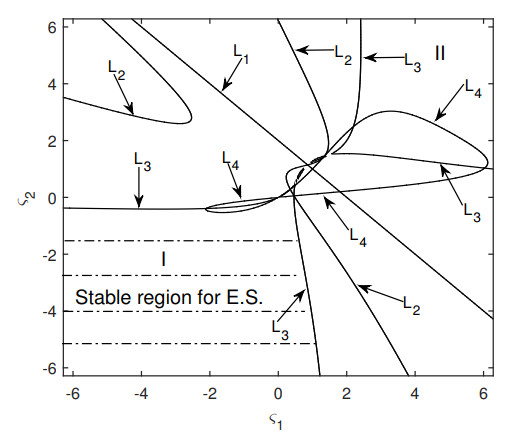
According to Eq (4.4), the following four transition curves are obtained as shown in Figure 2.

It is obvious that the E.S. is stable when the parameters ${\varsigma _1}$ and ${\varsigma _2}$ are located in region Ⅰ shown in Figure 2. Possible bifurcations may occur from the stable solution $x_i = 0$ $(i = 1, 2, 3, 4)$ when the parameters ${\varsigma _1}$ and ${\varsigma _2}$ are chosen from region Ⅱ.

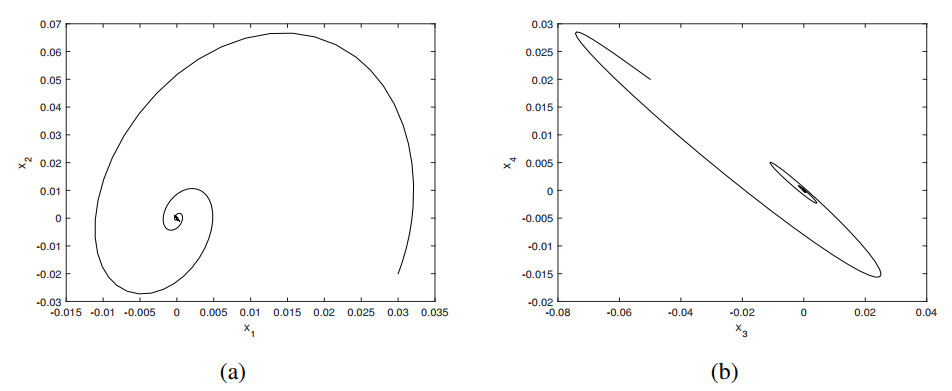
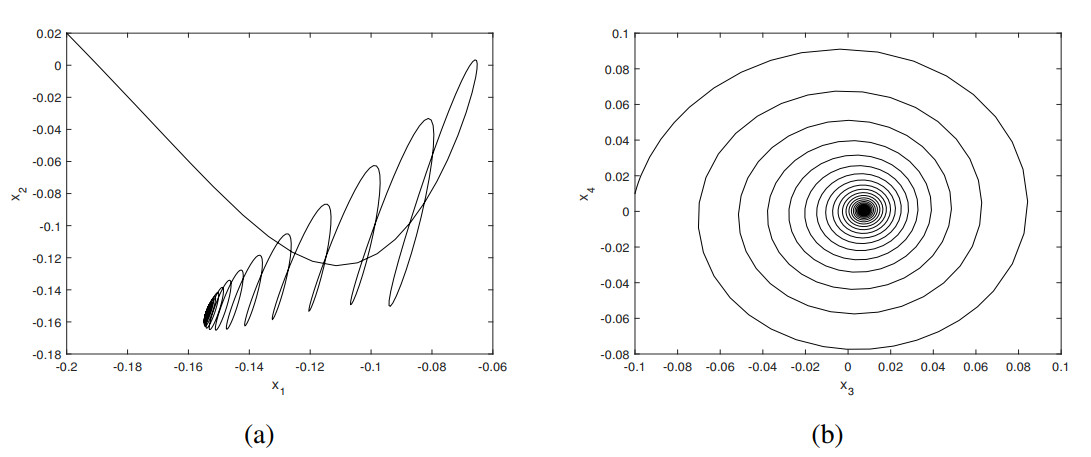
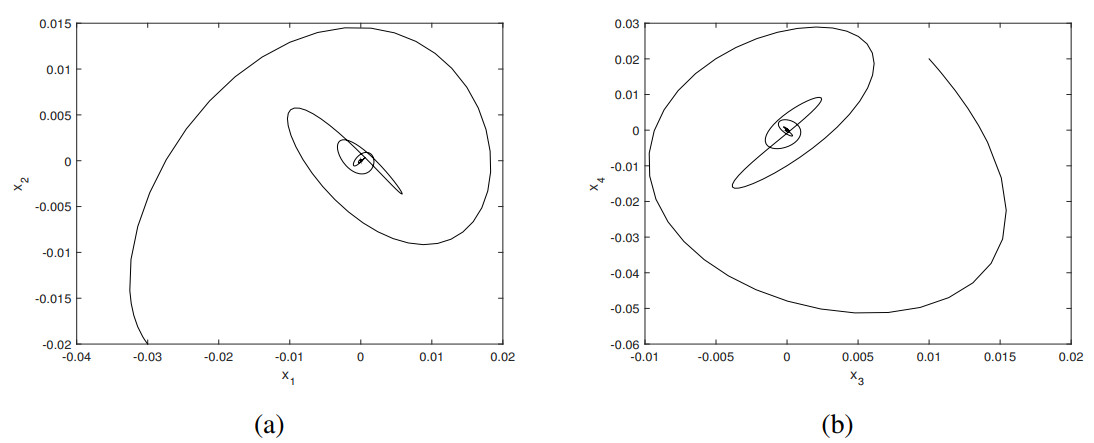
Employing the fourth-order Runge-Kutta method, numerical results have been obtained on the basis of the Eq (3.20). Choosing the parameter values $({\varsigma _1}, {\varsigma _2}) = (0.1, -0.5)$ from region Ⅰ, a numerical solution starting from an initial point $({x_1}, {x_2}, {x_3}, {x_4}) = (0.03, -0.02, -0.05, 0.02)$ asymptotically converges to the region of the origin, shown in Figure 3, and it is proved that the E.S. is stable. See Figure 3 for the phase trajectories on the ${x_1} - {x_2}$ and ${x_3} - {x_4}$ subspaces. If the values of ${\varsigma _1}$ and ${\varsigma _2}$ are determined from the region Ⅱ, the E.S. becomes unstable.

4.2.   The case of a simple zero and a pair of pure imaginary eigenvalues

In case (2), the parameter values are selected as

${\mu _1} = - 1$, ${\mu _2} = 0$, ${\alpha _1} = 0$, ${\alpha _2} = 1$, ${\beta _1} = 0$, ${\beta _2} = -2$, ${k_{21}} = \frac{{1}}{2}$, ${k_{81}} = \frac{{3}}{2}$, ${k_{22}} = {k_{31}} = {k_{32}} = {k_{82}} = {k_{91}} = {k_{92}} = 0$, ${a_{01}} = {a_{02}} = {a_{03}} = {a_{04}} = {a_{05}} = {a_{06}} = 1$, ${b_{01}} = {b_{02}} = {b_{03}} = {b_{04}} = {b_{05}} = {b_{06}} = 1$.

Choosing ${\mu _1}$ and ${\mu _2}$ as the perturbation parameters, letting ${\mu _1} = -1 + {\varsigma _1}$, ${\mu _2} = {\varsigma _2}$, and applying the state variable transformation

onto Eq (3.20) yield

where the nonlinear functions $Nf_2^i\, (i = 1, 2, 3, 4)$ are listed in the Appendix. Evaluating on the solution ${z_i} = 0$ at the critical point ${\varsigma _{1c}} = {\varsigma _{2c}} = 0$, the Jacobian matrix of Eq (4.7) can be achieved as

Note that the local dynamical behaviors of the system in the vicinity of the critical point are related to the critical variables ${z_1}$, ${z_2}$, and ${z_3}$. According to Eq (4.7), the research in ^[20] are applied to determine the normal form of system (4.7) as follows:

and

Letting $\dot y = \dot r = 0$ in Eq (4.9) yields the following steady state solutions.

The initial equilibrium solution (E.S.):

The static bifurcation solution (S.B.):

The Hopf bifurcation solution (H.B. with frequency ${\omega _1}$):

The secondary Hopf bifurcation or the secondary static bifurcation solution (2nd H.B. or 2nd S.B. with frequency ${\omega _2}$):

Note that the characters of Eqs (4.11)–(4.14) can be verified based on the Jacobian matrix of (4.9), given by

Evaluating (4.15) on (4.11) reveals that the stability of the E.S. can be rigorously established under the following conditions:

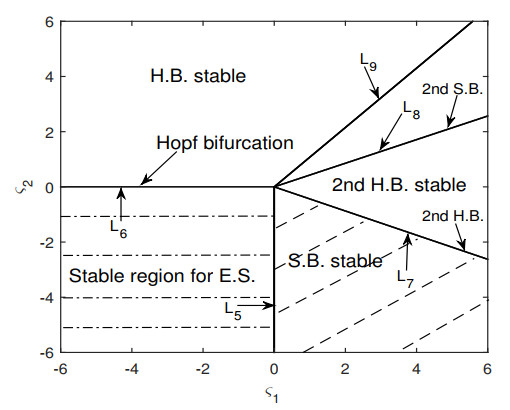
The region obtained by Eq (4.16) is exhibited in Figure 4, which illustrates the stability boundaries for the E.S., which are

where the S.B. solution given by Eq (4.12) bifurcates from the E.S. (4.11). The other critical line is

along which the H.B. solution (4.13) naturally emerges.

To determine the stability conditions for (4.12), the Jacobian matrix (4.15) on the S.B. solution (4.12) is evaluated as

which means that the S.B. solution maintains its stability if

The stability boundaries decided by conditions (4.20) comprise both the critical line ${L_5}$ and an additional critical line

It is confirmed that the stability criterion for the S.B. solution (4.12) is strictly satisfied within the domain enclosed between ${L_5}$ and ${L_7}$ (see Figure 4).

Similarly, the Jacobian matrix (4.15) on Eq (4.13) is calculated to yield

which implies the stability of the H.B. solution when the following conditions hold:

and the frequency of (4.13) is expressed as

Consequently, the stability region of the H.B. solution is bounded between two critical boundaries: the critical line ${L_6}$ and an additional critical line characterized by

It is noted that the critical boundary ${L_7}$ is intersected with the change of the parameter values, and the S.B. solution given by Eq (4.12) loses stability and undergoes a bifurcation, giving rise to a family of limit cycles known as the 2nd H.B. solution (4.14). It is further demonstrated that the H.B. solution presented in (4.13) becomes unstable when crossing the critical boundary ${L_8}$, from which another family of limit cycles identified as the 2nd S.B. solution (4.14) emerges. The frequency of the 2nd H.B./2nd S.B. solution is determined as

To analyze the stability of (4.14), the Jacobian matrix (4.15) on Eq (4.14) is computed to derive

The stability conditions for (4.14) are determined by analyzing the trace and determinant of (4.27) given as follows:

Obviously, the fulfillment of condition (4.29) becomes inherently guaranteed whenever the 2nd H.B. solution exists. Setting the determinant equal to zero results in ${L_7}$ and ${L_8}$ that demarcate the parameter region for the existence of the 2nd H.B. solutions. Letting the trace equal zero, an additional critical line is established as

Theoretical analysis suggests the potential emergence of a two-dimensional (2-D) torus through secondary bifurcation. However, our investigation reveals that the critical line ${L_9}$ (with slope 1.076) lies strictly above ${L_8}$ (slope 0.428). Consequently, the 2nd H.B. solutions cannot undergo a bifurcation into a two-dimensional torus. Therefore, the existence of a 2nd H.B. solution ensures its stability. The corresponding critical bifurcation lines are depicted in Figure 4.

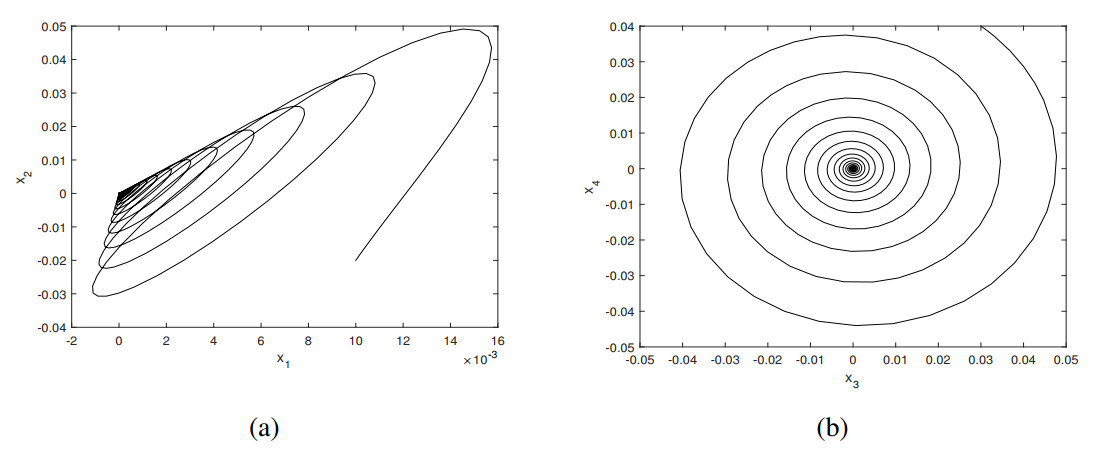
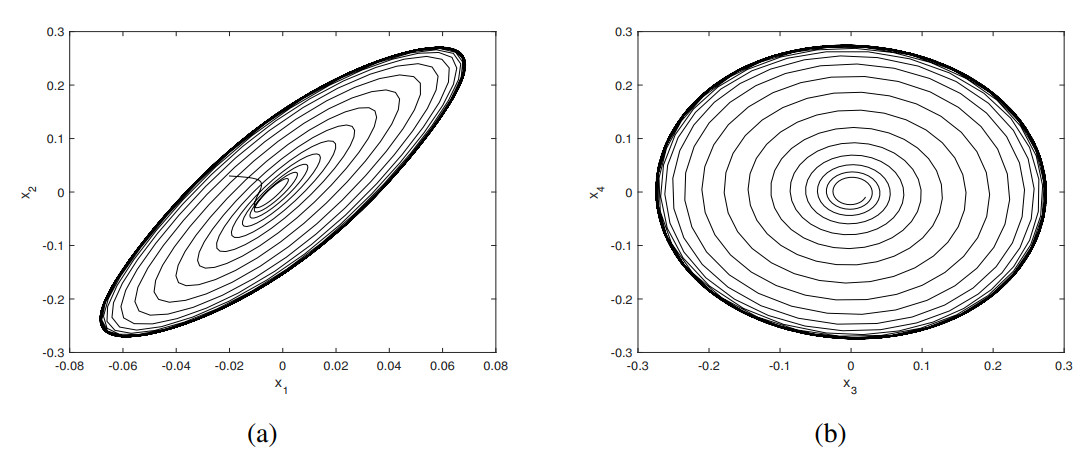
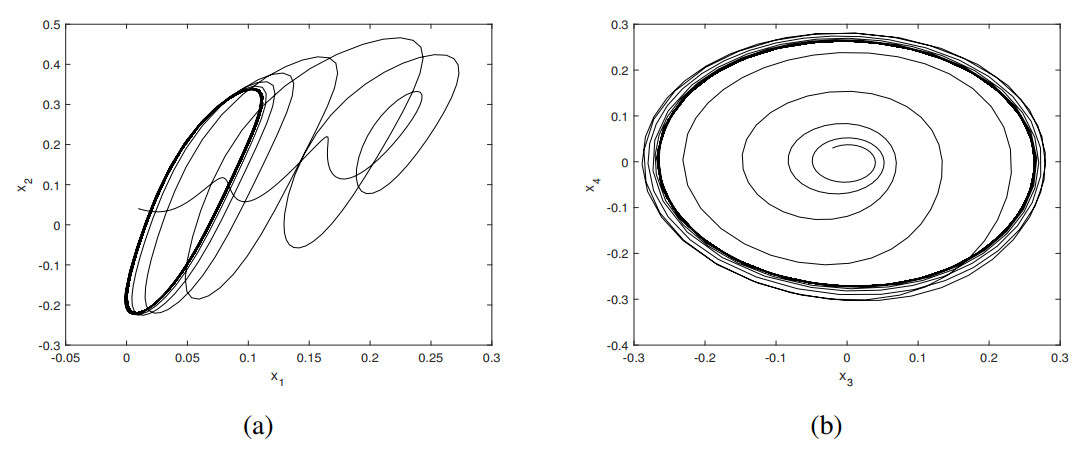
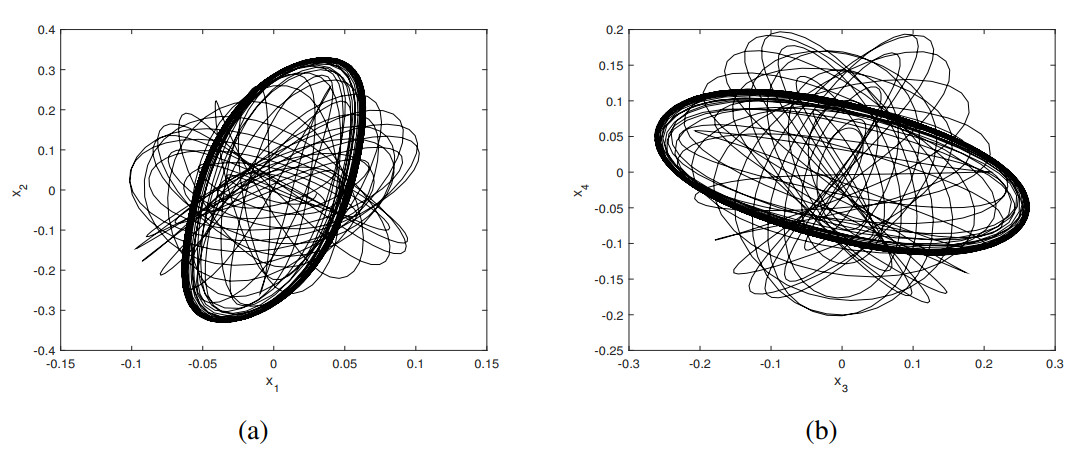
Similar to the case in Subsection 3.1, parameter values are selected from distinct regions in Figure 4 to verify the analytical results derived in this section. Choosing the parameter values $({\varsigma _1}, {\varsigma _2}) = (-0.1, -0.1)$ within the stable region of the E.S., the trajectory originating from $({x_1}, {x_2}, {x_3},$ ${x_4}) = (0.01, - 0.02, 0.03, 0.04)$ asymptotically converges to the origin, as demonstrated in Figure 5. When the parameter values are set to $({\varsigma _1}, {\varsigma _2}) = (0.1, -0.1)$ within the stable region of the S.B. solution, numerical simulation demonstrates that the trajectory originating from the initial condition $({x_1}, {x_2}, {x_3}, {x_4}) = (-0.2,$ $0.02, -0.1, 0.01)$ asymptotically converges to the S.B. solution shown in Figure 6. When selecting $({\varsigma _1}, {\varsigma _2}) = (-0.1, 0.1)$, numerical simulations reveal a stable limit cycle as demonstrated in Figure 7. The periodic trajectory associated with the H.B. solution originates from the initial condition $({x_1}, {x_2}, {x_3}, {x_4}) = (-0.02,$ $0.03, 0.02, -0.01)$. Furthermore, when employing parameter values $({\varsigma _1}, {\varsigma _2}) = (0.3, 0.1)$ within the stable region for the 2nd H.B. solution, the system generates another stable limit cycle from initial coordinates $({x_1}, {x_2}, {x_3}, {x_4}) = (0.01, 0.04, -0.02, 0.03)$, as illustrated in Figure 8. Notably, all numerical simulations show qualitative agreement with analytical predictions.

4.3.   The case of two pairs of pure imaginary eigenvalues

Similarly, for the third case described above, the parameter values can be established as

${\mu _1} = 1$, ${\mu _2} = -1$, ${\alpha _1} = {\alpha _2} = 0$, ${\beta _1} = {\beta _2} = 0$, ${k_{21}} = 2$, ${k_{31}} = 3$, ${k_{81}} = {k_{91}} = 1$, ${k_{22}} = {k_{32}} = {k_{82}} = {k_{92}} = 0$, ${a_{01}} = {a_{02}} = {a_{03}} = {a_{04}} = {a_{05}} = {a_{06}} = 1$, ${b_{01}} = {b_{02}} = {b_{03}} = {b_{04}} = {b_{05}} = {b_{06}} = 1$.

Choosing ${\mu _1}$ and ${\mu _2}$ as the perturbation parameters, applying the parameter transformation ${\mu _1} = 1+{\varsigma _1}$, ${\mu _2} = -1+{\varsigma _2}$, and taking into account the state variable transformation

Equation (3.20) becomes

where the nonlinear functions $Nf_3^i\, (i = 1, 2, 3, 4)$ are presented in the Appendix. At the critical point ${\varsigma _{1c}} = {\varsigma _{2c}} = 0$, the Jacobian matrix of Eq (4.32) evaluated with respect to the initial equilibrium solution ${z_i} = 0$ takes the following canonical form:

Applying the normal form theory, performing a near-identity nonlinear transformation ${z_i} = {y_i} + {g_i}({y_j})$, and then implementing a transformation ${y_1} = {r_1}\cos {\theta _1}$, ${y_2} = {r_1}\sin {\theta _1}$, ${y_3} = {r_2}\cos {\theta _2}$, ${y_4} = {r_2}\sin {\theta _2}$, the normal form of Eq (4.32) can be derived as follows ^[20]:

and

According to Eq (4.34), the steady state solutions can be acquired by setting ${\dot r_1} = {\dot r_2} = 0$.

The initial equilibrium solution (E.S.):

The incipient Hopf bifurcation solution (H.B.(I) with frequency ${\omega _1}$):

The secondary Hopf bifurcation solution (H.B.(II) with frequency ${\omega _2}$):

Quasi-periodic solution (2-D tori):

The Jacobian matrix of Eq (4.34) can be expressed in the following form:

which can be applied to assess the stability of the four steady state solutions mentioned above. Evaluating (4.42) on (4.36) yields the stability region of E.S. as

which gives the critical line defined by

from which a family of limit cycles emerges from the E.S. through a Hopf bifurcation, with the H.B.(II) solution being expressed as Eq (4.39).

Evaluating the Jacobian matrix (4.42) on (4.37) leads to the stability conditions

which are contradictive, which reveals that the H.B.(I) exhibits instability.

Similarly, evaluating (4.42) on (4.39) yields the stability condition as

The next task is to find the stability conditions for 2-D tori given by Eq (4.41), while the expression of the quasi-periodic solution shows that no quasi-periodic solutions exist unless ${r_1} = {r_2} = 0$.

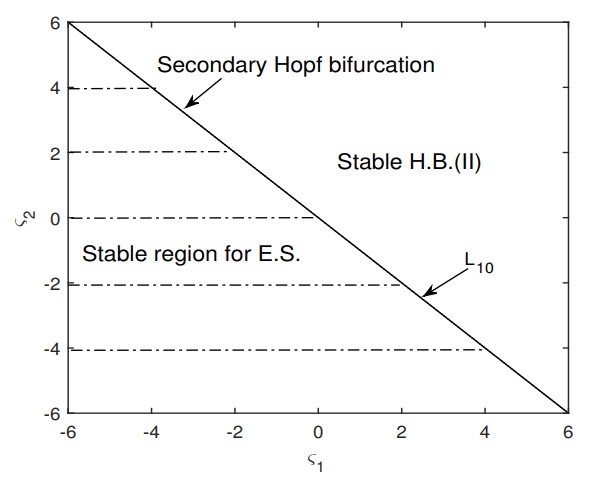
From the previous analysis, it can be concluded that when ${L_{10}}$ is intersected with the change of the parameter values, the E.S. (4.36) loses stability and undergoes a Hopf bifurcation, resulting in the emergence of stable limit cycles (H.B.(II) solution). The critical bifurcation line is illustrated in Figure 9.

In this case, the parameter values are selected from distinct regions in Figure 9 to find the numerical solutions. Choosing $({\varsigma _1}, {\varsigma _2}) = (-0.8, 0.1)$ within the stable region of the E.S., the trajectory originating from $({x_1}, {x_2}, {x_3}, {x_4}) = (-0.03, -0.02, 0.01, 0.02)$ asymptotically converges to the origin, as can be seen in Figure 10. Choosing the parameter values as $({\varsigma _1}, {\varsigma _2}) = (0.2, - 0.1)$ within the stable region of the H.B.(II) solution, the system's trajectory evolves into a stable limit cycle from initial coordinates $({x_1}, {x_2}, {x_3}, {x_4}) = (0.03, -0.01, -0.02, 0.04)$, depicted in Figure 11. It is observed that all numerical solutions exhibit excellent agreement with analytical results.

5.   Conclusions

In this paper, stability and bifurcation behaviors of an axially moving beam subjected to two frequency parametric excitations are studied. Simultaneous principal parametric resonance as well as combination parametric resonance with 3:1 internal resonance is considered. Three types of degenerated equilibrium points are discussed in detail. Based on the aforementioned research, the following conclusions are obtained:

(1) The steady state solutions are analytically derived and their stability conditions are determined as explicit expressions of the parameters ${\varsigma _1}$ and ${\varsigma _2}$, which are obtained by using the parameter transformations in three cases: (1) ${\mu _1} = - 2 + {\varsigma _1}, {\mu _2} = {\varsigma _2}$; (2) ${\mu _1} = - 1 + {\varsigma _1}$, ${\mu _2} = {\varsigma _2}$; (3) ${\mu _1} = 1 + {\varsigma _1}$, ${\mu _2} = - 1 + {\varsigma _2}$, where ${\mu _1} = - \mu {C_{1R}} - \alpha {e_{1R}}$, ${\mu _2} = - \mu {C_{2R}} - \alpha {e_{2R}}$. ${\mu}$ is a coefficient that denotes the nondimensional viscous (external) damping. $\alpha$ is another coefficient of nondimensional material (internal) damping. ${C_{iR}}$ and ${e_{iR}}$ ($i = 1, 2$) are the real parts of the nonlinear interaction coefficients $C_i$ and $e_i$. As mentioned above, the parameters ${\varsigma _1}$ and ${\varsigma _2}$ are related to ${\mu}$, $\alpha$, ${C_{iR}}$, and ${e_{iR}}$ ($i = 1, 2$), which indicates that the stability conditions and the dynamical behaviors are affected by the viscous (external) damping ${\mu}$, the material (internal) damping $\alpha$, and the nonlinear interaction coefficients ${C_{iR}}$ and ${e_{iR}}$ ($i = 1, 2$) of the system. It is further demonstrated that complex dynamical behaviors of the traveling viscoelastic beams can be controlled by modifying the parameters ${\mu}$ and $\alpha$. Therefore, the theoretical studies obtained here can help us to optimize the design of the structural parameters of accelerating beams. In addition, transition curves giving rise to static bifurcation, Hopf bifurcation, and 2-D torus bifurcation are discussed applying normal form theory, stability, and bifurcation theory.

(2) In order to confirm the analytical predictions, system (3.20) is chosen to conduct numerical simulations. The fourth-order Runge-Kutta algorithm through the software MATLAB is employed to indicate stability of the steady state solutions. It is observed that all the numerical simulations agree with the theoretical predictions. In the design of vehicles, such as spacecrafts, automobiles, and aerial cable tramways, the structural components may demonstrate a significant nonlinear behavior that requires careful consideration and precise control. The results of this study could provide critical insights for mechanical engineers specializing in the nonlinear vibration analysis of axially moving beams.

Author contributions

Fengxian An: Methodology, Software, Writing-original draft; Liangqiang Zhou: Methodology, Writing-reviewing and editing. All authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was supported by the Open Foundation of Key Laboratory of Mathematical Modelling and High Performance Computing of Air Vehicles (NUAA) (No. 202301) and the National Natural Science Foundation of China (No. 11772148).

Conflict of interest

The authors declare no conflict of interest in this paper.

Appendix

The nonlinear functions $Nf_1^i\, (i = 1, 2, 3, 4)$ in (3.20) are

The functions $h_i(\mu_1, \mu_2, \alpha_1, \alpha_2, \beta_1, \beta_2, k_{21}, k_{22}, k_{31}, k_{32}, k_{81}, k_{82}, k_{91}, k_{92})\, (i = 2, 3, 4)$ in (3.23) are

The nonlinear functions $Nf_2^i\, (i = 1, 2, 3, 4)$ in (4.7) are

The nonlinear functions $Nf_3^i\, (i = 1, 2, 3, 4)$ in (4.32) are