Soliton solutions of the nonlinear dynamics in the Boussinesq equation with bifurcation analysis and chaos

1.   Introduction

The Boussinesq equation was first presented in 1871; nonlinear wave equations have attracted a lot of interest. Numerous solutions and weak variants of these equations have been thoroughly studied by researchers, and we carry on that tradition. Researchers have concentrated on thorough analyses of higher-order models and the two-dimensional Boussinesq equation because these equations become more difficult when higher-order elements are included or when the two-dimensional Boussinesq equation is taken into account. Additionally, the Korteweg–de Vries hierarchy and non-integrable additional interactions between two solitons have been taken into consideration while examining convergence to asymptotic behavior. Together, these works show that the Boussinesq equation may be used to evaluate wave behavior and nonlinearity in a wide range of applications, such as shallow water transport and other physical systems. This equation will continue to inspire mathematical physics study because of its characteristics and importance in both theoretical and applied mathematics. Numerous application areas covered in the current study can be investigated with the help of this equation. The Boussinesq equation, broadly used in modeling long surface waves in shallow water, attains robust physical significance from basic studies in sediment transport and wave dynamics. Grass in 1981 studied sediment transport together with the effect of waves and currents, setting base for wave–current interaction models supporting Boussinesq-type models ^[1]. Moreover, Qian et al. in 2018 and Castro et al. in 2008 developed numerical techniques for sediment transport model in shallow water, which depend on similar expectations to those supporting the Boussinesq equation ^[2,3]. In 1965, De Vries examined non-steady bed-load transport in open channels, presenting important visions into unsteady flow systems where Boussinesq frameworks are useable ^[4]. Armanini in 2018 extended on river hydraulics and sediment dynamics, further supporting the requirement of higher-order shallow water formulations like the Boussinesq equation ^[5]. Mayer et al. in 1998 explored a fractional step method for unsteady free-surface flows, strengthening the usefulness of nonlinear wave models, particularly in demonstrating wave interactions and propagation ^[6]. Together, these researchers created the physical explanation for using the Boussinesq equation in modeling dispersive, nonlinear, and sediment-influenced wave phenomena in shallow environments.

In present day studies, dealing with nonlinear PDEs, various analytical methods have been applied to obtain exact soliton solutions. The bilinear method, mainly Hirota's approach, has proven useful in constructing soliton, breather, and rogue wave solutions, as observed in the work of Wang et al. and others, in which interactive behaviors in Boussinesq-type and Schrödinger type systems are discovered ^[7,8].

The Boussinesq water wave equation is widely used in many different mathematical and practical domains; hence it is essential to create and identify mathematical models for particular equation systems. These models include solutions to solitary waves, conservation laws, and Lie symmetry analysis. Several important techniques include the modified F-expansion approach ^[9], He's variational iteration method and Adomian's decomposition method ^[10], the New extended (G'/G)-expansion method ^[11], (G′/G, 1/G)-expansion method ^[12], (G'/G)-expansion method ^[13], Exp-function method ^[14], (G'/G²)-expansion method ^{[15,16,17,18]}, Novel (G'/G²)-expansion method ^[19], modified (G'/G²)-expansion method ^[20,21]. Our developed, novel modified (G'/G²)-expansion method ^[22] is a major step forward within the understanding of soliton waves for non-linear fractional differential conditions. This approach moves forward the effectiveness and quality of these examinations, opening the door for more in-depth discoveries in consequent studies.

New advances in solving nonlinear evolution equations using methods such as fractional and extended function methods have gained important visions through modeling wave dynamics in shallow water systems. Researchers have applied techniques such as Khater Method and the modified extended tanh function method to Boussinesq-type and shallow water wave equations, producing bright, dark, singular, and periodic type soliton solutions ^[23,24]. These methods increase the usefulness of the models in nonlinear physical systems like optics, particle physics, and ocean engineering.

On the other hand, many of these studies are conducted to mostly solitary wave or traveling wave solutions without discovering the qualitative behavior of the system in detail. We discriminate by using the novel (G'/G²)-expansion method to obtain new exact traveling wave solutions and by performing a detailed bifurcation and chaotic analysis of the system. Unlike other studies, we discover the multistability, periodic, quasi-periodic, and chaotic behaviors of the Boussinesq equation with phase portraits and time-series analysis. This combination of dynamical and analytical method gives new intuitions into the complex behavior of nonlinear dispersive models, which has not been widely studied in other works.

In this work, we employ novel (G'/G²)-expansion method, which was first presented by Shakeel et al. ^[19] in 2022, to obtain the exact solutions to the fourth-order nonlinear Boussinesq water wave equation. The recommended approach is special, and steady, and has advantages over other approaches to discover a compelling solution for PDE. The importance of handling of nonlinear equations is highlighted within the paper, so that it may be utilized in models with distinctive sorts of nonlinearity. When utilized with particular free parameters, the novel (G'/G²)-expansion method gives a significant range of exact traveling wave solutions. The resulting solutions are exact and can be utilized to depict both physical and visual nonlinear systems. The novel (G'/G²)-expansion method is better suited for the Boussinesq equation than other methods such as Hirota's bilinear method or inverse scattering because of its capability to deal with the complex nonlinearities of the equation. Hirota's method is typically restricted to integrable equations with soliton solutions, while inverse scattering needs integrability conditions that are not usually applicable to the Boussinesq equation. Contrary, the novel (G'/G²)-expansion method, provides exact solutions for a broader range of nonlinear wave equations and efficiently captures soliton and non-soliton behaviors. This flexibility makes it useful for practical applications where exact integrability is not attainable.

Multiple wave interactions make it significant to consider how these waves carry on in liquid elements and plasma physics. Although a few conventional equations have been created, such as the Kortewegâ-de Vries (KdV) equation, wave soundness does not bolster them ^[25]. This can be the case for the Benjamin–Bona–Mahony (BBM) equation and the regularized long-wave condition (RLWE), which are less susceptible to these issues than the KdV and give interesting characteristics for the examination of marvels like shallow water and plasma waves ^[26]. Because of its versatility, RLWE is the best model for nonlinear dispersive work. It is pivotal to understand how water carries on when it shows long, minor undulations. Our objective of this work is to solve the Boussinesq condition in a logical and successive way.

A thorough examination of liquid flow is made easier by the Boussinesq condition, which addresses issues counting shoaling, diffraction, and weak nonlinearities in shallow waters. Its usefulness goes beyond fluid dynamics and includes string vibrations, plasma sound wave propagation, and lattice wave modelling. These different applications highlight the significance of the equation in hypothetical and viable settings, which empowers continued study of its behaviors and solutions in a range of scientific and physical situations. The Boussinesq condition is composed underneath:

A classical model used in shallow-water wave analysis, the Boussinesq equation is essential for analyzing the dynamics of phenomena like wave wrinkling. In this case, u_tt measures the wave's acceleration, is the second partial derivative of u with respect to time. The wave's curvature is shown by the term u_xx, which is the second derivative with respect to space x. The second spatial partial derivative of u² scaled by β is included in the nonlinear term β(u²)_xx. Moreover, higher-order dispersion effects are taken into account by δu_xxx, the third partial derivative of u with respect to xxx scaled by δ.

Shoaling weak non-linearities, diffraction, and refraction are among the different liquid elements issues in shallow waters that can be examined with this equation. The importance of this finding amplifies beyond physics since it has applications in a number of areas, counting nonlinear string vibrations, particle sound waves in plasma, long wave engendering in intertidal zones, and one-dimensional linear cross section wave approximation. Its wide appropriateness and continuous research are illustrated in the literature ^[27,28].

This equation contains major that define various features of wave forms. Together with, it also contains δu_xxxx, a higher order dispersion phenomena which is fourth order partial derivative of u with respect to x. The second order partial derivative of u with the temporal derivative is αu_xt in which illustrates the time–space coupling in wave evolutions is a significant term. Parameter α effects the speed and shape changes of waves and indicates the temporal-spatial influence on their structures. A wave process's nonlinearity is shown by β, which describes the degree of nonlinear effects on parameters like amplitude and waveform space time deviation. Finally, δ represents higher order dispersion with respect to the wave distribution or ripple formation throughout the formation process of flow. All these concepts deliver a comprehensive framework for assessing many aspects of complex wave behavior, especially in shallow water and other related situations.

Bifurcation analysis is a crucial tool in nonlinear dynamical frameworks, enabling the investigation of subjective changes in system behavior as control parameters are changed. These changes, known as bifurcations, happen when little perturbation in system parameters lead to critical moves in system dynamics, such as the emergence of periodic, quasi-periodic, or chaotic behavior. Within the setting of our system, bifurcation investigation gives basic bits of knowledge into the move from stable to unstable directions, distinguishing the onset of complex dynamics, including chaos, multistability, and Lyapunov exponents. By analyzing the bifurcation structure, we can identify basic limits where subjective shifts happen, offering a more thoughtful understanding of the exchange between system parameters (e.g., damping, perturbation amplitude, and frequency). Such examinations are fundamental in deciding the stability and chaos of the system, as well as in recognizing parameter areas where particular dynamic states, like periodicity or chaos, prevail. Bifurcation analysis hence serves as an effective tool in revealing the rich dynamical behaviour in nonlinear systems, which is a main concern of our ^[29,30].

Our fundamental objective of this work is to investigate the dynamic behavior of the condition utilizing bifurcation and to analytically examine the water wave condition by novel (G'/G²)-expansion method. This strategy produces a wide range of solutions, comprising periodic soliton, bright solitons, hybrid solitons, and asymmetric solitons. Contrary to other studies, our solutions incorporate free parameters, which cover a more extensive range of physical phenomena. Our results are generalized by the expansion of arbitrary constants, which empowers intensive depiction utilizing two and three dimensional plots. By using this comprehensive method, we can improve our comprehension of nonlinear dynamics and offer new visions on how Eq (1.2) works in different scenarios, leading to more broad applications in fields like building, engineering, ecology, and telecommunications.

The motivation for our work is in the requirement to understand the nonlinear wave behavior in shallow water systems. The Boussinesq equation is important in studying long waves in fluids, and gathering its various dynamical features, together with solitons and chaos, is vital for applications in wave examination and ocean engineering.

We offer a comprehensive combination of analytical soliton solutions with bifurcation and chaos analysis. As the novel (G'/G²)-expansion method itself is conventional, its application to the Boussinesq equation, together with dynamical analysis, is innovative and unique.

2.   The description of novel (G'/G²)-expansion method

In this section, we discuss the algorithm of novel (G'/G²)-expansion method ^[19].

Consider the NLPDE as follows:

where $u = u\left( {x, t} \right)$ is an unknown function, N is a polynomial in $u = u\left( {x, t} \right)$ and its partial derivatives. The major steps of the proposed method are given below:

Step 1: Suppose the wave variable has the following representation $\eta = x - \omega {\kern 1pt} t$, where $\omega$ represents the speed of wave. In light of this, Eq (2.1) can be simplified to the following nonlinear ODE:

where $u = u\left( {x, t} \right){\kern 1pt} \, = U\left( \eta \right)\, .$

Step 2: Let us assume that the solution of Eq (2.2) can be expressed as a finite power series of the form $\left( {H + G'/{G^2}} \right)$:

where ${a_0}, {a_i}, {b_i}, (i = 1, ..., n),$ and H are un-known constants to be calculated later, and ${a_n}\, , {b_n}$ cannot be zero at the same time. By considering the homogeneous balance principle, which involves balancing the highest-order derivative term with the nonlinear term in Eq (2.2), we can determine the degree of the positive integer n. It is supposed that $G = G(\eta )$ satisfies the Riccati equation:

in which $A \ne 1\, , \,$ and $B \ne 0$ are arbitrary integers.

Step 3: If the degree of $U(\eta ) = {\text{Deg}}[U(\eta )] = n$, then, following formulas can be used to determine the degree of the terms listed below.

Step 4: By plugging Eqs (2.3) and (2.4) into Eq (2.2), we derive a polynomial in $\left( {H + G'/{G^2}} \right)$ By gathering the coefficients of the similar powers of ${\left( {H + G'/{G^2}} \right)^i}$, represented as $i = 0, \, \, 1, \, \, 2, \, ..., \, n,$ we can establish a set of nonlinear algebraic equations. To solve this set, we set each coefficient of ${\left( {H + G'/{G^2}} \right)^i}$ equal to zero, which yields a set of equations with unknown constants ${a_0}, {a_i}, {b_i}, k, \, {\text{and }}H.$ We can utilize a symbolic software like Maple to potentially solve this algebraic system and find the unknown constants.

Step 5: Based on the values of A and B, the solutions to Eq (2.4) are divided into three cases given below:

Case 1: If AB > 0, then Eq (2.4) has a solution in the form of trigonometric functions, which can be expressed as:

where A and B represent arbitrary integers, while P and Q denote nonzero constants.

Case 2: If AB < 0, then Eq (2.4) has the following solution:

This can also be written in the form of hyperbolic function solution as:

where P and Q are non-zero constants.

Case 3: If A = 0 and $B \ne 0$, then Eq (2.4) has the solution:

By putting the acquired values of ${a_0}, {a_i}, {b_i}, \left( {i = 1, ..., n} \right), k, \, {\text{and }}H$ and the solutions (2.6)–(2.9) into Eq (2.3) and using the transformation stated above, we can derive the precise traveling wave solution of Eq (1.2). This process allows us to determine the complete expression for the traveling wave solutions.

3.   Applications of the novel (G'/G²)-expansion method

In this section, Eq (1.2) is solved, and exact solutions are obtained using the novel (G'/G²)-expansion method. Using the transformation $\eta = k\, x - \omega {\kern 1pt} t$ into Eq (1.2), we obtain the following equation:

After twice integration, Eq (3.1) can be transformed into a nonlinear ordinary differential equation of the form:

Now by homogeneous balancing between the highest-order derivative and the nonlinear term in Eq (3.2), we get $N = 2.$ Hence, from Eq (2.3), we obtain:

Putting Eq (3.3) into Eq (3.2) along with Eq (2.4), then equating the coefficients of ${\left( {H + (G'/{G^2})} \right)^i}\, (i = 0, \pm 1, \pm 2, ...)$ to zero, we obtain a system of nonlinear algebraic equations. By solving this system with the help of Maple 18, we obtain the following solution sets.

Set 1:

By substituting the above constants in Eq (3.3), using different conditions stated in Eqs (2.6) to (2.9), we get three cases for Set 1 which are given below:

Case 1: If $AB > 0, \,$ then we get the following solution:

Case 2: If $AB < 0$, then we have the following hyperbolic solution:

Case 3: If $A = 0\, , B \ne 0\,$, then we get the following rational solution:

Set 2:

By substituting the above constants in Eq (3.3), using different conditions stated in Eqs (2.6) to (2.9), we get three cases for Set 2 which are given below:

Case 1: If $AB > 0, \,$ then we get the following solution:

Case 2: If $AB < 0$, then we have the following hyperbolic solution:

Case 3: If $A = 0\, , B \ne 0\,$, then we get the following rational solution:

Set 3:

By substituting the above constants in Eq (3.3), using different conditions stated in Eqs (2.6) to (2.9), we get three cases for Set 3 which are given below:

Case 1: If $AB > 0, \,$ then we get the following solution:

Case 2: If $AB < 0$, then we have the following hyperbolic solution:

Case 3: If $A = 0\, , B \ne 0\,$, then we get the following rational solution:

4.   Graphical representation

In this section, we explore the obtained solutions and analyze their distinct characteristics by examining the physical structure of the solutions for the governing equation. The dynamic behaviour of these solutions is demonstrated through a series of graphical representations. All the parameter sets are chosen to reflect shallow water or plasma wave models, confirming that the solution lies within a physically realistic and mathematically stable range.

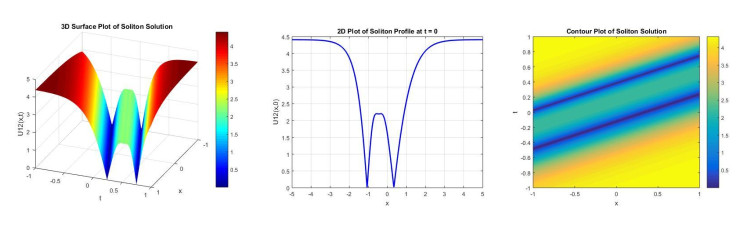
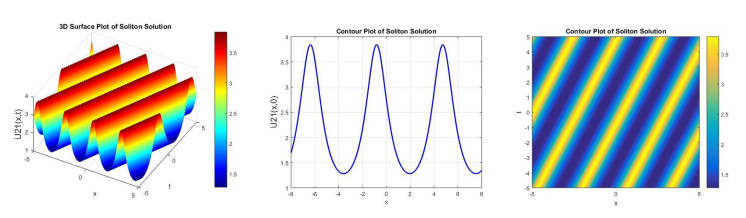
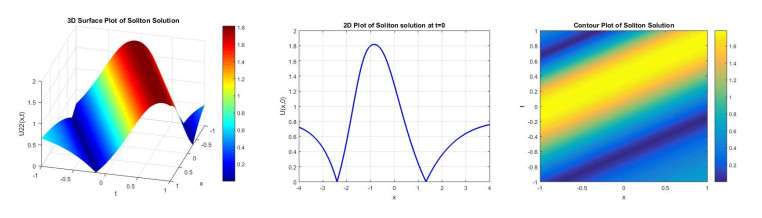
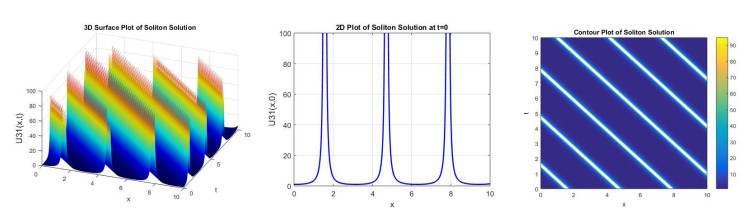
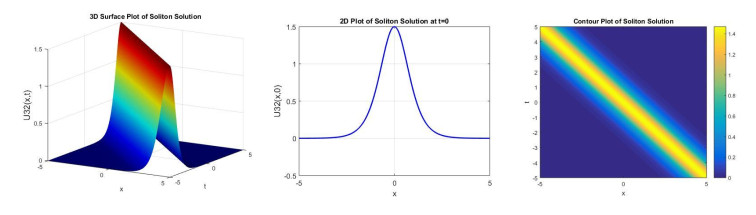
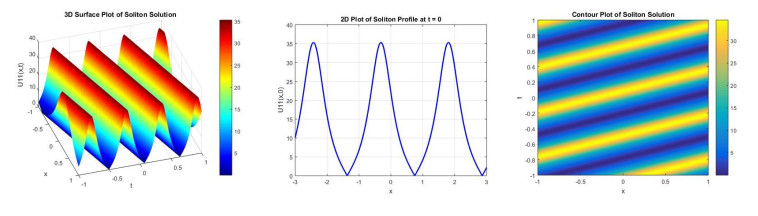
Figure 1 demonstrates the 3D, 2D, and contour plot of the soliton solution ${u_{11}}(x, t)$ obtained for the parameters k = 1.05, A = 2, B = 1, α = 1, β = 1, H = 1, δ = 1, P = 0.5, Q = 1. The 3D plot with x ∈ [−1, 1] and t ∈ [−1, 1] discloses a periodic wave-like structure propagating along the spatial temporal domain, whereas the 2D plot over x ∈ [−3, 3] displays regular oscillations, specify a cnoidal wave. The contour plot over x ∈ [−1, 1] and t ∈ [−1, 1] also confirms the space-temporal symmetry and periodic pattern. These plots indicate that the solution preserves its periodic shape during propagation, signifying a balance between nonlinearity and dispersion. Figure 2 displays 3D, 2D, and contour plots of the soliton solution u₁₂(x, t) obtained for the parameters k = 1.05, A = 1, B = −1, α = 4, β = 1, H = 1, δ = 1, P = 0.5, Q = 1. The 3D and contour plots are displayed over x ∈ [−1, 1] and t ∈ [−1, 1] whereas the 2D plot is displayed at t = 0 and x ∈ [−5, 5]. The soliton solution presented is of bright-type W shaped, characterized by a localized peak that remains stable over time. The balance between dispersion and nonlinearity governed by the chosen parameters leads to this clear wave pattern. Figure 3 shows 3D, 2D, and contour plots of the soliton solution ${u_{21}}(x, t)$ obtained for the parameters k = 0.4, A = 2, B = 1, α = 1, β = 1, δ = −1, P = 0.5, Q = 1. The 3D and contour plots are showed over x ∈ [−5, 5] and t ∈ [−5, 5], whereas the 2D plots is displayed at t = 0 and x ∈ [−8, 8]. The resulting soliton is a bright-type periodic soliton, displaying repeated localized peaks. Figure 4 demonstrates 3D, 2D, and contour plots of the soliton solution ${u_{22}}\left( {x, t} \right)$ obtained for the parameters k = 0.4, A = 2, B = −1, α = 1, β = 1, H = 1, δ = 1, P = 0.5, Q = 1. The 3D and contour plots are displayed over x ∈ [−1, 1] and t ∈ [−1, 1], whereas the 2D plots is displayed over t = 0 and x ∈ [−4, 4]. The 2D and 3D plots show single-peaked bright-type soliton, demonstrating a localized increase in amplitude that remains stable over time and space. The wave is regular and smooth, with energy localized around the center. Figure 5 displays 3D, 2D, and contour plots of the soliton solution ${u_{31}}\left( {x, t} \right)$ obtained for the parameters k = 1, A = 1, B = 1, α = 1, β = 1.5, H = 0, ω = 1, P = 0, and Q = 1. The 3D and contour plots are shown over x ∈ [0, 10] and t ∈ [0, 10], whereas the 2D plot is displayed over t = 0 and x ∈ [0, 10], showing a periodic formation of soliton peaks. The solution is of bright-type that is characterized by sharp, localized positive amplitude peaks that repeat over time. Figure 6 demonstrates 3D, 2D, and contour plots of the soliton solution ${u_{32}}\left( {x, t} \right)$ obtained for the parameters k = 1, A = 1, B = −1, α = 1, β = 1, H = 0, ω = −1, P = 1, and Q = −1. The 3D and contour plots are displayed over x, t ∈ [−5, 5], showing a sharply peaked single, localized bright soliton structure propagating along the spatial temporal domain. The 2D plot is displayed over t = 0 and x ∈ [−5, 5], disclosing a smooth, bell-shaped soliton centered at the origin.

5.   Comparison table

The comparison table shows a comparative analysis of the exact solutions constructed in our study and those formerly established by Almusawa et al. ^[31]. It shows the conditions under which both sets of solutions are obtained, representing their differences and similarities. These solutions specify that, under specific selection of parameters, the results in our work become those obtained by Almusawa et al., hence verifying the method. Furthermore, Table 1 illustrates that the choice of parameters has an impact on the solutions, supporting the applicability and flexibility of the present method in solving nonlinear PDEs.

6.   Bifurcation analysis

Bifurcation analysis looks at dynamical systems and observes how the system behaves at different parameter values, regardless of whether the parameters are dependent on one another or not. The observed second-order differential Eq (3.2) may be transformed into two first-order differential equations by applying the Galilean transformation ^[32]:

where ${F_1} = \left( {{\omega ^2} - {k^2} + \alpha \, k\, \omega } \right)/\beta \, {k^4}\, {\text{and}}\, {F_2} = - \alpha \, {k^2}/\beta \, {k^4}.$ The equilibrium points of dynamic system (6.1) are (0, 0) and $\left( { - {F_1}/{F_2}} \right)$. Once we have the fixed points, we can analyze the stability of these points by computing the Jacobian matrix of the system (6.1). It is given by:

where det (J) = ${F_1} + 2{F_2}u.$

To investigate the system's stability (6.1), we calculate the eigenvalues by solving the following equation.

This gives the eigenvalues: $\lambda = \pm \sqrt {{F_1} + 2{F_2}u} \, .$

The physical interpretation of eigenvalues, depends on the sign of (F₁+2F₂u), which is discussed below:

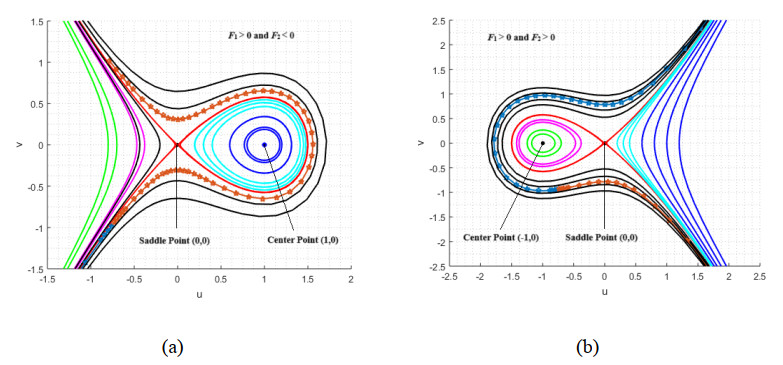
Case 1: When F₁ > 0, F₂ > 0 ⟹ F₁+2F₂u > 0, this leads to real and opposite eigenvalues. This corresponds to a saddle point, and small perturbations cause the system to diverge in at least one direction, causing an unstable equilibrium.

Case 2: When F₁ > 0, F₂ < 0. In this case, the sign of (F₁+2F₂u) decides the stability.

If (F₁+2F₂u) > 0, the eigenvalues are real and opposite, resulting to a saddle point.

If (F₁+2F₂u) < 0, the eigenvalues become pure imaginary, resulting in oscillatory behavior.

Case 3: When F₁ < 0, F₂ < 0 ⟹ (F₁+2F₂u) < 0, this leads to pure imaginary eigenvalues. This then leads to a center, i.e., small perturbations that cause periodic oscillations.

Case 4: When F₁ < 0, F₂ > 0, the sign of (F₁+2F₂u) determines the stability.

If (F₁+2F₂u) > 0, the eigenvalues are real and opposite, resulting in a saddle point.

If (F₁+2F₂u) < 0, the eigenvalues become pure imaginary, resulting in oscillatory behavior.

The Jacobian gives a linear approximation of the system near the fixed or equilibrium points and helps classify these points as saddle points or center points based on the eigenvalues. This analysis is fundamental in understanding the local stability of a dynamical system.

Phase space analysis is used in this paper to examine the qualitative behavior of the nonlinear dynamical system obtained from the Boussinesq equation. By transforming the equation into a system of first-order ODEs, the trajectories in phase space give graphical analysis of the dynamics of the system. This examination is beneficial to recognize different attractors, such as fixed points or more complex trajectories related with chaos. It also discloses the sensitivity of the system to initial conditions, which is important for intuitions of multistability and chaotic behavior. Moreover, it clarifications on the nature of oscillations, differentiating periodic, quasi-periodic, and chaotic behaviors. Thus, the phase space analysis facilitates a stronger understanding of how the system changes over time and gives a visual understanding of stability and chaos, proving it a useful tool for investigating the complex nonlinear wave models.

The two phase portraits in Figure 7(a, b) illustrate how the sign of F₂ influence the stability flow patterns of the system. In both cases, the saddle point (0, 0) displays the instability, affecting the trajectories to diverge in at least one direction. On the other hand, the location of the center point shown that oscillatory behavior changes location due to the sign of F₂. In Figure 7a, when F₂ < 0 the center lies at (1, 0), establishing bounded oscillations around the center. Moreover, in Figure 7b, when F₂ > 0 the center shifts to (-1, 0), keeping oscillatory behavior but changing the region where it lies. These portraits show that the saddle point frequently causes instability, and the sign of F₂ decides the location of the oscillatory areas.

7.   Chaotic analysis

In this section, we add an external force in the dynamical system (6.1) to make it perturbed as shown below:

where $\rho \cos \left( {\tau \, \eta } \right)$ is known as perturbation term. In your system of equations, τ represents the frequency of the external perturbation, determining how often the external force oscillates over time, while ρ is the amplitude of the perturbation, controlling the strength of the external force ^[33]. The term ρcos(τ) models this periodic forcing. A higher τ means faster oscillations, and a larger ρ means a stronger force. Together, they define the nature of the perturbation, with stronger and more frequent forces potentially driving the system toward more complex or chaotic behavior, while weaker or slower perturbations tend to produce smoother, more regular dynamics.

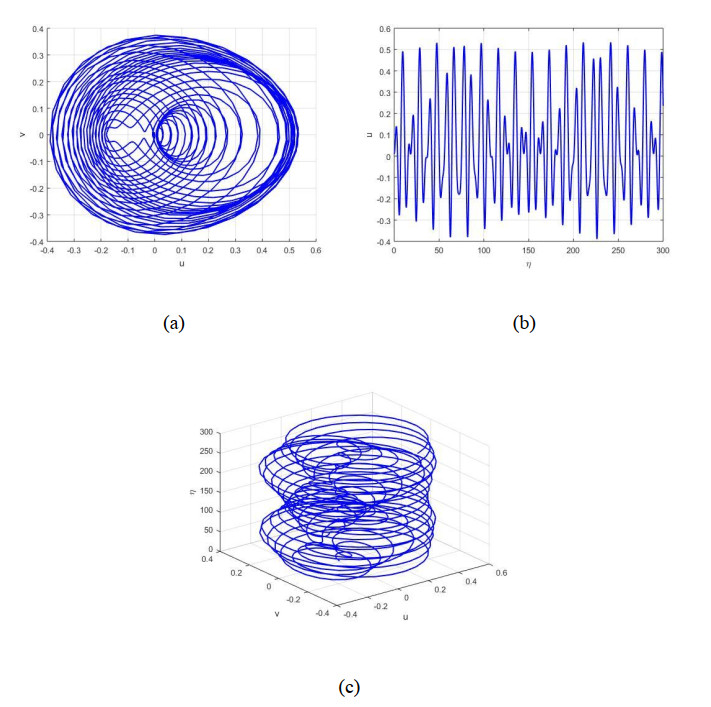
To deeply investigate the chaotic behavior of the dynamic system, we study its phase portraits and time series figures. The behavior of the system is estimated through Figures 8 and 9 with initial conditions [0.01, 0.01]. Figure 8 is displayed with the parameter sets $\rho = 0.1, \, \omega = 1, \, \alpha = - 0.5,$ and $\beta = 1$. In Figure 8a, the examination of the 2D phase portrait shows a pattern categorized by nested trajectories that do not settle into a fixed limit cycle. They form complex, intertwined loops, signifying quasi-periodicity instead of strict periodicity. Unlike chaotic attractors that show sensitivity to initial conditions, the system is not exponentially divergent to nearby trajectories but shows organized yet non-repeating arrangements. In Figure 8b, the time series plot confirms this behavior by showing oscillations with uneven frequencies and amplitudes. The absence of periodic behavior in these oscillations shows multiple irregular frequencies leading the system's motion. In Figure 8c, the 3D phase portrait illustrates a constrained, toroid type pattern with spiralling curves. This shows that the system changes in a bounded yet non-repeated way, approving the quasi-periodic nature. On the other hand, Figure 9 demonstrates the periodic motion with the parameters $\rho = 0.01, \, \omega = 1, \, \alpha = - 0.5,$ and $\beta = 1$. In Figure 9a, the 2D phase portrait shows organized, bounded trajectories, a characteristic of periodic motions. In Figure 9b, the time series plot shows regular, stable motions, confirming the presence of a single frequency governing the dynamics of the system. Furthermore, the 3D phase portrait in Figure 9c displays a regular cylindrical pattern, a symbol of periodic behavior. However, Figures 8 and 9 depict quasi-periodic and periodic behaviors, respectively. In this no obvious sign of deterministic chaos is detected. In real-world systems, weak chaos describes a condition where minor perturbations can cause major, unpredictable changes in behavior as time progresses. This sensitivity to initial conditions makes long-term forecasting challenging, particularly in systems such as economics, ecosystems, or weather, where even small variations can lead to significant effects.

To enhance the understanding of chaotic behavior and multistability in nonlinear system's dynamics, researchers have highlighted the importance of phase space analysis methods, including strange attractors, Lyapunov exponents, and fractal basin boundaries, in diagnosing complex transitions between periodic, quasi-periodic, and chaotic behaviors ^[34]. Taking motivation from these studies, we use tools, such as 2D and 3D phase portraits, multistability figures, time series analysis, and Lyapunov exponents, to deeply examine the dynamics of the system under different initial conditions and perturbation parameters. These tools enable us to detect the coexisting attractors and sensitivity to initial conditions, which are important signs of chaos detection. The observed behaviors support the phenomena reported in ^[34], hence strengthening the validity and complexity of this study, illustrating the strong dynamical behavior of the perturbed Boussinesq system.

8.   Multistability

Multistability refers to the presence of multiple stable states or behaviors that a dynamical system can exhibit under the same set of system parameters. It shows that the system can settle into different long-term behaviors depending on its initial conditions. In a multistable system, different trajectories can lead to periodic, quasi-periodic, or chaotic outcomes, even though the system's parameters remain unchanged. This phenomenon highlights how sensitive the system is to initial conditions, where small variations in starting points can result in vastly different dynamics ^[35,36].

In practical terms, multistability is important because it indicates that the system can respond to perturbations or initial differences in a variety of ways, revealing complex underlying structures like attractors. It is commonly observed in systems like biological processes, climate dynamics, and mechanical systems, where different operational modes can coexist.

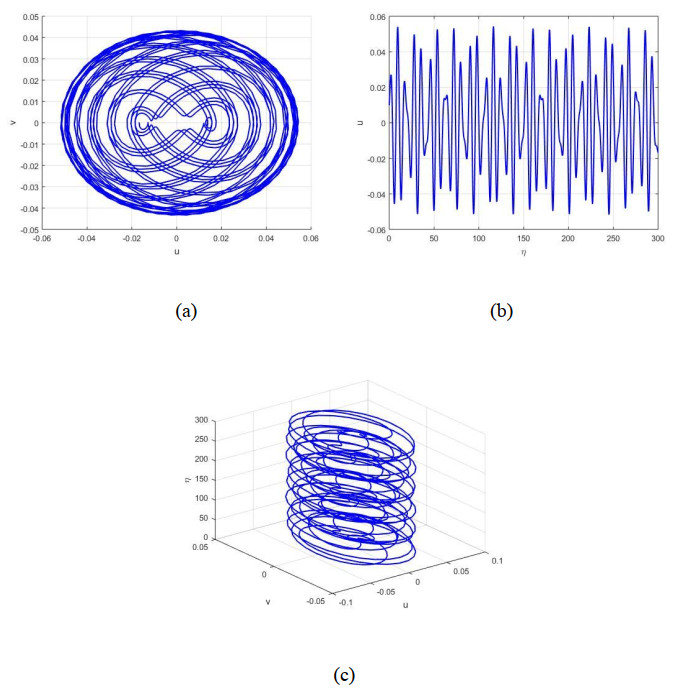
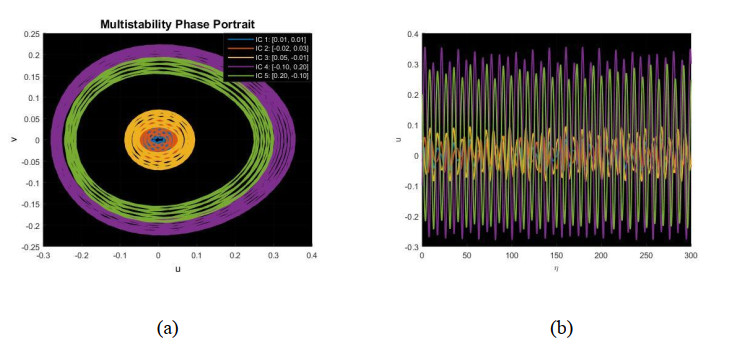
The analysis of the system's dynamics through the multistability phase portrait and time series plot in Figure 10(a, b) highlights the presence of periodic multistability, where multiple stable attractors coexist.

The multistability phase portrait and time series analysis in Figure 10 use $\rho = 0.01, \, \omega = 1, \,$ $\alpha = - 0.5, \beta = 1,$ and five distinct initial conditions: [0.01, 0.01], [-0.02, 0.03], [0.05, -0.01], [-0.10, 0.20], and [0.20, -0.10]. Each trajectory is represented with unique colours, i.e., blue, orange, yellow, green, and purple, respectively, to distinguish the states and their corresponding stable attractors in the system. Figure 10(a) uncovers well-defined and distinct trajectories, each corresponding to unique initial conditions, highlighting the sensitivity of the system to its initial conditions. The time series analysis encourages this periodic behavior, presenting stable oscillations with shifting amplitudes and phases for different initial conditions. The regular and controlled nature of these trajectories shows the absence of chaos, affirming that the system remains predictable, stable, and periodic. This multistable behavior highlights the nonlinear dynamics of the system, making it an appropriate prospect for future investigation in multistability phenomena and nonlinear stability investigation.

In practical applications, like wave control in ocean engineering, multistability plays an important character in modelling effective frameworks. The capability of the system to settle into diverse steady states depends on initial conditions that can be used to develop efficient wave energy converters, where various parameters correspond to changing environmental conditions. Moreover, coexisting attractors assist in the design of complex control techniques for moderating undesirable oscillations in marine structures, thus improving their flexibility beside external perturbations. Future research can reveal how variation in parameters affects the attractor transferring, giving strong understandings of the optimization and controllability of such systems in engineering field. The resilience of multistability to noise and parameter variations is an important feature in defining the dependability of the system. If the system keeps its attractors, even with small perturbations, it shows strong multistability, confirming periodic behavior. On the other hand, if minor changes cause a switch in the attractors, this means that the system is sensitive to noise, which can show instability.

Depending on the application, the presence of multistability can be advantageous or mitigated. In wave control and energy harvesting systems, multiple attractors support adaptation to changing conditions, enhancing system performance. On the other hand, unexpected state shifts can be problematic in control systems. In such situations, using feedback control or adjusting parameters can keep the system in a stable state, making it more reliable. Grasping these aspects can result in designed systems where the effect of multistability can be advantageous or suppressed, depending on the desired result.

9.   Lyapunov exponent

Lyapunov exponents are utilized to analyze the sensitivity of a system to its initial conditions by evaluating the rate of convergence or divergence of adjacent trajectories in phase portraits. A positive Lyapunov exponent demonstrates a chaotic conduct, where small perturbations develop exponentially over time, whereas a negative exponent recommends steadiness, stability or convergence to a fixed point or periodic trajectory. These exponents are basic for recognizing and characterizing chaos, stability, and consistency in nonlinear dynamical systems ^[37].

Figure 11 demonstrates the system's behaviors using Lyapunov exponents, which help recognize chaotic dynamics by measuring the rate of convergence or divergence between trajectories. In this case, the Lyapunov exponents (λ₁ and λ₂) are analyzed for the given parameter set: ρ = 0.01, ω = 1.0, F₁ = − 0.5, F₂ = 0.5, with an initial condition of [0.01, 0.01]. The results express that λ₁ (red) converges to a positive value 0.003, whereas λ₂ (blue) stabilizes to a negative value −0.0029. The positive λ₁ shows a divergence in the trajectories of the system, showing sensitivity to initial conditions and signifying the existence of chaotic behavior. On the other hand, the negative λ₂ reveals dispersion in another direction, demonstrating stability in the system. The approximately equal values of the two exponents, having opposite sign, propose that the system is near-conservative with weak chaos. This combination of parameters and initial conditions highlights the complex balance of stability and instability inside the system dynamics. Such results are important for understanding the long-term performance of the system beneath perturbations and variations in parameters.

10.   Conclusions

We present a comprehensive investigation of the Boussinesq equation by applying the novel (G'/G²)-expansion method, yielding various soliton solutions such as periodic solitons, bright solitons, W type, and bell shaped solitons. We identify the complex dynamical behaviors including periodic, quasi-periodic, and weak chaos, using techniques like phase portraits and time series analysis. Bifurcation analysis shows a variation in the dynamics of the system as F₂ varies. It shows that the center point shifts from (1, 0) to (−1, 0) when F₂ changes sign, while the saddle point remains unstable. This indicates a shift in oscillatory behavior and stability structure due to bifurcation. Chaos analysis, together with 2D phase portraits and time series plots, confirms the quasi-periodic nature of the system, where trajectories show non-repeating, bounded structures. The multistability analysis exhibits the coexistence of different stable attractors, highlighting the nonlinear stability of the system and its reliance on initial conditions. Finally, the Lyapunov exponents assess the stability and chaotic behavior of the system, with positive and negative exponents demonstrating weak chaos and directional stability, respectively. Our results hold notable significance for different areas of applied mathematics and nonlinear science. The study of solitonic solutions contributes to understanding wave propagation in optics, plasma physics, and fluid dynamics, where localization and transport of energy are a matter of interest. This research serves as a benchmark for future investigation of higher-order soliton solutions, multi-dimensional chaotic attractors, and their stability under perturbations. By continuing the understanding of solidness, stability, chaos, and multistability in nonlinear systems, this study sets the foundation for practical applications and encourages research in related scientific fields. However, we focus on a specific parameter range without considering environmental noise. To further advance the research, researchers should examine how these phenomena behave under random fluctuations and uncertainties and expand the research to include more realistic boundary conditions and control strategies. This will enable the practical use of these findings in ocean engineering, including wave energy harvesting and coastal structure design.

Author contributions

Muhammad Shakeel: Writing – original draft, Conceptualization. Amna Mumtaz: Software, Resources. Abdul Manan: Methodology, Investigation, Formal analysis. Marouan Kouki: Visualization, Validation, Resources. Nehad Ali Shah: Writing – review & editing, Validation. All authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA for funding this research work through the project number "NBU-FPEJ-2025-2570-04".

Conflict of interest

The authors declare that they have no conflicts of interest.