1.
Introduction
Mathematical realms have seen some fascinating research in the exploration of new spaces and their applications. Based on this advancement, the concept of b-metric space is currently gaining a lot of attention. The foundation of b-metric spaces was initially laid by Czerwik [1], whose work established a more flexible alternative to the traditional triangle inequality. This framework has since enabled significant advancements within b-metric spaces, such as hybrid contractions, which have been applied in both linear and nonlinear contexts and examined by Karapinar and Fulga [2].
There is a lot of ambiguity, imprecision, and uncertainty in the real world. The concepts we encounter in daily life are more ambiguous than specific. Due to the fact that many real-world issues in disciplines including biology, economics, engineering, environmental sciences, and medicine require data with a variety of uncertainties, researchers have recently showed a strong interest in modeling vagueness. Due to the existence of several types of imperfect information, one cannot effectively use standard mathematical methods to manage the complexity of vagueness. There are four theories for handling faulty knowledge in the previous literature. Among these theories, probability theory, fuzzy set theory, and rough set theory were the three that were used the most. A few settings must be pre-assigned for each of the aforementioned tools. When these pre-specifications are considered against the background of insufficient knowledge, everyday issues arise. Molodtsov [3] developed the idea of soft set theory in response to this worry, attempting to address concepts and phenomena related to vague, ambiguous, and imprecise contexts. A soft set allows for approximative descriptions of things instead of requiring pre-specified parameters. Molodtsov [3] underlined the relationship between the fuzzy set and soft set models. Yang et al. [4] noted that in order to broaden the application of soft set theory to new domains, it needs to be developed in several ways. Many researchers have now improved upon the idea of soft sets. Maji et al. [5] introduced the concept of fuzzy soft sets and explored its numerous characteristics by fusing the concepts of soft sets and fuzzy sets. The reader may review [6] and a few citations therein for related advances in fuzzy soft sets. The idea of soft set-valued maps was recently researched by Mohammad and Azam [6,7,8], who also presented the concepts of e-soft fixed points and E-soft fixed points of maps whose range set is a family of soft sets. Every fuzzy mapping is a specific type of soft set-valued map, as demonstrated in [7]. The idea of soft fixed point theorems is an extension of fuzzy fixed points and fixed points of crisp set-valued mappings since every fuzzy mapping has a matching multifunction analogue [9].
Our study builds upon these principles, advancing hybrid contractions by incorporating £-fuzzy soft set mappings. These mappings provide enhanced fixed point frameworks applicable to real-world problems, offering a robust model for managing complex, uncertain data. Recent advancements in cognitive processes increasingly highlight sophisticated models like generalized fuzzy soft sets for complex evaluation scenarios. A comprehensive study was conducted on generalized fuzzy soft sets, demonstrating their applications in cognitive processes and illustrating their advantages over traditional fuzzy sets. Fixed point theorems in b-metric spaces with intuitionistic fuzzy parameters have been explored, laying the groundwork for foundational applications relevant to differential and integral inclusions. In this context, hesitant fuzzy soft sets have been applied in multi-attribute decision-making, offering a comparative perspective that supports the approach using £-fuzzy soft sets. Previous studies have demonstrated the advantages of lattice-valued fuzzy soft sets under uncertainty. Building on these concepts, this approach incorporates lattice structures within £-fuzzy soft sets to further improve their applicability. This lattice-based membership structure enables multi-level evaluation and prioritization essential for nuanced data handling in complex decision-making scenarios, such as project management. This concept has proven beneficial in settings like project or operations management, where hierarchical relationships among attributes allow for effective prioritization of decision criteria. Research on fractional differential equations with fuzzy solutions provides a foundation for this approach, reinforcing its significance in addressing fractional inclusion issues.
In practical applications, £-fuzzy soft set models employ lattice-based memberships rather than traditional binary or real values to create a nuanced decision framework. This model assigns each attribute a lattice value, providing a hierarchical structure essential in cognitive processes where criteria such as budget compatibility, quality expectations, or expertise need to be evaluated across multiple importance levels. By using operators like join (supremum) and meet (infimum), the £-fuzzy soft set framework derives comprehensive scores that enable informed decisions. Applying fuzzy soft fixed points in engineering has proven effective, emphasizing the usefulness of fixed-point frameworks in practical scenarios, which this methodology builds upon. Hybrid models incorporating fuzzy and soft set theories further reinforce the cognitive framework within £-fuzzy soft sets, particularly in decision-making applications. The combination of fuzzy soft set theory with decision rules, such as selecting an alternative based on the highest join value, maximizes satisfaction across criteria, a benefit essential for applications in scenarios requiring structured, multi-level analysis. The £-fuzzy soft set model is thus positioned as a refined approach to managing data ambiguity and uncertainty, setting it apart from traditional models and underscoring its applicability in multi-criteria evaluations for complex project and operational management scenarios.
2.
Preliminaries
We collect the specific b-metric space foundation in the following section. We utilize throughout this manuscript R+ = J+.
Definition 1. [1] Assume a set Υ that is not empty and ϱ≥1 is a constant. Consider the following conditions to be met by the mapping d:Υ×Υ→J+ for each ζ,η,θ∈Υ:
(1) d(ζ,η)=0 iff ζ=η;
(2) d(ζ,η)=d(η,ζ);
(3) d(ζ,θ)≤ϱ[d(ζ,η)+d(η,θ)] for all ζ,η,θ∈Υ.
Then the triplet (Υ,d,ϱ) is called a b-metric space.
Example 1. Let Υ=N and define d:Υ×Υ→Υ by
where φ>0 is a constant. Then (Υ,d) is a b-metric space with coefficient ϱ=5>1. But (Υ,d) is not a triangular metric space as d(1,3)=6φ>2φ=d(1,5)+d(5,3).
Remark 1.
(1) All metrics have the parameter ϱ=1 and are defined as b-metrics.
(2) A b-metric is typically not continuous.
Definition 2. [10] Let (Υ,d,ϱ) represents a b-metric space.
(1) A sequence {ϑϕ}ϕ∈N is convergent if and only if we can find ϑ∈Y for which d(ϑn,ϑ)→0 as n→∞, and we write this as limn→∞d(ϑn,ϑ)=0.
(2) A sequence {ϑϕ}ϕ∈N is Cauchy Sequence if and only if d(ϑn,ϑm)→0 as n,m→∞.
(3) A b-metric space (Υ,d,ϱ) is complete if all Cauchy sequences are convergent in Υ.
Definition 3. [10] We will consider (Υ,d,ϱ) to be a b-metric space. Then, a subset Λ of Υ is called:
(1) Compact if and only if, for every sequence of elements of Λ, we can find a subsequence that converges to an element of Λ.
(2) Closed if and only if, for every sequence {ϑn}n∈N of elements of Λ that converges to an element ϑ, we have ϑ∈Υ.
Definition 4. [11] A non-empty subset Λ of Υ is called proximal if, for each y∈Υ, we can find a∈Λ for which d(y,a)=d(y,Λ).
Definition 5. [2,12] A function ∇:J+→J+ that does not decrease is said to be:
(1) a c-comparison function if ∇ϕ(ρ)→0 as ϕ→∞ for every ρ∈J+;
(2) a b-comparison function if it is possible to find q0∈N, λ∈(0,1), and a series ∑∞ϕ=1ϑϕ that is convergent but non-negative, for which ϱq+1∇q+1(ρ)≤λϱq∇q(ρ)+ϑq, for ϱ≥1, q≥q0, and any ρ≥0, where ∇ is iterated ϕ times denoted by ∇ϕ.
Shown by Π, the group of functions ∇:J+→J+ meet the requirements listed below:
(1) ∇ is a b-comparison function;
(2) ∇(ρ)=0 only if ρ=0;
(3) ∇ is not discontinuous.
Remark 2. [2] A b-comparison function is a c-comparison function when ϱ=1.
Lemma 1. [12] For a b-comparison function ∇:J+→J+, the following characteristics hold true:
(1) Every time you repeat ∇ϕ, ϕ∈N is also a b-comparison function;
(2) ∇(ρ)<ρ for every ρ>0.
Lemma 2. [12] Assuming that ∇:J+→J+ represents a b-comparison function, then each ρ∈J+ leads to the convergence of series ∑∞q=0ϱq∇q(ρ).
Remark 3. [2] As each b-comparison function is considered a comparison function in Lemma 2, they also satisfy ∇(ρ)<ρ in Lemma 1.
2.1. Fuzzy set
Definition 6. Let Υ be an initial universe. Recall that an ordinary subset ϝ of Υ is determined by its characteristics function χϝ, defined by χϝ:Υ→{0,1}, where:
This function indicates whether or not an element belongs to ϝ. By extending this idea, a fuzzy set allows elements y∈Υ to have membership degree μϝ(y) in the interval [0,1]. Thus, a fuzzy set ϝ in Υ is represented as a set of ordered pairs:
where μϝ:Υ→[0,1] is called the membership function, denoting the degree to which y belongs to the fuzzy set ϝ.
For a fuzzy set ϝ in Υ, the α-level set (also known as α-cut) for any α∈(0,1] is the set:
which includes elements belonging to ϝ to at least the degree α. Similarly, the strong α-level set or strong α-cut is defined as:
Let IΥ represents the family of all fuzzy sets in Υ. A mapping V:Υ→IΥ is termed as a fuzzy mapping, and an element u∈Υ is a fuzzy fixed point of V if there exists an α∈(0,1] such that u∈Υ.
The precise foundations for soft sets and fuzzy soft sets are compiled hereafter. Thus, let Υ represent the discourse universe and Ξ represent the set of parameters Λ⊆Ξ and the power collection Υ is expressed via P(Υ).
2.2. Soft set
Let Λ be a set of parameters, Λ⊆Ξ, and P(Υ) represent the powerset of the universe Υ. Molodtsov introduced the concept of soft sets with the following definition:
Definition 7. [3] A pair (V,Λ) is called a soft set over Υ with respect to Ξ, where Λ⊆Ξ and V is a mapping V:Λ→P(Υ). In this context, a soft set represents a collection of subsets of Υ, each corresponding to a parameter in Ξ. For example, if Ξ represents various traits or characteristics, then for each ϵ∈Ξ, V(ϵ) might represent the set of elements in Υ that approximately satisfy trait ϵ.
Example 2. Suppose Υ is the set of all books in a library, and Ξ = {fiction, non-fiction, science, art} represents categories of books. Define a soft set (V,Ξ) where:
● V(fiction) = {y1,y2,y3}, meaning books y1,y2,y3 are classified as fiction;
● V(non-fiction) = {y4,y5}, indicating books y4,y5 as non-fiction;
● V(science) = {y2,y6}, meaning books y1,y2,y3 are related to science;
● V(art) = {y3}, representing that y3 is related to art.
Under Ξ, the set of all soft sets over Υ is denoted by [P(Υ)]Ξ.
Definition 8. [7] There is a type of mapping V:Υ→[P(Υ)]Ξ] called a soft set-valued mapping. The term "ϖ-soft fixed point" of V refers to a point β∈Υ if β∈(Vβ)(ϖ), for few ϖ∈Ξ. Alternatively, this can be written as β∈Vβ, as a quick recap. If DomVβ=Ξ and β∈(Vβ)(ϖ) for each ϖ∈Ξ, then β is referred to as a Ξ-soft fixed point of V. The interval I=[0,1] and IΥ refer to the family of fuzzy sets in Υ.
2.3. Fuzzy soft set
Fuzzy soft sets were introduced to handle situations where elements may belong to sets to varying degrees. Maji et al. defined a fuzzy soft set as follows:
Definition 9. [5] A pair (V,Ξ) is called a fuzzy soft set over Υ if Λ⊆Ξ and V:Λ→IΥ. In a fuzzy soft set, each parameter ϵ∈Λ maps to a fuzzy soft subset of Υ, allowing partial memberships.
Example 3. Following the library scenario, suppose we want to measure the extent to which each book belongs to different genres. Then, a fuzzy soft set (V,Λ) might be:
● V(fiction) = {y1/0.9,y2/0.7,y3/0.5} where y1 has a 0.9 degree of membership in the "fiction" category
● V(non-fiction) = {y4/0.8,y5/0.9}
● V(science) = {y2/0.6,y6/0.7}
● V(art) = {y3/0.4}.
Definition 10. [5] Fuzzy soft set-valued maps refer to the mapping V:Υ→I(Ξ;Υ).
Definition 11. [8] Take V:Υ→I(Ξ;Υ) as a map that has a fuzzy soft set value, w∈Υ, ϖ∈DomV, and α∈(0,1]. Afterwards, we have V's α-level set as follows:
Keep in mind that for w∈Υ, Vw∈I(Ξ;Υ), that is, Vw:Ξ→IΥ. This means that (Vw)(ϖ)=V(w;ϖ)∈IΥ. Accordingly, V(w;ϖ):Υ→I, and hence V(w;ϖ)(y)∈I. So for α∈I, [V(w;ϖ)]α is well-provided.
Definition 12. A point w is called a fuzzy soft fixed point of V:Υ→I(Ξ;Υ) if we can find ϖ∈Ξ, α∈(0,1] for which w∈[V(w;ϖ)]α. The point w is said to be a common fuzzy soft fixed point of U,V:Υ→I(Ξ;Υ) if w∈[U(w;ϖ)]α⋂[V(w;ϖ)]α.
Definition 13. A partially ordered set (£,≼£) is referred to as
(1) a lattice, if ζ∨η∈£, ζ∧η∈£ for any ζ,η∈£;
(2) a complete lattice, if ∨Λ∈£, ∧Λ∈£ for any Λ⊆£;
(3) distributive, if ζ∨(η∧θ)=(ζ∨η)∧(ζ∨θ), ζ∧(η∨θ)=(ζ∧η)∨(ζ∧θ) for any ζ,η,θ∈£.
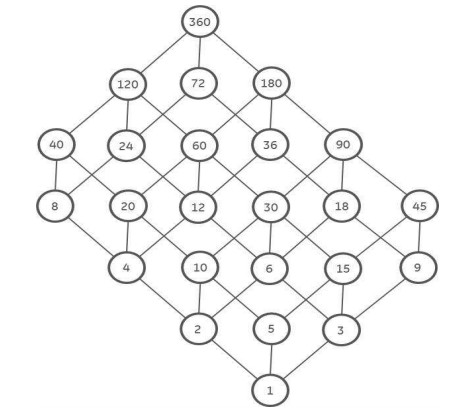
Example 4. Consider the set (N,≼) of integers without negatives, partially ordered by division, that is, ϖ≼ρ if ϖ divides ρ. Let the join and meet for any ϖ,ρ∈N be defined as:
Then (N,≼) is a lattice. Moreover, this is a complete distributive lattice with 0 and 1 as bottom and top elements, respectively. The accompanying outline portrays a limited sublattice having whole number divisors of 360 in Figure 1.
Definition 14. A £-fuzzy set Λ on a not-empty set Υ is a function Λ:Υ→£ with £ being a complete distributive lattice with 1£ and 0£.
Definition 15. We can consider any set Θ as arbitrary and Υ is a metric space. A mapping T is called a £-fuzzy mapping if V:Θ→F£(Υ). A £-fuzzy mapping V is a £-fuzzy set on Θ×Υ with membership function V(x)(y). V(x)(y) depicts the grade of membership of y in V(x).
Definition 16. Assuming that (Υ,d) represents a b-metric space and V:Υ→F£(Υ) is a £-fuzzy mapping, a point z∈Υ is the α£-fuzzy fixed point of V if z∈[Vz]α£ for few α£∈£∖{0£}.
Remark 4. The class of £-fuzzy sets exceeds the class of fuzzy sets since a £-fuzzy set is a fuzzy set if £=[0,1].
2.4. £-Fuzzy soft set
Over Υ under Ξ, £(Ξ;Υ) symbolizes a family of £-fuzzy soft sets. By Λ∈£(Ξ;Υ) we mean the mapping Λ:Ξ→£Υ.
Definition 17. (V,Λ) is a pair of £-fuzzy soft sets over Υ, where Λ⊆Ξ and V:Λ→£Υ represents a mapping.
Definition 18. An α£-level set for £-fuzzy set Λ is denoted by Λα£ and is given as follows:
We mean £Υ as a family of £-fuzzy soft sets within Υ.
Example 5. Suppose a £-fuzzy soft set (V,Ξ) which indicates the attractiveness of a collection of shirts in relation to the parameters given by the wearer.
The set Υ={z1,z2,z3,z4,z5} is the best of all the shirts considered. £={ζ,η,θ,ϑ} is a set of complete distributive lattices with ζ≤£η≤£ϑ and ζ≤£θ≤£ϑ, where η and θ cannot be compared.
Interpretation of £: ζ = neutral for both, η = attractive for girl, θ = attractive for boy, and ϑ = best for both.
£Υ is a collection of all £-fuzzy subsets of Υ. Also, let Ξ={ϖ1="colorful",ϖ2="bright",ϖ3="cheap",ϖ4="warm"}, and let £-fuzzy subsets of Υ for each parameter; V(ϖ1)={z1ζ,z2η,z3ϑ,z4ζ,z5θ}, V(ϖ2)={z1η,z2θ,z3ζ,z4η,z5ϑ}, V(ϖ3)={z1θ,z2ϑ,z3η,z4ζ,z5θ}, V(ϖ4)={z1ϑ,z2θ,z3η,z4θ,z5ϑ}.
The family {V(ϖi,i=1,2,3,4} of £Υ is a £-fuzzy soft set (V,Ξ) as shown in Table 1:
For each parameter ˘u∈Ξ, we can generate alpha cuts for each element in the £-fuzzy soft set as: Consider the parameter ϖ1 = colorful:
Apply the definition of the £-fuzzy soft set V:Λ→£Υ, and we have V(ϖ1)∈£Υ V(ϖ1):Υ→£ V(ϖ1)(z)∈£, which can be written as V(z,ϖ1). So, [V(z,ϖ1)ζ={z∈V:V(z,ϖ1)≤ζ}, which gives [V(z;ϖ1)]ζ = {z1,z4}.
Similarly, by using the same definition, we will get all other alpha cut sets for all parameters as follows:
ϖ2: bright
ϖ3: cheap
ϖ4: warm
Since η and θ are not comparable, we cannot combine alpha cuts for η and θ. These alpha cuts provide a way to analyze the £-fuzzy soft set (V,Ξ) at different levels of granularity.
Task: Choose a shirt for a girl that is cheap but not colorful. From V(ϖ3) and [V(ϖ1), we see that:
● z4 is cheap ζ.
● z5 is not colorful ζ.
Considering the requirements, z4 is the best choice.
Task: Choose a shirt for a boy that is colorful and warm. From V(ϖ1) and [V(ϖ4), we see that:
● z5 is somewhat colorful θ for a boy.
● z5 is warm ϑ for both.
Considering the requirements, z5 is the best choice.
Definition 19. A set-valued map V:Υ→£(Ξ;Υ) is known as a £-fuzzy soft set.
Definition 20. A point w is called a £-fuzzy soft fixed point of V:Υ→£(Ξ;Υ), if we can find ϖ∈Ξ, α£∈£∖{0£} for which w∈[V(w;ϖ)]α£. The point w is referred to as a common £-fuzzy soft fixed point of U,V:Υ→£(Ξ;Y) if w∈[U(w;ϖ)]α£⋂[V(w;ϖ)]α£.
For each y∈Υ, an array of all proximal and proximal bounded subsets of Υ under Ξ are referred to as cPα£(y;ϖ) and cPα£(y;ϖ)b, respectively.
3.
Common £-fuzzy soft fixed points of £-fuzzy soft set-valued maps
In this section, we will discuss the idea of a common £-fuzzy soft fixed point of £-fuzzy soft set-valued maps, which is inspired by the idea of a common fuzzy soft fixed point of fuzzy soft set-valued maps.
Definition 21. Let (Υ,d,ϱ) be a b-metric space and U,V:Υ→£(Ξ;Υ) be £-fuzzy soft set-valued maps. Then, (U,V) forms a BCLFSC, if for all y,ω∈Υ and ϖ∈Ξ, there exist α£(y;ϖ),α£(ω,ϖ)∈£∖{0£}, such that
where
Definition 22. Let (Υ,d,ϱ) be a b-metric space and U,V:Υ→£(Ξ;Υ) be £-fuzzy soft set-valued maps. Then pair (U,V) is referred to as Hausdorff continuous ({H}-continuous) at u∈Υ, if for any sequence {yn}n∈N in Υ,
implies that
and
where ϖ∈Ξ and α£∈£∖{0£}.
We discuss our main finding as follows:
Theorem 1. Let (Υ,d,ϱ) be a complete b-metric space and U,V:Y→£(Ξ;Υ) be £-fuzzy soft set-valued maps. For ϖ∈Ξ, suppose that
(1) for each y∈Υ, we can find α£(y;ϖ)∈£∖{0£}, such that [U(y;ϖ)]α£(y;ϖ) and [V(y;ϖ)]α£(y;ϖ) are in cPα£(ω,ϖ)b(Υ).
(2) (U,V) is a b-Ciric £-fuzzy soft contraction.
(3) U and V are Hausdorff continuous.
Then, U and V have a common £-fuzzy soft fixed point in Υ.
Proof. Consider y0∈Υ, then, by assumptions, we can find α£(y0;ϖ)∈£∖{0£}, such that [U(y0;ϖ)]α£(y0;ϖ)∈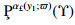 . As ϖ is made fixed, we may write α£(y0) instead of α£(y0;ϖ). Choose y1∈[U(y0;ϖ)]α£(y0), such that d(y0,y1)=d(y0,[U(y0;ϖ)]α£(y0)). Similarly, we can find α£(y1)∈£∖{0£}, such that [V(y1;ϖ)]αL(y1)∈
. As ϖ is made fixed, we may write α£(y0) instead of α£(y0;ϖ). Choose y1∈[U(y0;ϖ)]α£(y0), such that d(y0,y1)=d(y0,[U(y0;ϖ)]α£(y0)). Similarly, we can find α£(y1)∈£∖{0£}, such that [V(y1;ϖ)]αL(y1)∈ . So, we can find y2∈[V(y1;ϖ)]α£(y1), such that
. So, we can find y2∈[V(y1;ϖ)]α£(y1), such that
Continuing in this fashion, we can find a sequence {yn}n∈N of elements of Υ such that
and
By the above relations and the proximality of [U(y2r;e)]α£(y2r) and [V(y2r−1;ϖ)]α£(y2r−1), we have
Assume that y2r=y2r+1, for some p∈N and k>0. Now suppose that y2r+1≠y2r+2. Then,
It gives
Hence, using the continuity of ∇ and the proximality of [U(y2r;ϖ)]α£(y2r) and [V(y2r+1;ϖ)]α£(y2r+1), we obtain
It implies that
which is impossible.
It follows that d(y2r+1,y2r+2)=0. Therefore,
and
So, y2r turns out to be a common £-fuzzy soft fixed point of U and V.
Case Ⅰ. Suppose that d(y2r,y2r+1)≥d(y2r−1,y2r). From (3.6):
(ⅰ) If the maximum is d(y2r−1,y2r) then from (3.1) and (3.6),
Since ∇ is a b-comparison function, then (3.8) implies that
which results in impossibility (a contradiction).
(ⅱ) If maximum = d(y2r−1,y2r+1)2ϱ, again, from (3.1) and (3.6), we have
Since ∇ is a b-comparison function, we get
which is impossible. It follows that
Setting n=2r∈N in (3.6), we have
From (3.1), we have
Now let m,n∈N with m>n:
Applying the limit as n→∞ on both sides, we get d(yn,ym)→0 indicating that {yn}n∈N is a Cauchy sequence in Υ.
As Υ is complete, we can get a point u∈Υ such that
Now, by using the triangular inequality in Υ, we have
Using the Hausdorff continuity of the (U,V) pair, by applying the limit as n→∞ in (3.12) and considering (3.11), we attain
which implies that
Correspondingly, we can prove that
which means that u∈[V(u;ϖ)]α£(u).
Thus, we have
that is, u is a common £-fuzzy soft fixed point of U and V. □
Example 6. Let Υ=[0,∞) and d:Υ×Υ→J+ is given as d(x,y)= ∣x−y∣2=(x−y)2 where k=2 and then (Υ,d,k=2) is a complete b-metric space. Moreover, let £={θ,ϕ,η,ζ} with θ≤£ϕ≤£ζ, θ≤£η≤£ζ where ϕ and η are not comparable. Then (£,≤£) is a complete distributive lattice.
For each ϖ∈Ξ and y,w∈Υ consider the £-fuzzy soft set-valued maps
which are defined as the following, if y =w=1:
If y≠1,w≠1:
Let α£=ζ and then
Case Ⅰ. If y=w=1:
Thus (3.1) becomes
Since ∇ is a b-comparison function, therefore, (3.13) implies
Case Ⅱ. If y = 2, w = 3:
Thus (3.1) becomes
Since ∇ is a b-comparison function, therefore, (3.14) gives us
Moreover, it is clear that the pair (U, V) is H-continuous and [U(y;ϖ)]α£(y), [V(y;ϖ)]α£(y) are proximal for each y∈Υ.
As the conditions mentioned in Theorem 1 are fulfilled, we see that U and V have a common £-fuzzy soft fixed point.
4.
Solvability of fractional integral inclusions via £-fuzzy soft set-valued maps
Motivation:
● Dhage [13] investigated the existence and uniqueness of solutions to nonlinear integral equations using fixed-point methods.
● Baleanu et al.[14] investigated the existence and uniqueness of fractional integral equation solutions using fixed-point results.
● Shahid et al.[15] used fixed point theory to establish the existence results for the non-linear fractional differential inclusion under certain conditions.
These prior experiments show that employing integral equations and inclusions, as well as fixed-point results, can be used to derive integral equation solutions in terms of fixed or shared fixed points.
In this section, the existence theorem of the solution for the following two types of fractional integral (Riemann-Liouville and Atangana-Baleanu integral) inclusion systems [16] is proved using the obtained results for a common fixed point of £-fuzzy soft set-valued maps.
Consider the following fractional Riemann-Liouville integral inclusion system:
where x,y,U,V∈C([a,b],R), T,S,Q,R∈C([a,b]×R,R), [a,b]⊆R+, Q and R are bounded and
is a fractional integral of function τ∈C([a,b]×R,R) and of order k∈R+. By a common solution of (4.1), we mean a continuous function y(t) such that
where T,S,Q,R∈C([a,b]×R,R).
Theorem 2. Suppose that for every t∈[a,b], ϱ≥1, and y,ω∈Υ, the following inequality holds:
Then, the Riemann-Liouville fractional integral inclusion (4.1) possesses a solution in C[a,b].
Proof. Let Υ=C[a,b] and define d:Υ×Υ→R+ by d(x,y)=|x(t)−y(t)| for all x,y∈Υ. Then (Υ,d) is a complete b-metric space. Now, let £={θ,ϕ,η,ζ} with θ≤£ϕ≤£ζ and θ≤£η≤£ζ where ϕ,η are not comparable. Then (£,≤£) is a complete distributive lattice. Assume that U,V:Υ→(0,1] are two arbitrary mappings.
Now, let α£=ζ and define a pair of £-fuzzy soft set-valued mappings A,B:Υ→£(Ξ;Υ) as follows:
such that
and
Now, for ℘(t)∈[A(y;ϖ)]α£(y),
Also, for some ℑ(t)∈[B(ω;ϖ)]α£(ω), we have
For ℘(t)∈[A(y;ϖ)]α£(y) and ℑ(t)∈[B(ω;ϖ)]α£(ω),
Hence, by Theorem 1, there exists a common £-fuzzy soft fixed point of mappings A and B. □
The major goal of this calculation is to find a common fixed point for the fractional integral inclusion. This shared fixed point is a solution to the inclusion, which is a generalization of classical integral equations.
By applying Theorem 1, we have obtained:
(1) A rigorous mathematical framework for investigating fractional integral inclusions;
(2) The existence and uniqueness of the answer to the inclusion;
(3) That the solution demonstrates stability and robustness;
(4) An application of classical integral equation results to fractional integral inclusions.
5.
Advantages and disadvantages of b-metric space with BCLFSC
In this study, we used the b-metric space framework with a BCLFSC, specifically aiming to address complex decision-making scenarios that involve both uncertain and multi-level data. We acknowledge the importance of clarifying the advantages and limitations of this model to illustrate its utility, as well as its contributions to the field of fixed point theory.
Advantages: Enhanced Handling of Uncertainty and Ambiguity: The BCLFSC model improves upon traditional problem-solving tools by incorporating £-fuzzy soft sets, which allow for more nuanced evaluations through lattice-valued memberships. This approach is particularly useful in contexts where decision criteria are uncertain, complex, or vaguely defined, offering a structured way to represent ambiguity.
Multi-criteria problem-solving: By utilizing lattice structures, BCLFSC supports multi-level attribute assessments, making it well-suited for applications involving a hierarchy of criteria, as is common in real-world problems. This allows for flexible, ordered satisfaction levels and facilitates cognitive processes by aligning attribute importance with lattice weights.
Broader applicability: The models flexibility allows it to be applied to a wide range of domains, including differential equations and soft set theory applications. This generalizability makes it an asset for solving both theoretical and applied problems, from project evaluation to multi-criteria assessments in environmental sciences and healthcare.
Improved convergence in fixed point theory: The BCLFSC model introduces new types of contractive inequalities in b-metric spaces, enabling fixed-point solutions that extend existing results. This is especially advantageous in settings where conventional contractive mappings may fail, providing a more robust framework for theoretical development.
Disadvantages of computational complexity: The introduction of lattice-based memberships and BCLFSC requires additional computational resources to handle the complexity of lattice structures, especially when applied to large datasets. This can limit the models scalability and make it less accessible for real-time applications where computational efficiency is critical.
Need for specialized knowledge: Implementing the BCLFSC model in practical settings may require specialized knowledge of lattice theory, b-metric spaces, and fuzzy set logic. This can pose a barrier to adoption for practitioners unfamiliar with these concepts, potentially limiting the models use outside academic and highly technical fields.
Limited empirical validation: Although the BCLFSC model is theoretically sound, empirical validation in real-world scenarios remains limited. As a result, the practical effectiveness and accuracy of the model in applied decision-making contexts warrant further exploration to establish its reliability across diverse domains.
6.
Conclusions
In this study, we explore fixed point theory within the context of £-fuzzy soft set-valued mappings, offering a dual contribution to both theoretical and applied mathematics. The research presents novel fixed-point results that support stable, consistent cognitive frameworks, especially in contexts where uncertainty and incomplete information challenge conventional cognitive processes. Additionally, these fixed-point theorems facilitate practical applications in solving integral equations, broadening the utility of £-fuzzy soft sets in mathematical modeling. Our framework provides tools for accurate decision-making and effective integral inclusion solutions, particularly in fields such as engineering, economics, and healthcare, where ambiguity is a critical factor. This work not only advances the theoretical underpinnings of £-fuzzy soft sets but also underscores their practical value in complex, real-world applications, establishing a foundation for further research in both science and analytical methods for integral inclusions.
Author contributions
Maliha Rashid: Conceptualization, Formal analysis, Supervision, Writing original draft preparation, Writing review and editing; Akbar Azam: Conceptualization, Writing original draft preparation; Maria Moqaddas: Investigation, Writing original draft preparation; Naeem Saleem: Conceptualization, Formal analysis, Investigation, Writing review and editing; Maggie Aphane: Formal analysis, Investigation, Writing review and editing. All authors have reviewed and consented to the finalized version of the manuscript for publication.
Use of Generative-AI tools declaration
The authors declare that AI was not involved in any manner during the writing of this manuscript.
Acknowledgements
The authors are grateful to the reviewers for their insightful comments and constructive suggestions, which have greatly contributed to enhancing the quality and clarity of our paper. Their valuable criticism has been instrumental in refining our work.
Conflict of interest
The authors declare no competing interests.









 DownLoad:
DownLoad:
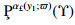 . As
. As  . So, we can find
. So, we can find 


