Speed determinacy of traveling waves for a lattice stream-population model with Allee effect

1.   Introduction

In this paper, we mainly study the speed determinacy of traveling waves in a reaction-diffusion-advection lattice stream-population model

where $u_n(t)$ and $v_n(t)$ are the sequence of real functions representing population density in the drift layer and benthic layer at the time $t$ and the location $n$, respectively. $\sigma > 0$ is the per capita rate of organisms from the drifting to the benthic layer; $\mu > 0$ is the per capita rate of organisms from the benthic layer to the drifting; $\alpha > 0$ is the advection speed of water in the drift layer; $d > 0$ and $\varepsilon > 0$ are the diffusion coefficients of populations in the drift layer and benthic layer, respectively. It is important to note that $\varepsilon$ is a small positive number because organisms in the benthic layer hardly spread.

It is well-known among the scientific community that lattice systems play an important role in mathematical models of biological distributions, neuronal dispersions, quantum mechanics, chemical material processing, fluid dynamics, and so on; see, for instance, the classical nonlinear Klein-Gordon lattice model in ^[1], the NP system in ^[2], and the LBM model in ^[3]. In comparison to continuous models, lattice differential systems are more realistic in describing problems such as propagation barriers. In particular, Van Vleck et al. ^[4] found the phenomenon of "propagation failure" by studying a lattice system, which is not found in a continuous model. Based on these observations, the lattice system has attracted considerable attention from mathematical groups; see ^{[5,6,7,8,9,10]}.

The Allee effect in biological systems is used to describe a state of low population growth. Allee ^[11] revealed that beetle growth is positively influenced by population density, unlike previous analyses from the perspective of biological uptake of resources, and can accelerate extinction at low density. Scholars are interested in the influence of the Allee effect on invasion rate, biological stability and species diversity ^[12,13,14]. Indicating a state with no Allee effect by assuming $f(v) < f^{\prime}(0)v$, Hans Weinberger ^[15] improved the original hypothetical condition and analyzed the speed selection in the Allee condition.

The determinacy of biological minimal speed governs the spreading rate of organisms, and its study is relevant to the development of populations. The conjecture that the minimal and linear speeds are equal was first proposed by Hosono and preliminar tested by numerical means ^[16]. Alhasanat and Ou showed that when $c = c_0+\varepsilon_1$ for sufficiently small $\varepsilon_1$, there exists an upper solution, and they proved theoretically that the minimal wave speed and the linear speed are equal by means of the upper and lower solutions method and the comparison principle ^[17]. According to a similar approach, conclusions are obtained for the speed selection of the lattice system in ^[18,19]. Wang and Kot analyzed the invasion speed under the strong and weak Allee effects, respectively ^[12]. The results show that if the Allee effect is sufficiently weak then the invasion speed can be approximated with the minimal invasion speed.

For lattice systems, the influence of the Allee effect on speed selection has been less studied. Based on it, this paper focuses on the influence of the weak Allee effect on the dynamical properties of the traveling wave solutions and obtains sufficient conditions for linear and nonlinear selections. The reaction term $f(v_n)$ is a benthic biological reaction term with the Allee effect. The conditions for the weak Allee effect are usually denoted as $f(0) = f(1) = 0, f^{\prime}(1) < 0 < f^{\prime}(0)$, and $f(v_n) > 0$ with $v_n\in(0, 1)$. This system has two equilibrium points, $e_0 = (0, 0)$ and $e_1 = (\frac{\mu}{\sigma}, 1)$, and $e_0$ is unstable and $e_1$ is stable. In order to study the traveling wave solution of the system (1.1), a variable transformation of $z = n-ct$ is first performed, which gives

where the unknown constant $c > 0$ is the wave speed. By substituting $(u_n(t), v_n(t)) = (\phi(z), \psi(z))$ into (1.1), we obtain

where

We focus on the speed selection of traveling wave solutions satisfying the boundary conditions

By using the conclusions in ^[20] and theorem 1.1 in ^[7], the existence of the critical value $c_{\rm{min}}$ can be obtained and given as

In general, it is difficult to directly obtain the minimal wave speed of the system (1.3). However, the linear speed $c_0$ determined by the linearizing system around $e_0$ provides an estimation for $c_{\rm{min}}$. Furthermore, the selection mechanism of the wave speed can be obtained by comparing the relationship between $c_0$ and $c_{\rm{min}}$. In the following we give the definition of speed selection.

Definition 1.1. If $c_{\rm{min}} = c_0$, we say that the minimal wave speed of the system (1.3) is linearly selected; otherwise, if $c_{\rm{min}} > c_0$, we say that the minimal wave speed is nonlinearly selected.

The goal of this paper is to investigate the speed selection mechanism for the system (1.3) by means of the upper and lower solution methods and the comparison principle. Firstly, the asymptotic behavior of the traveling wave solution at the equilibrium point $e_0$ is obtained. Secondly, based on the asymptotic behavior, the sufficient conditions for linear selection of the wave speed are obtained by constructing the suitable upper solution, and the sufficient conditions for nonlinear selection are obtained by constructing the lower solution. Then, in order to obtain the effect of the Allee effect on the wave speed, this paper investigates the selection mechanism of the minimal wave speed of the system with the reaction term $f(\psi) = \psi (1-\psi)(1+\rho \psi)$ and skillfully obtains the explicit conditions for linear and nonlinear selections. Further, we find that there exists a critical value $\rho_{1}$ such that the minimal wave speed is linearly selected for $\rho < \rho_{1}$. Finally, the sufficient conditions are proved to be nonempty sets by numerical simulations, and our conjecture is verified.

2.   The asymptotic behavior at $e_0$

In this section, we consider the asymptotic behavior of the traveling wave $(\phi, \psi)(z)$ at $e_0$. First, the system (1.3) is linearized at $e_0$ as follows:

Letting $(\phi, \psi)(z) = (A_1, A_2)e^{-\lambda z}$, where $A_1, \ A_2$, and $\lambda$ are positive constants, and substituting it into (2.1), we get

The matrix form of Eq (2.2) is as follows:

where $A = (A_1, \ A_2)^{\rm{T}}.$ We further simplify it to

Here $k(\lambda)$ = $c\lambda$, and the matrix $B(\lambda)$ is represented as

where

The system (2.4) has nontrivial solutions if and only if $k(\lambda)$ satisfies

By calculating, we get

thus, Eq (2.5) has two real roots, which are obtained by

where $k_- < k_+$. By substituting $B_1$ and $B_2$ into $k_+$, we can obtain the exact expression as

The first-order derivative of $k_+$ with respect to $\lambda$ can be obtained as follows:

where $\eta = (d-\varepsilon) (e^{-\lambda}+e^{\lambda}-2) -\sigma -\alpha (e^{-\lambda}-1)+\mu-f^{\prime}(0)$. Since $\varepsilon$ is a small positive number and the rest of the parameters are positive, we have $k_+^{\prime}(\lambda) > 0$ and $k_+ > 0$ for $\lambda \in(0, +\infty)$. The principal eigenvalues of the coefficient matrix $B(\lambda)$ are expressed as

It should be noted that unlike the eigenvalues in a continuous system, the principal eigenvalues here are not always convex functions. After a laborious calculation, for $2d\geq \alpha +2\varepsilon$, the function $k^{* \prime \prime} (\lambda)\geq 0$ with $\lambda \in (0, +\infty)$, so $k^*(\lambda)$ is the continuous convex function. The solutions are determined by the number of crossing points between the function $y = k^*(\lambda)$ and the primary function $y = c\lambda$. Based on the correspondence between $c$ and $\lambda$, the following lemma is given:

Lemma 2.1. If we define

which is the linear speed, then the equation $k(\lambda)$ = $c\lambda$ has

(1) No solutions if $c < c_0$;

(2) One solution $\lambda_0$ if $c = c_0$;

(3) Two solutions, $\lambda_1$ and $\lambda_2$, satisfying $\lambda_1 < \lambda_2$ if $c > c_0$.

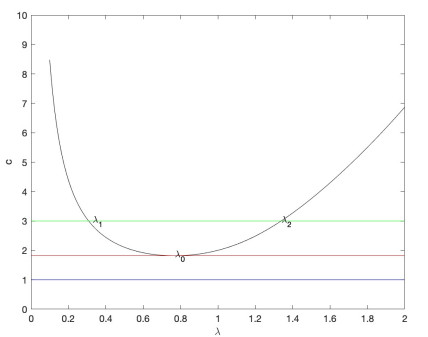
Letting $d = 3, \ \sigma = 4, \ \alpha = 1, \ \varepsilon = 0.1$ and $\mu = 1, \ f^{\prime}(0) = 1$, we obtain the curve of $c = \frac{k^{*}(\lambda)}{\lambda}$; see Figure 1. By numerical calculation, we know $c_0 = 1.82$ and $\lambda_0 = 0.77$. Further, there are no solutions (see the blue line) when $c < c_0$; there is only one exact solution $\lambda_0$ when $c = c_0$ (see the red line); and there are two solutions denoted by $\lambda_1$ and $\lambda_2$ when $c > c_0$ (see the green line). Then, we shall study the asymptotic behavior of the traveling wave solutions $(\phi, \psi)(z)$ as $z \rightarrow \infty$.

If $c > c_0$ and $A_2 = 1$, the corresponding characteristic equation can be obtained as:

And the traveling wave $(\phi, \psi)(z)$ around $e_0$ is represented as

its equivalence is expressed as

where $C_1 > 0$ or $C_1 = 0 \ and \ C_2 > 0$. The two forms (2.9) and (2.10) can represent all nonzero solutions of Eq (2.1).

3.   Speed selection mechanisms

In this section, the selection mechanism for the minimal wave speed will be obtained by using the upper and lower solution methods. For convenience, we use the following notations:

Next, we give the definition of the upper and lower solutions of the system (1.3).

Definition 3.1. (Upper and lower solutions) For a given $c\geq c_0$, if the binary continuous function $(\phi, \psi)(z)$ is differentiable on $\mathbb{R}$, such that

and $(\phi, \psi)(z_i^-)\geq (\phi, \psi)(z_i^+)$ for all $z_i$, $i = 1, 2, ..., n$, then $(\phi, \psi)(z)$ is called the upper solution (the lower solution) of the system (1.3).

From now on, we discuss the linear selection mechanism of the system (1.3), and the key is to find a pair of suitable upper solutions. When $c = c_0+\varepsilon_1$ with sufficiently small $\varepsilon_1$, there exists $0 < \lambda_1(c) < \lambda_2(c)$ with $c$. According to the asymptotic behavior of $\phi(z)$ and $\psi(z)$, we define a pair of functions $(\overline{\phi}(z), \overline{\psi}(z))$ as below

which satisfy the boundary conditions $\left(\overline{\phi}(z), \overline{\psi}(z)\right) (\infty) = (0, 0)$ and $\left(\overline{\phi}(z), \overline{\psi}(z)\right) (-\infty) = \left(\frac{\mu}{\sigma}, 1\right),$ where $A_1^{1} = A_1\left(\lambda_{1}(c)\right) = \frac{\mu}{c\lambda_{1}-B_{1}(\lambda_{1})}$. Their first-order derivatives can be obtained as

We need to do some preparation to prove that $(\overline{\phi}(z), \overline{\psi}(z))$ is a pair of upper solutions. By combining with (1.4), we can obtain

where

The representations of $q_i(\lambda_1, \kappa)(i = 1, 2, 3, 4, 5, 6)$ in (3.5)-(3.10) are as follows:

where

In the above formulas, $q_i(\lambda_1, \kappa)$ is a continuous function with respect to $\kappa \in [0, \infty)$. Next, substituting (3.3)–(3.11) into $L_1(\psi, \phi)$ and combining with (2.10), we obtain

where

If the inequality

holds, then we have $L_1(\overline{\psi}, \overline{\phi})\leq 0$. $Q(z)$ can be regarded as a quadratic function of $\overline{\psi}$ in inequality (3.12). And analyzing optimal value through the symmetry axis $\overline{\psi}_a$, we have three cases: $\overline{\psi}_a < 0$, $\overline{\psi}_a > 1$, or $\overline{\psi}_a$ in $(0, 1)$. But since $Q(z)$ in (3.12) is a function of $\kappa$, it is a function with a higher exponent with respect to z. Therefore, we give the proof that the set $Q \leq 0$ is not empty.

Remark 3.2. Letting $d = 8$, $\sigma = 1$, $\alpha = 7$, $\mu = 10$, $\varepsilon = 4.5$, and $f^{\prime}(0) = 1$, we can calculate that $c_0 = 7.66$, $\lambda_0 = 0.14$, and $A_1^1 = 9.98$. Upon setting $a = 1$, we obtain that $Q(z)$ is less than or equal to 0, which leads to the conclusion that $L_1(\overline{\phi}, \overline{\psi})\leq 0.$

Next, substituting (3.3)–(3.4) into $L_2(\phi, \psi)$ and combining the second equation of (2.8), we get

where

Obviously, if the inequality

holds, then we get $L_2(\overline{\phi}, \overline{\psi})\leq 0$.

To demonstrate the linear selection mechanism of the wave speed, we also give a pair of lower solutions as follows:

The proof of the lower solution $(\underline{\phi}^0, \underline{\psi}^0)$ is similar to that in the literature ^[21], and we omit it for convenience.

Based on the above description, when $c = c_0+\varepsilon_1$ with a small enough $\varepsilon_1$, we find suitable upper and lower solutions. By comparing the principles, we can obtain sufficient conditions for the linear selection of the minimal traveling wave speed of the system (1.3).

Theorem 3.3. (Linear selection) When $2d\geq \alpha +2\varepsilon$, the minimal wave speed of the system (1.3) is linearly selected if (3.12) and (3.13) hold.

Then, we will construct the lower solutions to prove the nonlinear selection mechanism. It is worthwhile to note that the traveling wave speed of the system (2.1) can be nonlinear selection when the lower solution can perform asymptotical propagation with $(A_1(\lambda_2) e^{-\lambda_2 z}, e^{-\lambda_2 z})$. Next, we state it with following lemma:

Lemma 3.4. For $c_1 > c_0$, we can assume that there exits a pair of lower solutions $(\underline{\phi}, \underline{\psi})(z)$ to the system

The solution satisfies $\limsup\limits_{z \rightarrow -\infty}\underline{\psi}(z) < 1$ and $\underline{\psi}(z)$ approaches $Ce^{-\lambda_2z}$ (i.e., the faster decay rate) for $C > 0$ as $z \rightarrow \infty$. Here, $\lambda_2$ is the larger solution of $k(\lambda) = c\lambda$ and $z = n-c_1t$. Then no traveling wave solutions to (3.14) exist for the speed $c\in [c_0, c_1)$.

Proof of Lemma 3.4. We prove this lemma by contradiction. Assume to the contrary, there exists a pair of monotone and positive traveling wave solutions $(\phi, \psi)(z)$, $z = x-ct$ with $c\in [c_0, c_1)$, subject to the initial conditions

Recall that $\lambda_1$ decreases monotonically to $c$ while $\lambda_2$ increases; thus, we usually assume (by shifting if necessary) that $(\underline{\phi}, \underline{\psi})(n)\leq (\phi, \psi)(n)$ for all $n \in \mathbb{Z}$. Since $(\underline{\phi}, \underline{\psi})(n-c_1 t)$ is the lower solution to (3.14), we can obtain

for all $(n, t)\in (\mathbb{Z}, \mathbb{R}^+)$. If $z = n-c_1 t$, then we have

Therefore, $\underline{\psi}(z)\leq 0$ is paradoxical with $\psi(z) > 0$, which yields a contradiction. The proof is complete. □

Remark 3.5. Due to the lemma, for the nonlinear selection, we only need to find a lower solution with asymptotic behavior $\left(A_1(\lambda_2(c)) e^{-\lambda_2 z}, e^{-\lambda_2 z}\right)$ as $z \rightarrow +\infty$ for $c > c_0$.

By the above lemma, when $c > c_0$, we give a pair of new traveling waves as follows:

where $A_1^{2} = A_1\left(\lambda_2(c)\right) = \frac{\mu}{c\lambda_{2}-B_{1}(\lambda_{2})}$. The first-order derivatives of (3.15) and (3.16) are

Utilizing the notations

we can derive a continuous function $q_{i}(\lambda_2, \zeta)$ by replacing all values of $\lambda_1$ and $\kappa$ in $q_i(\lambda_1, \kappa)$ with $\lambda_2$ and $\zeta$ respectively. Thus, we obtain

where

If the inequality

holds, we have $L_1(\underline{\psi}, \underline{\phi})\geq 0$.

Remark 3.6. Based on the given values of $d = 5000$, $\sigma = 100$, $\alpha = 1$, $\mu = 200$, $\varepsilon = 10$, and $f^{\prime}(0) = 1$, the calculation indicates that $c_0 = 67.38$, $\lambda_0 = 0.01$, and $A_1^2 = 2.00$. When $a = 0.11$, it is possible to obtain $F(z)\geq0$, which leads to $L_1(\underline{\phi}, \underline{\psi})\geq0$.

Taking (3.15) and (3.16) into $L_2(\phi, \psi)$, next we get

where

If

holds, then $L_2(\underline{\phi}, \underline{\psi})\geq 0$. These conditions lead to the nonlinear selection of the minimal wave speed.

Theorem 3.7. (Nonlinear selection) When $2d\geq \alpha +2\varepsilon$, if (3.17) and (3.18) hold, the minimal wave speed of the system (1.3) is nonlinearly selected.

4.   Applications

In this section, we consider the speed selection of a system with the reaction term $f(\psi) = \psi(1-\psi)(1+\rho \psi)$, where $\rho$ is a non-negative constant. The system (1.1) becomes

And the corresponding traveling wave system is as follows:

Many scholars have given that the minimal wave speed is linearly selected as $\rho \leq1$ under the assumption $f(\psi) < f^{\prime}(0)\psi$; see ^[23,24] for details. We conjecture that there exists a critical value $\rho_1 > 1$, such that the minimal wave speed is linearly selected for $\rho < \rho_1$. There also exists a critical value $\rho_2$, such that the traveling wave speed is nonlinearly determined for $\rho > \rho_2$. Our conjecture is supported by the following lemma, which yields the existence of critical values.

Lemma 4.1. If the minimal wave speed is linearly selected for a positive $\rho = \rho_1$, then it is also linearly selected for any $\rho \leq \rho_1$. On the other hand, if the minimal wave speed is nonlinearly selected for any positive $\rho_2$, it will also be nonlinearly selected for any $\rho \geq \rho_2$.

Proof of Lemma 4.1. When $\rho = \rho_1$, assume that there exists $(\phi^*, \psi^*)$ as a pair of solutions with $c = c_0+\epsilon_2$ for any sufficiently small $\epsilon_2 > 0$, such that

Next, we can deduce that the minimal wave speed of the system (4.3) is linearly selected. For any $\rho < \rho_1$, taking $(\phi^*, \psi^*)$ into (4.2), the first equation of (4.3) is permanent, while the second equation becomes

So $(\phi^*, \psi^*)$ is a pair of upper solutions of (4.2), and the minimal wave speed of the system (4.2) is linearly selected with $\rho < \rho_1$.

The proof of $\rho > \rho_2$ is similar to $\rho < \rho_1$, and we omit it for convenience. □

Substituting the reaction term $f(\overline{\psi}) = \overline{\psi}(1-\overline{\psi})(1+\rho \overline{\psi})$ into $L_2(\overline{\phi}, \overline{\psi})$, we obtain

If $\rho\leq 2e^{-\lambda_1}\varepsilon \gamma +\sigma a$, then $L_2(\overline{\phi}, \overline{\psi}) \leq 0$. Further, when $\rho < 1$, $f(\overline{\psi})$ possesses the property of subhomogenity. Thus, the minimal wave speed is linearly selected. Let

Based on the above discussion, we can get the linear selection mechanism for the minimal wave speed.

Theorem 4.2. If there exist $d, \alpha, \sigma, \mu, \varepsilon$, and $c$ satisfying $2d\geq \alpha +2\varepsilon$ and (3.13), then the minimal wave speed of the system (4.2) is linearly selected when $\rho \leq \rho_1$.

Next, substituting the reaction term $f(\underline{\psi})$ into $L_2(\underline{\phi}, \underline{\psi})$, we obtain

Let

If $\rho\geq \rho_2$, then we get $L_2(\underline{\phi}, \underline{\psi})\geq 0.$

Theorem 4.3. When $d, \alpha, \sigma, \mu, \varepsilon, c$ and $A_1(\lambda_2(c))$ satisfy $2d\geq \alpha +2\varepsilon$, there exists the constant $a$ such that (3.17) holds when $\rho\geq \rho_2$. Then the minimal wave speed of the system (4.2) is nonlinearly selected.

Conclusion 4.4. Lemma 4.1 implies the existence of $\rho_c$, so that the speed is linearly selected if and only if $\rho \leq \rho_c$. Now $\rho_1$ and $\rho_2$ founded in theorems 4.2 and 4.3 are considered as estimations of $\rho_c$.

Next, we verify that $\rho_c > 1$ through numerical calculations. Based on theorem 4.2, under the parameter conditions of remark 3.2, we can calculate $\rho_1 = 1.203$. When $\rho \leq 1.203$, the minimal wave speed is linearly selected. On the other hand, if we consider the nonlinear selection of the minimal wave speed, we can use the parameter conditions of Remark 3.6 and Theorem 4.3 to calculate $\rho_2 = 11.002$. This means that when $\rho \geq 11.002$, the minimal wave speed of the system (4.2) is nonlinearly selected. Therefore, we have successfully verified that the conjecture holds.

5.   Conclusions

In this paper, we investigate the speed selection mechanism of the traveling wave solution by the upper and lower solutions method for the reaction-diffusion-advection lattice stream-population model with a weak Allee effect. We construct a pair of upper solutions by applying the asymptotic behavior in Section 2, which allows us to obtain the linear selection mechanism. By constructing suitable lower solutions with a faster propagation speed, we demonstrate that the minimal wave speed is nonlinearly selected. Further, we introduce the reaction term $f(\psi) = \psi(1-\psi)(1+\rho \psi)$ with the classical weak Allee effect in theorem 3.3. Further, when $\rho \leq \rho_1$, the minimal wave speed of the system (4.2) is linearly selected. Additionally, we identify a critical value $\rho_2$ such that the minimal wave speed of the system (4.2) is nonlinearly selected when $\rho > \rho_2$. Finally, we further verify our conjecture and theoretical results with numerical calculations, which yield $\rho_1 = 1.203$ and $\rho_2 = 11.002$ when $c$ tends to $c_0$.

Author contributions

Chaohong Pan: Application of statistical, mathematical, computational, or other formal techniques to analyze or synthesize study data; Xiaowen Xu: Validated the research outputs and wrote the original draft of this research; Yong Liang: Prepared and created the published work by those from the original research group and helped to create the final form of this research after revision stages.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare there are no conflicts of interest