Family of right conoid hypersurfaces with light-like axis in Minkowski four-space

1.   Introduction

Hadamard or $H$-matrix is proved to be of a great value in many classical problems in numerical linear algebra. This matrix class provides a frame for extensive research on stability of dynamical systems with emphasis on matrix spectra and spectra-related parameters. The information on eigenvalue localization within a prescribed area in the complex plane as a sufficient condition for a certain type of stability could be obtained from analysis of special $H$-matrices. Special $H$-matrices have their role in dealing with linear complementarity problems when considering questions of existence and uniqueness of solutions and in error analysis.

$H$-matrices are closely related to well-known Minkowski or $M$-matrices. A matrix $A = [a_{ij}]\in \mathbb C^{n, n}$ is an $H$-matrix if its comparison matrix $\langle A \rangle = [m_{ij}]$ defined by

is an $M$-matrix, i.e., $\langle A \rangle ^{-1} \geq 0$; for more details, see ^[3,14]. $H$-matrices are also related to $P$-matrices, real square matrices with all principal minors positive. A real $H$-matrix with positive diagonal entries is a $P$-matrix. In literature, $H$-matrices also appear as $GSDD$ matrices, or generalized strictly diagonally dominant matrices, as they represent a generalization of strictly diagonally dominant ($SDD$) matrices.

Motivation for the research on special $H$-matrices comes from the fact that diagonal dominance and related matrix properties play an important role in matrix splitting methods and convergence analysis of iterative procedures for solving large sparse systems of linear equations, eigenvalue localization problems, norm for the inverse and condition number estimation, and linear complementarity problems. As the $SDD$ condition is very limiting, results developed for $SDD$ matrices, such as Varah norm bound for the inverse (see ^[46]) cannot be applied to wider matrix classes. Therefore, we are motivated to consider modifications of the $SDD$ condition and obtain new estimates applicable to new classes of matrices.

In this paper, we obtain new bounds for the norm of the inverse that work in some cases when well-known bounds cannot be applied. Also, for some matrices, both new bounds and some already known bounds are applicable, and we show through numerical examples that new bounds can give tighter results. As the condition number of a matrix is defined as

results on norm bounds directly imply estimates for the condition number. Condition number helps us recognize ill-conditioned problems, with high relative change in output for a relative change in input data. Therefore, upper estimates for condition number have important applications in engineering, in control of perturbation effects.

Another important benefit of new estimates for the inverse is the possibility to apply new results to block $H$-matrices. It is important to emphasize that block $H$-matrices do not have to be $H$-matrices in the classical sense. In these cases, bounds developed for $H$-matrices cannot be applied, but block approach could still work. This is of great importance in ecological models describing interactions between several populations (see ^[24]) with self-interactions in community matrices equal to zero. Matrices with zero diagonal entries, or 'hollow matrices', do not belong to $H$-matrices in the classical sense, but they could be block $H$-matrices with respect to some partition of the index set and they could be approached using tools of $H$-matrix theory.

New norm estimations are further applied in linear complementarity problems. Also, we obtain eigenvalue localization for the Schur complements of special $H$-matrices that can be applied in convergence analysis in Schur-based iterative methods.

Concept of diagonal dominance and related subclasses of $H$-matrices are widely applied in analysis of stability and other dynamical properties of complex real systems, in wireless sensor networks, structural engineering, and economy.

The paper by Fiedler and Pták (see ^[17]) brought a characterization of $H$-matrices through their scaling relation to $SDD$ matrices. Fiedler and Pták proved that a matrix $A = [a_{ij}] \in {\mathbb C}^{n, n}$ is an $H$-matrix if, and only if, there exists a diagonal non-singular matrix $W$ such that $AW$ is $SDD$. This definition of (non-singular) $H$-matrices is also known as the 'scaling characterization', while the diagonal matrix $W$ (that can be chosen to have all positive diagonal entries) is called the 'scaling matrix'. A complex square matrix $A = [a_{ij}]\in \mathbb C^{n, n}$ is an $SDD$ matrix if, for all indices $i \in N$,

While the $SDD$ condition is expressed in a very elegant manner and easily checkable with low calculation cost, identification of $H$-matrices was never that simple. In literature, there are various iterative or direct criteria for recognizing special $H$-matrices; see ^{[4,10,15,16,25,26,30,42]}. Through slight relaxations of the $SDD$ condition, using different approaches, new special subclasses of $H$-matrices were defined. These new conditions could be seen as different ways of 'breaking the $SDD$ condition'.

Although scaling characterization connects $H$-matrices to $SDD$ matrices through a very simple diagonal scaling transformation, in most cases these scaling relations are unknown to us, as we are not able to easily determine the scaling matrix. In ^[8], new criteria for identifying non-singular $H$-matrices were presented based on a special form of scaling. Motivated by these results, in this paper we introduce new criteria for identifying special $H$-matrices based on special scaling relation of the new class to the class of Nekrasov matrices; see ^[25,34].

It is worth mentioning that scaling methods could be interpreted in different ways and prove to be useful in a wide range of practical applications when the purpose of scaling is to obtain prescribed row and column sums in a nonnegative matrix see ^[2,3]. In analysis of budget allocation problems, transportation problems, Leontief input-output systems, Markov chains, and related mathematical models of real-life systems, the concept of scaling plays an important role.

In the remainder of this section, we recall well-known criteria for identifying some special $H$-matrices. In Section 2, we introduce a new subclass of $H$-matrices and discuss relation of the new class to well-known matrix classes. In Section 3, we present possible applications of the new class: Estimation of the infinity norm of the inverse, bounds for minimal singular value, error estimation for linear complementarity problems, and preliminary eigenvalue localizations for Schur complements of matrices in the new class. The fourth section consists of concluding remarks.

In ^[8], a scaling-based condition for identifying non-singular $H$-matrices was given as follows. Let $A = [a_{ij}] \in \mathbb C^{n, n}$, $n \geq 2$ be a matrix with nonzero diagonal entries. Denote

If

then $A$ is an $H$-matrix. In further consideration, we say that a matrix is an $O$-scal matrix if it satisfies the condition (1.1). The proof of the statement that $O$-scal matrices are non-singular $H$-matrices, given in ^[8], relies on the special scaling relation between $O$-scal matrices and well-known Ostrowski matrices; see ^[41]. Recall that a matrix $A = [a_{ij}] \in \mathbb C^{n, n}$, $n \geq 2$ is an Ostrowski matrix if

In ^[8], it was proved that for an $O$-scal matrix $A$ and diagonal matrix

the matrix $AQ$ is an Ostrowski matrix.

Now we recall Nekrasov matrices; see ^[25,34]. Consider recursively defined row sums:

A matrix $A = [a_{ij}] \in {\mathbb C}^{n, n}, n\geq 2$ is a Nekrasov matrix if, for each $i \in N$, it holds that

In literature, there are different propositions by different authors on how to construct a scaling matrix for the given Nekrasov matrix. We recall a construction presented in ^[45].

Theorem 1.1. ^[45] Let $A = [a_{ij}] \in {\mathbb C}^{n, n}$ be a Nekrasov matrix with all nonzero Nekrasov row sums. Then, for a diagonal positive matrix $\; Y = diag(y_{i})$, where $y_{i} = \varepsilon_{i}\frac{h_{i}(A)}{|a_{ii}|}, \; i \in N,$ and $(\varepsilon_{i})_{i = 1}^{n}$ is an increasing sequence of numbers with $\; \varepsilon_{1} = 1$ and $\varepsilon_{i}\in\left(1, \frac{|a_{ii}|}{h_{i}(A)}\right), \; i = 2, \dots, n,$ the matrix $AY$ is an $SDD$ matrix.

In ^[42], Peña presented a class of matrices named $SDD_1$ matrices via a condition that generalizes the $SDD$ condition by imposing on the rows that are not $SDD$ of a weaker demand.

Definition 1.2. A matrix $A = [a_{ij}]\in \mathbb C^{n, n}, \; n\geq 2, \;$ is an $SDD_1$ matrix if

where

$N_A = \{i \in N \, | \, |a_{ii}| \leq r_i(A) \}$ \, and \, $\overline{N_A} = \{i \in N \, | \, |a_{ii}| > r_i(A) \}$.

As $SDD_1$ matrices were researched recently by different authors, we are going to discuss relations of the $SDD_1$ condition to new criteria we presented in the Section 2.

Well-known classes of Ostrowski (see ^[41]) or Dashnic-Zusmanovich (see ^[15,16]) were defined based on a special treatment of one index in the index set; Nekrasov matrices (see ^[26,34,44]) were introduced via recursively defined row sums and further generalized through conditions involving permutations of the index set (see ^[10]); while $SDD_1$ matrices (see ^[42]) involve a new type of row sums. All of these conditions (i.e., matrix classes) were further applied in estimations of the norm of the inverse matrix (see ^{[13,18,28,29,37,38]}), estimations of errors in linear complementarity problems (see ^{[1,20,21,22,33,38]}), eigenvalue localizations (see ^[47]), and analysis of Schur complements, (see ^[9,11,12,39]).

2.   New criteria for non-singular $H$-matrices

2.1.   Introducing $N$-scal matrices

In this section, we introduce new conditions defining a subclass of non-singular $H$-matrices. These new criteria are obtained as scaling modifications of the Nekrasov condition.

Given a matrix $A = [a_{ij}]\in {\mathbb C}^{n, n}, n\geq 2,$ with nonzero diagonal entries, let

Definition 2.1. Given a matrix $A = [a_{ij}]\in {\mathbb C}^{n, n}, n\geq 2,$ with nonzero diagonal entries, then $A$ is an $N$-scal matrix if

Theorem 2.2. If a matrix $A = [a_{ij}]\in {\mathbb C}^{n, n}, n\geq 2,$ is an $N$-scal matrix, then $A$ is a non-singular $H$-matrix.

Proof. Let us consider the diagonal matrix $X = diag(x_{k}),$ with

For the diagonal matrix $X$ defined in that way, let us prove that $AX$ is a Nekrasov matrix. It is easy to see that

We now prove by induction that for all $i \in N,$

First, for $i = 1,$

Consider $i \in \{2, 3, \ldots, n\}.\;$ Assume that for all indices $k\in \{1, 2, \ldots, i-1\}, \;$ it holds that

Then,

Therefore, $A$ is an $H$-matrix.

$N$-scal class is derived from Nekrasov class and, just like the Nekrasov class, it is not closed under simultaneous permutations of rows and columns, as the following example shows.

Example 2.3. Consider

The matrix $A_0$ is an $N$-scal matrix, but for $P$ being a counter-identical permutation, $P^TA_0P$ is not an $N$-scal matrix.

2.2.   Relations between classes

Let us now discuss relations of the $N$-scal condition to other well-known criteria for identifying $H$-matrices.

Example 2.4. Consider the following matrix

The matrix $A_1$ belongs to some of the matrix classes presented in Table 1.

Consider the matrix

The matrix $A_2$ belongs to some of the matrix classes presented in Table 2.

Consider the matrix

The matrix $A_3$ belongs to some of the matrix classes presented in Table 3.

Consider the matrix

The matrix $A_4$ belongs to some of the matrix classes presented in Table 4.

Consider the matrix

The matrix $A_5$ belongs to all of the matrix classes presented in Table 5.

Consider the matrix

The matrix $A_6$ belongs to some of the matrix classes presented in Table 6.

Remark 2.5. If we consider the matrix $A_3,$ we see that the $N$-scal class is not contained in any of the following classes: $SDD$, $SDD_1$, Ostrowski, Nekrasov. Considering the matrix $A_1,$ we see that the $N$-scal class is not contained in $O$-scal.

Remark 2.6. Neither of the classes $SDD$, $SDD_1$, Ostrowski, Nekrasov is contained in $N$-scal, as seen from the matrix $A_4.$ Considering $A_2$, we see that $O$-scal is not a subclass of $N$-scal.

Remark 2.7. The matrix $A_5$ belongs to the new class $N$-scal and also to all of the classes $SDD$, $SDD_1$, Ostrowski, Nekrasov, $O$-scal, so the intersection of these classes is nonempty.

Remark 2.8. If we consider matrices $A_2$ and $A_3$, we see that $O$-scal matrices can have more than one non-$SDD$ row. This is not the case with Ostrowski matrices.

Remark 2.9. If we consider matrix $A_6$, we see that it is an $N$-scal matrix, but it does not belong to any of the classes $SDD$, $SDD_1$, Ostrowski, Nekrasov, $O$-scal.

The previous remarks show that the new class $N$-scal stands in a general relation to each of the classes $SDD$, $SDD_1$, Ostrowski, Nekrasov, $O$-scal.

3.   Applications of $N$-scal criteria

3.1.   Norm of the inverse and minimal singular value estimations

In ^[46], a max-norm bound is given for the inverse of $SDD$ matrices.

Theorem 3.1. ^[46] Given an $SDD$ matrix $\; A = [a_{ij}] \in {\mathbb C}^{n, n}, \;$ the following bound applies,

This result of Varah served as a starting point for defining new norm estimations applicable to wider classes of matrices.

Theorem 3.2. ^[32] Let $A \in \mathbb C^{n, n}, \ n \geq 2,$ be an Ostrowski matrix. Then,

In ^[40], in a slightly different form, one can find the following result.

Theorem 3.3. Let $A \in \mathbb C^{n, n}, \ n \geq 2,$ be an $O$-scal matrix. Then,

Theorem 3.4. ^[31] Given a Nekrasov matrix $\; A = [a_{ij}] \in {\mathbb C}^{n, n}, \;$ the following bound applies,

where

Based on the $N$-scal condition, we now define a new norm estimation as follows.

Theorem 3.5. If a matrix $A = [a_{ij}]\in {\mathbb C}^{n, n}, n\geq 2,$ is an $N$-scal matrix, then the following bound applies:

where

Proof. As $A$ is an $N$-scal matrix, for $X = diag(x_k),$ with $x_k = \frac{h_k(A)}{|a_{kk}|}, \ k \in N, \;$ we know that the matrix $B = AX\;$ is a Nekrasov matrix.

Also, $B^{-1} = (AX)^{-1} = X^{-1}A^{-1}, \;$ i.e., $A^{-1} = XB^{-1}.\;$ Therefore,

It is easy to prove that $z_i(B) = z_i(A), \;$ for all $i \in N, \;$ by induction.

Namely, for $i = 1, \;$ it holds that $z_1(A) = z_1(B) = 1, \;$ by definition. If we assume that $z_j(B) = z_j(A), \;$ for all $j = 1, 2, \ldots, i-1, \;$ then

Applying the upper bound for the norm of the inverse given in Theorem 3.4 to the matrix $B,$ we obtain

It follows that

Example 3.6. Consider the matrix

The matrix $B_1$ belongs to the $N$-scal class and the norm estimation from Theorem 3.5 is

while the exact value is

The matrix $B_1$ does not belong to any of the classes $SDD$, Ostrowski, Nekrasov, $O$-scal; therefore, the corresponding norm bounds cannot be applied.

Example 3.7. Consider

The matrix $B_2$ belongs to the $N$-scal class and the norm estimation from Theorem 3.5 is

while the exact value is

The matrix $B_2$ does not belong to any of the classes $SDD$, Ostrowski, Nekrasov, $SDD_1$; therefore, the corresponding norm bounds cannot be applied. It does belong to the $O$-scal class and the norm estimation from Theorem 3.3 is 1.035986.

Example 3.8. Consider

Norm bounds for the inverse for $B_3$ are presented in Table 7.

The matrix $B_3$ belongs to classes $O$-scal and $N$-scal. Exact value for the norm of the inverse matrix is

Also, the matrix $B_3$ belongs to the $SDD_1$ class. Applying the norm bound given in ^[4]HY__HY, Theorem 8] for the $SDD_1$ class, we obtain $||B_3^{-1}||_{\infty} \leq 4.215686.$ Therefore, in this case, the bound obtained for $N$-scal matrices gave a more precise result than the bound for $SDD_1.$

Example 3.9. In mathematical models in ecology, when modeling interactions between species, stochastic matrices represent corresponding transition probabilities between stages in life cycles. If we consider predator and prey species in juvenile or adult life stage, probabilities of transitions between different states could be represented with the following matrix:

Coming from real systems, these matrices often possess properties related to diagonal dominance. Here, the matrix $B_4$ is neither $SDD$ nor Ostrowski, but it belongs to the $N$-scal class and the norm estimation from Theorem 3.5 is

which is tighter than bounds obtained for Nekrasov (24.1429) or the $O$-scal class (18.85714).

Example 3.10. In mathematical models in structural engineering, when applying the finite element method, matrices representing relationships between forces and displacements occur. In some cases, these matrices can be analyzed via tools of the $H$-matrix theory. Consider a tridiagonal matrix of order 10, $B_5 = tridiag[−6, 12, −6],$ having a form that often appears in modeling systems in engineering or economics. The matrix $B_5$ is neither $SDD$ nor Ostrowski, but it belongs to the $N$-scal class and the norm estimation from Theorem 3.5 is

which is tighter than the bound obtained for Nekrasov (85.16666).

In order to bound the smallest singular value of a special $H$-matrix $A$, let us denote

For the given matrix $A \in \mathbb C^{n, n},$ let $||A||_1, ||A||_2,$ and $||A||_{\infty}$ represent the $1$-norm, $2$-norm, and $\infty$-norm of $A$, respectively. It is well-known that the following relation between the norms hold

Applying this inequality, the lower bound for the minimal singular value of special $H$-matrices is obtained.

Theorem 3.11. Let $A \in \mathbb C^{n, n}, \ n \geq 2$ be a matrix with nonzero diagonal entries. If

for all $i \in N,$ then

where $\sigma_n(A)$ is the smallest singular value of $A.$

Proof. Matrices $A$ and $A^T$ are both $N$-scal matrices. From the previous theorem, we have

As

we obtain

i.e.,

Remark 3.12. We can apply obtained results to other norms as well. If matrices $A$ and $A^T$ are both $N$-scal matrices, from the previous consideration, it follows that

Remark 3.13. One can consider block generalizations of $H$-matrices and subclasses and define infinity norm estimation for the inverse in the block-case as well. Block $H$-matrices were researched in ^[43,47].

For $A = [a_{ij}]\in\mathbb C^{n, n}\;$ and a partition $\; \pi = \{p_j\}_{j = 0}^l, \; p_0 = 0 < p_1 < p_2 < ... < p_l = n\;$ of the index set $N$, consider the block matrix $[A_{ij}]_{l\times l}$ with the index set $L = \{1, 2, ..., l\}.$

The relation between point-wise and the block case (see ^[7]) implies the following estimation.

For a given $\; A = [a_{ij}]\in\mathbb C^{n, n} \;$ and a given partition $\; \pi = \{p_j\}_{j = 0}^l$ of the index set $\; N, \;$ if $\; \rangle A \langle^\pi\;$ is an $N$-scal matrix, then

Here, comparison matrix is defined in a usual manner. The matrix $\; \rangle A \langle^\pi = [p_{ij}]_{l\times l}\;$ is given by

Example 3.14. When considering a continuous-time dynamical ecological system composed of several populations resting at a feasible equilibrium point (see ^[24]) self-interactions are often removed from the community matrix, meaning that diagonal entries are equal to zero. Matrices with zero diagonal, by the name 'hollow matrices', do not belong to the class of $H$-matrices in the classical sense; therefore, they cannot be treated nor analyzed via bounds obtained for special classes of $H$-matrices. However, the community matrix often has a certain block structure and we can apply results developed for block $H$-matrices. Consider

This matrix is not an $H$-matrix, as it is hollow, but with respect to partition $\pi = \{0, 2, 4, 6, 8\}$, we obtain the comparison matrix $\; \rangle G \langle^\pi$, which is an $N$-scal matrix; therefore, we obtain

3.2.   Error bounds for the solution of linear complementarity problem

Assume that $A = [a_{ij}] \in {\mathbb R}^{n, n}\;$ and $\; q\in {\mathbb R}^{n}.$ The linear complementarity problem LCP($A, q$) is defined as follows. Find $x \in {\mathbb R}^{n}\;$ satisfying

or show that such a vector does not exist. In modern game-theory, as well as in economy and engineering, there are certain problems that can be formulated as LCP problems. Special matrix classes, including $P$-matrices, $Q$-matrices, and $M$-matrices, have always played an important role in analysis of linear complementarity problems, whether in establishing conditions for existence and uniqueness of the solution, or in construction of procedures for solving LCP. Necessary and sufficient condition for LCP($A, q$) to have a unique solution with respect to any $\; q\in {\mathbb R}^{n}\;$ is the demand on matrix $A$ to be a $P$-matrix, a real square matrix with all its principal minors positive; see ^[6].

For a $P$-matrix $A$, let $x^{\ast}$ denote the solution of the LCP($A, q$) and denote $\; r(x) = min(x, Ax+q),$ $D = diag(d_i), 0 \leq d_i \leq 1.$ In ^[5], the following estimate for the error of the solution was presented:

It is well-known that an $H_+$ matrix, a real $H$-matrix with positive diagonal entries, is a $P$-matrix.

Therefore, it is convenient to apply the upper error bound for error of the solution of the given LCP($A, q$) presented in ^[19] that can be used in cases when we know how to construct a scaling matrix for the given $H_+$ matrix.

Theorem 3.15. ^[19] Let $\; A = [a_{ij}]\in\mathbb R^{n, n}\;$be an $H$-matrix with $a_{ii} > 0$ for all $i \in N.\;$ Let $W = diag(w_1, \ldots, w_n)\;$ with $w_i > 0, \;$ for all $i = 1, \ldots, n, \;$ be a diagonal scaling matrix for $A$, such that $AW$ is $SDD$. Then,

where for each $\; i = 1, 2, \ldots, n, \; \; \beta_i = a_{ii}w_i-\sum_{i\in N\backslash\{i\}} |a_{ij}|w_j$.

In what follows, we denote

Note that the norm estimation depends both on the entries of the given matrix $A$ and the choice of scaling matrix $W$.

As we know how to construct a scaling matrix for a given $N$-scal matrix, we directly obtain the following error estimation.

Theorem 3.16. Let $A = [a_{ij}]\in\mathbb R^{n, n}, \; n\geq2$ be an $N$-scal matrix with positive diagonal entries. Then,

where $W = diag(w_i)\;$ and for each $\; i = 1, 2, \ldots, n, \; \; w_i = \varepsilon_i\frac{H_i(A)}{a_{ii}}, \; \;$ and $\; (\varepsilon_i)_{i = 1}^n$ is an increasing sequence of numbers with $\varepsilon_1 = 1, \; \varepsilon_i\in \left(1, \frac{h_i(A)}{H_i(A)}\right), \; i = 2, \ldots, n.$

Proof. Let $A = [a_{ij}]\in\mathbb R^{n, n}, \; n\geq2, \; a_{ii} > 0, \; i = 1, \ldots, n\;$ be an $N$-scal matrix. Then, for the diagonal matrix $X$, $\; X = diag(x_i)$ with

the matrix $AX\;$ is a Nekrasov matrix. Notice that Nekrasov row sums are nonzero both in $A\;$ and $AX.\;$ Therefore, we can construct the scaling matrix $Y\;$ for the Nekrasov matrix $AX\;$ as proposed in Theorem 1.1. This implies that the matrix $AXY, \;$ with $Y = diag(y_i), \;$

is an $SDD$ matrix, for $(\varepsilon_i)_{i = 1}^n$ being an increasing sequence of numbers with

Applying Theorem 3.15 with $W = XY = diag(w_i), \; i = 1, \ldots, n, \;$ where

the proof is completed.

Assume that $A = [a_{ij}] \in \mathbb C^{n, n}$ is an Ostrowski matrix with positive diagonal entries, with the only non-$SDD$ row indexed by $l.$ The estimation $\eta(A, W)$ given in Theorem 3.15 can be applied to Ostrowski matrix $A$ with scaling matrix $W$ defined as $W = diag(w_k),$

where $\tilde I_1 = \frac{r_l(A)}{|a_{ll}|} < \tilde \gamma < \min\limits_{i \neq l, a_{il} \neq 0} \frac{|a_{ii}|-r_i(A)+|a_{il}|}{|a_{il}|} = \tilde I_2,$ and if $a_{il} = 0$, for all $i \neq l$, then $\tilde I_2 = \infty$.

The estimation $\eta(A, W)$ of Theorem 3.15 can also be applied to an $O$-scal matrix $A = [a_{ij}] \in \mathbb C^{n, n}$ with positive diagonal entries, with the following choice of the scaling matrix $W$. Let $W = diag(w_i),$

$l$ is the index of the only non-$SDD$ row in $AQ$, $Q = diag(q_k)$ and $q_k = \frac{r_k(A)}{|a_{kk}|}, \; \; k \in N.$ If there is no such index $l$, we choose $\gamma = 1$.

In the following numerical examples, we compare $\eta$ estimations for LCP obtained from Theorem 3.15 with corresponding choices of scaling matrices.

Example 3.17. Consider

The matrix $B$ is an $N$-scal matrix, so we apply Theorem 3.16 for $\varepsilon_i = 1+0.0362i, \; i = 0, \ldots, 9.\;$ We obtain $\eta$ estimation 2.729348. As $B$ does not belong to any of the classes $SDD$, Ostrowski, $O$-scal, Nekrasov, the corresponding bounds obtained for these classes cannot be applied. In all the examples $\varepsilon_1 = 1$ and $\varepsilon_i, \; i = 2, \ldots, n,$ are chosen equidistantly inside the interval $\left(1, \min\limits_{i = 2, \ldots, n}\frac{h_i(A)}{H_i(A)}\right).$

Example 3.18. Consider

The matrix $C$ belongs to all of the classes we considered; therefore, we apply bounds developed for all these classes and compare them. Results are presented in Table 8.

For this matrix, we see that the best bound for the norm of the inverse matrix is the bound from Theorem 3.3 for the $O$-scal class, while the best $\eta$ bound for LCP is the bound from Theorem 3.16 for the $N$-scal class.

3.3.   Eigenvalue localizations for the Schur complement matrix and mLCP

The Schur complement matrix can be viewed as a side product of block-Gaussian elimination. It allows transformation of a given large dimensional system to problems of smaller dimensions.

The Schur complement of $A = [a_{ij}]\in {\mathbb C}^{n, n}$ with respect to a proper subset $\alpha$ of the index set $N$ is denoted by $A / \alpha$ and defined to be

Here, $A(\alpha, \beta)$ denotes the sub-matrix of $A\in {\mathbb C}^{n, n}$ formed by the rows indexed by $\alpha$ and the columns indexed by $\beta$, while $A(\alpha, \alpha)$ is abbreviated to $A(\alpha)$. In our considerations, we assume that $A(\alpha)$ is a non-singular matrix.

Results on the Schur complement of special $H$-matrices including spectra localizations and closure properties can be found in ^{[9,11,12,27,39,48]}.

Denoting by $\sigma (A)$ the spectrum of matrix $A$, i.e., the set of all eigenvalues of the matrix $A$, we now recall the famous Geršgorin theorem; see ^[23]. It states that for any matrix $A \in {\mathbb C}^{n, n},$

where the set $\; \Gamma_{i}(A) = \{z \in {\mathbb C}||z - a_{ii}|\leq r_i(A)\}\;$ is called the $i$-th Geršgorin disk, while $\Gamma (A)$ is the Geršgorin set.

In what follows, we apply the scaling method in order to obtain information on spectra of Schur complements. For this purpose, the scaling will be performed in the form of a similarity transformation, as similar matrices have the same set of eigenvalues. Notice that if $W$ is a diagonal scaling matrix for the given matrix $A$, i.e., if $AW$ is $SDD$, then the matrix $W^{-1}AW$ is also $SDD$, as scaling the rows does not affect $SDD$ property. Having this in mind, for a given non-singular diagonal matrix $W$, we denote

and

We also make use of another convenient property of the Schur complement. Namely, Schur complements agree well with multiplications with diagonal non-singular matrices, both from right and left. More precisely, for a diagonal non-singular $W,$ it holds that

and also

In ^[36], the authors provided information on spectra of the Schur complement of an $SDD$ matrix as follows.

Theorem 3.19. ^[36] Let $A \in {\mathbb C}^{n, n}$ be an $SDD$ matrix with real diagonal entries, and let $\alpha$ be a proper subset of the index set. Then, $A / \alpha$ and $A(\overline \alpha)$ have the same number of eigenvalues whose real parts are greater (less) than $f(A)$ (resp., $-f(A)$), where

In ^[35], the authors presented another interesting result on spectra of the Schur complement.

For $A \in {\mathbb C}^{n, n}$, $\alpha = \{ i_{1}, i_{2}, \ldots, i_{k}\} \subseteq \overline{N_A}, \; \overline \alpha = \{ j_{1}, j_{2}, \ldots, j_{l}\}$ and for every eigenvalue $\lambda$ of $A/\alpha$, there exists $1 \leq t \leq l$ such that

In other words, the eigenvalues of $A/\alpha$ are contained in the union of those Geršgorin disks for the original matrix $A$ whose indices are in $\overline \alpha.$

In further considerations, we apply this result and we obtain information on spectra of Schur complements of $N$-scal matrices.

Theorem 3.20. Let $A \in {\mathbb C}^{n, n}$ be an $N$-scal matrix with real diagonal entries, and let $\alpha$ be a proper subset of the index set. Then, $A / \alpha$ and $A(\overline \alpha)$ have the same number of eigenvalues whose real parts are greater (less) than $f(W^{-1}AW)$ (resp., $-f(W^{-1}AW)$), where $f(A)$ is defined as in (3.4) and $W = diag(w_i)$ is a diagonal scaling matrix for $A$, with $\; w_i = \varepsilon_i\frac{H_i(A)}{a_{ii}}, \; \; \; i = 1, 2, \ldots, n, \;$ where $(\varepsilon_i)_{i = 1}^n$ is an increasing sequence of numbers with $\varepsilon_1 = 1, \; \varepsilon_i\in \left(1, \frac{h_i(A)}{H_i(A)}\right), \; i = 2, \ldots, n.$

Proof. Since $A$ is an $N$-scal matrix with real diagonal entries and $W$ is the corresponding scaling matrix, $W^{-1}AW$ is an $SDD$ matrix with real diagonal entries. Notice that matrices $(W^{-1}AW)/\alpha$ and $A/\alpha$ are similar, as well as matrices $(W^{-1}AW)(\overline \alpha)$ and $A(\overline \alpha)$, so their spectra coincide. Now, the statement is proved by applying Theorem 3.19.

The method of the proof holds for all $H$-matrices with real diagonal entries and their scaling matrices.

Now, we obtain a Geršgorin-like spectra localization for the Schur complement of an $N$-scal matrix using scaling matrices.

Theorem 3.21. Let $A \in {\mathbb C}^{n, n}$ be an $N$-scal matrix, let $\alpha \subseteq N$, and let $W = diag(w_i)$ be a diagonal scaling matrix for $A$, with $\; w_i = \varepsilon_i\frac{H_i(A)}{a_{ii}}, \; \; \; i = 1, 2, \ldots, n, \;$ where $(\varepsilon_i)_{i = 1}^n$ is an increasing sequence of numbers with $\varepsilon_1 = 1, \; \varepsilon_i\in \left(1, \frac{h_i(A)}{H_i(A)}\right), \; i = 2, \ldots, n.$ Then,

Proof. It is easy to see that $(W^{-1}AW)/\alpha$ is similar to $A/\alpha$. Similarity implies that spectra of these matrices coincide. Applying results from ^[35] to $SDD$ matrix $\; W^{-1}AW, \;$ we complete the proof.

In this way, we obtain Geršgorin-like eigenvalue localization area for the Schur complement of an $N$-scal matrix using only the entries of the original matrix $A$. Again, the method of the proof holds for any $H$-matrix $A$ and its scaling matrix $W$; see ^[12,39].

Results on spectra of Schur complements can be interpreted in light of the mLCP.

Consider mLCP($A, B, C, D, a, b$) with a non-singular matrix $A$. For $A \in \mathbb R^{n, n}$, $B \in \mathbb R^{m, m}$, $C \in \mathbb R^{n, m}$, $D \in \mathbb R^{m, n}$, $a \in \mathbb R^n$ i $b \in \mathbb R^m$, the problem can be formulated as follows. Find

such that

For a non-singular $A,$ the given problem can be transformed to a classical LCP($B-DA^{-1}C, b-DA^{-1}a$). Denote by $M$ the block matrix

Then, the matrix that appears in classical LCP is the Schur complement $M / A = B-DA^{-1}C$. If the matrix $M$ belongs to some special class, we are able to obtain results on eigenvalues as follows.

● If $M \in {\mathbb C}^{n+m, n+m}$, $n+m \geq 2$ is an $N$-scal matrix with real diagonal entries, then $M / A$ and $B$ have equal number of eigenvalues with real parts greater (less) than $f(W^{-1}MW)$ ($-f(W^{-1}MW)$). Here, $f(M)$ is defined as in Theorem 3.19 and $W = diag(w_i)$ is a diagonal scaling matrix for $M$.

● For $M \in {\mathbb C}^{n+m, n+m}$ of order $n+m \geq 2$ being an $N$-scal matrix, let $W = diag(w_i)$ be a corresponding diagonal scaling matrix. Then,

Example 3.22. Consider

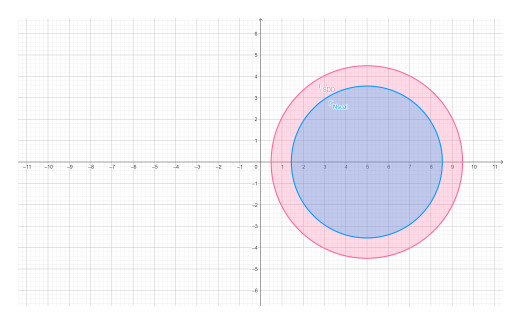
It belongs both to the $SDD$ class and $N$-scal class. Let $\alpha = \{1, 2\}.$ Applying (3.5), we obtain $\; \Gamma_{3}(A) = \{z||z-5| \leq 4.5\}, \;$ $\Gamma_{4}(A) = \{z||z-5| \leq 2.5\},$

From Theorem 3.21 for $N$-scal matrices, with $\; \varepsilon_i = 1+0.375i, \; i = 0, 1, 2, 3, \;$ we obtain $\Gamma_{3}^W(A) = \{z||z-5| \leq 2.6335\}, \;$ $\Gamma_{4}^W(A) = \{z||z-5| \leq 3.549\}, \;$ and

We see that $\Gamma_{Nscal}(A / \alpha)$ (blue) gives tighter localization than $\Gamma_{SDD}(A / \alpha)$ (pink); see Figure 1.

Example 3.23. Consider, again, the matrix $B$ given in (3.3) and set $\alpha = \{1, 2, 3, 4, 5, 6, 7\}.$ As $N_B$ $= \{1, 2, 3, 5\}$ and $\alpha \not\subseteq \overline N_B,$ we cannot use localization from ^[35].

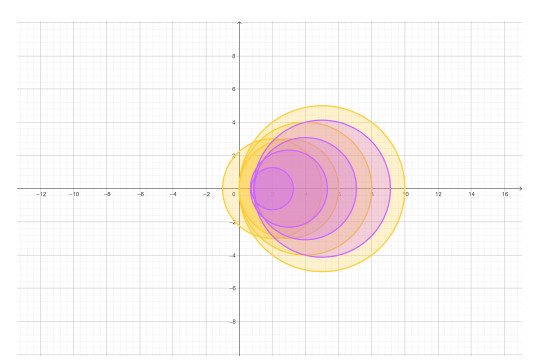
However, we obtain the spectra localization for $B/\alpha$ given in Figure 2 applying Theorem 3.21, with $\; \varepsilon_i = 1+0.0362i, \; i = 0, \ldots, 9.\;$ Here, $\Gamma_{8}^W(B) = \{z||z-8| \leq 6.68754\}$, $\Gamma_{9}^W(B) = \{z||z-9| \leq 7.398684\},$ and $\Gamma_{10}^W(B) = \{z||z-10| \leq 8.547165\}.$

Now, let $\alpha = \{4, 6, 7, 8, 9, 10\}.$ As $\alpha \subseteq \overline N_B,$ we are able to apply results for both the $SDD$ case and $N$-scal case. From (3.5) for the $SDD$ case, we obtain

where $\Gamma_{1}(B) = \{z||z-4| \leq 4\}$, $\Gamma_{2}(B) = \{z||z-2| \leq 3\}$, $\Gamma_{3}(B) = \{z||z-3| \leq 3\},$ and $\Gamma_{5}(B) = \{z||z-5| \leq 5\}.$

Applying Theorem 3.21 for the $N$-scal class, we obtain

where $\Gamma_{1}^W(B) = \{z||z-4| \leq 3.077659\}$, $\Gamma_{2}^W(B) = \{z||z-2| \leq 1.607273\}$, $\Gamma_{3}^W(B) = \{z||z-3| \leq 2.320485\},$ and $\Gamma_{5}^W(B) = \{z||z-5| \leq 4.128828\}.$

If we compare localization areas, we see that $\Gamma_{Nscal}(B / \alpha)$ (violet) is tighter than $\Gamma_{SDD}(B / \alpha)$ (yellow); see Figure 3.

4.   Conclusions

In this paper, we presented a new sufficient condition for non-singularity of matrices by the name $N$-scal condition. We proved that matrices satisfying this condition belong to the $H$-matrix class. We discussed the relation of the new $N$-scal matrix class to some well-known subclasses of non-singular $H$-matrices, such as $SDD$, Ostrowski, $SDD_1$, $O$-scal, and the Nekrasov class. Numerical examples show that the new class stands in a general relation to each of these classes. We used new criteria to obtain bounds for the infinity norm of the inverse matrix. Numerical examples illustrate that these bounds can give better results in some cases than existing bounds developed for some well-known matrix classes. Due to relations among classes, it is obvious that new estimates developed for $N$-scal matrices can work in some cases when already known estimates cannot be applied. Applying scaling relations between the new class and the well-known matrix classes, we defined error estimation for linear complementarity problems that involve $N$-scal matrices. Also, Schur complements of $N$-scal matrices are considered. Spectra localizations for Schur complements are obtained via diagonal scaling in the form of similarity transformation. If the matrix in consideration is both $SDD$ and $N$-scal, numerical examples show that new localization can give tighter estimate due to the scaling method.

Author contributions

Both authors have equally contributed to conceptualization, investigation, methodology, formal analysis, writing and editing, validation, inspection. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

The authors would like to thank the editor and the anonymous referees for their valuable suggestions and comments. This research has been supported by the Ministry of Science, Technological Development and Innovation (Contract No. 451-03-65/2024-03/200156) and the Faculty of Technical Sciences, University of Novi Sad through project ''Scientific and Artistic Research Work of Researchers in Teaching and Associate Positions at the Faculty of Technical Sciences, University of Novi Sad" (No. 01-3394/1).

Conflict of interest

The authors declare that there are no conflict of interest.